A Bus Passenger Flow Prediction Model Fused with Point-of-Interest Data Based on Extreme Gradient Boosting
Abstract
:1. Introduction
- A novel bus passenger flow prediction model is proposed. The model takes the predicting accuracy and the predicting efficiency into account. The model improves the dimensionality of bus IC card data by fusing POI, so that large-scale low-dimensional data have more feature representation, which ensures the accuracy of prediction. The XGBoost algorithm has the advantage of fast operation, contributing to reducing the total training time of the passenger flow prediction model for multiple lines to achieve the goal of efficient training.
- Extensive experiments were conducted on historical passenger flow datasets of Beijing. After preprocessing the original data and matching the POI data, the XGBoost algorithm can be used to build a unified prediction model for different stations of the bus line, which can effectively improve the training efficiency of the model. In addition, comparison with the existing methods verifies the practicability and effectiveness of the proposed model.
2. Related Work
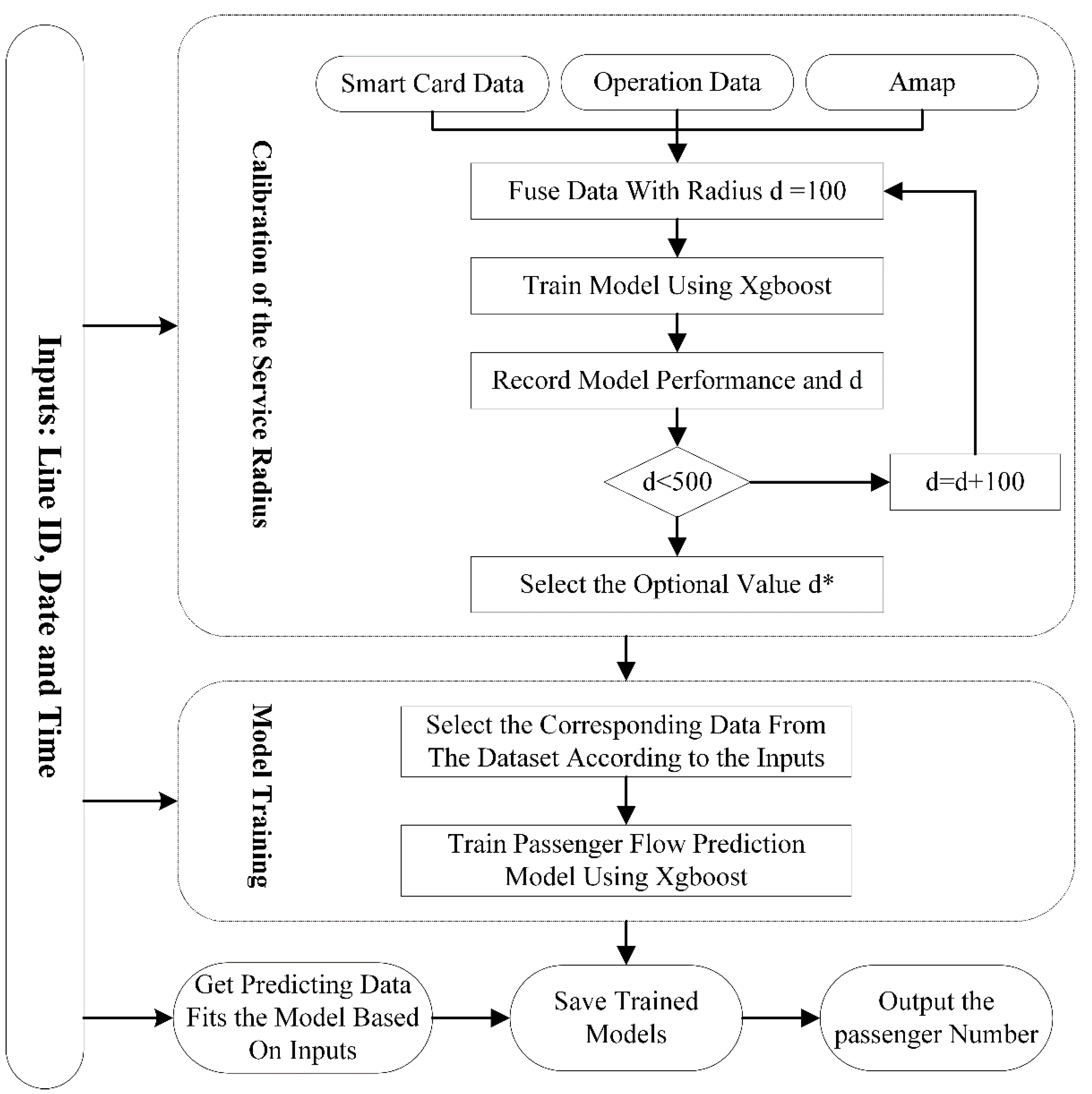
3. Methodology
3.1. IC Card Data Processing and POI Description
3.2. Passenger Flow Prediction Model
3.3. Model Training
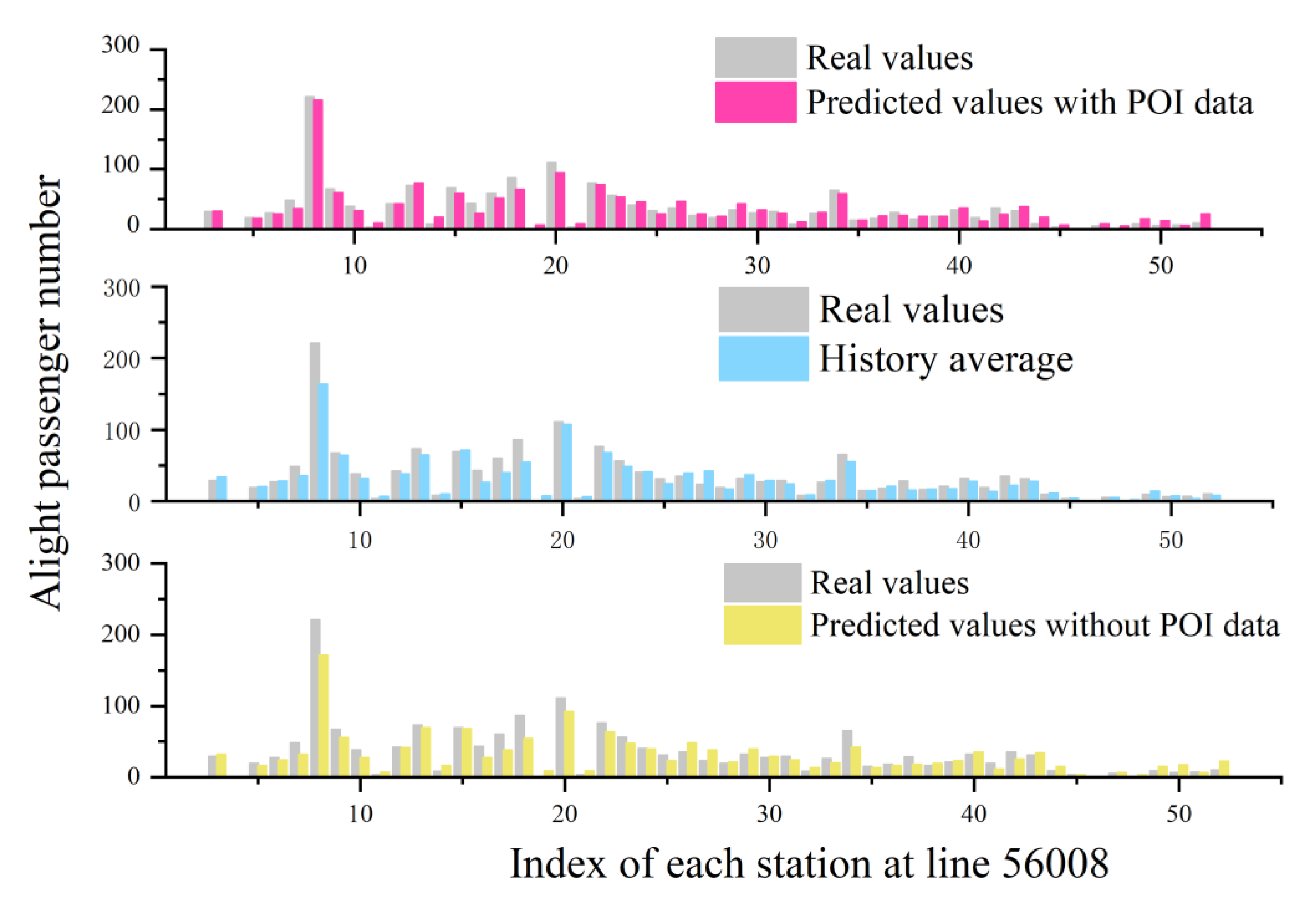
4. Results and Discussion
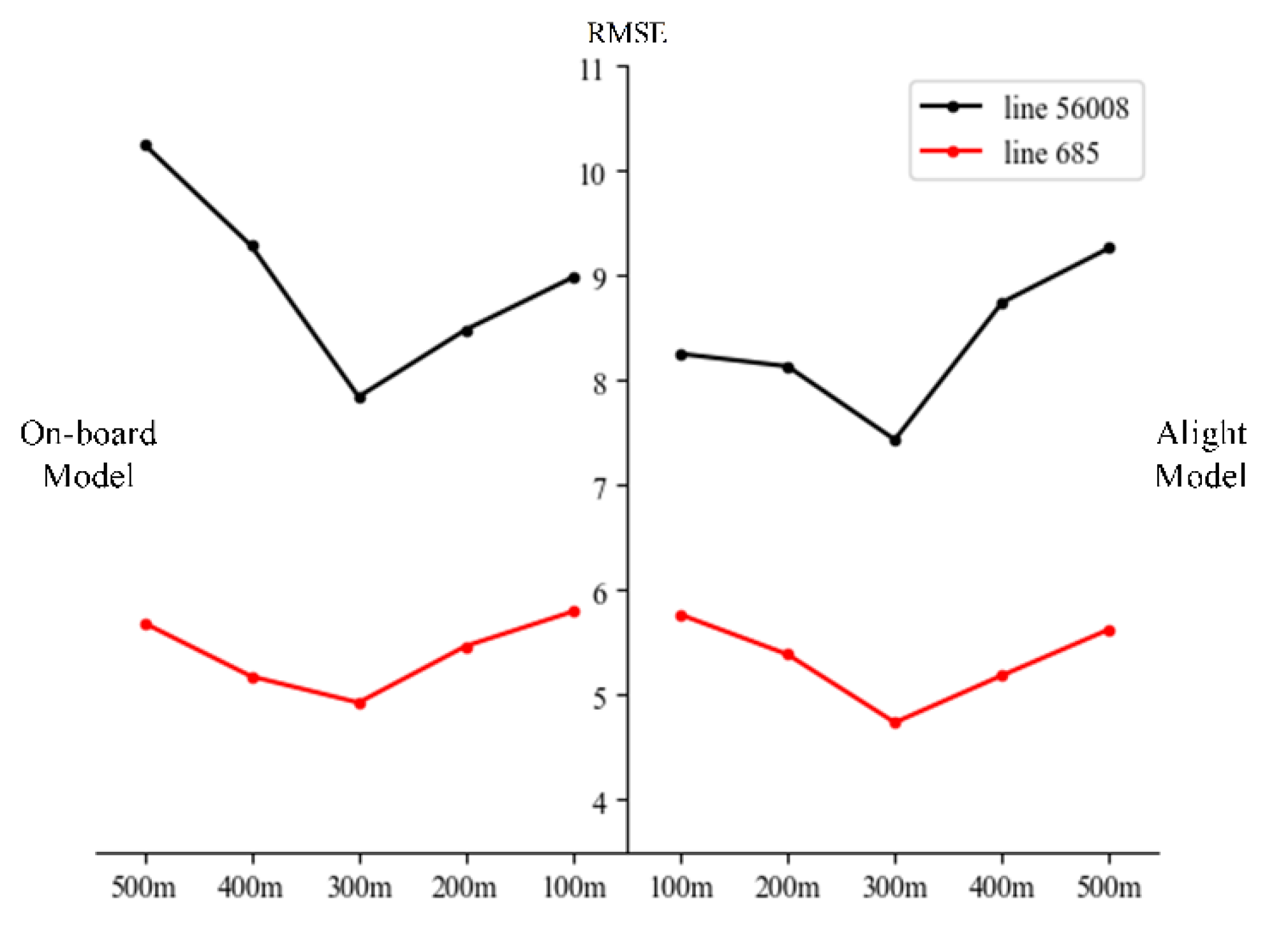
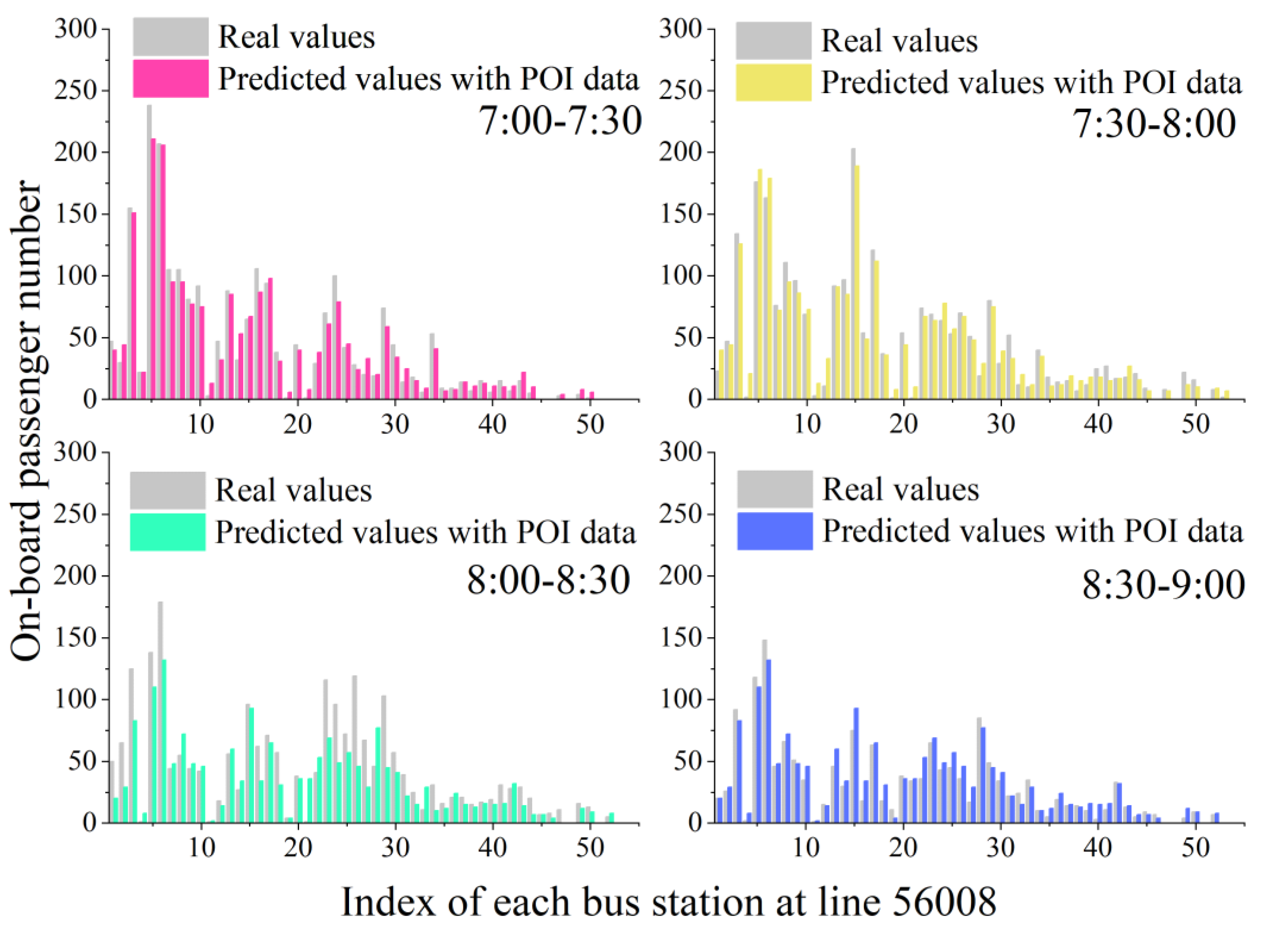
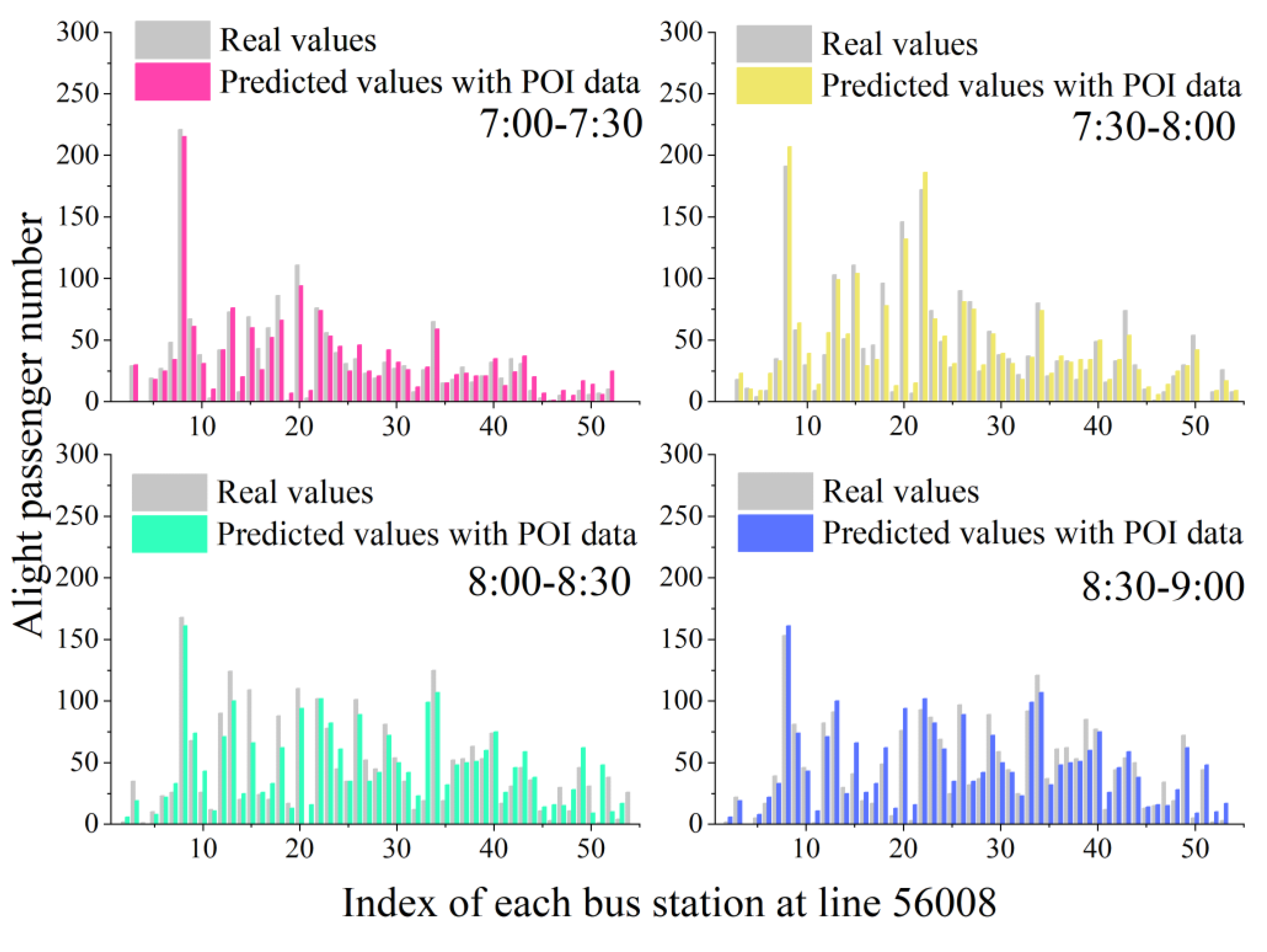
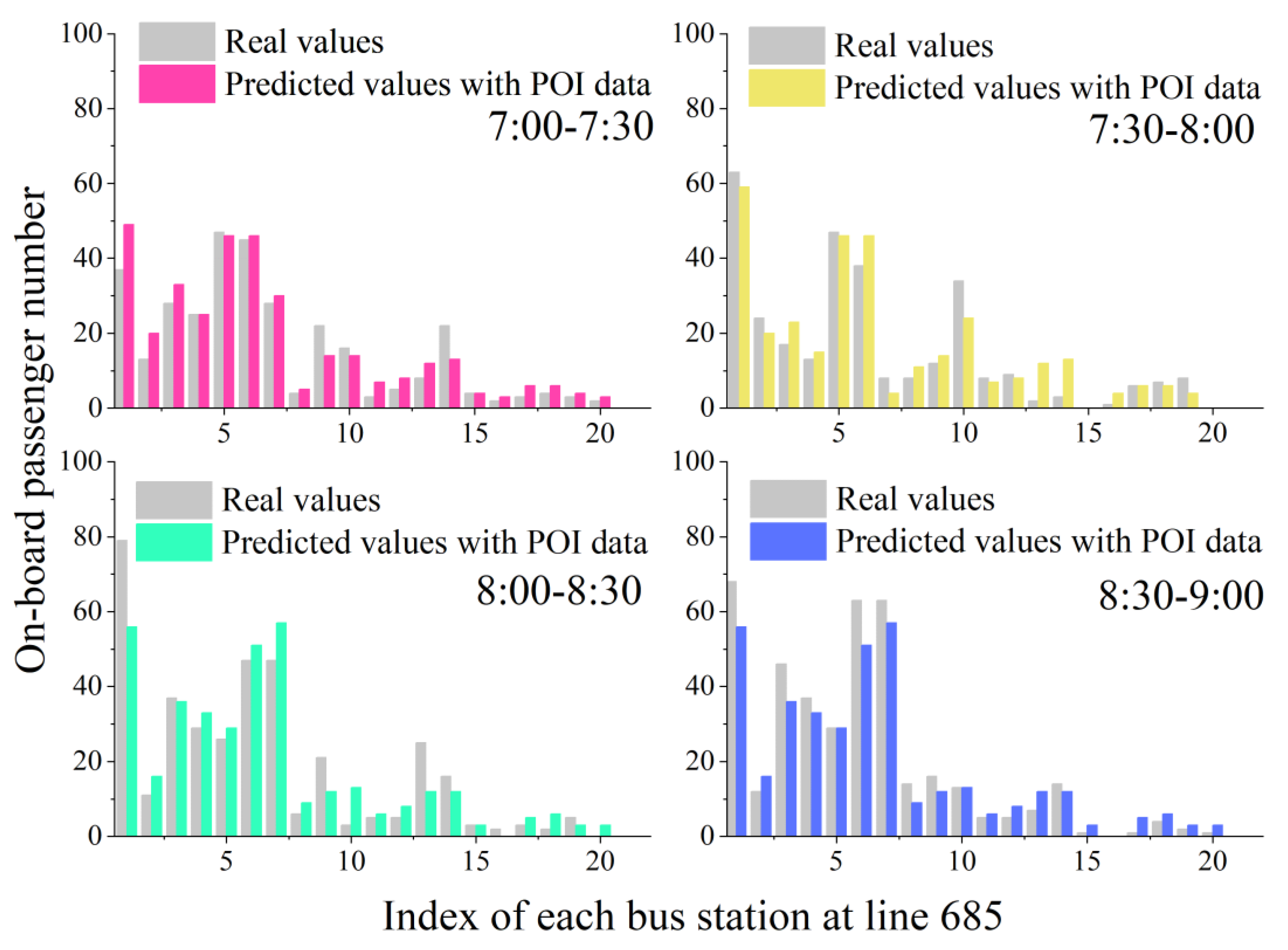
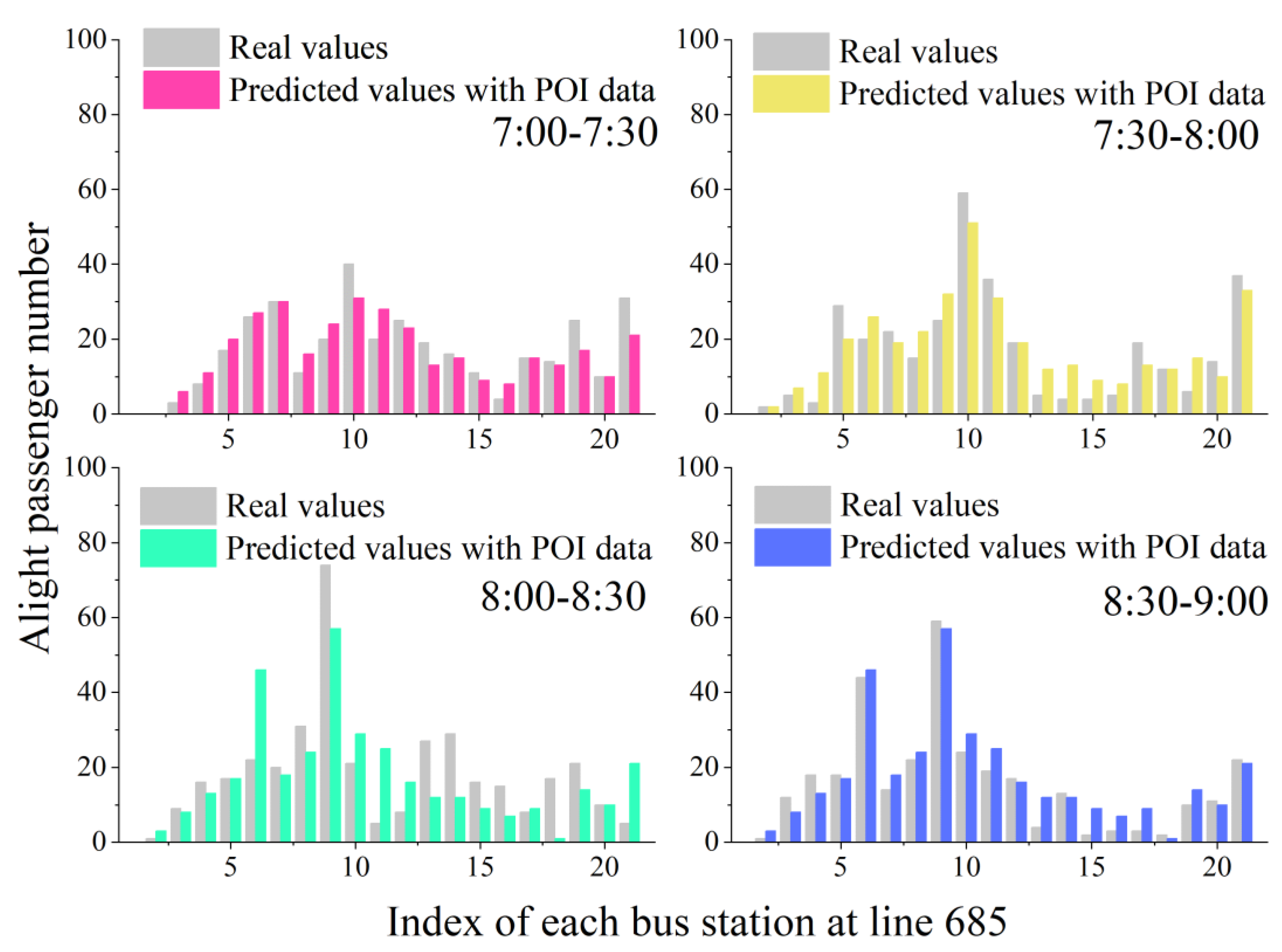
4.1. Peak Period Experiments
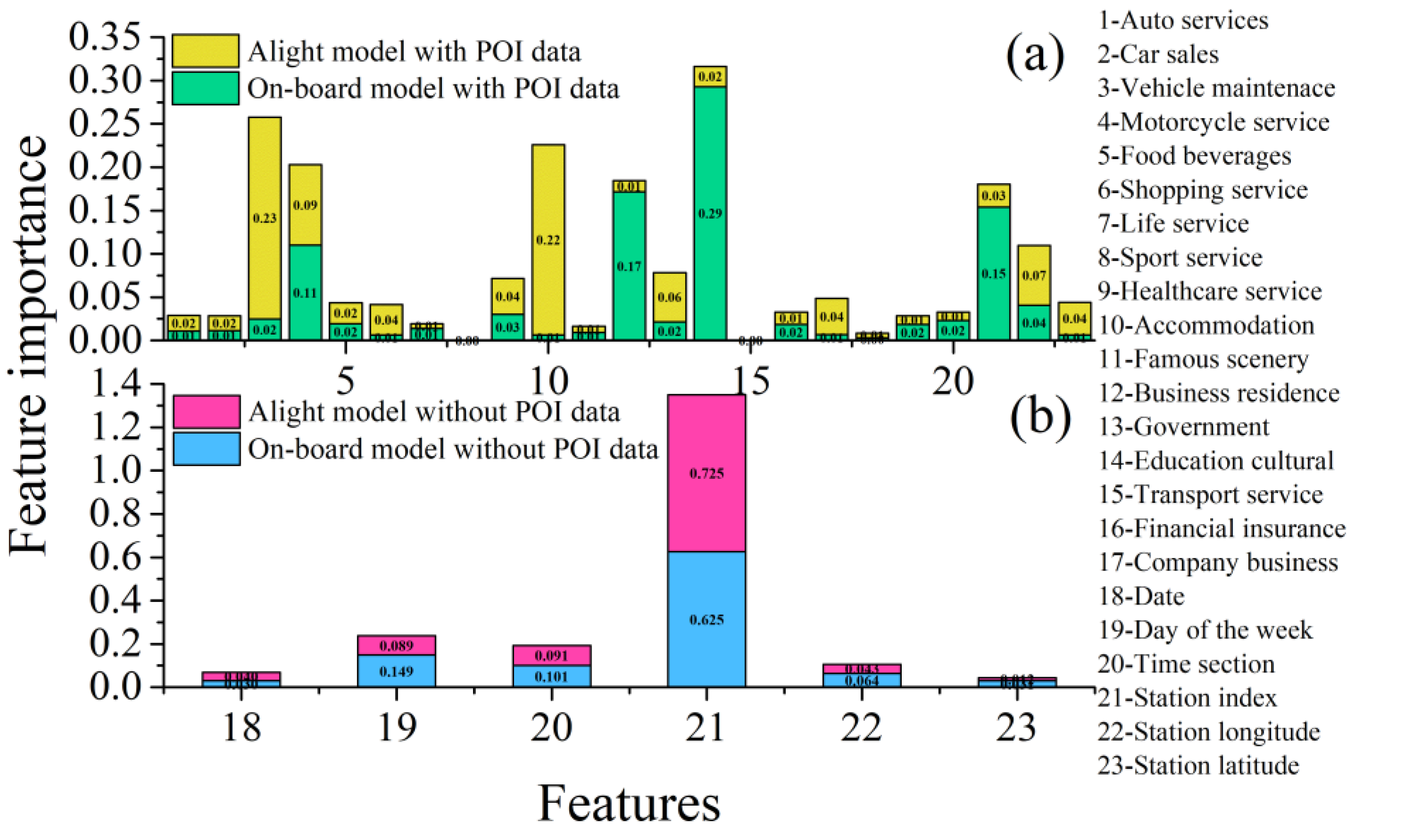
4.2. Impact Analysis of POI
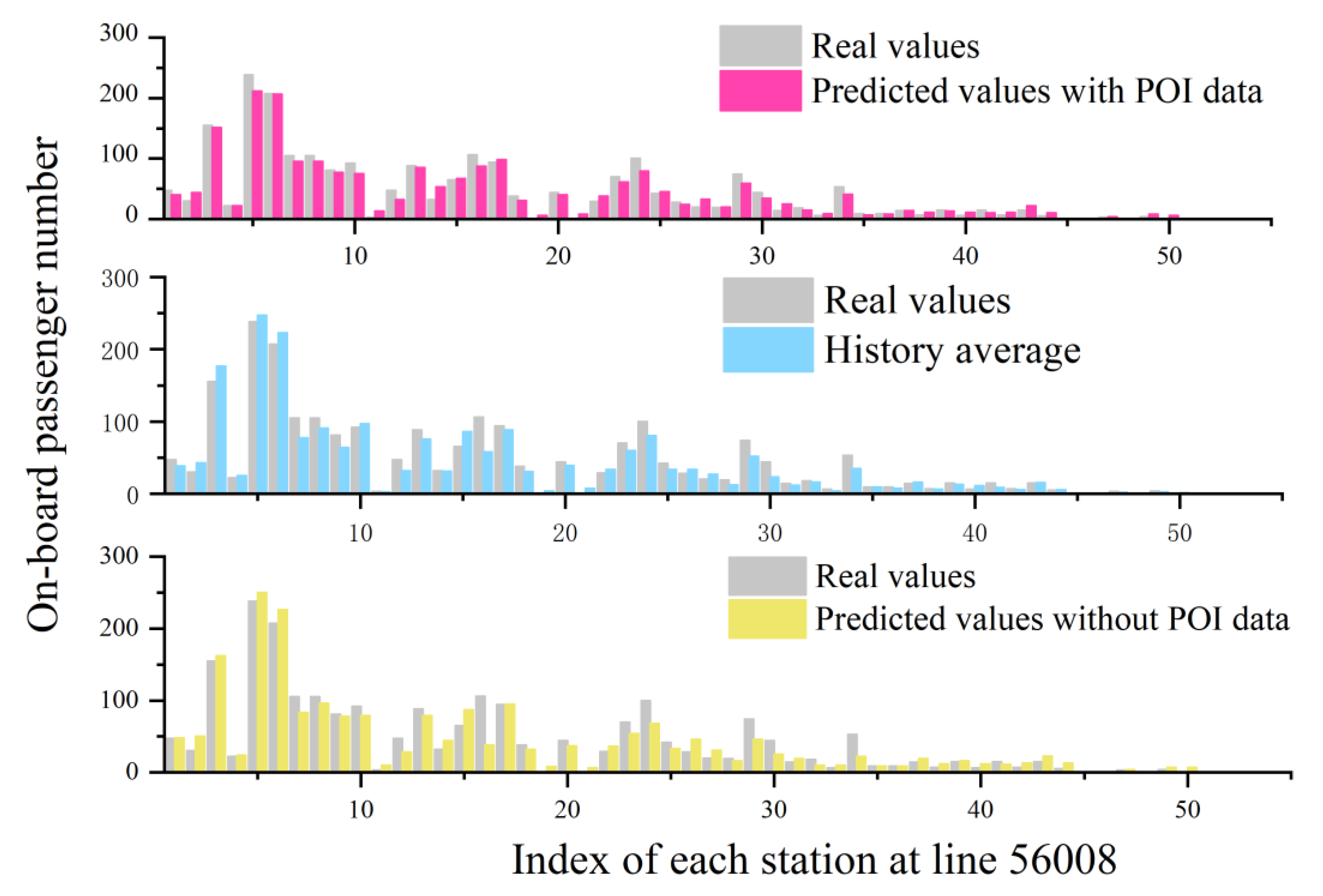
4.3. Comparison with Multiple Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beijing Public Transport Corporation. Available online: http://www.bjbus.com/home/index.php (accessed on 23 December 2021).
- Pelletier, M.P.; Trepanier, M.; Morency, C. Smart card data use in public transit: A literature review. Transp. Res. C-Emerg. 2011, 19, 557–568. [Google Scholar] [CrossRef]
- Noekel, K.; Viti, F.; Rodriguez, A.; Hernandez, S. Modelling Public Transport Passenger Flows in the Era of Intelligent Transport Systems; Gentile, G., Noekel, K., Eds.; Springer Tracts on Transportation and Traffic; Springer International Publishing: Cham, Switzerland, 2016; Volume 1, ISBN 978-3-319-25080-9. [Google Scholar]
- Zhai, H.W.; Cui, L.C.; Nie, Y.; Xu, X.W.; Zhang, W.S. A Comprehensive Comparative Analysis of the Basic Theory of the Short Term Bus Passenger Flow Prediction. Symmetry 2018, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Iliopoulou, C.; Kepaptsoglou, K. Combining ITS and optimization in public transportation planning: State of the art and future research paths. Eur. Transp. Res. Rev. 2019, 11, 27. [Google Scholar] [CrossRef]
- Milenkovic, M.; Svadlenka, L.; Melichar, V.; Bojovic, N.; Avramovic, Z. Sarima Modelling Approach for Railway Passenger Flow Forecasting. Transp.-Vilnius 2018, 33, 1113–1120. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.Y.; Bi, J.; Li, Z.Y. Passenger Flow Forecasting Research for Airport Terminal Based on SARIMA Time Series Model. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Singapore, 22–25 December 2017; IOP Publishing Ltd.: Bristol, UK, 2017. [Google Scholar]
- Ni, M.; He, Q.; Gao, J. Forecasting the Subway Passenger Flow Under Event Occurrences with Social Media. IEEE Trans. Intell. Transp. 2017, 18, 1623–1632. [Google Scholar] [CrossRef]
- Tang, T.L.; Fonzone, A.; Liu, R.H.; Choudhury, C. Multi-stage deep learning approaches to predict boarding behaviour of bus passengers. Sustain. Cities Soc. 2021, 73, 103111. [Google Scholar] [CrossRef]
- Wang, P.F.; Chen, X.W.; Chen, J.X.; Hua, M.Z.; Pu, Z.Y. A two-stage method for bus passenger load prediction using automatic passenger counting data. IET Intell. Transp. Syst. 2021, 15, 248–260. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Cook, A.R. Analysis of freeway traffic time-series data by using Box-Jenkins techniques. Transp. Res. Rec. 1979, 722, 1–9. [Google Scholar]
- Li, L.C.; Wang, Y.G.; Zhong, G.; Zhang, J.; Ran, B. Short-to-medium Term Passenger Flow Forecasting for Metro Stations using a Hybrid Model. KSCE J. Civ. Eng. 2018, 22, 1937–1945. [Google Scholar] [CrossRef]
- Gong, M.; Fei, X.; Wang, Z.H.; Qiu, Y.J. Sequential Framework for Short-Term Passenger Flow Prediction at Bus Stop. Transp. Res. Rec. 2014, 2417, 58–66. [Google Scholar] [CrossRef]
- Ming, W.; Bao, Y.K.; Hu, Z.Y.; Xiong, T. Multistep-Ahead Air Passengers Traffic Prediction with Hybrid ARIMA-SVMs Models. Sci. World J. 2014, 2014, 567246. [Google Scholar] [CrossRef]
- Sun, Y.X.; Leng, B.; Guan, W. A novel wavelet-SVM short-time passenger flowprediction in Beijing subway system. Neurocomputing 2015, 166, 109–121. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Liu, Z.Y.; Jia, R. DeepPF: A deep learning based architecture for metro passenger flow prediction. Transp. Res. C-Emerg. 2019, 101, 18–34. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lv, Y.B.; Ma, J.H.; Li, J. An LSTM-Based Method Considering History and Real-Time Data for Passenger Flow Prediction. Appl. Sci. 2020, 10, 3788. [Google Scholar] [CrossRef]
- Yang, X.; Xue, Q.C.; Ding, M.L.; Wu, J.J.; Gao, Z.Y. Short-term prediction of passenger volume for urban rail systems: A deep learning approach based on smart-card data. Int. J. Prod. Econ. 2021, 231, 107920. [Google Scholar] [CrossRef]
- Martinez-de-Pison, F.J.; Fraile-Garcia, E.; Ferreiro-Cabello, J.; Gonzalez, R.; Pernia, A. Searching Parsimonious Solutions with GA-PARSIMONY and XGBoost in High-Dimensional Databases. In Proceedings of the International Joint Conference SOCO’16-CISIS’16-ICEUTE’16, San Sebastian, Spain, 19–21 October 2016; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Nielsen, D. Tree Boosting with XGBoost—Why Does XGBoost Win "Every" Machine Learning Competition? Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Dong, X.C.; Lei, T.; Jin, S.T.; Hou, Z.S. Short-Term Traffic Flow Prediction Based on XGBoost. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference, Enshi, China, 25–27 May 2018. [Google Scholar]
- Lee, E.H.; Kim, K.; Kho, S.Y.; Kim, D.K.; Cho, S.H. Estimating Express Train Preference of Urban Railway Passengers Based on Extreme Gradient Boosting (XGBoost) using Smart Card Data. Transp. Res. Rec. 2021, 2675, 64–76. [Google Scholar]
- Aslam, N.S.; Ibrahim, M.R.; Cheng, T.; Chen, H.F.; Zhang, Y. ActivityNET: Neural networks to predict public transport trip purposes from individual smart card data and POIs. Geo-Spat. Inf. Sci. 2021, 24, 711–721. [Google Scholar] [CrossRef]
- Faroqi, H.; Mesbah, M. Inferring trip purpose by clustering sequences of smart card records. Transp. Res. C-Emerg. 2021, 127, 103131. [Google Scholar] [CrossRef]
- Bao, J.; Xu, C.C.; Liu, P.; Wang, W. Exploring Bikesharing Travel Patterns and Trip Purposes Using Smart Card Data and Online Point of Interests. Netw. Spat. Econ. 2017, 17, 1231–1253. [Google Scholar] [CrossRef]
| Parameter | Meaning |
|---|---|
| key | Users apply for API types on the official website of AMap. |
| location | Longitude and latitude are divided by “,”. Longitude is the former and latitude is the latter. The decimal point of latitude and longitude should not exceed 6 digits. |
| coordsys | The original coordinate system. |
| types | POI types. The classification code consists of six digits. The first two numbers represent large categories, the middle two represent medium categories and the last two represent small categories. |
| city | City of inquiry. |
| radius | Radius of the inquiry. The value range is from 0 to 50,000. |
| Output | Return to data format type. |
| On-Board Passenger Prediction Models in Line 56008 | RMSE | MAE | R-Squared |
|---|---|---|---|
| PFP-XPOI | 7.84 | 7.32 | 0.912 |
| XGBoost | 8.79 | 8.16 | 0.889 |
| LSTM | 8.69 | 8.12 | 0.892 |
| SVM | 8.89 | 8.25 | 0.887 |
| Historical Average | 8.96 | 8.34 | 0.885 |
| Alighting Passenger Prediction Models in Line 56008 | RMSE | MAE | R-Squared |
|---|---|---|---|
| PFP-XPOI | 7.43 | 6.98 | 0.931 |
| XGBoost | 8.06 | 7.52 | 0.919 |
| LSTM | 7.49 | 7.13 | 0.929 |
| SVM | 7.96 | 7.48 | 0.921 |
| Historical Average | 8.12 | 7.65 | 0.917 |
| On-Board Passenger Prediction Models in Line 685 | RMSE | MAE | R-Squared |
|---|---|---|---|
| PFP-XPOI | 4.92 | 4.53 | 0.890 |
| XGBoost | 5.76 | 4.74 | 0.849 |
| LSTM | 5.32 | 4.66 | 0.871 |
| SVM | 6.09 | 4.90 | 0.831 |
| Historical Average | 5.53 | 4.92 | 0.861 |
| Alighting Passenger Prediction Models in Line 685 | RMSE | MAE | R-Squared |
|---|---|---|---|
| PFP-XPOI | 4.73 | 4.34 | 0.925 |
| XGBoost | 5.48 | 5.02 | 0.899 |
| LSTM | 5.13 | 4.97 | 0.912 |
| SVM | 5.53 | 5.12 | 0.898 |
| Historical Average | 5.69 | 5.14 | 0.892 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Lv, Y.; Ouyang, Q.; Ren, Y. A Bus Passenger Flow Prediction Model Fused with Point-of-Interest Data Based on Extreme Gradient Boosting. Appl. Sci. 2022, 12, 940. https://doi.org/10.3390/app12030940
Lv W, Lv Y, Ouyang Q, Ren Y. A Bus Passenger Flow Prediction Model Fused with Point-of-Interest Data Based on Extreme Gradient Boosting. Applied Sciences. 2022; 12(3):940. https://doi.org/10.3390/app12030940
Chicago/Turabian StyleLv, Wanjun, Yongbo Lv, Qi Ouyang, and Yuan Ren. 2022. "A Bus Passenger Flow Prediction Model Fused with Point-of-Interest Data Based on Extreme Gradient Boosting" Applied Sciences 12, no. 3: 940. https://doi.org/10.3390/app12030940
APA StyleLv, W., Lv, Y., Ouyang, Q., & Ren, Y. (2022). A Bus Passenger Flow Prediction Model Fused with Point-of-Interest Data Based on Extreme Gradient Boosting. Applied Sciences, 12(3), 940. https://doi.org/10.3390/app12030940






