PTRNet: Global Feature and Local Feature Encoding for Point Cloud Registration
Abstract
:1. Introduction
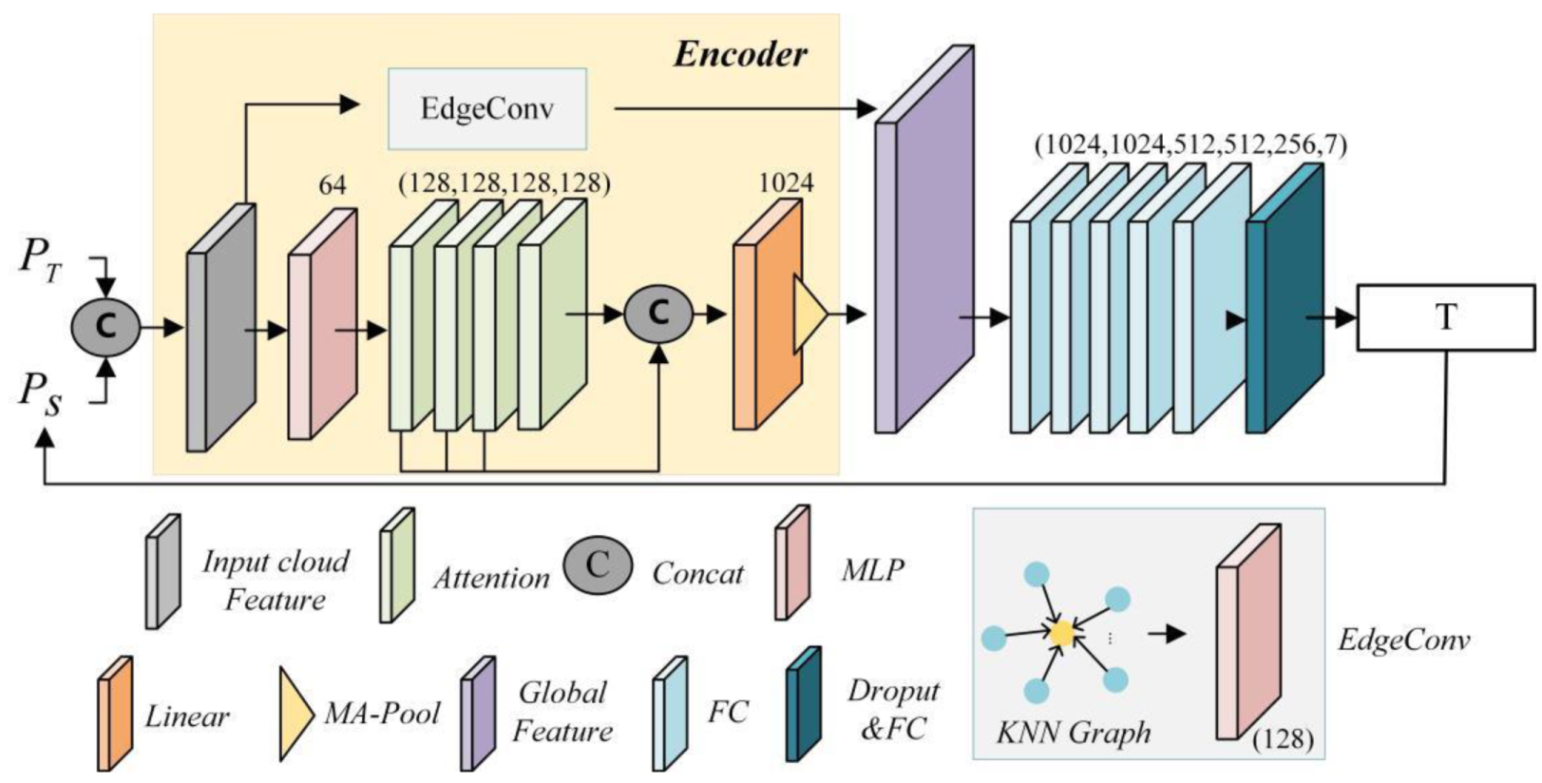
2. Method
2.1. Local Features
2.2. Transformer
2.3. PTRNet for Point Cloud Registration
2.4. Loss Function
3. Experiments
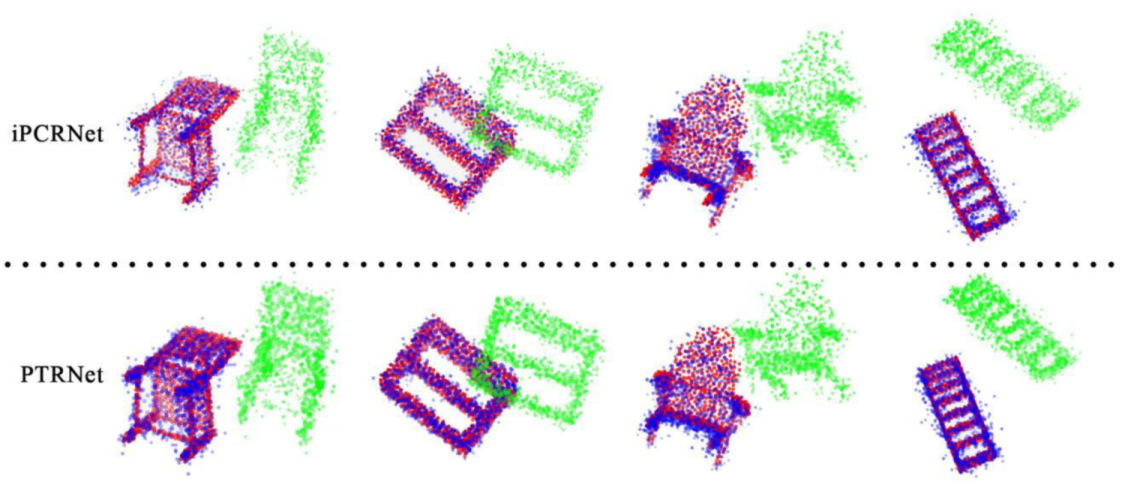
4. Results
4.1. Training and Testing on Different Object Classes
4.2. Training and Testing on the Same Object Class
4.3. Robustness Experiment
4.4. Efficiency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Besl, P.J.; Mckay, H.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Lin, G.C.; Tang, Y.C.; Zou, X.J. Point Cloud Registration Algorithm Combined Gaussian Mixture Model and Point-to-Plane Metric. J. Comput. -Aided Des. Comput. Graph. 2018, 30, 642–650. [Google Scholar] [CrossRef]
- Yang, H.; Carlone, L. A Polynomial-time Solution for Robust Registration with Extreme Outlier Rates. arXiv 2019, arXiv:1903.08588. [Google Scholar]
- Le, H.; Do, T.T.; Hoang, T.; Cheung, N. SDRSAC: Semidefinite-based randomized approach for robust point cloud registration without correspondences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 124–133. [Google Scholar]
- Cheng, L.; Song, C.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of Laser Scanning Point Clouds: A Review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [Green Version]
- Zhan, X.; Cai, Y.; He, P. A three-dimensional point cloud registration based on entropy and particle swarm optimization. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Yuan, W.; Eckart, B.; Kim, K.; Jampani, V.; Fox, D.; Kautz, J. DeepGMR: Learning Latent Gaussian Mixture Models for Registration. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 733–750. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Zeng, A.; Xiao, J. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1802–1811. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. 3D Local Features for Direct Pairwise Registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3244–3253. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully Convolutional Geometric Features. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 8958–8966. [Google Scholar]
- Yang, J.; Zhao, C.; Xian, K.; Zhu, A.; Cao, Z. Learning to Fuse Local Geometric Features for 3D Rigid Data Matching. Inf. Fusion 2020, prepublish. [Google Scholar] [CrossRef] [Green Version]
- Valsesia, D.; Fracastoro, G.; Magli, E. Learning Localized Representations of Point Clouds with Graph-Convolutional Generative Adversarial Networks. IEEE Trans. Multimed. 2020, 23, 402–414. [Google Scholar] [CrossRef]
- Dai, J.L.; Chen, Z.Y.; Ye, Z.X. The Application of ICP Algorithm in Point Cloud Alignment. J. Image Graph. 2007, 3, 517–521. [Google Scholar]
- Wang, Y.; Solomon, J. Deep Closest Point: Learning Representations for Point Cloud Registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3523–3532. [Google Scholar]
- Yan, Z.; Hu, R.; Yan, X.; Chen, L.; Van Kaick, O.; Zhang, H.; Huang, H. RPM-Net: Recurrent prediction of motion and parts from point cloud. ACM Trans. Graph. 2019, 38, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Wang, M.J.; Mao, W.D.; Gong, M.L.; Liu, X.P. SiamesePointNet: A Siamese Point Network Architecture for Learning 3D Shape Descriptor. Comput. Graph. Forum 2020, 39, 309–321. [Google Scholar] [CrossRef]
- Gro, J.; Osep, A.; Leibe, B. AlignNet-3D: Fast Point Cloud Registration of Partially Observed Objects. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec, QC, Canada, 15–19 September 2019; pp. 623–632. [Google Scholar]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative Distance-Aware Similarity Matrix Convolution with Mutual-Supervised Point Elimination for Efficient Point Cloud Registration. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 378–394. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. PCRNet: Point Cloud Registration Network using PointNet Encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3DRegNet: A Deep Neural Network for 3D Point Registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 7193–7203. [Google Scholar]
- Wang, L.; Chen, J.; Li, X.; Fang, Y. Non-Rigid Point Set Registration Networks. arXiv 2019, arXiv:1904.01428. [Google Scholar]
- Zi, J.Y.; Lee, G.H. 3DFeat-Net: Weakly supervised local 3d features for point cloud registration. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 630–646. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J. Feature-Metric Registration: A Fast Semi-Supervised Approach for Robust Point Cloud Registration Without Correspondences. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics & Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2018, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. PCT: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Engel, N.; Belagiannis, V.; Dietmayer, K. Point Transformer. IEEE Access 2021, 9, 134826–134840. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Processing Syst. 2017, 30, 5998–6008. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szilam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A Deep Representation for Volumetric Shapes. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. PointNetLK: Robust & Efficient Point Cloud Registration Using PointNet. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]

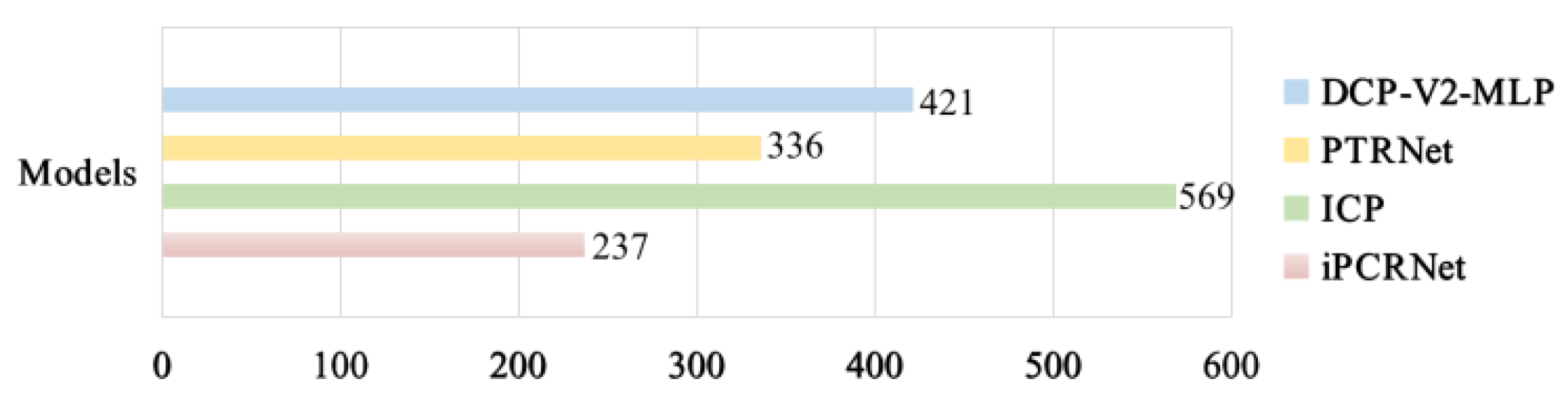
| Model | MSE (R) | RMSE (R) | MAE (R) | MSE (t) | RMSE (t) | MAE(t) |
|---|---|---|---|---|---|---|
| iPCRNet | 9.521 | 3.086 | 3.811 | 0.793 | 0.891 | 0.025 |
| DCP-V2-MLP | 682.279 | 26.120 | 22.603 | 0.015 | 0.122 | 0.094 |
| ICP | 12.314 | 3.509 | 5.387 | 9.604 | 3.100 | 0.063 |
| Model-V1 | 4.874 | 2.208 | 2.083 | 0.022 | 0.148 | 0.011 |
| Model-V2 | 7.262 | 2.695 | 3.296 | 0.034 | 0.184 | 0.012 |
| PTRNet | 4.434 | 2.106 | 1.778 | 0.003 | 0.055 | 0.005 |
| Model | MSE (R) | RMSE (R) | MAE (R) | MSE (t) | RMSE (t) | MAE(t) |
|---|---|---|---|---|---|---|
| iPCRNet | 1.220 | 1.104 | 2.715 | 7.844 | 2.801 | 0.006 |
| DCP-V2-MLP | 919.594 | 30.325 | 24.013 | 0.046 | 0.214 | 0.170 |
| ICP | 9.638 | 3.105 | 4.587 | 6.509 | 2.551 | 0.017 |
| Model-V1 | 4.180 | 2.045 | 2.057 | 0.023 | 0.152 | 0.007 |
| Model-V2 | 1.315 | 1.146 | 1.976 | 0.158 | 0.397 | 0.010 |
| PTRNet | 1.143 | 1.069 | 1.601 | 0.003 | 0.055 | 0.005 |
| Model | MSE (R) | RMSE (R) | MAE (R) | MSE (t) | RMSE (t) | MAE(t) |
|---|---|---|---|---|---|---|
| iPCRNet | 1.973 | 1.405 | 3.518 | 1.863 | 1.365 | 0.013 |
| DCP-V2-MLP | 779.542 | 27.920 | 23.173 | 0.084 | 0.290 | 0.225 |
| ICP | 9.638 | 3.105 | 4.587 | 6.509 | 2.551 | 0.017 |
| Model-V1 | 7.003 | 2.646 | 2.907 | 0.239 | 0.489 | 0.015 |
| Model-V2 | 4.273 | 2.067 | 4.012 | 0.000 | 0.010 | 0.020 |
| PTRNet | 1.340 | 1.158 | 2.739 | 0.036 | 0.190 | 0.011 |
| Model | MSE (R) | RMSE (R) | MAE (R) | MSE (t) | RMSE (t) | MAE(t) |
|---|---|---|---|---|---|---|
| iPCRNet | 1.274 | 1.129 | 2.771 | 5.700 | 2.388 | 0.016 |
| DCP-V2-MLP | 679.070 | 26.059 | 22.583 | 0.139 | 0.373 | 0.295 |
| ICP | 10.446 | 3.232 | 4.760 | 0.000 | 0.010 | 0.015 |
| Model-V1 | 1.134 | 1.065 | 2.767 | 0.193 | 0.439 | 0.006 |
| Model-V2 | 3.315 | 3.027 | 2.125 | 0.018 | 0.134 | 0.012 |
| PTRNet | 1.242 | 1.821 | 1.936 | 0.001 | 0.032 | 0.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Yang, S.; Shi, L.; Liu, Y.; Li, Y. PTRNet: Global Feature and Local Feature Encoding for Point Cloud Registration. Appl. Sci. 2022, 12, 1741. https://doi.org/10.3390/app12031741
Li C, Yang S, Shi L, Liu Y, Li Y. PTRNet: Global Feature and Local Feature Encoding for Point Cloud Registration. Applied Sciences. 2022; 12(3):1741. https://doi.org/10.3390/app12031741
Chicago/Turabian StyleLi, Cuixia, Shanshan Yang, Li Shi, Yue Liu, and Yinghao Li. 2022. "PTRNet: Global Feature and Local Feature Encoding for Point Cloud Registration" Applied Sciences 12, no. 3: 1741. https://doi.org/10.3390/app12031741
APA StyleLi, C., Yang, S., Shi, L., Liu, Y., & Li, Y. (2022). PTRNet: Global Feature and Local Feature Encoding for Point Cloud Registration. Applied Sciences, 12(3), 1741. https://doi.org/10.3390/app12031741






