Survey on Implementations of Generative Adversarial Networks for Semi-Supervised Learning
Abstract
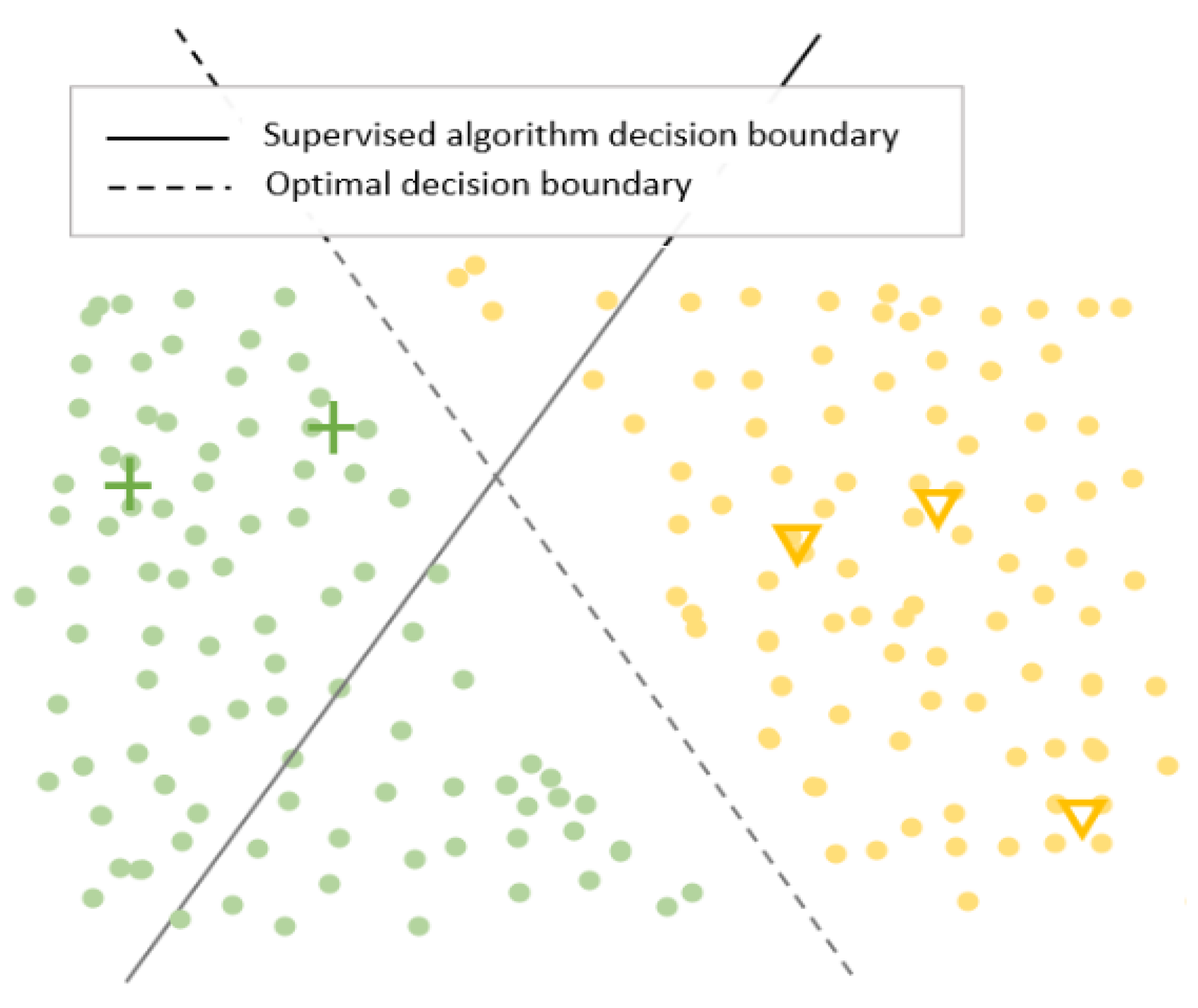
:1. Introduction
2. Common Techniques Used in Semi-Supervised Learning
2.1. Consistency Regularization
2.2. Pseudo-Labeling
2.3. Entropy Minimization
3. Literature Review of GANS for SSL
3.1. Taxonomy
3.2. Notation
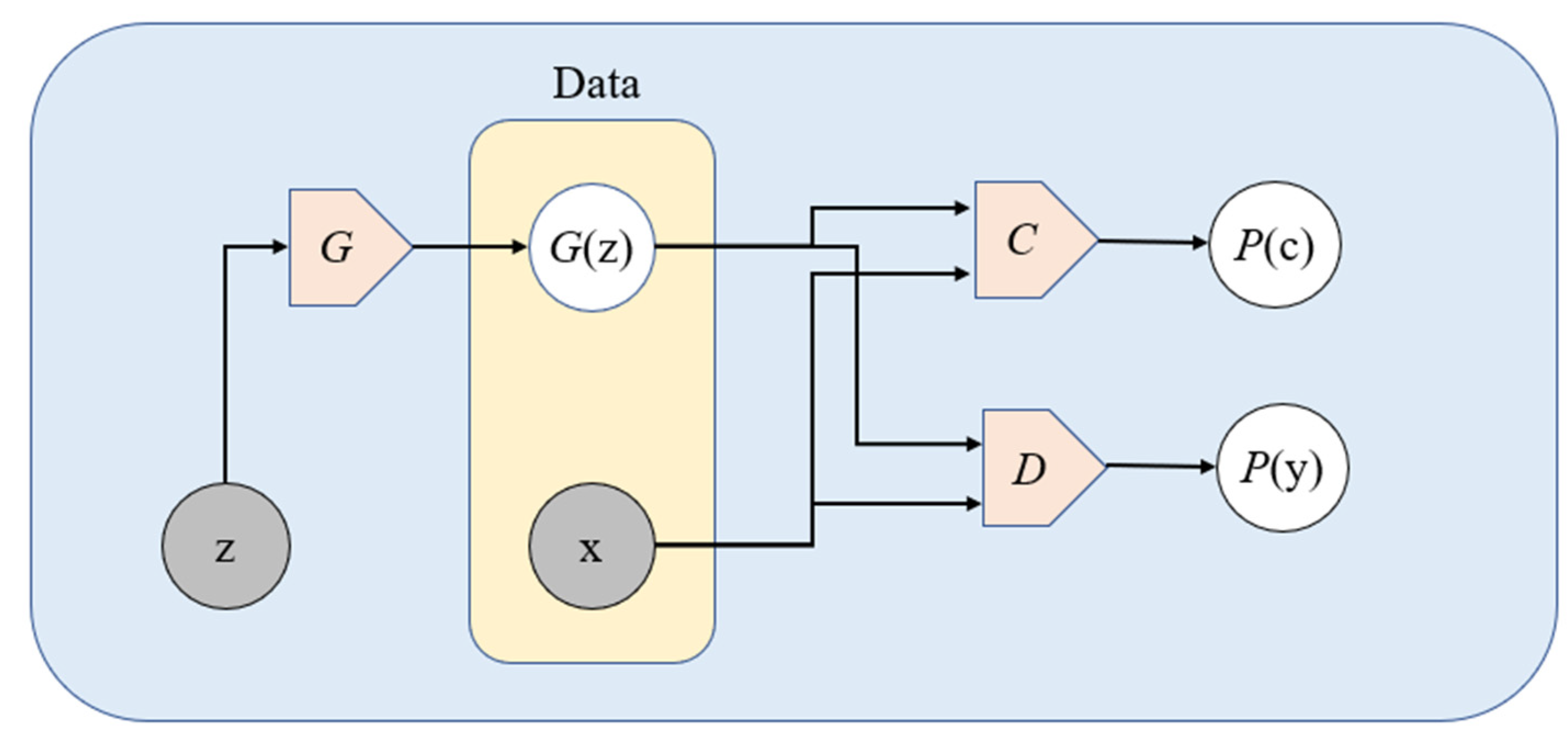
3.3. Extensions Using Pseudo-Labeling and Classifiers
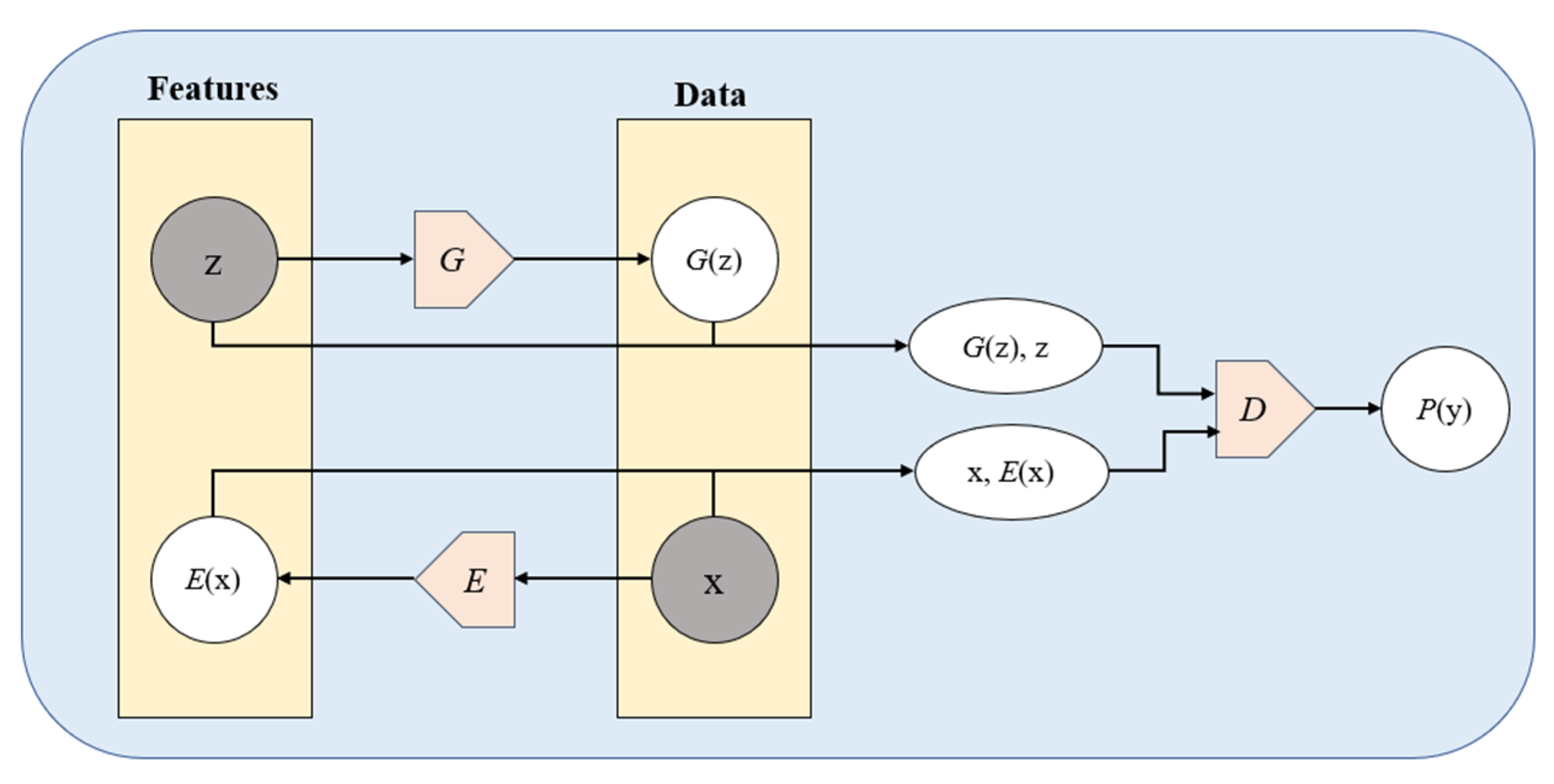
3.4. Encoder-Based Approaches
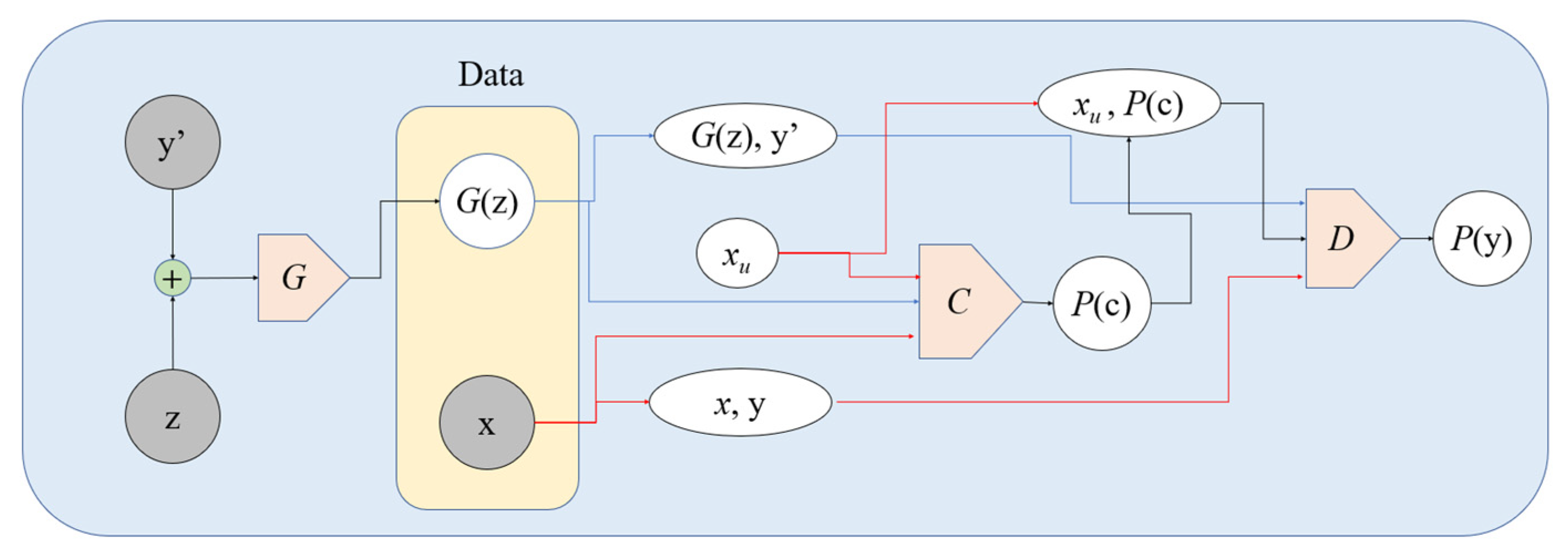
3.5. The TripleGAN Approach
3.6. Manifold Regularization-Based Methods
3.7. Two-GAN Approaches
3.8. GAN Using Stacked Discriminator
4. Results
5. Discussion
5.1. Quantitative Analysis
5.2. Qualitative Analysis
6. Future Directions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- van Engelen, J.E.; Hoos, H.H. A Survey on Semi-Supervised Learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef] [Green Version]
- Károly, A.I.; Fullér, R.; Galambos, P. Unsupervised Clustering for Deep Learning: A Tutorial Survey. Acta Polytech. Hung. 2018, 15, 29–53. [Google Scholar]
- Ouali, Y.; Hudelot, C.; Tami, M. An Overview of Deep Semi-Supervised Learning. arXiv 2020, arXiv:2006.05278. [Google Scholar]
- Yang, X.; Song, Z.; King, I.; Xu, Z. A Survey on Deep Semi-Supervised Learning. arXiv 2021, arXiv:2103.00550. [Google Scholar]
- Chapelle, O.; Zien, A. Semi-Supervised Classification by Low Density Separation. In Proceedings of the Tenth International Workshop on Artificial Intelligence and Statistics, AISTATS 2005, Bridgetown, Barbados, 6–8 January 2005; Cowell, R.G., Ghahramani, Z., Eds.; PMLR: London, UK; Volume R5, pp. 57–64. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–17 December 2011. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.-L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence. arXiv 2020, arXiv:2001.07685. [Google Scholar]
- Oliver, A.; Odena, A.; Raffel, C.; Cubuk, E.D.; Goodfellow, I.J. Realistic Evaluation of Deep Semi-Supervised Learning Algorithms. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 3239–3250. [Google Scholar]
- Zhang, H.; Zhang, Z.; Odena, A.; Lee, H. Consistency Regularization for Generative Adversarial Networks. In Proceedings of the International Conference on Learning Representations, Shenzhen, China, 15–17 February 2020. [Google Scholar]
- Sajjadi, M.; Javanmardi, M.; Tasdizen, T. Regularization with Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 1171–1179. [Google Scholar]
- Laine, S.; Aila, T. Temporal Ensembling for Semi-Supervised Learning. arXiv 2017, arXiv:1610.02242. [Google Scholar]
- Tarvainen, A.; Valpola, H. Mean Teachers Are Better Role Models: Weight-Averaged Consistency Targets Improve Semi-Supervised Deep Learning Results. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 1195–1204. [Google Scholar]
- Luo, Y.; Zhu, J.; Li, M.; Ren, Y.; Zhang, B. Smooth Neighbors on Teacher Graphs for Semi-Supervised Learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8896–8905. [Google Scholar]
- Miyato, T.; Maeda, S.; Koyama, M.; Ishii, S. Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1979–1993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.; Park, J.-K.; Shin, S.-J.; Moon, I.-C. Adversarial Dropout for Supervised and Semi-Supervised Learning. arXiv 2017, arXiv:1707.03631. [Google Scholar]
- Verma, V.; Lamb, A.; Kannala, J.; Bengio, Y.; Lopez-Paz, D. Interpolation Consistency Training for Semi-Supervised Learning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; International Joint Conferences on Artificial Intelligence Organization: Macao, China, 2019; pp. 3635–3641. [Google Scholar]
- Berthelot, D.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Sohn, K.; Zhang, H.; Raffel, C. ReMixMatch: Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring. arXiv 2020, arXiv:1911.09785. [Google Scholar]
- Wei, X.; Gong, B.; Liu, Z.; Lu, W.; Wang, L. Improving the Improved Training of Wasserstein GANs: A Consistency Term and Its Dual Effect. arXiv 2018, arXiv:1803.01541. [Google Scholar]
- Chen, Z.; Ramachandra, B.; Vatsavai, R.R. Consistency Regularization with Generative Adversarial Networks for Semi-Supervised Learning. arXiv 2020, arXiv:2007.03844. [Google Scholar]
- Zhao, Z.; Singh, S.; Lee, H.; Zhang, Z.; Odena, A.; Zhang, H. Improved Consistency Regularization for GANs. arXiv 2020, arXiv:2002.04724. [Google Scholar]
- Lee, D.-H. Pseudo-Label: The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks. In Proceedings of the Workshop on Challenges in Representation Learning, Atlanta, GA, USA, 21 June 2013; Volume 3. [Google Scholar]
- Shi, W.; Gong, Y.; Ding, C.; Ma, Z.; Tao, X.; Zheng, N. Transductive Semi-Supervised Deep Learning Using Min-Max Features. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 311–327. [Google Scholar]
- Iscen, A.; Tolias, G.; Avrithis, Y.; Chum, O. Label Propagation for Deep Semi-Supervised Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5065–5074. [Google Scholar]
- Arazo, E.; Ortego, D.; Albert, P.; O’Connor, N.E.; McGuinness, K. Pseudo-Labeling and Confirmation Bias in Deep Semi-Supervised Learning. arXiv 2020, arXiv:1908.02983. [Google Scholar]
- Li, C.; Xu, K.; Zhu, J.; Zhang, B. Triple Generative Adversarial Nets. arXiv 2017, arXiv:1703.02291. [Google Scholar]
- Dong, J.; Lin, T. MarginGAN: Adversarial Training in Semi-Supervised Learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Liu, Y.; Deng, G.; Zeng, X.; Wu, S.; Yu, Z.; Wong, H.-S. Regularizing Discriminative Capability of CGANs for Semi-Supervised Generative Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5719–5728. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, F.; Cohen, W.W.; Salakhutdinov, R. Good Semi-Supervised Learning That Requires a Bad GAN. arXiv 2017, arXiv:1705.09783. [Google Scholar]
- Springenberg, J.T. Unsupervised and Semi-Supervised Learning with Categorical Generative Adversarial Networks. arXiv 2016, arXiv:1511.06390. [Google Scholar]
- Odena, A. Semi-Supervised Learning with Generative Adversarial Networks. arXiv 2016, arXiv:1606.01583. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved Techniques for Training GANs. arXiv 2016, arXiv:1606.03498. [Google Scholar]
- Sun, J.; Bhattarai, B.; Kim, T.-K. MatchGAN: A Self-Supervised Semi-Supervised Conditional Generative Adversarial Network. arXiv 2020, arXiv:2006.06614. [Google Scholar]
- Wu, S.; Deng, G.; Li, J.; Li, R.; Yu, Z.; Wong, H.-S. Enhancing TripleGAN for Semi-Supervised Conditional Instance Synthesis and Classification. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10083–10092. [Google Scholar]
- Gan, Z.; Chen, L.; Wang, W.; Pu, Y.; Zhang, Y.; Liu, H.; Li, C.; Carin, L. Triangle Generative Adversarial Networks. arXiv 2017, arXiv:1709.06548. [Google Scholar]
- Deng, Z.; Zhang, H.; Liang, X.; Yang, L.; Xu, S.; Zhu, J.; Xing, E.P. Structured Generative Adversarial Networks. arXiv 2017, arXiv:1711.00889. [Google Scholar]
- Haque, A. EC-GAN: Low-Sample Classification Using Semi-Supervised Algorithms and GANs. arXiv 2021, arXiv:2012.15864. [Google Scholar]
- Donahue, J.; Krähenbühl, P.; Darrell, T. Adversarial Feature Learning. arXiv 2017, arXiv:1605.09782. [Google Scholar]
- Dumoulin, V.; Belghazi, I.; Poole, B.; Mastropietro, O.; Lamb, A.; Arjovsky, M.; Courville, A. Adversarially Learned Inference. arXiv 2017, arXiv:1606.00704. [Google Scholar]
- Kumar, A.; Sattigeri, P.; Fletcher, P.T. Semi-Supervised Learning with GANs: Manifold Invariance with Improved Inference. arXiv 2017, arXiv:1705.08850. [Google Scholar]
- Lecouat, B.; Foo, C.-S.; Zenati, H.; Chandrasekhar, V.R. Semi-Supervised Learning with GANs: Revisiting Manifold Regularization. arXiv 2018, arXiv:1805.08957. [Google Scholar]
- Lecouat, B.; Foo, C.-S.; Zenati, H.; Chandrasekhar, V. Manifold Regularization with GANs for Semi-Supervised Learning. arXiv 2018, arXiv:1807.04307. [Google Scholar]
- Xiang, X.; Yu, Z.; Lv, N.; Kong, X.; Saddik, A.E. Attention-Based Generative Adversarial Network for Semi-Supervised Image Classification. Neural Process. Lett. 2020, 51, 1527–1540. [Google Scholar] [CrossRef]
- Tang, X.; Yu, X.; Xu, J.; Chen, Y.; Wang, R. Semi-Supervised Generative Adversarial Networks Based on Scalable Support Vector Machines and Manifold Regularization. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4264–4269. [Google Scholar]
- Motamed, S.; Khalvati, F. Multi-Class Generative Adversarial Nets for Semi-Supervised Image Classification. arXiv 2021, arXiv:2102.06944. [Google Scholar]
- Motamed, S.; Khalvati, F. Vanishing Twin GAN: How Training a Weak Generative Adversarial Network Can Improve Semi-Supervised Image Classification. arXiv 2021, arXiv:2103.02496. [Google Scholar]
- Motamed, S.; Rogalla, P.; Khalvati, F. Data Augmentation Using Generative Adversarial Networks (GANs) for GAN-Based Detection of Pneumonia and COVID-19 in Chest X-Ray Images. arXiv 2021, arXiv:2006.03622. [Google Scholar] [CrossRef] [PubMed]
- Sricharan, K.; Bala, R.; Shreve, M.; Ding, H.; Saketh, K.; Sun, J. Semi-Supervised Conditional GANs. arXiv 2017, arXiv:1708.05789. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y. CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features. arXiv 2019, arXiv:1905.04899. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. arXiv 2017, arXiv:1703.05921. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Li, W.; Wang, Z.; Li, J.; Polson, J.; Speier, W.; Arnold, C. Semi-Supervised Learning Based on Generative Adversarial Network: A Comparison between Good GAN and Bad GAN Approach. arXiv 2019, arXiv:1905.06484. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. RandAugment: Practical Automated Data Augmentation with a Reduced Search Space. arXiv 2019, arXiv:1909.13719. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mané, D.; Vasudevan, V.; Le, Q.V. AutoAugment: Learning Augmentation Strategies From Data. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 113–123. [Google Scholar]
- Xie, Q.; Dai, Z.; Hovy, E.; Luong, M.-T.; Le, Q.V. Unsupervised Data Augmentation for Consistency Training. arXiv 2020, arXiv:1904.12848. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on Deep Learning with Class Imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]




| Term | Definition |
|---|---|
| x | Original labeled data points |
| y | Original labels |
| xu | Unlabeled data points |
| y’ | Labels of generated data |
| z | Randomly generated latent space |
| G(z) | Generator |
| E(z) | Encoder |
| D | Discriminator |
| C | Classifier |
| P(y) | Probability—Discriminator output |
| P(c) | Probability—Classifier output |
| H(x) | Entropy of a given distribution over data x |
| Laplacian Norm |
| Citation | Authors | Date of Publication | Proposed Model | Baseline Models |
|---|---|---|---|---|
| [49] | Goodfellow et al. | June 2014 | GAN (Original) | n/a |
| [30] | J. Springenberg | April 2016 | CatGAN (Categorical) | MTC, PEA, PEA+, VAE + SVM, SS-VAE, Ladder T-model, Ladder-full |
| [32] | Salimans et al. | June 2016 | Improved GAN | DGN, Virtual Adversarial, CatGAN, Skip Keep Generative Model, Ladder network, Auxiliary Deep Generative Model |
| [31] | A. Odena | October 2016 | SGAN (Semi-Supervised) | CNN (isolated classifier, unspecified) |
| [29] | Dai et al. | November 2017 | GoodBadGAN | CatGAN, SDGM, Ladder network, ADGM, FM, ALI, VAT small, TripleGAN, Π model, VAT + EntMin + Large |
| [19] | Wei et al. | March 2018 | CT-GAN | Ladder, VAT, CatGAN, Improved GAN, TripleGAN |
| [33] | Sun et al. | October 2020 | MatchGAN | StarGAN |
| Citation | Authors | Date of Publication | Proposed Model | Baseline Models |
|---|---|---|---|---|
| [38]. | Donahue et al. | May 2016 | BiGAN | - |
| [39] | Dumoulin et al. | February 2017 | ALI (Adversarially Learned Inference) | CIFAR-10: Ladder network, CatGAN, GAN (Salimans 2016); SVHN: VAE, SWWAE, DCGAN + L2SVM, SDGM, GAN (Salimans 2016) |
| [40] | Kumar et al. | December 2017 | Augmented BiGAN |
| Citation | Authors | Date of Publication | Proposed Model | Baseline Models |
|---|---|---|---|---|
| [26] | Li et al. | November 2017 | TripleGAN | M1 + M2, VAT, Ladder, Conv-Ladder, ADGM, SDGM, MMCVA, CatGAN, Improved GAN, ALI |
| [35] | Gan et al. | November 2017 | TriangleGAN | CatGAN, Improved GAN, ALI, TripleGAN |
| [36] | Deng et al. | November 2017 | SGAN (Structured) | Ladder, VAE, CatGAN, ALI, Improved GAN, TripleGAN |
| [27] | J. Dong and T. Lin | November 2019 | MarginGAN | NN, SVM, CNN, TSVM, DBN-rNCA, EmbedNN, CAE, MTC |
| [34] | Wu et al. | January 2020 | EnhancedTGAN (Triple) | Ladder network, SPCTN, Π model, Temporal Ensembling, Mean Teacher, VAT, VAdD, VAdD + VAT, SNTG + Π model, SNTG + VAT, CatGAN, Improved GAN, ALI, TripleGAN, GoodBadGAN, CT-GAN, TripleGAN |
| [28] | Liu et al. | August 2020 | R3-CGAN (Random Regional Replacement Class-Conditional) | Ladder network, SPCTN, Π model, Temporal Ensembling, Mean Teacher, VAT, VAdD, SNTG + Π model, Deep Co-Train, CCN, ICT, CatGAN, Improved GAN, ALI, TripleGAN, Triangle-GAN, GoodBadGAN, CT-GAN, EnhancedTGAN |
| [43] | A. Haque | March 2021 | EC-GAN (External Classifier) | DCGAN |
| Citation | Authors | Date of Publication | Proposed Model | Baseline Models |
|---|---|---|---|---|
| [41] | Lecouat et al. | May 2018 | Laplacian-based GAN | Ladder network, Π model, VAT, VAT + EntMin, CatGAN, Improved GAN, TripleGAN, Improved semi-GAN, Bad GAN |
| [42] | Lecouat et al. | July 2018 | Monte Carlo-based GAN | Π model, Mean Teacher, VAT, Vat + EntMin, Improved GAN, Improved Semi-GAN, ALI, TripleGAN, Bad GAN, Local GAN |
| [43] | Xiang et al. | November 2019 | SelfAttentionGAN | CatGAN, Improved GAN, TripleGAN, Bad GAN, Local GAN, Manifold-GAN, CT-GAN, Ladder network, π-model, Temporal Ensembling w/augmentation, VAT + EntMin w/ aug, MeanTeacher, MeanTeacher w/aug, VAT + Ent + SNGT w/aug |
| [44] | Tang et al. | August 2020 | SSVM-GAN (Scalable SVM) | Ladder Network, CatGAN, ALI, VAT, FM GAN, Improved FM, GAN, TripleGAN, Π model, Bad GAN |
| Citation | Authors | Date of Publication | Proposed Model | Baseline Models |
|---|---|---|---|---|
| [48] | Sricharan et al. | August 2017 | SS-GAN (Semi-Supervised) | C-GAN (conditional GAN on full dataset), SC-GAN (conditional GAN only on labeled dataset), AC-GAN (supervised auxiliary classifier GAN on full dataset), SA-GAN (semi-supervised AC-GAN) |
| [47] | Motamed et al. | January 2021 | IAGAN (Inception-Augmentation) | AnoGAN, AnoGAN w/traditional augmentation, DCGAN |
| [45] | S. Motamed and F. Khalvati | February 2021 | MCGAN (Multi-Class) | DCGAN |
| [46] | S. Motamed and F. Khalvati | March 2021 | VTGAN (Vanishing Twin) | OC-SVM, IF, AnoGAN, NoiseGAN, Deep SVDD |
| Citation | Proposed Model | Datasets Evaluated On | Results |
|---|---|---|---|
| [49] | GAN (Original) | MNIST, TFD | Gaussian Parzen window: MNIST: 225, TDF: 2057 |
| [30] | CatGAN (Categorical) | MNIST | 1.91% PI-MNIST test error w/100 labeled examples, outperforms all models except Ladder-full (1.13%) |
| [32] | Improved GAN | MNIST, CIFAR-10, SVHN | MNIST: 93 incorrectly predicted test examples w/ 100 labeled samples, outperforms all other; CIFAR-10: 18.63 test error rate w/4000 labeled samples, outperforms all other; SVHN: 8.11% incorrectly predicted test examples w/1000 labeled samples, outperforms all other |
| [31] | SGAN (Semi-Supervised) | MNIST | 96.4% classifier accuracy w/1000 labeled samples, comparable to isolated CNN classifier (96.5%) |
| [29] | GoodBadGAN | MNIST, SVHN, CIHAR-10 | MNIST: 79.5 # of errors, outperforms all; SVHN: 4.25% errors, outperforms all; CIFAR-10: 14.41% errors, outperforms all except Vat + EntMin + Large |
| [19] | CT-GAN | MNIST | 0.89% error rate, outperformed all |
| [33] | MatchGAN | CelebA, RaFD | (For both datasets, 20% of training data labeled) CelebA: 6.34 FID, 3.03 IS; RaFD: 9.94 FID, 1.61 IS; outperformed StarGAN in all metrics |
| Citation | Proposed Model | Datasets Evaluated On | Results |
|---|---|---|---|
| [38] | BiGAN | ImageNet | Max Classification accuracy: 56.2% with conv classifier |
| [39] | ALI (Adversarially Learned Inference) | CIFAR-10, SVHN, CelebA, ImageNet (center-cropped 64 × 64 version) | CIFAR-10: 17.99 misclassification rate w/4000 labeled samples, outperforms all; SVHN: 7.42 misclassification rate w/1000 labeled samples, outperforms all |
| [40] | Augmented BiGAN | SVHN, CIFAR-10 | SVHN: 4.87 test error w/500 labeled, 4.39 test error w/1000 labeled, outperforms all for both; CIFAR-10: 19.52 test error w/1000 labeled, outperforms all, 16.20 test error w/4000 labeled, outperforms all except Temporal Ensembling |
| Citation | Proposed Model | Datasets Evaluated On | Results |
|---|---|---|---|
| [26] | TripleGAN | MNIST, SVHN, and CIFAR-10 | MNIST: 0.91% error rate w/100 labeled samples, outperforms all except Conv-Ladder; SVHN: 5.77% error rate w/1000 labeled samples, outperforms all except MMCVA; CIFAR-10: 16.99% error rate w/4000 labeled samples, outperforms all |
| [35] | Triangle-GAN | CIFAR-10 | 16.80% error rate w/4000 labeled samples, outperforms all |
| [36] | SGAN (Structured) | MNIST, SVHN, CIFAR-10 | MNIST: 0.89% error rate w/100 labeled, outperforms all but equal as Ladder; SVHN: 5.73% error rate w/1000 labeled, outperforms all; CIFAR-10: 17.26% error rate w/4000 labeled, outperforms all |
| [27] | MarginGAN | MNIST | 2.06% error rate w/3000 labels, outperformed all |
| [34] | EnhancedTGAN (Triple) | MNIST, SVHN, CIFAR-10 | MNIST: 0.42% error rate w/100 labels, outperforms all; SVHN: 2.97% error rate w/1000 labels, outperforms all; CIFAR-10: 9.42% error rate w/4000 labels, outperforms all |
| [28] | R3-CGAN (Random Regional Replacement Class-Conditional) | SVHN, CIFAR-10 | SVHN: 2.79% error rate w/1000 labels, outperformed all except equal with EnhancedTGAN; CIFAR-10: 6.69% error rate w/4000 labels, outperformed all |
| [43] | EC-GAN (External Classifier) | SVHN, X-ray Dataset | SVHN: 93.93% accuracy w/25% of dataset, outperformed DCGAN; X-ray: 96.48% accuracy w/25% of dataset, outperformed DCGAN |
| Citation | Proposed Model | Datasets Evaluated On | Results |
|---|---|---|---|
| [41] | Laplacian-based GAN | SVHN, CIFAR-10 | SVHN: 4.51% error rate w/1000 labeled, outperformed all except Vat + EntMin, Improved semi-GAN, and Bad GAN; CIFAR-10: 14.45% error rate w/4000 labeled, outperformed all except Vat + EntMin and Bad GAN |
| [42] | Monte Carlo-based GAN | CIFAR-10, SVHN | CIFAR-10: 14.34% error rate w/4000 labels, outperformed all except VAT, VAT + EntMin, and Local GAN; SVHN: 4.63% error rate w/1000 labels, outperformed VAT + EntMin and Improved semi-GAN |
| [43] | SelfAttentionGAN | SVHN, CIFAR-10 | CIFAR-10: 9.87% error rate w/4000 labels, outperformed all; SVHN: 4.30% error rate w/1000 labels, outperformed all except Bad GAN, VAT + EntMin w/aug, MeanTeacher w/aug, VAT + Ent + SNGT w/aug |
| [44] | SSVM-GAN (Scalable SVM) | CIFAR-10, SVHN | CIFAR-10: 14.27% error rate w/4000 labels, outperformed all; SVHN: 4.54% error rate w/1000 labels, outperformed all except Bad GAN |
| Citation | Proposed Model | Datasets Evaluated on | Results |
|---|---|---|---|
| [48] | SS-GAN (Semi-Supervised) | MNIST, CelebA, CIFAR-10 | MNIST: 0.1044 class prediction error, outperforms only SA-GAN, 0.0160 reconstruction error, outperforms SA-GAN and SC-GAN (both metrics w/20 labeled samples); CelebA: 0.040 reconstruction error, outperforms all except C-GAN; CIFAR-10: 0.299 class pred error, outperforms only AC-GAN and SC-GAN, 0.061 recon error, outperforms all except C-GAN |
| [47] | IAGAN (Inception-Augmentation) | Pneumonia X-rays: Dataset I (3765 imgs), Dataset II (4700 imgs) | Dataset I: 0.90 AUC, outperformed all; Dataset II: 0.76 AUC, outperformed all |
| [45] | MCGAN (Multi-Class) | MNIST, F-MNIST | MNIST: 0.9 AUC unknown class classification and 0.84 known class classification, outperformed DCGAN; F-MNIST: 0.79 AUC unknown & 0.65 known, outperformed DCGAN |
| [46] | VTGAN (Vanishing Twin) | MNIST, F-MNIST | MNIST: 0.90, 0.92, 0.85, and 0.86 AUC, outperformed all in all 4 experiments; F-MNIST: 0.87, 0.76, 0.70, 0.57, 0.62, 0.70 AC, outperformed all in 4 out of 6 experiments |
| Citation | Category | Proposed Model | Results |
|---|---|---|---|
| [30] | Pseudo-labeling and Classifiers | CatGAN | 1.91% PI-MNIST test error w/100 labeled examples, outperforms all models except Ladder-full (1.13%) |
| [39] | Encoder-based | ALI | CIFAR-10: 17.99 misclassification rate w/4000 labeled samples, outperforms all; SVHN: 7.42 misclassification rate w/1000 labeled samples, outperforms all |
| [26] | TripleGAN | TripleGAN | MNIST: 0.91% error rate w/100 labeled samples, outperforms all except Conv-Ladder; SVHN: 5.77% error rate w/1000 labeled samples, outperforms all except MMCVA; CIFAR-10: 16.99% error rate w/4000 labeled samples, outperforms all |
| [44] | Manifold Regularization | SSVM-GAN | CIFAR-10: 14.27% error rate w/4000 labels, outperformed all; SVHN: 4.54% error rate w/1000 labels, outperformed all except Bad GAN |
| [28] | TripleGAN | R3-CGAN | SVHN: 2.79% error rate w/1000 labels, outperformed all except equal with EnhancedTGAN; CIFAR-10: 6.69% error rate w/4000 labels, outperformed all |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajun, A.R.; Zualkernan, I. Survey on Implementations of Generative Adversarial Networks for Semi-Supervised Learning. Appl. Sci. 2022, 12, 1718. https://doi.org/10.3390/app12031718
Sajun AR, Zualkernan I. Survey on Implementations of Generative Adversarial Networks for Semi-Supervised Learning. Applied Sciences. 2022; 12(3):1718. https://doi.org/10.3390/app12031718
Chicago/Turabian StyleSajun, Ali Reza, and Imran Zualkernan. 2022. "Survey on Implementations of Generative Adversarial Networks for Semi-Supervised Learning" Applied Sciences 12, no. 3: 1718. https://doi.org/10.3390/app12031718
APA StyleSajun, A. R., & Zualkernan, I. (2022). Survey on Implementations of Generative Adversarial Networks for Semi-Supervised Learning. Applied Sciences, 12(3), 1718. https://doi.org/10.3390/app12031718






