Abstract
Changes in climatic conditions are expected globally resulting in a higher rainfall intensity and longer duration of rainfall. The increase in the rainwater infiltration into the soil contributes to many geotechnical issues, such as excessive settlement, retaining wall failure and rainfall-induced slope failures. These geotechnical problems could be mitigated by the improvement of the problematic soil with the incorporation of the unsaturated soil mechanic principles. Dual-porosity soils or soils with bimodal water retention curve (WRC) are able to retain more water during prolonged drying and they would be able to drain out water faster during intense rainfall to maintain the slope stability. The objective of this study is to investigate the characteristics of the unsaturated shear strength of soil with bimodal WRC. In addition, the new mathematical equation is proposed to estimate the unsaturated shear strength of soils with a bimodal WRC. The results of the study indicated that the nonlinearity of the unsaturated shear strength is a function of the shape of bimodal WRC limited by the first and second air-entry value (AEV) of dual-porosity soils. The proposed equation agreed well with the experimental data of the unsaturated shear strength for dual-porosity soil.
1. Introduction
Many regions in the world have a geological profile that is characterized by a deep groundwater table. Since the location of the groundwater table varies from 5 to 20 m underneath ground surface, the vadose zone or the unsaturated soil zone cannot be neglected for geotechnical-related issues in many parts of the world [1,2,3,4,5,6]. One such issue is slope instability due to rainfall. Prolonged rainfall would result in an increased occurrence of rainfall-induced slope failures and prolonged drought would adversely affect the water content in soil and plant health [7,8,9,10]. The changes in rainfall intensity would affect the groundwater fluctuations, which may significantly impact the quality of surface water [11]. These adverse effects of climate change could be mitigated by having a comprehensive knowledge about hydraulic properties of unsaturated soils—bimodal water retention curve (WRC) and permeability functions. Past studies [12,13,14] indicated that compacted soils with bimodal pore size distribution (PSD) are less susceptible to changes in the external environment (prolonged drying and intense rainfall). As a result, bimodal soils would be beneficial for plant health, as they would be able to retain more water during prolonged drying and for slope stability because they would be able to drain out water faster during intense rainfall [15,16].
Soils with a bimodal grain-size distribution can exhibit bimodal characteristics in their WRC, however, a bimodal grain-size distribution does not guarantee the bimodality of the WRC [17,18,19,20,21]. Bimodality can be exhibited in the WRC and, consequently, in the permeability function since the permeability function takes up the shape of the WRC [22,23,24]. A bimodal PSD is highly associated with a bimodal WRC [25,26,27]. A bimodal PSD consists of two pore series, the larger of the two corresponds to the macropores, while the smaller one corresponds to the micropores [27].
Zhai et al. [28] investigated the pore-size distribution of compacted kaolinite soil, a type of fine-grained soil, which was compacted at three distinct water contents across the compaction curve: dry of optimum, optimum moisture content, and wet of optimum. Only the specimen compacted in the dry of optimum exhibits a bimodal PSD. Based on the relations of the pores to the PSD, the inter-aggregate pores and intra-aggregate pores can be seen as equivalent to the macropores and micropores mentioned by Satyanaga et al. [17], respectively. The inter-aggregate pores referred to by Zhai et al. [12] correspond to the first sub-curve of the bimodal WRC, whereas the intra-aggregate pores correspond to the second sub-curve, very similar to the macropores referred to by Satyanaga et al. [17], which correspond to the first sub-curve and the micropores that correspond to the second sub-curve. The terms micropores and macropores will be used in this paper for consistency.
Shear strength of unsaturated soil is required for addressing numerous geotechnical problems such as slope stability [29,30]. An increase in shear strength is closely related to an increase in matric suction as governed by unsaturated shear strength angle (ϕb). ϕb is equal to effective friction angle ϕ′ for matric suction up to the air-entry value (AEV) of soil [29]. Therefore, a linear relationship between shear strength and matric suction is normally obtained experimentally at matric suctions up to AEV. Beyond AEV, the soil starts to become unsaturated and the shear strength envelope become non-linear and ϕb is not equal to ϕ′ anymore but ϕb decreases with increasing matric suctions [31]. Beyond residual matric suction, the shear strength of an unsaturated soil may increase, decrease or remain constant when the matric suction increases [32].
Laboratory measurement of unsaturated shear strength is costly and time-consuming. Hence, there are many shear strength prediction equations that use WRC with the saturated shear strength parameters to estimate the unsaturated shear strength of soil. One of the most widely utilized models is by correlating shear strength with pore size distribution of soil, which actually depends on WRC [32]. Numerous research works have been performed on bimodal soil, but those studies are generally limited to WRC and permeability of soil. Therefore, this study investigates the characteristics of the unsaturated shear strength of soil with bimodal WRC. In addition, the new mathematical equation is proposed to estimate the unsaturated shear strength of soils with a bimodal WRC.
2. Investigated Soil and Methodology
2.1. Investigated Soils
In this experiment, there were two soil mixtures produced by mixing coarse kaolin and Ottawa sand, specifically 70%Sand-30%Kaolin (70S30K) and 50%Sand-50%Kaolin (50S50K). For each composition, specimens were prepared for WRC tests, and for saturated and unsaturated triaxial tests. The soil mixtures were selected to avoid non-homogeneity of the soil specimen in order to ensure the results from different specimens were comparable and could be used to establish the characteristics of soil [33]. The specimens in this study were prepared with water content corresponding to 90% of maximum dry density on the dry side of optimum of the compaction curve. The specimens were then statically compacted at 1 mm/min loading rate with 10 mm thickness per layer as described in [34], to produce homogenous specimens. This procedure was selected to ensure the specimens used in each laboratory testing have similar soil properties. Specifically, specimens of 100 mm in height and 50 mm in diameter were used for multistage consolidated undrained and consolidated drained saturated and unsaturated triaxial tests, correspondingly. Moreover, specimens of 20 mm in height and 50 mm in diameter were used for WRC measurements.
2.2. Methodology
Index properties tests were performed based on the ASTM standards (Table 1) [35,36,37,38,39]. The compacted soil specimens underwent a saturation process using Tempe cell until the mass equalizes before WRC tests and shrinkage tests were conducted. WRC tests were carried out using Tempe cell setup for matric suction from 1 kPa to 100 kPa and pressure plate setup for matric suction from 100 kPa to 900 kPa, in accordance with procedures explained in ASTM D6836-16 [40] and Satyanaga et al. [41]. WRC tests using both Tempe cell and pressure plate were conducted using the axis-translation method [42]. The ceramic disks in Tempe cell and pressure plate setups were saturated with distilled water prior to the test and regularly flushed to ensure they were saturated. The WRC measurement followed a small increment of matric suction to obtain WRC with greater accuracy. Moreover, the low matric suction (1 to 5 kPa) at the beginning of the test was controlled using a manometer set up to ensure the accuracy of the matric suction. The specimens were weighed every 15 min for the first 1 h at the beginning of each suction and twice a day thereafter. The matric suction level was increased only when the mass of the specimens reached a constant value.

Table 1.
ASTM standard for laboratory testing.
There were two types of shear strength tests, namely, saturated and unsaturated shear strength tests carried out in this study. Both tests were started with saturation of the specimens in order to have a uniform initial condition. Saturation was performed by applying cell pressure (σ3) and back pressure (uw) to the specimens. To avoid significant swelling of specimens, a net confining pressure (σ3–uw) of 10 kPa was retained until pore-water pressure parameter (B) was larger than 0.95, as recommended by Fredlund and Rahardjo [28]. Multistage testing was performed by loading and unloading procedure on each specimen. Compared to single stage testing, multistage testing consumes less time to obtain comprehensive data. However, it should be expected that the measured shear strength would be slightly lower than the actual, due to cumulative strain in the specimen. So, the maximum allowable axial strain in this study is limited to 20% according to Goh et al. [43].
The cohesion intercept (c′) and friction angle (ϕ′) of the specimens were obtained from the multistage consolidated undrained triaxial tests by plotting Mohr-Coulomb failure envelope using the peak deviator stresses acquired from the stress versus strain curves. Firstly, the specimens were isotropically consolidated until there was no volume change in the specimens. The specimens were then sheared under three effective confining pressures (i.e., 25, 50, and 75 kPa) with pore-water pressure measurements at the base of specimens. The shearing rate used was 0.05 mm/min according to Goh et al. [43].
A modified triaxial apparatus was used for multistage consolidated drained triaxial testing to investigate shear strength of an unsaturated soil, as described by Fredlund and Rahardjo [28]. The setup procedure was started by placing a high air-entry ceramic disk with diameter of 50 mm on the pedestal. The specimens were then put directly on the saturated ceramic disk. Filter paper, porous stone and top cap were positioned to the top of the specimen while a rubber membrane was used to enclose the specimen. Eventually, O-rings secured the membrane at the top cap and pedestal.
After saturation process, the specimen was isotropically consolidated and the consolidation was stopped when pore-water volume change reached equilibrium. Pore-water, pore-air (ua), volume changes and cell pressures were set and controlled by Digital Pressure and Volume Controller. Next, the shearing stage was started with a strain rate of 0.0009 mm/min, as suggested by Goh et al. [43], in order to ensure excess pore-water pressure was zero, which implied that the pore-air and pore-water pressures remained the same as those before the shearing. Eventually, the shearing stage was stopped when the deviator stress showed a constant value. The measured parameters such as total volume changes, displacement and load were recorded using Triax 4.0 software [43]. In this experiment, the test was conducted under a constant net confining pressure and varying matric suctions. The net confining pressure (σ3–ua) was set to remain constant at 50 kPa, while the matric suction (ua–uw) was varied from 5, 20, 30, 50, 75, 100 to 200 kPa. Therefore, from this multistage CD test, unsaturated shear strength parameter (ϕb) of the specimens could be obtained.
The laboratory testing to obtain the water retention curve and the unsaturated shear strength is tedious and time-consuming. The duration of 1 set of the unsaturated shear strength testing is around 6 months. The duration of 1 set of water retention curve testing is around 3 months. Therefore, only two sets of the unsaturated shear strength testing and two sets of water retention curve testing were performed in this study. The results from the unsaturated shear strength testing were used to evaluate the unsaturated shear strength data, which were estimated using the proposed equation.
3. Mathematical Equation
3.1. Applicable Theory
Various best-fitting methods for the WRC had been developed with great accuracy. In this study, a mathematical equation (Equation (1)) from Satyanaga et al. [17] was used for best fitting the experimental data of the bimodal WRC. This equation was used since the parameter of this equation has a physical definition [12,23,33]. The term of physical definition for parameters in the WRC equation refers to the ability of the parameters in the proposed equation to represent the variables of the WRC, such as: air-entry value of soil, inflection point of WRC, and residual suction and residual water content of soil.
where:
- θs1 = saturated volumetric water content
- θs2 = volumetric water content related to air-entry value 2
- β1 = 0 when ψ ≤ ψa1; β1 = 1 when ψ > ψa1
- β2 = 0 when ψ ≤ ψa2; β2 = 1 when ψ > ψa2
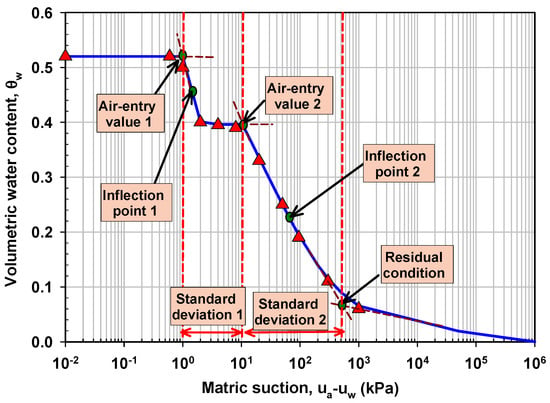 Figure 1. Variables of bimodal water retention curve.
Figure 1. Variables of bimodal water retention curve.- Cr = input parameter according to Fredlung and Xing [43] (kPa)
- erfc = the complementary error function,
- ψm1 = parameter related to suction at the inflection point 1 (Figure 1)
- ψm2 = parameter related to suction at the inflection point 2 (Figure 1)
- θr = parameter related to volumetric water content at residual condition (Figure 1)
- s1 = parameter related to standard deviation 1 (Figure 1)
- s2 = parameter related to standard deviation 2 (Figure 1)
The subscript 1 and 2 in the equation are associated with sub-curve 1 (macro pores) and sub-curve 2 (micro pores) of dual-porosity soils, respectively. The details of explanation of each parameter can be seen in Satyanaga et al. [17].
Many equations had been developed to model the unsaturated shear strength. In this study, the mathematical equation (Equation (2)) from Goh et al. [44], was used to model the experimental data from the unsaturated shear strength in the initial stage.
where ϕ′ = ϕb if (ua − uw) < AEV
if (ua − uw) ≥ AEV
where:
- AEV = air-entry value of soil (kPa)
- y and b = fitting parameters.
- Ip = plasticity index.
- n = fitting parameter from Fredlund and Xing [43] equation for fitting WRC
3.2. Proposed Equation
Many studies showed that pore size distribution (PSD) of the soil can be determined from the differentiation of water retention curve [43,45]. In this study the PSD of the soil mixtures was differentiated from its corresponding WRC which has been modelled using Satyanaga et al. [17], equation. Therefore, the equation from Satyanaga et al. [17], was differentiated to generate a PSD of the soil mixtures. The PSD equation used in this study is presented in Equation (7).
where all parameters were taken from Equation (1) after Satyanaga et al. [17]
In this study, a new equation that can be used for a best fitting of the unsaturated shear strength with bimodal WRC is proposed. The shear strength equation for suction lower than AEV1 is the same as Goh et al. [44] equation. The new equation (Equation (8)) was proposed since the experimental data from the unsaturated shear strength of soil with bimodal characteristics has unique behavior for suctions higher than AEV1. The rationale behind the development of the new equation is simply to incorporate the characteristics of the first sub-curve of the bimodal WRC into the equation.
The parameters related to standard deviation in the bimodal WRC (s1 and s2) have been studied by Satyanaga et al. [17,23], Zhai et al. [12]. They concluded that the parameters related to standard deviation can be used to estimate bimodal WRC based on grain-size distribution. Therefore, the parameters related to standard deviation were used in the development of the new bimodal unsaturated shear strength equation. The parameter s1 and s2 from Equation (1) are incorporated in the new shear strength equation (Equation (10)) to replace parameter “n” from Fredlund and Xing [43] model because shear strength of bimodal soil is affected by dual-porosity characteristics of PSD within the soil. The parameters S1 and S2 are discrete values representing the width of sub-curve 1 and sub-curve 2 in bimodal WRC (Figure 1). The reader is referred Satyanaga et al. [17,23], and Zhai et al. [12] for details of these parameters. In the proposed equations, the parameter s1 is used to represent the effect of sub-curve 1 of bimodal WRC on the unsaturated shear strength for suctions between AEV1 and AEV2. Additionally, the parameter s2 is used to represent the effect of sub-curve 2 of bimodal WRC on the unsaturated shear strength for suctions beyond AEV2. Void ratio and fine content are selected as the parameters in the Equation (11) since these properties play important role in clay materials. Soil with bimodal WRC are commonly associated with the presence of clay materials [12]. In addition, the equation was developed to take into account the characteristics of the second sub-curve of the bimodal WRC.
For AEV1 < matric suction < AEV2:
s1 = parameter related to geometric standard deviation 1.
For matric suctions > AEV2:
Equations (8) and (11) were developed for the estimation of the unsaturated shear strength of soil. The proposed equations require four (4) variables of water retention curve and three (3) soil properties. The required variables of water retention curve include AEV1, AEV2, s1 and s2. The required soil properties include plasticity index (Ip), void ratio (e) and percentage of fines.
4. Results of Laboratory Testing
Figure 2 shows both 70S30K and 50S50K specimens are in the dry optimum of their corresponding compaction curves. The maximum dry densities for specimens 70S30K and 50S50K are 1.95 Mg/m3 and 1.845 Mg/m3, respectively. The optimum water content for specimens 70S30K and 50S50K are 9.5% and 14%, respectively. The compaction curve for 70S30K illustrates that a higher maximum dry density is observed at a lower optimum water content as compared to 50S50K. Dry optimum of water content was selected to improve the possibility of producing compacted sand-kaolin bimodal soils, as suggested by Sivakumar and Wheeler [46].
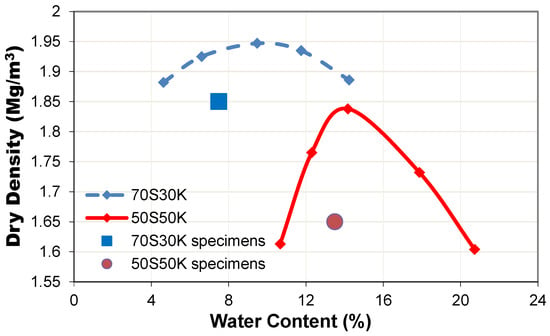
Figure 2.
Compaction curve.
Figure 3 shows a double-humped grain size distribution for both specimens. It can be observed that the main constituents for both specimens are medium-sized sand and silt-sized kaolin. The soil properties of the specimens are listed in Table 2.
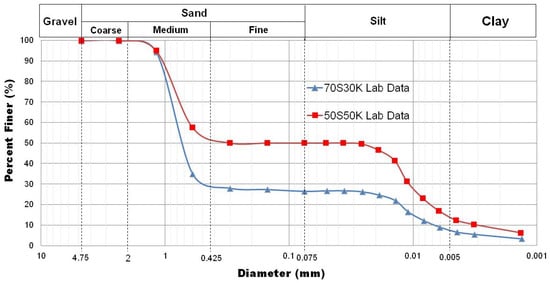
Figure 3.
Grain size distribution curve.

Table 2.
Summary of Soil Properties.
Figure 4 and Figure 5 depict volumes of water for different matric suctions that were calculated from mass of water divided by unit weight of water. The volume of water should reach equilibrium before increasing matric suction to a higher value during WRC testing. Moreover, Figure 3 and Figure 4 show that a significant drop in volume of water does not necessarily mean that the corresponding suction is the AEV of the specimen. For example, there is a significant decrease in the volume of water between matric suction 95 and 200 kPa, but none of them is AEV.
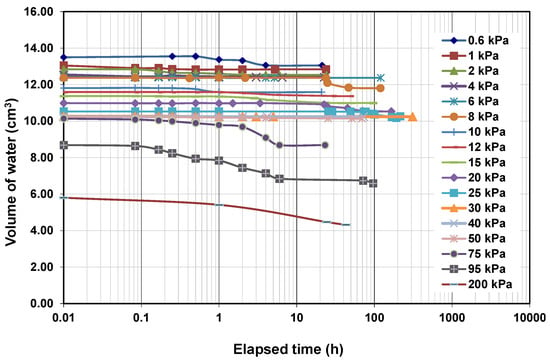
Figure 4.
Equalization time of soil specimen 70S30K.
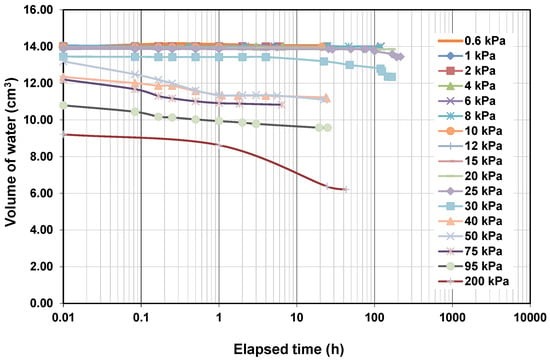
Figure 5.
Equalization time of soil specimen 50S50K.
Figure 6 exhibits WRC measurements that are fitted using Equation (1). The comprehensive fitting parameters of the equation are listed in Table 3. Table 3 shows that 70S30K has a higher AEV in the first and second sub-curves of WRC than the respective air-entry values of 50S50K. This can be explained by the fact that the percentage of coarse particles for 70S30K is higher than that for 50S50K, resulting in a faster water flow out of 70S30K than that of 50S50K. Table 3 also indicates that the Satyanaga et al. [16] equation performed very well, as shown by R2 close to 1.
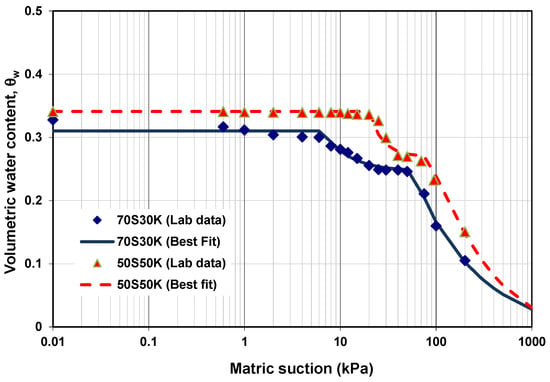
Figure 6.
WRC of 70S30K and 50S50K.

Table 3.
WRC fitting parameters based on bimodal equation proposed by Satyanaga et al. [17].
Figure 7 shows that 70S30K has two dominant pore sizes at radius 0.015 mm and 0.001 mm with frequency 0.017 and 0.057, respectively. Figure 6 also indicates that the dual porosity structure of 50S50K is observed at pore radius 0.004 mm and 0.001 mm, having frequencies of 0.014 and 0.111, correspondingly.
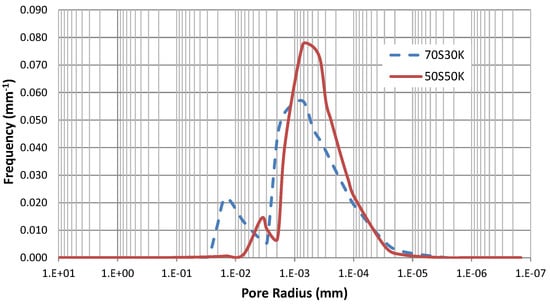
Figure 7.
Pore-size distribution curve of 70S30K and 50S50K.
Figure 8 and Figure 9 present the stress–strain curve and pore-water pressure changes from CU saturated triaxial testing. It demonstrates that 70S30K has a higher deviatoric stress than 50S50K, as expected due to the higher dry density of 70S30K. Furthermore, it also has a lower pore-water pressure during shearing as compared to 50S50K because of the lower void ratio of 70S30K. Figure 10 presents the Mohr–Coulomb failure envelope from the saturated shear strength test. It shows that soil specimen 70S30K has a lower effective cohesion as compared to soil specimen 50S50K. This is attributed to a higher percentage of sand within soil specimen 70S30K as compared to soil specimen 50S50K. Figure 11 depicts that 70S30K can be classified as ductile material, whereas 50S50K is brittle material based on the respective failure mechanism. This may be caused due to greater percentage of coarse-grained particles in 70S30K. Ductile behavior is indicated by constant load upon the failure of specimen 70S30K, whereas brittle behavior is shown by abrupt decrease of load upon the failure of specimen 50S50K.
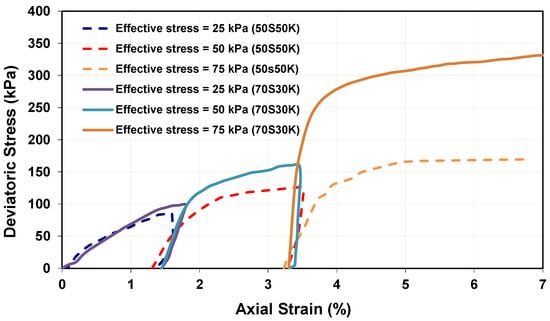
Figure 8.
Deviatoric stress against axial strain of soil specimen 70S30K and 50S50K from saturated shear strength.
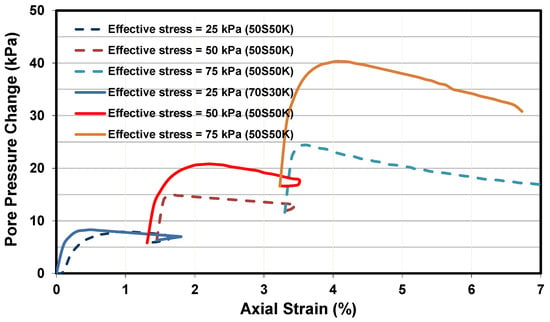
Figure 9.
Pore-water pressure changes against axial strain of soil specimen 70S30K and 50S50K from saturated shear strength.
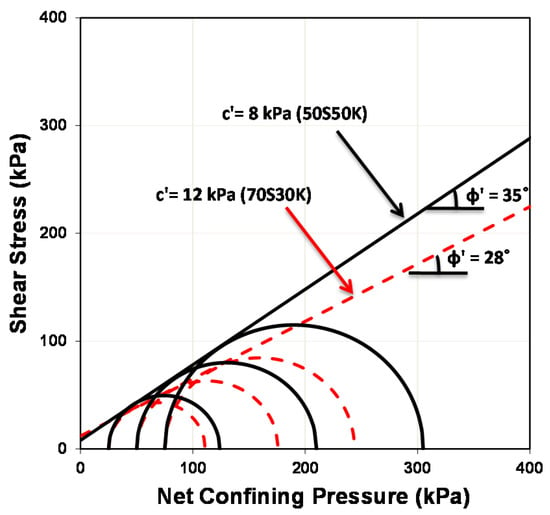
Figure 10.
Mohr circle of soil specimens 70S30K and 50S50K at matric suction of 0 kPa from saturated shear strength test.
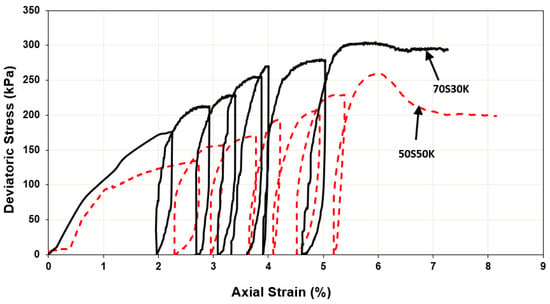
Figure 11.
Deviatoric stress against axial strain circle of soil specimens 70S30K and 50S50K from unsaturated shear strength test.
Cohesion intercept is attained by drawing tangent line to the Mohr Circle for different matric suction. Afterwards, cohesion intercept can be plotted against matric suction as shown in Figure 12 and Figure 13. Equation from Goh et al. [44] and the proposed unsaturated shear strength equations in this study were used to estimate the unsaturated shear strength of soil specimens 70S30K and 50S50K. The estimated unsaturated shear strength from both equations were compared with the experimental data to evaluate the performance of the proposed unsaturated shear strength equation. The Goh et al. [44] model requires the use of parameter “n” from Fredlund and Xing [43] unimodal WRC fitting. Figure 5 shows that AEV according to Fredlund and Xing [43] model (i.e., AEV = 15 kPa for 70S30K and AEV = 25 kPa for 50S50K) as shown in Table 4 is different with either AEV1 or AEV2 from equation proposed by Satyanaga et al. [17] (i.e., AEV1 = 6 kPa and AEV2 = 50 kPa for 70S30K and AEV1 = 20 kPa and AEV2 = 75 kPa for 50S50K), as shown in Table 5. This occurs due to the fact that the Fredlund and Xing [43] equation can only be used to best fit unimodal WRC, whereas equation proposed by Satyanaga et al. [17] can be used to best fit bimodal WRC.
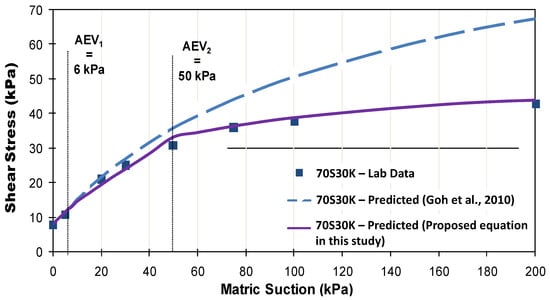
Figure 12.
Comparison between Goh et al. [44] and the proposed equation in this study for predicting shear strength of 70S30K.
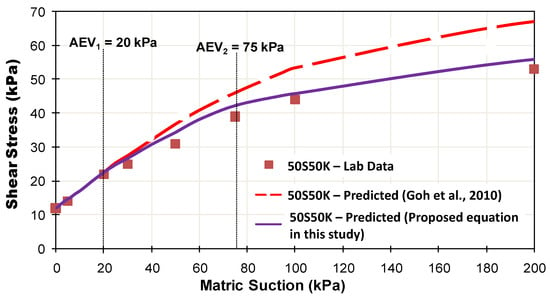
Figure 13.
Goh et al. [44] and the proposed equation in this study for predicting shear strength of 50S50K.

Table 4.
Shear strength prediction parameters based on Goh et al. [44] Equation.

Table 5.
Parameters of the proposed equation for predicting bimodal unsaturated shear strength in this study.
Table 6 shows that when matric suction is less than AEV1, ϕb is equal to ϕ′ because all pores inside the specimen are within the saturated condition. When matric suction is between AEV1 and AEV2, ϕb is less than ϕ′ since micropores are still saturated but macropores already come into an unsaturated state as the water starts to flow out. The relationship between shear strength and matric suction is non-linear and ϕb is much smaller than ϕ′ for matric suctions beyond their corresponding AEV2. This can happen because both macropores and micropores will go into an unsaturated condition and ultimately will be in a dry state when matric suction is increased continually.

Table 6.
ϕb angle for different matric suctions.
5. Discussion
The saturated volumetric water content of 70S30K is lower than that of 50S50K, as shown in Table 3. It can happen because 70S30K has a lower void ratio, which indicates less amount of void to be filled with water at saturation. The experimental results from this study are in agreement with the previous studies from Zhai et al. [12], and Satyanaga et al. [17,23], who stated that bimodal grain size distribution may lead to bimodal WRC if the soil is compacted in dry optimum with certain percentages of fine and coarse-grained particles. There are two main constituent particles (i.e., medium-sized sand and silt-sized kaolin) for both specimens that can be correlated to two AEVs of the respective specimens. The AEVs and inflection points of the first and second sub-curves of WRC for 70S30K are lower than those of 50S50K (Table 3), indicating a smaller water storage of 70S30K as compared to that of 50S50K. This can occur since 70S30K has larger particle sizes and lower liquid and plastic limits than those of 50S50K. Additionally, it indicates that 70S30K has larger sizes of dominant macropore and micropore than those for 50S50K. Kelvin’s equation describes that pore sizes of soil are inversely proportional to the ability of soil to retain water at high matric suction [27].
Furthermore, the lower saturated volumetric water content of 70S30K shows that total amount or frequency of pores inside 70S30K are less than those inside 50S50K. At a fully saturated state, water is equivalent to all available pores inside the specimen by assuming water cannot penetrate into solid particles. Based on Table 3, standard deviation of first and second sub-curves of WRC correspond to the width of the dominant macropore and micropore sizes in PSD, respectively. In this research, lower standard deviations are observed in WRC of 50S50K, which has a higher number of fine-grained particles. Therefore, the greater percentages of fine contents, the more unlikely the appearance of two dominant pore sizes in the PSD.
Mohr–Coulomb failure envelopes of both specimens (Figure 10) demonstrate that typically 70S30K has a lower effective cohesion intercept than that of 50S50K. One of the possible reasons is that the inter-particle bonding inside 70S30K is weaker than that of 50S50K since 70S30K has a smaller proportion of fine-grained particles. Figure 12 and Figure 13 illustrate that equation from Goh et al. [44] tends to significantly overestimate the measured shear strength of both specimens especially at high matric suctions or beyond AEV2. The possible reason is that equation from Goh et al. [44] incorporates parameters from the Fredlund and Xing [43] equation which cannot fit the experimental data of the unsaturated shear strength with bimodal WRC data well. Therefore, the equation from Goh et al. [44] is not applicable to predict the shear strength of soil with bimodal WRC. The proposed shear strength equation in this study can predict the measured data reasonably accurately, as observed in Figure 12 and Figure 13. For both specimens, the linear relationship between shear strength and matric suction is observed when matric suction is less than their respective AEV2.
Table 6 indicates that ϕb of 70S30K is higher than that of 50S50K for the entire matric suction range. This trend may occur due to the higher percentage of the coarse-grained particles and the lower void ratio in 70S30K than those of 50S50K. This study was carried out on soil, which is associated with bimodal WRC without significant volume change. Therefore, the proposed bimodal shear strength equation in this study is not applicable to soil with bimodal WRC with significant volume change.
In summary, the proposed bimodal shear strength equation can be used to minimize the cost and complexity of the unsaturated shear strength testing on soil with bimodal WRC. The outcome of this study is beneficial for geotechnical or geo-environmental engineers who needs to design slope cover. Future works should be carried out to incorporate the use of soil with bimodal WRC to minimize the rainwater infiltration into the slope as well as maintain some water contents to ensure the health of the plants. Based on the bimodal shear strength characteristics of the investigated soil in this study, the suction of soil for the slope cover should be maintained between AEV1 and AEV2.
Previous studies by Santamarina and Fam [47], and also Jang and Santamarina [48] indicated the influence of fine particles especially those with significant volume change on shear strength characteristics. Other researchers [49,50,51,52] also indicated that particle shape has an effect on the characteristics of shear strength. This study is limited to soils with negligible volume change. No investigation was carried out on the effect of particle shape on this study.
6. Conclusions
From this research, several conclusions can be deducted as follows:
- Lower air-entry value and lower inflection point of soil WRC signify larger sizes of dominant macropore and micropore in PSD of soil.
- Dual porosity structure in PSD is more unlikely if there are higher percentages of fine-grained particles inside the soil.
- For matric suctions less than AEV1, the relationship between shear strength and matric suction is linear and ϕb is the same with ϕ′.
- For matric suctions between AEV1 and AEV2, the relationship between shear strength and matric suction is still linear but ϕb is less than ϕ′.
- For matric suctions beyond AEV2, the relationship between shear strength and matric suction is non-linear and ϕb is much smaller than ϕ′.
- A new mathematical equation has been proposed to estimate the unsaturated shear strength of soil with bimodal water retention curve. The proposed equation has been evaluated and it is in agreement with the experimental data of the unsaturated shear strength carried out in this study.
Author Contributions
A.S., S.-W.M. and J.R.K. conceptualized the study; A.S. and N.B. implemented data processing under the supervision of S.-W.M. and J.R.K.; the original draft of the manuscript was written by A.S. and N.B. with editorial contributions from S.-W.M. and J.R.K.; the funding acquisition was made by S.-W.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors appreciate the financial support from the Nazarbayev University, Faculty Development Competitive Research Grant Program (FDCRGP) Grant No 110119FD4508, and Collaborative Research Project (CRP) Grant No. 11022021CRP1508. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Nazarbayev University.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.H.; Zhang, L.M. Geometric parameters and REV of a crack network in soil. Comput. Geotech. 2010, 37, 466–475. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhou, B.; Wu, S.R.; Shi, J.S.; Li, B. Characteristic analysis of large-scale loess landslides: A case study in Baoji City of Loess Plateau of Northwest China. Nat. Hazards Earth Syst. Sci. 2011, 11, 1829–1837. [Google Scholar] [CrossRef]
- Pu, J.; Wallwork, J.; Khan, A.; Pandey, M.; Pourshahbaz, H.; Satyanaga, A.; Hanmaiahgari, P.; Gough, T. Flood Suspended Sediment Transport: Combined Modelling from Dilute to Hyper-Concentrated Flow. Water 2021, 13, 379. [Google Scholar] [CrossRef]
- Zhanabayeva, A.; Sagidullina, N.; Kim, J.; Satyanaga, A.; Lee, D.; Moon, S.-W. A comparative analysis of Kazakhstani and European design specifications: Raft foundation, pile foundation, and piled raft foundation. Appl. Sci. 2021, 11, 3099. [Google Scholar] [CrossRef]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of hysteresis on the stability of residual soil slope. Int. Soil Water Conserv. Res. 2019, 7, 226–238. [Google Scholar] [CrossRef]
- Satyanaga, A.; Rahardjo, H. Role of Unsaturated Soil Properties in The Development of Slope Susceptibility Map. Proc. Inst. Civ. Eng.-Geotech. Eng. 2020, 1–44. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; Leong, E.C.; Ng, Y.S.; Foo, M.D.; Wang, C.L. Slope failures in Singapore due to rainfall. In Proceedings of the 10th Australia New Zealand Conference on Geomechanics “Common Ground”, Brisbane, Australia, 21–24 October 2007; Volume 2, pp. 704–709. [Google Scholar]
- Nistor, M.M.; Rahardjo, H.; Satyanaga, A.; Koh, Z.H.; Qin, X.; Sham, A.W.L. Investigation of groundwater table distribution using borehole piezometer data interpolation: Case study of Singapore. Eng. Geol. 2020, 271, 105590. [Google Scholar] [CrossRef]
- Satyanaga, A.; Rahardjo, H.; Hua, C.J. Numerical Simulation of Capillary Barrier System under Rainfall Infiltration. ISSMGE Int. J. Geoengin. Case Hist. 2019, 5, 43–54. [Google Scholar]
- Ip, S.C.; Rahardjo, H.; Satyanaga, A. Three-dimensional slope stability analysis incorporating unsaturated soil properties in Singapore. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2020, 15, 98–112. [Google Scholar] [CrossRef]
- Tamm, T.; Nõges, T.; Järvet, A.; Bouraoui, F. Contributions of DOC from surface and groundflow into Lake Võrtsjärv (Estonia). In European Large Lakes Ecosystem Changes and Their Ecological and Socioeconomic Impacts. Developments in Hydrobiology; Nõges, T., Ed.; Springer: Dordrecht, The Netherlands, 2007; Volume 199. [Google Scholar]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Priono. Effect of bimodal soil-water characteristic curve on the estimation of permeability function. Eng. Geol. 2017, 230, 142–151. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; Harnas, F.R.; Leong, E. Use of Dual Capillary Barrier as Cover System for a Sanitary Landfill in Singapore. Indian Geotech. J. 2016, 46, 228–238. [Google Scholar] [CrossRef]
- Syarifudin, A.; Satyanaga, A. Variability of bimodal soil-water characteristic curves under different confining pressure. Appl. Environ. Soil Sci. 2021, 2021, 5569491. [Google Scholar] [CrossRef]
- Wang, D.; Li, C.; Parikh, S.J.; Scow, K.M. Impact of biochar on water retention of two agricultural soils—A multi-scale analysis. Geoderma 2019, 340, 185–191. [Google Scholar] [CrossRef]
- Li, Y.; Satyanaga, A.; Rahardjo, H. Characteristics of unsaturated soil slope covered with capillary barrier system and deep-rooted grass under different rainfall patterns. Int. Soil Water Conserv. Res. 2021, 9, 405–418. [Google Scholar] [CrossRef]
- Satyanaga, A.; Rahardjo, H.; Leong, E.; Wang, J.-Y. Water characteristic curve of soil with bimodal grain-size distribution. Comput. Geotech. 2013, 48, 51–61. [Google Scholar] [CrossRef]
- Wijaya, M.; Leong, E. Equation for unimodal and bimodal soil-water characteristic curves. Soils Found. 2016, 56, 291–300. [Google Scholar] [CrossRef]
- Chen, R.-P.; Liu, P.; Liu, X.-M.; Wang, P.-F.; Kang, X. Pore-scale model for estimating the bimodal soil-water characteristic curve and hydraulic conductivity of compacted soils with different initial densities. Eng. Geol. 2019, 260, 105199. [Google Scholar] [CrossRef]
- Yan, W.; Birle, E.; Cudmani, R. A new framework to determine general multimodal soil water characteristic curves. Acta Geotech. 2021, 16, 3187–3208. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Huang, T.-T.; Lee, J.-W. Effect of Unimodal and Bimodal Soil Hydraulic Properties on Slope Stability Analysis. Water 2021, 13, 1674. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; D’Amore, G.A.R.; Leong, E.C. Soil-water Characteristic Curves of Gap-graded Soils. J. Eng. Geol. 2012, 125, 102–107. [Google Scholar] [CrossRef]
- Satyanaga, A.; Zhai, Q.; Rahardjo, H. Estimation of Unimodal Water Characteristic Curve for Gap-graded Soil. Soils Found. 2017, 57, 789–801. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effects of soil–water characteristic curve and Page 18 of 30 relative permeability equations on estimation of unsaturated permeability function. Soils Found. 2015, 55, 1400–1411. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G.; Zhuang, Y. Framework to estimate the soil-water characteristic curve for soils with different void ratios. Bull. Int. Assoc. Eng. Geol. 2020, 79, 4399–4409. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, H.; Priono; Dai, G. Role of the pore-size distribution function on water flow in unsaturated soil. J. Zhejiang Univ. Sci. A 2019, 20, 10–20. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. A pore-size distribution function based method for estimation of hydraulic properties of sandy soils. Eng. Geol. 2018, 246, 288–292. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. Variability in unsaturated hydraulic properties of residual soil in Singapore. Eng. Geol. 2016, 209, 21–29. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Satyanaga, A.; Rahardjo, H. Unsaturated shear strength of soil with bimodal soil-water characteristic curve. Geotechnique 2019, 69, 828–832. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Gan, J.K.M. Non-linearity of Strength Envelope for Unsaturated Soils. In Proceedings of the 6th International Conference on Expansive Soils, New Delhi, India, 1–4 December 1987; pp. 49–54. [Google Scholar]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Priono; Rahardjo, H.; Leong, E.C.; Chatterjea, K. Effects of mica content on hydraulic anisotropy of unsaturated soil. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; pp. 1675–1683. [Google Scholar]
- Rahardjo, H.; Satyanaga, A.; Mohamed, H.; Ip, S.; Shah, R.S. Comparison of Soil–Water Characteristic Curves from Conventional Testing and Combination of Small-Scale Centrifuge and Dew Point Methods. Geotech. Geol. Eng. 2018, 37, 659–672. [Google Scholar] [CrossRef]
- ASTM D422-63; Standard Test Method for Particle–Size Analysis of Soils. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM D4318-00; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2000.
- ASTM D854-02; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM D698-12E1; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12 400 ft-lbf/ft3 (600 kN-m/m3)). ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM D2487-00; Standard Practice for Classification of Soils for Engineering Purposes, Unified Soil Classification System. ASTM International: West Conshohocken, PA, USA, 2000.
- ASTM D6836-16; Standard Test Methods for Determination of the Soil Water Characteristic Curve for Desorption Using Hanging Column, Pressure Extractor, Chilled Mirror Hygrometer, or Centrifuge. ASTM International: West Conshohocken, PA, USA, 2016.
- Satyanaga, A.; Rahardjo, H.; Koh, Z.H.; Mohamed, H. Measurement of a Soil-water Characteristic Curve and Unsaturated Permeability using the Evaporation Method and the Chilled-Mirror Method. J. Zhejiang Univ. Sci. A 2019, 20, 368–375. [Google Scholar] [CrossRef]
- Hilf, J.W. An Investigation of Pore-Water Pressure in Compacted Cohesive Soils; U.S. Department of the Interior, Bureau of Land Reclamation, Design and Construction Division: Denver, CO, USA, 1956; Technical Memoranda No. 654.
- Fredlund, D.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Goh, S.G.; Rahardjo, H.; Leong, E.C. Closure to “Shear Strength Equations for Unsaturated Soil under Drying and Wetting” by Goh Shin Guan, Harianto Rahardjo, and Leong Eng Choon. J. Geotech. Geoenviron. Eng. 2011, 137, 1313–1315. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. HYDRAU uc properties of porous media. Hydrol. Pap. Colo. State Univ. 1964, 24, 37. [Google Scholar]
- Sivakumar, V.; Wheeler, S.J. Influence of Compaction Procedure on the Mechanical Behaviour of an Unsaturated Compacted Clay, Part 1: Wetting and Isotropic Compression. Géotechnique 2000, 50, 359–368. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Fam, M. Changes in dielectric permittivity and shear wave velocity during concentration diffusion. Can. Geotech. J. 1995, 32, 647–659. [Google Scholar] [CrossRef]
- Jang, J.; Santamarina, J.C. Fines Classification Based on Sensitivity to Pore-Fluid Chemistry. J. Geotech. Geoenviron. Eng. 2016, 142, 06015018. [Google Scholar] [CrossRef] [Green Version]
- Santamarina, J.C.; Cho, G.C. Soil behaviour: The role of particle shape. In Advances in Geotechnical Engineering: The Skempton Conference; Jardine, R.J., Potts, D.M., Higgins, K.G., Eds.; Thomas Telford: London, UK, 2004; Volume 1, pp. 604–617. [Google Scholar]
- Santamarina, J.C.; Klein, K.A.; Fam, M.A. Soils and Waves: Particulate Materials Behavior, Characterization and Process Monitoring; Wiley: Chichester, UK, 2001. [Google Scholar]
- Santamarina, J.C.; Shin, H. Friction in Granular Media. Meso-scale Shear Physics in Earthquake and Landslide Mechanics; CRC Press: London, UK, 2009; pp. 157–188. [Google Scholar]
- Santamarina, J.C.; Klein, K.A.; Wang, Y.-H.; Prencke, E. Specific surface: Determination and relevance. Can. Geotech. J. 2002, 39, 233–241. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).