Abstract
Hyperparameter tuning is a critical function necessary for the effective deployment of most machine learning (ML) algorithms. It is used to find the optimal hyperparameter settings of an ML algorithm in order to improve its overall output performance. To this effect, several optimization strategies have been studied for fine-tuning the hyperparameters of many ML algorithms, especially in the absence of model-specific information. However, because most ML training procedures need a significant amount of computational time and memory, it is frequently necessary to build an optimization technique that converges within a small number of fitness evaluations. As a result, a simple deterministic selection genetic algorithm (SDSGA) is proposed in this article. The SDSGA was realized by ensuring that both chromosomes and their accompanying fitness values in the original genetic algorithm are selected in an elitist-like way. We assessed the SDSGA over a variety of mathematical test functions. It was then used to optimize the hyperparameters of two well-known machine learning models, namely, the convolutional neural network (CNN) and the random forest (RF) algorithm, with application on the MNIST and UCI classification datasets. The SDSGA’s efficiency was compared to that of the Bayesian Optimization (BO) and three other popular metaheuristic optimization algorithms (MOAs), namely, the genetic algorithm (GA), particle swarm optimization (PSO) and biogeography-based optimization (BBO) algorithms. The results obtained reveal that the SDSGA performed better than the other MOAs in solving 11 of the 17 known benchmark functions considered in our study. While optimizing the hyperparameters of the two ML models, it performed marginally better in terms of accuracy than the other methods while taking less time to compute.
1. Introduction
Machine learning (ML) techniques are increasingly being used in a wide range of research areas including for object detection and classification [1,2], natural language processing and data-driven control [3]. Despite the relatively good performance obtained, selecting the optimal hyperparameter (HP) values for most ML models remains a significant challenge. These hyperparameters are usually classified as either continuous, discrete, or a combination of the two [4]. Continuous hyperparameter metrics that can be optimized include the learning rate, decay, momentum and regularization parameters [5,6]. Similarly, the number of layers in deep learning models and the number of trees in the random forest algorithm are examples of discrete hyperparameters that must be fine-tuned [7]. We could perhaps note that other conditional search spaces might be influenced by other hyperparameters, such as the type of optimizer used in training, which determines the types and number of hyperparameters to be used [8].
In terms of hyperparameter tuning, the random and grid search approaches are currently the most popular methods for fine-tuning the hyperparameters of many ML models [9,10]. However, because they tend to search every sample point in the hyperparameter space, regardless of the training configuration used, these search techniques are regarded as naive approaches. Consequently, such search methods are inefficient, and the computational complexity and cost of optimizing hyperparameter values increase. Several other optimization techniques, such as Bayesian optimization, evolutionary strategies, and tree pipeline approaches have been proposed for searching and selecting the optimal hyperparameter values of many ML models [11,12,13].
It has been demonstrated that the Bayesian optimization technique with Gaussian processes can effectively search for hyperparameter values in a continuous search space [14]. Tree-based Bayesian optimization and evolutionary algorithms have also been demonstrated to be flexible and applicable in a wide range of search spaces [13]. However, comparing the performance of different ML models is necessary, especially when different optimization techniques are used to optimize the hyperparameter values under different application conditions. As a result, in order to improve the training efficiency and accuracy performance of ML models, the present article proposes an improved optimization technique called the simple deterministic selection genetic algorithm (SDSGA) for hyperparameter optimization. Following the performance of the proposed technique, we summarize the current article’s contributions as follows:
- 1.
- A simple deterministic selection genetic algorithm (SDSGA) was developed as an improved optimization technique for computing optimal HP values with a small number of fitness evaluations.
- 2.
- The proposed SDSGA has shown a high exploitative capability which makes it able to search more deeply within a region in the search space without sacrificing its exploratory capabilities.
The rest of the paper is structured as follows: Section 2 examines the related work, while our proposed SDSGA is described in Section 3. Our method of comparison and analysis is presented in Section 4. Experimental results were obtained, discussion is presented in Section 5, and Conclusions are drawn in Section 6.
2. Related Work
Several techniques have been proposed for optimizing the hyperparameters (HPs) of ML models. These include the grid search, random search, and Bayesian optimization techniques. The grid search approach was observed to be inefficient and time consuming in optimizing certain hyperparameters [14,15]. Similarly, the random search approach has been shown to be effective in optimizing the HPs of ML models within a small search space [9]. However, due to the random nature of the technique, its performance tends to be spurious and erratic, necessitating the use of more computational resources [15]. This is frequently associated with a lack of indicators and a guide for an optimization process that governs the expected improvement direction.
The Bayesian Optimization and Gaussian process approaches have also been used to optimize the HP values of ML models [16]. These algorithms are inherently sequential in nature since they rely on the results of the previous iteration to decide on the next HP sample to be evaluated [17]. Thus, this leads to their inability to use multiple CPU and GPU cores in speeding up the optimization process. Other HP optimization methods for speeding up the search space are documented in [14,18], with a popular approach being the Successive Halving Algorithm SHA [19]. In this approach, the HPs optimization problem was defined as a non-stochastic multi armed bandit problem, in which more resources are allocated to the HP samples that demonstrate more promising performance. Similarly, in [18], an early stop criteria mechanism was incorporated into the algorithm to prevent the model from being evaluated with unfavorable HP samples. Thus, this speeds up the search process as compared to the naïve random search approach.
Some other hybrid methods were also proposed to speed up the optimization process, among these is the adaptive Bayesian approach, in which dataset sizes were selected adaptively, and the model was evaluated using the Bayesian optimization algorithm [20]. Similarly, the Bayesian optimization approach was combined with the hyperband, thus harnessing the strength of both techniques to effectively search the solution space and to terminate the process [14]. Despite being highly parallel, the lack of consideration of previous experiences in searching for new solutions is a major drawback associated with random search-based approaches.
It has been demonstrated that the Gaussian Process (GP) and Bayesian Optimization (BO) are effective methods for optimizing HP configurations. However, they cannot fully take advantage of parallel computing platforms due to their inherently sequential nature. Other approaches that use the power of parallel computing platforms to accelerate HP optimization processes have been reported in [12,21]. For example, a metaheuristic-based approach called the covariance matrix adaptation evolutionary strategy (CMA-ES) has been proposed to optimize HPs in ML models. Similarly, the PSO-BO algorithm was proposed in [22], which uses the PSO algorithm to optimize the acquisition function of the BO algorithm. Other metaheuristic approaches for hyperparameter optimization are presented in [23,24]. In addition, a parallel approach referred to as the parallel PSO was proposed in [25] to scale up the HP optimization, while harnessing the strength of the multiple computing resources. The results obtained demonstrated performance improvement over the sequential PSO-BO technique. Other documented approaches entail the use of large population sizes in evaluating the performance of metaheuristics-based optimization of ML model HPs [26,27].
Various AutoML systems have been proposed in the literature for the practical application of hyperparameter optimization of ML models. The main goal is to automatically optimize the ML pipeline, such as optimizing the ML model selection and hyperparameters. These include Auto-Sklearn [28], Auto-Weka [29], Auto-Keras [15], and Auto-Pytorch [30], which are named after the ML packages they primarily support. Despite the fact that our research is not about AutoML, we should point out that, because our proposed optimization algorithm is model-free, an AutoML system can be built with little modification using the proposed optimization algorithm.
These approaches mentioned thus far can be summarized into those that fully evaluate the model and then optimize the results, such as the validation error or validation accuracy, and those that do not fully evaluate the model and do not optimize the results. There are several algorithms that fall into the category of those that fully evaluate the model, such as the BO and PSO-BO algorithms, as well as those that only evaluate the models for a limited number of iterations such as the SHA and its variants. Although these different classes and techniques have many advantages, they also have some significant drawbacks. For example, the first group requires algorithms that are highly parallel; otherwise, it may take a long time before any useful results can be generated—whereas the second class, on the other hand, may result in the possibility of losing good hyperparameters since the model are often not evaluated in its entirety.
However, in this article, we present the SDSGA with an aim to efficiently search for the optimal hyperparameters of ML models. A comparative analysis approach was then used in evaluating the performance of the developed SDSGA, which was then compared with other MOAs, such as the genetic algorithm (GA), particle swarm optimization (PSO), and biogeography-based optimization (BBO) techniques. We used small population sizes in order to conserve the computation resources involved in training ML models (CNN and RF). As a result, the fewer function evaluations used to find the optimal HP values, the less time will be spent on training the model.
3. Methodology
In this article, the selection method used in the typical GA is modified. The elitist GA as described in [31] was used as the base GA, as it has been shown to be very effective in finding global optima in unimodal and multimodal problems [32]. We note that the proposed approach was motivated by the desire to overcome the drawback of the original GA, which uses probabilistic selection techniques such as the roulette wheel. Because of this, the original GA has a tendency to become trapped in local optima, thus being a major weakness in the exploitation capabilities of the GA.
3.1. Crossover and Mutation in GA
When using the GA, a population of individuals is created that contains the variables that need to be optimized, which are known as chromosomes. A population is defined in (1) with the row vector representing the solution vector in a single iteration. X is a matrix of all individuals that take part in the optimization process. The total population throughout the run is defined in (2), where n represents the n-th iteration, and m represents the number of agents or chromosomes:
Furthermore, let P represent the percentage of the best fitness values to be chosen as the number of parents in the population; thus, assuming , the top 30% of the population in terms of fitness will be chosen for recombination/crossover. If represents the i-th individual in the n-th generation, and this individual’s fitness is in the top 30% of the population, it will be chosen as a parent; otherwise, it will not be chosen. This is represented in (3) as follows:
where is the whole population, t is the iteration count, is the parent array at the end of given iteration of the for loop in line 6 of Algorithm 1, is the parent array at the end of the previous iteration, the expression means that , which is the nth individual is appended to the parent array from the previous iteration. The first condition in (3) implies that an i-th individual will be appended to the parent array if its fitness value is in the best P% of the whole population, whereas the parent array remains the same if otherwise.
Regarding the crossover probability, for example, if the probability of crossover is set to 60%, then two randomly selected individuals will have a 0.6 probability of performing a crossover operation on each other. The same rule applies to the mutation operation as it does to the other operations. The number of parents, the probability of crossover, and the probability of mutation are typically provided as parameters to the GA algorithm before the optimization run is carried out. Notably, the individuals upon which these crossover and mutation operations are conducted are those whom are selected according to the criteria stated in (3).
3.2. Proposed Improved Genetic Algorithm (SDSGA)
In implementing the GA, it was discovered that, if the population is too low, there appears to be little to no diversity in the population after a few generations. Although increasing the mutation probability can inject diversity, the GA tends to diverge and is unable to exploit a promising region of the search space more effectively.
The strategy employed in this study is to enhance the highly exploitative property of GA by modifying the selection algorithm in such a way that the entire solution/chromosome set, including the fitness values, is considered rather than only the fitness value being used as a selection criterion as was previously done. On the other hand, we note that there have been several proposals in the literature for improving GA by specifically modifying the selection algorithms used for selecting parents who will participate in crossover operation [33,34]. Our proposal is different since it only involves a simple selection of individuals sorted in a decreasing order of fitness values making sure that all selected individuals are unique. Although this can help in highly exploitative search, it reduces diversity in the population, which makes the algorithm unable to search globally in the search space.
This challenge was addressed by increasing the mutation probability. It may be counter intuitive to increase the mutation probability as it causes divergence in the algorithm. However, since the system is already highly exploitative, this shows that the global search and the local search can be balanced using this method. The proposed algorithm for the modified GA selection algorithm is shown in Algorithm 1, whereas Figure 1 presents the flowchart for the proposed SDSGA. The performance of the proposed SDSGA was tested and evaluated by comparing with other well-known and popular metaheuristic optimization algorithms, particularly the GA, PSO and BBO algorithms, which will be described in Section 4. They were all tested for both benchmark function optimization and the tuning of the HPs of the ML models, specifically the CNN and RF algorithms. For tuning the hyperparameters, Bayesian Optimization, as described in [11], was used as a basis for comparison.
| Algorithm 1 Pseudocode of the selection algorithm. | |
| Require: population | |
| Ensure: parent array | |
| 1: | Sort the population in decreasing order |
| 2: | Create array of zeros to contain parents |
| 3: | Set added, count to 0 |
| 4: | for each individual in population do |
| 5. | if individual does not exist in parent array then |
| 6. | Add copy of individual to parent array |
| 7. | Increment added |
| 8. | end if |
| 9. | if added is equal to parent size then |
| 10. | Break |
| 11. | end if |
| 12. | end for |
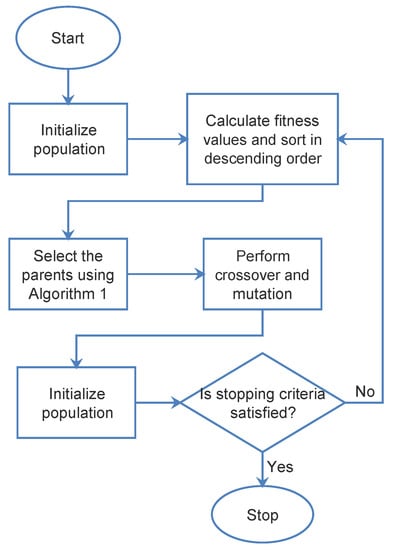
Figure 1.
Flowchart of the SDSGA.
4. Experimental Components
This section describes the datasets, benchmark functions, and optimization algorithms used in this study. The approach used is broken down into five sections: dataset description, overview of metaheuristic optimization algorithms, overview of ML models classifiers, our method of comparison, and the evaluation metrics used.
4.1. Description of Benchmark Functions
To validate the SDSGA’s suitability for optimizing the hyperparameters of ML models, its performance was compared to that of some well-known metaheuristic optimization algorithms. The proposed SDSGA was tested on 17 benchmark functions that included both unimodal and multimodal functions. The chosen functions have been widely used in the literature as alternative functions in place of real-world simulations. They also present various challenges to optimization algorithms, making them excellent tools for comparing and validating different metaheuristic algorithms. The mathematical expressions of some of these functions are described in [35].
A dimension of 10 was used for all the benchmark functions with a population size of 200 and iteration of 100, which is within the limit of the maximum number of fitness evaluations as noted in [36]. The use of dimension 10 generally introduces some level of complexity and difficulty into the optimization process with difficulty increasing as dimension increases. The initial population was generated randomly only once for every run and passed to each of the optimization algorithms. This is done to make sure that they all start under the same initial condition.
The optimization algorithms were run five times for each benchmark function and a pivot table was created. The mean and standard deviation of the runs were computed. These were used to compare the performance of the optimization algorithms.
4.2. Description of the Datasets
We used two different datasets from different application areas in this article. The first set of data used were obtained from the MNIST vision classification datasets [37], while the second sets of data were obtained from the UCI classification datasets [38]. The MNIST dataset consists of 70,000 gray scale images out of which 60,000 images were used for training and 10,000 for testing. These images have a resolution of 28 × 28, which gives a total of 784 pixels. These images have a resolution of 28 × 28, which gives a total of 784 pixels. We note that all the images belong to one of 10 classes contained in the datasets.
The objective was to optimize the HP values using each of the metaheuristic optimization algorithms (SDSGA, GA, PSO and BBO) and the BO algorithm for the CNN model in order to predict and classify an image into a category that is appropriate for the image. Some sample images contained in MNIST datasets are shown in Figure 2. In addition, five UCI image datasets were selected for this research including the car evaluation, breast cancer clinical trial, ADULT, LETTER and forest cover Type. Table 1 summarizes the key details of these datasets. The selected optimization algorithms were then used to optimize the hyperparameters of the RF model in predicting the classes in the datasets.

Figure 2.
Some of the images present in the MNIST dataset.

Table 1.
Summary of the UCI dataset.
4.3. Overview of the Metaheuristic Optimization Algorithms
The GA, PSO and BBO metaheuristic optimization algorithms [39,40,41], as well as our proposed SDSGA were used to optimize the HP values of each ML model. The selection of these algorithms was based on their widespread use as representative examples of their nature of optimization in general. We note that not too much effort has been put into optimizing the parameters of these metaheuristic optimization algorithms. Instead, good parameters are often selected based on reports from the literature. The BO algorithm was used as a baseline for comparison purposes in [11].
4.3.1. Particle Swarm Optimization (PSO)
The PSO is a population based-metaheuristic optimization algorithm, belonging to the class of Swarm Intelligence [42]. It models solutions to an optimization problem as a swarm of particles having specified positions and velocities. These particles also possess memory for storing their local best position and some means of communication of the global best position:
where v and x represent the velocity and position of a particle, respectively. The subscripts t and i are the iteration and an individual particle, respectively, whereas are the learning parameters used to fine-tune the algorithm per specific problem.
4.3.2. Genetic Algorithm (GA)
The GA is also a population-based metaheuristic algorithm that was developed based on Darwinian theory of evolution of genes [39]. The solution to an optimization problem is represented by GA as a population of chromosomes. These chromosomes then iteratively recombine and mutate to form new child chromosomes with the aim of producing better offspring as the generation progresses. Further details on the theoretical development of GA as an optimization algorithm can be found in [43]. We note the existence of another variant of GA known as Elitist GA, which ensures the preservation and propagation of the best results over the next generation [44]. This variant of the GA was adopted for the optimization of the HP values in this research.
4.3.3. Biogeography Based Optimization (BBO)
The BBO algorithm was proposed in [45], as a way of connecting the engineering field with that of biogeography. Biogeography was thus mathematically modelled in such a way that it describes the species migration from a one island to another, the rise of species, and the extinction of others. We note that an island in the context of optimization describes a habitat that is geographically isolated from other habitats around it. The objective function was modelled by the habitat suitability index (HSI), while the independent variables were modelled as the suitability index variables (SIVs). This optimization process follows the emigration and immigration of species from one island to another. The island with a high HSI has a high fitness value, and the island has a high emigration rate as the species migrate to explore other islands. The island with low HSI tends to have a high immigration rate. This is because there is less competition on the island, thus making it very attractive. However, species on the island tend to go extinct if the island does not get better, which, in turn, causes more immigration.
4.3.4. Metrics of Analysis for Optimizing Benchmark Functions
The performance of the four metaheuristic optimization algorithms, SDSGA GA, PSO and BBO algorithms for the optimization of benchmark functions were analyzed using metrics such as mean of the best solution reached by the algorithm and the standard deviation of the best solutions. By taking the mean of the best solutions found, it is possible to reduce the impact of outliers on the results. As a measure of variability or spread around a mean, the standard deviation of the solutions provides an indication of that variability or spread.
4.4. Overview of the Machine Learning Classifiers
A simple CNN model with two convolution layers was trained on the MNIST dataset. The convolution filter used has a size of 5 × 5, with a stride of 1 and no padding. The MaxPooling filter was used at the pooling layer after the convolution step with a size of 2 × 2. We added dropout to regularize the model to avoid overfitting. The Log SoftMax was used at the output of the model to select one of the 10 classes predicted for an image. The Adam optimizer was used with default parameters and the model’s loss was computed using a negative log likelihood loss function. The structure of the convolutional neural network used is depicted in Figure 3.
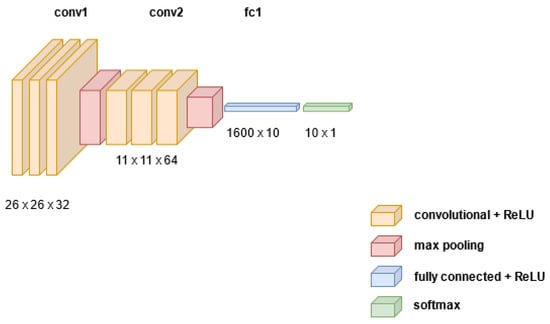
Figure 3.
Structure of CNN used, showing the results of all operations.
For the classification tasks, the RF classifier was trained on the UCI datasets. In order to keep the experiment simple, the same model was used for training all the four datasets. A preprocessing step was necessary for the ADULT dataset since it contains some missing data. This involves mainly filling the unavailable fields with the mode of the feature values.
4.4.1. Tuning the Hyperparameters of CNN Model
The CNN model was trained using the MNIST dataset. Two hyperparameters viz. learning rate, , and the batch size, s, were selected to be optimized. The selection of these HPs was guided by the results of the preliminary experimental investigation, which revealed that the learning rate and batch size have a significant impact on the accuracy of the CNN ML model when used for image classification problems. The ranges used for the two hyperparameters are and . The three algorithms used were limited to only a population size of 15. This was done in order to meet the goal of using smaller population sizes to evaluate the performance of the algorithms while utilizing limited computational resources.
4.4.2. Tuning the Hyperparameters of the Random Forest Model
The performance of the RF algorithm for classification depends highly on both the strength of a single tree and the correlation between trees [11]. The value that controls them is , where m is the number of features that a leaf node should be split, and M is the number of features in the dataset. An increase in m will increase the strength of the trees as well. However, this will increase the correlation between trees which will in turn increase the error rate of classification. Therefore, a trade-off needs to be made by finding the optimal value of m. The second hyperparameter is the number of trees in the RF model. A smaller number of trees implies having lower accuracy. Thus, the range of values used for these hyperparameters are and . We note that we have used the standard implementation of RF algorithm with classification and regression trees (CART) implementation of decision trees [46]. However, there are perhaps better alternatives such as the oblique RF [47,48], where, instead of simple partitioning as is done in standard RF, an oblique linear hyperplane is used in splitting the training data at each node. The heterogeneous oblique RF [49] is also a type of oblique RF where the authors proposed the use of multiple linear hyperplanes for the splitting of the features. The choice of which will be based on some optimization at the node. Another type of RF is the multinominal RF (MRF) [50] which is concerned about increasing the consistency and the differential privacy in RF with performance comparable to the standard RF.
4.4.3. Metrics of Analysis for HP Optimization
The BO and four metaheuristic optimization algorithms, SDSGA GA, PSO and BBO were evaluated for tuning the HPs of ML models using metrics such as mean validation accuracy, number of iterations and execution time. The validation accuracy is the most essential metric since the purpose of the HP optimization is to improve the classification accuracy of the ML models. Metaheuristic optimization algorithms are well known for their effectiveness in determining global optimal solution values in specific problems. However, a large number of fitness evaluations are required to accomplish this. The algorithm may find fitter solutions to the model as the number of iterations increases. Similarly, in this study, the number of iterations was used as a metric to compare the algorithms by using the worst performing algorithm as the baseline and comparing how long the competing algorithms took to reach a comparable solution. Furthermore, the execution time was computed to compare how long it takes each algorithm to perform the optimization process excluding the preprocessing step. It is noted that, due to the sequential nature of BO, a single fitness evaluation is the same as one iteration. This is in contrast to the other metaheuristic algorithms, which consider 15 fitness evaluations to be one iteration. To normalize this metric, 15 fitness evaluations were thus grouped as one iteration in the BO algorithm.
5. Results and Discussion
The performance of the SDSGA is compared to other metaheuristic algorithms in this section, both on the different benchmark functions and for fine-tuning the hyperparameters of two ML models. For the performance comparison of the benchmark functions, metrics such as mean accuracy and mean standard deviation were used for comparison. For tuning the hyperparameters of the two ML models, metrics such as accuracy, number of function evaluations, and execution time were used to make comparisons.
5.1. Effect of the Population Size on SDSGA Performance
This section discusses how the proposed SDSGA performs when different percentages P of the total population size were chosen as the number of parents, ranging from 10% to 90% with a 10% increment, when applied to the benchmark test functions, as well as how the considered ML models, namely the random forest and the CNN performed when trained on the MNIST and UCI datasets. Following Figure 4, the total number of best results recorded across the entire benchmark functions by the SDSGA was 13 at both and parent sizes.
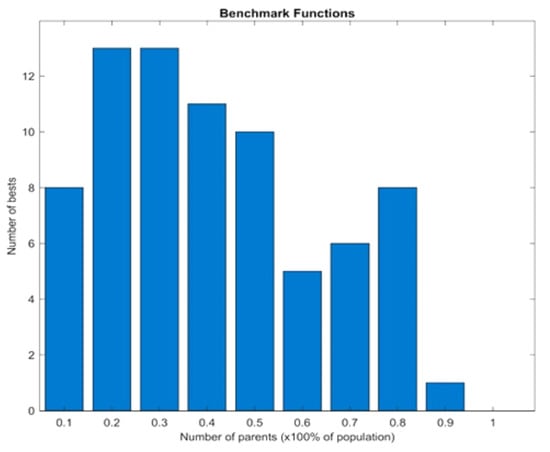
Figure 4.
Effect of varying the parent size.
The least performance was at , which may be attributed to the fact that almost the entire population was considered as parents, thus effectively reducing the chance for exploitation through recombination. Furthermore, the fact that the 20% and 30% parent sizes yielded the same number of the best outcomes shows that there were no statistical differences between the two parent sizes. As a result, selecting any of the two parent sizes will result in the same performance. Summarily, Figure 4 simply indicates that the SDSGA achieves the best performance in 13 of the benchmark functions when the parent size was set to 20% and 30% of the total population.
A similar study was performed on some UCI datasets, and it was discovered that a parent size of 20 and 30% yielded the best results when applied to different datasets, as shown in Figure 5. Nonetheless, we see a minor improvement in performance by the proposed SDSGA when a parent size of 20% was chosen and implemented on the LETTER and ADULT datasets as opposed to 30%. In the instance of the LETTER dataset, there was a modest improvement in accuracy from around 96.5% for a parent size of 30% to about 96.52% for the size of 20%, and, similarly, about 85.88% was recorded for the parent size of 20% compared to 85.86% recorded for the 30% parent size (see Figure 5). We should point out that the little change may not be statistically significant. As a result, the parent size of either 20 or 30% can be selected for evaluating the SDSGA.
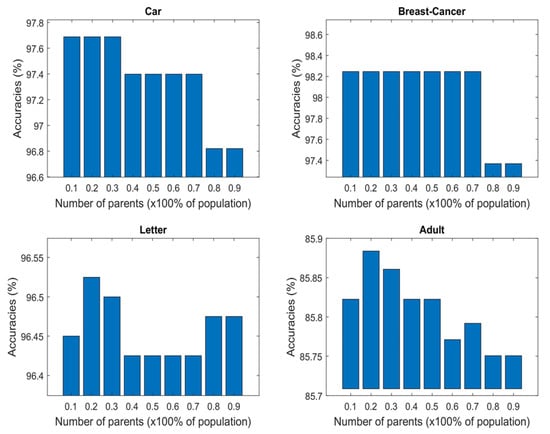
Figure 5.
Comparison of accuracy of the UCI datasets under varying parent population percentages.
5.2. Comparison and Evaluation of Optimization Algorithms on Benchmark Function
Table 2 shows the result of running the SDSGA on 17 benchmark functions and comparing its performance with that of the GA, PSO and BBO algorithms. The light green color in the table was used to highlight the best mean values per function, while the light brown color highlighted the highest standard deviation values. Table 2 shows that the developed SDSGA performed better than the three compared algorithms in terms of accuracy in 65% of the benchmark functions. In some cases where the SDSGA did not perform as well as other algorithms used for comparison, the standard deviation shows that the result does not deviate too far from the global optimum and that its results are stable across runs.

Table 2.
Result of comparison of metaheuristic algorithms on benchmark functions in 10D.
This is evident in the Griewank function results in Table 2 where it is noted that, while the SDSGA is not the best performing algorithm, its standard deviation is the best. Furthermore, when it came to optimizing the KTablet function, the GA came out on top in terms of both mean best solution and standard deviation (=, =). The SDSGA (=1.09 , =) is not far from the GA when compared to both BBO (, ) and PSO (, ).
5.3. CNN on the MNIST Dataset
This section summarizes the performance accuracy obtained when each of the optimization technique (SDSGA, GA, PSO, BBO and BO) were used to tune the HPs of the CNN on MNIST datasets. Due to the use of an early stopping strategy during the model training, if no further improvement is achieved, the execution time becomes a poor metric of evaluation. As an example, we discovered that, if the validation accuracy has not increased to 70% after three epochs of training, it fails to reach 90% even after 10 to 20 epochs. As a result, continuing to use such HP combinations wastes computational resources. Therefore, a better approach to measure the performance entailed selecting a baseline validation accuracy and comparing how many iterations it takes the algorithms to give such results. Table 3 shows the results of optimizing the CNN model on the MNIST dataset. It was observed that the BO algorithm performed the least with a value of 99.14%, which is slightly less than the PSO algorithm at 99.15% while the SDSGA performed the best with an average value of about 99.2% (see Table 3). Similarly, the BBO algorithm recorded the next best in terms of performance with about 99.18%, while the GA performed at 99.17%. Furthermore, it was discovered that the differences between the optimization algorithms are not significant. This could be due to the number of fitness evaluations chosen as 150 or it could be due to the optimal accuracy of the ML model having plateaued around that value. Nonetheless, we discovered that increasing the number of fitness evaluations beyond 150 resulted in no further improvement in the results.

Table 3.
Result of optimizing the CNN model on the MNIST dataset. The data have been prepared to show the best accuracy so far.
The BO algorithm performed the worst in terms of the number of fitness evaluations required for the algorithms to reach optimal, with 99.14% at the tenth iteration. This means that the BO had performed 150 fitness evaluations to reach this value. The best performing algorithm was the SDSGA, which achieved an accuracy of 99.2% at the fifth iteration. The BBO algorithm performed the next best and achieved an accuracy of 99.18% at the ninth iteration, whereas the GA achieved 99.17% at the second iteration. The accuracy of the BBO algorithm shows that it performed better than the GA and PSO algorithm. Despite gradually improving, its results have been consistently optimal across all runs. Figure 6 depicts a graph of the optimization algorithms’ accuracy as iteration progresses.
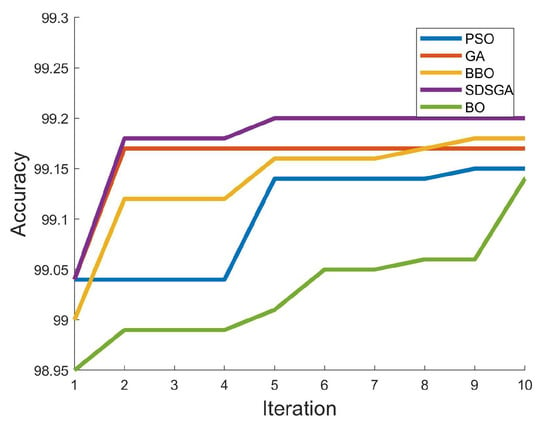
Figure 6.
Validation accuracy of CNN model as iteration progresses.
5.4. Random Forest on UCI Datasets
Table 4 shows the performance of the four metaheuristic algorithms when optimizing the hyperparameters of random forest (RF) model based on four UCI datasets. The “Time” column shows the execution time, the column “Best Pos” shows the values of the best hyperparameters after the optimization run. The column “Best Sol” is the accuracy obtained for that run when using the best hyperparameters for that run. The “Iter” column shows the number of iterations it takes for the algorithm to arrive at that accuracy. The variation of the prediction accuracies for all the optimization algorithms is shown in Figure 7.

Table 4.
Performance of the metaheuristic-based algorithms on RF trained on four different UCI datasets.
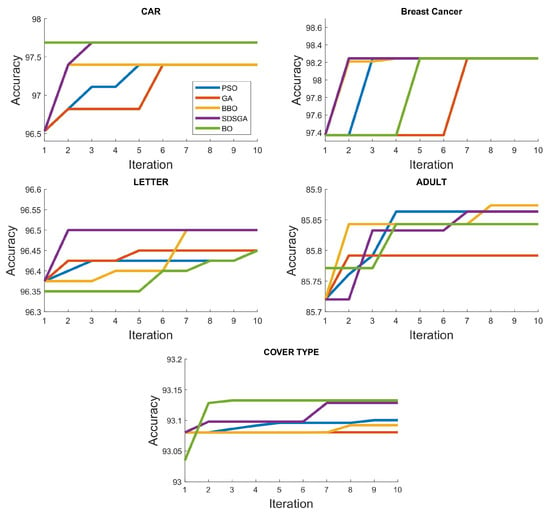
Figure 7.
Prediction accuracy for the different algorithms under the different UCI datasets.
We present in Table 4 the results obtained when training the RF model on five UCI datasets using the BO, SDSGA, GA, PSO and BBO algorithms to tune the HPs. In some cases, the best solution obtained by each optimization algorithm (BO, SDSGA, GA, PSO and BBO) was the same as demonstrated by the Breast Cancer dataset, where all optimization algorithms achieved an accuracy of 98.246% despite being obtained under different HPs values (see Table 4B). This is because the multiple hyperparameter combinations produced the same validation accuracy in this problem. Because the outcome is heavily dependent on the initial population, this can have a significant impact on the efficiency of metaheuristic optimization algorithms.
In the CAR dataset (Table 4A), it is noticed that both the BO and SDSGA algorithms performed the best at 97.688% while the rest of the optimization algorithms performed the same at a slightly lower value of 97.399%. In the LETTER dataset, SDSGA and BBO performed the best at 96.5%, whereas the BO, GA and PSO algorithms performed equally at 96.45%. The BBO algorithm performed better than the other algorithms in the ADULT dataset at 85.87%, whereas the PSO and SDSGA algorithms were tied at 85.86%. The BO algorithm performed at 85.843%, while GA performed the worst at 85.79%. The COVER TYPE dataset had the largest variation in accuracy with BO performing the best at 93.133%, whereas the SDSGA performed at 93.129%. The performance of the PSO is a little closer at 93.1%, BBO at 93.092% and the GA performed the least at 93.081%. From the hyperparameters of the Cover Type dataset (Table 4E), it was observed that the random forest algorithm’s accuracy can still be improved by increasing both m and n as those hyperparameters near the edges tend to have higher accuracies.
The time column in Table 4 refers to the time it takes to execute the whole optimization run excluding the preprocessing step. Here, it can be observed that, while there is no consistent pattern, the SDSGA performed the best in the three datasets (BREAST CANCER, LETTER and ADULT). Especially in the case of the LETTER dataset, where it took 422 s, or roughly half the time it took the PSO algorithm to execute at (787 s). We note that the PSO algorithm performed the best in terms of its execution time at 14.02 s when used to optimize the CAR dataset. This may be because the CAR dataset is the lightest and least complicated of the datasets considered. However, the BO algorithm at 79.47 s performed the worst with a large margin in the CAR dataset as compared to the BBO algorithm, which comes next at 38.5 s. We also note that the execution time of GA was close to that of SDSGA in three of the datasets (CAR, BREAST CANCER and LETTER) except in the case of ADULT and COVER TYPE datasets where they are very far apart. The SDSGA performed uncharacteristically poorly in the COVER TYPE dataset. This could be attributed to the population’s low diversity which makes it difficult for the selection algorithm to find suitable non-duplicate chromosomes to be selected as parents. This issue can be solved by using a different random seed or increasing the probability of mutation.
The Iter column in Table 4 refers to the number of iterations it took to get the best solution. Because the optimal value is unknown in advance in this optimization problem, it is impossible to predict the number of iterations or fitness evaluations. What determines this is the budget such as the amount of time or number of fitness evaluations available for the optimization to be completed in hopes of obtaining a nearly optimal value within this budget.
It has been observed that, because metaheuristic optimization algorithms are population-based, if the hyperparameter space is not large enough, these algorithms will converge very quickly to the optimal values. Because of its sequential nature, the BO tends to approach optimal values gradually. The progression of the BO algorithm in Figure 7 shows a straight line for the car dataset. This is due to the fact that the BO algorithm achieved its best solution during the first 15 fitness evaluations. Following that, it never achieved a higher value in any of the subsequent evaluations. It is observed in the BREAST CANCER dataset that, despite all algorithms being convergent to the same accuracy value, the number of iterations required to achieve this accuracy varies as it does in the other datasets. We note that GA’s remains average across all datasets, in contrast to the proposed SDSGA, which performed competitively well against the other optimization algorithms.
6. Conclusions
An improved GA called the simple deterministic selection genetic algorithm (SDSGA) with highly exploitative capabilities has been developed for hyperparameter optimization of machine learning (ML) models. To accomplish this, the GA selection algorithm was modified so that only the populations with the highest fitness are allowed to perform recombination/crossover as parents. In order to prevent drastic decrease in the diversity of the population, constraints were introduced to ensure that all chromosomes remain unique within the parent population. To increase the diversity further, the SDSGA was designed to have a high support for high mutation probability. The SDSGA was created to allow for high accuracy search for hyperparameters in machine learning models when time is limited. The optimization results of the proposed method on benchmark functions were compared with that of the GA, PSO and BBO algorithms, and the results obtained show that, overall, the SDSGA performed better than the other algorithms in 65% of the benchmark functions in terms of mean accuracy, albeit marginally. It is worth noting that the BBO algorithm performed the worst in all of the test functions evaluated herein. This is not necessarily due to the BBO being inferior as other factors such as the type of function and parameters used may have contributed for performance degradation. The comparison of the SDSGA with other optimization algorithms including the BO algorithm showed that our improved GA performed well, particularly in optimizing the CNN model on the MNIST dataset with an accuracy of 99.2%. For the case of the random forest model, our SDSGA performed marginally better than the other algorithms in most cases except in few cases where the PSO performed best, particularly on the CAR dataset in terms of its execution time. Despite this, we note that the better performances of our method, albeit marginally, were achieved at faster computing times than the other methods, emphasizing the proposed method’s advantage. It is possible to compare the SDSGA with other popular metaheuristic algorithms such as the artificial bee colony (ABC), differential evolution (DE), covariance matrix adaptation evolutionary strategy (CMA-ES), and the grey wolf optimization (GWO) algorithms for hyperparameter tuning of ML models, which serves to provide a direction for further research. Additionally, its consistency can be tested on high-dimensional spaces and multi-objective problems to determine how well it performs in these environments.
Author Contributions
I.D.R., H.B.-S., I.J.U., A.J.O., M.A.A. and A.T.S. contributed equally to this work. Conceptualization, H.B.-S., I.D.R., I.J.U. and A.J.O.; methodology, H.B.-S. and I.D.R.; writing—original draft preparation, H.B.-S. and I.D.R.; writing—review and editing, H.B.-S., A.J.O., M.A.A. and A.T.S.; supervision, H.B.-S., A.J.O., M.A.A. and A.T.S.; funding acquisition, M.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Khurana, D.; Koli, A.; Khatter, K.; Singh, S. Natural Language Processing: State of The Art, Current Trends and Challenges. arXiv 2017, arXiv:1708.05148. [Google Scholar]
- Friedman, C.; Rindflesch, T.C.; Corn, M. Natural language processing: State of the art and prospects for significant progress, a workshop sponsored by the National Library of Medicine. J. Biomed. Inform. 2013, 46, 765–773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, Z.A.; Feng, Z.; Irfan Uddin, M.; Mast, N.; Shah, S.A.A.; Imtiaz, M.; Al-Khasawneh, M.A.; Mahmoud, M. Optimal policy learning for disease prevention using reinforcement learning. Sci. Prog. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Mendoza, H.; Klein, A.; Feurer, M.; Springenberg, J.T.; Hutter, F. Towards Automatically-Tuned Neural Networks. In Automated Machine Learning; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; Volume Part F128815, pp. 847–855. [Google Scholar] [CrossRef]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. BI-Population CMA-ES Algorithms with Surrogate Models and Line Searches. In Proceedings of the 15th Annual Conference Companion on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 1177–1184. [Google Scholar] [CrossRef]
- Yu, T.; Zhu, H. Hyper-Parameter Optimization: A Review of Algorithms and Applications. arXiv 2020, arXiv:2003.05689. [Google Scholar]
- Levesque, J.C.; Durand, A.; Gagne, C.; Sabourin, R. Bayesian optimization for conditional hyperparameter spaces. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 286–293. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms. In Proceedings of the 12th Python in Science Conference, Austin, TX, USA, 24–29 June 2013; pp. 13–19. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. CMA-ES for Hyperparameter Optimization of Deep Neural Networks. arXiv 2016, arXiv:1604.07269. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Wang, J.; Xu, J.; Wang, X. Combination of Hyperband and Bayesian Optimization for Hyperparameter Optimization in Deep Learning. arXiv 2018, arXiv:1801.01596. [Google Scholar]
- Jin, H.; Song, Q.; Hu, X. Auto-keras: An efficient neural architecture search system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1946–1956. [Google Scholar] [CrossRef] [Green Version]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 4, 2951–2959. [Google Scholar]
- Li, L.; Jamieson, K.; Rostamizadeh, A.; Gonina, E.; Hardt, M.; Recht, B.; Talwalkar, A. A System for Massively Parallel Hyperparameter Tuning. arXiv 2018, arXiv:1810.05934. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2018, 18, 6765–6816. [Google Scholar]
- Jamieson, K.; Talwalkar, A. Non-stochastic best arm identification and hyperparameter optimization. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, AISTATS 2016, Cadiz, Spain, 9–11 May 2016; pp. 240–248. [Google Scholar]
- Klein, A.; Falkner, S.; Bartels, S.; Hennig, P.; Hutter, F. Fast Bayesian hyperparameter optimization on large datasets. Electron. J. Stat. 2017, 11, 4945–4968. [Google Scholar] [CrossRef]
- Friedrichs, F.; Igel, C. Evolutionary tuning of multiple SVM parameters. Neurocomputing 2005, 64, 107–117. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y. Hyper-parameter estimation method with particle swarm optimization. arXiv 2020, arXiv:2011.11944. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing convolutional neural network hyperparameters by enhanced swarm intelligence metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Gondro, C.; Reid, K.; Steibel, J.P. Heuristic hyperparameter optimization of deep learning models for genomic prediction. G3 Genes Genomes Genet. 2021, 11, 398800. [Google Scholar] [CrossRef]
- Lorenzo, P.R.; Nalepa, J.; Ramos, L.S.; Pastor, J.R. Hyper-parameter selection in deep neural networks using parallel particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017; pp. 1864–1871. [Google Scholar] [CrossRef]
- Mantovani, R.G.; Horvath, T.; Cerri, R.; Vanschoren, J.; De Carvalho, A.C. Hyper-Parameter Tuning of a Decision Tree Induction Algorithm. In Proceedings of the 2016 5th Brazilian Conference on Intelligent Systems (BRACIS), Recife, Brazil, 9–12 October 2016; pp. 37–42. [Google Scholar] [CrossRef]
- Tani, L.; Rand, D.; Veelken, C.; Kadastik, M. Evolutionary algorithms for hyperparameter optimization in machine learning for application in high energy physics. Eur. Phys. J. C. 2021, 81, 1–9. [Google Scholar] [CrossRef]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Auto-sklearn: Efficient and Robust Automated Machine Learning. In Automated Machine Learning; Springer International Publishing: Berlin, Germany, 2019; pp. 113–134. [Google Scholar] [CrossRef] [Green Version]
- Kotthoff, L.; Thornton, C.; Hoos, H.H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA. In Automated Machine Learning; Springer International Publishing: Berlin, Germany, 2019; pp. 81–95. [Google Scholar] [CrossRef] [Green Version]
- Zimmer, L.; Lindauer, M.; Hutter, F. Auto-Pytorch: Multi-Fidelity MetaLearning for Efficient and Robust AutoDL. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3079–3090. [Google Scholar] [CrossRef]
- Bhandari, D.; Murthy, C.A.; Pal, S.K. Genetic Algorithm with Elitist Model and ITS Convergence. Int. J. Pattern Recognit. Artif. Intell. 1996, 10, 731–747. [Google Scholar] [CrossRef]
- Liang, Y.; Leung, K.S. Genetic Algorithm with adaptive elitist-population strategies for multimodal function optimization. Appl. Soft Comput. 2011, 11, 2017–2034. [Google Scholar] [CrossRef]
- Aibinu, A.M.; Bello Salau, H.; Rahman, N.A.; Nwohu, M.N.; Akachukwu, C.M. A novel Clustering based Genetic Algorithm for route optimization. Eng. Sci. Technol. Int. J. 2016, 19, 2022–2034. [Google Scholar] [CrossRef] [Green Version]
- Bello-Salau, H.; Aibinu, A.M.; Wang, Z.; Onumanyi, A.J.; Onwuka, E.N.; Dukiya, J.J. An optimized routing algorithm for vehicle ad-hoc networks. Eng. Sci. Technol. Int. J. 2019, 22, 754–766. [Google Scholar] [CrossRef]
- Allawi, Z.T.; Ibraheem, I.K.; Humaidi, A.J. Fine-tuning meta-heuristic algorithm for global optimization. Processes 2019, 7, 657. [Google Scholar] [CrossRef] [Green Version]
- Arıcı, F.; Kaya, E. Comparison of Meta-heuristic Algorithms on Benchmark Functions. Acad. Perspect. Procedia 2019, 2, 508–517. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2323. [Google Scholar] [CrossRef] [Green Version]
- Frank, A.; Asuncion, A. UCI Machine Learning Repository; University of California: Irvine, CA, USA, 2010. [Google Scholar]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Eberhart; Shi, Y. Eberhart; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), Seoul, Korea, 27–30 May 2001; Volume 1. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D.; Siarry, P.; Yang, Z.; Fei, M. Biogeography-Based Optimization: A 10-Year Review. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 391–407. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications [in engineering design]. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Singh, V.K.; Sharma, V. Elitist Genetic Algorithm Based Energy Balanced Routing Strategy to Prolong Lifetime of Wireless Sensor Networks. Chin. J. Eng. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2009, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Loh, W. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Zhang, L.; Suganthan, P.N. Oblique Decision Tree Ensemble via Multisurface Proximal Support Vector Machine. IEEE Trans. Cybern. 2015, 45, 2165–2176. [Google Scholar] [CrossRef] [PubMed]
- Menze, B.H.; Kelm, B.M.; Splitthoff, D.N.; Koethe, U.; Hamprecht, F.A. On Oblique Random Forests; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef] [Green Version]
- Katuwal, R.; Suganthan, P.N.; Zhang, L. Heterogeneous oblique random forest. Pattern Recognit. 2020, 99, 107078. [Google Scholar] [CrossRef]
- Bai, J.; Li, Y.; Li, J.; Yang, X.; Jiang, Y.; Xia, S.T. Multinomial random forest. Pattern Recognit. 2022, 122, 108331. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).