Reconstruction of Epidemiological Data in Hungary Using Stochastic Model Predictive Control
Abstract
:1. Introduction
Notations and Abbreviations
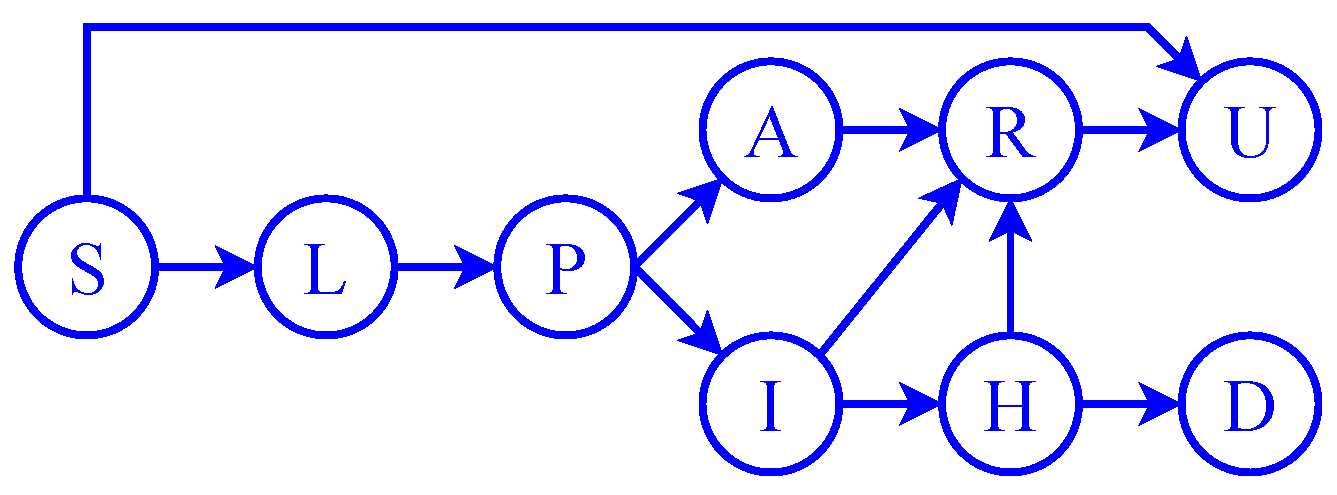
2. Compartmental Model of the Spread of the COVID-19 Epidemic in Hungary
2.1. Transitions between the Phases of the Disease
2.2. Vaccination Model
With this simplification, the people in the and compartments do not transmit the disease any more, as well as those who are still in the hospital. It is worth remarking that a positive IgG test does not necessarily ensure immunity in this sense. Serological tests suggest that even a relatively high IgG level does not exclude the possibility of reinfection [59].an individual is said to be immune to the disease if he/she will not be infected within the modeled time horizon.
2.3. Computing the Reproduction Number
2.4. Available Measurements
3. Optimization-Based Reconstruction of Past Epidemiological Data
State-Space Model Representation and Problem Statement
4. Statistical Analysis for Normally Distributed Model Parameters
4.1. Gaussian Assumptions
4.2. Closed-Loop Control Policy
4.3. Probabilistic Cost and Input Constraint
4.4. Linear Approximation of the State Dynamics around the Expectation
4.5. Initial Solution for the -NMPC Problem
| Algorithm 1 Computing a pseudo-optimal solution for Problem 2. |
|
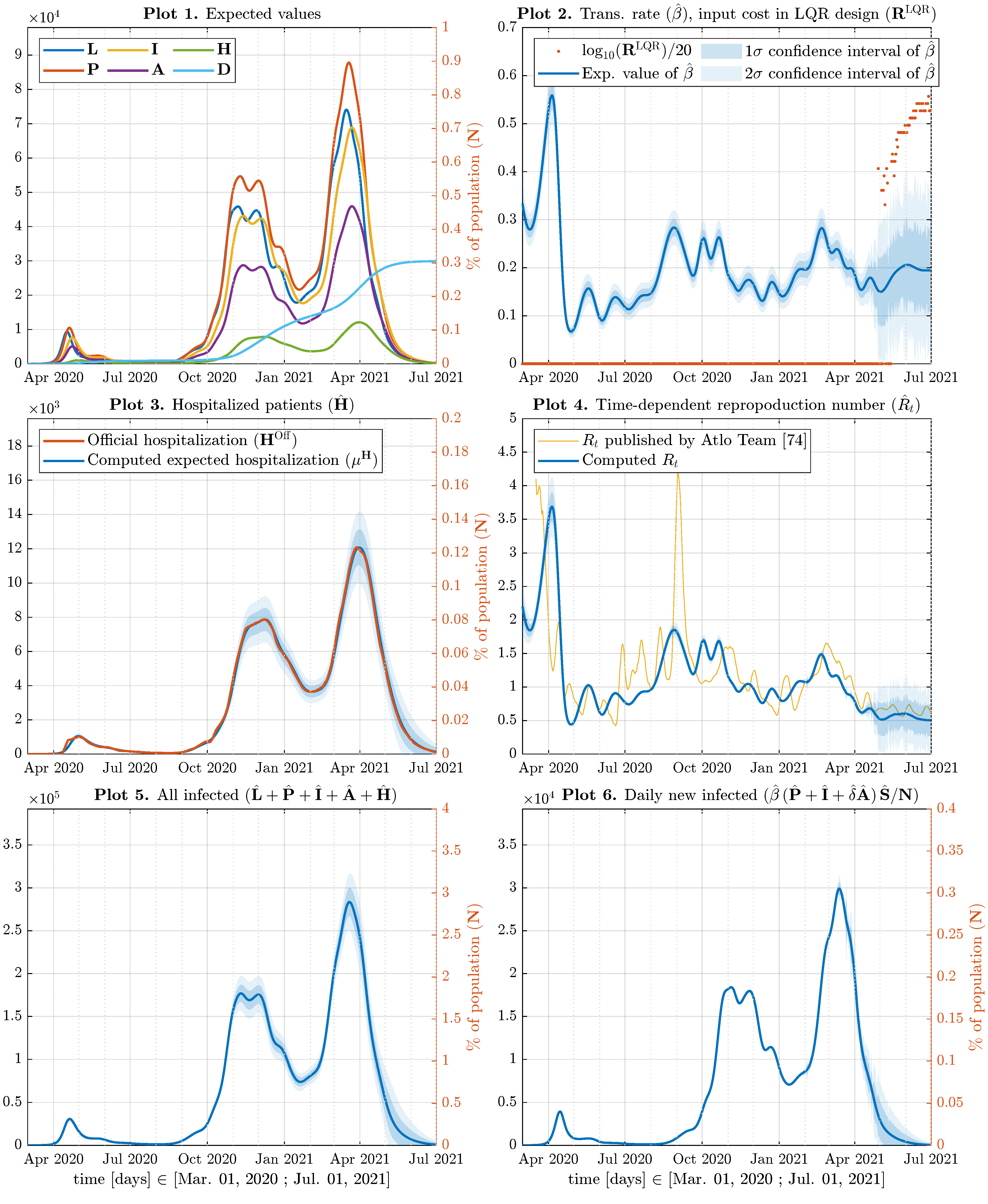
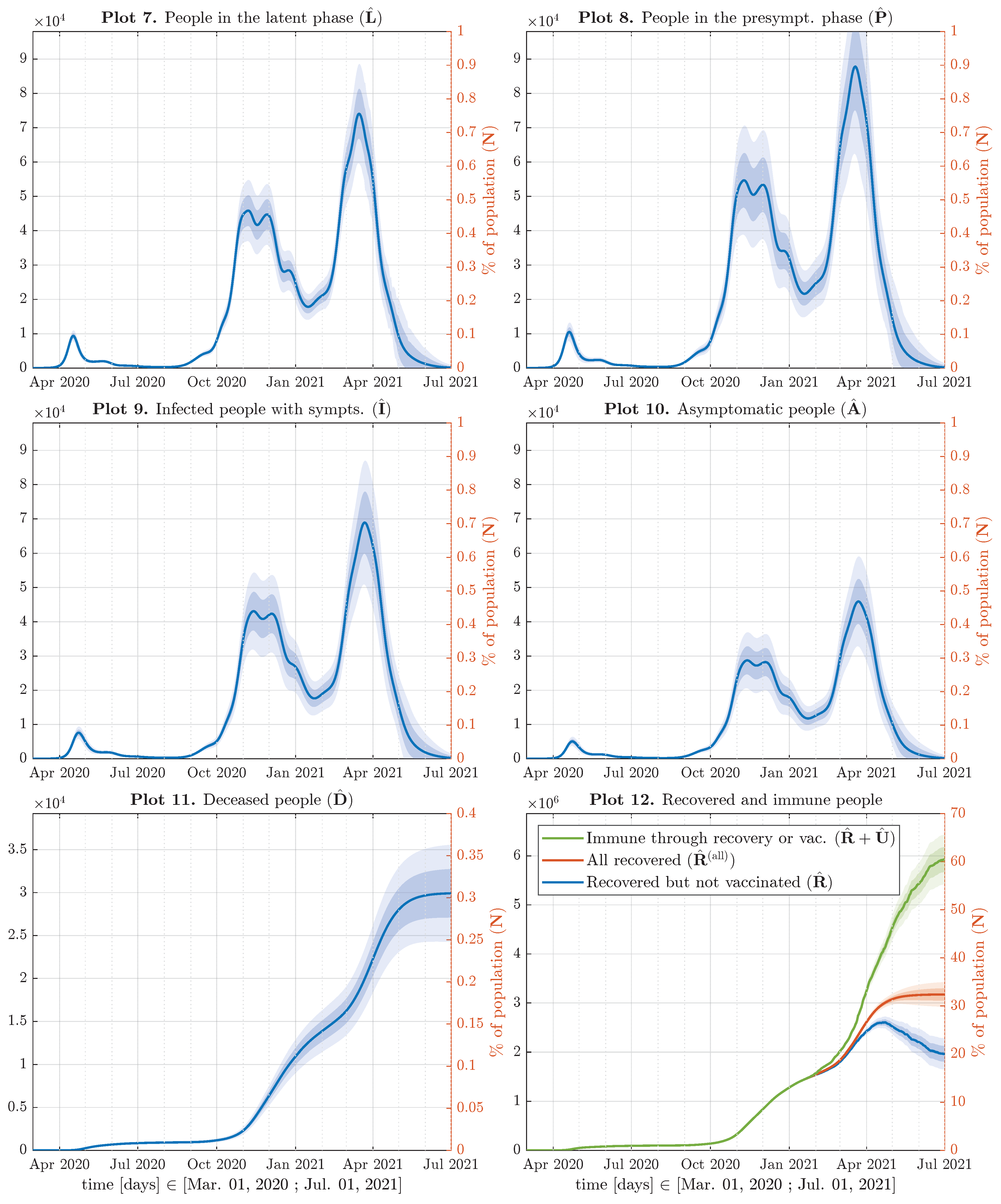
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SEIR | Susceptible–exposed–infected–recovered (compartmental model) |
| IgG | Immunoglobulin G |
| CT | Continuous-time |
| DT | Discrete-time |
| ODE | Ordinary differential equation |
| i.i.d. | Independent identically distributed |
| LTI | Linear time-invariant |
| MPC | Model predictive controller |
| NMPC | Nonlinear model predictive controller |
| SNMPC | Stochastic nonlinear model predictive controller |
| LQR | Linear quadratic regulator |
| -… | Mean-variance equations/dynamics/recursion/prediction model/NMPC |
| -NMPC | Mean-variance nonlinear model predictive controller |
Appendix A
References
- Miller, I.F.; Becker, A.D.; Grenfell, B.T.; Metcalf, C.J.E. Disease and healthcare burden of COVID-19 in the United States. Nat. Med. 2020, 26, 1212–1217. [Google Scholar] [CrossRef] [PubMed]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Terry, S.J. COVID-Induced Economic Uncertainty; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar] [CrossRef]
- Cao, L.; Liu, Q.; Hou, W. COVID-19 modeling: A review. arXiv 2021, arXiv:2104.12556. [Google Scholar]
- Shinde, G.R.; Kalamkar, A.B.; Mahalle, P.N.; Dey, N.; Chaki, J.; Hassanien, A.E. Forecasting models for coronavirus disease (COVID-19): A survey of the state-of-the-art. SN Comput. Sci. 2020, 1, 197. [Google Scholar] [CrossRef] [PubMed]
- Biswas, M.H.A.; Paiva, L.T.; de Pinho, M. A SEIR model for control of infectious diseases with constraints. Math. Biosci. Eng. 2014, 11, 761–784. [Google Scholar] [CrossRef]
- Brauer, F. Compartmental models in epidemiology. In Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 19–79. [Google Scholar] [CrossRef]
- He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Röst, G.; Bartha, F.A.; Bogya, N.; Boldog, P.; Dénes, A.; Ferenci, T.; Horváth, K.J.; Juhász, A.; Nagy, C.; Tekeli, T.; et al. Early phase of the COVID-19 outbreak in Hungary and post-lockdown scenarios. Viruses 2020, 12, 708. [Google Scholar] [CrossRef]
- Rajabi, A.; Mantzaris, A.V.; Mutlu, E.C.; Garibay, O.O. Investigating dynamics of COVID-19 spread and containment with agent-based modeling. Appl. Sci. 2021, 11, 5367. [Google Scholar] [CrossRef]
- Reguly, I.Z.; Csercsik, D.; Juhasz, J.; Tornai, K.; Bujtar, Z.; Horvath, G.; Keomley-Horvath, B.; Kos, T.; Cserey, G.; Ivan, K.; et al. Microsimulation based quantitative analysis of COVID-19 management strategies. PLoS Comput. Biol. 2022, 18, 1–14. [Google Scholar] [CrossRef]
- Rzadkowski, G.; Figlia, G. Logistic wavelets and their application to model the spread of COVID-19 pandemic. Appl. Sci. 2021, 11, 8147. [Google Scholar] [CrossRef]
- Lalmuanawma, S.; Hussain, J.; Chhakchhuak, L. Applications of machine learning and artificial intelligence for COVID-19 (SARS-CoV-2) pandemic: A review. Chaos Solitons Fractals 2020, 139, 110059. [Google Scholar] [CrossRef] [PubMed]
- Satu, M.; Howlader, K.C.; Mahmud, M.; Kaiser, M.S.; Shariful Islam, S.M.; Quinn, J.M.W.; Alyami, S.A.; Moni, M.A. Short-term prediction of COVID-19 cases using machine learning models. Appl. Sci. 2021, 11, 4266. [Google Scholar] [CrossRef]
- Ghafouri-Fard, S.; Mohammad-Rahimi, H.; Motie, P.; Minabi, M.; Taheri, M.; Nateghinia, S. Application of machine learning in the prediction of COVID-19 daily new cases: A scoping review. Heliyon 2021, 7, e08143. [Google Scholar] [CrossRef] [PubMed]
- Gostic, K.M.; McGough, L.; Baskerville, E.B.; Abbott, S.; Joshi, K.; Tedijanto, C.; Kahn, R.; Niehus, R.; Hay, J.A.; De Salazar, P.M.; et al. Practical considerations for measuring the effective reproductive number, Rt. PLoS Comput. Biol. 2020, 16, e1008409. [Google Scholar] [CrossRef] [PubMed]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar] [CrossRef] [PubMed]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [Green Version]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Koyama, S.; Horie, T.; Shinomoto, S. Estimating the time-varying reproduction number of COVID-19 with a state-space method. PLoS Comput. Biol. 2021, 17, e1008679. [Google Scholar] [CrossRef] [PubMed]
- Tsay, C.; Lejarza, F.; Stadtherr, M.A.; Baldea, M. Modeling, state estimation, and optimal control for the US COVID-19 outbreak. Sci. Rep. 2020, 10, 10711. [Google Scholar] [CrossRef] [PubMed]
- Péni, T.; Csutak, B.; Szederkényi, G.; Röst, G. Nonlinear model predictive control with logic constraints for COVID-19 management. Nonlinear Dyn. 2020, 102, 1965–1986. [Google Scholar] [CrossRef] [PubMed]
- Csutak, B.; Polcz, P.; Szederkényi, G. Computation of COVID-19 epidemiological data in Hungary using dynamic model inversion. In Proceedings of the 15th IEEE International Symposium on Applied Computational Intelligence and Informatics (SACI 2021), Timișoara, Romania, 19–21 May 2021; pp. 91–96. [Google Scholar] [CrossRef]
- Sereno, J.; D’Jorge, A.; Ferramosca, A.; Hernandez-Vargas, E.; González, A. Model predictive control for optimal social distancing in a type SIR-switched model. IFAC-PapersOnLine 2021, 54, 251–256. [Google Scholar] [CrossRef]
- Phipps, S.J.; Grafton, R.Q.; Kompas, T. Robust estimates of the true (population) infection rate for COVID-19: A backcasting approach. R. Soc. Open Sci. 2020, 7, 200909. [Google Scholar] [CrossRef]
- Rocchetti, I.; Böhning, D.; Holling, H.; Maruotti, A. Estimating the size of undetected cases of the COVID-19 outbreak in Europe: An upper bound estimator. Epidemiol. Methods 2020, 9, 20200024. [Google Scholar] [CrossRef]
- Bartha, F.A.; Karsai, J.; Tekeli, T.; Röst, G. Symptom-based testing in a compartmental model of COVID-19. In Analysis of Infectious Disease Problems (COVID-19) and Their Global Impact; Springer: Berlin/Heidelberg, Germany, 2021; pp. 357–376. [Google Scholar] [CrossRef]
- Lemaitre, J.C.; Perez-Saez, J.; Azman, A.; Rinaldo, A.; Fellay, J. Assessing the impact of non-pharmaceutical interventions on SARS-CoV-2 transmission in Switzerland. Swiss Med. Wkly. 2020, 150, w20295. [Google Scholar] [CrossRef]
- Allgöwer, F.; Zheng, A. (Eds.) Nonlinear Model Predictive Control, 1st ed.; Progress in Systems and Control Theory 26; Birkhäuser Basel: Basel, Switzerland, 2000. [Google Scholar] [CrossRef]
- Apte, A.; Jones, C.K.R.T.; Stuart, A.M.; Voss, J. Data assimilation: Mathematical and statistical perspectives. Int. J. Numer. Methods Fluids 2008, 56, 1033–1046. [Google Scholar] [CrossRef]
- Bröcker, J. On variational data assimilation in continuous time. Q. J. R. Meteorol. Soc. 2010, 136, 1906–1919. [Google Scholar] [CrossRef] [Green Version]
- Schumann-Bischoff, J.; Parlitz, U.; Abarbanel, H.D.I.; Kostuk, M.; Rey, D.; Eldridge, M.; Luther, S. Basin structure of optimization based state and parameter estimation. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 053108. [Google Scholar] [CrossRef] [Green Version]
- Schumann-Bischoff, J.; Parlitz, U. State and parameter estimation using unconstrained optimization. Phys. Rev. E 2011, 84, 056214. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Kirkby, N.F.; Jena, R. Optimal dosing of cancer chemotherapy using model predictive control and moving horizon state/parameter estimation. Comput. Methods Programs Biomed. 2012, 108, 973–983. [Google Scholar] [CrossRef]
- Das, A. Chance-constrained optimization-based parameter estimation for Muskingum models. J. Irrig. Drain. Eng. 2007, 133, 487–494. [Google Scholar] [CrossRef]
- Das, A. Parameter estimation for Muskingum models. J. Irrig. Drain. Eng. 2004, 130, 140–147. [Google Scholar] [CrossRef]
- Al-Hemeary, N.; Polcz, P.; Szederkényi, G. Optimal solar panel area computation and temperature tracking for a cubesat system using model predictive control. SPIIRAS Proc. 2020, 19, 564–593. [Google Scholar] [CrossRef]
- Courtier, P.; Talagrand, O. Variational assimilation of meteorological observations with the direct and adjoint shallow-water equations. Tellus A Dyn. Meteorol. Oceanogr. 1990, 42, 531–549. [Google Scholar] [CrossRef] [Green Version]
- Blackmore, L.; Açıkmeşe, B.; Carson, J.M. Lossless convexification of control constraints for a class of nonlinear optimal control problems. Syst. Control Lett. 2012, 61, 863–870. [Google Scholar] [CrossRef]
- Mao, Y.; Szmuk, M.; Açıkmeşe, B. Successive convexification of non-convex optimal control problems and its convergence properties. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 3636–3641. [Google Scholar] [CrossRef] [Green Version]
- Andersson, J.; Gillis, J.; Diehl, M. User Documentation for CasADi v3.4.4. 2018. Available online: http://casadi.sourceforge.net/v3.4.4/users_guide/casadi-users_guide.pdf (accessed on 17 December 2021).
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2018, 11, 1–36. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2005, 106, 25–57. [Google Scholar] [CrossRef]
- Zanelli, A.; Domahidi, A.; Jerez, J.; Morari, M. Forces NLP: An efficient implementation of interior-point methods for multistage nonlinear nonconvex programs. Int. J. Control 2017, 93, 13–29. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic model predictive control: An overview and perspectives for future research. IEEE Control. Syst. Mag. 2016, 36, 30–44. [Google Scholar] [CrossRef] [Green Version]
- de la Penad, D.; Bemporad, A.; Alamo, T. Stochastic programming applied to model predictive control. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 1361–1366. [Google Scholar] [CrossRef]
- Bernardini, D.; Bemporad, A. Stabilizing model predictive control of stochastic constrained linear systems. IEEE Trans. Autom. Control 2012, 57, 1468–1480. [Google Scholar] [CrossRef] [Green Version]
- Thangavel, S.; Paulen, R.; Engell, S. Robust multi-stage nonlinear model predictive control using sigma points. Processes 2020, 8, 851. [Google Scholar] [CrossRef]
- Thangavel, S.; Paulen, R.; Engell, S. Dual multi-stage NMPC using sigma point principles. IFAC-PapersOnLine 2020, 53, 11243–11250. [Google Scholar] [CrossRef]
- Bonzanini, A.D.; Paulson, J.A.; Makrygiorgos, G.; Mesbah, A. Fast approximate learning-based multistage nonlinear model predictive control using Gaussian processes and deep neural networks. Comput. Chem. Eng. 2021, 145, 107174. [Google Scholar] [CrossRef]
- Ostafew, C.J.; Schoellig, A.P.; Barfoot, T.D. Conservative to confident: Treating uncertainty robustly within learning-based control. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 421–427. [Google Scholar] [CrossRef]
- Hewing, L.; Kabzan, J.; Zeilinger, M.N. Cautious model predictive control using Gaussian process regression. IEEE Trans. Control. Syst. Technol. 2020, 28, 2736–2743. [Google Scholar] [CrossRef] [Green Version]
- Candela, J.Q.; Girard, A.; Rasmussen, C.E. Prediction at an Uncertain Input for Gaussian Processes and Relevance Vector Machines Application to Multiple-Step Ahead Time-Series Forecasting; Technical Report IMM-2003-18; Technical University of Denmark: Kgs. Lyngby, Denmark, 2003. [Google Scholar]
- Deisenroth, M.P. Efficient Reinforcement Learning Using Gaussian Processes—Revised Version. Ph.D. Thesis, Faculty of Informatics, Institute for Anthropomatics, Intelligent Sensor-Actuator-Systems Laboratory (ISAS), Karlsruhe, Germany, 2017. [Google Scholar]
- de Moura, D.T.H.; McCarty, T.R.; Ribeiro, I.B.; Funari, M.P.; de Oliveira, P.V.A.G.; de Miranda Neto, A.A.; do Monte Júnior, E.S.; Tustumi, F.; Bernardo, W.M.; de Moura, E.G.H.; et al. Diagnostic characteristics of serological-based COVID-19 testing: A systematic review and meta-analysis. Clinics 2020, 75, e2212. [Google Scholar] [CrossRef] [PubMed]
- Merkely, B.; Szabó, A.J.; Kosztin, A.; Berényi, E.; Sebestyén, A.; Lengyel, C.; Merkely, G.; Karády, J.; Várkonyi, I.; Papp, C.; et al. Novel coronavirus epidemic in the Hungarian population, a cross-sectional nationwide survey to support the exit policy in Hungary. GeroScience 2020, 42, 1063–1074. [Google Scholar] [CrossRef]
- Sedaghat, A.; Oloomi, S.A.A.; Malayer, M.A.; Band, S.; Mosavi, A.; Nadai, L. Modeling and sensitivity analysis of coronavirus disease (COVID-19) outbreak prediction. In Proceedings of the 2020 IEEE 3rd International Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 18–19 November 2020; pp. 000261–000266. [Google Scholar] [CrossRef]
- Sedaghat, A.; Oloomi, S.A.A.; Malayer, M.A.; Band, S.; Rezaei, N.; Mosavi, A.; Nadai, L. Coronavirus (COVID-19) outbreak prediction using epidemiological models of Richards Gompertz Logistic Ratkowsky and SIRD. In Proceedings of the 2020 IEEE 3rd International Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 18–19 November 2020; pp. 000289–000298. [Google Scholar] [CrossRef]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S.; et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef]
- Hu, X.; Lindquist, A. Geometric Control Theory; Royal Institute of Technology: Stockholm, Sweden, 2012. [Google Scholar]
- González Cisneros, P.S.; Werner, H. Nonlinear model predictive control for models in quasi-linear parameter varying form. Int. J. Robust Nonlinear Control 2020, 30, 3945–3959. [Google Scholar] [CrossRef]
- Bemporad, A.; Ricker, N.L.; Morari, M.; Model Predictive Control Toolbox™User’s Guide (R2019b). MathWorks. 2019. Available online: https://www.mathworks.com/help/pdf_doc/mpc/mpc_ug.pdf (accessed on 17 December 2021).
- Data on COVID-19 Vaccination in the EU/EEA. Available online: https://www.ecdc.europa.eu/en/publications-data/data-covid-19-vaccination-eu-eea (accessed on 17 December 2021).
- Atlo Team. Koronamonitor: Hungarian Status of Coronavirus Vaccination. 2021. Available online: https://atlo.team/vakcinacio (accessed on 11 November 2021).
- Salath, M.; Althaus, C.L.; Neher, R.; Stringhini, S.; Hodcroft, E.; Fellay, J.; Zwahlen, M.; Senti, G.; Battegay, M.; Wilder-Smith, A.; et al. COVID-19 epidemic in switzerland: On the importance of testing, contact tracing and isolation. Swiss Med. Wkly. 2020. [Google Scholar] [CrossRef]
- Steinbrook, R. Contact tracing, testing, and control of COVID-19—Learning from Taiwan. JAMA Intern. Med. 2020, 180, 1163–1164. [Google Scholar] [CrossRef]
- Data on Hospital and ICU Admission Rates and Current Occupancy for COVID-19. 2021. Available online: https://www.ecdc.europa.eu/en/publications-data/download-data-hospital-and-icu-admission-rates-and-current-occupancy-covid-19 (accessed on 11 November 2021).
- Mesbah, A.; Streif, S.; Findeisen, R.; Braatz, R.D. Stochastic nonlinear model predictive control with probabilistic constraints. In Proceedings of the 2014 IEEE American Control Conference, Portland, OR, USA, 4–6 June 2014. [Google Scholar] [CrossRef]
- De Larminat, P. Analysis and Control of Linear Systems; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lorenzen, M.; Dabbene, F.; Tempo, R.; Allgöwer, F. Constraint-tightening and stability in stochastic model predictive control. IEEE Trans. Autom. Control 2017, 62, 3165–3177. [Google Scholar] [CrossRef] [Green Version]
- MathWorks. Control System Toolbox™Reference (R2021b). 2021. Available online: https://www.mathworks.com/help/pdf_doc/control/control_ref.pdf (accessed on 17 December 2021).
- Amestoy, P.; Duff, I.S.; Koster, J.; L’Excellent, J.Y. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–41. [Google Scholar] [CrossRef] [Green Version]
- Amestoy, P.; Buttari, A.; L’Excellent, J.Y.; Mary, T. Performance and scalability of the block low-rank multifrontal factorization on multicore architectures. ACM Trans. Math. Softw. 2019, 45, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Polcz, P.; Epidemiological Data Reconstruction for Hungary Using Stochastic Nonlinear MPC Computations. GitHub Repository. 2021. Available online: https://github.com/ppolcz/MPC-monitoring-for-COVID-19 (accessed on 17 December 2021).
- Atlo Team. Koronamonitor: Detailed Diagrams of the Coronavirus Outbreak. 2021. Available online: https://atlo.team/koronamonitor-reszletesadatok (accessed on 11 November 2021).
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.C.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, Á.; et al. Transmission of SARS-CoV-2 lineage B.1.1.7 in England: Insights from linking epidemiological and genetic data. medRxiv 2021. [Google Scholar] [CrossRef]
- Institute for Health Metrics and Evaluation. COVID-19 Results Briefing, European Union 1 July 2021. 2021. Available online: https://www.healthdata.org/sites/default/files/files/Projects/COVID/2021/4743_briefing_European_Union_23.pdf (accessed on 17 December 2021).
| Description | Nominal Value | Uncertainty |
|---|---|---|
| The population of Hungary | ||
| Inverse of … (1/day) | ||
| latent period | ||
| presymptomatic infectious period | ||
| infectious period of symptomatic individuals | ||
| infectious period of asymptomatic individuals | ||
| average length of hospitalization | ||
| Relative infectiousness of asymptomatic | ||
| Probability of developing symptoms | ||
| Hospitalization probability of symptomatic cases | ||
| Probability of fatal outcome (if already hospitalized) | ||
| Effectiveness of vaccination |
| Quantitative Properties of the Optimization | Problem 1 | Problem 2 |
|---|---|---|
| Total number of variables | 4869 | 70,614 |
| Number of variables with only lower bounds | 4383 | 4383 |
| Number of variables with lower and upper bounds | 486 | 486 |
| Total number of equality constraints | 4383 | 70,128 |
| Number of nonzeros in the Lagrangian Hessian | 10,826 | 386,575 |
| Number of iterations | 212 | 74 |
| Elapsed time (s) | 8 | 1187 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polcz, P.; Csutak, B.; Szederkényi, G. Reconstruction of Epidemiological Data in Hungary Using Stochastic Model Predictive Control. Appl. Sci. 2022, 12, 1113. https://doi.org/10.3390/app12031113
Polcz P, Csutak B, Szederkényi G. Reconstruction of Epidemiological Data in Hungary Using Stochastic Model Predictive Control. Applied Sciences. 2022; 12(3):1113. https://doi.org/10.3390/app12031113
Chicago/Turabian StylePolcz, Péter, Balázs Csutak, and Gábor Szederkényi. 2022. "Reconstruction of Epidemiological Data in Hungary Using Stochastic Model Predictive Control" Applied Sciences 12, no. 3: 1113. https://doi.org/10.3390/app12031113
APA StylePolcz, P., Csutak, B., & Szederkényi, G. (2022). Reconstruction of Epidemiological Data in Hungary Using Stochastic Model Predictive Control. Applied Sciences, 12(3), 1113. https://doi.org/10.3390/app12031113






