A Comparative Review of the Current Methods of Analysis and Design of Stiffened and Unstiffened Steel Liners

Abstract

There are significant levels of concern about both the safety assessment and financial evaluation of the whole hydropower system, especially at early project stages. In addition, there is a variety of reliable and accurate methods for analysis, design, and optimization of steel pressure liners in hydropower plants. Several countries have developed specific regulations and codes for the design, installation, and safety evaluation of under-pressure piping, as well as estimates of the potential risks associated with failure. This paper reviews the current methodologies and codes available for design and safety assessment of either unstiffened or stiffened pressure steel liners in hydropower plants. After examining the main guidelines and practical conclusions drawn from recent research in the field of liners subjected to either internal or external pressure, this article then discusses the relevant regulations and codes. The scope of this work is to summarize the advantages, disadvantages, and main characteristics of the existing design criteria, analysis methods, and other issues related to steel liners. Afterwards, this paper compares the main reliable formulations and modelling techniques, even the most recent or sophisticated ones. Lastly, we draw some conclusions regarding their accuracy and scope of applicability.

1. Introduction

Over the past decades, large hydroelectric power stations have been built worldwide, with many others currently at the project or construction stage. According to estimates, power installed at pumped-storage hydroelectric power stations is expected to increase significantly during the present decade. Such plants are often designed for high flow rates and heads, which entail large-diameter and high-pressure penstocks. The increasing development of new and large-scale hydropower projects has involved a renewed research effort over the past decade with specific attention being paid to pressure steel liners [1].

The suitability of steel liner design methods is a highly relevant issue for either the technical development of new hydroelectric projects or the safety assessment of existing hydroelectric power plants in operation for more than 50 years. The accuracy of formulations traditionally used for steel-liner design, both with and without stiffeners, under external pressure is questionable. In addition, these may yield either conservative or non-conservative results depending on their ranges of application. This has led to the development of more refined, reliable, and safer design and analysis methods during the past few years. Traditional design approaches previously only considered the existing gap between the steel liner and the encasing concrete and piping out-of-roundness as the most relevant geometric imperfections. However, little focus had been given to those imperfections caused either by welding or by wall-thickness loss in corroded areas.

The aims of this paper are to gather and compare the available methods for the design and the safety assessment of steel pressure liners in current hydropower plants.

2. Layout and Components of a Pressure Tunnel

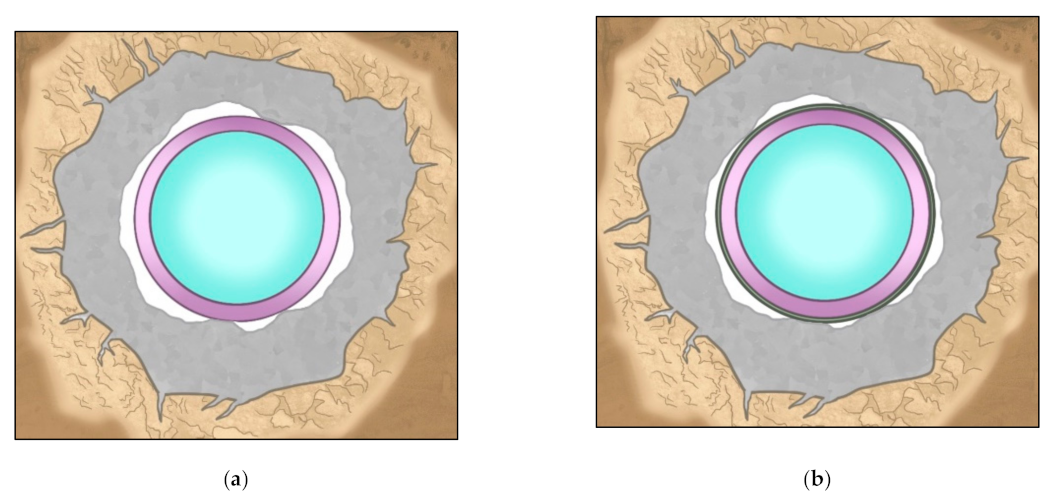
Figure 1 depicts the typical layout of a pressure tunnel and its components:

• Steel pressure liner that conveys water under pressure.
• Reinforced or mass-concrete backfill that encases the steel liner.
• An existing gap between the steel liner and the surrounding concrete.
• Grouted rock (if any) for either waterproofing or improvement of the terrain.
• Damaged rock that remains in place after blasting or excavation. The values of the outer radius of such zone may range between one and five times that of the piping. An estimate of the thickness of fissured rock may be from 0.3 to 1 m with the use of a tunnel borer and 1–2 m with blasting [1].
• Sound rock, usually assumed to be uniform, isotropic and elastic with a deformation modulus Er.
• Stiffeners that are attached to increase the moment of inertia of the pipe wall.
• Steel connectors anchored in concrete.

The main variables involved in the design of a steel liner have been compiled in

Table 1. Main variables involved in the design of a steel liner.

Main Variables
R	Liner Radius 1	Average value between the external and internal radius
D	Diameter	$D=2R$
t	Wall thickness of the liner
I	Moment of inertia of the stiffeners
g	Gap
L	Span length between stiffeners
Rfis	Radius of the fissured rock
Ec	Moduli of elasticity of the concrete backfill
Es	Moduli of elasticity of the steel
E′	Moduli of elasticity of the steel under plane strain assumption
fsy	Yield stress of the steel
Ps	Internal pressure absorbed by the steel liner
Pcr	Critical Buckling Pressure
ν	Poisson’s ratio
n	Number of lobes formed in a stiffened liner. It also indicates the buckling failure mode

¹ Also expressed as Rs by many authors.

and are indicated in Figure 2, and the main parameters are the following: $D/t$(the ratio between the diameter and wall-thickness of the pipeline), $L/D$ or $L/t$ (spacing between stiffeners), I (the moment of inertia of the stiffeners), the quality of the steel, $g/R$ (ratio between the initial gap and the pipe radius), and Ec/Es (between the moduli of elasticity of the concrete backfill and the steel liner). The usual values of the geometrical parameters are shown in

Table 2. Usual values of the geometrical parameters of a steel liner.

Parameter	Range
D/t	100–400
L/t	60–240
$g/R$	0.0003–0.001

. The influence of the different parameters was studied in depth by Wang et al. [2]. During this past decade, many authors have focused on analysing in depth these variables for their particular cases [3,4].

3. Types of Steel Liners

The project of a pressure tunnel involves a choice between an unstiffened liner with sufficient thickness and one thinner but with ring-stiffeners. Besides, using higher-strength steel is an additional option. The final design should draw on financial considerations and construction ease. Both types are depicted in Figure 3.

3.1. Unstiffened Liners

The liner consists of a steel cylindrical shell. It is often used when the external pressure is low and the minimum thickness imposed by transportation and installation is sufficient. It has the following advantages [5]:

• Design and calculation methods are developed with significant depth [6,7]
• Its outer diameter is smaller than that of a steel casing with stiffeners, by which the tunnel excavation diameter will be smaller.
• Implementation is simpler, especially for wall thicknesses less than 30 mm. For greater values, welds may be more complex and entail a higher financial cost.

Use of stiffeners for wall thicknesses $t$ greater than 38 mm is considered to be financially prudent. Up to such a thickness, the lining may be installed by using internal full-penetration welding, without any need to apply later thermal treatments to the weld (with medium- and low-strength steels).

3.2. Stiffened Liners

The stiffeners, which are equally-spaced installed along the pipe, are welded to its outer circumferential perimeter. They have the following advantages [1,5,8]:

• They provide the steel cylinder with greater rigidity and, depending on their shape, may bind the sheet steel to the concrete (thus behaving as connectors).
• Due to their greater moment of inertia, they are lighter than a liner with the same resistance capacity.

Figure 4 shows instability modes of liners with various degrees of spacing. The formation of a larger number of lobes (n) for closer spacing between the stiffeners may be noted.

4. Limitations to Stresses

Steel pressure liners have customarily been designed with a criterion that limits the allowable stress in the steel below 80% of yield strength (for thicknesses over 50 mm) and 90% for thinner cylinders.

The steel used in liners may be classified in the following categories: conventional steels with yield strength of up to 355 MPa, medium-strength steels with between 355 and 500 MPa, high-strength steels with between 500 and 690 MPa, and extra-high-strength steels for larger ones. However, in the existing national codes, there is no distinction between conventional and high-strength steels, which may be considered a non-conservative assumption [9].

The safety factors for allowable stress under water hammering conditions, given by Gordon [9], are shown in

Table 3. Safety factor for limiting steel stress, as proposed by Gordon (1978).

Design Criteria	Safety Factor
	Yield Strength	Ultimate Strength
Normal water hammering	1.67	2.63
Emergency water hammering	1.04	1.64

.

If the entire internal pressure is assumed to be withheld exclusively by the liner, the working stress is limited to 75–100% of the yield strength and 50–67% of the ultimate strength. However, if the contribution of rock and concrete backfill is considered in the model, the allowable working stress must lie between 33% of the ultimate strength and 67% of the yield stress [1]. Such criteria are practically equivalent.

5. Geometric Imperfections of the Liner

The majority of liners are highly sensitive to small imperfections, of which the following are most likely to affect their behavior in penstocks: the out-of-roundness of the liner, the existing gap between the liner and the surrounding concrete, circumferential weld-induced imperfections [10], those having emerged during manufacture, as well as localised dents, cracks, and reduced thicknesses in corroded areas. Pachoud [11] does a remarkable job at analysing the influence of geometrical imperfections and flaws at welds of steel liners on fatigue response of pressure tunnels and shafts in anisotropic rock.

5.1. Pipeline Ovality

In order to monitor the geometry of the liner, there are certain limitations in manufacturing and installation. The United States Army Corps of Engineers (USACE) [12] and the European Committee for Boilermaking and Kindred Steel Structures (Comité Européen de la Chaudronnerie et de la Tôlerie, CECT) [6] in large-diameter liners allow a degree of geometric imperfection of approximately 0.25% of the radius. In many cases, a temporary support such as spider bracing is used. These braces are adjustable in order to obtain the required circularity during the setting of the backfill concrete.

5.2. The Gap g

The gap between the liner and the encasing concrete can originate from diverse causes, such as the effects of heat during concrete hardening, retraction, and temperature changes in steel and concrete during construction, as well as changes in ambient temperature due to either natural or forced ventilation in the tunnel or execution difficulties during the constructive process. Its span g can range from 0 to 0.001 times the tunnel radius R depending on various factors. In

Table 4. Recommended values of the gap g between the liner and the encasing concrete.

Regulation	Conditions		Recommended Gap (g)
USACE [12]	Initial		0 < g < 0.001 R
	Initial		0.0002 R < g < 0.001 R
CECET [6]	In service	Highly compacted rock	g ≥ 0.0002 R (0.0005 R)
	In service	Cracked rock without injection	g = 0.0010 R
	In service	Steel liner highly subjected to internal pressure	g ≥ 0.0007 R

, the initial values are provided by European and United States regulations, according to the radius of the tunnel.

6. Actions to Consider in Calculations Associated with Pressure Penstocks

Safety assessment of a pressure liner encompasses the following issues:

• Examination of its stress response to internal pressure (including water hammering).
• Analysis of its stability and mechanical capacity when subjected to external pressure (either hydrostatic or grouting pressures in the backfill).
• Verification of the resistance of the surrounding rock. This involves the application of the theory of rock mechanics (not considered in this study).

6.1. Internal Pressure

The methodology provided by the USACE [12] is compared with that offered by Jacobsen [13]. Both formulations consider a distribution of internal pressure between the liner and the rock mass based on the assumption of displacement compatibility. The parameters that condition such a distribution are the following: the ratio of the concrete backfill and the steel liner moduli of elasticity, the existing gap between the liner and the concrete, and the relationship between the liner radius $Rs$ and that of the fissured rock Rfis.

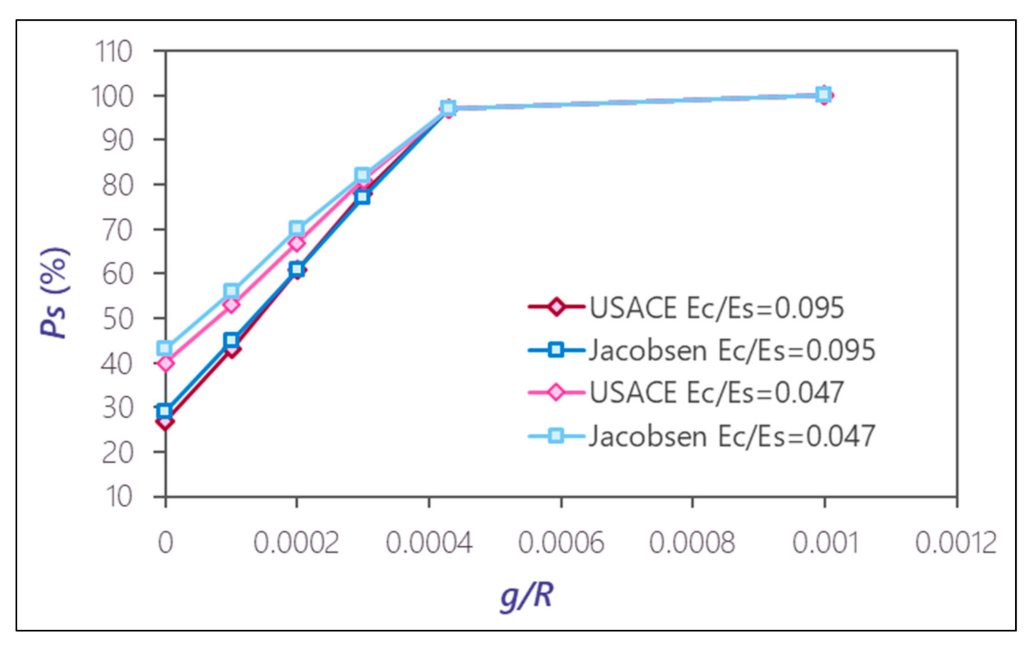
Figure 5 shows the percentage of internal pressure absorbed by the steel liner $Ps$ for a ratio between the radii of Rfis $=4Rs$. The calculation is performed for a cylinder with $D/t$ = 285.7 and for two values of the relation between the modulus of elasticity of the concrete backfill and that of the liner: $Ec/Es$ = 0.095 and 0.047. Such values are typical of liners in penstocks.

Figure 5 shows that the liner can withstand only around 25% of the total internal pressure when complete containment is ensured. This percentage increases as the gap is larger so that from around $g/R=0.0004$, the liner supports 100% of the internal pressure.

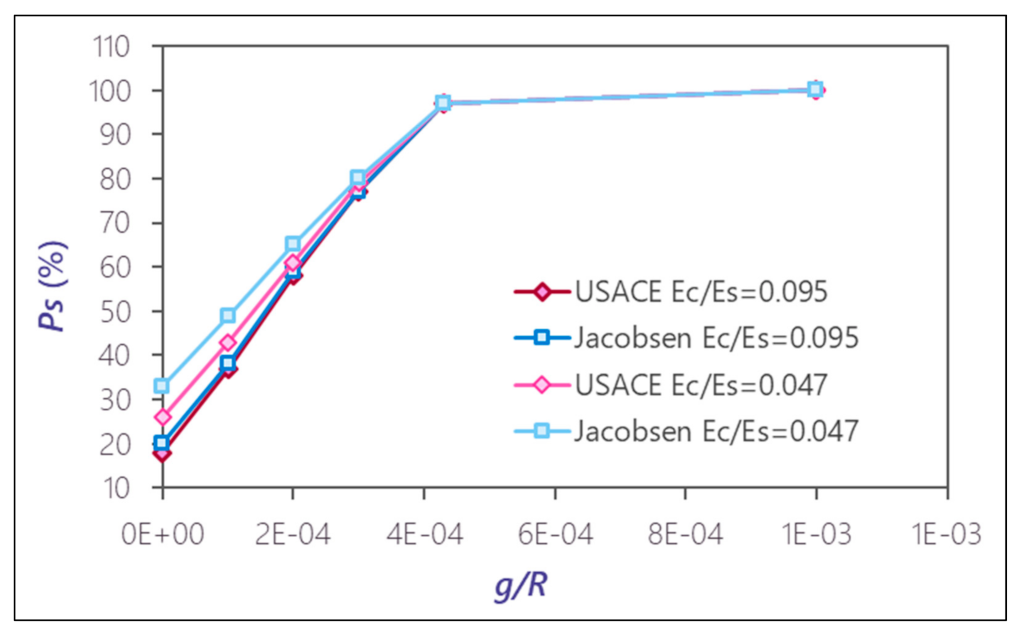
Figure 6 shows the percentage of the internal pressure that is carried by the liner for a relation between the radii of Rfis $=1.5 Rs$. This shows that the stiffer the surrounding rock, the lower the percentage of internal pressure that the liner receives as compared with the case of Rfis = 4 Rs.

Figure 5 and Figure 6 show that both methodologies (those of the USACE and Jacobsen) offer highly similar results that are closer for high values of $g/R$. By contrast, the results show a greater degree of discrepancy for low values of Ec/Es. However, it should be noted that the distribution of pressure is only relevant for significantly low values of $g/R$, with the liner absorbing 100% of the pressure from $g/R$ = 0.0004.

In usual practice, it is recommended to disregard the contribution of both the encasing concrete and rock mass when calculating the liner response to internal pressure. Given the results obtained, although slightly conservative, this assumption would be correct.

Mazzochi et al. [14] proposed a non-intrusive monitoring method of pressurized pipes to control the pressure wave generated actively by a cavitation bubble.

6.2. External Pressure

External pressure due to hydrostatic load may be present in pressure tunnels which, for inspection and maintenance purposes, are quickly emptied. There may also be conditions of external pressure when a tunnel subject to low pressure crosses an area with a high phreatic level or when excessive grouting pressure has been applied in the backfill during construction [5].

In certain cases, an external drainage system has been constructed, which consists of pipes that run parallel to the tunnel axis. In addition, sometimes pressure relief valves have been installed too [1,15]. Regardless, a liner should be designed to withstand a proportion of the total external hydrostatic load given that drainage cannot fully dissipate the external pressure and that it may become blocked or even not function correctly. Environmental factors should also be taken into account when implementing a permanent drainage system in the tunnel since they may result in permanent drainage at the ground surface or even in the depletion of aquifers.

The most frequent failure modes of steel liners due to external pressure are overall instability or local instability of the span between stiffeners; both often entail the formation of a single lobe parallel to the tunnel axis [5,16]. The term instability encompasses both elastic and inelastic buckling. Other types of failure can be localised yielding of the steel and weld breakage. Figure 7 shows the overall buckling of a steel liner under external pressure.

Yielding of the most stressed cross-section is the most common failure mode for thin walled unstiffened liners with a ratio $D/t$ between 100 and 300 [16]. Only for very slender liners with high-strength steels may geometric instability occur. In this case, the material is not used to the full. Regardless, geometric nonlinearity should be considered in the model [17].

Calculation Methods for a Liner Submitted to External Pressure

In the case of steel-lined pressure shafts and tunnels, the liner is confined by the concrete backfill, which prevents outward displacements once the gap is closed. This involves a resistance to instability significantly higher (up to 20 times greater) than that of an unconfined or an aerial pipeline with similar characteristics.

Since the 1950s, several researchers have examined the theory of instability of steel liners in hydraulic shafts and tunnels. As the various solutions have produced different results, it is necessary to carry out a comparative analysis of the respective methodologies to determine the critical pressure at which buckling occurs.

There are three main approaches associated with the phenomenon: the theory of multiple-lobe instability, that of radially symmetric buckling, and that of single-lobe buckling [5].

• Multiple-lobe instability approach

This is used to define the critical pressure at which instability occurs in the span between two consecutive stiffeners or adjacent supports for aerial pipes. It considers a cylindrical steel pipeline with unrestrained radial displacements and subjected to uniform external pressure. The pipeline tends to buckle symmetrically with two or more lobes. The formulations of von Mises [5] and Donnell and Roark [12] serve as references for the calculation of local buckling in piping circumferentially fixed at both ends.

• Radially symmetric buckling approach

This takes into account the radial confinement provided by the concrete backfill encasing the cylinder. The existing gap is assumed uniform around the entire perimeter. Its use is less frequent given that it provides less conservative results than single-lobe buckling theories. The formulations of Vaughan (1956) [12] and Borot [12] enable calculation of the instability under radial restraint.

• Single-lobe instability approach

Here, it is assumed that the cylinder is unlikely to remain centered with an initial uniform and all-round gap. The cylinder will finally lean against the surrounding material at some point and will have twice the radial gap on the opposite side. When the external pressure reaches a critical value, the cylinder will buckle with a single lobe. However, it should be noted that Boot [18] proposes two lobes for this case.

The principal theories for the buckling calculation through formation of a single lobe are the following:

▪

Glock [7]. This analytical method is applicable to unstiffened liners under the assumptions of elastic behavior and complete containment (gap = 0).

$$Pcr=E^{\prime }{\left(\frac{t}{R}\right)}^{2.2},$$

(1)

where Pcr is the critical pressure and E′ is the modulus of elasticity under plane strain assumption.

▪

Boot [18]. This analytical method modifies the Glock equation to account for an initial gap and applies this to unstiffened liners.

▪

Amstutz [6]. This study entails an analytical method assuming inelastic behavior; it is applicable to both stiffened and unstiffened liners.

▪

Jacobsen [19]. This contribution assumes plane strain and involves an analytical approach that considers inelastic response and is, despite its practical complexity, the most extensively used today. It is applicable both to stiffened liners and, with some simplifications, to unstiffened liners. The approach requires three non-linear simultaneous equations to be addressed. Jacobsen establishes that stress in the extreme fibre of the liner reaches the yielding value. This does not explicitly entail either the elastic or inelastic stability of the penstock, but assumes that the critical buckling pressure corresponds to the condition of plastification of a first fiber at any point on the liner.

In order to validate the calculated critical pressure that causes instability, tangential stresses in the liner must not exceed 80% of the yield stress of the steel. When the stress level exceeds this value, the stress-strain behavior of steel tends to become nonlinear.

$$\sigma ·FS=\frac{Pcr·R}{t}FS\le 0.8 f_{sy},$$

(2)

In the above expression, $f_{sy}$ is the yield stress of the steel and FS is the required safety factor, with σ being the design stress.

▪

Montel [20]. This work, which develops an empirical formula assuming inelastic behavior, is restricted to unstiffened liners.

▪

El Sawy and Moore [21]. This research entails a finite element method (FEM) approach and provides a parametric study of unstiffened liners that involves a formulation for failure through elastic buckling.

$$Pcr=\frac{E^{\prime }}{4}·{\left(\frac{t}{R}\right)}^3\left[\frac{25+350\frac{t}{R}+315\frac{g}{R}}{0.15+65\frac{t}{R}+350{\left(\frac{t}{R}\right)}^2+145\frac{g}{R}}\right],$$

(3)

FEM has become the most used alternative in the past decade. It is widely used in the literature to carry out simulations [22,23,24,25].

▪

Thepot [26]. This work develops an approach for unstiffened liners by application of the FEM and assuming elastic buckling.

$$\frac{Pcr}{E^{\prime }}=\frac{0.218}{1.0+0.41\delta -0.006{\delta }^2}{\left(\frac{t}{R}\right)}^{2.2},$$

(4)

$$\delta =3^{0.6}\left(\frac{g}{R}\right){\left(\frac{R}{t}\right)}^{1.2}$$

(5)

with δ being a dimensionless parameter, a function of the initial gap g.

The most referred-to theories for instability analysis in both stiffened and unstiffened liners (overall instability) are those provided by Amstutz (1970) [5,12] and Jacobsen [19].

In addition, in a parametric study El Sawy [27], determined values for inelastic instability (yielding) of unstiffened liners. Finally, other valuable studies that involve the application of FEM are as those of Prabu [28] and Das [29].

7. Comparison of Methods for Instability Analysis of Liners

7.1. Local Instability of Penstocks and Instability of Aerial Pipes

Local instability is the failure mode that may be applied both to the calculation of the steel shell span between stiffeners (in the case of penstocks) and the span of aerial pipes between supports.

Earlier work included a comparison of some analytical methods, such as those of Donnell, Roark and von Mises [17]. The applied data set for that comparison is shown in

Table 5. Data used in the comparison of the local instability analysis methods of penstocks.

Parameter	Value
D/t	285.71
E	210 MPa
ν	0.3
L/t	0.625
t	7.5 mm

.

Table 6. Critical pressure for linear elastic buckling of a thin-walled steel liner.

Critical Buckling Pressure PCR [MPa]
Spacing of Stiffeners [mm]	Failure Mode (Number of Lobes) n	Analysis Method
		FEM	Roark	Donnel	Von Mises
30.000	2	---	0.050	0.092	0.078
	3	0.080	0.050	0.075	0.057
	4	0.111	0.050	0.111	0.100
	5	0.169	0.050	0.167	0.159
	6	0.244	0.050	0.238	0.231
	7	0.334	0.050	0.324	0.317
	Pcr	0.080	0.050	0.075	0.057
2.500	5	---	0.596	34.890	2.710
	6	2.350	0.596	14.220	1.236
	7	1.419	0.596	6.610	0.788
	8	1.051	0.596	3.520	0.649
	9	0.933	0.596	2.190	0.700
	10	0.940	0.596	1.617	0.783
	11	1.016	0.596	1.391	0.900
	12	1.136	0.596	1.340	1.049
	13	1.286	0.596	1.394	1.200
	14	1.420	0.596	1.504	1.374
	15	1.655	0.596	1.653	1.563
	Pcr	0.940	0.596	1.340	0.783

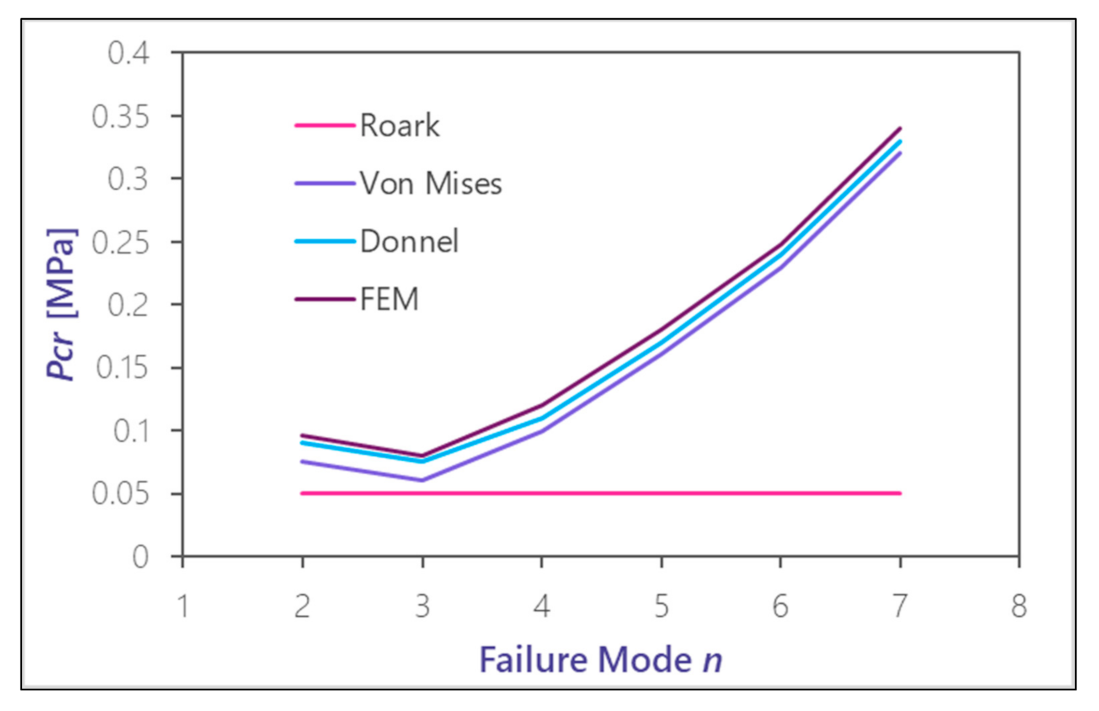
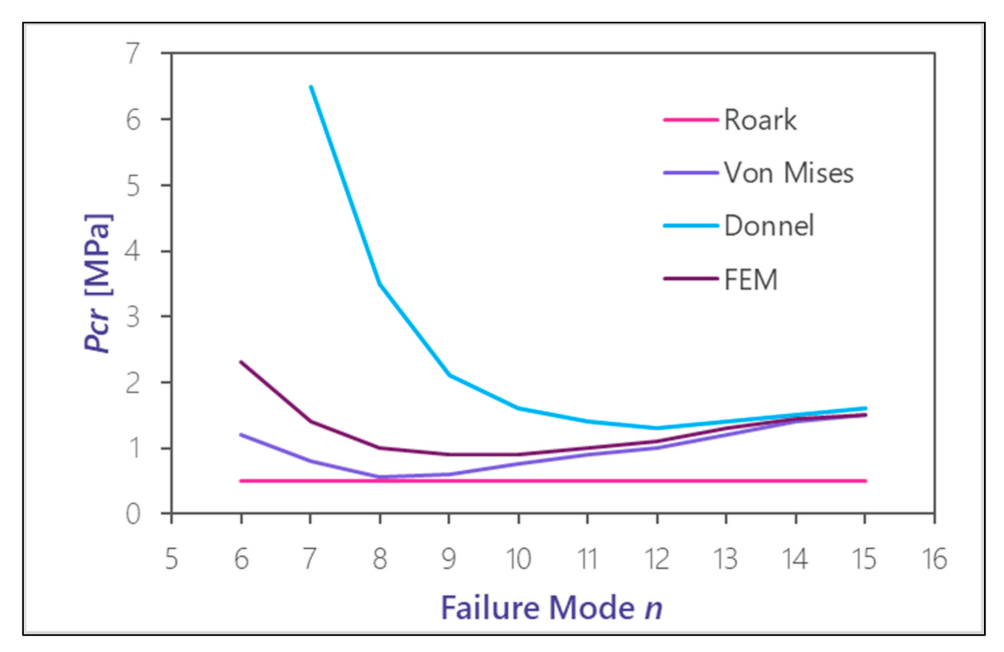
shows the critical pressure values resulting both from analytical formulations and a three-dimensional linear FEM model. Two cases with different degrees of spacing of 2.5 m and 30 m (with the latter being practically unstiffened) between stiffeners are shown.

It is notable that there is a significant spread in the results obtained, given that Roark does not consider the failure mode (the number of lobes) but the minimum critical pressure of instability. Hence, the Roark formula provides the most conservative values for critical pressure.

Figure 8 and Figure 9 show how the Roark line is practically the tangent at the lower point of the von Mises curve.

Given the results shown in Figure 8 and Figure 9, although it seems suitable that the critical pressure be assessed through different formulations, the development of a finite element model, even though there is a linear eigenvalue analysis [30], is recommended. As it can be seen, different stiffener lengths (L = 30 m in Figure 8 and L = 2.5 m in Figure 9) show very different results of the critical buckling pressure. Some formulations are more appropriate and conservative than other for different geometries. Nevertheless, Roark is always the most conservative formulation, irrespective of the geometry used, and Donnel and the FEM offer the most optimistic values. This shows the importance of trying out different formulations.

7.2. Instability of Unstiffened Steel Liners

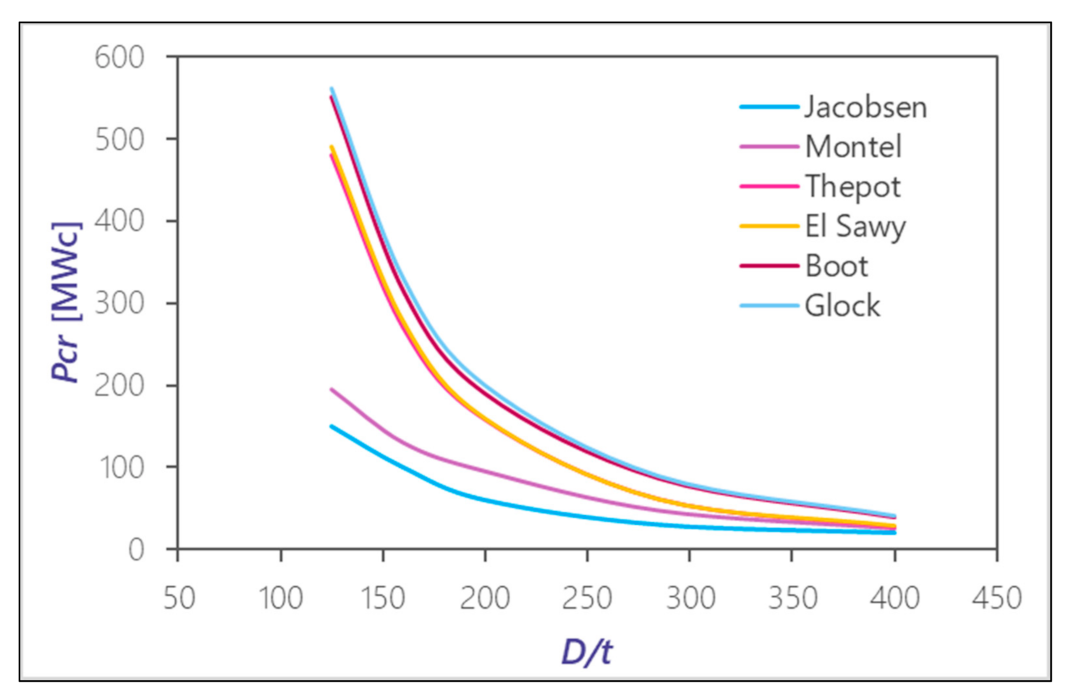
Across the analytical formulations, the basic parameters involved in the design of liners are the relations D/t (slenderness) and $g/R$ (relative gap), provided that the steel modulus of elasticity is 210 MPa and Poisson’s ratio ν = 0.3. Figure 10 shows the values for the critical buckling pressure assessed by various methods depending on the ratio $D/t$ and for a gap ratio of $g/R=1.5\times {10}^{-3}$.

The similarity of the Glock equation to that of Euler for unrestrained cylinders [31,32] and to other formulations is notable. Remember that Glock’s equation is expressed as follows:

$$Pcr=b·E^{\prime }{\left(\frac{D}{t}\right)}^m,$$

(6)

whereas for the case of a free cylinder (Euler), $b=2$, $m=-3$, for that of Glock, $b=1, m=$ 2.2. Such values are the formal limits of the parameters, with the real solution therefore varying with respect to a free cylinder and a completely constrained one (without a gap).

It should be noted that whereas the formulations offered by Amstutz, Jacobsen, and Montel are applicable when failure is produced by yielding [17], the remainder consider only failure due to geometric instability, which is uncommon for $D/t$ ratios of between 100 and 300.

One simple manner for comparing such formulations involves determining the factor K, which depends on the material of the liner, geometry, and size of the gap [33,34]. Thus, with $Pc{r}^{ideal}$ being the critical pressure of Euler, K may be defined so that:

$$Pcr=K·Pc{r}^{ideal}$$

(7)

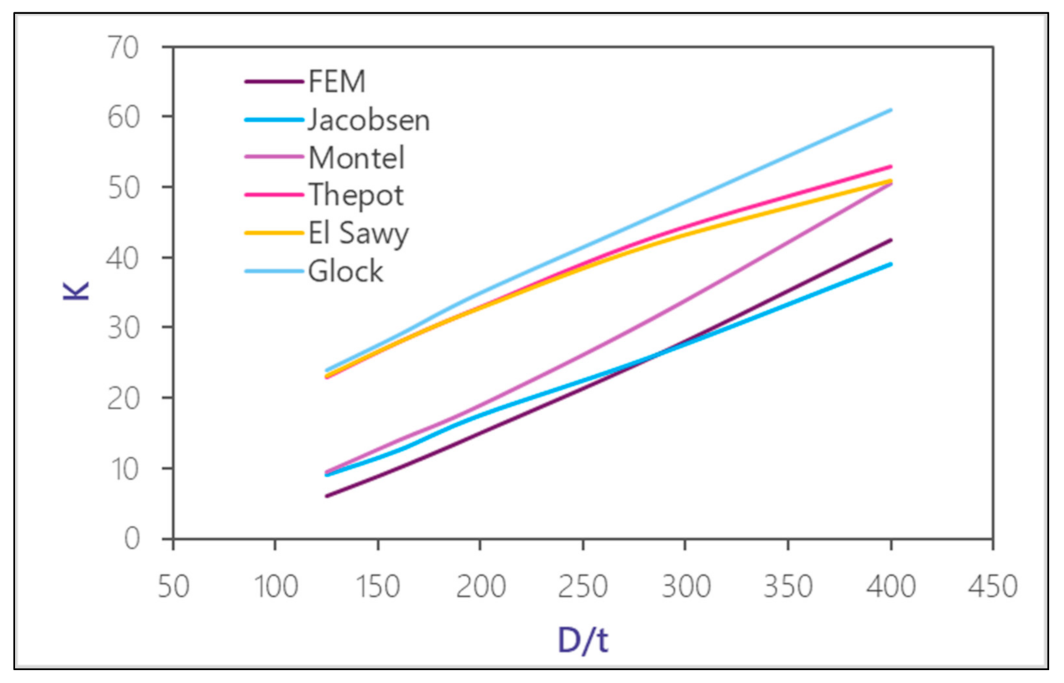
Figure 11 shows the parameter K, for the various formulations assuming a gap of $g=3$ mm. Nonlinearity is apparent for those obtained through the FEM, as well as the strong dependence of all on the parameter D/t.

As may be observed, both the value of K and its scatter are greater as the liner slenderness increases ($D/t$). Moreover, given that in some approaches the relation is nonlinear, an approximate formulation of the following type could be suitable:

$$Pcr=c_1\left(\frac{D}{t}\right)Pc{r}^{ideal}$$

(8)

which may resemble the variability of K with $D/t$. Indeed, this relation is equivalent to that expressed above in Equation (6).

Table 7. Calibration parameters for different formulations.

Calibration Parameters
Design method	g = 3 mm		g = 8 mm
	$g/R$ = 0.00075		$g/R=$ 0.002
	b	m	b	m
Thepot	3.85	−2.51	9.77	−2.74
El Sawy	3.14	−2.46	5.89	−2.63
Boot	1.39	−2.27	2.22	−2.38
Glock	1.00	−2.20	1.00	−2.20
Jacobsen	0.12	−2.03	0.10	−2.07
Montel	0.05	−1.79	0.11	−2.02

shows the estimate of parameters $b$ and $m$ in the aforementioned formulations from results obtained upon considering two values of the gap $g$: 8 mm and 3 mm.

From a comparison of Figure 10 and Figure 11 and Table 7 with the values of the parameters obtained, it may be deduced that the influence of the initial gap, $g$, in the determination of the critical pressure should be considered, with the influence of the parameter $D/t$ being insufficient. Additionally, it may be observed that the relation is not linear but exponential:

$$Pcr=b_0{\left(\frac{g}{D}\right)}^{b_1}{E}^{\prime }{\left(\frac{D}{t}\right)}^{n_0{\left(\frac{g}{D}\right)}^{n_1}}$$

(9)

in which $b_0$, $b_1$, $n_0$, and $n_1$ are constants.

In another case study [17], for a gap of 0.6 mm, the results obtained by different methods were compared with those achieved through a finite element model. Figure 12 shows that the latter follow the values obtained by Montel and Jacobsen. The reason is that the failure is due to steel yielding.

There is a significant scatter across the results of the models traditionally used (Montel and Jacobsen) and those obtained through elastic finite element models or the subsequent formulations derived. The reason is that the former assume that failure occurs by yielding, whereas the latter consider the geometric instability of the cylinder.

7.3. Instability of Stiffened Steel Liners

The parameters that define the slenderness of a stiffened liner are D/t and L/D (spacing of stiffeners). Since the most commonly used method is that of Jacobsen [19], its results were compared with those from three-dimensional finite element models [17]. 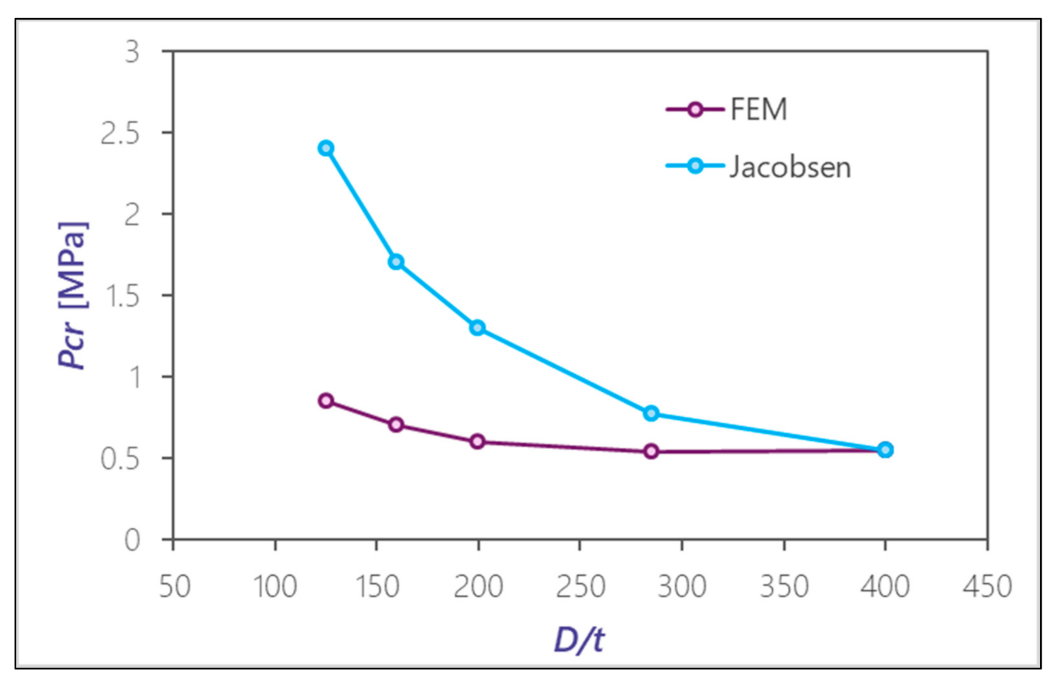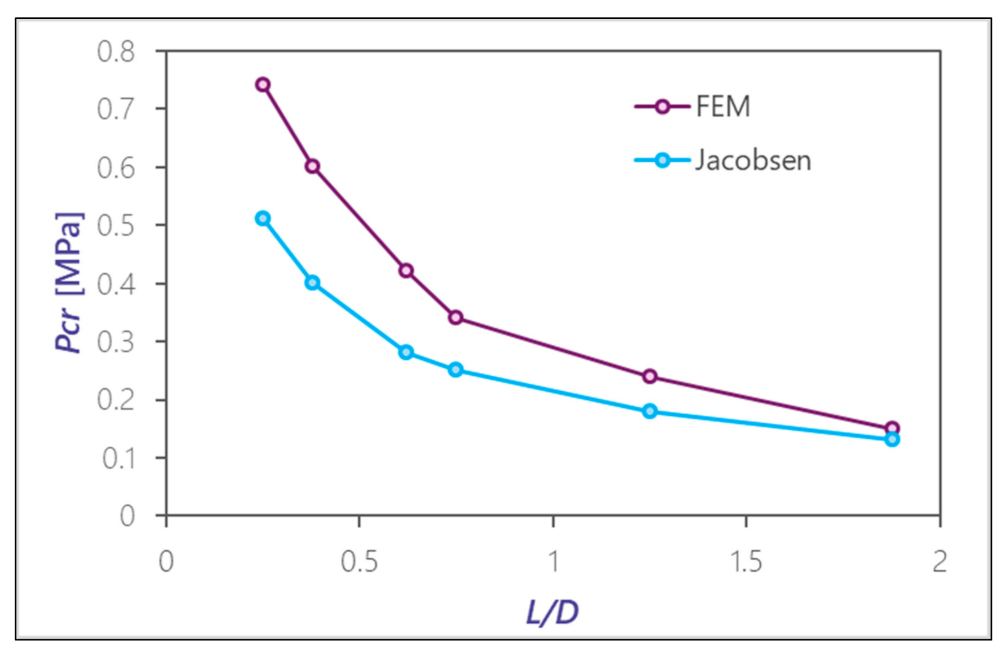El Sawy [21,27] compared the values obtained for unstiffened liners with the Jacobsen formulation, showing that the latter is conservative for usual $D/t$ values; however this would not be so for thin-walled liners. Regarding stiffened liners, the results of a three-dimensional finite element model were compared with those of the Jacobsen formulation, with the aforementioned conclusion being reached. Hence, it is recommended that results obtained through the Jacobsen formulation be verified with those from a finite element model. Otherwise the liner could become oversized in the case of high thicknesses whereas the design could fall out of the safety side for thin-walled liners.

Figure 13 compares the results of critical pressure depending on slenderness ($D/t$).

Figure 14 compares the results obtained for the critical pressure depending on the ratio L/D.

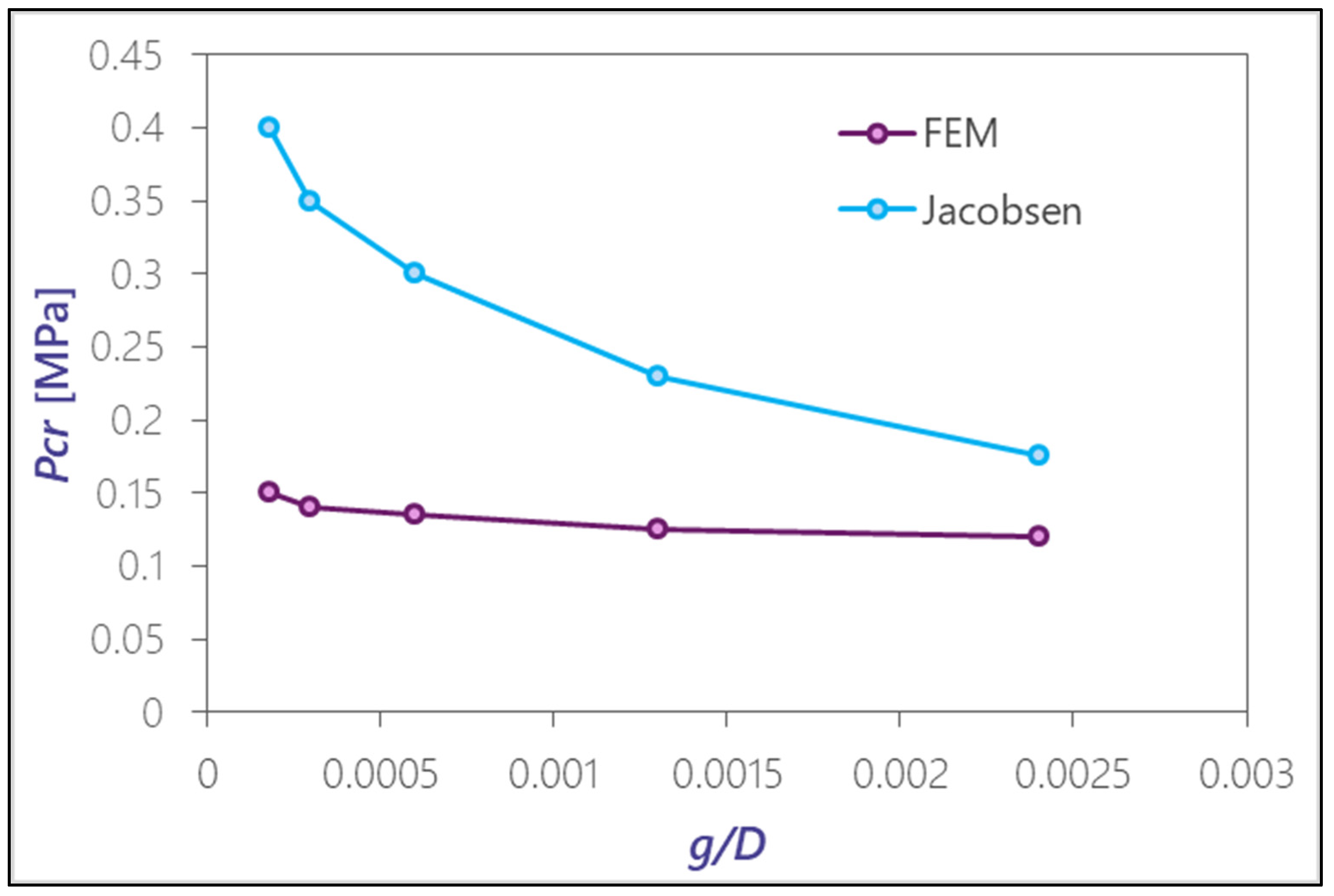
Figure 15 compares the results in the case of a very slender liner for different values of the gap ($g/D$). It is notable that the Jacobsen formula offers non-conservative values.

As can be seen in Figure 15 for very slender tubes (g/D ∈ (0.0005; 0.003)), it is more conservative to use the FEM formulation, whilst when the liner is not so slim, Figure 14 proves that Jacobsen formulation can be more conservative.

7.4. Responses to Vibration

Although this paper does not intend to cover the vibration effects in depth, the responses of the liner to external vibrations are highly influenced by the geometric imperfections of the liner (inner and outer radius of the tube, L/t, etc.), as well as the weight homogenization [35,36,37]. Vibration can be generated due to external causes, such as seismicity, but also because of internal reasons such as cavitation. Combating corrosion and vibration generated by cavitation of liners remains important because the life of liners with regard to cavitation erosion is approximately four times shorter than that with regard to the cylinder face wear [38]. This is not only of great importance for water supply systems but also in the field of nuclear power plants, where ambient vibration is a common danger. In such cases, the structural integrity of liners carrying hazardous materials must be studied in depth [39].

7.5. Cylindrical Shell Parallelism

Unstiffened steel liners can be considered cylindrical shells. A lot of research has been done on cylindrical shells and their response to vibrations. As mentioned in the previous section, this paper does not intend to delve into vibration effects, but Zhaoye Qin et al. [40] compares three different well-known formulations to analyse how free vibrations affect the shells: Fourier series, the Orthogonal polynomials, and the Chebyshev polynomials. The results show that the Chebyshev polynomials offer high computational efficiency.

As for mechanical buckling of cylindrical shells, it has been proven that an elastic foundation has a significant effect on the critical buckling load [41]. Pogorelov’s Geometrical method [42,43] has stablished as the most well-known mathematical model for describing features of local buckling of the shells.

8. Regulations and Codes Regarding Steel Liner Design

The most known codes are:

• The CECT issued a regulation [6] that explicitly makes reference to the calculation of steel liners. It includes equations and nomograms derived from the Amstutz formulation and requires a safety factor greater than 1.6.
• The USACE Code [12] recommends the methods provided by Amstutz, Jacobsen, and Vaughan with regard to overall instability. For analysis of local buckling of the span between stiffeners, it recommends the formulations of von Mises and Donnell. Indeed, design is considered to be acceptable when the calculated stresses do not exceed 80% of the yield stress.

Other related codes are the following:

• The Boiler and Pressure Vessel Code (2001), provided by the American Society of Mechanical Engineers (ASME).
• The Technical Guide on Pipelines for the Transport of Pressurised Water, provided by the Centre for Studies and Experimentation in Public Works: (Centro de Estudios y Experimentación de Obras Públicas, CEDEX, Spain), that gathers an extensive range of Standards associated with calculation methods in pressurised water tunnels (based on the American Water Works Association Manual M11).
• ASTM F1216 (1998), published by the American Society for Testing and Materials (ASTM) [34].
• The Recommended Practice DNV-RP-C202 for the Buckling Strength of Shells, published by Det Norske Veritas [8].
• Buckling of Steel Shells: European Recommendations, provided by the European Convention for Constructional Steelwork (ECCS) [44].
• Design Guidelines for Pressure Tunnels and Shafts AP-5273, provided by the Electric Power Research Institute (EPRI) [1].

However, design guidelines for the application of high-strength steel for steel liners are still missing [11]. For that, Pachaud et al. [45,46,47] proposed methodology for a safety assessment of the steel liners of pressure tunnels and shafts, particularly for the weakness that welding imperfections may affect the liners.

9. Conclusions

This study has reviewed and summarised, from a comparative perspective, the main calculation methods in the analysis of stiffened and unstiffened liners located in pressure tunnels at hydroelectric power plants. It has also examined the calculation and current design codes that were derived from the 1960s onwards.

The main parameters that determine the critical pressure that liners may withstand are the relationship between the thickness and diameter, quality of steel, inertia of stiffeners and their spacing (should this apply), initial gap, and geometric imperfections. In addition, it is recommended that the beneficial effect of the encasing concrete and rockfill be neglected when analysing a liner submitted to interior pressure, unless it can be assured that there is no gap between the liner and its grouting.

The analytical methods available (Amstutz and Jacobsen) for calculating the instability of stiffened liners only consider that failure is caused by plastic instability. Indeed, the scope of the Amstutz approach is rather limited. Instead, it is paramount to determine the failure mode, whether by geometric instability or yielding.

In the case of unstiffened liners, the Jacobsen values agree with the FEM results for common values of the D/t relationship, though it should be noted that for slender thin-walled liners, the Jacobsen approach does not consider failure due to geometric instability but by yielding.

The FEM serves as a valuable tool not only for determining the critical pressure of steel liners but also in addressing a given problem. Such an approach may be implemented for assessing the critical pressure when failure occurs by local instability (shell buckling), by overall buckling of the pipeline wall along with stiffeners or through inelastic instability.

The selection of the steel-liner type should be performed after examination of practical and financial criteria, which involve the choice of either stiffened or unstiffened liners, quality of steel, as well as spacing between stiffeners.

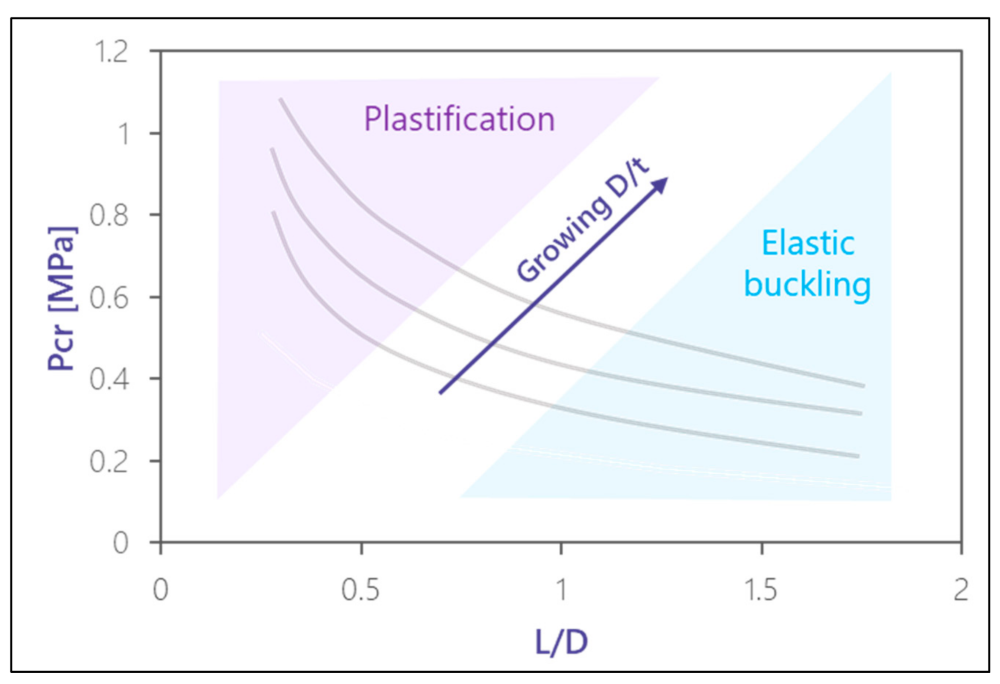
10. Future Research Lines

From the aforementioned conclusions, further research should involve the following issues:

• Behavior of stiffened liners:

  ▪

  FEM modelling for assessing the response of the shell-stiffener system.

  ▪

  Identification of the limits that allow discerning elastic failure from inelastic instability (plastification) of steel liners, as shown in Figure 16.

  ▪

  Behavioral differentiation between stiffeners and connectors.

• Influence of the stiffness of the backfill (concrete/rock) on the critical pressure value.
• Influence of imperfections arising from corrosion, dents, and welds in stiffened liners.
• Setting of suitable and up-to-date design criteria for stiffened liners, especially with high-resistance steels.