Semi-Active Control of Seismic Response on Prestressed Concrete Continuous Girder Bridges with Corrugated Steel Webs
Abstract
1. Introduction
2. Semi-Active Control Theory
2.1. Controlled System Status Description
2.2. LQR Optimal Active Control Algorithm
2.3. Semi-Active Control Algorithm
- 1.
- Simple bang–bang control algorithm
- 2.
- Optimal bang–bang control algorithm
- 3.
- Bounded Hrovat control algorithm
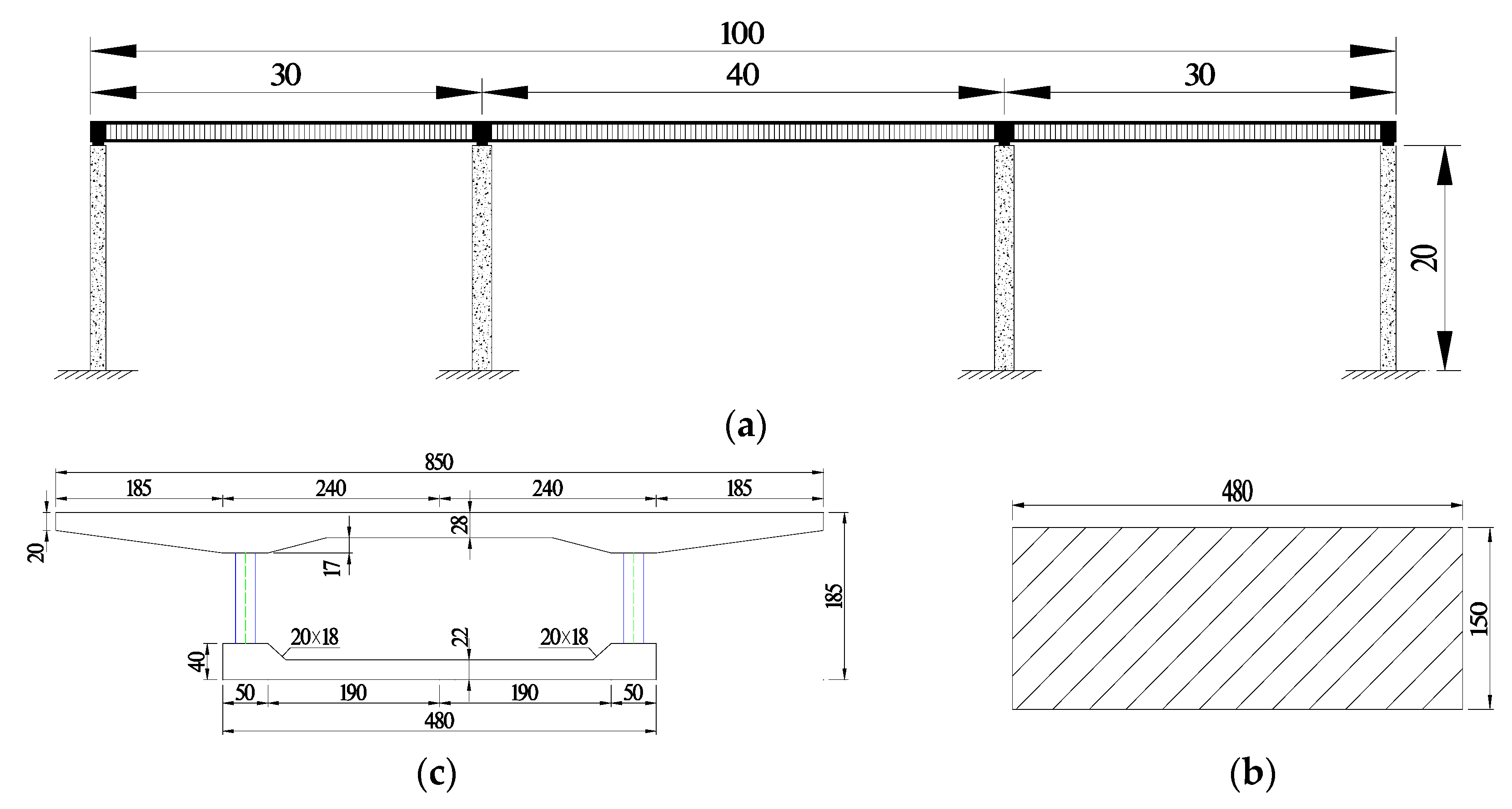
3. Project Profile
4. Finite Element Modeling
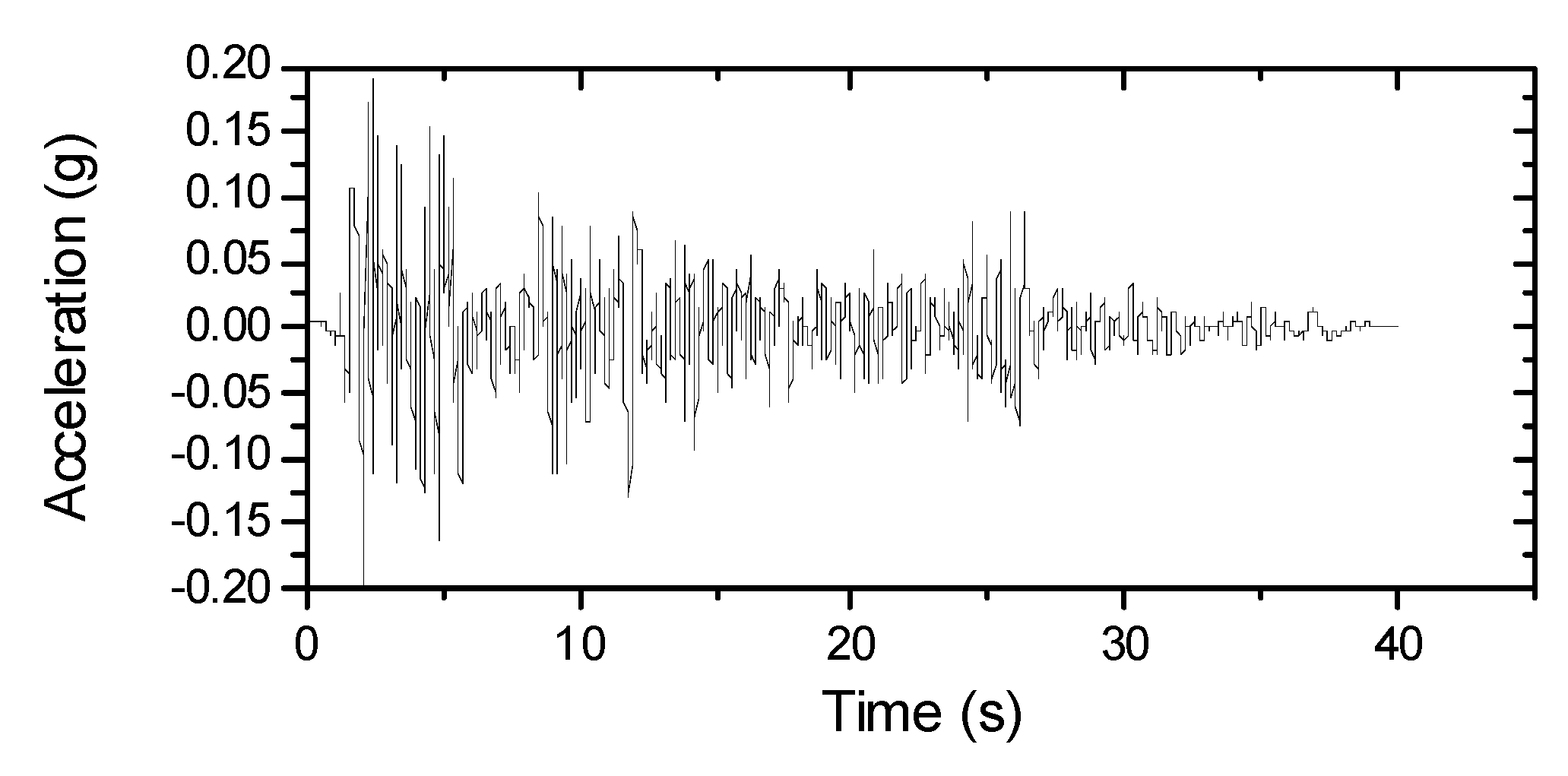
5. Ground Motion Input
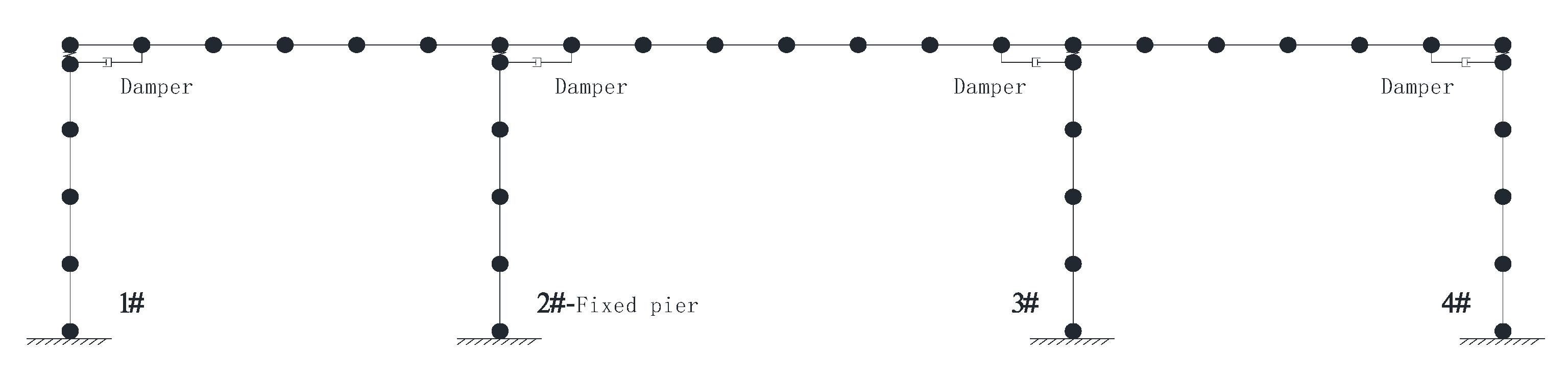
6. Establishment of Semi-Active Control System
6.1. Determination of Weight Matrix Coefficient
6.2. Design Parameters of the Semi-Active Control System
7. Analysis of Semi-Active Vibration Absorption Effect
7.1. Analysis of MR Damper Energy Dissipation
7.2. Analysis of Peak Vibration Absorption Effect
8. Analysis of Structural Vibration Absorption Effect
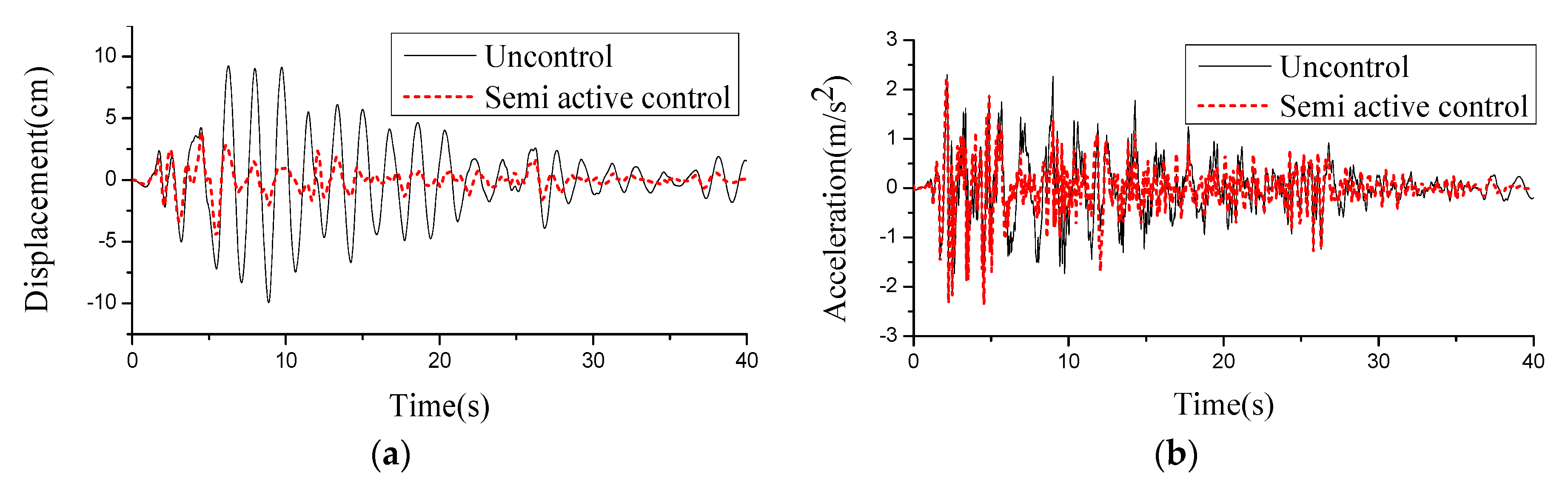
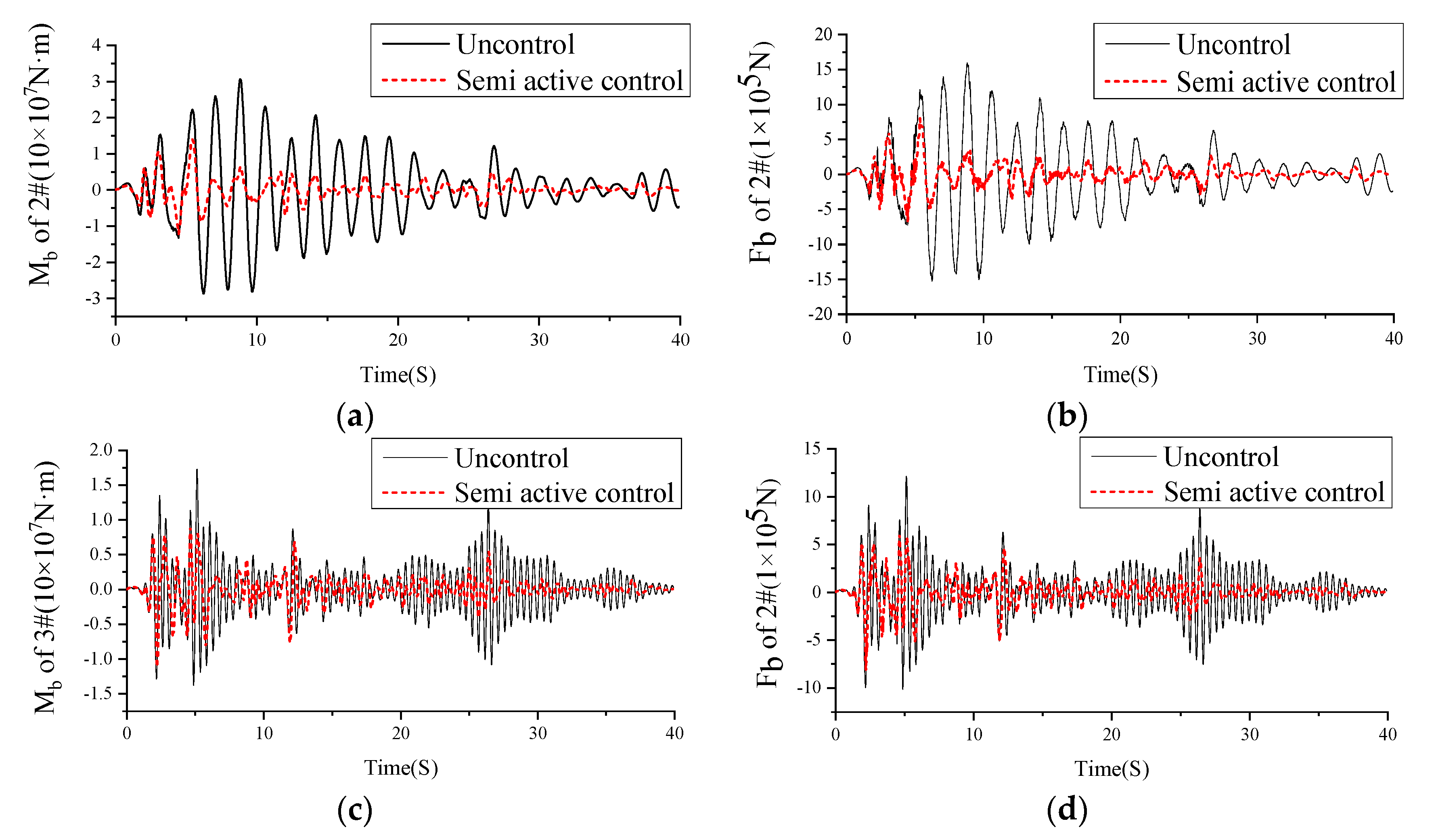
8.1. Time History Analysis of Main Beam Control
8.2. Time History Analysis of Pier Internal Force Control
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, R.J.; Kwong, A.F.; Xiao, Y.F. Prestressed concrete girder bridges with corrugated steel webs: Review. J. Struct. Eng. 2015, 141, 04014108. [Google Scholar] [CrossRef]
- Mo, Y.L.; Jeng, C.H.; Krawinkler, H. Experimental and analytical studies of innovative prestressed concrete box-girder bridges. Mater. Struct. 2003, 36, 99–107. [Google Scholar] [CrossRef]
- El, M.A.; Loov, R.E. Corrugated steel webs for prestressed concrete girders. Mater. Struct. 2003, 36, 127–134. [Google Scholar]
- Zhou, M.; Yang, D.; Zhang, J.D.; Lin, A. Stress analysis of linear elastic non-prismatic beams with corrugated steel webs. Thin Wall Struct. 2017, 119, 653–661. [Google Scholar] [CrossRef]
- Nie, J.G.; Zhu, L.; Tao, M.X.; Tang, L. Shear strength of trapezoidal corrugated steel webs. J. Constr. Steel Res. 2013, 85, 105–115. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Shear buckling behavior of tapered bridge girders with steel corrugated webs. Eng. Struct. 2014, 74, 157–169. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, J.; Xu, T. The shear-lag effect of composite box girder bridges with corrugated steel webs and trusses. Eng. Struct. 2019, 181, 617–628. [Google Scholar] [CrossRef]
- Mo, Y.L.; Fan, Y.L. Torsional design of hybrid concrete box girders. J. Bridge Eng. 2006, 11, 329–339. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, K.B.; Liu, Y.W. Nonlinear analysis for PC box-girder with corrugated steel webs under pure torsion. Thin Wall Struct. 2012, 51, 167–173. [Google Scholar] [CrossRef]
- Shen, K.; Wan, S.; Mo, Y.L.; Li, X.Y.; Song, A.M. A softened membrane model for composite box-girders with corrugated steel webs under pure torsion. Eng. Struct. 2018, 173, 357–371. [Google Scholar] [CrossRef]
- Cao, L.; Liu, J.; Chen, Y.F. Theoretical and numerical study on the natural frequencies of bridges with corrugated steel webs. Structures 2018, 15, 224–231. [Google Scholar] [CrossRef]
- Ji, W.; Deng, L.; Liu, S.Z.; Lin, P.Z. Study of vertical bending vibration behavior of continuous prestressed concrete box girders with corrugated steel webs. Adv. Struct. Eng. 2016, 19, 953–965. [Google Scholar] [CrossRef]
- Moon, J.; Ko, H.J.; Sung, I.H.; Lee, H.E. Natural frequency of a composite girder with corrugated steel web. Steel Compos. Struct. 2015, 18, 255–271. [Google Scholar] [CrossRef]
- Zheng, S.M.; Wan, S.; Cheng, H.G. Research on the dynamic characteristics of multi-room single box composite girder with corrugated steel webs. J. Railw. Eng. Soc. 2017, 9, 41–46. (In Chinese) [Google Scholar]
- Deng, W.Q.; Liu, D.; Xiong, Y.; Zhang, J. Experimental study on asynchronous construction for composite bridges with corrugated steel webs. J. Constr. Steel Res. 2019, 157, 93–102. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Li, C.; Correia, J.; Zhou, M. A novel asynchronous-pouring-construction technology for prestressed concrete box girder bridges with corrugated steel webs. Structures 2020, 27, 1940–1950. [Google Scholar] [CrossRef]
- Hung, C.; Lin, G.W.; Syu, H.S.; Chen, C.W.; Yen, H.Y. Analysis of the Aso-Bridge landslide during the 2016 Kumamoto earthquakes in Japan. B Eng. Geol. Environ. 2017, 77, 1439–1449. [Google Scholar] [CrossRef]
- Garlock, M. (New York State Department of Transportation, Albany, NY, USA). Private communication. 2008.
- Tabar, A.M.; Domenico, D.D.; Dindari, H. Seismic rehabilitation of steel arch bridges using nonlinear viscous dampers: Application to a case study. Pract. Period. Struct. Des. Constr. 2021, 26, 04021012. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J. Design and optimization of seismic isolation and damping devices for highway bridges based on probabilistic repair cost ratio. J. Struct. Eng. 2018, 144, 04018125. [Google Scholar] [CrossRef]
- Jansen, L.M.; Dyke, S.J. Semiactive Control Strategies for MR Dampers: Comparative Study. J. Eng. Mech. 2000, 126, 795–803. [Google Scholar] [CrossRef]
- Dyke, S.J.; Jr, B.F.S.; Sain, M.K.; Carlson, J.D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater. Struct. 1996, 5, 565–575. [Google Scholar] [CrossRef]
- Sheikh, M.N.; Xiong, J.; Li, W.H. Reduction of seismic pounding effects of base-isolated RC highway bridges using MR damper. Struct. Eng. Mech. 2012, 41, 791–803. [Google Scholar] [CrossRef][Green Version]
- Guo, A.; Li, Z.; Li, H. Experimental and analytical study on pounding reduction of base-isolated highway bridges using MR dampers. Earthq. Eng. Struct. D 2009, 38, 1307–1333. [Google Scholar] [CrossRef]
- Sahasrabudhe, S.S.; Nagarajaiah, S. Semi-active control of sliding isolated bridges using MR dampers: An experimental and numerical study. Earthq. Eng. Struct. D 2010, 34, 965–983. [Google Scholar] [CrossRef]
- Ok, S.Y.; Kim, D.S.; Park, K.S. Semi-active fuzzy control of cable-stayed bridges using magneto-rheological dampers. Steel Constr. 2007, 29, 776–788. [Google Scholar] [CrossRef]
- Lin, W.; Li, Z.; Ding, Y. Trust-region based instantaneous optimal semi-active control of long-span spatially extended structures with MRF-04K damper. Earthq. Eng. Eng. Vib. 2008, 7, 447–464. [Google Scholar] [CrossRef]
- El-Khoury, O.; Kim, C.; Shafieezadeh, A.; Hur, J.E.; Heo, G.H. Mitigation of the seismic response of multi-span bridges using MR dampers: Experimental study of a new SMC-based controller. J. Vib. Control. 2016, 24, 83–99. [Google Scholar] [CrossRef]
- Heo, G.; Seo, S.; Jeon, S.; Kim, C. Development of a hybrid control algorithm for effective reduction of drift in multispan isolated bridges. Soil Dyn. Earthq. Eng. 2021, 143, 106659. [Google Scholar] [CrossRef]
- Omrani, R.; Mobasher, B.; Liang, X.; Gunay, S.; Mosalam, K.M.; Zareian, F.; Taciroglu, E. Guidelines for Nonlinear Seismic Analysis of Ordinary Bridges: Version 2.0; Caltrans Final Report; Caltrans: Sacramento, CA, USA, 2015. [Google Scholar]
- Ou, J.P. Structural Vibration Control—Active, Semi-Active and Intelligent Control; Science Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Qi, X.J. Research on Semi-Active Control of Bridge Damping; Institute of Geophysics, China Seismological Bureau: Beijing, China, 2006. (In Chinese) [Google Scholar]


| α | Xmax | Xrms | Mmax | Mrms | Fmax | Frms | Fc_2#/N | Fc_3#/N |
|---|---|---|---|---|---|---|---|---|
| 40 | 0.57 | 0.72 | 0.57 | 0.72 | 0.52 | 0.72 | 894.6936 | 2.53 × 105 |
| 100 | 0.60 | 0.74 | 0.60 | 0.74 | 0.55 | 0.74 | 1.92 × 103 | 2.98 × 105 |
| γ | 5.26% | 2.78% | 5.26% | 2.78% | 5.77% | 2.78% | 114.64% | 17.65% |
| Ground Motion | EI Centro (PGA = 0.2 g) | |||
|---|---|---|---|---|
| Coefficient of Weight Matrix | α = 40 | β = 0.00001 | ||
| Number of MR damper | #1 | #2 | #3 | #4 |
| Active optional control force(N) | 253,280 | 894.6936 | 253,480 | 253,540 |
| Point in time (s) | 2.34 | 2.23 | 2.34 | 2.34 |
| Relative velocity (m/s) | 0.3889 | −0.0008959 | 0.3897 | 0.3900 |
| Adjustable multiple of damping force | 8 | 8 | 8 | 8 |
| Viscous damping coefficient of MR damper (N·s/m) | 81,409.10 | 124,838.64 | 81,306.13 | 81,262.82 |
| Maximum Coulomb force of MR variable damper (N) | 221,620.00 | 782.86 | 221,795.00 | 221,847.50 |
| Minimum Coulomb force of the MR variable damper (N) | 0 | 0 | 0 | 0 |
| Control Algorithm | Semictrl1 | Semictrl2 | Semictrl3 | Active |
|---|---|---|---|---|
| Energy consumption (MJ) | 4.39 | 9.09 | 4.03 | 4.07 |
| Seismic Response | Disp-Beam (cm) | Acce-Beam (m/s2) | Move-2# (1 × 107 N·m) | Shear-2# (1 × 105 N) | Move-3# (1 × 107 N·m) | Shear-3# (1 × 105 N) | |
|---|---|---|---|---|---|---|---|
| Unctrl | Peak | 9.93 | 2.30 | 3.07 | 15.92 | 1.73 | 12.12 |
| RMS | 3.18 | 0.55 | 0.98 | 5.08 | 0.36 | 2.55 | |
| Semictrl1 | Peak | 5.77 | 2.84 | 1.83 | 9.96 | 0.81 | 5.50 |
| RMS | 1.34 | 0.66 | 0.42 | 2.23 | 0.26 | 1.76 | |
| VBR1 | Peak | 42% | −23% | 40% | 37% | 53% | 55% |
| RMS | 58% | −20% | 57% | 56% | 28% | 31% | |
| Semictrl2 | Peak | 4.47 | 2.99 | 1.39 | 8.50 | 1.21 | 7.76 |
| RMS | 1.24 | 0.59 | 0.39 | 2.06 | 0.31 | 1.87 | |
| VBR2 | Peak | 55% | −30% | 55% | 47% | 30% | 36% |
| RMS | 61% | −7% | 60% | 59% | 14% | 27% | |
| Semictrl3 | Peak | 4.51 | 2.35 | 1.39 | 8.01 | 1.12 | 8.19 |
| RMS | 0.93 | 0.44 | 0.29 | 1.50 | 0.21 | 1.33 | |
| VBR3 | Peak | 55% | −2% | 55% | 50% | 35% | 32% |
| RMS | 71% | 20% | 70% | 70% | 42% | 48% | |
| Active | Peak | 4.29 | 2.37 | 1.32 | 7.61 | 1.20 | 7.99 |
| RMS | 0.88 | 0.43 | 0.27 | 1.43 | 0.21 | 1.37 | |
| VBR4 | Peak | 57% | −3% | 57% | 52% | 31% | 34% |
| RMS | 72% | 22% | 72% | 72% | 42% | 46% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Shen, Q.; Guan, C.; Cheng, H.; Zhuang, H.; Zhou, M. Semi-Active Control of Seismic Response on Prestressed Concrete Continuous Girder Bridges with Corrugated Steel Webs. Appl. Sci. 2022, 12, 12881. https://doi.org/10.3390/app122412881
Zheng S, Shen Q, Guan C, Cheng H, Zhuang H, Zhou M. Semi-Active Control of Seismic Response on Prestressed Concrete Continuous Girder Bridges with Corrugated Steel Webs. Applied Sciences. 2022; 12(24):12881. https://doi.org/10.3390/app122412881
Chicago/Turabian StyleZheng, Shangmin, Qiang Shen, Chong Guan, Haigen Cheng, Haiyan Zhuang, and Man Zhou. 2022. "Semi-Active Control of Seismic Response on Prestressed Concrete Continuous Girder Bridges with Corrugated Steel Webs" Applied Sciences 12, no. 24: 12881. https://doi.org/10.3390/app122412881
APA StyleZheng, S., Shen, Q., Guan, C., Cheng, H., Zhuang, H., & Zhou, M. (2022). Semi-Active Control of Seismic Response on Prestressed Concrete Continuous Girder Bridges with Corrugated Steel Webs. Applied Sciences, 12(24), 12881. https://doi.org/10.3390/app122412881








