Predicting Geotechnical Parameters from Seismic Wave Velocity Using Artificial Neural Networks

Abstract

Geotechnical investigation plays an indispensable role in site characterization and provides necessary data for various construction projects. However, geotechnical measurements are time-consuming, point-based, and invasive. Non-destructive geophysical measurements (seismic wave velocity) can complement geotechnical measurements to save project money and time. However, correlations between geotechnical and seismic wave velocity are crucial in order to maximize the benefit of geophysical information. In this work, artificial neural networks (ANNs) models are developed to forecast geotechnical parameters from seismic wave velocity. Specifically, published seismic wave velocity, liquid limit, plastic limit, water content, and dry density from field and laboratory measurements are used to develop ANN models. Due to the small number of data, models are developed with and without the validation step in order to use more data for training. The results indicate that the performance of the models is improved by using more data for training. For example, predicting seismic wave velocity using more data for training improves the R² value from 0.50 to 0.78 and reduces the ASE from 0.0174 to 0.0075, and MARE from 30.75 to 18.53. The benefit of adding velocity as an input parameter for predicting water content and dry density is assessed by comparing models with and without velocity. Models incorporating the velocity information show better predictability in most cases. For example, predicting water content using field data including the velocity improves the R² from 0.75 to 0.85 and reduces the ASE from 0.0087 to 0.0051, and MARE from 10.68 to 7.78. A comparison indicates that ANN models outperformed multilinear regression models. For example, predicting seismic wave velocity using field plus lab data has an ANN derived R² value that is 81.39% higher than regression model.

1. Introduction

Seismic wave velocity is a practical, non-destructive, non-invasive, cost-effective measurement related to the inherent mechanical properties of geomaterials [1]. However, seismic wave velocity is not used directly in most designs of engineering structures. Developing correlations between seismic wave velocity and different engineering soil properties could facilitate the use of seismic information for designing engineering structures.

Researchers have extensively studied the correlation between seismic wave velocity and different soil properties. Dikmen developed correlations between shear wave velocity (V_s) and uncorrected Standard Penetration Test (SPT-N) values for sandy, silty, and clayey soils [2]. It was shown that SPT-N and shear wave velocity were strongly correlated but the type of soil had no significant effect on the estimation of V_s. Gautam established correlations between shear wave velocity and uncorrected standard penetration resistance [3]. This study used 500 measurements on various sand and silt soils. The coefficient of determination for silty and sandy soils was relatively low in comparison to using all soils together. He also compared his results with existing correlations from the literature and showed significant similarities with existing correlations. Hasancebi developed correlations between shear wave velocity and penetration resistance for sandy, clayey, and all soil (i.e., sandy and clay) using regression analysis [4]. Correlations between shear wave velocity and SPT-N were found to be significant. For sandy soil, the R-value was 0.65, for clayey soil the R-value was 0.75, and the combined data had an R-value of 0.73. Hasancebi also concluded that the blow count was a significant parameter for the correlation, but the soil type had no significant influence. A good correlation was established between S-wave velocity and the degradation factor (G_PMT/G_o), where G_PMT is intermediate strain shear modulus from the PMT and G_o is low strain modulus from S-wave velocity. However, the correlations between SPT-N and field measured S-wave velocity and P-wave velocity were poor. Correlations were also developed between shear wave velocity and cone penetration resistance. Mayne and Rix worked on field clay soil and found empirical correlations between shear wave velocity (V_s) and cone penetration tip resistance (q_c) [5]. An increasing trend in shear wave velocities with cone penetration resistance was observed with consistency from soft to stiff to hard clay materials. Log regression analysis returned a coefficient of regression of 0.736. Inazaki established correlations between S-wave velocity and SPT-N, bulk density, solidities as the complement of porosity, and mean grain size of surficial unconsolidated sediments [6]. S-wave velocities were measured in boreholes using the PS suspension logging tool. The results showed that it is possible to express N-values in terms of S-wave when N-value data have good accuracy. The correlation between S-wave velocities and solidities was good but was dependent on lithofacies and depositional age. The data also showed a good relationship between S-wave velocity and density but a weak relation between S-wave velocity and mean grain size. Even though most of the researchers found good correlations between S-wave velocity and N-values, studies by some researchers could not find out good correlations between S-wave velocity and N-values. A large number of researchers worked on developing correlation between shear wave velocity and SPT-N [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21].

Some other researchers attempted to develop correlation between seismic wave velocity and other geotechnical parameters. Evans worked with sand and clay soils to establish correlations between geophysical and geotechnical parameters [22]. Seismic refraction surveys were performed to collect S-wave and P-wave velocities. Pressure Meter Test (PMT), SPT, Atterberg limit tests, and dry unit weight data were also collected from the Salt River Project (SRP) [23,24]. Heureux and Long developed correlations between S-wave velocity, cone penetration parameters, undrained shear strength, and 1-D compression parameters for Norwegian clay [25]. Data used for this research was collected from 29 sites; in south-eastern and mid-Norway. Regression analyses were performed to establish the correlation between in situ S-wave velocity (V_s) and cone net resistance (q_net), collected from the cone penetration test. The coefficient of determination R² was 0.73. The undrained shear strength values obtained from direct shear tests were correlated with V_s. with a regression coefficient (R²) of 0.91. Their analysis also showed a good correlation between pre-consolidation stress (P_c^’) and V_s with an R² value of 0.81. Johora developed ANN models to predict geotechnical parameters from S-wave and P-wave velocity separately using laboratory data for compacted clay and sandy clay soil [26]. The results indicated that P-wave velocity and S-wave velocity were more sensitive to dry density and void ratio than to saturation and water content. The performance of the ANN models to predict geotechnical parameters from soil mix proportion and either P-wave or S-wave velocity was better when multiple geotechnical parameters were predicted at a time. Empirical correlations were developed by Imai et al. between index properties and seismic velocities [27]. Foti and Lancellotta used velocity data published by Hunter and showed the dependency of porosity with S-wave and P-wave velocity [28,29]. Alshameri and Madun showed a direct positive linear correlation exists between seismic wave velocity and cohesion and shear strength for compacted sand-kaolin mixtures. They also attempted to establish correlation between seismic wave velocity and friction angle but found that it is insignificant [30]. Duan et al. developed correlations between shear wave velocity with vertical effective stress, unit weight, preconsolidation stress and undrained shear strength for clay type soil [31].

ANN is gaining popularity as a problem-solving tool in the field of civil engineering. Researchers are using ANN to predict concrete compressive strength [32,33,34], ultrasonic pulse velocity [35], slump of concrete [36,37,38]. Zeh showed the application of ANN to assess the nonlinear behavior of steel structures [39]. ANN was used to forecast flexure and initial stiffness of beam column joints [40]. In geotechnical engineering ANN was used to study slope stability [41], pile analysis [42,43], developing correlation between ER and geotechnical parameters [44], analysis of liquefaction potential [45,46]. In transportation engineering researchers applied ANN to develop transportation systems [47].

ANN can solve complex problems, but the performance depends on the size and accuracy of the data set. Using a big data set can help to train the network efficiently. In many fields big data sets are not always easily available. Researchers are working on developing ANN models using small data sets. Pasini described a particular neural network tool which is capable of handling small data sets and its application to a specific case study [48]. Feng et al. used deep neural network to predict material defects using small data set [49].

Literature contains a good number of correlations between seismic wave velocity and blow counts. There are fewer correlations with other important geotechnical parameters, such as water content, dry density, cohesion, angle of friction, saturation, void ratio, etc. More study is necessary to establish the correlation between seismic wave velocity and different types of geotechnical parameters. Many of the existing studies employ conventional regression methods to develop the correlations between geotechnical and seismic wave velocity, even though ANN was used in many fields of civil engineering In this study, multi regression analysis and the ANNs approach were used to develop the relationships between seismic wave velocity and geotechnical parameters or, conversely, to predict geotechnical parameters from seismic wave velocity and other geotechnical parameters using data from the literature. The performance of the ANN and regression analysis was compared. Two different ANN approaches with and without validations were also discussed to handle the small size data set.

2. Seismic Wave Velocity

Soil allows for the propagation of different types of seismic waves. Waves that deform the material through shear are referred to as shear waves, and those that produce volumetric deformations are referred to as compressional waves. These are often referred to as S-wave and P-wave, respectively. Seismic wave velocity is related to the maximum shear modulus, bulk modulus, Young’s modulus, bulk density, and Poisson’s ratio of the soil [50].

The longitudinal P-wave and the transverse S-wave velocity in an infinite elastic continuum are related to the elastic properties by

$${\mathrm{V}}_{\mathrm{p}}=\sqrt{\frac{\mathrm{M}}{\mathsf{\rho }}}=\sqrt{\frac{\mathrm{B}+\frac{4}{3}\mathrm{G}}{\mathsf{\rho }}}\hspace{1em}\mathrm{P}\text{-}\mathrm{waves}$$

(1)

$${\mathrm{V}}_{\mathrm{s}}=\sqrt{\frac{\mathrm{G}}{\mathsf{\rho }}}\hspace{1em}\mathrm{S}\text{-}\mathrm{waves}$$

(2)

where M (Pa) is the constraint modulus, B (Pa) is the bulk modulus, G (Pa) is the shear modulus, and $\mathsf{\rho }$(kg/m³) is the mass density of the medium. Hence, the propagation velocity increases with the material stiffness and decreases with its mass density (inertia). Velocity of S-waves is always smaller than the velocity of P-waves [50].

For fluid-filled porous media, the effective bulk modulus is provided by Gassmann [50].

$${\mathrm{B}}_{\mathrm{eff}}={\mathrm{B}}_{\mathrm{SK}}+\frac{{\left(1-\frac{{\mathrm{B}}_{\mathrm{SK}}}{{\mathrm{B}}_{\mathrm{g}}}\right)}^2}{\frac{\mathsf{\phi }}{{\mathrm{B}}_{\mathrm{f}}}+\frac{1-\mathsf{\phi }}{{\mathrm{B}}_{\mathrm{g}}}-\frac{{\mathrm{B}}_{\mathrm{SK}}}{{\mathrm{B}}_{\mathrm{g}}^2}}$$

(3)

where B_SK (Pa) is the bulk modulus of the skeleton_, ${\mathrm{B}}_{\mathrm{g}}$ (Pa) is the bulk modulus of the grains, ${\mathrm{B}}_{\mathrm{f}}$ (Pa) is the bulk modulus of the fluid phase, and φ is the porosity. In the Gassmann model, the shear modulus of the soil, G_eff, (Pa) remains unaffected by the presence of the fluid at low excitation frequencies:

G_eff = G_SK.

(4)

For partially saturated soils, the mass density of the mixture ρ_mix, changes due to the different densities of the saturating fluids. By ignoring granular effects, fluid substitution can be used to modify the expression for the effective bulk modulus of the soil. For soil with water saturation of S_w, the fluid bulk modulus in Equation (5) given by

$$\frac{1}{{\mathrm{B}}_{\mathrm{f}}}=\frac{{\mathrm{S}}_{\mathrm{w}}}{{\mathrm{B}}_{\mathrm{w}}}+\frac{1-{\mathrm{S}}_{\mathrm{w}}}{{\mathrm{B}}_{\mathrm{a}}}$$

(5)

where ${\mathrm{B}}_{\mathrm{w}}$ (Pa) is the bulk modulus of the liquid phase and ${\mathrm{B}}_{\mathrm{a}}$ (Pa) is the bulk modulus of the air phase. Small volumes of air produce a large decrease in the modulus of the fluid phase. However, under dynamic loading, differences in inertia, shear stiffness, and bulk compressibility can add further complexity to the analysis.

Seismic wave propagation in granular soil materials is more complicated due to the complex behavior of the solid skeleton and the influence of capillary forces. The skeletons B_SK and G_SK depend on the “strength” of the grain contacts and are therefore dependent upon the applied effective stress. The concept of effective stress for soils at low saturation is still an area of active research because internal forces associated with capillary forces and electrical forces at the grain surface play an important role [50]. That is why empirical relationships are often necessary to predict seismic wave propagation in the partially saturated particulate medium.

There are numerous methods for measuring seismic wave velocity in the field and the laboratory. In the laboratory, the “time of flight” approach is common. A seismic wave is generated using a source in contact with one end of the sample, the disturbance passes through the soil and is detected by a receiver at the opposite end of the sample. Velocity is calculated by dividing the distance (sample length) by the measured travel time. The soil samples usually consist of remolded soil or a field sample with some degree of disturbance. The frequency of the seismic wave is usually in the 10–100 kHz range. Field measurements of seismic velocity can be performed using surface surveys such as refraction surveys or surface wave analysis. These approaches mitigate the problem of soil disturbance since no samples are required. However, they are less repeatable and have larger uncertainty in measure values. The frequency of the seismic wave is in the 10 Hz to several 100 Hz ranges. It should be noted that field-measured seismic velocities are usually lower than laboratory-measured velocities.

3. Data Collections

This study uses data from a report on seismic wave velocity (P wave) published by the Engineering Research Institute of Iowa State University, Ames, Iowa [51]. Field measurement of seismic wave velocity was conducted on highway embankments. The embankments were constructed with three types of soil namely, clay loam, silty clay (two weathering variations, gray and brown), and silty loam. For laboratory measurements, samples were collected from the side slope of the highway embankment adjacent to the field measurement location. One additional soil type was used for the laboratory measurements defined as loess. The types of soils investigated, and their liquid limit and plasticity index are shown in

Table 1. Type of soil used for the tests.

Soil Type	Liquid Limit	Plasticity Index
Clay loam	23	9
Silty clay (gray)	30	13
Silty clay (brown)	40	18
Silty loam	32	6
Loess	32	6

.

Micro-seismic refraction tests were conducted at 34 different locations to measure seismic velocities in the field. The equipment consists of three components: an impact source, a receiving transducer, and a seismic timer. A model 217 Micro-Seismic Timer and a transducer were used for these micro-seismic refraction tests. A tack hammer was used as the impact source on a 5/8-inch diameter steel ball-bearing to transmit the energy into the ground. Seismic measurements were taken along a 2 ft line by moving the receiver in 3-in intervals. A total of 10 first-arrival measurements were collected at each station. The seismic wave velocities were calculated from slope of the distance-time plots. At the midpoint of the seismic line, a standard rubber balloon volumetric density measurement and an in situ water content measurement were performed [52]. The range of values associated with the field measurements is listed in

Table 2. Parameters and ranges.

Type of Data	Parameters	Ranges
		Max	Min
General	Plasticity Index	21.87	2.03
	LL (%)	45.43	17.39
Field	Dry density (kg/m3)	2240.58	1465.69
	Water content (%)	18	3.87
	Velocity (m/s)	1128.99	67.12
Lab	Dry density (kg/m3)	2240.58	1465.69
	Water content (%)	20.53	4.74
	Velocity (m/s)	1675.07	57.48
Field plus Lab	Dry density (kg/m3)	2246.59	1484.71
	Water content (%)	20.96	3.13
	Velocity (m/s)	1705.07	7.23

.

In the laboratory, 35 different soils samples were compacted in 4-inch diameter by 4.58 inch high molds. Standard and modified AASHO compaction tests procedures were followed to prepare the samples. Water content, dry density of all the samples (total 35) were determined in lab. Liquid limit (LL), plasticity index (total 5 samples) were determined on for the different soil types. Seismic velocities were measured on all samples (total 35) using the pulse-transmission method.

4. Artificial Neural Networks Approach

During the past few years, artificial neural networks (ANNs) based modeling has been gaining popularity in the field of geotechnical engineering [53]. ANNs can learn complex nonlinear relationships between parameters from many data [54]. The methodology of ANN is based on the human brain activity of processing data. Much like the human brain, ANN has a large number of interconnected cells called neurons [55]. There are connection links between the neurons to transfer signals from one neuron to the other. ANN consists of three different layers (i.e., input layer, hidden layers, and output layer). Information is passed from the input layer through hidden layers to the output layer. The hidden layers process the received signals from the input layer then transmit the information to the output layer. The output layer receives the processed information from the hidden layer and executes the outputs. ANN is capable of learning highly complex relationships which are difficult to solve by traditional computational techniques. The performance of an ANN model depends on the quality and the size of the database. Erroneous and too small databases affect the accuracy of the model performance. ANN can be of different types, i.e., feed-forward neural networks, recurrent networks, and stochastic neural networks depending on the number of layers, the activation function and training algorithm [55]. The vital part of ANNs approach is the activation function, which introduces nonlinearity to the network to solve complex problems. Examples of different activation functions that can be used are linear, binary step, sigmoidal, and hyperbolic tangent sigmoid.

5. ANN Model Development

The architecture of an ANN model is determined based on the characteristics of the problem and knowledge of ANN. In this study, the feed-forward back propagation technique is used, and the nonlinear sigmoid function is chosen as the activation function. ANN models are usually developed following four different steps. In the first step, a database is divided into three different classes namely training, testing, and validation. Training sets include around 50% of the total data and are selected randomly, including minimum and maximum values of the input data. Testing and validation sets are also selected randomly and contain about 25% of the data in each set. In the second step, the optimum number of hidden nodes and iteration of the network is determined by training and testing the network. The three best-performing networks are chosen based on their statistics for comparison. In the third step, the three best networks are validated using a validation data set. For the final step, the selected three networks are re-trained using all the data to increase the prediction accuracy on the network structure that was determined in the previous step. The performance of the selected three networks is evaluated based on Mean Absolute Relative Error (MARE), Coefficient of Determination (R²), and normalized Average Squared Error (ASE) and calculated using the following equations.

$$\mathrm{MARE}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1(}^{\mathrm{N}}\left|{\mathrm{X}}_{\mathrm{i}}^{\mathrm{P}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}\right|)/{\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}}{\mathrm{N}}*100$$

(6)

$${\mathrm{R}}^2=1-\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{p}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}-\overline{{\mathrm{X}}_{\mathrm{i}}}\right)}^2}$$

(7)

$$\mathrm{ASE}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{p}}\right)}^2}{\mathrm{N}}$$

(8)

where, ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}$ = Actual value,${\mathrm{X}}_{\mathrm{i}}^{\mathrm{P}}$ = Predicted value, $\overline{{\mathrm{X}}_{\mathrm{i}}}=$ Mean of $X_i^A$, N = Total number of data.

6. ANN Models

ANN models are developed to predict seismic wave velocity, water content, and dry density using the data from the lab and field experiments. Separate ANN models are developed using lab data, field data, and lab and field data combined. Since the number of data is limited, two different ANN approaches are used for predicting seismic wave velocity. The first approach is the typical approach, where the data is used for training, testing, and validation. Around 50% of data is used for training, 25% for testing, and 25% for validation. In the second approach, the validation stage is excluded so that 75% data is used for training and 25% for testing. The parameters used for developing models are shown in Table 2, along with their ranges.

6.1. ANN Models for Predicting Seismic Wave Velocity

Six different models are developed to predict seismic wave velocity. Models are using lab data, field data and both lab and field data together following the two approaches, with validation and without validation. Correlation matrix analysis was used before selecting the input and output parameters for prediction model development.

The best three networks selected based on the statistical measures and optimal hidden nodes to predict seismic velocity using field data from LL, plasticity index, water content, and dry density are presented in

Table 3. Statistical accuracy measures of model for predicting seismic wave velocity using field data, with validation).

Model Architecture	4_ (1_1_2100) _1	4_ (2_2_2100) _1	4_ (4_4_3100) _1
Training
ASE	0.0151	0.0152	0.0152
MARE	19.61	19.87	19.75
R2	0.30	0.30	0.30
Testing
ASE	0.0122	0.0121	0.0121
MARE	21.72	21.70	21.56
R2	0.26	0.28	0.27
Validation
ASE	0.0153	0.0149	0.0147
MARE	18.54	18.63	18.49
R2	0.25	0.28	0.29
All
ASE	0.0132	0.0132	0.0133
MARE	18.87	19.01	19.04
R2	0.34	0.34	0.34

. The best model is the model which has lower the ASE, MARE and higher the R². The statistics show that ASE, MARE and R² of all three networks are very close to each other in training, testing, and all-trained. From these three networks, network 4_ (4_4_3100) _1 (where network structure is denoted as input_ (initial hidden nodes_final hidden nodes_iteration) _output) is chosen as the best model depending on the best statistics in testing. The predicted versus actual graph is shown in Figure 1a. The statistics and predicted versus actual graph indicate that the accuracy of predicting velocity is marginal. The best model for predicting velocity using field data without the validation stage is network 4_ (2_4_2900) _1. The predicted versus actual graph for network 4_ (2_4_2900) _1 is shown in Figure 1b. The statistics are presented in

Table 4. Comparing ANN models (predicting seismic wave velocity).

Source of Data	Model	Model Structure	ASE	MARE	R2
Field	with validation	4_ (4_4_3100) _1	0.0133	19.04	0.34
	without validation	4_ (2_4_2900) _1	0.0128	19.34	0.37
Lab	with validation	4_ (2_2_200) _1	0.0079	14.86	0.71
	without validation	4_ (1_5_100) _1	0.0058	13.33	0.80
Field plus Lab	with validation	4_ (1_2_2900) _1	0.0174	30.75	0.50
	without validation	4_ (5_10_20000) _1	0.0075	18.53	0.78

. The accuracy of predicting velocity is increased after omitting validation, but the overall performance is still marginal.

The best model using lab data to predict velocity is network 4_ (2_2_200) _1. The statistics in Table 4 and predicted versus actual graph shown in Figure 1c indicate that the accuracy of the velocity prediction is good. The best model to predict velocity without validation is network 4_ (1_5_100) _1. The predicted versus actual graph shown in Figure 1d and the statistics presented in Table 4 indicate that the accuracy of the velocity predictions is good. Again, excluding the validation helps to slightly minimize the errors and increases the R² values. The results also show that the errors are much lower, and the R² values are much higher for the networks trained using lab data in comparison to the network trained using field data.

The best model using field and lab data together to predict the seismic wave velocity is network 4_ (1_2_2900). The statistics are shown in Table 4. and the predicted versus actual graphs for the best network shown in Figure 1e. indicates that the accuracy is marginal. The ASE and MARE are higher after combining lab and field data in comparison to the models trained with lab and field data separately. The R² values are improve. The model developed without the validation stage is network 4_ (5_10_20000) _1 The statistics are shown in Table 4. and the predicted versus actual graphs for the best network shown in Figure 1f. indicates that the accuracy is good This model has significantly smaller errors and increased R² values compared to the model with validation.

In summary, of the results in Table 4 indicates that developing models without the validation stage in order to have more data for training results in slightly better models. The errors are lower and the R² values are higher for the network trained using lab data than using field data. The models using field data and lab data together perform in between models based solely on lab data or field data.

6.2. ANN Models for Predicting Water Content

Water content is an important index property of soil. The amount of water gives an indication of grading of soil and porosity. Soil compaction and strength is highly affected by water content. ANN models are developed to predict water content using lab and field data independently and in combination. Based on the previous models for velocity this analysis is developed without validation. Models are developed with and without velocity as input to evaluate if velocity helps in predicting water content. The statistics for the six different models are presented in

Table 5. Comparing ANN models (predicting water content).

Source of Data	Model	Model Structure	ASE	MARE	R2
Field	without velocity	3_ (2_3_1000) _1	0.0087	10.68	0.75
	with velocity	4_ (1_5_100) _1	0.0051	7.78	0.85
Lab	without velocity	3_ (4_4_100) _1	0.0051	7.69	0.82
	with velocity	4_ (3_3_100) _1	0.0043	6.63	0.89
Field plus Lab	without velocity	3_ (5_12_100) _1	0.006	10.69	0.74
	with velocity	4_ (3_3_1000) _1	0.0083	11.61	0.67

.

The best model to predict water content from LL, plasticity index, and dry density using field data is Network 3_ (2_3_1000) _1. The predicted versus actual graph for the best network is shown in Figure 2a indicates that the accuracy of predicting water content is good. Predicting water content from field data by including seismic wave velocity into the input parameters is Network 4_ (1_5_100). The predicted versus actual graph is shown in Figure 2b and the statistics indicate better accuracy in predicting water content. So, the results indicate that including seismic wave velocity improves the prediction of water content.

Using lab data to predict water content from LL, plasticity index, and dry density is best for network 3_ (3_3_100) _1 The predicted versus actual graphs are shown in Figure 2c and statistics indicate that the accuracy of predicting moisture content is higher than the model derived from field data. Adding the velocity as additional input to traditional lab data results in network 4_ (3_3_100) _1 with even better accuracy. The predicted versus actual graph for this network is shown in Figure 2d and the statistics shown in Table 5 indicate this is the best model for predicting moisture content. In summary, the models for predicting moisture content are better using laboratory data than field data and the addition of seismic velocity information enhances the models

Combining lab and field data to develop ANN models to predict water content reduces the performance of the models. Network 3_ (5_12_100) _1 is the best network without the velocity. The predicted versus actual graph, is shown in Figure 2e. The statistics indicate that the errors are higher and the R² values are lower for the network built using field data and lab data together in comparison to the network built using lab data and field data separately. So combining field and lab data together lowers the performance of the model. The predicted versus actual graph for the best network 4_ (3_3_100) _1 including seismic wave velocity into the input parameters is shown in Figure 2f. Contrary to the previous models, based on solely lab or field data, the addition of velocity as input causes the ASE, MARE to increase and the R² to decrease. In summary, models for predicting water content are more accurate when using lab data than field data. Combining the data results in much poorer models. The addition of velocity as an input to either the lab or field data results in more accurate models. Adding velocity as in input to the combined lab and field data results in poorer models.

6.3. ANN Models for Predicting Dry Density

Soil dry density is used to determine the degree of compaction. The maximum dry density is very important to increase the soil ability to support the structure and to avoid excessive settlements. ANN models are developed to predict dry density using lab and field data independently and in combination. Based on the previous models for velocity this analysis is developed without validation. Models are developed with and without velocity as input to evaluate if velocity helps in predicting dry density. The statistics for the six different models are presented in

Table 6. Comparing ANN models (predicting dry density).

Source of Data	Model	Model Structure	ASE	MARE	R2
Field	without velocity	3_ (4_4_2000) _1	0.0068	2.90	0.80
	with velocity	4_ (3_5_100) _1	0.0032	1.81	0.91
Lab	without velocity	3_ (4_4_500) _1	0.0051	2.42	0.86
	with velocity	4_ (4_4_100) _1	0.0056	2.52	0.85
Field plus Lab	without velocity	3_ (3_11_19800) _1	0.0087	2.94	0.75
	with velocity	4_ (9_9_400) _1	0.0077	3.00	0.78

.

The best model to predict dry density from LL, plasticity index and water content using field data is Network 3_ (4_4_2000) _1. The predicted versus actual graph for the best network shown in Figure 3a indicates that the accuracy of predicting dry density is good. The best ANN model developed to predict dry density with the same number of classified data and ranges but including seismic wave velocity into the input parameters is network 4_ (3_5_100) _1. The predicted versus actual graph is shown in Figure 3b and the statistics indicate better accuracy in predicting dry density So, the results indicate that including seismic wave velocity improves the prediction of dry density. The best network using lab data to predict dry density from LL, plasticity index, and dry density is network 3_ (4_4_500) _1. The predicted versus actual graphs are shown in Figure 3c and statistics indicate that the accuracy of predicting dry density is lower than the model derived from similar field data. Adding the velocity as additional input to traditional lab data results in network 4_ (4_4_100) _1.

The predicted versus actual graph for this network is shown in Figure 3d and the statistics shown in Table 6 indicate the addition of velocity in the lab data did not help to improve the results.

The models for predicting dry density are better using field data than laboratory data. This is in contrast to the results for water content shown previously. Combining lab and field data to develop ANN models to predict dry density reduces the performance of the models. Network 3_ (3_11_19800) _1 is for without the velocity. The predicted versus actual graph is shown in Figure 3e. The statistics indicate that the errors are higher and the R² values are lower for this network in comparison to the networks built using lab data or field data. The predicted versus actual graph for the best network 4_ (9_9_400) _1 including seismic wave velocity into the input parameters is shown in Figure 3f. The addition of velocity as input causes the MARE to increase but the R² is higher, and ASE is lower. This suggests a slight to insignificant improvement of the model after adding velocity as an input.

In summary, models for predicting dry density are more accurate when using field data with velocity as an input. The model based on lab data is comparable to field data-based models without the additional of velocity. Combining the lab and field data results in much poorer models. The addition of velocity as an input to either field data and lab plus field data results in more accurate models but did not help to improve the accuracy of the model build using lab data.

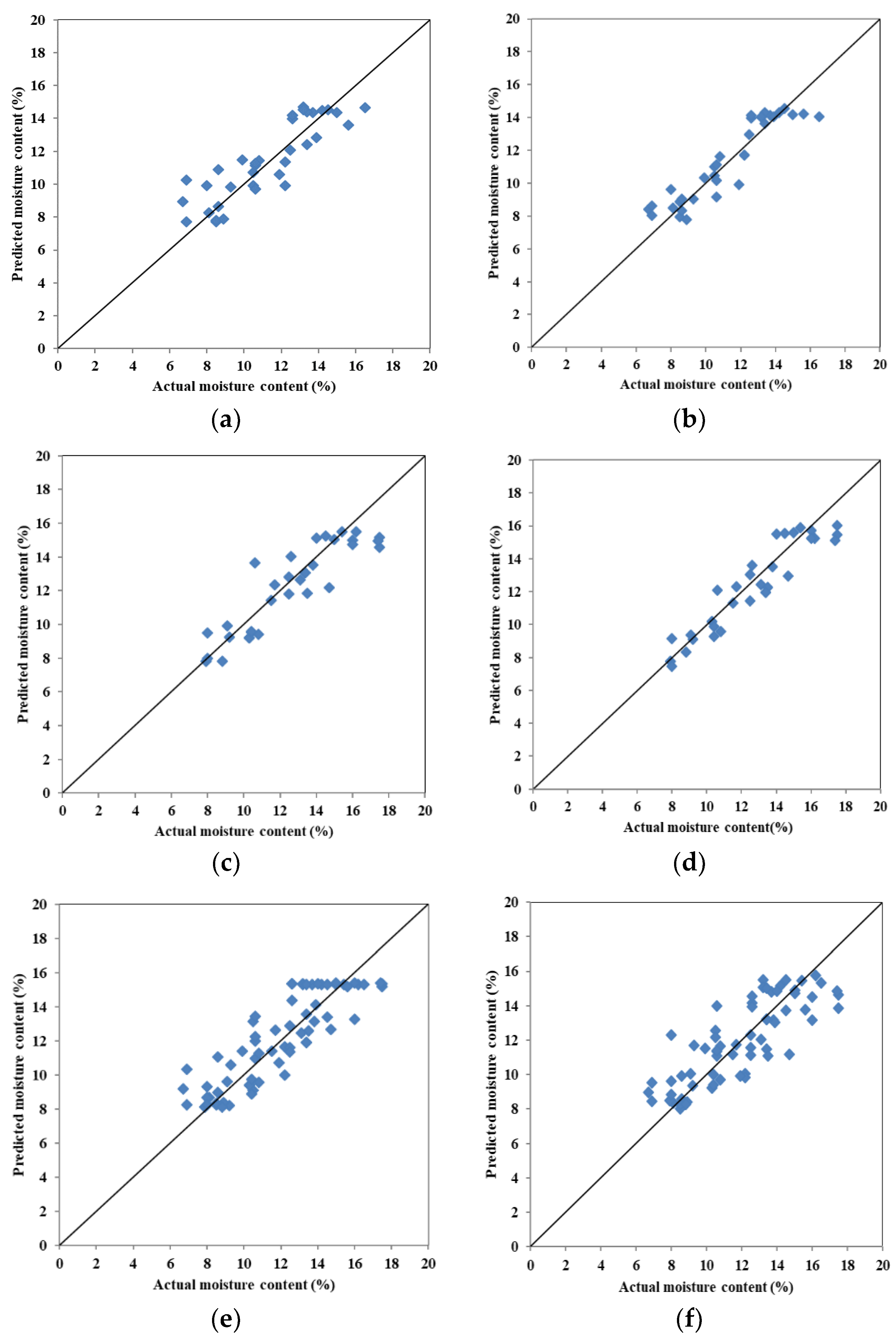
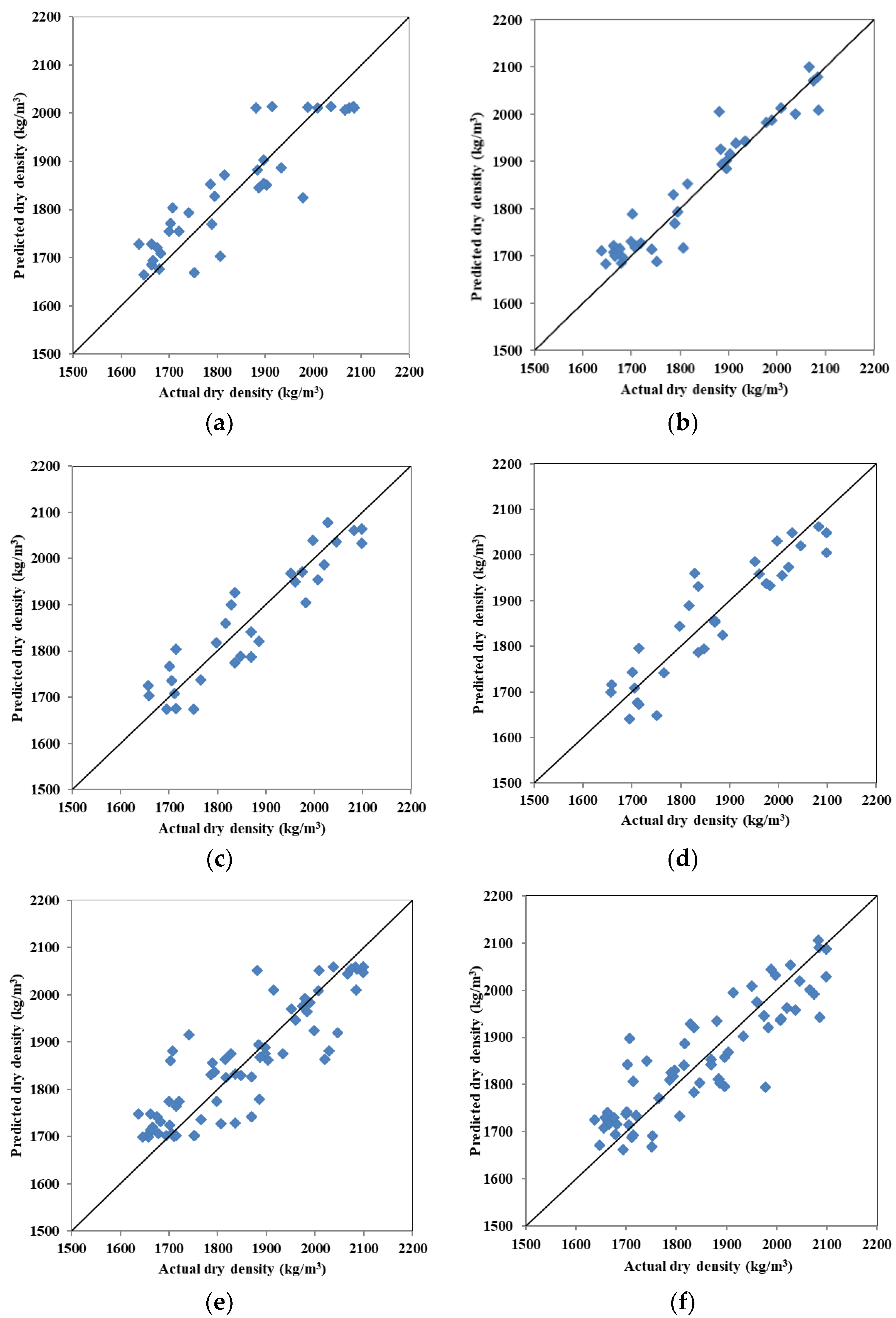
7. Comparison between ANN and Regression Models

Regression analysis is a conventional way to determine the relationship between independent and dependent variables. It determines how strongly the independent variables affect the depended variables. Multiple-linear regression analyses are performed using the same databases used for the ANN models. The performance of the models is determined based on RMSE, MARE, unnormalized ASE and R². For predicting seismic wave velocity three different data set: lab data, field data and both lab and field data are used. Input parameters for predicting seismic wave velocity models are LL, plasticity index, water content and dry density.

For predicting water content LL, plasticity index, dry density and velocity are used as input parameters. Models are developed for lab, field and both lab and field data sets. For predicting dry density same type of data set and approach are used except the input parameters are LL, plasticity index, water content and seismic wave velocity. The results of regression analysis are shown in

Table 7. Comparison of ANN and regression models.

Model	Source of Data	ANN				Regression
		RMSE	ASE	MARE	R2	RMSE	ASE	MARE	R2
Predicting velocity	F	394	155,616	19.3	0.37	403	162,712	18.8	0.34
	L	403	162,650	13.3	0.80	465	216,368	15.4	0.72
	F + L	483	233,701	18.5	0.78	772	596,434	30.8	0.43
Predicting water content	F	1.0	1.0	7.7	0.85	1.5	2.3	12	0.66
	L	1.0	1.0	6.6	0.89	0.9	0.9	6.5	0.88
	F + L	1.6	2.6	11.6	0.67	1.6	2.7	12	0.66
Predicting dry density	F	2.7	7.5	1.8	0.91	4.9	24.2	3.3	0.69
	L	3.4	11.6	2.5	0.85	3.3	11.0	2.4	0.85
	F + L	4.1	17.5	3	0.78	4.4	19.5	3.1	0.75

Note: Field (F), Lab (L).

.

Table 7 presents the statistics for ANN (without validation) and regression models. To compare ANN models with regression models the unnormalized ASE is calculated using the unnormalized actual and predicted values. Additionally, root mean squared error (RMSE) is also calculated using.

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{A}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{p}}\right)}^2}{\mathrm{N}}}$$

(9)

For predicting seismic wave velocity, the regression model using laboratory data showed the higher R² value and lower MARE but higher. ASE and RMSE than field data models. Combining the field and lab data increased errors and a R² value in between the models using individual lab and field data. For predicting water content, the regression models based on lab data also showed the best performance The performance of field data and field plus lab data are very close to each other. For predicting dry density, the best performance is also observed for the lab data model. The second-best model is field plus lab data and lowest performance is observed for the field data.

For all the cases, ANN models resulted in better R2 values in comparison to regression analysis. Significant improvements are observed for the case of field data for predicting water content, the R2 increases 22.35%, using field data for predicting dry density the R2 increase 24.18% and for using field & lab data for predicting seismic wave velocity the R2 increase 44.87%. Errors are lower for ANN models in comparison to regression models with some minor exceptions. ANN models showed significantly reduced errors than regression models using with field data for predicting water content RMSE decreases 50%, ASE decreases 130%, MARE decreases 55.84%, for predicting dry density the RMSE decreases 81.48%, ASE decreases 222.67%, 83.33%. The model build with field and lab data for predicting velocity the RMSE decreases 59.83%, ASE decreases 155.21% and MARE decreases 66.49%. So, it appears that ANN shows better accuracy in prediction when compared to regression analysis.

8. Conclusions

This study used ANN and regression analysis to predict geotechnical parameters from seismic wave velocity and other geotechnical parameters using a published data. The geotechnical parameters used here are plasticity index, LL, dry dry density, and water content. The aim was to evaluate the use of seismic wave velocity to predict geotechnical parameters so that it can save time and cost by minimizing the number of geotechnical tests.

From the analysis this can be concluded that seismic wave velocity helps to predict water content and dry density. This validates that seismic wave velocity is sensitive to change in water content and dry density. Combination of other geophysical parameters may increase the accuracy of the prediction model. The study shows that the performance of the prediction models is better when lab and filed data are used separately. However, combining lab and field data resulted in poorer models and requires further investigation. From the comparison of ANN and regression models it is proved that ANN can predict better with more accuracy than traditional regression analysis. This study showed the correlation between seismic wave velocity and water content, dry density for four types of soil using field and lab data. Other geotechnical parameters such as angle of friction, cohesion, saturation, void ratio can be considered for developing correlations. Correlations can also be developed for other soil types.