ConDPC: Data Connectivity-Based Density Peak Clustering
Abstract
1. Introduction
- (1)
- Constructing connected groups based on the idea of connectivity. Points in the same group are connectable to each other, whereas points in different groups are not.
- (2)
- Adjusting the calculation method of neighbor distance based on the idea of connectivity to improve the accuracy of determining the cluster center.
- (3)
- Adjusting the neighbor allocation strategy based on the idea of connectivity to improve the accuracy of clustering.
2. Original Algorithm
3. Proposed Algorithm
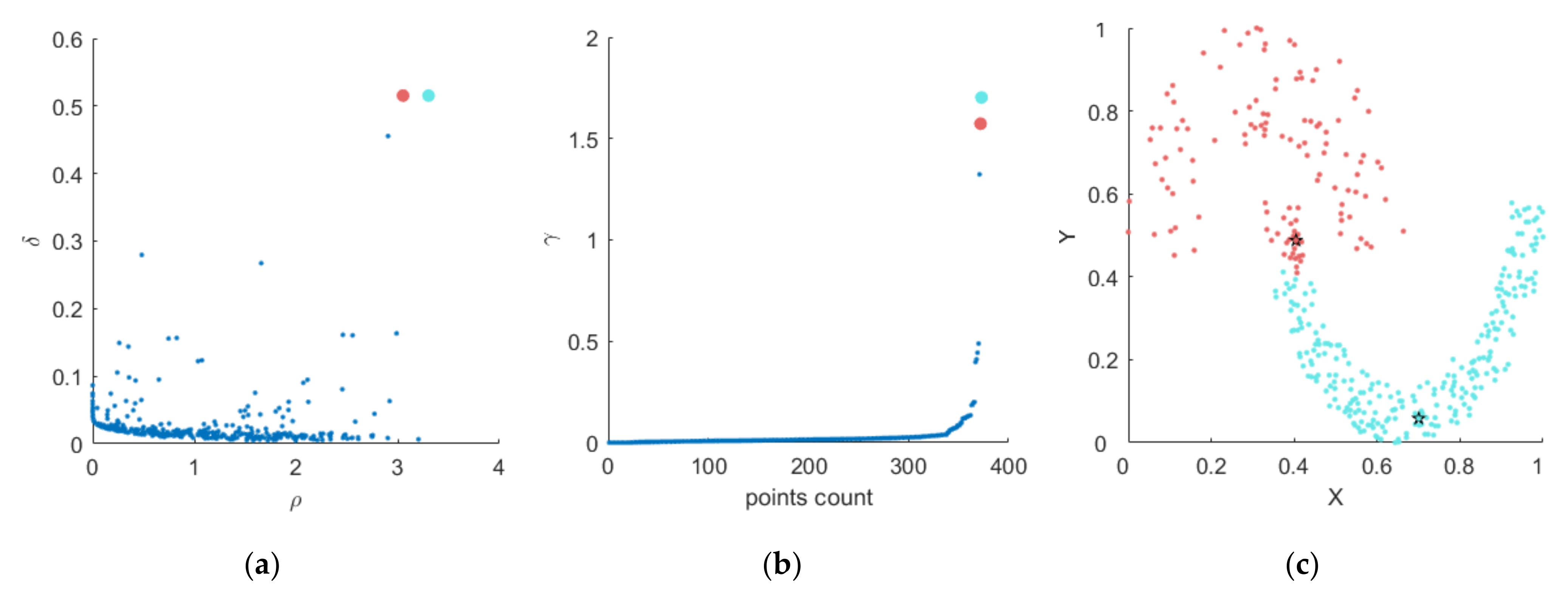
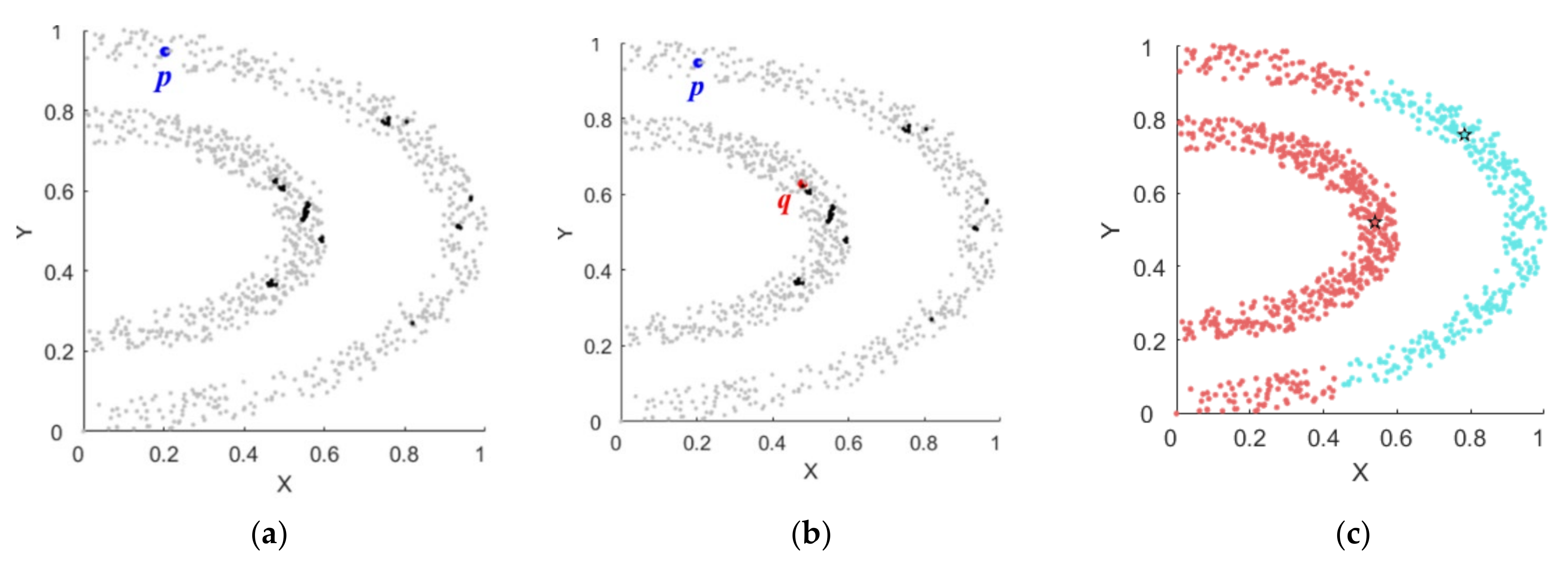
3.1. Basic Definitions
3.2. Steps of the Proposed Algorithm
| Algorithm 1 Calculate connected groups |
| Input: input dataset; cutoff distance Output: connected groups 1. Mark all points as ungrouped; 2. For each point that has not been grouped 3. Create a new group G, mark point as grouped in G, and add its directly connectable point set to G; 4. For each point in G that has not been grouped 5. Mark point as grouped in G, and add its directly connectable point set to G; 6. End For 7. End For 8. Return connected groups; |
| Algorithm 2 Calculate and neighbor assignment |
| Input: local density matrix; distance matrix; connected groups Output: and neighbor assignment matrix 1. Sort all points in descending order of density; 2. For each point that has no neighbors assigned 3. In the set of all points with a density larger than point , if there is a subset connectable to point (that is, there are big neighbors of point in the same connected group as ), select the point closest to point in as the neighbor of point , and update to ; 4. In the set , if there is no point connectable to point (that is, there is no big neighbor in the same connected group as point ), select the point closest to point in as the neighbor of point , and update to the maximum value; 5. End For 6. Return and neighbor assignment matrix; |
| Algorithm 3 Identifying cluster centers and Label assignment |
| Input: input dataset Output: clustering result 1. Normalize the dataset; 2. Calculate distance matrix ; 3. Calculate the local density of each point according to Formula (1); 4. Call Algorithm 1 to obtain connected groups; 5. Call Algorithm 2 to obtain and neighbor assignment matrix; 6. Calculate decision value according to Formula (4); 7. Draw the decision diagram and select the appropriate cluster centers according to the decision value; 8. Assign other points to corresponding categories according to the neighborassignment results in Algorithm 2; |
4. Experiments and Results
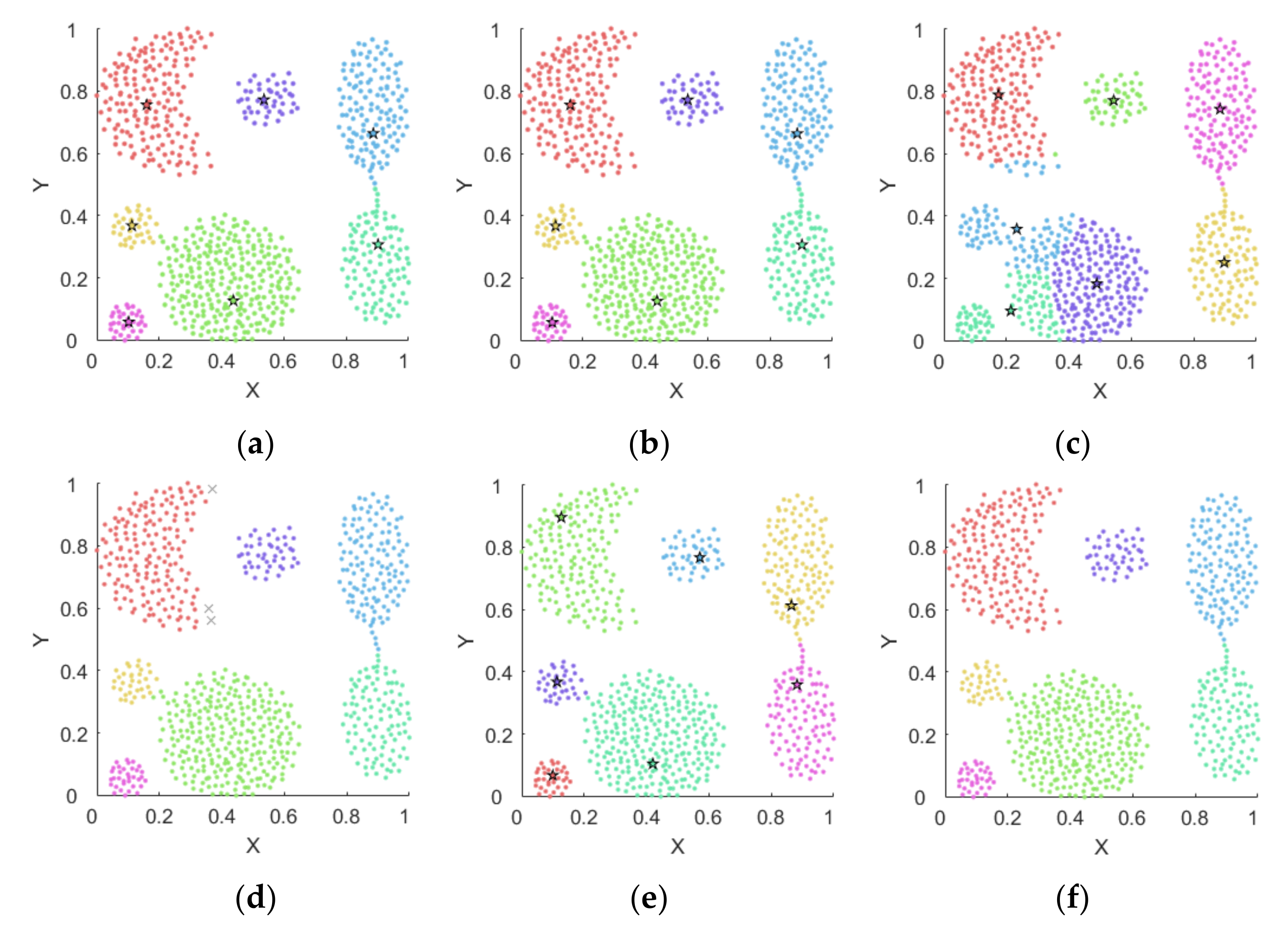
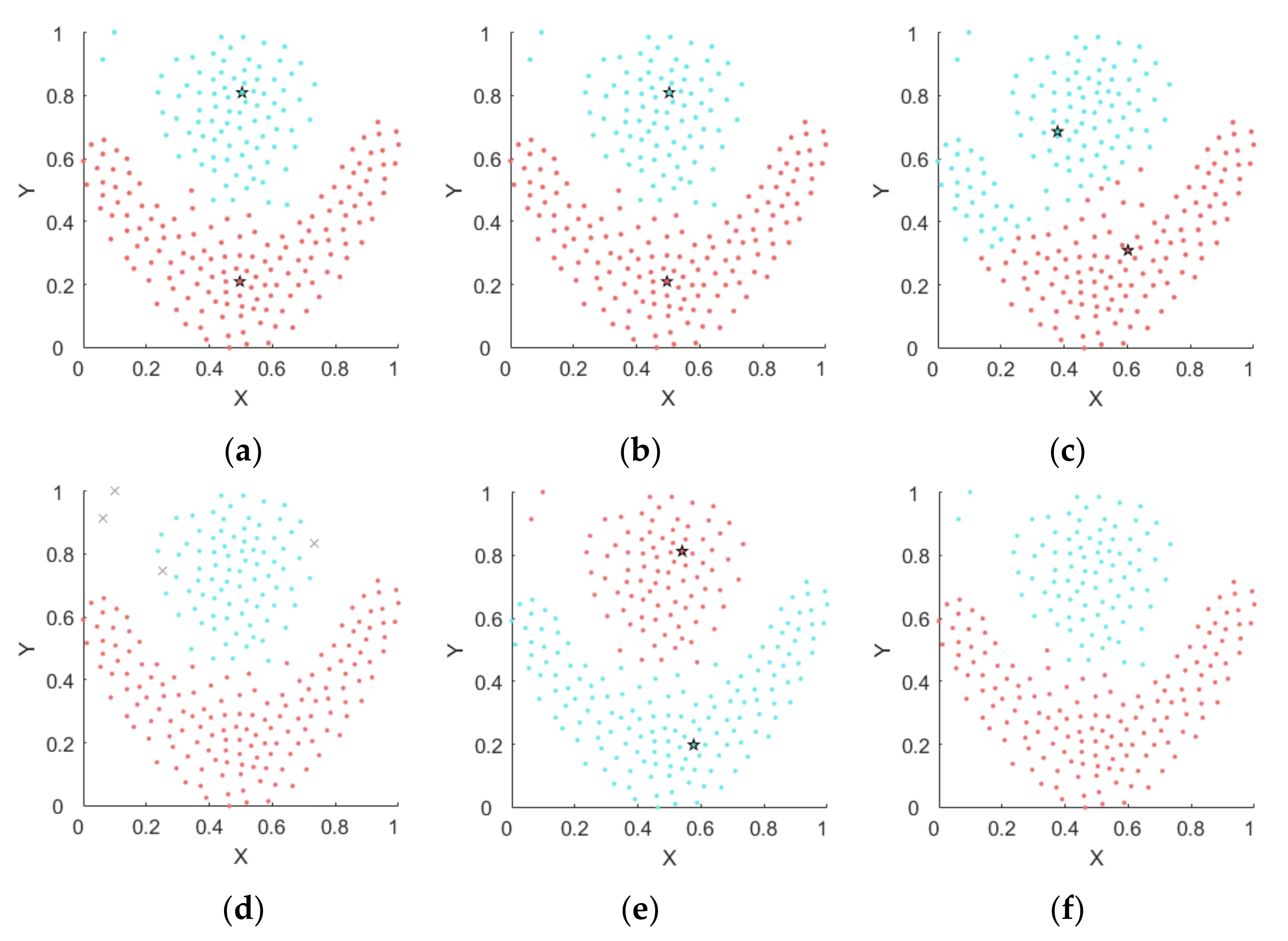
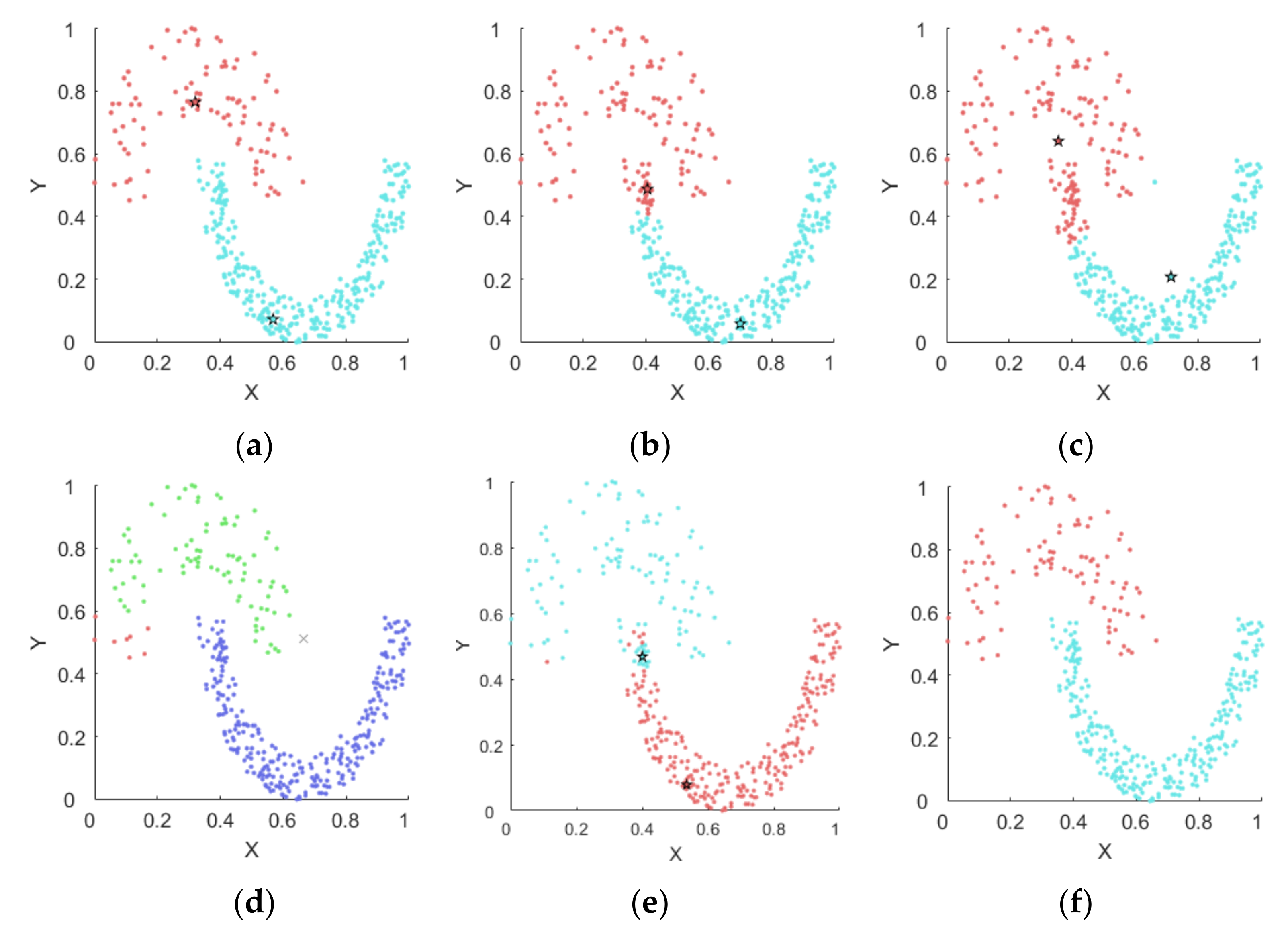
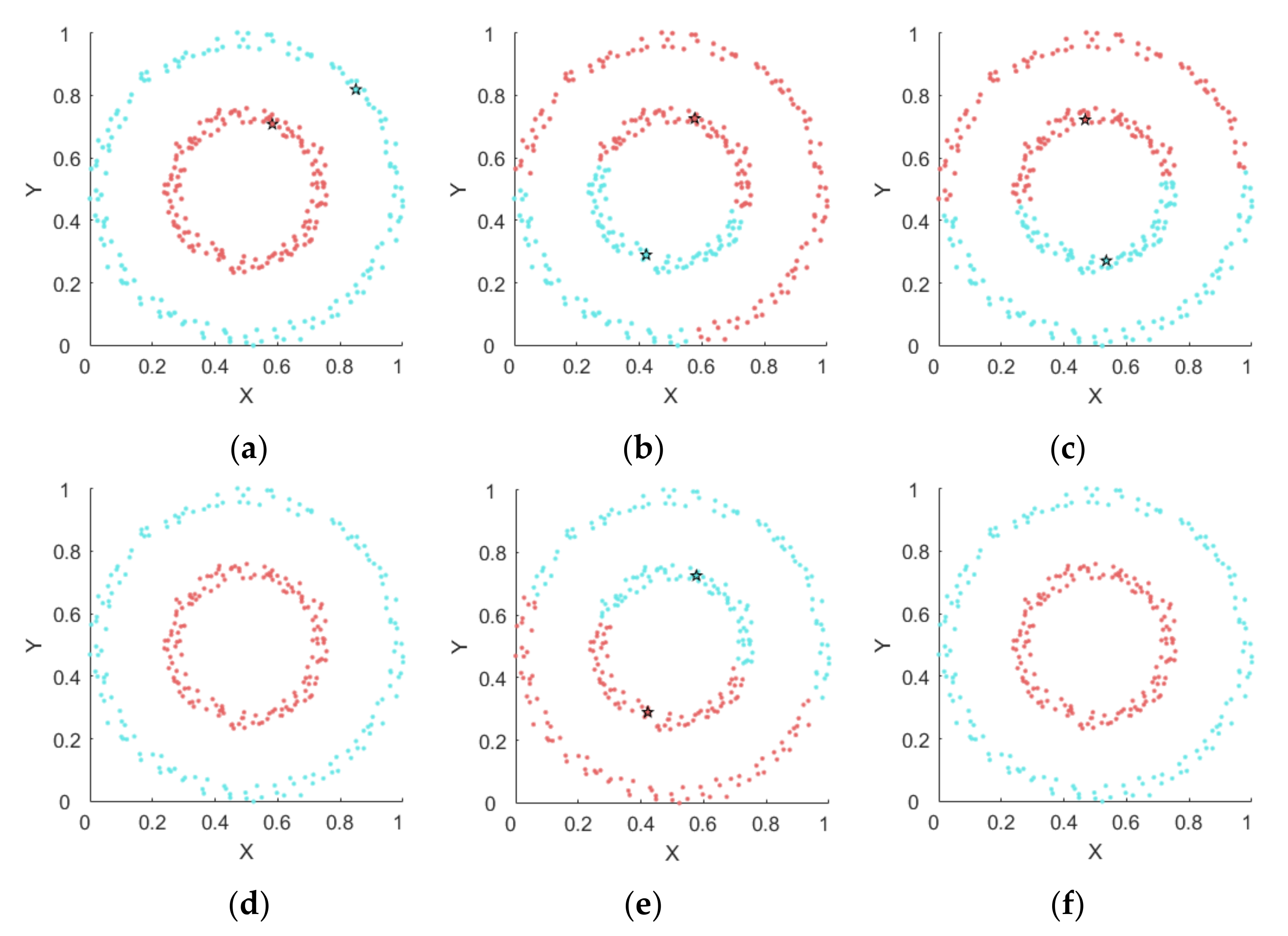
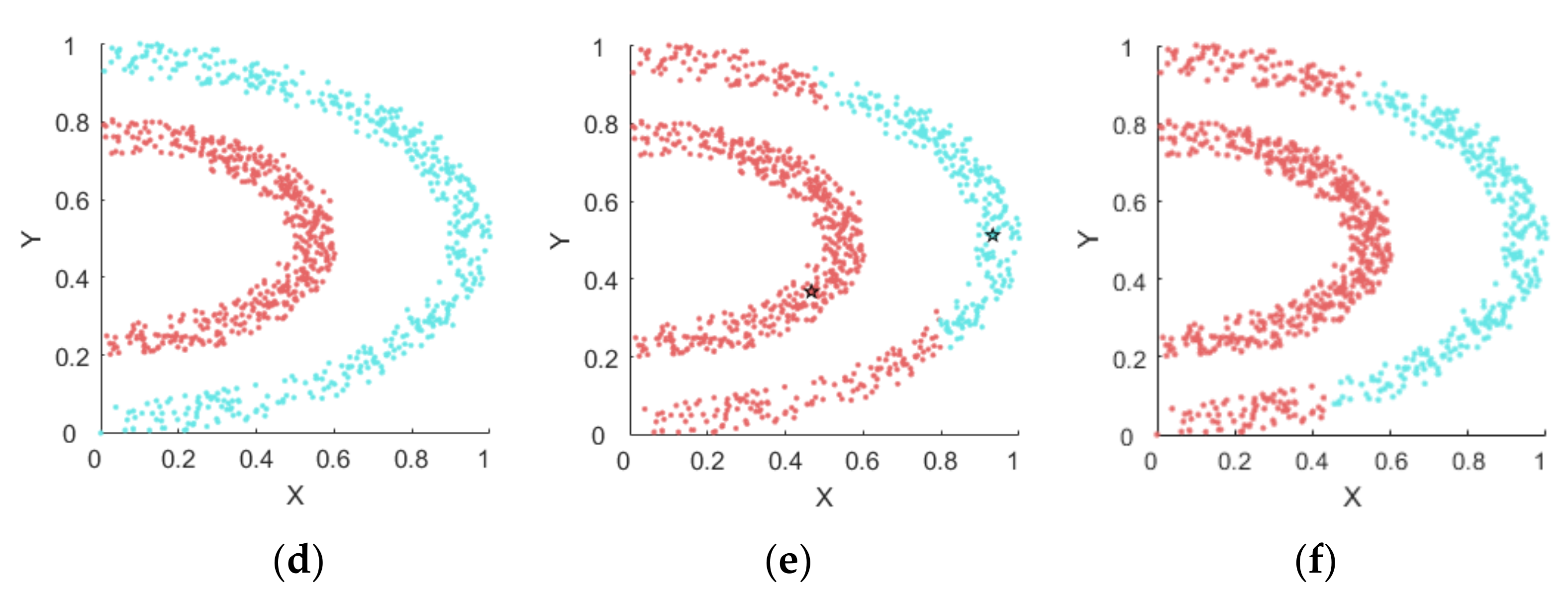
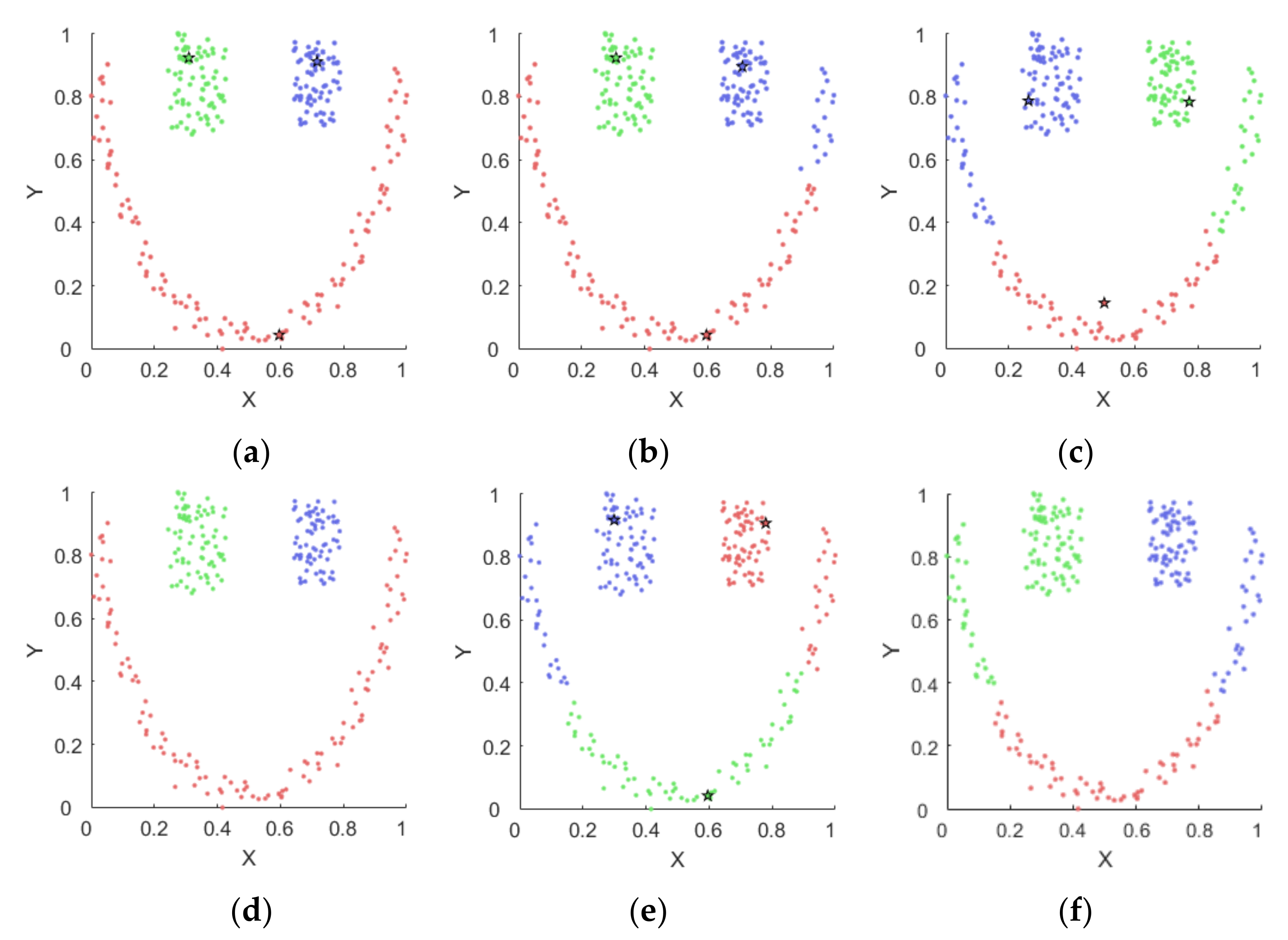
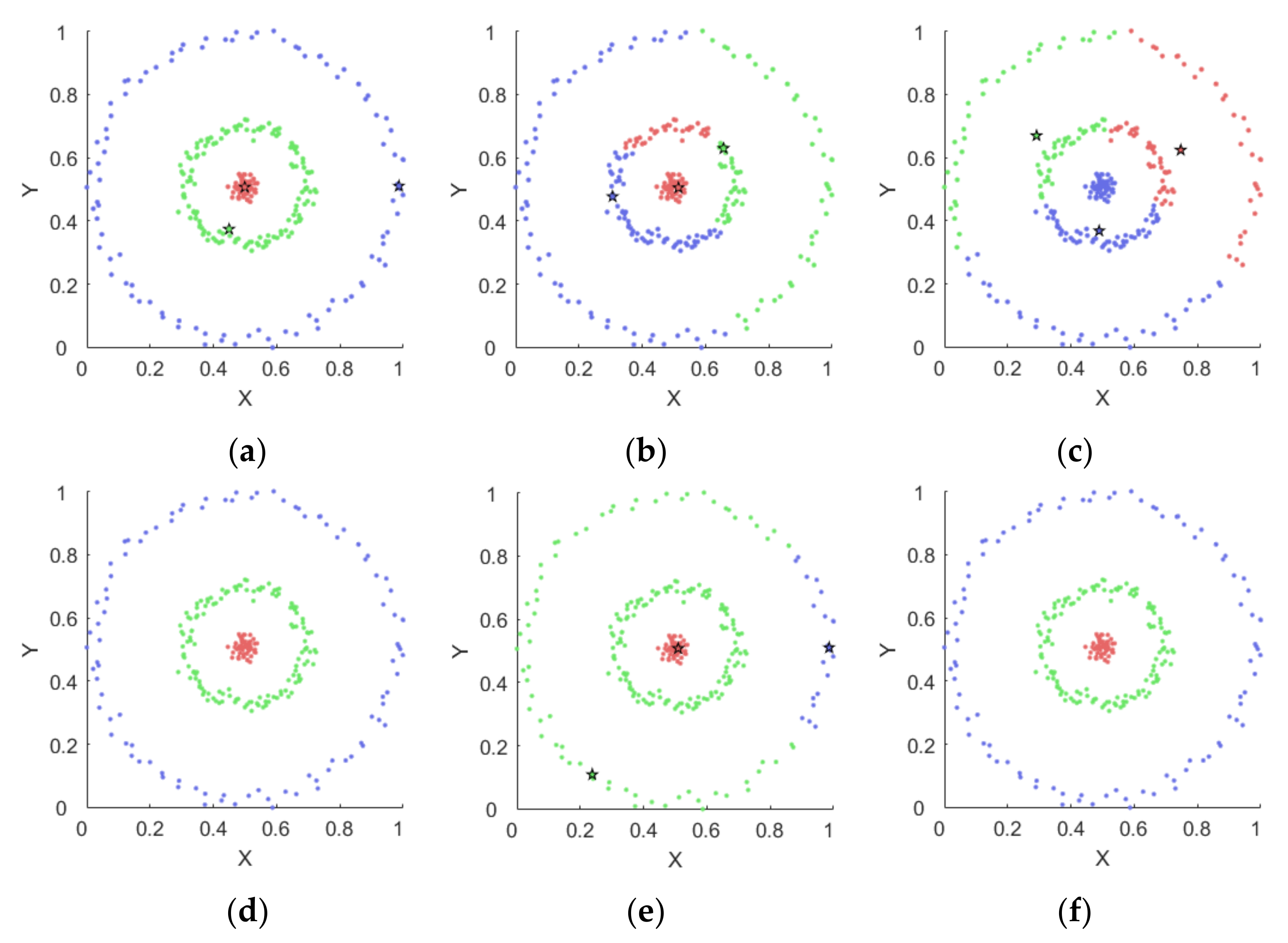
4.1. Experiments on Synthetic Datasets
4.1.1. Synthetic Datasets
4.1.2. Results on Synthetic Datasets
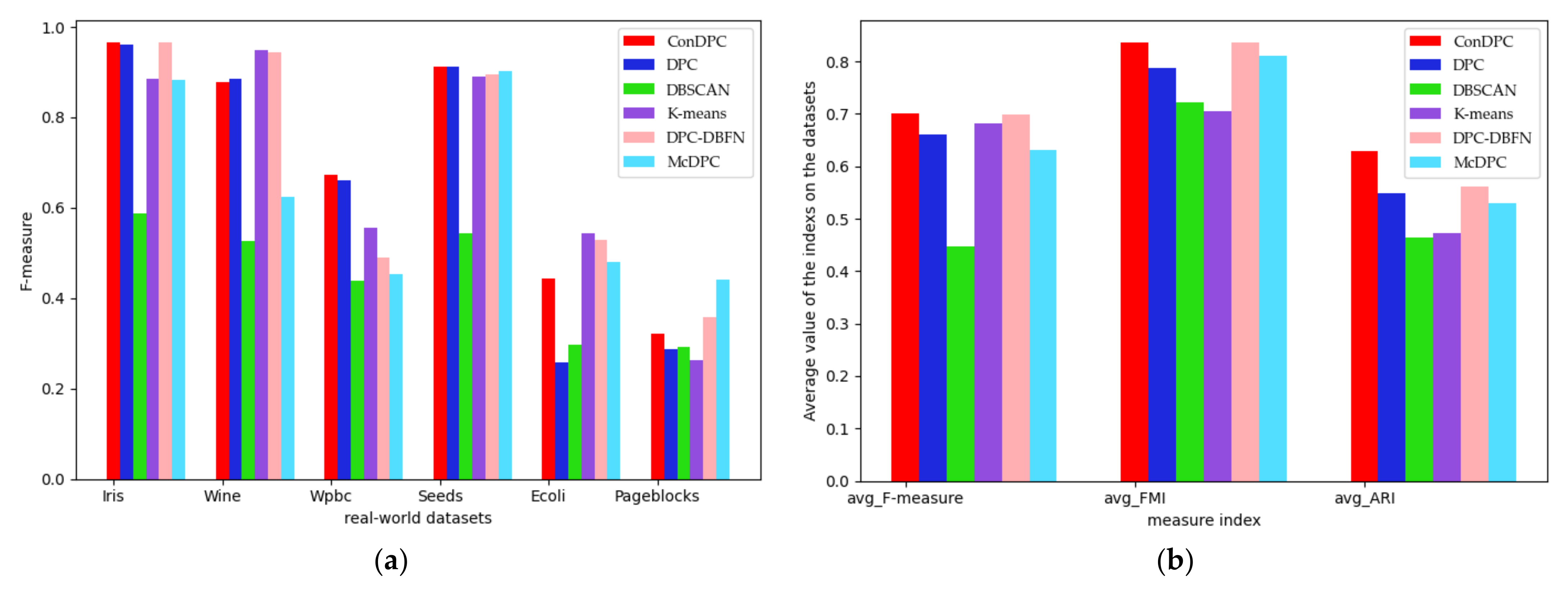
4.2. Experiments on Real-World Datasets
4.2.1. Real-World Datasets
4.2.2. Results on Real-World Datasets
4.3. Experimental Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Waltham, MA, USA, 2011; pp. 443–450. [Google Scholar]
- Zhu, Y.; Ting, K.M.; Carman, M.J. Density-ratio based clustering for discovering clusters with varying densities. Pattern Recognit. 2016, 60, 983–997. [Google Scholar] [CrossRef]
- Pavithra, L.K.; Sree, S.T. An improved seed point selection-based unsupervised color clustering for content-based image retrieval application. Comp. J. 2019, 63, 337–350. [Google Scholar] [CrossRef]
- Sun, Z.; Qi, M.; Lian, J.; Jia, W.; Zou, W.; He, Y.; Liu, H.; Zheng, Y. Image Segmentation by Searching for Image Feature Density Peaks. Appl. Sci. 2018, 8, 969. [Google Scholar] [CrossRef]
- Akila, I.S.; Venkatesan, R. A Fuzzy Based Energy-aware Clustering Architecture for Cooperative Communication in WSN. Comp. J. 2016, 59, 1551–1562. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, M.; Li, Q.; Qian, L. Fault Diagnosis Method Based on Time Series in Autonomous Unmanned System. Appl. Sci. 2022, 12, 7366. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD 96, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 49–60. [Google Scholar]
- Hinneburg, A.; Gabriel, H.H. Denclue 2.0: Fast clustering based on kernel density estimation. In Proceedings of the 7th International Symposium on Intelligent Data Analysis, Ljubljana, Slovenia, 6–8 September 2007; pp. 70–80. [Google Scholar]
- Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. Density-based clustering in spatial databases: The algorithm GDBSCAN and its applications. Data Min. Knowl. Disc. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Madhulatha, T.S. An overview on clustering methods. IOSR J. Eng. 2012, 2, 719–725. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Du, M.; Ding, S.; Jia, H. Study on density peaks clustering based on k-nearest neighbors and principal component analysis. Knowl. Based Syst. 2016, 99, 135–145. [Google Scholar] [CrossRef]
- Xie, J.; Gao, H.; Xie, W.; Liu, X.; Grant, P.W. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors. Inf. Sci. 2016, 354, 19–40. [Google Scholar] [CrossRef]
- Lotfi, A.; Moradi, P.; Beigy, H. Density peaks clustering based on density backbone and fuzzy neighborhood. Pattern Recognit. 2020, 107, 107449. [Google Scholar] [CrossRef]
- Du, M.; Ding, S.; Xue, Y.; Shi, Z. A novel density peaks clustering with sensitivity of local density and density-adaptive metric. Knowl. Inf. Syst. 2018, 59, 285–309. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Zhang, X.; Pang, W.; Miao, C.; Tan, A.; Zhou, Y. McDPC: Multi-center density peak clustering. Neural Comput. Appl. 2020, 32, 13465–13478. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Z.; Yu, F. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy. Knowl. Based Syst. 2017, 133, 208–220. [Google Scholar]
- Tao, X.; Guo, W.; Ren, C.; Li, Q.; He, Q.; Liu, R.; Zou, J. Density peak clustering using global and local consistency adjustable manifold distance. Inf. Sci. 2021, 577, 769–804. [Google Scholar] [CrossRef]
- Supplementary Materials for Clustering by Fast Search and Find of Density Peaks. Available online: https://www.science.org/doi/suppl/10.1126/science.1242072 (accessed on 20 September 2022).
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January1966; pp. 281–297. [Google Scholar]
- Rijsbergen, V. Foundation of Evaluation. J. Doc. 1974, 30, 365–373. [Google Scholar] [CrossRef]
- Fowlkes, E.B.; Mallows, C.L. A method for comparing two hierarchical clusterings. J. Am. Stat. Assoc. 1983, 78, 553–569. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Guan, J.; Li, S.; He, X.; Zhu, J.; Chen, J. Fast hierarchical clustering of local density peaks via an association degree transfer method. Neurocomputing 2021, 455, 401–418. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, L.; Han, X.; Li, M. A novel deviation density peaks clustering algorithm and its applications of medical image segmentation. IET Image Process. 2022, 16, 3790–3804. [Google Scholar] [CrossRef]
- Gionis, A.; Mannila, H.; Tsaparas, P. Clustering aggregation. In Proceedings of the 21st International Conference on Data Engineering, Tokyo, Japan, 5–8 April 2005; pp. 341–352. [Google Scholar]
- Fu, L.; Medico, E. Flame, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinf. 2007, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Veenman, C.J.; Reinders, M.J.T.; Backer, E. A maximum variance cluster algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1273–1280. [Google Scholar] [CrossRef]
- Jain, A.K.; Law, M.H.C. Data clustering: A user’s dilemma. In Proceedings of the Pattern Recognition and Machine Intelligence, Kolkata, India, 20–22 December 2005; pp. 1–10. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; pp. 849–856. [Google Scholar]
- Zelnik-Manor, L.; Perona, P. Self-tuning spectral clustering. In Proceedings of the 17th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 1 December 2004; pp. 1601–1608. [Google Scholar]
- Liu, R.; Wang, H.; Yu, X. Shared-nearest-neighbor-based clustering by fast search and find of density peaks. Inf. Sci. 2018, 450, 200–226. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 20 September 2022).


| Algorithm | Parameter(s) and the Search Range |
|---|---|
| ConDPC | |
| DPC | |
| DBSCAN | , |
| K-means | : number of clusters |
| DPC-DBFN | |
| McDPC | , , |
| Dataset | Source | Instances | Features | Clusters |
|---|---|---|---|---|
| Aggregation | [28] | 788 | 2 | 7 |
| Flame | [29] | 240 | 2 | 2 |
| R15 | [30] | 600 | 2 | 15 |
| Jain | [31] | 373 | 2 | 2 |
| Twocircle | [32] | 314 | 2 | 2 |
| Halfkernal | [17] | 1000 | 2 | 2 |
| Halfcircle | [33] | 238 | 2 | 3 |
| Threecircle | [33] | 299 | 2 | 3 |
| Algorithm | Aggregation | Flame | R15 | Jain | Twocircle | Halfkernal | Halfcircle | Threecircle | |
|---|---|---|---|---|---|---|---|---|---|
| ConDPC | F-measure | 0.998 | 1 | 0.997 | 1 | 1 | 1 | 1 | 1 |
| FMI | 0.997 | 1 | 0.993 | 1 | 1 | 1 | 1 | 1 | |
| ARI | 0.996 | 1 | 0.993 | 1 | 1 | 1 | 1 | 1 | |
| Parameter | 3.1 | 2.7 | 3.4 | 3 | 2.7 | 1.5 | 3.8 | 7.2 | |
| DPC | F-measure | 0.998 | 1 | 0.997 | 0.910 | 0.610 | 0.819 | 0.943 | 0.586 |
| FMI | 0.997 | 1 | 0.993 | 0.882 | 0.534 | 0.729 | 0.884 | 0.492 | |
| ARI | 0.996 | 1 | 0.993 | 0.715 | 0.050 | 0.422 | 0.824 | 0.214 | |
| Parameter | 3.1 | 2.7 | 3.4 | 0.3 | 0.2 | 0.1 | 4.2 | 0.2 | |
| DBSCAN | F-measure | 0.996 | 0.979 | 0.994 | 0.976 | 1 | 1 | 1 | 1 |
| FMI | 0.994 | 0.974 | 0.988 | 0.990 | 1 | 1 | 1 | 1 | |
| ARI | 0.992 | 0.944 | 0.987 | 0.976 | 1 | 1 | 1 | 1 | |
| Parameter | 0.08/21 | 0.1/10 | 0.05/30 | 0.08/2 | 0.07/4 | 0.08/5 | 0.08/5 | 0.09/5 | |
| K-Means | F-measure | 0.834 | 0.833 | 0.997 | 0.864 | 0.510 | 0.522 | 0.798 | 0.451 |
| FMI | 0.788 | 0.736 | 0.993 | 0.820 | 0.497 | 0.506 | 0.665 | 0.403 | |
| ARI | 0.730 | 0.453 | 0.993 | 0.577 | −0.003 | 0.002 | 0.488 | 0.053 | |
| Parameter | 7 | 2 | 15 | 2 | 2 | 2 | 3 | 3 | |
| DPC-DBFN | F-measure | 0.995 | 0.991 | 0.998 | 0.925 | 0.503 | 0.743 | 0.818 | 0.712 |
| FMI | 0.994 | 0.985 | 0.997 | 0.906 | 0.497 | 0.674 | 0.687 | 0.715 | |
| ARI | 0.993 | 0.967 | 0.996 | 0.768 | −0.003 | 0.267 | 0.522 | 0.476 | |
| Parameter | 30 | 6 | 39 | 14 | 4 | 7 | 3 | 17 | |
| McDPC | F-measure | 0.998 | 1 | 0.997 | 1 | 1 | 0.819 | 0.798 | 1 |
| FMI | 0.997 | 1 | 0.993 | 1 | 1 | 0.729 | 0.665 | 1 | |
| ARI | 0.996 | 1 | 0.993 | 1 | 1 | 0.422 | 0.488 | 1 | |
| Parameter | 0.1/0.01/0.21/1 | 0.1/0.01/ 0.4/5 | 0.05/0.01/ 0.05/2 | 0.3/0.3/0.23/5 | 0.2/0.5/0.08/2 | 0.01/0.01/ 0.21/5 | 0.3/0.5/0.3/2 | 0.3/0.5/0.08/2 |
| Dataset | Source | Instances | Features | Clusters |
|---|---|---|---|---|
| Iris | [35] | 150 | 4 | 3 |
| Wine | [35] | 178 | 13 | 3 |
| Wpbc | [35] | 198 | 32 | 2 |
| Seeds | [35] | 210 | 7 | 7 |
| Ecoli | [35] | 336 | 7 | 8 |
| Pageblocks | [35] | 5473 | 10 | 5 |
| Algorithm | Iris | Wine | Wpbc | Seeds | Ecoli | Pageblocks | Average | |
|---|---|---|---|---|---|---|---|---|
| ConDPC | F-measure | 0.967 | 0.879 | 0.673 | 0.913 | 0.444 | 0.322 | 0.700 |
| FMI | 0.935 | 0.775 | 0.762 | 0.844 | 0.777 | 0.926 | 0.837 | |
| ARI | 0.904 | 0.660 | 0.244 | 0.767 | 0.692 | 0.498 | 0.628 | |
| Parameter | 2.5 | 0.8 | 0.4 | 0.7 | 0.6 | 2.7 | ||
| DPC | F-measure | 0.960 | 0.885 | 0.661 | 0.913 | 0.259 | 0.287 | 0.661 |
| FMI | 0.923 | 0.783 | 0.760 | 0.844 | 0.506 | 0.908 | 0.787 | |
| ARI | 0.886 | 0.672 | 0.227 | 0.767 | 0.349 | 0.387 | 0.548 | |
| Parameter | 0.2 | 2.0 | 7.4 | 0.7 | 0.4 | 8 | ||
| DBSCAN | F-measure | 0.587 | 0.526 | 0.439 | 0.543 | 0.298 | 0.293 | 0.448 |
| FMI | 0.753 | 0.718 | 0.563 | 0.694 | 0.763 | 0.848 | 0.723 | |
| ARI | 0.625 | 0.538 | 0.034 | 0.524 | 0.669 | 0.392 | 0.464 | |
| Parameter | 0.13/9 | 0.51/23 | 0.64/4 | 0.3/35 | 0.23/30 | 0.08/33 | ||
| K-Means | F-measure | 0.885 | 0.949 | 0.555 | 0.891 | 0.543 | 0.263 | 0.681 |
| FMI | 0.811 | 0.903 | 0.579 | 0.803 | 0.559 | 0.583 | 0.706 | |
| ARI | 0.716 | 0.854 | 0.032 | 0.705 | 0.425 | 0.108 | 0.473 | |
| Parameter | 3 | 3 | 2 | 3 | 8 | 5 | ||
| DPC-DBFN | F-measure FMI ARI Parameter | 0.967 0.935 0.904 5 | 0.945 0.888 0.832 3 | 0.489 0.721 0.004 19 | 0.896 0.809 0.715 4 | 0.530 0.755 0.658 3 | 0.358 0.914 0.254 39 | 0.698 0.837 0.561 |
| McDPC | F-measure FMI ARI Parameter | 0.883 0.816 0.720 0.1/0.1/0.34/1 | 0.625 0.680 0.439 0.2/0.3/0.6/1 | 0.452 0.787 0.008 0.2/0.52/0.3/0.3 | 0.903 0.826 0.742 0.02/0.02/0.3/0.3 | 0.480 0.822 0.739 0.02/0.01/0.3/0.5 | 0.440 0.928 0.524 0.01/0.01/ 0.33/1 | 0.631 0.810 0.529 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Wang, Z. ConDPC: Data Connectivity-Based Density Peak Clustering. Appl. Sci. 2022, 12, 12812. https://doi.org/10.3390/app122412812
Zou Y, Wang Z. ConDPC: Data Connectivity-Based Density Peak Clustering. Applied Sciences. 2022; 12(24):12812. https://doi.org/10.3390/app122412812
Chicago/Turabian StyleZou, Yujuan, and Zhijian Wang. 2022. "ConDPC: Data Connectivity-Based Density Peak Clustering" Applied Sciences 12, no. 24: 12812. https://doi.org/10.3390/app122412812
APA StyleZou, Y., & Wang, Z. (2022). ConDPC: Data Connectivity-Based Density Peak Clustering. Applied Sciences, 12(24), 12812. https://doi.org/10.3390/app122412812





