Experimental and Numerical Study of the Flow Field Structure of High-Speed Train with Different Nose Lengths Head at 15° Yaw
Abstract
1. Introduction
2. Experimental
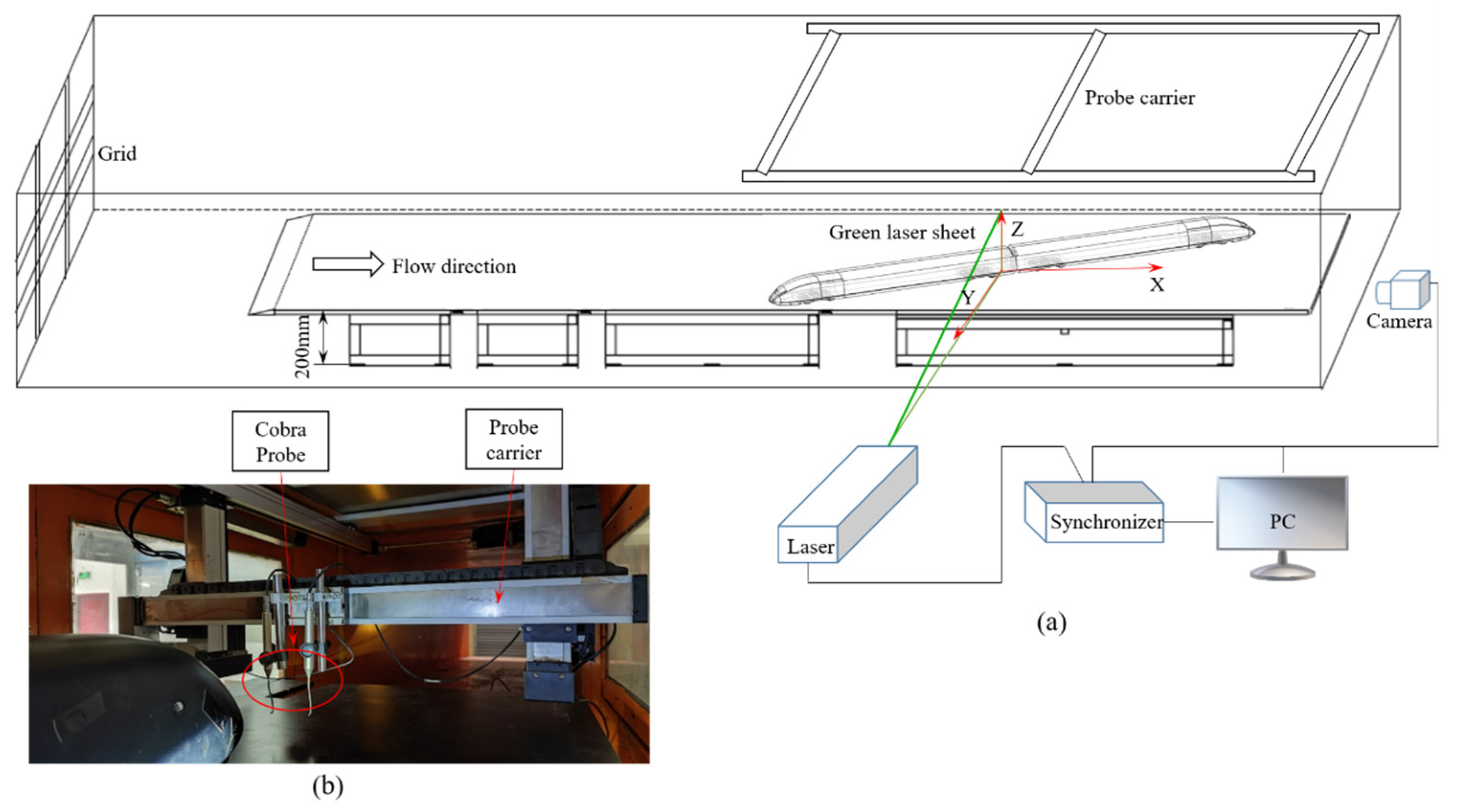
2.1. Experimental Setup and Wind Tunnel
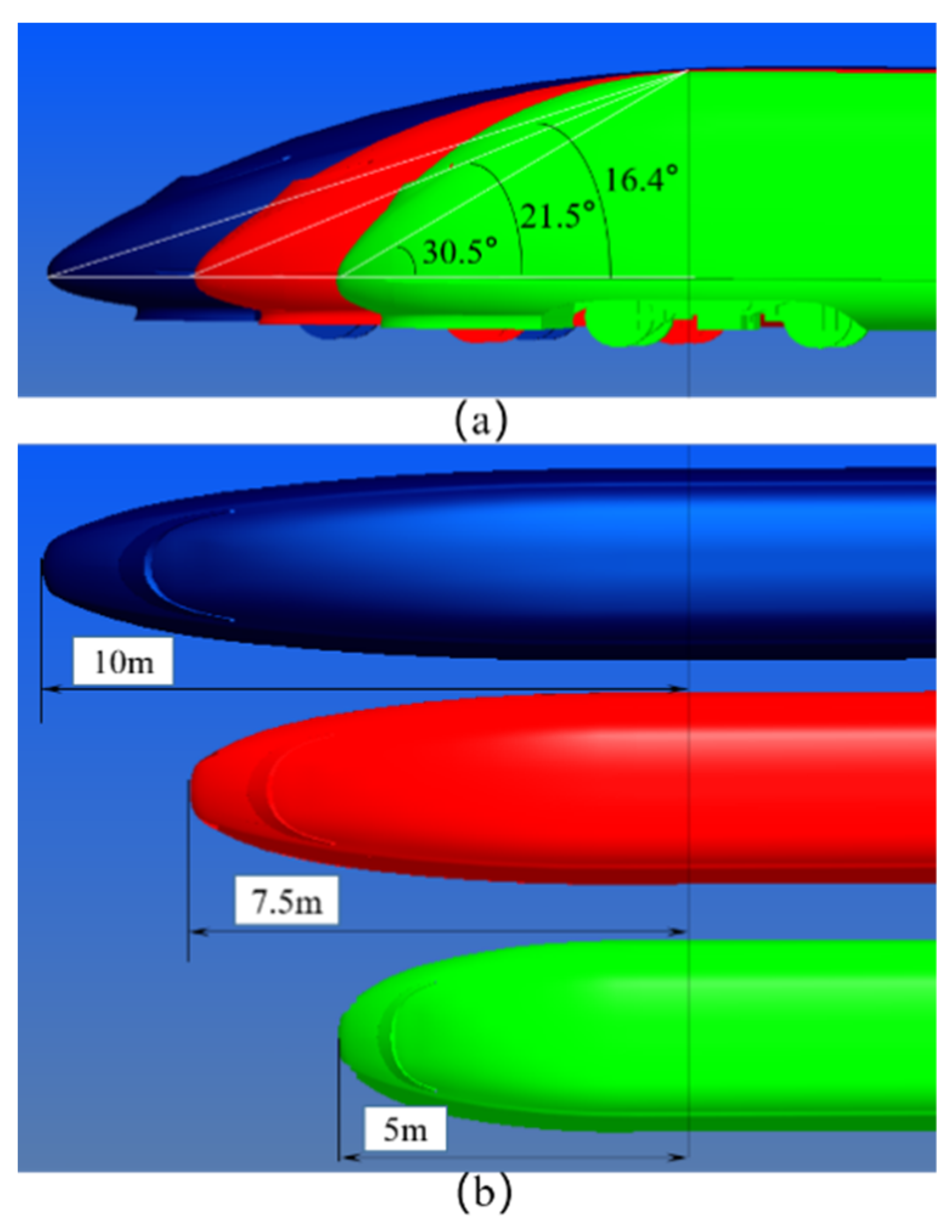
2.2. Models
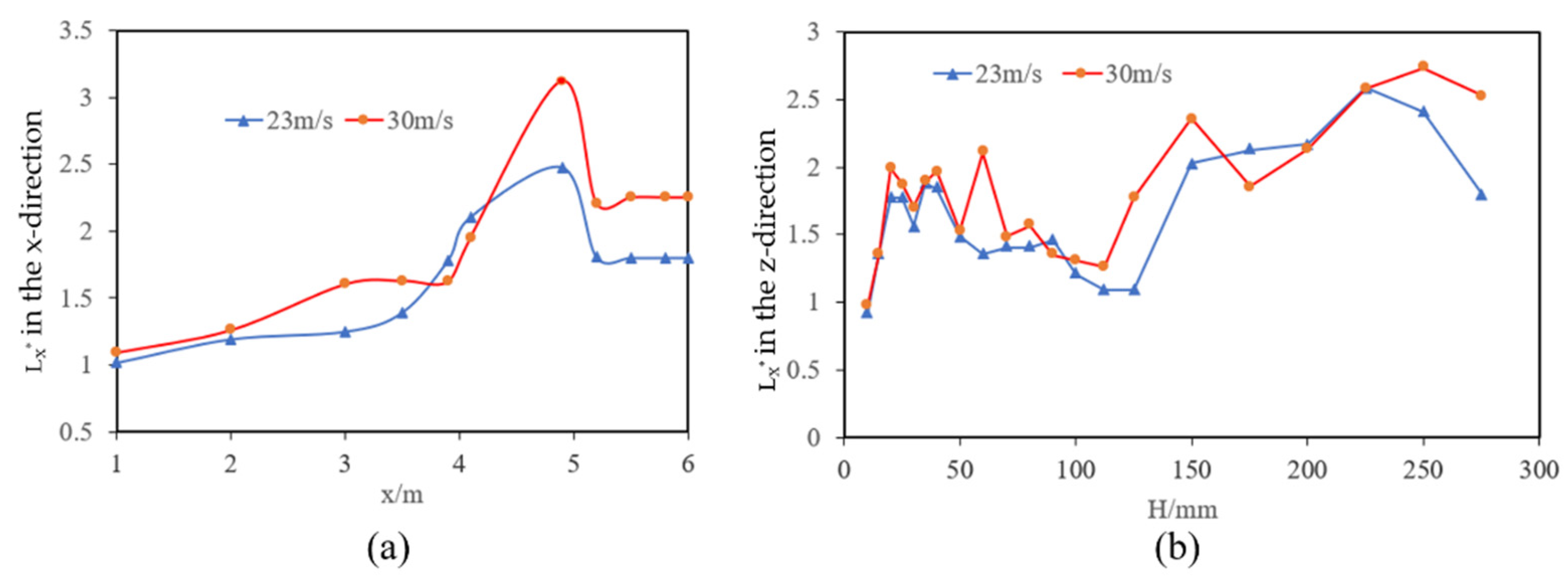
2.3. Roof Boundary Layers
3. Numerical Algorithms
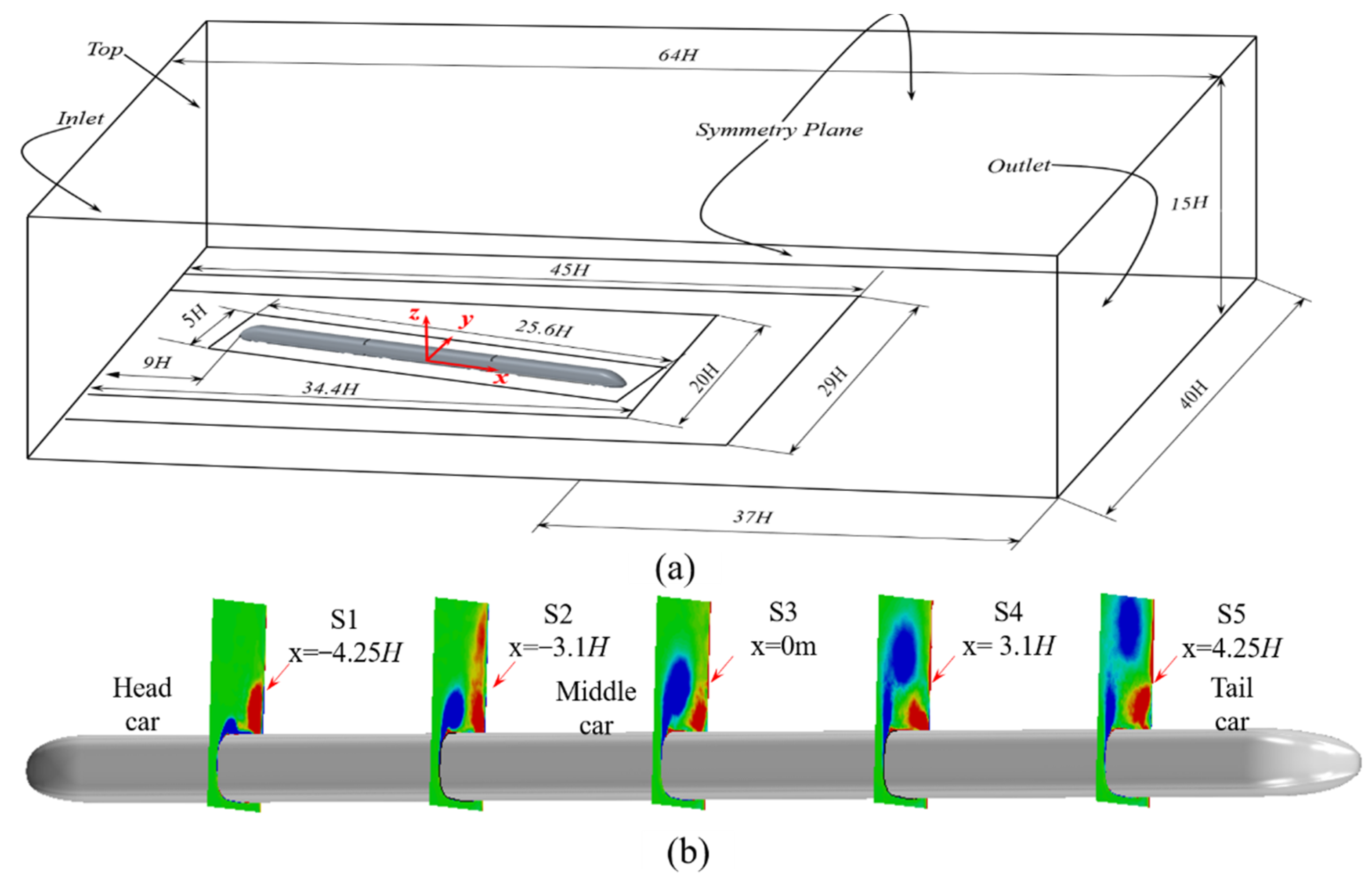
3.1. Simulation Models and Computational Cases
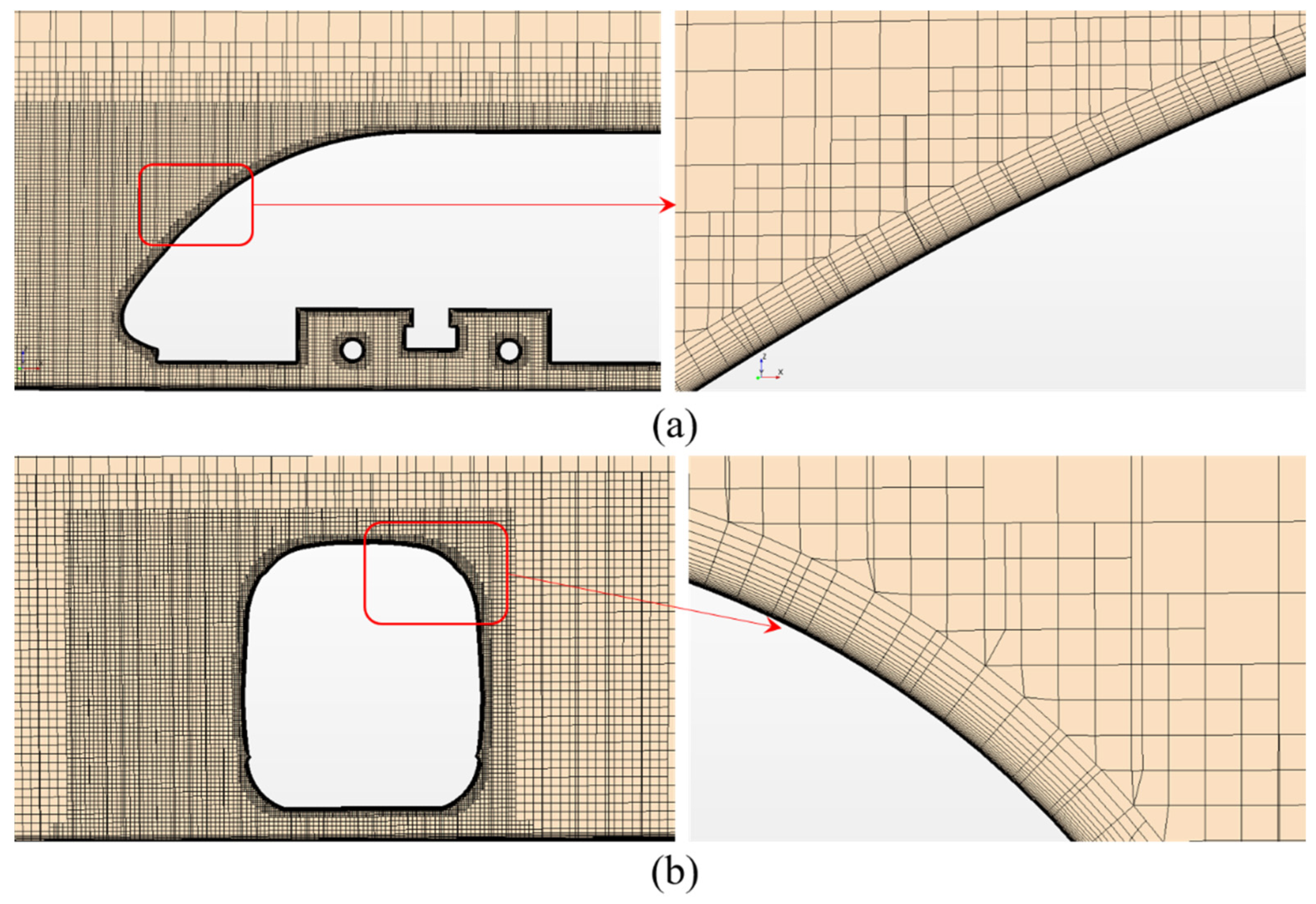
3.2. Computational Grids
4. Results and Discussion
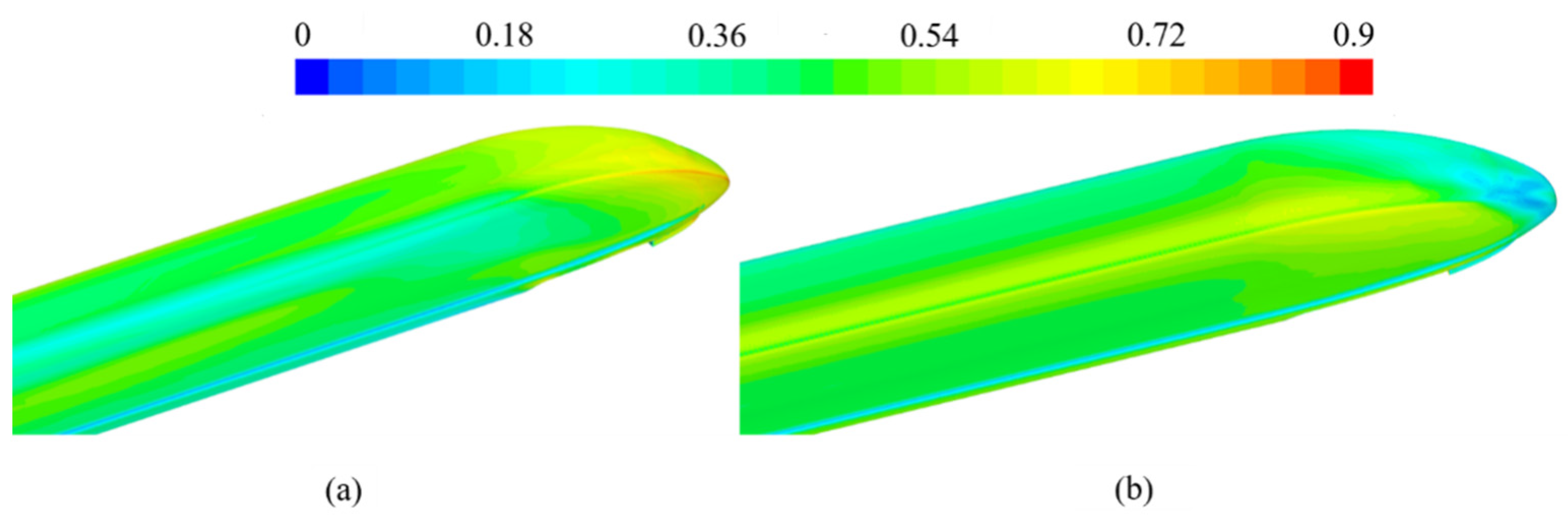
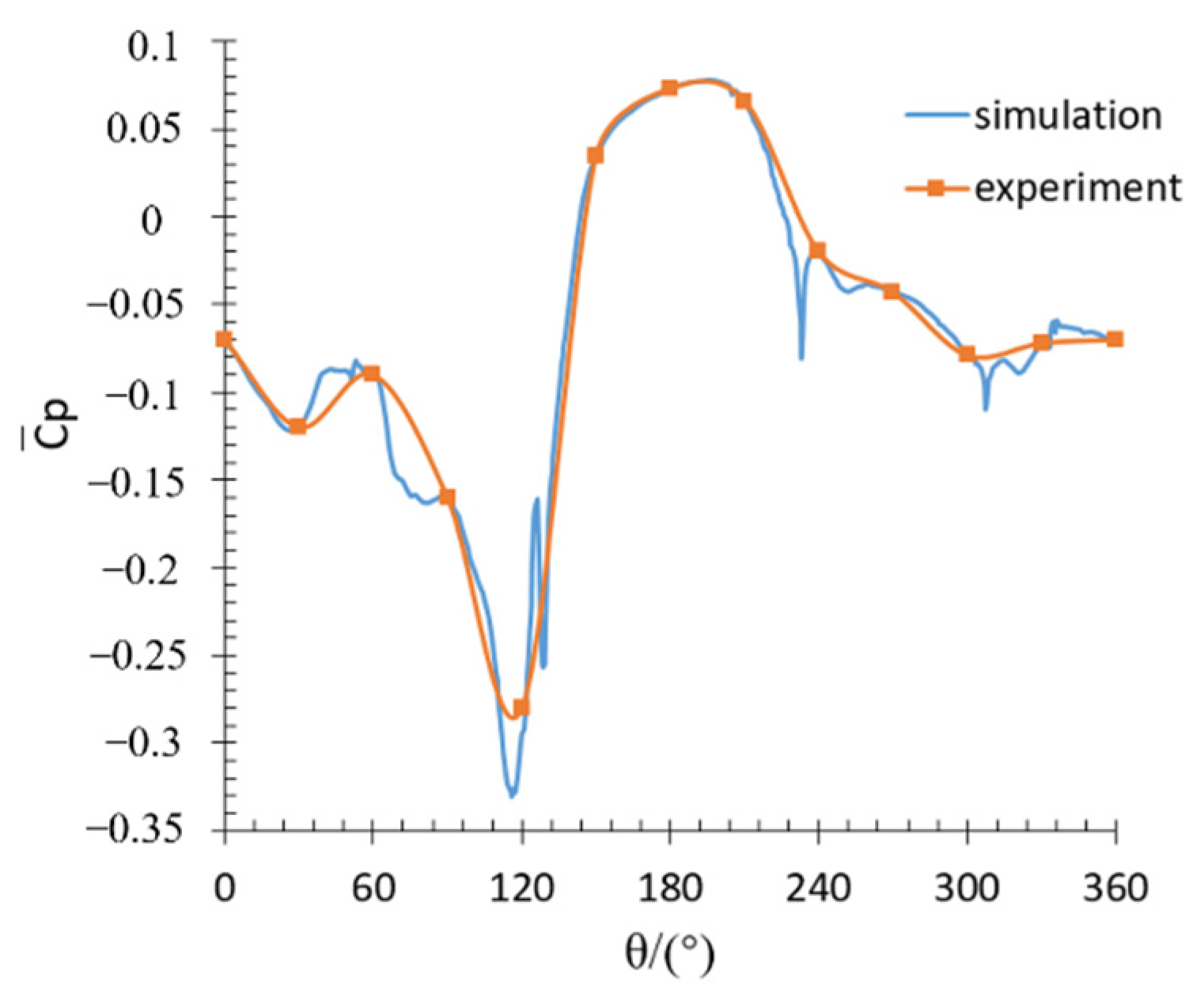
4.1. The Aerodynamic Force Coefficients and Pressure under Smooth Condition
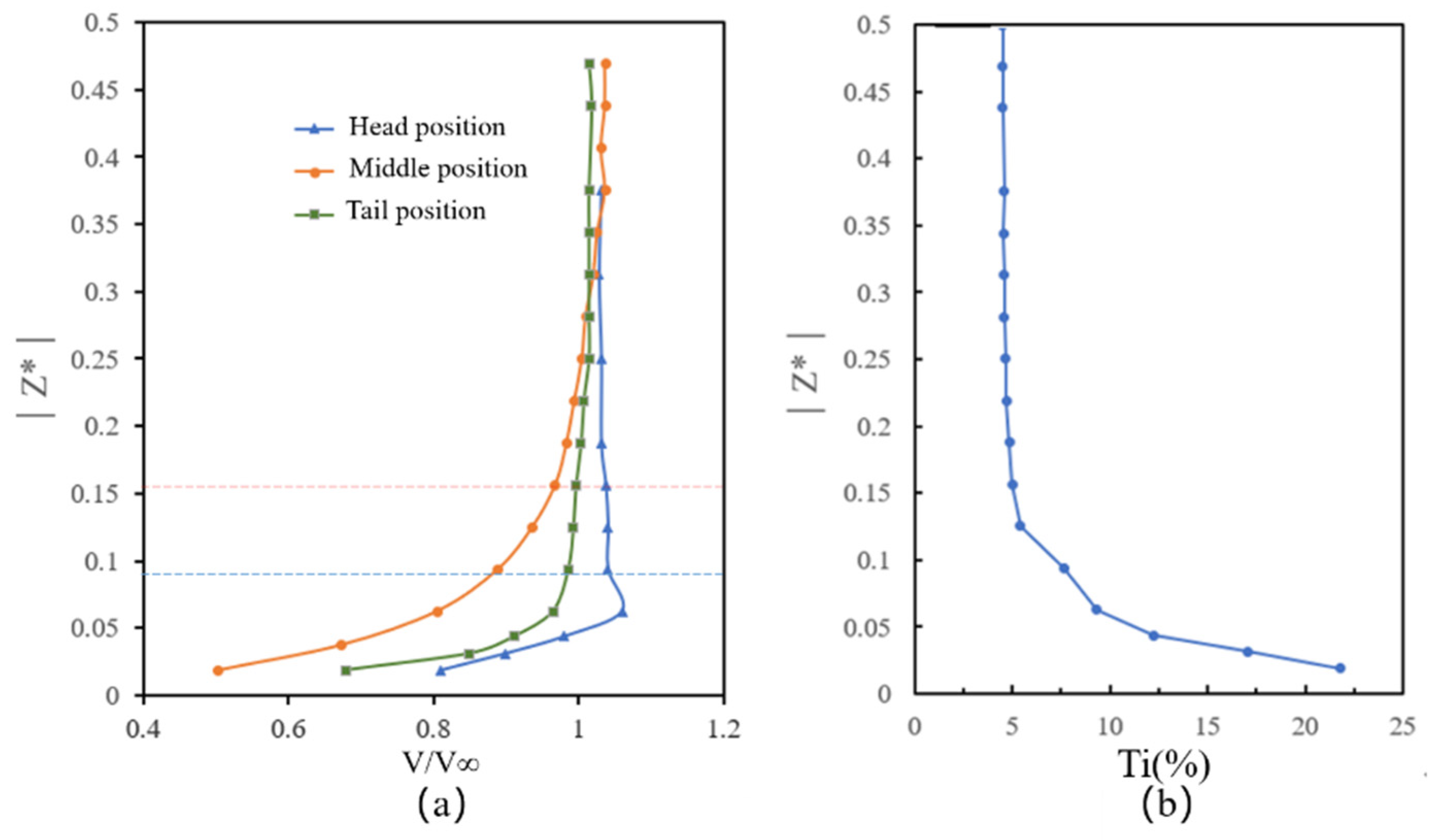
4.2. Effect of Turbulence
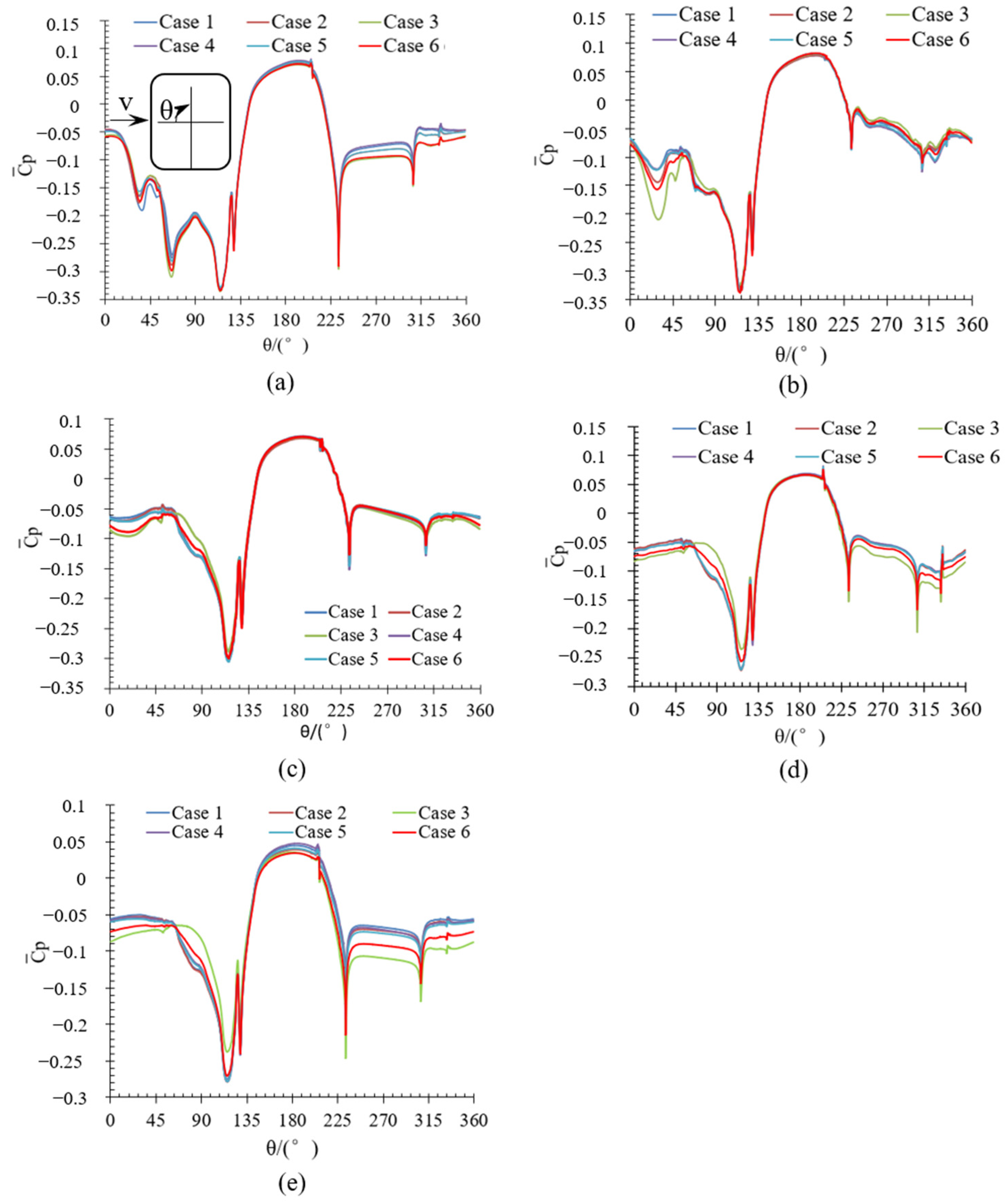
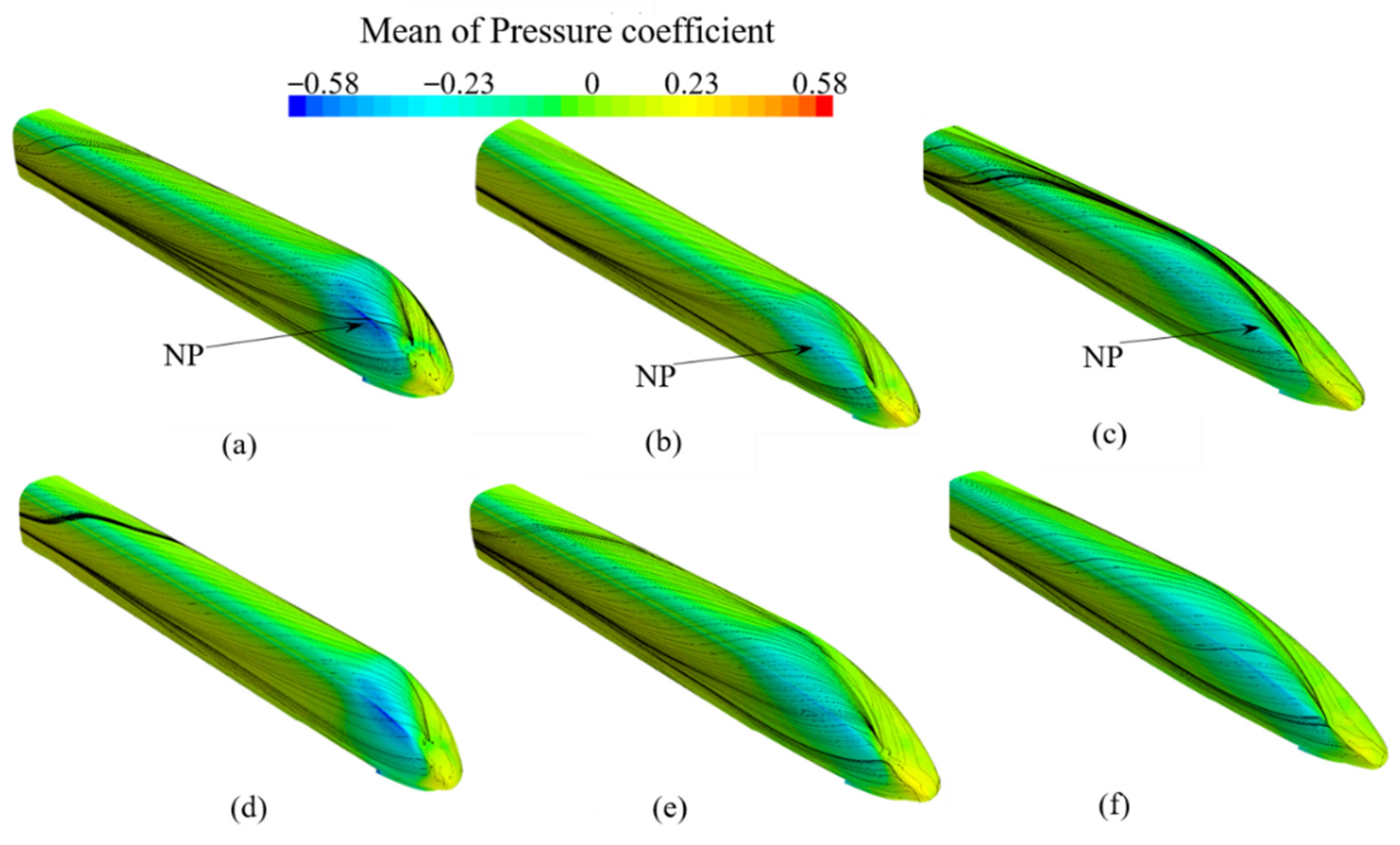
4.2.1. Pressure Distribution Analysis of the Train Surface
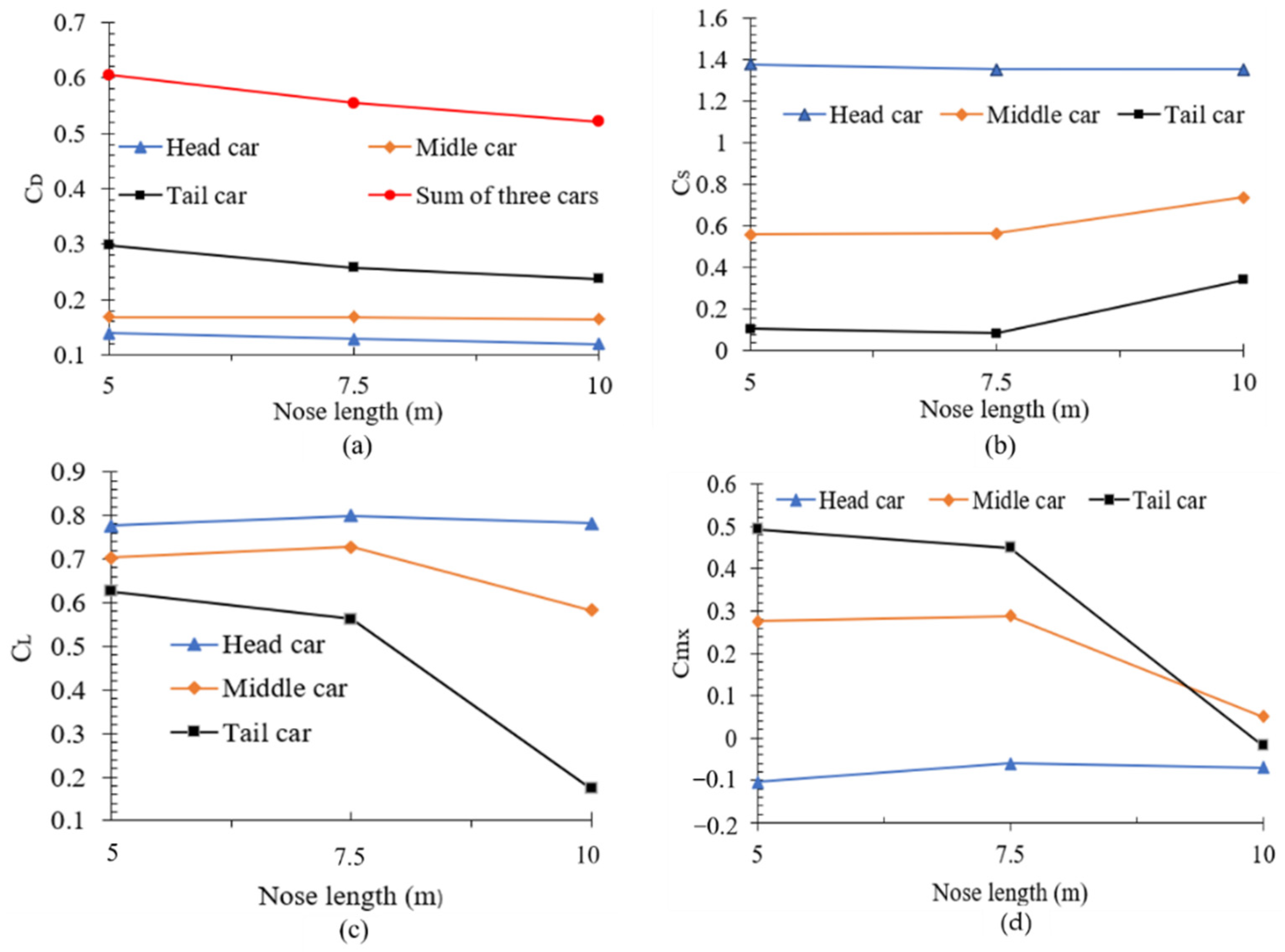
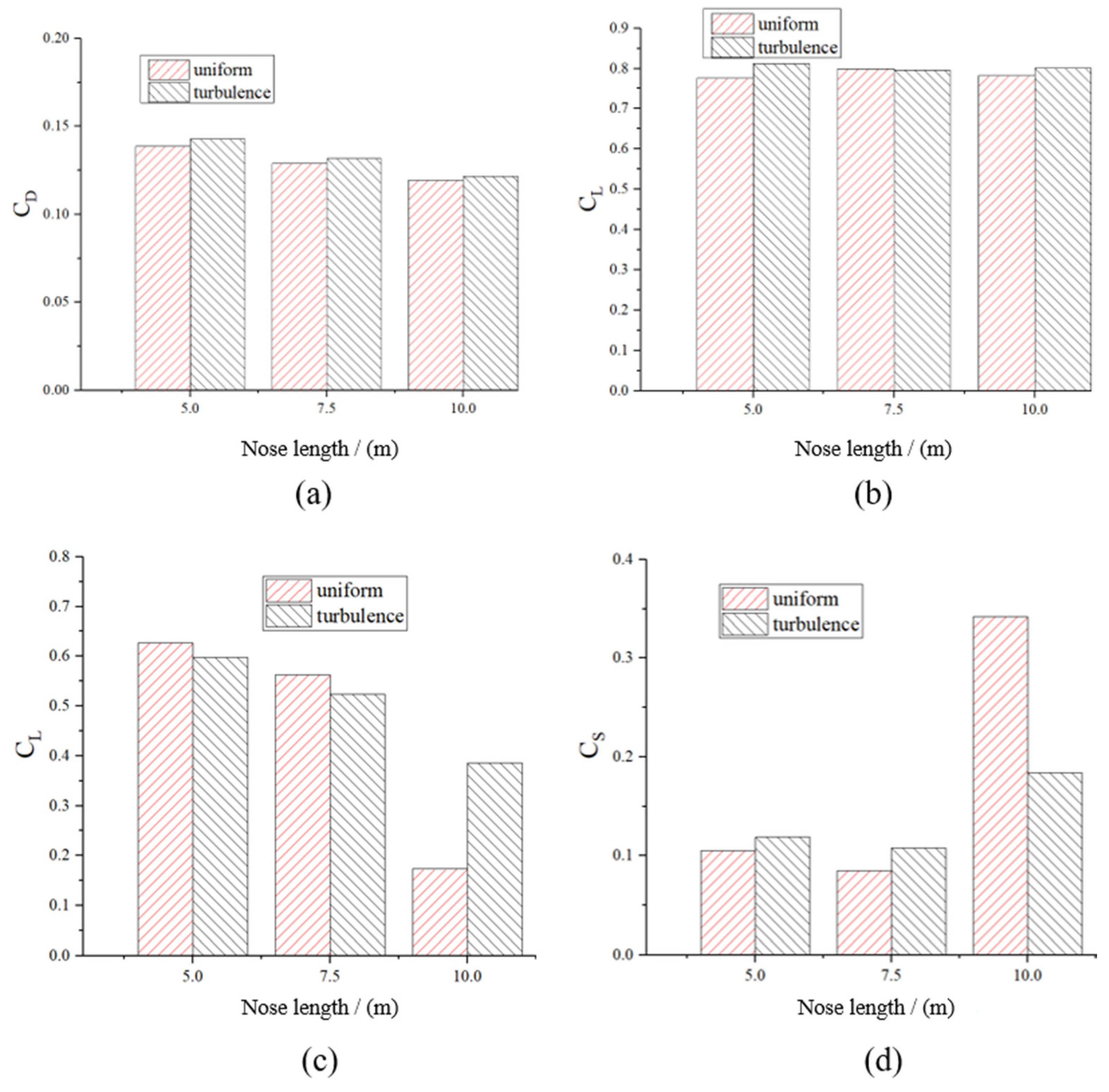
4.2.2. Force Coefficient
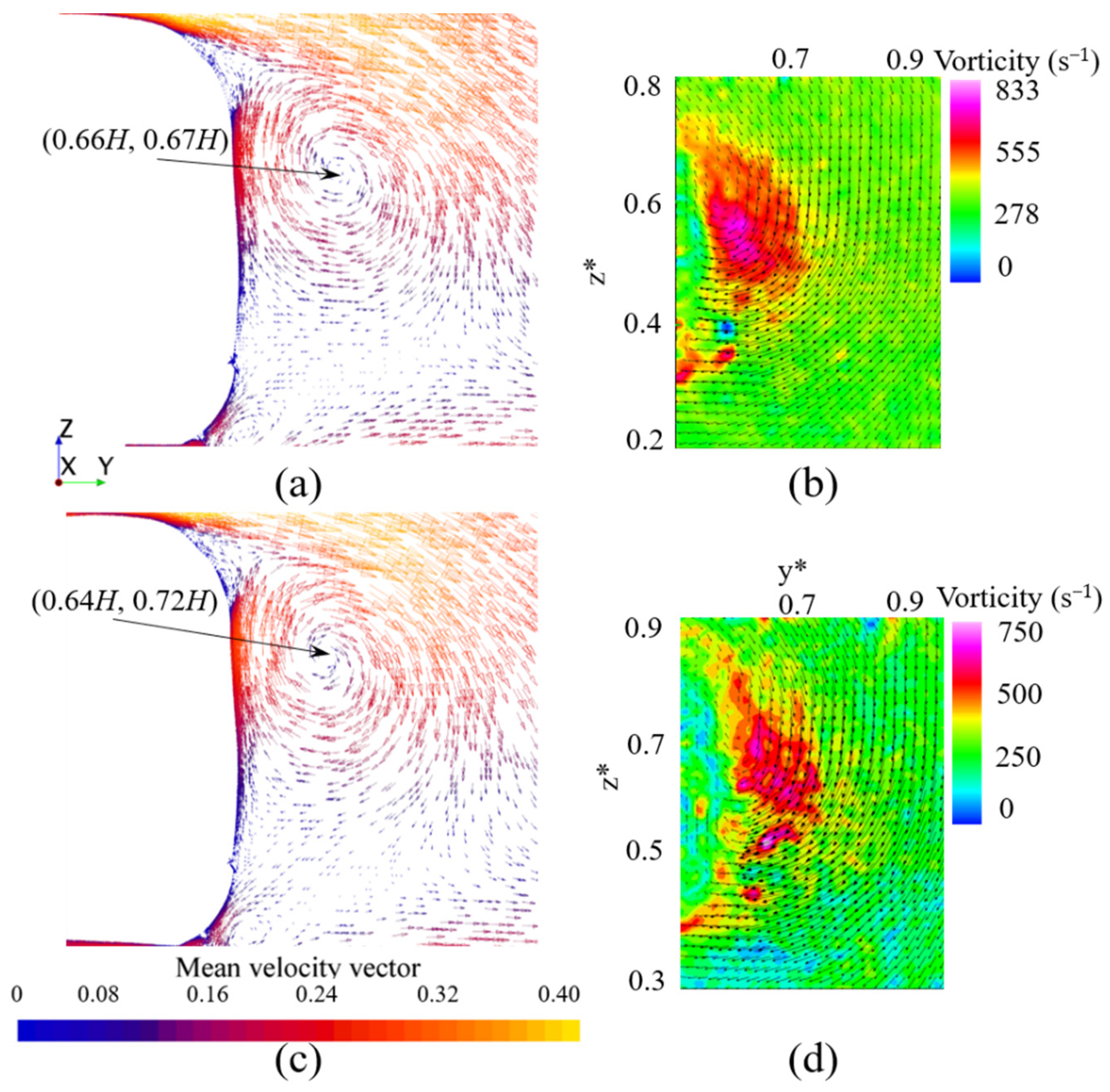
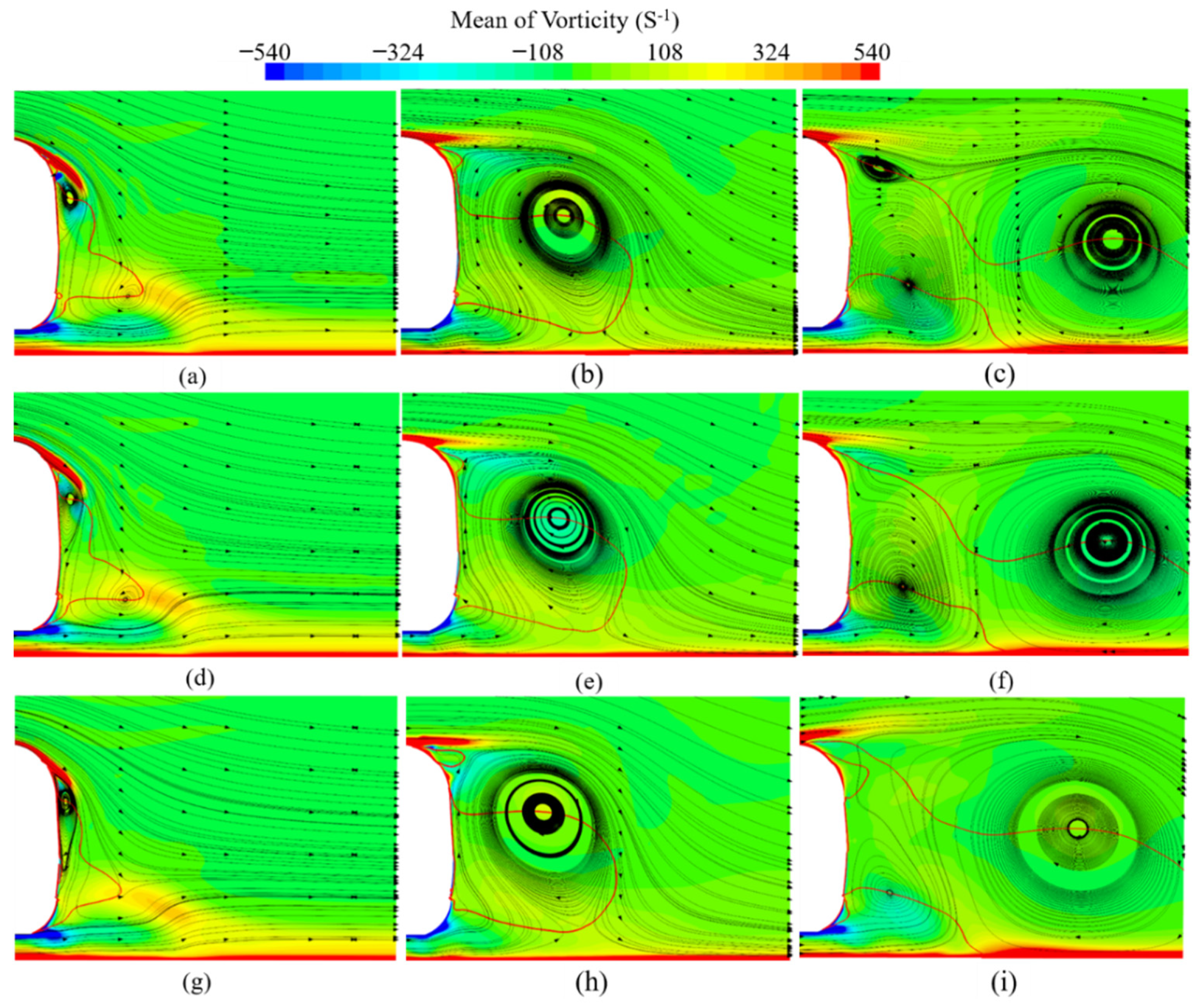
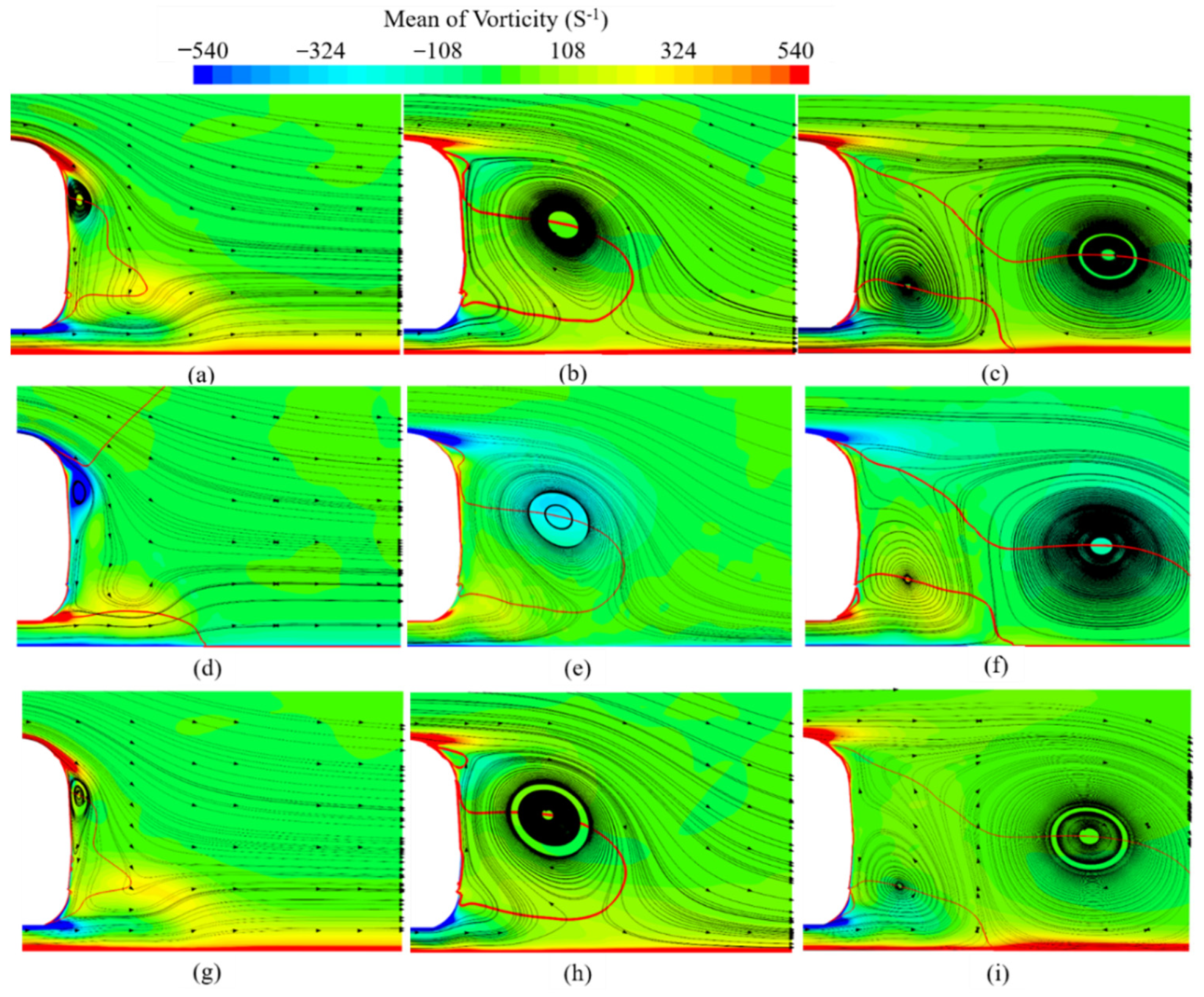
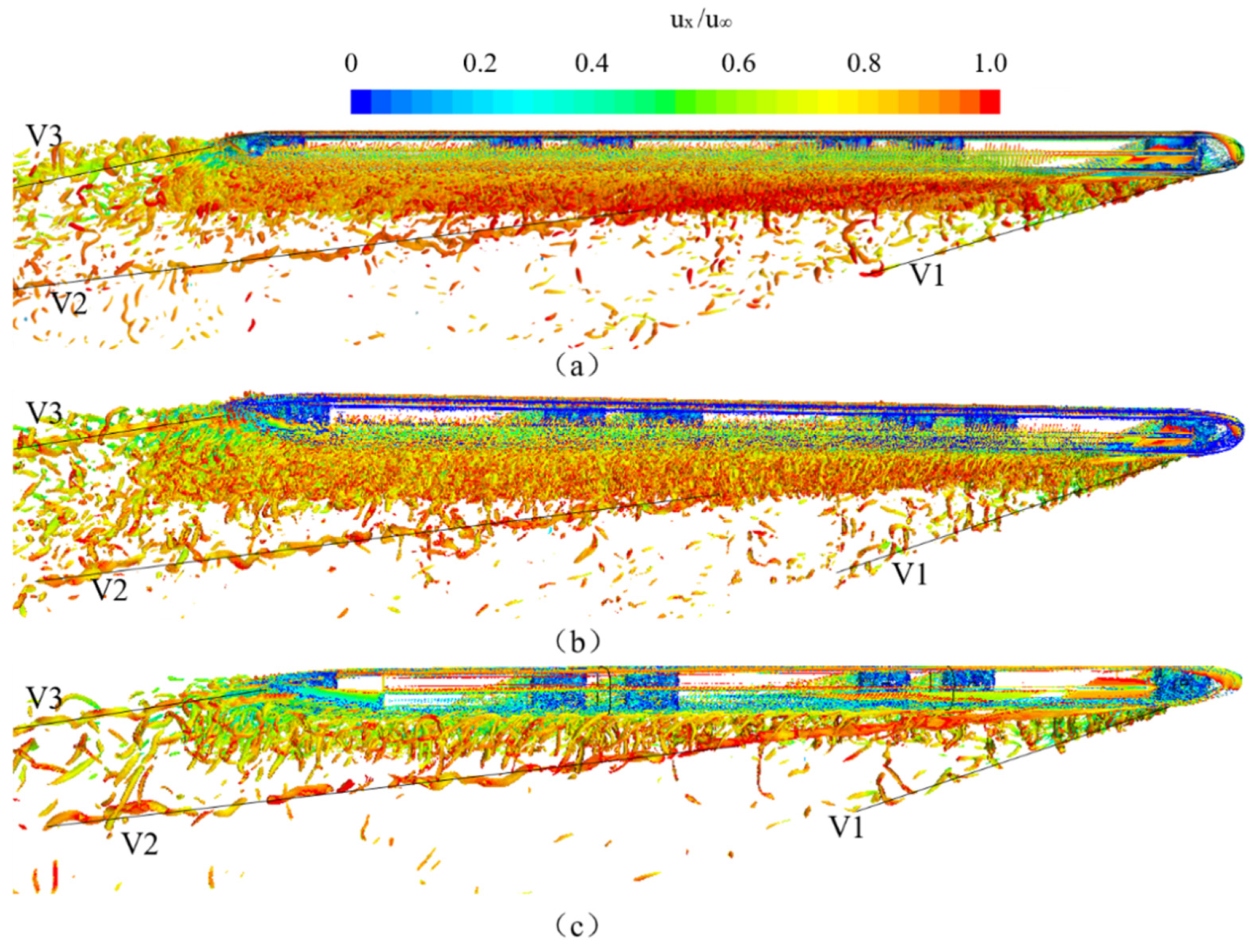
4.2.3. Lateral Flow Field
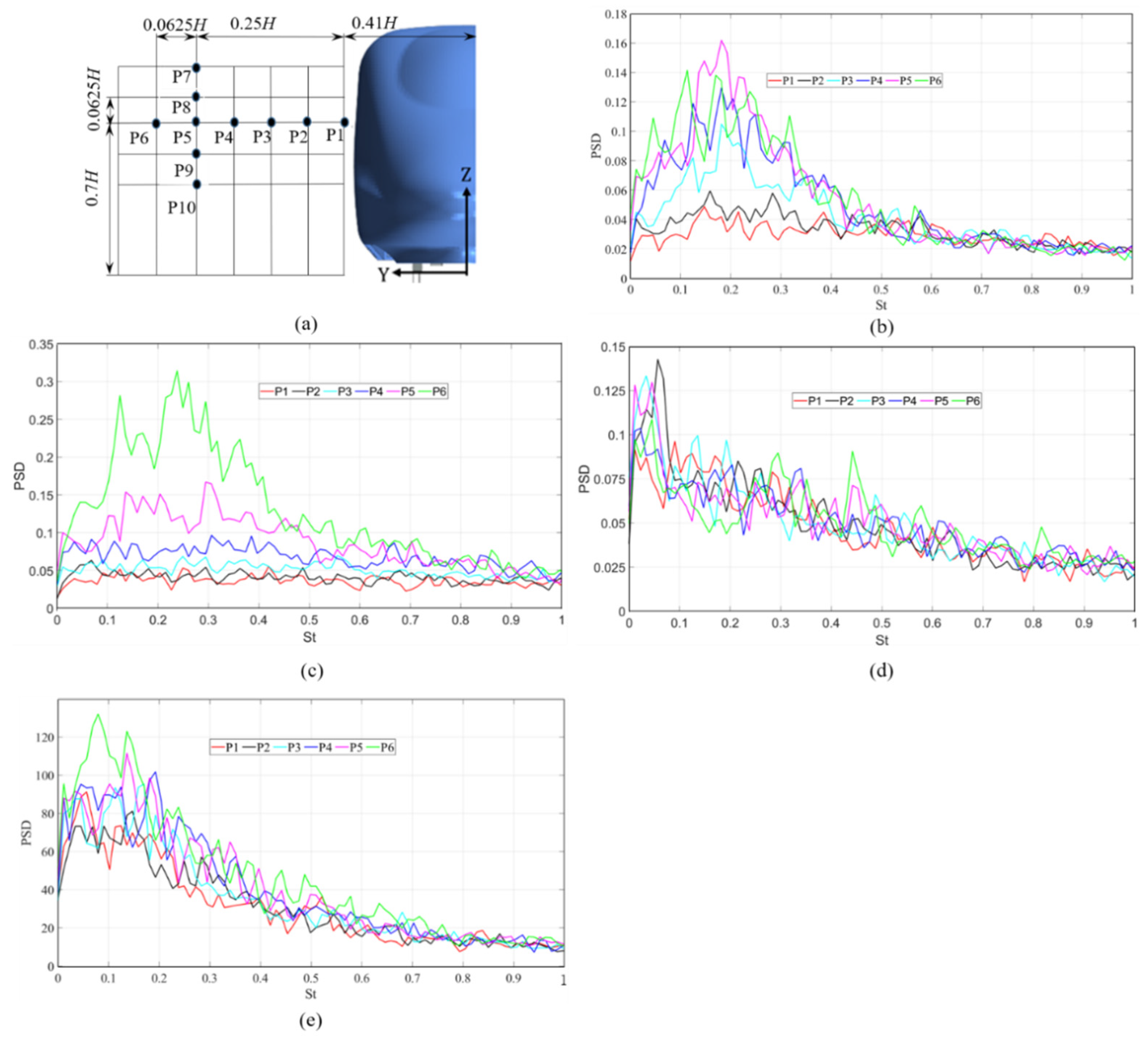
4.2.4. The Power Spectral Density or Spectrum
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Z.W.; Liu, T.H.; Jiang, Z.H.; Guo, Z.J.; Zhang, J. Comparative analysis of the effect of different nose lengths on train aerodynamic performance under crosswind. J. Fluids Struct. 2018, 78, 69–85. [Google Scholar] [CrossRef]
- Hemida, H.; Krajnović, S. LES study of the influence of the nose shape and yaw angles on flow structures around trains. J. Wind Eng. Ind. Aerodyn. 2010, 98, 34–46. [Google Scholar] [CrossRef]
- Baker, C.J.; Jones, J.; Lopez-Calleja, F.; Munday, J. Measurements of the crosswind forces on trains. J. Wind Eng. Ind. Aerodyn. 2004, 92, 547–563. [Google Scholar] [CrossRef]
- Baker, C.J. Some complex applications of the wind loading chain. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1791–1811. [Google Scholar] [CrossRef]
- Suzuki, M.; Tanemoto, K.; Maeda, T. Aerodynamic characteristics of train/vehicles under cross winds. J. Wind Eng. Ind. Aerodyn. 2003, 91, 209–218. [Google Scholar] [CrossRef]
- Hoppmann, U.; Koening, S.; Tielkes, T.; Matschke, G. A short-term strong wind prediction model for railway application, design and verification. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1127–1134. [Google Scholar] [CrossRef]
- Niu, J.Q.; Wang, Y.M.; Zhang, L.; Yuan, Y.P. Numerical analysis of aerodynamic characteristics of high-speed train with different train nose lengths. Int. J. Heat Mass Transfer 2018, 127, 188–199. [Google Scholar] [CrossRef]
- Sun, Z.X.; Yao, S.B.; Wei, L.; Yao, Y.; Yang, G.W. Numerical Investigation on the Influence of the Streamlined Structures of the High-Speed Train’s Nose on Aerodynamic Performances. Appl. Sci. 2021, 11, 784. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.B.; Liu, Z.; Zhou, D.; Wang, Z.; Liang, X.F.; Krajnovic, S. Dynamic analysis of the effect of nose length on train aerodynamic performance. J. Wind Eng. Ind. Aerodyn. 2019, 184, 198–208. [Google Scholar] [CrossRef]
- Volpe, R.; Ferrand, V.; Silva, A.D.; Moyne, L.L. Forces and flow structures evolution on a car body in a sudden crosswind. J. Wind Eng. Ind. Aerodyn. 2014, 128, 114–125. [Google Scholar] [CrossRef]
- Baker, C.J. The flow around high speed trains. In Proceedings of the BBAA VI International Colloquium on: Bluff Bodies Aerodynamics & Applications, Milano, Italy, 20–24 July 2008. [Google Scholar]
- Baker, C.J.; Quinn, A.; Sima, M.; Hoefener, L.; Licciardello, R. Full-scale measurement and analysis of train slipstreams and wakes. Part 1: Ensemble averages. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 451–467. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.; Herbst, A.; Sheridan, J. Wind tunnel analysis of the slipstream and wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2014, 134, 122–138. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.C.; Herbst, A.H.; Sheridan, J. Moving model analysis of the slipstream and wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2015, 136, 127–137. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.C.; Herbst, A.H.; Sheridan, J. Dynamics of trailing vortices in the wake of a generic high-speed train. J. Fluids Struct. 2016, 65, 238–256. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.C.; Herbst, A.H.; Sheridan, J. Flow topology and unsteady features of the wake of a generic high-speed train. J. Fluids Struct. 2016, 61, 168–183. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.C.; Herbst, A.H.; Sheridan, J. The effect of tail geometry on the slipstream and unsteady wake structure of high-speed trains. Exp. Therm. Fluid Sci. 2017, 83, 215–230. [Google Scholar] [CrossRef]
- Avadiar, T.; Bell, J.; Burton, D.; Cormaty, H.; Li, C. Analysis of High-speed Train Flow Structures Under Crosswind. J. Mech. Sci. Technol. 2016, 30, 3985–3991. [Google Scholar] [CrossRef]
- Raghuathan, S.; Kim, H.D.; Setoguchi, T. Aerodynamics of high-speed railway train. Prog. Aerosp. Sci. 2002, 8, 469–514. [Google Scholar]
- Liu, T.H.; Su, X.C.; Zhang, J.; Chen, Z.W.; Zhou, X.S. Aerodynamic performance analysis of trains on slope topography under crosswinds. J. Cent. South Univ. 2016, 23, 2419–2428. [Google Scholar] [CrossRef]
- Hooper, J.D.; Musgrove, A.R. Reynolds stress, mean velocity, and dynamic static pressure measurement by a four-hole pressure probe. Exp. Therm. Fluid Sci. 1997, 15, 375–383. [Google Scholar] [CrossRef]
- Xia, C.; Shan, X.; Yang, Z. Comparison of different ground simulation systems on the flow around a high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 135–147. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.Y.; Li, T.; Zhang, Y.D. Multi-objective aerodynamic optimization design of high-speed train head shape. J. Zhejiang Univ. Sci. A 2017, 18, 841–854. [Google Scholar] [CrossRef]
- Yang, B.; Xiong, X.H.; He, Z.; Li, X.B.; Xie, P.H.; Tang, M.Z. Feasibility of replacing the 3-coach with an 1.5-coach grouping train model in wind tunnel experiment at different yaw angles. J. Cent. South Univ. 2022, 29, 2062–2073. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Wang, H.F.; Zeng, L.W.; Alam, M.; Zhao, X. Effects of oncoming flow turbulence on the near wake and forces of a 3D square cylinder. J. Wind Eng. Ind. Aerodyn. 2021, 214, 104674. [Google Scholar] [CrossRef]
- Flay, R.G.J.; Stevenson, D.C. Integral length scales in strong winds below 20 m. J. Wind Eng. Ind. Aerod. 1998, 28, 21–30. [Google Scholar] [CrossRef]
- Du, S.B.; Li, M.; Yang, Y. Effects of turbulence integral scales on characteristics of fluctuating wind pressure. J. Wind Eng. Ind. Aerod. 2020, 204, 104245. [Google Scholar] [CrossRef]
- Vita, G.; Hemida, H.; Andrianne, T. Generating atmospheric turbulence using passive grids in an expansion test section of a wind tunnel. J. Wind Eng. Ind. Aerodyn. 2018, 178, 91–104. [Google Scholar] [CrossRef]
- Roach, P.E. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Flow 1987, 8, 82–92. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Ghasemian, M.; Nejat, A. Aerodynamic noise prediction of a Horizontal Axis Wind Turbine using Improved Delayed Detached Eddy Simulation and acoustic analogy. Energy Convers. Manag. 2015, 99, 210–220. [Google Scholar] [CrossRef]
- He, K.; Minelli, G.; Wang, J.; Gao, G.J.; Krajnovic, S. Assessment of LES, IDDES and RANS approaches of a notchback bluff body. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104737. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.F.; Shan, X.; Yang, Z.; Li, Q. Effects of ground configurations on the slipstream and near wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2017, 168, 177–189. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.B.; Liang, X.F. IDDES simulation of the performance and wake dynamics of the wind turbines under different turbulent inflow conditions. Energy 2022, 238, 121772. [Google Scholar] [CrossRef]
- Chiu, T.W.; Squire, L.C. An experimental study of the flow over a train in a crosswind at large yaw angles up to 90°. J. Wind Eng. Ind. Aerodyn. 1992, 45, 47–74. [Google Scholar] [CrossRef]
- Hunt, J.; Wray, A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows; Center for Turbulent Research Report CTR-S88; Stanford University: Stanford, CA, USA, 1998. [Google Scholar]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Chong, M.S.; Perry, A.E. A general classification of three- dimensional flow fields. Phys. Fluids A 1990, 2, 765–777. [Google Scholar] [CrossRef]
- Graftieaux, L.; Michard, M.; Grosjean, N. Combining piv, pod and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 2001, 12, 1422–1429. [Google Scholar] [CrossRef]
- Vino, G.; Watkins, S.; Mousley, P.; Watmuff, J.; Prasad, S. Flow structures in the near wake of the ahmed model. J. Fluids Struct. 2005, 20, 673–695. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Y.; Pin, Y.; Chan, T. Turbulent near wake of an ahmed vehicle model. Exp. Fluids 2013, 54, 1490. [Google Scholar] [CrossRef]
- Minguez, M.; Pasquetti, R.; Serre, E. High-order large-eddy simulation of flow over the ahmed body car model. Phys. Fluids 2008, 20, 095101. [Google Scholar] [CrossRef]


| Grids | First Layer Mesh Thickness | Number of Mesh Layers in Boundary Layer | Boundary Layer Grid Growth Rate | Total Numbers |
|---|---|---|---|---|
| Coarse | 5.5 × 10−5 mm | 30 | 1.2 | 47.11 million |
| Medium | 5.0 × 10−5 mm | 30 | 1.2 | 70.97 million |
| Fine | 4.5 × 10−5 mm | 30 | 1.2 | 99.54 million |
| Case | Condition | Iu/(%) | Lhead/(m) | Total Numbers | y+ | s+ | l+ |
|---|---|---|---|---|---|---|---|
| 1 | Smooth | 1 1 1 | 5 | 71.62 million | 0.33 | 87.5 | 87.5 |
| 2 | 7.5 | 70.97 million | 0.33 | 88 | 88 | ||
| 3 | 10 | 63.31 million | 0.33 | 99 | 99 | ||
| 4 | turbulence | 5 5 5 | 5 | 71.62 million | 0.33 | 87.5 | 87.5 |
| 5 | 7.5 | 70.97 million | 0.33 | 88 | 88 | ||
| 6 | 10 | 63.31 million | 0.33 | 99 | 99 |
| Grids | ||||
|---|---|---|---|---|
| Coarse | 0.1296 | 0.1625 | 0.2506 | 0.0578 |
| Medium | 0.1288 | 0.1681 | 0.2572 | 0.0608 |
| Fine | 0.1283 | 0.1682 | 0.2569 | 0.0597 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
|---|---|---|---|---|---|---|
| Head car | 0.0196 | 0.0151 | 0.0156 | 0.1165 | 0.1000 | 0.0992 |
| Middle car | 0.0203 | 0.0210 | 0.0197 | 0.0896 | 0.0869 | 0.0989 |
| Tail car | 0.0195 | 0.0181 | 0.0243 | 0.0653 | 0.0634 | 0.0848 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Xiong, X.-H.; Chen, G.; Xue, R.-D. Experimental and Numerical Study of the Flow Field Structure of High-Speed Train with Different Nose Lengths Head at 15° Yaw. Appl. Sci. 2022, 12, 12712. https://doi.org/10.3390/app122412712
Yang B, Xiong X-H, Chen G, Xue R-D. Experimental and Numerical Study of the Flow Field Structure of High-Speed Train with Different Nose Lengths Head at 15° Yaw. Applied Sciences. 2022; 12(24):12712. https://doi.org/10.3390/app122412712
Chicago/Turabian StyleYang, Bo, Xiao-Hui Xiong, Guang Chen, and Ru-Dai Xue. 2022. "Experimental and Numerical Study of the Flow Field Structure of High-Speed Train with Different Nose Lengths Head at 15° Yaw" Applied Sciences 12, no. 24: 12712. https://doi.org/10.3390/app122412712
APA StyleYang, B., Xiong, X.-H., Chen, G., & Xue, R.-D. (2022). Experimental and Numerical Study of the Flow Field Structure of High-Speed Train with Different Nose Lengths Head at 15° Yaw. Applied Sciences, 12(24), 12712. https://doi.org/10.3390/app122412712






