1. Introduction
To reduce interference in the communication process and enable the system to automatically check and correct errors to improve the reliability of data transmission, channel coding technology is widely used in various wireless communication systems. Currently, commonly used coding techniques include Reed–Solomon (RS) codes [
1], low-density parity-check (LDPC) codes [
2,
3], turbo codes [
4,
5], Bose–Chaudhuri–Hocquenghem codes [
6,
7,
8], convolutional codes [
9], and polar codes [
10]. Polar codes have been strictly proven to reach the Shannon limit under the binary discrete memoryless channel and binary erasure channel when the code length tends to infinity [
11], and due to their excellent short-code performance, they became the control channel selection coding scheme for 5G enhanced mobile broadband scenarios at the 2016 3GPP RAN1#87 conference [
12]. As the only channel coding that has been proven to reach the Shannon limit, polar codes are very important for 5G communication and future 6G communication. In the field of wireless communication, the decoding of polar codes has received extensive attention globally. Examples are the traditional belief propagation (BP) algorithm [
13], the successive-cancelation (SC) algorithm [
14], the early stop BP algorithm [
15], other low complexity BP algorithms [
16], the fast SC decoding scheme [
17,
18,
19], and successive cancellation stack [
20]. These traditional algorithms and their improvements can only reduce the decoding complexity or improve the decoding performance but cannot satisfy the requirements of improving communication quality and reducing decoding steps at the same time.
In recent years, the rapid development of deep learning in computer vision and language translation has attracted widespread attention from experts and scholars in the field of communication. Some algorithms directly train deep learning as a polar decoder, Chao, Z.W. et al. explored a polar code residual network decoder with a denoiser and a decoder. The denoiser used a multi-layer perceptron (MLP) [
21], a convolutional neural network (CNN) [
22], and a recurrent neural network (RNN) [
23], while the decoder used a CNN [
24]. The decoding performances nearly reached those of a traditional successive cancelation list (SCL) [
25] algorithm when the code length was less than 32. In terms of reducing decoding complexity, Xu, W.H. et al. applied a neural network to polar code decoding, but the application was only used for limited code length [
26]. Hashemi, S. et al. used the deep learning algorithm to reduce the complexity of the SC algorithm [
27]. However, all of them cannot be directly applied to decoding longer polar codes. To apply the machine learning in polar code decoding, researchers combine machine learning with traditional polar decoding algorithms.
There are many combinations of BP algorithm and machine learning. In terms of reducing the complexity, Gruber, T. et al. proposed a neural network BP decoder that can be executed at any code length, which reduced the decoding bit error rate (BER) and saved 50% of the hardware cost [
28]. Cammerer, S. et al. proposed a segmentation decoding scheme based on neural networks, which complied with the BP decoding law and divided polar codes into single-parity checks (SPCs) and repetition code (RC) nodes and decoded them using a neural network to achieve the same bit error performance as the SC and BP algorithms with lower complexity [
29]. In terms of improving decoding performance, Teng, C.F. et al. used the check relationship between the cyclic redundancy check (CRC) remainder and the decoding result to propose a comprehensive loss function of polar code frozen bits, which realized the unsupervised decoding of the polar codes, and the decoding performance was better than that of the traditional BP decoding algorithm [
30]. Gao, J. et al. proposed a BP structure similar to the res-net network, which achieved better decoding performance than the standard BP algorithm [
31]. In terms of simultaneously improving decoding performance and reducing complexity, Xu, W. et al. used deep learning to improve the decoding performance of the BP algorithm and used lower computational complexity to achieve a bit error performance close to that of the CRC-aided SCL (CA-SCL) algorithm [
32].
The SC algorithm and machine learning are less frequently combined. Doan, D. et al. divided the polar code into equal-length nodes and decoded them using neural networks [
33] and obtained a lower complexity than [
29]. However, when the code length is longer, the number of neural network models that need to be called for decoding is higher, and the increase in the calculation amount is not negligible. None of the above studies have achieved a low-complexity low-bit-error decoding performance by combining the SC algorithm and machine learning.
To achieve a low-complexity low-bit-error decoding performance by combining SC algorithm and machine learning, this paper proposes a decoding method combining neural network nodes (NNNs) and traditional nodes. This scheme avoids the extra complexity caused by frequent calls of the neural network model and proposes a decoding scheme that can not only reduce the delay, but also improve the decoding performance.
The remainder of this paper is organized as follows:
Section 2 introduces the knowledge required for polar code decoding, including the SC decoding scheme, traditional special nodes, and the fast SC decoding scheme.
Section 3 introduces the system model and the decoding scheme based on the NNN and CNN structure and then analyzes the performance of the model in decoding. Two NNN recognition strategies are explored.
Section 4 presents the simulation results over the additive white Gaussian noise (AWGN) and Rayleigh channel.
Section 5 summarizes the paper.
3. Neural Network-Assisted Polar Code Decoding Scheme
Considering that the traditional fast SC decoding algorithm can effectively reduce the decoding time step, in this paper, we will reduce the BER of fast SC decoding structure. Xu Xiang studied the decoding performance of the polar code neural network decoder based on CNNs, RNNs, long short-term memory, and MLP under different network designs and parameter settings [
34]. In comparison, it can be seen that the CNN-based decoder can achieve a better performance with fewer parameters. Therefore, we consider using the CNN to improve the decoding performance and call the scheme neural network assisted (NNA) decoding scheme.
3.1. System Model
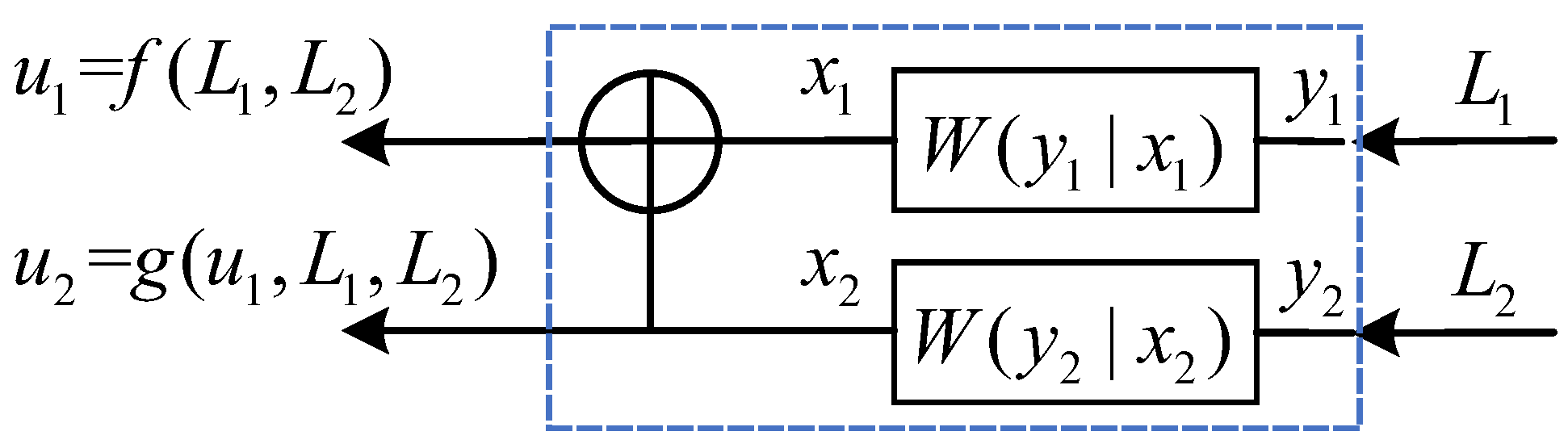
Figure 7 shows the block diagram of the proposed decoding scheme system, which is composed of training and decoding parts. The “Training Part” is executed first, followed by the “Decoding Part”. The Training Part is composed of “Polar Encoder1” and “Neural Network Training”; the Decoding Part comprises “Polar Encoder2”, “Mapper”, “Noise”, and “NNA Decoding Scheme”. Note that the Mapper Layer, Noise Layer, and Decoder Layer are trained in the training part, but only the model of the Decoder Layer is saved and called in NNA Decoding. Although the decoder layer decodes
to obtain
, the purpose of the training part is to obtain the trained Decoder Layer model and not the
.
and
denote the code length and information length of the codewords to be trained, respectively, while
and
denote the code length and information length of the codewords to be decoded, respectively.
denotes a row vector
. The two parts have different inputs,
and
, and different diagram structures, but
and
are mapped in the same way. Taking
as an example, consider single-carrier signaling in which
binary streams
are encoded with a channel encoder that generates a codeword of length
. The codeword
is then mapped to binary phase-shift keying (BPSK) symbols
by the mapper. Then,
is transmitted over noisy channels by the noise block, and finally, the signal
is received. When the channel noise is additive gaussian white noise (AWGN),
is given by
,
. Similarly,
can be obtained from
. Note that
is determined by the Node Recognizer. We can obtain the LLR values through
, where
denotes Gaussian noise power. In this paper, the channel-side information is assumed to be known at the receiver. The details of the neural network (NN) model and decoding scheme are introduced in the following section.
3.2. Neural Network Model and NNN
The NN model is trained by the training part in
Figure 7. We write matrix
with size
to denote all the possible information sequences and matrix
with size
to denote all the possible codewords, resulting in,
. Let
denote the position set of the information bits. The decoder layer is trained to find the
corresponding to
, with
. To fully train the NN, additional layers without trainable parameters are added to perform certain actions, namely mapping the codewords to BPSK symbols and adding noise. Therefore, the NN model approximates
to
. Therefore,
represents the training data in this machine learning problem and
is the label. We can generate as much training data as desired by Monte Carlo simulations. The activation functions used in the decoder layer are sigmoid functions and a rectified linear unit (ReLU), which are defined as follows:
Mini-batch gradient descent is used to train the NN, and in each batch, different data are fed into the NN.
Table 1 summarizes the architecture of the proposed NN model. In this scheme, the batch size, which is equal to the size of the label set and that of the codeword set, is
. Thus, the training complexity scales exponentially with
, which makes training the NN decoder for long polar codes not feasible in actuality. To solve this problem, we define the short codes (
is generally less than 32) decoded by the NN decoder as NNNs and combine them with the traditional special nodes mentioned in
Section 2.2 to derive an NNA decoding scheme. Note that an NNN could be one of the R1, R0, Rep, or SPC nodes, or none of them. Arıkan’s system polar code coding scheme [
35] is used in this paper unless otherwise stated.
The neural network structure in this paper consists of a mapper layer, a noise layer, and a decoding layer. All three layers need to be trained. In real-life decoding, only the decoding layer is needed. The structure of the NN is shown in
Table 1. The mapper layer and the noise layer are both custom-function layers generated by the Keras tool in Tensorfow2. In this paper, Gaussian white noise is used unless otherwise stated; the Gaussian construction method is used to generate polar codes; the modulation method is BPSK. The input of the network during training is
. The label is
. Each round of training adds different noises, i.e., the data of each round of training are different from each other to prevent overfitting.
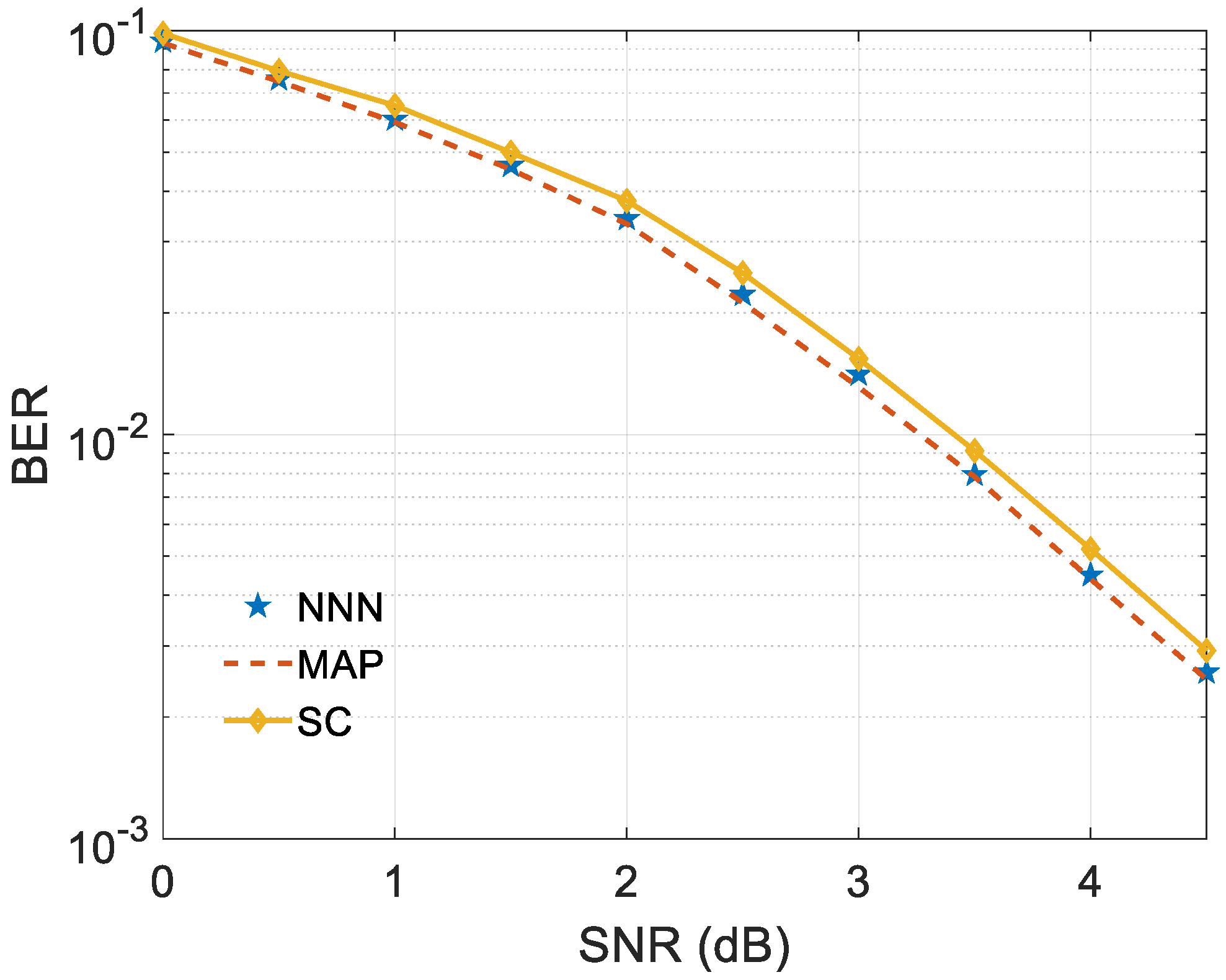
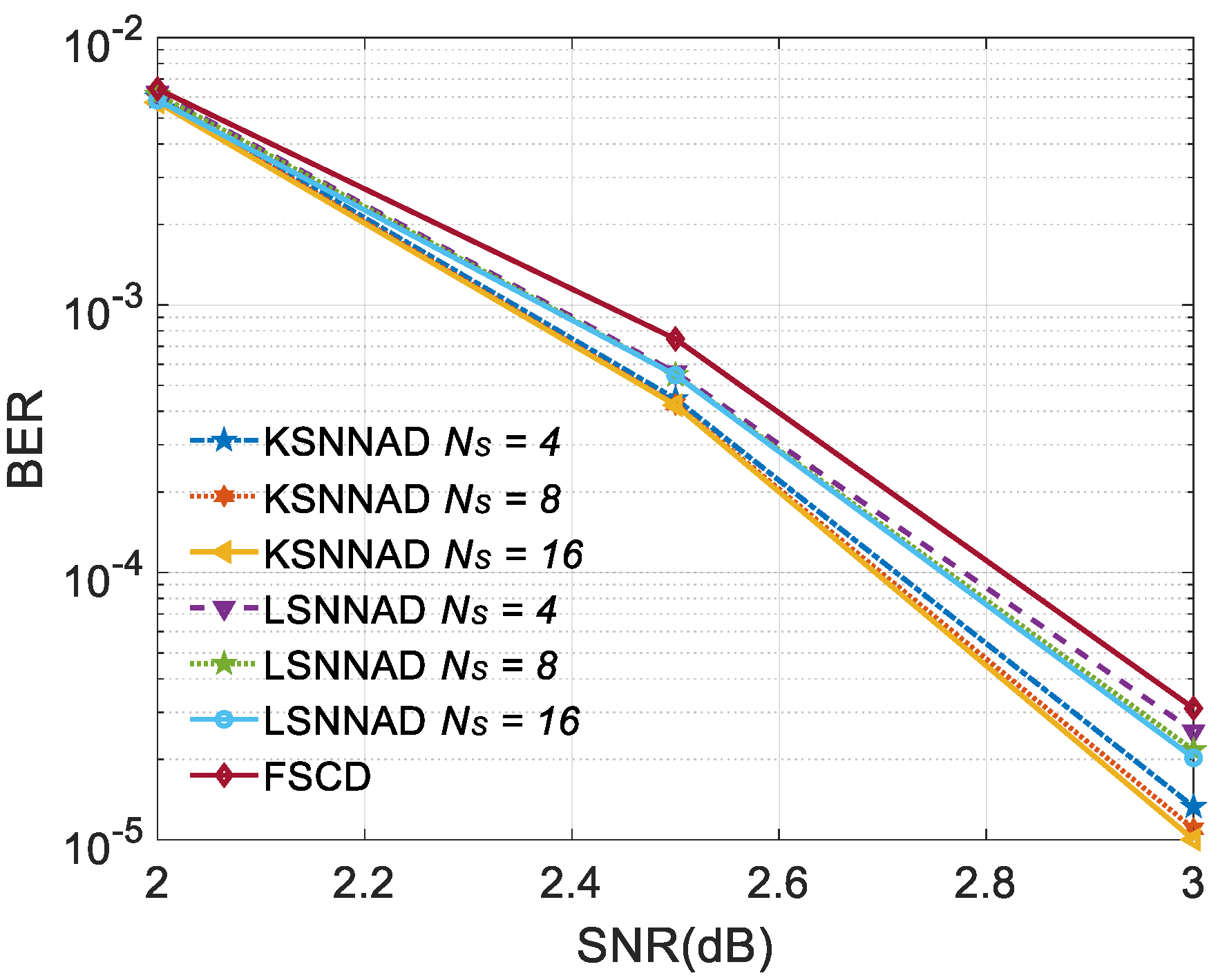
A trained CNN can classify the received signal, find the corresponding information sequence, and finally decode the polar code. A well-trained neural network can achieve the performance of MAP decoding [
26]. The decoding results of the NNN with
and
are shown in
Figure 8.
As shown in
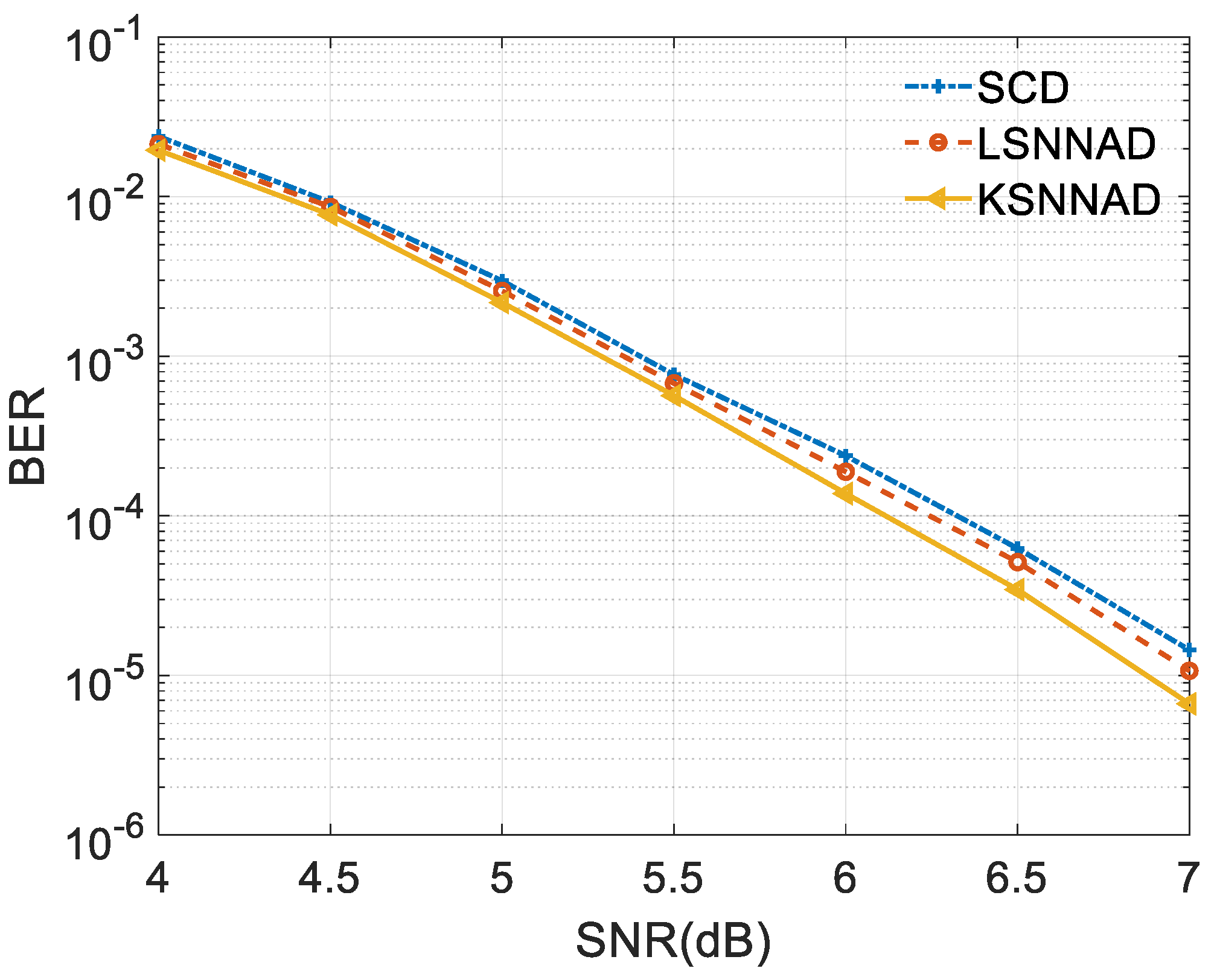
Figure 8, NNN decoding performance is better than SC algorithm, almost the same as the optimal MAP decoding algorithm, while the traditional fast decoding adopts a suboptimal decoding algorithm, and its decoding performance is similar to SC. Therefore, using well-trained CNN to decode subcodes can obtain better decoding performance than traditional classified subcodes.
3.3. Neural Network-Assisted (NNA) Decoding
The NNA decoding scheme is composed of a node recognizer and a decoder. The former recognizes the code as a concatenation of smaller constituent codes that were simply named nodes, which includes the NNN, and then the latter decodes these nodes. Note that the NNN is decoded by the trained model from the neural network model. Since the decoding scheme proposed in this paper is only for the receiving end, we use BER as the metric to measure the decoding performance. To avoid the computational complexity of the recursive structure of the successive-cancellation decoder (SCD), a vector of size is used to store the intermediate calculation results of the SC decoding algorithm. The decoding error rate will decrease as the SNR increases, i.e., when a BER is at a lower signal noise rate (SNR), the BERs at higher SNRs with the same parameters are definitely lower than . Let denote BER threshold. If a BER is lower than the threshold, it will not be displayed in the figures. Therefore, the calculations of higher SNRs with BERs lower than can be skipped to further improve the calculation speed.
To determine how to recognize the NNN, we must determine how it works. The progress of the signal process is shown in the training part of
Figure 7. When
,
ranges from 1 to 16. As shown in
Figure 7 and as explained in
Section 3.1, “Polar Encoder1” generates
possible codewords of
bits size in the training part. Considering the multiple possibilities of node recognition, we trained the polar code with
,
, with
,
, and with
,
in epochs. The gradient of the loss function is calculated in each epoch using the Adam optimizer [
36], and the trained model is finally saved to be used in the decoding part.
When only four kinds of traditional special nodes need to be identified, we first identify the polar code with the entire length of and judge whether the code is one of the above four kinds of nodes. If so, we directly perform maximum likelihood decoding. If not, we continue to identify the first half and the second half, and the above process is repeated until the original code is completely decomposed into nodes. Although the recognition process is a recursive process, this process is only performed once, and the computational complexity increase is limited. This method of transferring half of the original sequence into the recursive operation to identify the subcode is called dichotomy.
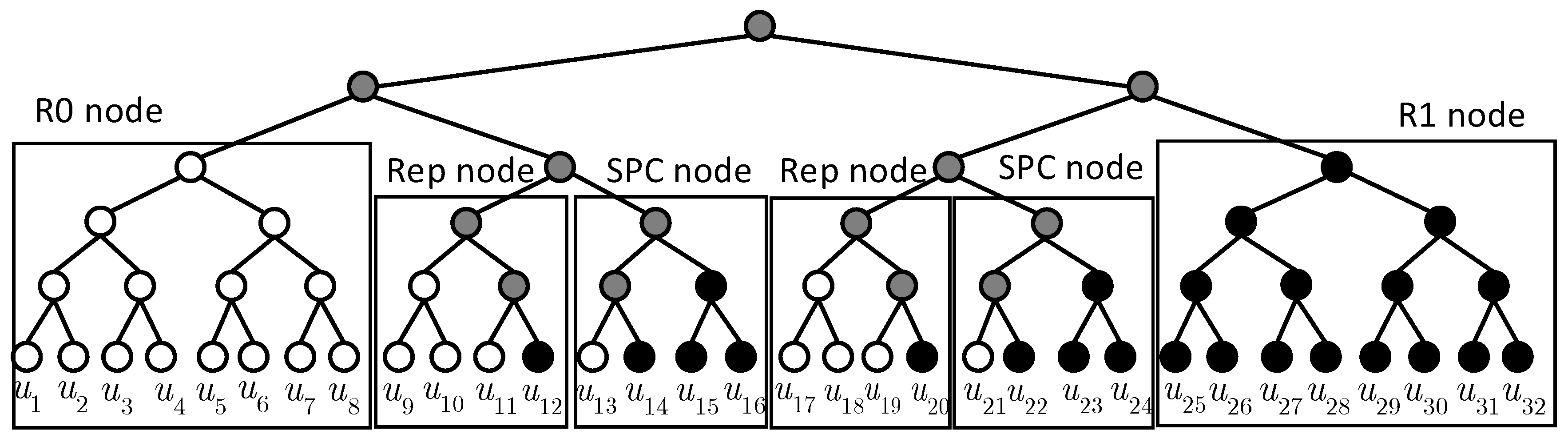
Assuming that the length of the NNN is 8, if we execute dichotomy, when the subcode with a code length of 8 does not belong to the four traditional special nodes mentioned before, it will be recognized as an NNN. In practice, the decoding performance will be greatly reduced in some cases. To find the reasons and explore a proper division method of the NNN, we recognized and decoded polar codes with a code length of 16 and information bit length 1–16. In this experiment, the codewords were constructed using the GA method. Taking polar codes with and as an example, we write R0(8) to denote an R-0 node with a code length of 8, SPC(4) to denote the SPC node with a code length of 4, and NNN(8/3) to denote an NNN with and . When the code is recognized in the traditional way, the node-type structure is R0(8) + R0(4) + SPC(4) and the node can be recognized as R0(8) + NNN(8/3) by the node recognizer as well, that is, the NNN structure is R0(4) + SPC(4). Note that when , the code can also be recognized as NNN(16/3).
We simulated multiple times and found that when the NNN is the last node of the original code, the decoding performance is always better than that of the traditional fast SC decoding algorithm. When an NNN is decoded as the non-last subcode, the polarization effect cannot be generated sometimes. This is because the information bits position determined by encoder 1 is different from the actual NNN determined by the recognizer. So, the decoding model is mismatched and errors are propagated in the decoding tree, resulting in decoding failure.
There are two ways to solve the abovementioned problems: one is to use an NNN as the last decoded subcode directly, and the other is to consider adapting the model and improving the correct probability of the first error, thus preventing the decoding error propagation. The two solutions lead to two decoding schemes, which are described below.
3.4. Last Subcode Neural Network-Assisted Decoding (LSNNAD) Scheme
Let
denote the code length of the last subcode neural network node (LSNNN). The main idea of this scheme is to identify the last subcode as LSNNN. Note that at this time, LSNNN may be one of the four traditional subcodes mentioned above, or it may be different from the above four subcodes. The type, length, position, and order are determined at the moment when the codeword is constructed. In this experiment, 0 and 1 are used to represent the frozen bits and information bits, i.e., the sequence
of code length
N is obtained after the codeword is constructed. When
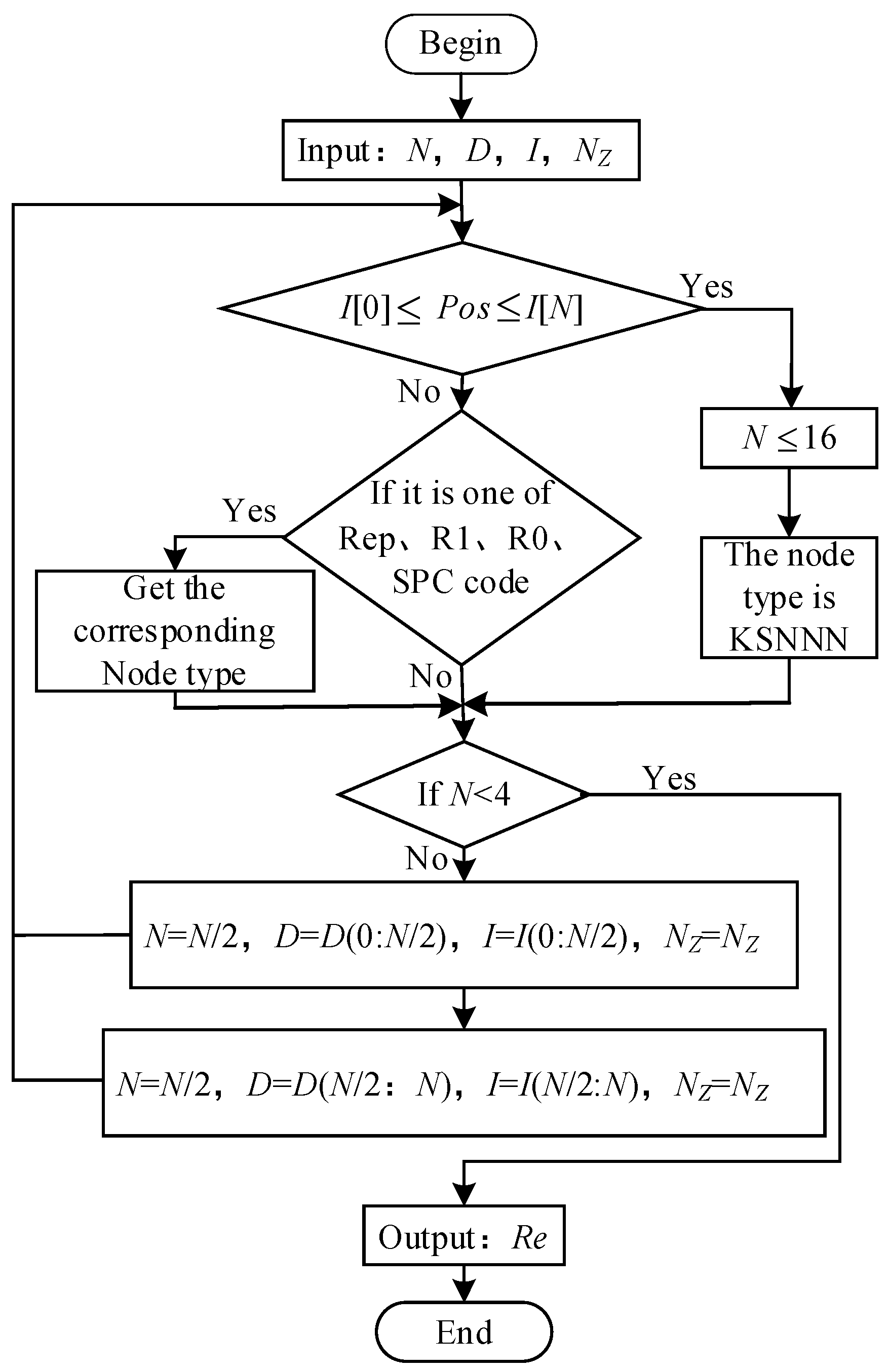
, the information bits are stored. Otherwise, the frozen bits are stored. In this experiment, all frozen bits are 0. The LSNNN identification flowchart is shown in
Figure 9.
The input
is the same as in
Figure 1. Let
denote the position of bits and
, an arbitrary subset of
, denote the position of information bits.
denotes the vector of the index, the initial content of which is in the range
, and it represents the sequence position currently being processed.
denotes the first element of the vector
and represents the starting position of the code being processed.
,
, and
constantly change during the calculation process depicted in the flowchart (
Figure 9).
denotes the first half of the vector
,
denotes the second half of the vector
, and
denotes the starting point of the NNN that is already fixed when the total code length and length of the NNN are determined. The output
is a matrix with five rows, with the first to the last rows denoting the node type, the starting point,
,
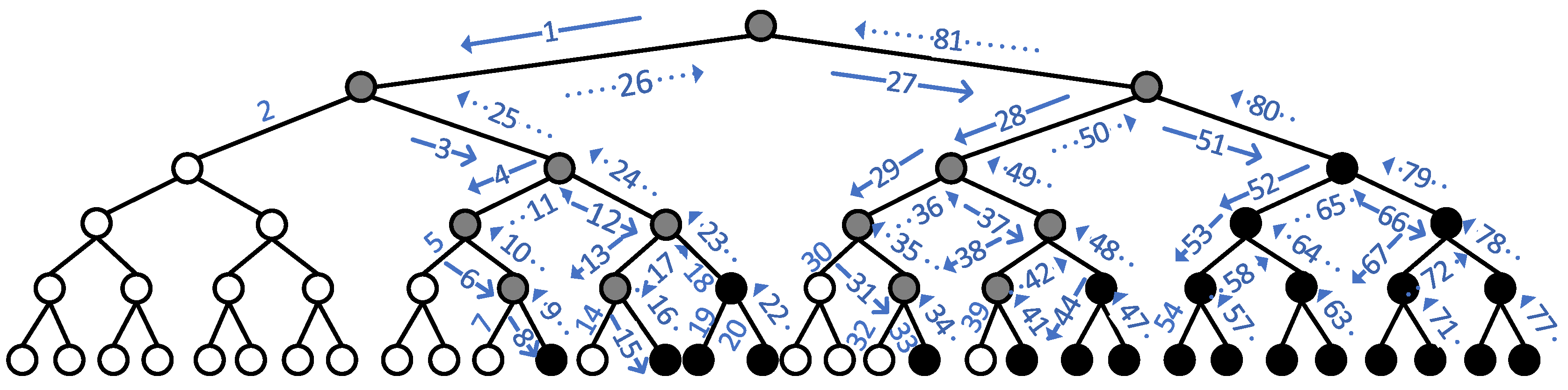
, and the information position of every node, respectively. In the node identification process, the decoding depth of each node is recorded, i.e., the node position in the SC decoding tree is recorded. The decoding tree after dividing the subcodes according to the above rules is shown in
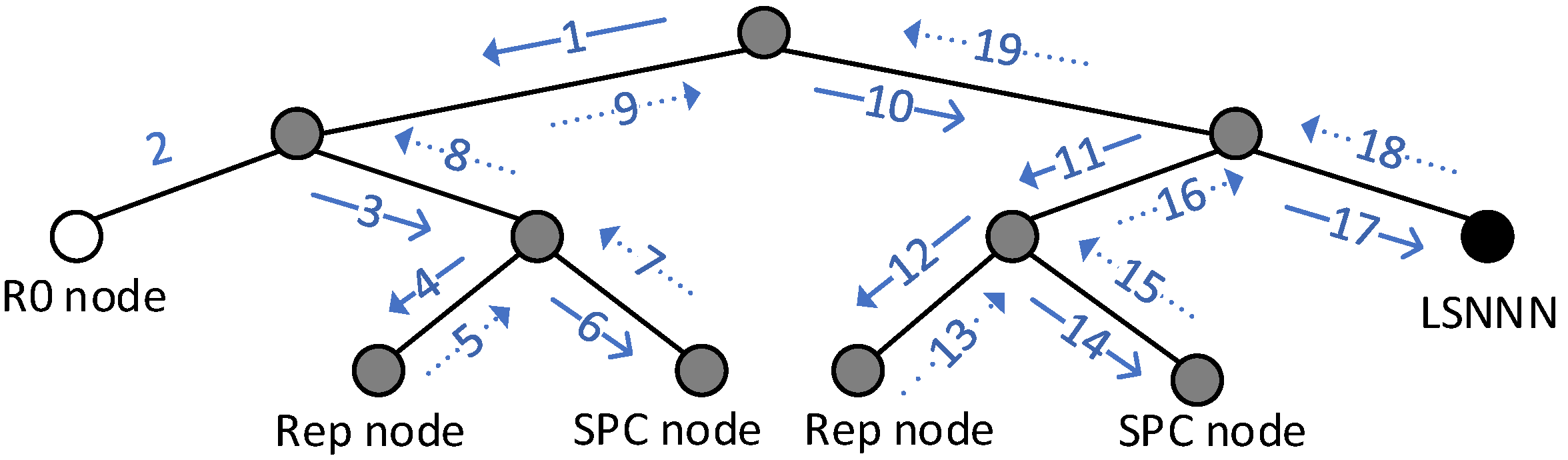
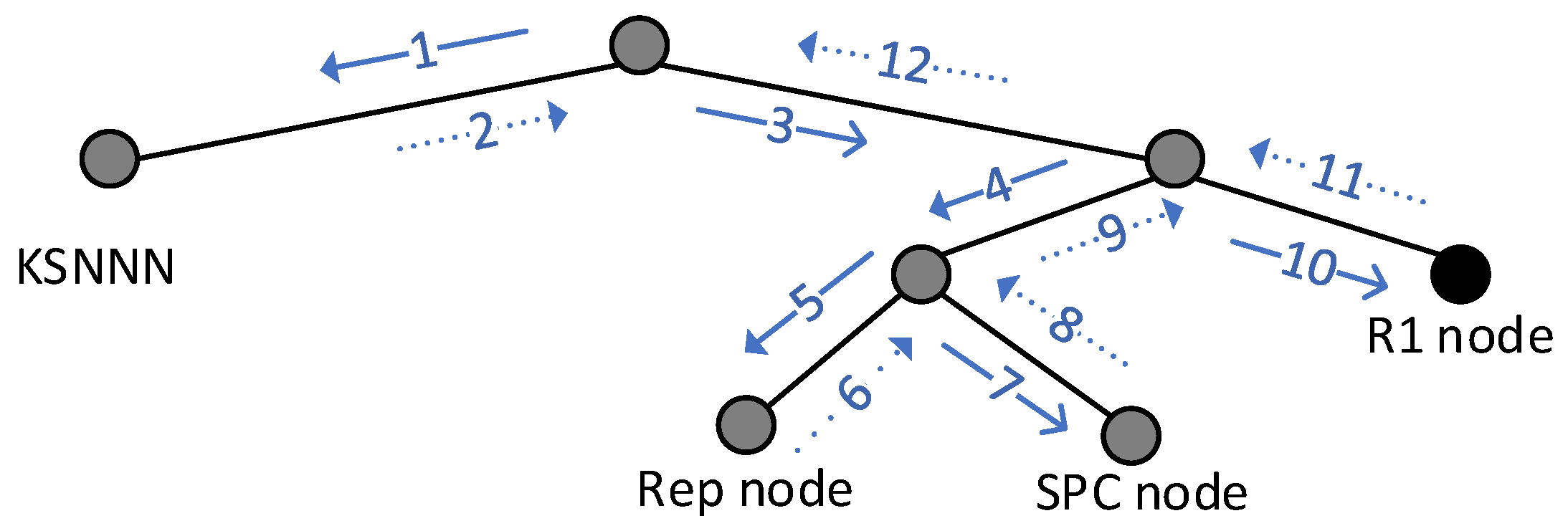
Figure 10.
3.5. Key-Bit-Based Subcode Neural Network-Assisted Decoding (KSNNAD) Scheme
Although the LSNNAD minimizes the loss of decoding errors caused by model mismatches, the performance improvement is limited. So, we must find another scheme to improve the decoding performance.
Ref. [
37] analyzed the SC decoding error of polar codes and found that the first error is usually caused by channel noise, and the frequency of decoding failure caused by this error increases with the increase of code length. Ref. [
38] analyzed and proved that when the polar code is divided into several R1 nodes, the first error in SC decoding of the polar code is likely to occur at the first information bit of the R1 nodes. Therefore, the decoding performance of the SC algorithm can be improved as long as the first error is correct. It can be seen from the above analysis that the first error is likely to occur at the first information bit position. This bit is defined as a key bit, and the node containing this bit is recognized as an NNN. In this scheme, all the NNNs are recorded and trained, and the models are saved to be called in the decoding part so that the model mismatched error is solved. Note that the label
is the decoding result whose key bit is flipped in the decoding process. So, the training part of the KSNNAD does not need a polar encoder.
The scheme is called a KSNNAD scheme, and the NNN is called the key bit based neural network node (KSNNN). We solve another problem: how to recognize a KSNNN.
The simplest idea of recognizing a KSNNN is to select the key bit as the first bit of the KSNNN. Assuming that the position is
and the subcode length is
, the position of the last bit of the KSNNN is
. However, the dichotomy does not ensure that the key bit is the first position of the KSNNN; it may be the middle position. Next, we need to recognize a polar code with a KSNNN and the other four traditional subcodes mentioned above. Considering the complexity, the code length of KSNNN is limited to
. The identification flowchart is shown in
Figure 11.
Taking the polar code with
, which is mentioned above as an example, the recognized result and decoding process are shown in
Figure 12.
As shown in
Figure 13, the time step required for decoding at this time is 12. The structure of the KSNNN is R0(8) + Rep(4) + SPC(4), compared with
Figure 6. The structure of the original polar code is KSNNN(16) + Rep(4) + SPC(4) + R1(8). In the actual execution process, the subcode classification procedure is first executed. All possible forms of KSNNN are recorded. The key bit flip results corresponding to all possible situations of each specific form are trained as labels. Finally, the models are saved and called in the decoding part separately.
.