Evaluation of Criteria for Out-of-Plane Stability of Steel Arch Bridges in Major Design Codes by FE Analysis
Abstract
1. Introduction
2. Outline of Out-of-Plane Stability Provisions in Each Code
2.1. Chinese Code
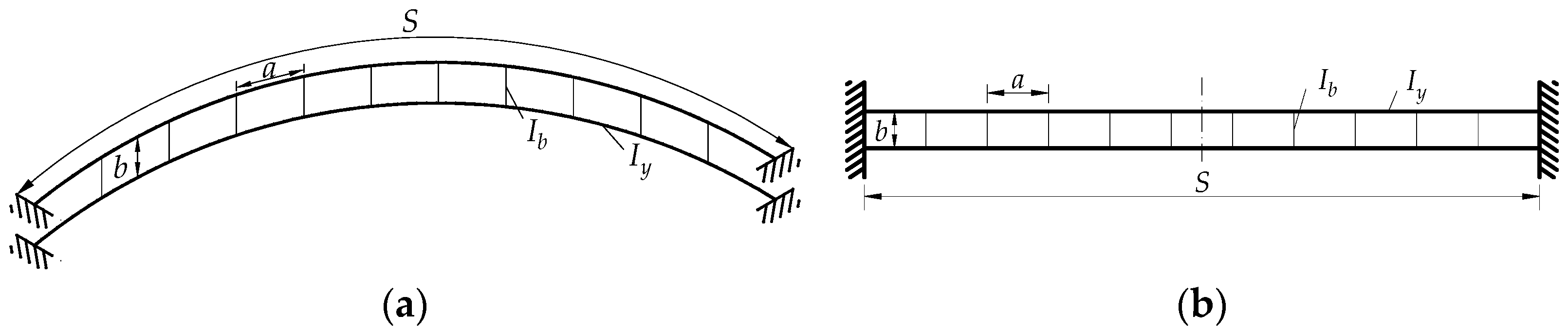
2.2. Japanese Code
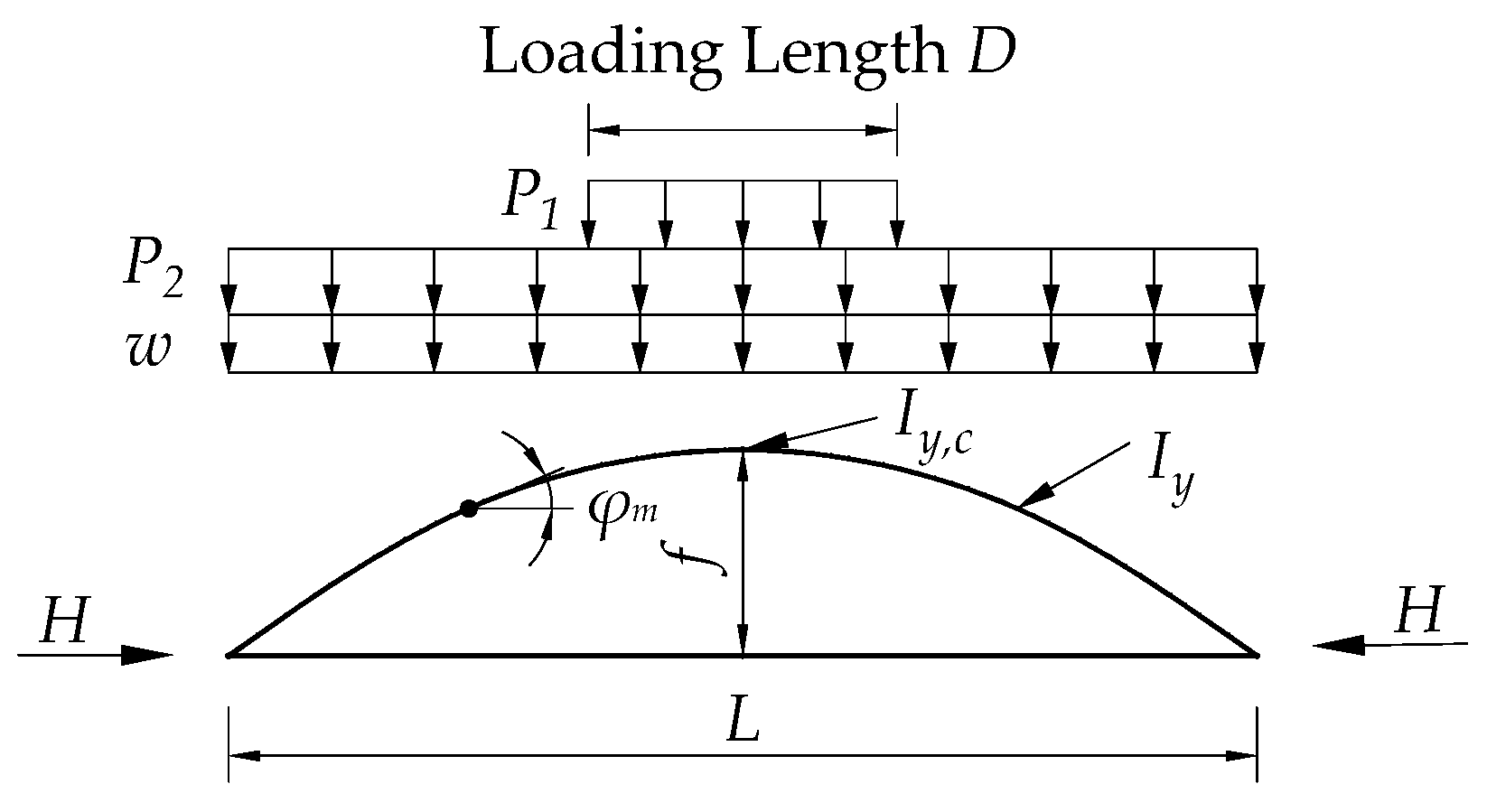
2.3. Eurocode 3
3. Bridges Analyzed and Method of FE Analysis
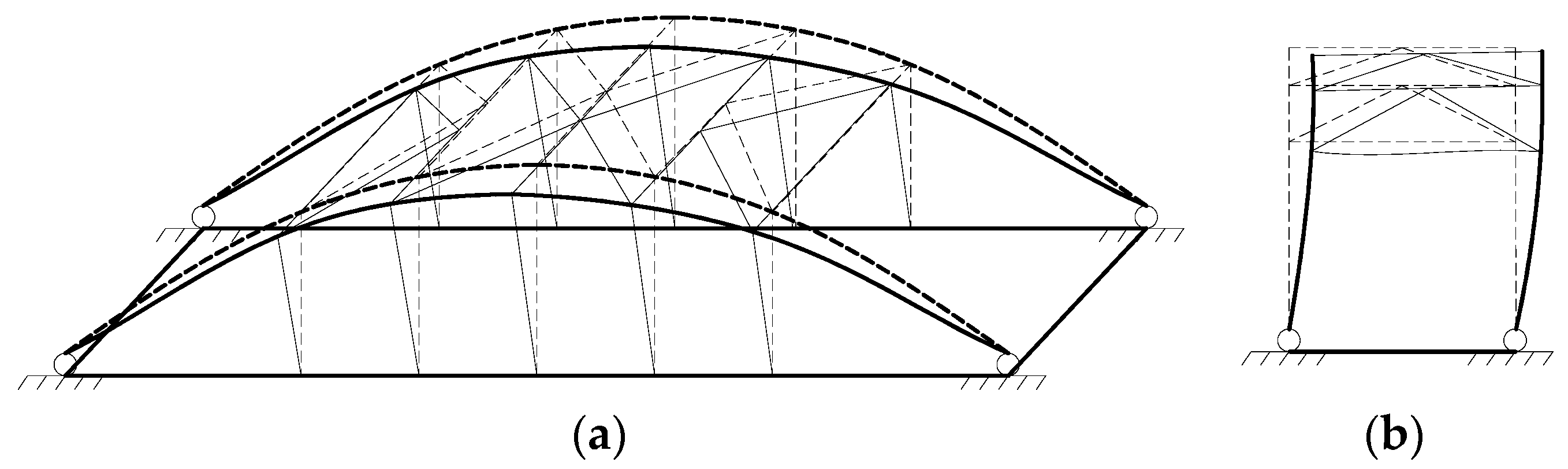
3.1. Bridges Analyzed and Study Parameters
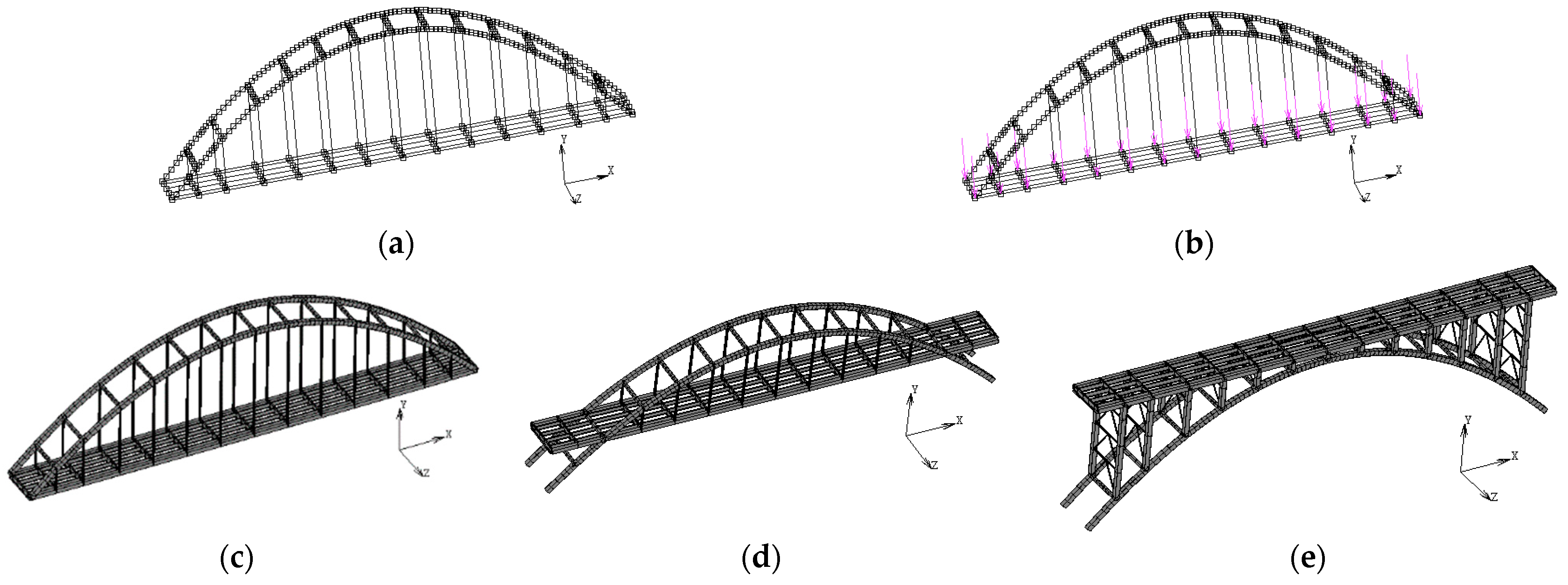
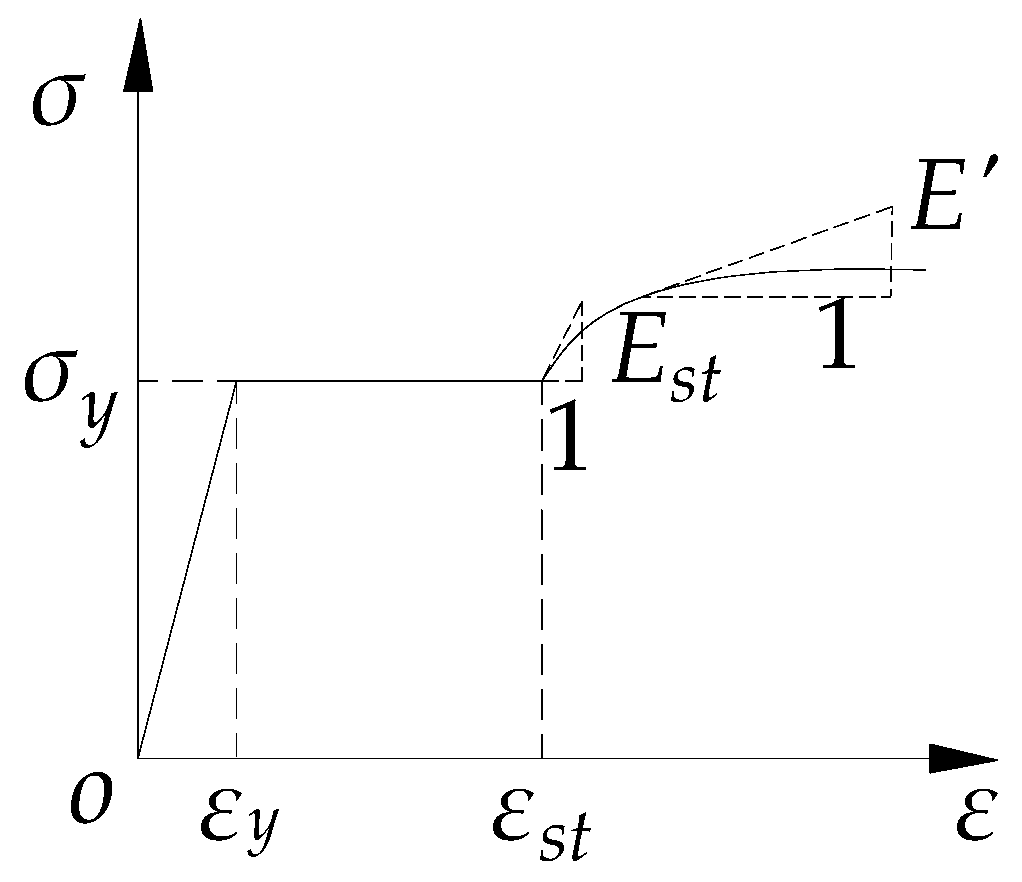
3.2. FE Analysis
3.2.1. FE Modeling
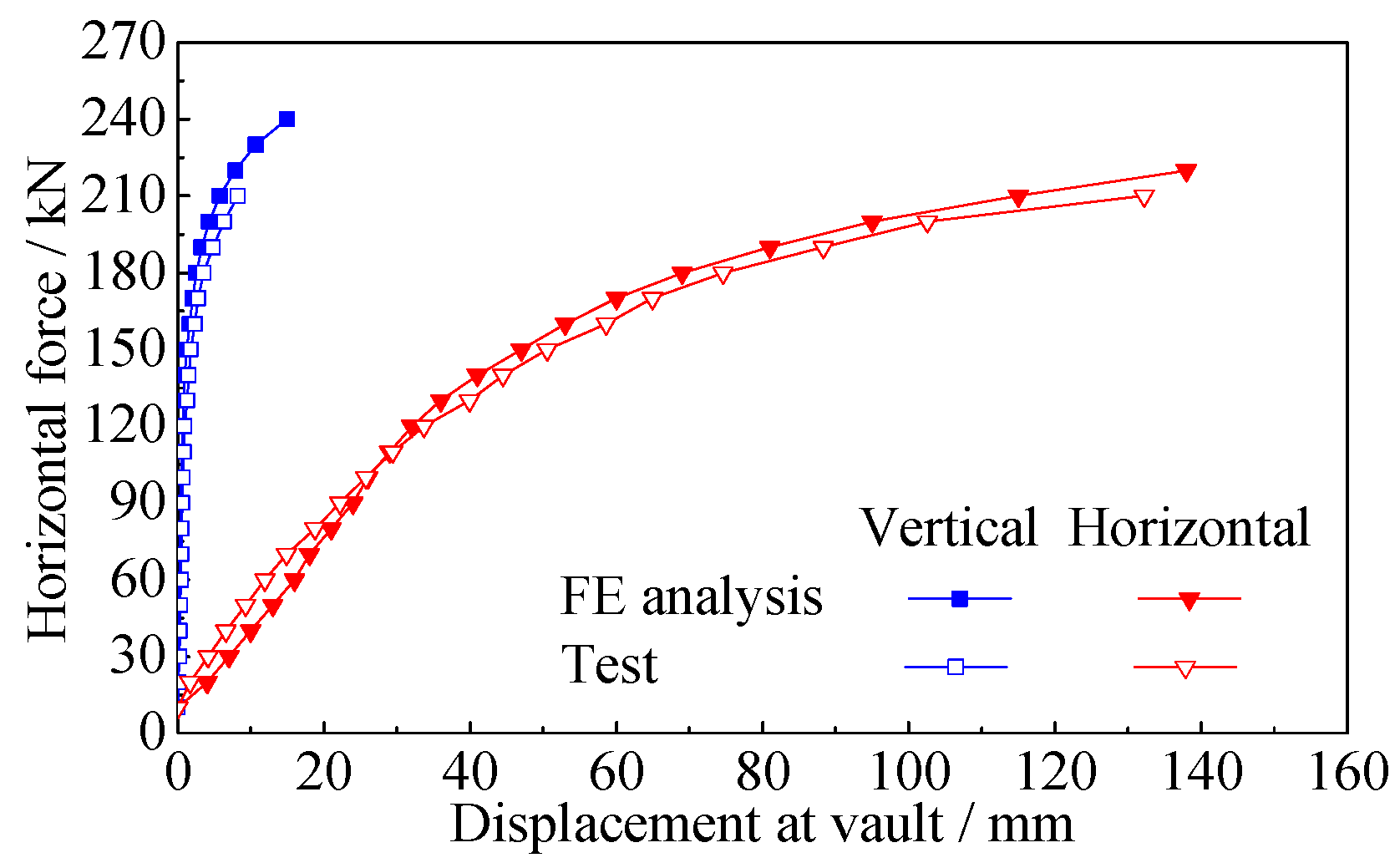
3.2.2. Accuracy Verification of FE Analysis
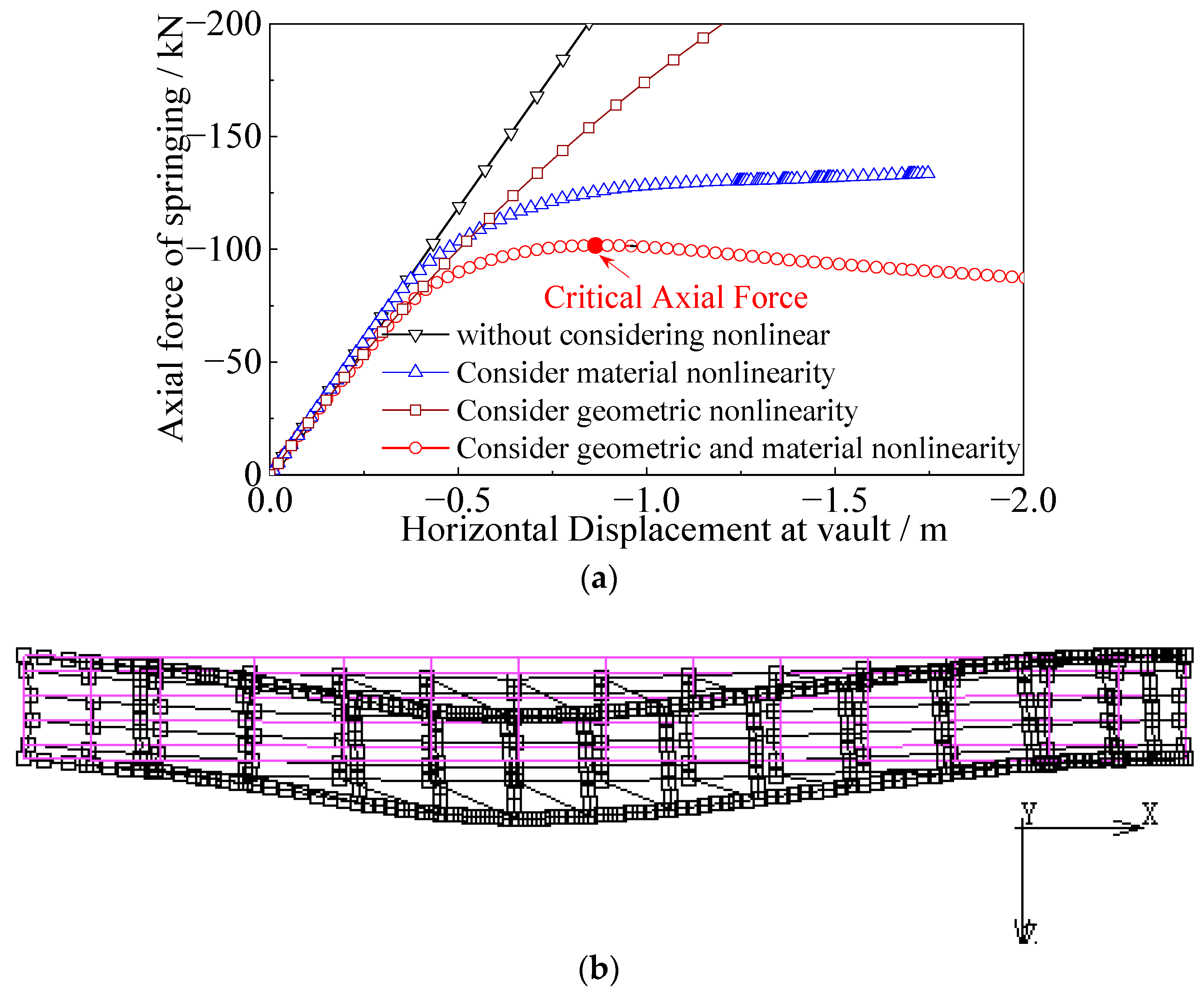
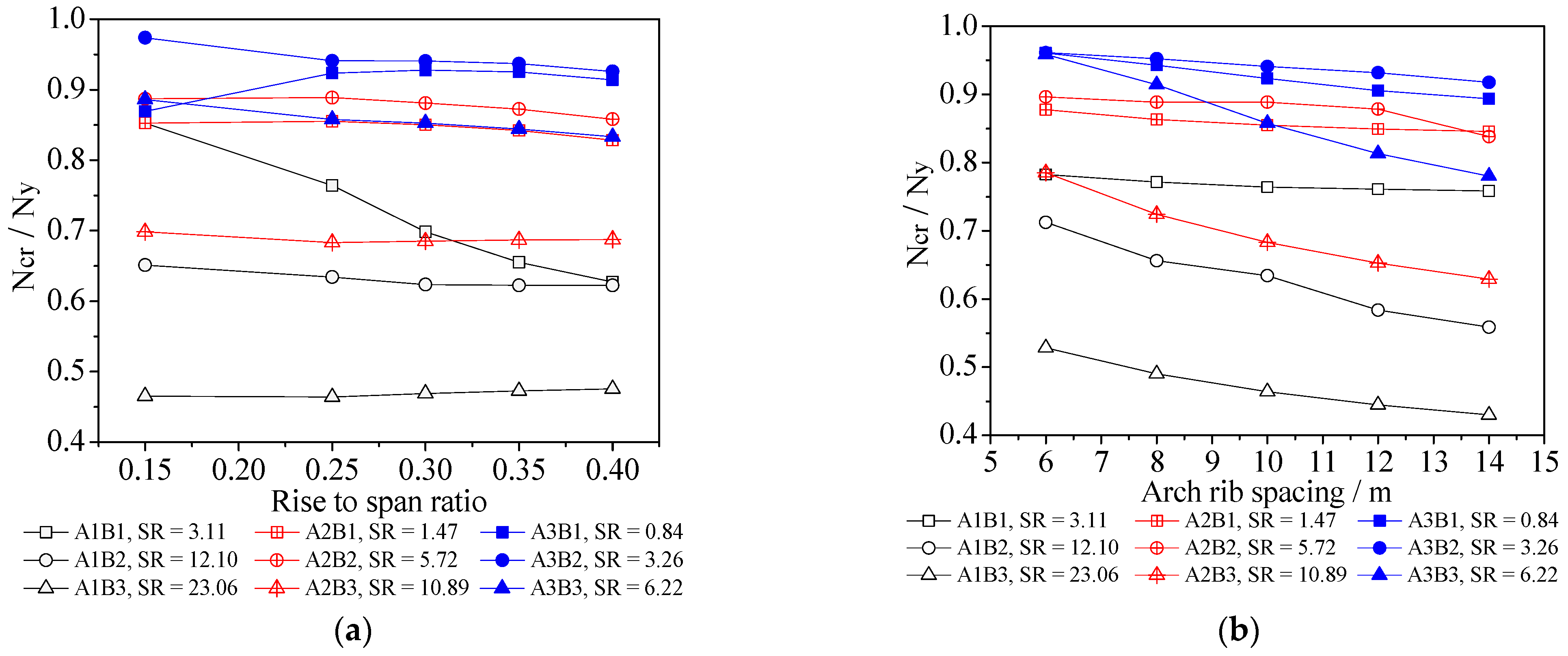
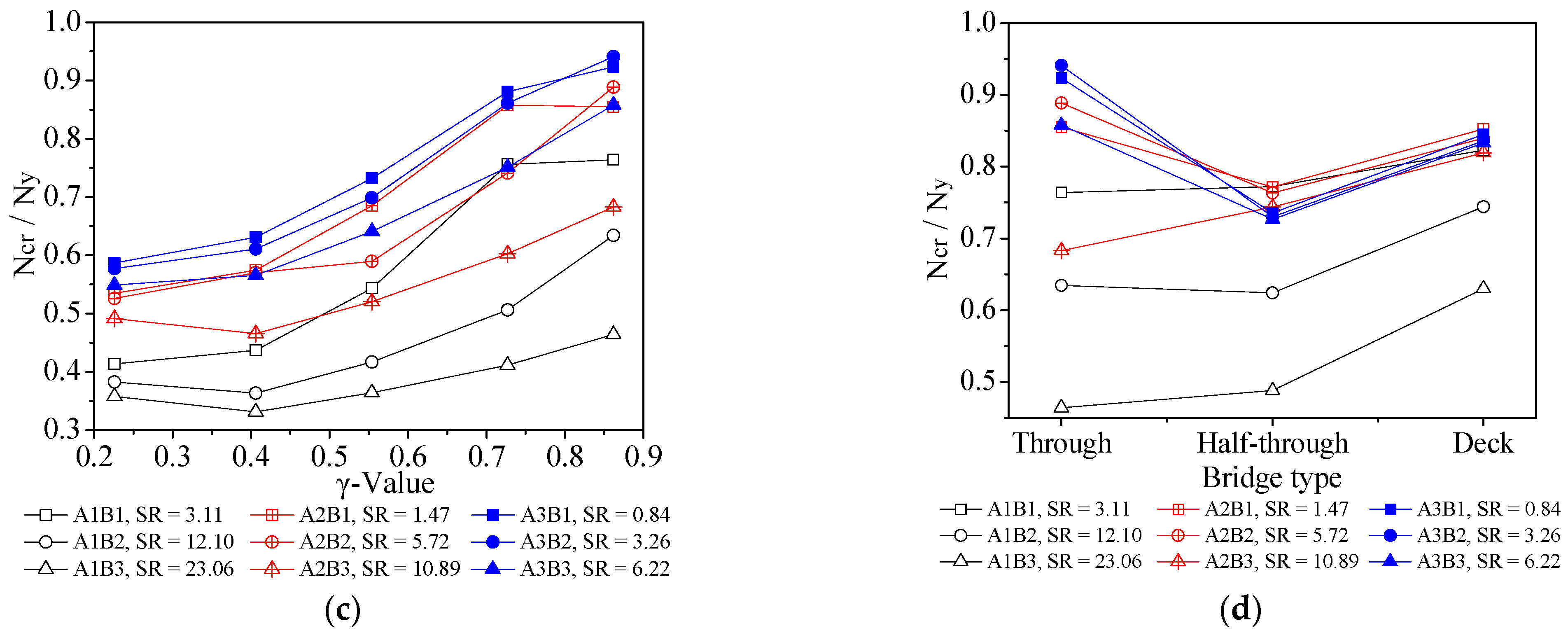
4. Discussion of FE Analysis Results
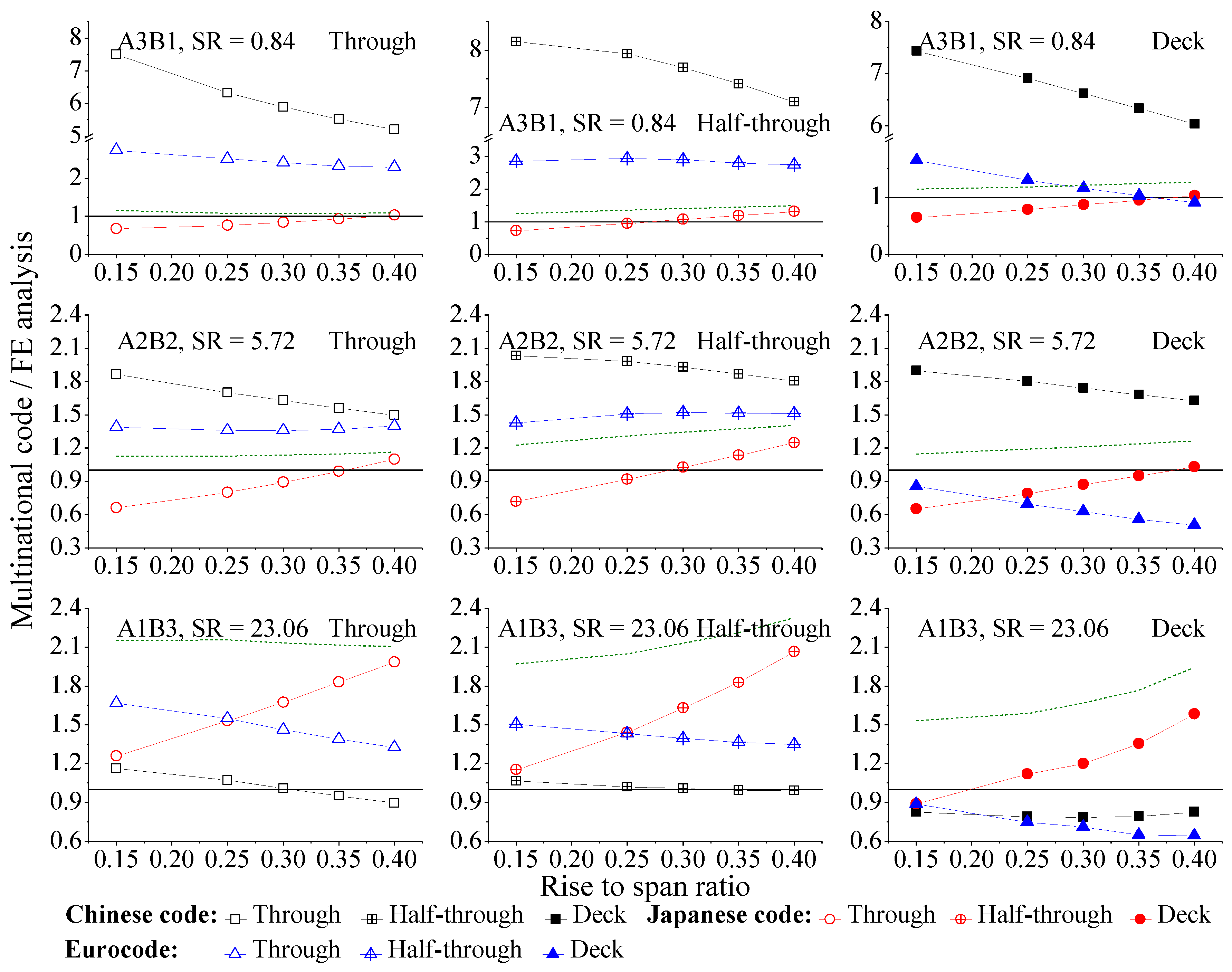
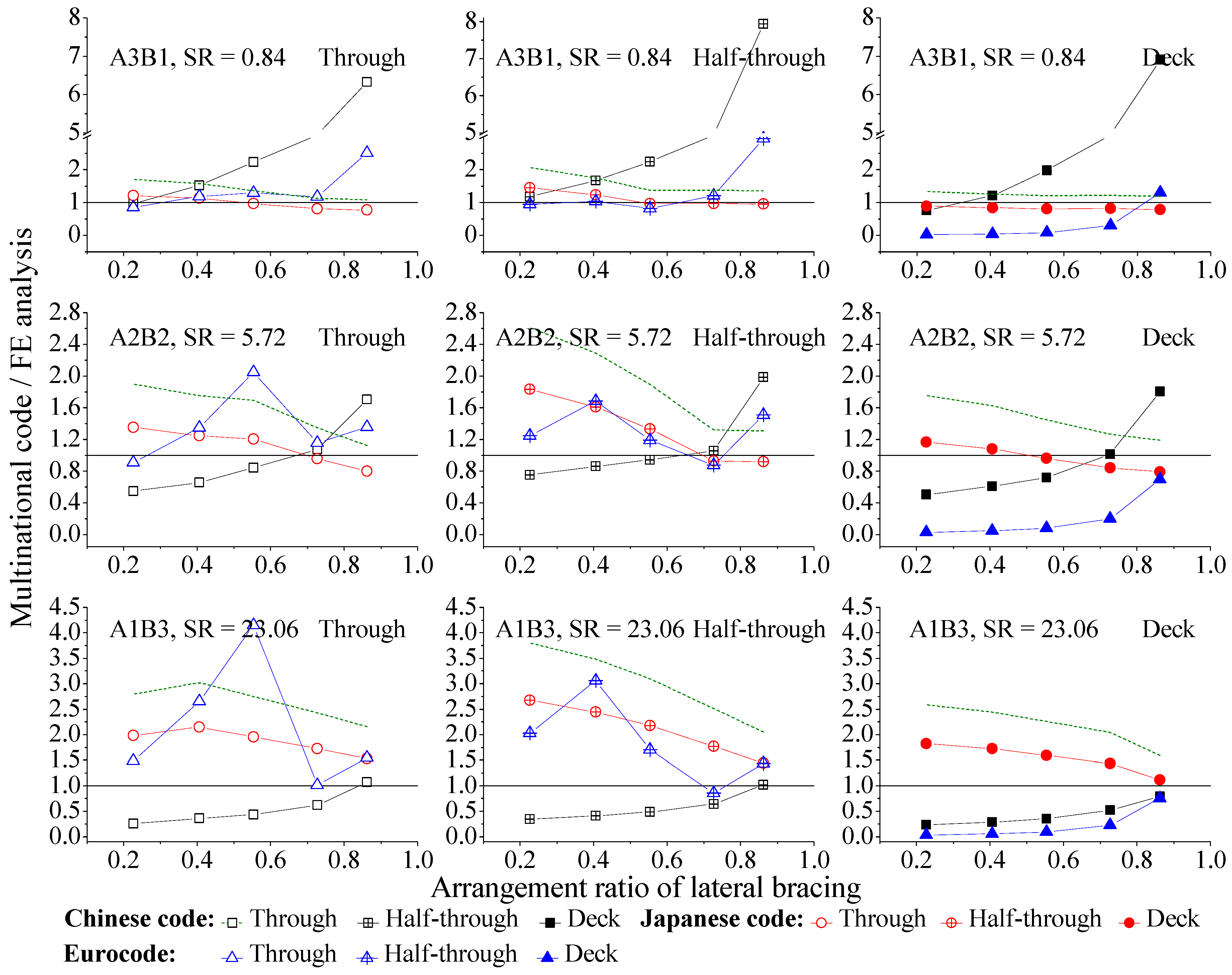
5. Evaluation of Major Design Codes Based on Results of FE Analysis
5.1. Influence of Rise-to-Span Ratio
5.2. Influence of Range of Lateral Bracing Arrangements
5.3. Influence of Arch Rib Spacing
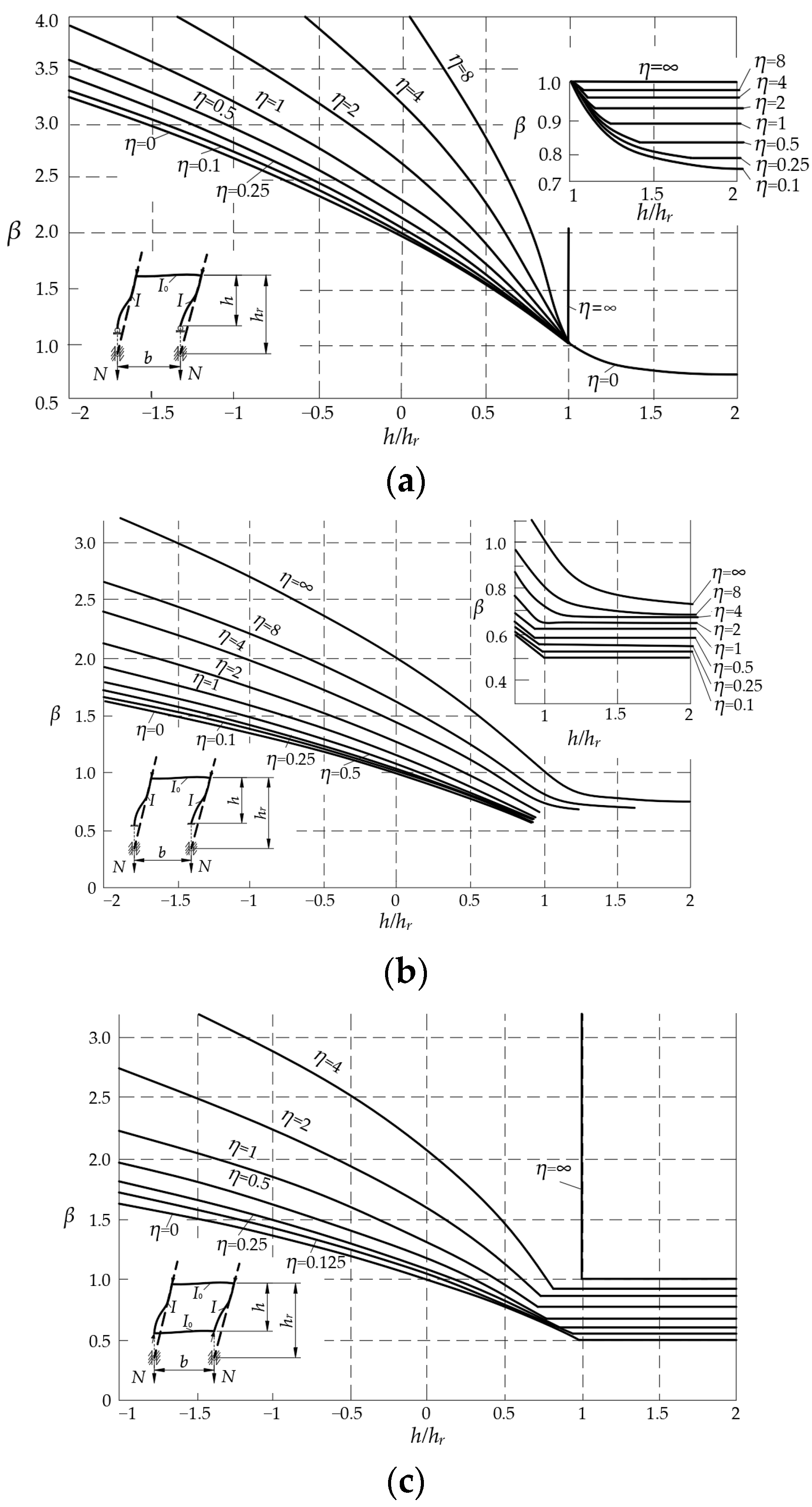
5.4. Influence of Stiffness Ratio
5.5. Influence of Bridge Type
5.6. Factors for Improving Code Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Timoshenko, S.; Gere, J. Theory of Elastic Stability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Demuts, E. Lateral Buckling of Circular Arches Subjected to Uniform Gravity Type Loading. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 1969. [Google Scholar]
- Lu, H.; Liu, A.; Bradford, M.A.; Pi, Y. Experimental investigation of out-of-plane buckling of circular arches under a central radial point load. Thin-Walled Struct. 2020, 148, 106198. [Google Scholar] [CrossRef]
- Tokarz, F.J.; Sandhu, R.S. Lateral-torsional buckling of parabolic arches. J. Struct. Div. 1972, 98, 1161–1179. [Google Scholar] [CrossRef]
- Kee, C.F. Lateral inelastic buckling of tied arches. J. Struct. Div. 1961, 87, 23–40. [Google Scholar] [CrossRef]
- Tokarz, F.J. Experimental Study of Lateral Buckling of Arches. J. Struct. Div. 1971, 97, 545–559. [Google Scholar] [CrossRef]
- Papangelis, J.P.; Trahair, N.S. Flexural-torsional buckling tests on arches. J. Struct. Eng. 1987, 113, 1433–1443. [Google Scholar] [CrossRef]
- Papangelis, J.P.; Trahair, N.S. Flexural-torsional buckling of arches. J. Struct. Eng. 1987, 113, 889–906. [Google Scholar] [CrossRef]
- Almeida, P.N. Lateral Buckling of Twin Arch Ribs with Transverse Bars. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 1970. [Google Scholar]
- Sakimoto, T.; Namita, Y. Out-of-plane buckling of solid rib arches braced with transverse bars. Proc. Jpn. Soc. Civ. Eng. 1971, 191, 109–116. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sakimoto, T.; Komatsu, S. A possibility of total breakdown of bridge arches due to buckling of lateral bracings. In Proceedings of the Final Report of the 2nd International Colloquium on Stability of Steel Structures, Liege, Belgium, 13–15 April 1977; pp. 299–301. [Google Scholar]
- Kuranishi, S.; Yabuki, T. Required out-of-plane rigidities of steel arch bridge with two main ribs subjected to vertical and lateral loads. Technol. Rep. Tohoku Univ. 1977, 46, 47–72. [Google Scholar]
- Guo, Y.; Zhao, S.; Dou, C. Out-of-plane elastic buckling behavior of hinged planar truss arch with lateral bracings. J. Constr. Steel Res. 2014, 95, 290–299. [Google Scholar] [CrossRef]
- Sakimoto, T.; Komatsu, S. Ultimate strength of arches with bracing systems. J. Struct. Div. 1982, 108, 1064–1076. [Google Scholar] [CrossRef]
- Sakimoto, T.; Komatsu, S. Ultimate strength formula for steel arches. J. Struct. Div. 1983, 109, 613–627. [Google Scholar] [CrossRef]
- Sakimoto, T.; Sakata, T.; Kobori, T. An effective length procedure for out-of-plane buckling strength estimation of steel arch bridges. In Proceedings of the 3rd Pacific Structural Steel Conference, Tokyo, Japan, 26–28 October 1992. [Google Scholar]
- Pi, Y.L.; Trahair, N.S. Out-of-Plane Inelastic Buckling and Ultimate Strength of Steel Arches; Research Report No. R737; University of Sydney: Camperdown, NSW, Australia, 1997. [Google Scholar]
- Lim, N.H.; Kang, Y.J. Out of plane stability of circular arches. Int. J. Mech. Sci. 2004, 46, 1115–1137. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A. Out-of-plane strength design of fixed steel I-section arches. J. Struct. Eng. 2005, 131, 560–568. [Google Scholar] [CrossRef]
- Spoorenberg, R.C.; Snijder, H.H.; Hoenderkamp, J.C.D. A theoretical method for calculating the collapse load of steel circular arches. Eng. Struct. 2012, 38, 89–103. [Google Scholar] [CrossRef][Green Version]
- Liu, A. Experimental research on stable ultimate bearing capacity of leaning-type arch rib systems. J. Constr. Steel Res. 2015, 114, 281–292. [Google Scholar] [CrossRef]
- Bouras, Y.; Vrcelj, Z. Out-of-plane stability of concrete-filled steel tubular arches at elevated temperatures. Int. J. Mech. Sci. 2020, 187, 105916. [Google Scholar] [CrossRef]
- Zhong, Z.; Liu, A.; Fu, J.; Lin, P.; Jian, D.; Xie, Z. Analytical and experimental studies on out-of-plane dynamic parametric instability of a circular arch under a vertical harmonic base excitation. J. Sound Vib. 2021, 500, 116011. [Google Scholar] [CrossRef]
- Chan, S. Non-linear behavior and design of steel structures. J. Constr. Steel Res. 2001, 57, 1217–1231. [Google Scholar] [CrossRef]
- Standardization Administration of the People’s Republic of China. Fundamental Code for Design on Railway Bridge and Culvert; China Railway Publishing House Co., LTD.: Beijing, China, 2005. [Google Scholar]
- Japan Road Association. Specifications for Highway Bridges Part II; Marusan Publishing Division: Tokyo, Japan, 2012. [Google Scholar]
- European Committee for Standardization. Eurocode3: Design of Steel Structures-Part 2: Steel Bridge; European Committee for Standardization: Brussels, Belgium, 2003. [Google Scholar]
- American Association of State Highway and Transportation Officials. LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010.
- Wan, P. Research on Synthetical Three Factors Check Method for Ultimate Load Carrying Capacity of Long-Span Steel Arch Bridges. Ph.D. Thesis, Southwest Jiaotong University, Chendu, China, 2005. [Google Scholar]
- Usami, T. Guidelines for Stability Design of Steel Structures; Marusan Publishing Division: Tokyo, Japan, 2005. [Google Scholar]
- Sakimoto, T.; Sakata, T. The out-of-plane buckling strength of through-type arch bridges. J. Constr. Steel Res. 1990, 16, 307–318. [Google Scholar] [CrossRef]
- Sakimoto, T.; Sakata, T.; Tsuruta, E. Elastic-plastic out-of-plane buckling strength of through type and half-through type arch bridges. Struct. Eng./Earthq. Eng. 1989, 2, 137–148. [Google Scholar]





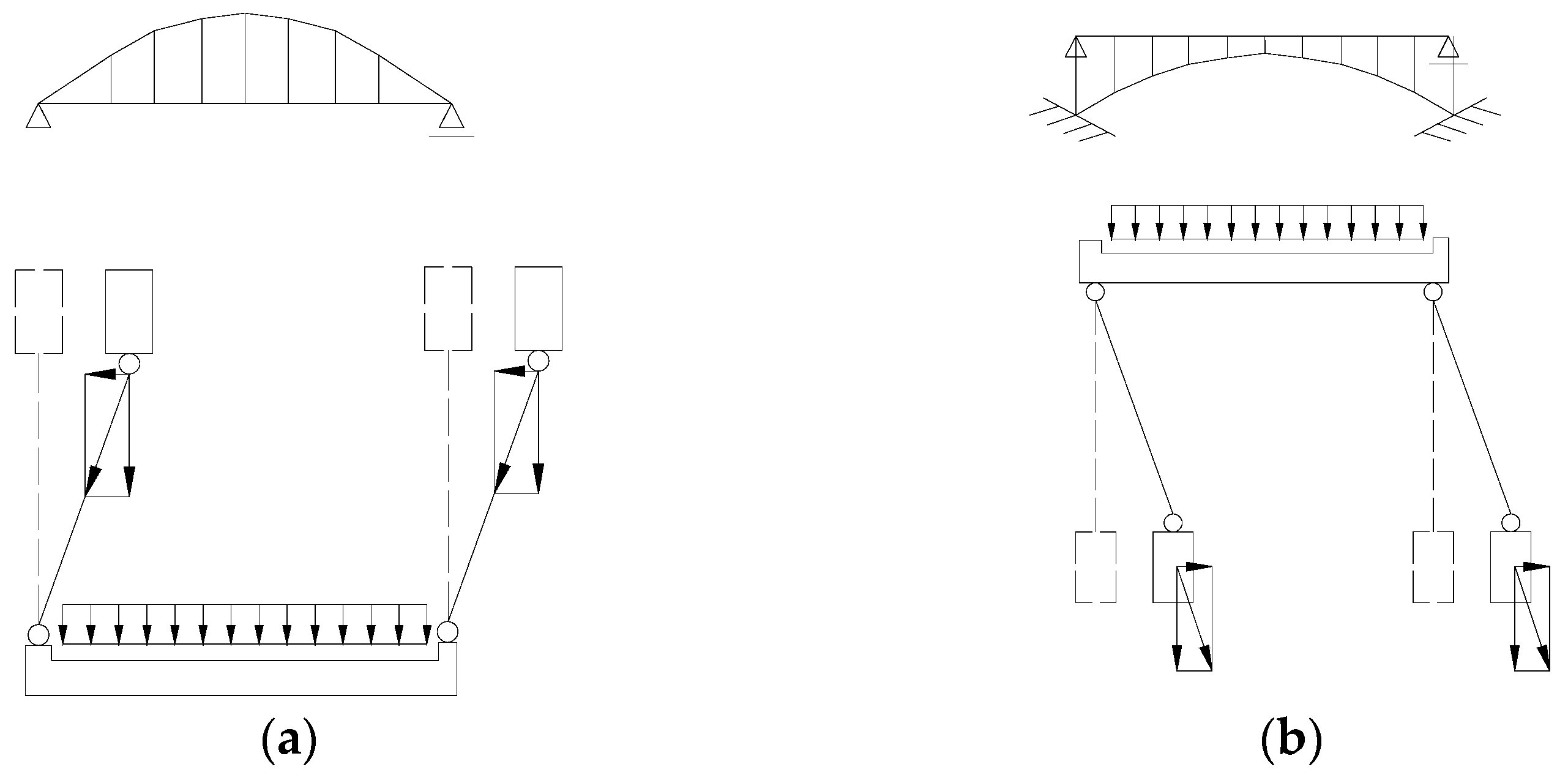
| Section | Rise Ratio f/L | ||||
|---|---|---|---|---|---|
| 0.05 | 0.10 | 0.20 | 0.30 | 0.40 | |
| Iy = constant | 0.50 | 0.54 | 0.65 | 0.82 | 1.07 |
| Iy = Iy,c/cosφm | 0.50 | 0.52 | 0.59 | 0.71 | 0.86 |
| Section | Height | Width | Thickness of Flange | Thickness of Web Plate |
|---|---|---|---|---|
| Arch rib 1 | 1752 | 1100 | 26 | 26 |
| Arch rib 2 | 1200 | 1000 | 22 | 20 |
| Arch rib 3 | 1000 | 900 | 20 | 16 |
| Lateral brace 1 | 1000 | 900 | 18 | 15 |
| Lateral brace 2 | 700 | 600 | 14 | 12 |
| Lateral brace 3 | 600 | 500 | 12 | 10 |
| Case | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
|---|---|---|---|---|---|---|---|---|---|
| Section of arch rib | 1 | 2 | 3 | ||||||
| Section of lateral brace | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Stiffness ratio | 3.11 | 12.10 | 23.06 | 1.47 | 5.72 | 10.89 | 0.84 | 3.26 | 6.22 |
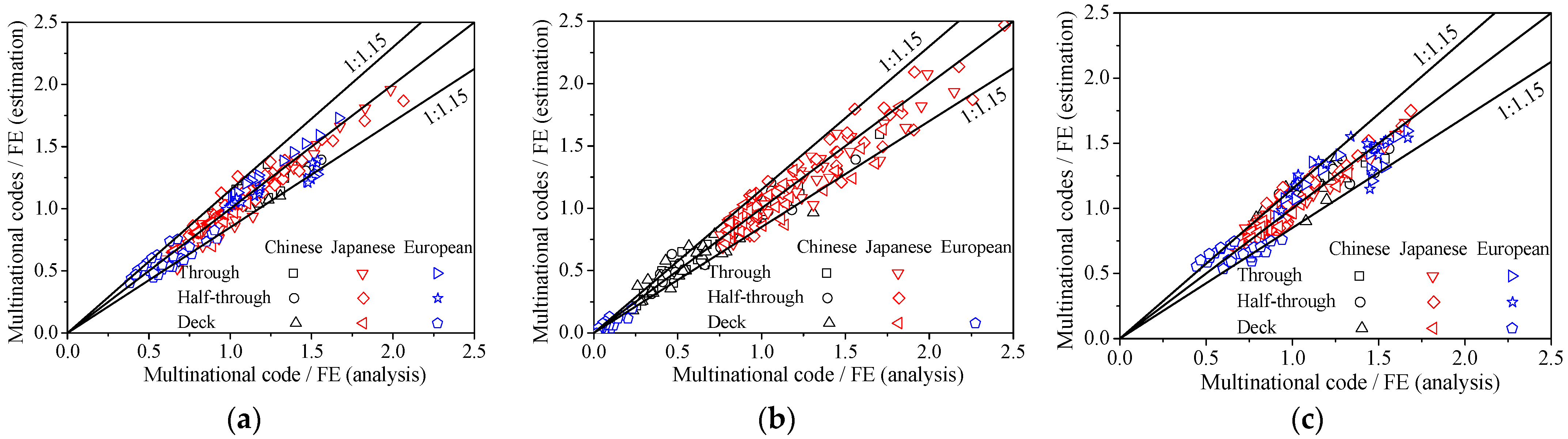
| Code | Bridge Type | A | B | C | D |
|---|---|---|---|---|---|
| Chinese code | Through | 1.602 | −0.008 | −0.919 | −0.009 |
| Half-through | 1.751 | −0.025 | −0.778 | 0.015 | |
| Deck | 1.704 | −0.036 | −1.179 | 0.044 | |
| Japanese code | Through | 0.267 | 0.022 | 1.506 | 0.063 |
| Half-through | 0.360 | 0.010 | 2.140 | 0.046 | |
| Deck | 0.413 | 0.003 | 1.553 | −0.007 | |
| Eurocode | Through | 0.751 | 0.051 | 0.712 | −0.091 |
| Half-through | 0.768 | 0.034 | 1.593 | −0.178 | |
| Deck | 0.929 | 0.001 | −1.436 | 0.016 |
| Code | Bridge Type | A | B | C | D |
|---|---|---|---|---|---|
| Chinese code | Through | 0.333 | −0.012 | 1.193 | −0.020 |
| Half-through | 0.530 | −0.015 | 1.212 | −0.030 | |
| Deck | 0.275 | −0.008 | 1.215 | −0.034 | |
| Japanese code | Through | 1.356 | 0.039 | −0.811 | 0.001 |
| Half-through | 1.629 | 0.076 | −1.018 | −0.053 | |
| Deck | 0.899 | 0.050 | −0.228 | −0.035 | |
| Eurocode | Deck | −0.048 | −0.001 | 0.187 | 0.008 |
| Code | Bridge Type | A | B | C | D |
|---|---|---|---|---|---|
| Chinese code | Through | 1.848 | −0.001 | −0.058 | −0.001 |
| Half-through | 2.922 | −0.044 | −0.116 | 0.002 | |
| Deck | 2.658 | −0.050 | −0.110 | 0.002 | |
| Japanese code | Through | 0.663 | 0.015 | 0.004 | 0.002 |
| Half-through | 0.778 | 0.007 | 0.006 | 0.002 | |
| Deck | 0.603 | −0.002 | 0.012 | 0.002 | |
| Eurocode | Through | 1.978 | −0.011 | −0.088 | 0.003 |
| Half-through | 2.563 | −0.042 | −0.125 | 0.005 | |
| Deck | 0.974 | −0.014 | −0.033 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Lin, Y.; Chen, K. Evaluation of Criteria for Out-of-Plane Stability of Steel Arch Bridges in Major Design Codes by FE Analysis. Appl. Sci. 2022, 12, 12632. https://doi.org/10.3390/app122412632
Wang W, Lin Y, Chen K. Evaluation of Criteria for Out-of-Plane Stability of Steel Arch Bridges in Major Design Codes by FE Analysis. Applied Sciences. 2022; 12(24):12632. https://doi.org/10.3390/app122412632
Chicago/Turabian StyleWang, Wenping, Yanyu Lin, and Kangming Chen. 2022. "Evaluation of Criteria for Out-of-Plane Stability of Steel Arch Bridges in Major Design Codes by FE Analysis" Applied Sciences 12, no. 24: 12632. https://doi.org/10.3390/app122412632
APA StyleWang, W., Lin, Y., & Chen, K. (2022). Evaluation of Criteria for Out-of-Plane Stability of Steel Arch Bridges in Major Design Codes by FE Analysis. Applied Sciences, 12(24), 12632. https://doi.org/10.3390/app122412632






