Abstract
Due to the characteristics of soil–rock composites and large-span arches, the surrounding rock parameters of stations are difficult to obtain accurately under soft upper and hard lower geological conditions when the arch cover method is used to carry out the construction of a large-span underground excavation station. To optimize the design of stations and guide the next step of construction, an intelligent inverse analysis method, the Gaussian process differential evolution co-optimization algorithm (GP-DE algorithm), is proposed for the arch cover method for station construction. Taking the Shikui Road station of the Dalian Metro Line Five as the engineering background, the finite element model of FLAC3D is established. By combining the measured data of the sensor and the monitoring data obtained using the orthogonal scheme, this algorithm is used for the joint back analysis of displacement stress and the accuracy of the inversion parameters is verified by forwarding the calculation for FLAC3D. By using the obtained surrounding rock parameters, the demolition length of the center diaphragm to the Shikui Road station is optimized. Under different numbers of training samples, the inversion effect of the GP-DE algorithm and the other three common back-analysis algorithms is compared and analyzed. Finally, based on the iteration rate and convergence effect, the value range of the differential evolution algorithm parameters F and CR is given. The results show that the forward calculation results of the parameters obtained from the back analysis are in good agreement with the actual values, and the accuracy of the back-analysis results is high.
1. Introduction
In the construction of subway stations under complex geological conditions, the arch cover method is widely used because of its outstanding advantages, such as less impact on the surrounding environment, fewer procedures, high efficiency, and safe and reliable construction [1]. In construction using the arch cover method, due to the complexity and heterogeneity of the rock mass structure, it is difficult to accurately describe the failure mechanism of the rock mass, and it is also difficult to give accurate rock mass parameters in the project [2]. Because of the large span, the geological conditions of the crossing are more complex, so the accuracy of the rock stratum information in the exploration process is difficult to guarantee, and some parameters can only give the corresponding interval range, which cannot provide a certain reference value for the input parameters of the numerical simulation. Therefore, the back-analysis method combined with the field-measured data becomes one of the most effective methods to accurately obtain rock mechanical parameters [3,4].
At present, the back-analysis method is widely used. In the study of the back analysis, Kavanagh first put forward the method of the back analysis of displacement in 1971. According to the amount of deformations after tunnel excavation, the mechanical parameters of rock mass were calculated with the finite element method [5]. Gioda calculated some mechanical parameters of rock mass by monitoring information on displacement [6]. Gao proposed a new neural network back-analysis method based on the black hole algorithm. Based on the measured converging displacement, the physical parameters of the surrounding rock of two deep roadways in the Huainan coal mine of China were back-calculated [7]. Su used FLAC3D to initialize the stochastic mechanical parameters, and, then, based on the differential evolution algorithm, the displacement difference between the numerical value and the in situ measurement value was regarded as the fitness value for the identification of rock mechanical parameters [8]. Zhao proposed an inverse analysis method for identifying rock mass parameters around tunnels using the ELM extreme learning machine model optimized with particle swarm optimization (PSO), taking into account displacement loss and spatial effects [9]. Jiang and others, through a differential evolution algorithm, combined the automatic acquisition system with a numerical simulation to conduct a displacement stress joint back analysis of surrounding rock parameters in tunnel engineering [10]. Jin and others inversed the joint surface parameters of the rock mass of the Baihetan hydropower station by combining the discrete element method and neural network, applying the results to the model, and comparing them with the measured values [11]. Wang and others conducted a back analysis on surrounding rock parameters by compiling an intelligent displacement back-analysis program based on a differential evolution algorithm and using tunnel convergence and arch crown settlement displacement values [12]. Huang and others used a genetic algorithm to invert the surrounding rock parameters of a highway tunnel and then took the obtained parameters into the numerical model for a forward analysis. The difference between the results and the measured values was small [13]. In previous studies, some algorithms were mainly used to back-analyze the rock parameters surrounding a tunnel in combination with the actual site displacement, but only relying on the displacement for the back analysis, which has certain limitations, and there have only been a few intelligent back-analysis studies for the stations constructed using the arch cover method. In practical projects, especially under soft upper and hard lower geological conditions, the unique arch cover construction method of large span concealed excavation makes it difficult to predict the mechanical parameters of the surrounding rock. Therefore, an accurate prediction of surrounding rock parameters has a certain guiding role for the station constructed with the arch cover method.
Table 1 shows the application research of the Gaussian process machine learning algorithm. After 2009, the application of the Gaussian process in civil engineering increased, mainly in the time series prediction of rock and soil mass deformation during the construction process. There are only a few studies on the algorithm being used for the inversion of rock and soil mechanical parameters. The Gaussian process for machine learning can better solve the problem of supervised learning. Two well-known algorithms, the neural network (ANN) and support vector machine (SVM), do not handle some aspects well. For example, the neural network has certain limitations in dealing with small-sample problems, and the support vector machine is also difficult to use for determining its kernel function and loss function. With the continuous development of machine learning, the GP algorithm has become a focus point in the field of international machine learning, and has been successfully applied to regression classification. Based on the Bayesian learning theory, this algorithm has significant advantages in dealing with small samples, nonlinearity, and other problems, and the GP algorithm has flexible nonparametric inference, adaptive parameter acquisition, and a simple implementation process [14].

Table 1.
Application research of Gaussian process machine learning algorithm.
This paper takes the Shikui Road Station of the Dalian Metro as the engineering background. First, according to 25 groups of orthogonal design schemes, the forward calculation is carried out through the established three-dimensional FLAC3D numerical model. After the results are obtained, a sensitivity analysis is carried out on the results, the key parameters are found, and 25 groups of displacement stress results are normalized. Then, the Gaussian process differential evolution (GP-DE) algorithm is used to train the 25 groups of normalized orthogonal design results and the measured displacement and stress are taken as the input samples for the inversion to obtain accurate surrounding rock parameters, which intend to provide a theoretical basis and reference value for the optimization design of the station and the guidance of the next step of construction in arch cover construction.
The remainder of this article is organized as follows. Section 2 introduces the geological uncertainty in the construction of a large-span arch cover station. Section 3 introduces the station parameter identification method based on the GP-DE arch cover method. Section 4 introduces the application of this method in engineering. Section 5 optimizes and analyzes the project’s temporary support removal scheme according to the determined parameters. Section 6 discusses the inversion effect of GP-DE and the influence of differential evolution parameters on the back-analysis effect. Finally, Section 7 concludes.
2. The Problem of Geological Uncertainty in the Large-Span Arch Cover Station Construction
The geotechnical environment has a great influence on underground engineering because geotechnical mass is not only the generating medium of underground engineering, but also the source of load [25]. In particular, the core idea of the arch and cover method construction is to make use of the bearing capacity and stability of the underlying surrounding rocks, as the rock mass bears and disperses the load to different degrees, with multiple identities as well as functions [26,27]. Rock mechanical parameters are one of the most important factors affecting the mechanical characteristics of tunnel construction, together with the access point for disaster control and structure design [6]. However, the limitations of measurement technologies and equipment, especially the incomprehensibility and spatial variations in the geological environment, bring great challenges to the identification of mechanical parameters of surrounding rocks. Therefore, a reasonable determination of physical and mechanical parameters of rocks as well as soil mass has a great influence on the design and construction of underground engineering.
To ensure the safety of station construction through the arch and cover method, it is necessary to design or adjust the construction scheme, while an optimization analysis of the excavation methods, temporary support, and demolition measures are necessary [28,29]. One of the ways to optimize the rationality of the scheme is to use the numerical simulation of the site [27,30], as is shown in Figure 1. To ensure the effect and accuracy of the numerical model, it is necessary to ensure the accuracy of the formation parameters in the simulation process.
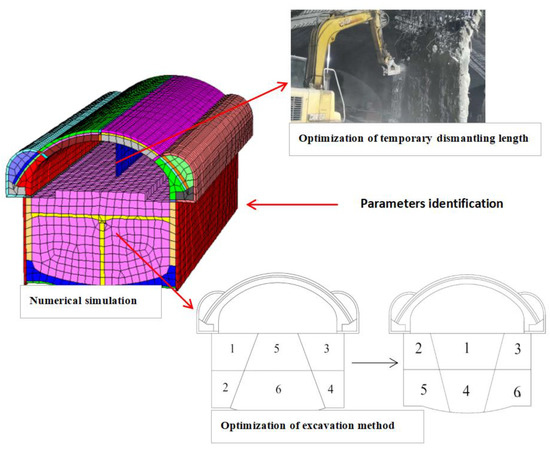
Figure 1.
Relationship among parameter identification, numerical simulation and construction scheme optimization.
3. Parameter Identification Methods for Stations through Arch Cover Method Based on GP-DE
In the excavation process of a station through the arch cover method, if the joint reverse analysis of the displacement stress is used, we can more comprehensively consider the relationship between the changes of station surrounding rocks and parameters, and the accuracy of the inversion results should be higher. Combined with the automatic monitoring data and a reasonable optimization model, the optimal mechanical parameters of the surrounding rocks are obtained through the reverse analysis method, and then the actual deformation law of surrounding rocks is found, so as to provide a scientific basis for the subsequent optimization design of the station [31]. How to minimize the number of function evaluations in the optimization process while achieving the global optimal solution becomes the key. To this end, a joint inverse analysis of displacement stress based on the GP-DE algorithm is used.
3.1. The GP Respond Surface Optimized by DE
GP algorithm is mainly determined by the mean function and covariance function. Consider regression model [16,20,32].
This is example 1 of an equation:
where x is the input variation; y is the observed value; Noise . The expectation and variance of the predicted value y′ can be obtained from the Bayesian posterior probability formula:
This is example 1 of an equation:
In GP, the covariance function is equivalent to the kernel function, and the squared exponential covariance function is the commonly used covariance function.
where: is the signal variance of the kernel function, is the diagonal matrix of the hyperparameter, is the variance scale, and is the Kronecker symbol.
is made the hyperparameter, and the optimal hyperparameter can be obtained using the log function maximum likelihood method. The partial derivatives of the negative log-likelihood function and the hyperparameter are:
The DE algorithm is a differential evolution algorithm, which is also a population-based evolutionary algorithm. In the DE algorithm, the initial population is generated first, all the new individuals in the initial population are selected as the same parent probability, and better individuals are selected as the next generation between new and parent individuals. If the population generation is G and the number is , the population vector of generation G is represented as . Each vector individual contains D components. The basic process of the DE algorithm is as follows [8,33].
3.1.1. Generate Initial Population
In D-dimensional space, chromosomes satisfying the upper and lower bounds of independent variables are randomly generated. The formula is:
where: , are the upper and lower bounds of the jth component in the ith vector; is a random number between (0,1).
3.1.2. Mutation Operation
During evolution, the variable of the difference between any two target vector individuals is superimposed on a third vector individual according to a certain law, so that it becomes a brand-new variable, which is the variation vector. Through mutation operation, not only the searchability of the population is enhanced, but the diversity of the population is also maintained. For the target vector of generation G, the jth component of the variation vector is:
where: r1, r2, and r3 are arbitrary and mutually different integers in [1, ]; F is the scaling factor, which plays the role of adjusting the step amplitude of vector difference.
3.1.3. Cross Operation
The target vector and the variation vector are hybridized according to Formula (4) to generate a new test vector .
where is a random number, which corresponds to the jth component of the vector; is the cross probability, and a new individual is randomly generated by probability; and is an integer randomly selected in , that is, one or more components of the variation vector shall be ensured to be applied by the test vector.
3.1.4. Select Action
The greedy search method is selected for the selection operation. The fitness function is used to compare each objective vector of DE with the test vector. If the value of the objective function corresponding to the test vector is small, the test vector is selected; if not, it is retained.
The Gaussian process machine learning algorithm is used as the GP-DE algorithm to establish the nonlinear mapping relationship among the learning samples. Taking the optimal hyperparameters of the GP as the population, the hyperparameters in the GP are optimized through the mutation cross-selection operation based on the DE algorithm, so as to optimize the GP model and predict an output value closer to the optimal solution. Using the square difference between the optimal output value and the control value predicted by the GP model as the fitness function, the prediction ability of the GP model is improved by optimizing the sample population to approach the optimal solution, so that the predicted target vector is closer to the optimal solution. This cycle is iterated until the global optimal solution of each optimal hyperparameter is found.
3.2. The Parameter Identification Flowchart
According to the meaning of the model parameters, the stress and displacement are taken as the objective function to control the target value as well as to reach the minimum objective function.
where is a function of the displacement control value; is the stress control value; and are the measured deformation and stress values of the surrounding rock; and are implicit functions with the surrounding rock parameters as independent variables, which need to be solved by numerical simulation; is a parameter; is the number of parameters; and are the upper and lower limits of the parameter ; and is the number of observation values.
The specific flow of displacement stress joint back analysis of surrounding rock parameters based on GP-DE is as follows:
- Orthogonal design of surrounding rock parameters includes: the tensile strength T, Poisson’s ratio μ, cohesion c, and internal friction angle . Different values of the five surrounding rock parameters of elastic modulus E are taken within a certain range for an orthogonal design, and an orthogonal scheme is formed.
- Second item, sample generation: FLAC3D is used to establish a numerical model, and the orthogonal scheme is used to simulate the model. The results of the orthogonal scheme are normalized after they are obtained, and the processed results are test samples, which are regarded as GP learning training samples and prediction test samples, and the influential factors obtained through a sensitivity analysis are used as the variables to be inverted.
- The following method is used to establish a nonlinear mapping relationship model of surrounding rock parameters: use GP technology to establish the nonlinear mapping relationship, use superparameters to carry out GP learning and prediction on the test samples, and evaluate the fitness of the obtained results obtained. Then, repeat the operation of mutation, crossover, selection, GP prediction, and fitness evaluation on the test samples. When the objective function reaches the preset value, the GP-DE algorithm has been optimized.
- Optimization of surrounding rock parameters: first of all, take the objective function of Formula (10) as the fitness function of the DE algorithm, generate a random group of parameters in the solution space as the initial population, and repeat the operation of mutation, crossover, selection, GP prediction, and fitness evaluation. The surrounding rock parameters that meet the minimum fitness are the back-analysis parameters. The detailed process is shown in Figure 2.
 Figure 2. Flow chart of back-analysis method based on GP-DE algorithm.
Figure 2. Flow chart of back-analysis method based on GP-DE algorithm.
Due to the different dimensions of displacement and stress in the results obtained based on the orthogonal design, a direct comparison and calculation will make the final results inaccurate, so they cannot be compared. To make the results accurate and reliable, normalization can be a good choice. After normalization processing, the data of different dimensions can be transformed into dimensionless data for subsequent processing. The normalization formula is as follows:
where: is the calculated value of the th output in the sample, is the minimum value of the output in the orthogonal scheme, is the maximum value of the output in the orthogonal scheme, and the normalized value of is .
4. Engineering Application
4.1. Engineering Overview
Shikui Road Station of Dalian Metro Line 5 is located in the urban area of Dalian, which is surrounded by residential and commercial areas, with numerous underground pipelines. The main body of the station is located directly below the road. The overall terrain of the site is a gentle slope, whose geomorphic unit belongs to denuded low hills. The soil in the upper part of the station is plain fill, and the lower part is mainly constructed with moderately to strongly weathered quartzite. The excavation diameter of the tunnel face of the station is about 21 m, and the soil thickness is 11.9~19.4 m. The stratum through which the station passes mainly consists of moderately weathered quartzite, which is a class-IV surrounding rock with a low compressibility foundation, a high bearing capacity of bearing stratums, a uniform foundation, and a large buried depth. The project is a large-span underground excavation project, where the arch cover method is adopted for construction. During construction, a small pilot tunnel is excavated first; then, a middle pilot tunnel is excavated; then, the side walls of the small pilot tunnel are removed; and finally, and the arch cover is formed. During excavation, it is easy to cause collapse along the fracture structural plane, and the excavation depth is large, making it easy to cause soil deformation. The longitudinal geological profile and the station cross-section are shown in Figure 3. The project location is Shikui Road Station of Dalian Metro Line 5 in Dalian, Liaoning Province, China. The project location is shown in Figure 4.

Figure 3.
The longitudinal geological profile and the station cross-section: (a) the longitudinal geological profile; (b) the station cross-section.

Figure 4.
The project location map.
4.2. Construction Procedure of Arch Cover Method
The construction sequence of symmetry is mainly adopted in the excavation of the Shikui Road arch cover pilot tunnel. First of all, a side pilot tunnel is excavated, then follows a middle pilot tunnel, and a supporting structure is timely constructed to prevent excessive settlement. Necessary monitoring measures shall also be taken during the construction to adjust the excavation footage and support scheme according to the monitoring data. The construction scheme is shown in Table 2. The specific construction process is as follows:

Table 2.
Schematic diagram of arch cover method construction process.
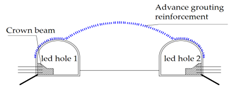
- (1)
- The side pilot tunnels 1 and 2 of the main body are grouted and reinforced with advanced small conduits, which are then excavated and supported in time. The mortar and foot lock anchor bolts are set at the arch foot, and a crown beam is set when the side pilot tunnel is through.
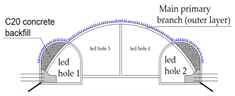
- (2)
- Advanced small tremie grouting reinforcement is carried out for pilot tunnel No. 3 and No. 4 in the main body, and then excavation is carried out, support is to be provided in time, and plain concrete is backfilled in the empty part of the side pilot tunnel.
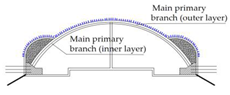
- (3)
- The side walls of side pilot tunnel No. 1 and No. 2 are dismantled, and secondary primary support is provided at the same time.
- (4)
- Advanced small tremie grouting reinforcement is carried out for pilot tunnel No. 3 and No. 4 in the main body; then, excavation is carried out, support is to be provided in time, and plain concrete is backfilled in the empty part of the side pilot tunnel.
- (5)
- The side walls of side pilot tunnel No. 1 and No. 2 are dismantled, and secondary primary support is provided at the same time.
- (6)
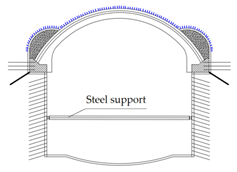
- According to the measured data, the middle partition is removed at a certain distance, a waterproof layer is laid on the bottom of the crown beam, and a secondary lining structure is constructed in time.
- (7)
- The lower soil mass is excavated layer by layer, and the side walls are initially supported, and at the same time, the side wall is provided with anchor cables and steel supports. After reaching the tunnel bottom elevation, a bottom cushion is constructed.
- (8)
- The waterproof layer is paved, the secondary lining structure and medium plate beam column are constructed, and then the internal structure of the station is constructed.
4.3. Numerical Simulation Model
A numerical calculation model is established using FLAC3D finite difference software. In order to eliminate the influence of the boundary effect, the left and right boundary of the model are taken as more than two times the station span, the lower boundary is taken as two times the station span, the upper boundary is taken vertically to the surface, and the depth direction of the three-dimensional model is taken as 50 m, with an overall model size of 100 m × 60 m × 74.2 m, whose size scale is simulated according to the data given in the geological survey report. The model includes 200,853 nodes and 126,890 units. Ansys 15.0 software is used to establish and grid the model, as well as densify the grid of main structures and surrounding rock areas. The numerical calculation and analysis are completed using FLAC3D3.0. The Mohr–Coulomb yield criterion is adopted in the analysis process of the model. A linear elastic model is used to simulate the primary support, secondary lining, backfill concrete, crown beam, and other structures. The boundary around the model is a normal constraint, the bottom boundary is a 3D fixed constraint, and the upper one is free. The input geotechnical parameters are based on Table 3. The numerical calculation model calculation model is shown in Figure 5. Note: the “e” in the figure represents “10”, and the number after it is his exponent. For example, 2.5000e-003 represents 2.5000 × 10−003.

Table 3.
Basic mechanical parameters of surrounding rock.
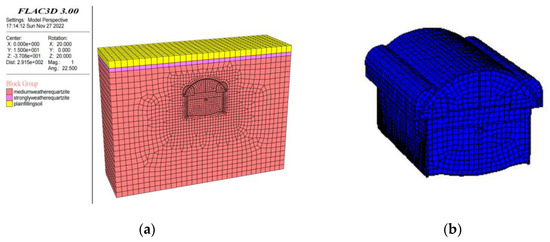
Figure 5.
Numerical calculation model: (a) overall model; (b) model of the station.
The Mohr–Coulomb yield criterion is adopted to the station. The first layer is constructed with plain fill, the second layer consists of strongly weathered quartzite, and the third layer is made of moderately weathered quartzite (parameter layer to be inverted). The basic mechanical parameters are shown in Table 3 regarding field investigation and investigation data.
4.4. Monitoring and Measurement
According to the basic requirements in the construction specifications of the Shikui Road Station, the construction methods and surrounding rock characteristics of Shikui Road Station were monitored, including changes in the stress and settlement of the arch cover during the construction period. To obtain a better inversion effect, it was necessary to select appropriate monitoring information for inversion. Therefore, an automatic monitoring section was set at the arch cover of the station, and an earth pressure box as well as a single-point displacement meter was used to monitor the stress and displacement changes in the arch cover in real time.
The earth pressure box (TY-1, TY-2, and TY-3) and single-point displacement meter (DW-1, DW-2, and DW-3) were arranged as shown in Figure 6.

Figure 6.
Automated sensor placement location.
The actual monitoring data and the calculation results were compared and analyzed. Figure 7 and Figure 8 show the actual monitoring data of the earth pressure box and the single-point displacement meter.

Figure 7.
Field monitoring data curve of earth pressure box.

Figure 8.
Field monitoring data curve of displacement measuring point.
4.5. Orthogonal Design
Orthogonal design is a multi-factor and multi-level test method, through which representative points can be selected for test design, thus reducing the difficulties caused by a large number of tests and the facilitation of efficient tests [34].
In the back analysis, the stability and displacement settlement of the station mostly depend on the surrounding rock parameters, and the influence of different surrounding rock parameters on the failure and deformation of rock mass is different; at the same time, if there are many inversion parameters, the authenticity of parameters obtained from the back analysis will also be affected. Therefore, the parameters of surrounding rocks that have a great impact on the station were obtained through a sensitivity analysis for back analysis.
An orthogonal design scheme was adopted, the parameter values were divided into five grades according to the determined parameter range, and then the values of different grades of each parameter were reasonably combined according to the orthogonal scheme; that is, 25 combinations were formed according to the L25 (55) orthogonal table (as is shown in Table 4). According to the field investigation and survey data, 25 combinations of five test parameters at five levels were designed. The parameter and value range: tensile strength t = 0.07~0.19 MPa, Poisson’s ratio μ = 0.3~0.35, cohesion c = 0.2~0.7 MPa, internal friction angle φ = 27°~39°, and elastic modulus E = 1.3~6 GPa. The parameters of each scheme were substituted into a three-dimensional finite element model for forward calculation, and the three points (as is shown in Figure 7), where the sensors were located at the station arch cover, were, respectively, selected to obtain the corresponding displacement and stress, whose results are shown in Table 4.

Table 4.
Parametric orthogonal experiment scheme.
In the back analysis, the mechanical parameters had a great relationship with the stability of the surrounding rocks. The failure and deformation of rock mass were different with different rock mass parameters. Moreover, the authenticity of the parameters obtained from back analysis decrease with the increase in the number of inversion parameters [35]. Therefore, sensitivity analysis was used in this paper to obtain the factors that have a greater impact on the stability of the station for an inverse analysis, and a range analysis was carried out on the settlement displacement value of the arch crown and arch waist. See Table 5 for the range value of DW-1, DW-2, and DW-3 as well as the order of their impact on the displacement.

Table 5.
Numerical calculation results (Cont).
In Table 4 and Table 5, DW-2 is the settlement displacement value at the left arch waist of the arch cover; DW-3 is that at its right arch waist; DW-1 is that at its arch crown; TY-1, TY-2, and TY-3 are the total stress at these three points of the arch cover of the station; and the range, order as well as average range of DW-1, DW-2, and DW-3 are the range value of the settlement displacement at the corresponding measuring points of at the arch cover, the primary and secondary relationship of the influence of various parameters, as well as the average range value.
As can be seen from Table 3, the order of sensitive factors affecting the three points at the arch cover is elastic modulus E, Poisson’s ratio μ, internal friction angle φ, tensile strength t, and cohesion force c. Elastic modulus has the greatest influence, followed by Poisson’s ratio and internal friction angle. Therefore, the first three factors with a great influence on the sensitivity factor analysis are selected for the analysis in this paper.
4.6. Parameter Identification Results
The back analysis of displacement and stress can be used to further solve not only the problem of the low accuracy, but also the problem of the low authenticity caused by the increase in back-analysis parameters. At the same time, real changes in the surrounding rocks of the station can be fully considered in the joint analysis of displacement and stress, so that it is more real and effective.
According to the actual monitoring, the settlement displacement of each point of the surrounding rocks was DW-1 = 12.53 mm, DW-2 = 10.75 mm, DW-3 = 10.71 mm, TY-1 = 176.97 kPa, TY-2 = 125.8 kPa, and TY-3 = 120.55 kPa. Taking the measured displacement and stress values as the control values while applying MATLAB to conduct a joint back analysis on displacement and stress, the initial parameters setting of differential evolution are shown in Table 6.

Table 6.
Initial parameters of differential evolution.
It was found that when the cross factor was CR = 0.7 and F = 0.8, the optimal mechanical combination parameter of moderately weathered quartzite obtained through inversion was E = 1.3 GPa, μ = 0.33, and φ = 35°, and the inversion results of surrounding rock parameters are shown in Table 7. The results obtained from the inversion were substituted into the finite-element software for a forward calculation, the results obtained from which were compared with the monitoring values at the monitoring section of Shikui Road Station and the single displacement back analysis. The results are shown in Table 8.

Table 7.
Inversion results of surrounding rock parameters.

Table 8.
Comparison of inversion calculation results and actual measurement results.
The back analysis of displacement and stress can be used to further solve not only the problem of the low accuracy, but also the problem of the low authenticity caused by the increase in back-analysis parameters. At the same time, the joint analysis of displacement and stress real changes in the surrounding rocks of the station can be fully considered, so that it is more real and effective.
According to the data in Table 4, only when the settlement value of the displacement at the arch cover of the station was used as the control value for the back analysis of surrounding rock parameters could the maximum relative error be 5.35%, while when the displacement and stress value at the arch cover of the station was combined for the back analysis, the maximum error was only 3.62%. The inversion effect was improved by 32.3% through a joint back analysis of displacement and stress compared with the single back analysis of displacement. This method further illustrates the applicability of the joint back analysis of displacement stress using the GP-DE algorithm through the arch and cover method. The surrounding rock parameters obtained from the joint back analysis can be applied to the problem of later scheme optimization, thus providing a reliable reference for the subsequent calculations.
5. Optimization Analysis of Temporary Dismantling Based on Determined Parameters
To analyze the stress characteristics of the center diaphragm wall of Shikui Road Station during the excavation process, the parameters obtained from the joint back analysis of displacement and stress based on the GP-DE algorithm were used as calculation parameters in the removal process of the center diaphragm wall support of the station. By analyzing the ground settlement and vault settlement of the station, the optimal length of the removal of its center diaphragm wall with class-IV surrounding rocks was studied. The overall model was consistent with Figure 9. A numerical simulation was carried out with FLAC3D 3.0 software. The stratum and constitutive as well as physical and mechanical parameters were consistent with Table 1. The center diaphragm wall was established with solid units. After the center diaphragm wall was removed, the two-layer primary support structure and the secondary lining structure were constructed immediately. The monitoring section was set as 3 m in the longitudinal direction of the station, and 35 monitoring points of the ground settlement were set in its transverse direction. The ground and vault settlement under the length of 6 m, 12 m, 18 m and 24 m were analyzed, respectively, to determine the optimal removal length of the center diaphragm wall of the station.

Figure 9.
Numerical model of demolition of partition walls in different length: (a) dismantle 6 m; (b) dismantle 12 m; (c) dismantle 18 m; (d) dismantle 24 m.
5.1. Surface Subsidence Analysis
To better analyze the suitable distance of the removal length of the center diaphragm wall in the station, the optimization was carried out based on the length range provided by the design institute. Four lengths were selected to analyze the removal length of the center diaphragm wall, so as to obtain a more appropriate removal length of the center diaphragm wall. The ground settlement under four schemes, namely 6 m, 12 m, 18 m, and 24 m, was compared, respectively, to determine the optimal removal length of the center diaphragm wall. The surface settlement curve is shown in Figure 10.

Figure 10.
Surface settlement curve.
It can be seen from the surface settlement curve that, during the removal of the center diaphragm, the surface was symmetrically distributed to both sides with the center diaphragm as the center, and the surface settlement was distributed in a “V” shape. All the maximum surface settlement values were on the tunnel axis. When the removal length of the center diaphragm of the station was 6 m, the maximum surface settlement value was 4.9 mm, which was 6.65 mm, 9.75 mm and 14.31 mm when the removal length of the station center diaphragm was 12 m, 18 m and 24 m, respectively. It could be found that, with the increase in the removal length of the center diaphragm, the maximum surface settlement gradually increased. When the center diaphragm was removed for 6 m, the minimum surface settlement occurred, and when it was removed for 24 m, the maximum surface settlement occurred. This is because the stress conversion of the main pilot tunnel of the station after excavation is relatively stable when the removal length of the center diaphragm is small, while when the removal length of the center diaphragm is too long, the stress conversion of the main pilot tunnel of the station after excavation is severe, which may lead to the instability of the structure, thus causing a greater settlement of the ground surface. It can be seen from the surface settlement curve that the removal length of the center diaphragm had a great impact on the surface settlement, which is not enough to be judged only by the surface settlement, so a further analysis is needed.
5.2. Settlement Analysis of Arch Crown
During the construction and removal of the center diaphragm wall of the station, the value of the arch crown settlement is a monitoring item that cannot be ignored. The monitoring of the arch crown settlement plays an important role in the safety of the tunnel. If the value of the arch crown settlement exceeds the control range, it may bring great dangers to the tunnel. Therefore, the monitoring of the arch crown settlement should be focused on. The demolition length of the center diaphragm wall can be further determined by the crown settlement through the value of the crown settlement of different demolition lengths of the center diaphragm wall. The Figure 11 shows the vertical displacement cloud diagram of the demolition length of each center diaphragm wall. Note: the “e” in the figure represents “10”, and the number after it is his exponent. For example, 2.5000e-003 represents 2.5000 × 10−003.

Figure 11.
Vertical displacement cloud diagram of each demolished length: (a) dismantle 6 m; (b) dismantle 12 m; (c) dismantle 18 m; (d) dismantle 24 m.
It can be seen from the vertical displacement program of the center diaphragm of different removal lengths in Figure 10 that different removal lengths had different effects on the settlement of the station vault. When the removal length of the center diaphragm was 6 m, 12 m, 18 m and 24 m, the settlement of the station vault was 15.57 mm, 16.43 mm, 18.12 mm and 21.87 mm, respectively. It could be found that, with the increase in the removal length of the center diaphragm, the settlement value of the station vault showed a significant increase. When the removal length of the center diaphragm was 24 m, the settlement value of the vault was the largest. According to the field monitoring and data, the control value of the station vault settlement was 20 mm, so when the removal length of the center diaphragm was 24 m, the control value was exceeded. If this is the removal length, the stability of the station will be weakened, which may affect the safety of the whole station.
It can be seen from the surface settlement curve and the dome top settlement cloud diagram that after a comprehensive comparison of the surface settlement value and the dome top settlement value, when the removal length of the center diaphragm wall at the arch cover of the station was 18 m, the value of surface settlement and dome top settlement was within the control value range. Through the removal of the center diaphragm wall with this length, not only the budget cost for the removal of the center diaphragm wall of the station can be reduced, but also the safe construction of the tunnel can also be ensured.
6. Discussion
6.1. Effect Analysis of Back Analysis of GP-DE Model
To verify the algorithm of GP-DE, the displacement stress in the construction process through the large-span arch cover method and numerical model simulation was used to analyze the inversion effect of the algorithm on the mechanical parameters of the upper soft stratum and the lower hard stratum. To further analyze the applicability of this algorithm, the methods including GP-DE, BP, LSSVM and GP commonly used in back analyses were used to compare and analyze the inversion effect of the mechanical parameters of the upper and lower hard layer through the large-span arch cover method for different training samples with an identical numerical model and mechanical parameter input. The Figure 12 shows the relative error of monitoring point values of different strategies.

Figure 12.
Relative error of monitoring point values of different strategies: (a) 5 samples; (b) 10 samples; (c) 25 samples; (d) 41 samples.
Training sets with 5, 10, 25 and 41 samples were used to train the above algorithms. A line chart of relative errors was drawn corresponding to the mechanical effect at each measurement point based on different training sets and different inversion algorithms, as is shown in the figure. Samples were obtained through numerical simulation. The rules for selecting samples from different sample sets were as follows: a number of samples (5 and 10 samples) were randomly selected from the table of Sample L25(55), respectively, and the training sample set 41 was the orthogonal scheme L25(55) plus L16(45).
When the number of samples was 5, there were fewer training samples at this time. It can be found from the figure that LSSVM and GP-DE inversion was significantly better than the BP neural network and GP, which shows that GP-DE and LSSVM can also have certain inversion performance of rock formation parameters when the sample size is small. BP and GP in this case, especially BP, are more likely to fall into a local solution state. When the number of trainings increased to 10, the GP inversion effect was significantly improved, and the GP-DE effect was the best. The BP neural network could easily fall into local solutions, and some relative errors were large.
When the number of training samples increased to 25, the results of the BP neural network had a better effect than LSSVM, so BP needs a sufficient number of training samples, which can better give play to the advantages of the algorithm. An advantage of LSSVM is that it can have a good effect when the number of training samples is small, which is suggested to be selected when the number of samples is small. When the number of training samples reached 41, little improvement could be found in the inversion results compared with 25, and the inversion results of the selected algorithm were at a better level. Compared with the other three algorithms, both the inversion results and the convergence speed had a good performance. The overall inversion effect of the GP-DE algorithm was excellent, which also had a good performance with a small sample size.
6.2. Influence of Differential Evolution Parameters on Optimization Results
In DE, variation factor F, cross factor CR, and population size NP, different strategies may affect the convergence rate. To obtain better calculation results, the control variable method was used in this paper to analyze the impact of key parameters such as DE, variation coefficient F, and cross coefficient CR on the DE algorithm under the above conditions with optimized parameters, 25 training samples, and the mechanical parameter input dimension of the numerical model; thus, the appropriate value range of variation coefficient F and cross coefficient CR was determined.
F represents the single search contraction range, and CR represents the probability of cross-recombination between newly generated mutants and individuals in the original population, which is used to enhance the diversity of the population. F was fixed as 0.3, 0.5, 0.7, and 0.9, respectively, and the convergence of CR that was between 0.3 and 0.9 was compared and analyzed, as is shown in Figure 13.

Figure 13.
Training convergence curve under different F and CR values: (a) F = 0.3; (b) F = 0.5; (c) F = 0.7; (d) F = 0.9.
From the perspective of the overall iterative effect, when CR was 0.7 and 0.9, the iteration effect and rate were relatively better. When the CR value was 0.3 and 0.5, the iteration rate was high in the beginning part, but slowed down significantly in the later part. When F was 0.5 and 0.7, the overall iteration rate was higher than 0.3 and 0.9. Based on the iteration rate and convergence effect, it is suggested that the parameters and the value of CR be selected, respectively, from 0.5 to 0.7 and from 0.7 to 0.9.
7. Conclusions
The GP-DE back-analysis method was used to back-analyze the rock strata parameters of the station constructed using the arch cover method. The main conclusions are as follows:
- The advantages of the GP-DE (Gaussian process differential evolution co-optimization) algorithm in establishing a nonlinear mapping relationship and its strong optimization ability are used to back-analyze the surrounding rock parameters of the power station. The calculation results showed that the error between the forward calculation of inversion parameters and the measured values was only 3.62%, which can meet the needs of the project to guide the next step of construction.
- The current content is “based on the parameters inversed by the GP-DE algorithm”; it was studied that the optimal length for removing the station middle partition (including Class-IV surrounding rocks) was 18m, which can not only reduce the budget cost for removing the station middle partition, but also ensure the safety and efficiency of tunnel construction.
- With different training samples, the inversion effect of the mechanical parameters of the upper soft rocks and the lower hard rocks through the long-span arch cover method was compared with that through the GP-DE, BP, LSSVM, and GP methods. Compared with the other three algorithms, the inversion effect of the GP-DE algorithm was generally good, which performed well with a small-sample training amount.
- For the key parameters of DE, the variation coefficient F, and the cross-coefficient CR, the control variable method was used to analyze the impact of these two parameters on the DE algorithm. Based on the iteration rate and convergence effect, it is recommended that the selection range of parameter F be 0.5~0.7 and the value of CR be 0.7~0.9.
Author Contributions
Conceptualization, F.Z. and A.J.; methodology, F.Z.; software, X.G.; validation, F.Z.; formal analysis, F.Z.; investigation, Q.M., Q.Y. and F.Z.; resources, A.J., Q.M. and Q.Y.; data curation, X.G., Q.M. and Q.Y.; writing—original draft preparation, F.Z. and X.G.; writing—review and editing, A.J.; visualization, A.J.; supervision, A.J.; project administration, A.J.; funding acquisition, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52078093; LiaoNing Revitalization Talents Program, grant number XLYC1905015; and Cultivation Program for the Excellent Doctoral Dissertation of Dalian Maritime University, grant number 2022YBPY009.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhong, G. Arch-Cover Method: A New Subsurface Excavation Construction for Metro Stations. J. Technol. 2012, 15, 145–148. [Google Scholar]
- Xu, J.; Ni, Y. Displacement ratio dichotomy back analysis of surrounding rock-initial support system of weathered rock tunnel. Arab. J. Geosci. 2019, 12, 181. [Google Scholar] [CrossRef]
- Wang, K.P.; Jian, D.L.; Liu, D.H. The Parameter Back Analysis of Rock Mass Based on Orthogonal Design. In Proceedings of the 2014 7th International Conference on Intelligent Computation Technology and Automation, Changsha, China, 25–26 October 2014; pp. 809–813. [Google Scholar]
- Feng, X.T.; Zhou, H.; Li, X.J.; Chen, B.R. Integrated Intelligent Feedback Analysis of Rock Mechanics and Engineering Problems and Its Applications. Chin. J. Rock Mech. Eng. 2007, 26, 1737–1744. [Google Scholar]
- Sakurai, S.; Takeuchi, K. Back Analysis of Measured Displacements of Tunnels. Rock Mech. Rock Eng. 1983, 16, 173–180. [Google Scholar] [CrossRef]
- Gioda, G. Some Remarks on Back Analysis and Characterization Problems. In Proceedings of the 5th International Conference on Numerical Methods in Geomechanics, Nagoya, Japan, 1–5 April 1985; Volume 1, pp. 47–61. [Google Scholar]
- Gao, W.; Chen, D.L.; Dai, S.; Dai, X. Back analysis for mechanical parameters of surrounding rock for underground roadways based on new neural network. Eng. Comput. 2017, 34, 25–36. [Google Scholar] [CrossRef]
- Su, G.S. A New Intelligent Back-Analysis Method Based on Differential Evolution Algorithm. In Proceedings of the 2019 International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009; pp. 212–214. [Google Scholar]
- Zhao, Y.; Feng, S.J. Back analysis of surrounding rock parameters of tunnel considering displacement loss and space effect. Bull. Eng. Geol. Environ. 2021, 80, 5675–5692. [Google Scholar] [CrossRef]
- Jiang, Z.B.; Jiang, A.N.; Hu, X.F.; Liu, Y.H.; Chen, W.; Liu, G.Y. Displacement-Stress Based Multi-Information Intelligent Back Analysis in Highway Tunnels. Mod. Tunn. Technol. 2017, 54, 145–152. [Google Scholar]
- Jin, C.Y.; Feng, X.T.; Zhang, C.S. Application of neural network to back analysis of mechanical parameters of columnar joint basalt. J. Hydroelectr. Eng. 2010, 29, 234–238. [Google Scholar]
- Wang, J.X.; Jiang, A.N. The analysis of monitoring data and intelligent inversion of parameters of Dalian subway tunnel. China Civ. Eng. J. 2011, 44, 135–138. [Google Scholar]
- Huang, C.T.; Wang, Y.; Zhang, Y.J. Application of displacement back analysis method in determination of surrounding rock parameters of highway tunnels. Yangtze River 2017, 48, 138–140. [Google Scholar]
- Xu, C.; Liu, B.G.; Liu, K.Y.; Guo, J.Q. Intelligent model for time series analysis and prediction of landslide displacement based on particle swarm optimization Gaussian process regression coupling algorithm. Geotech. Mech. 2011, 6, 1670–1675. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Brahim-Belhouari, S.; Bermak, A. Gaussian Process for Nonstationary Timeseries Prediction. Comput. Stat. Data Anal. 2004, 47, 705–712. [Google Scholar] [CrossRef]
- Kim, H.C.; Kim, D.J.; Ghahramani, Z.; Bang, S.Y. Appearance-Based Gender Classification with Gaussian Processes. Pattern Recognit. Lett. 2006, 27, 618–626. [Google Scholar] [CrossRef]
- Guo, S.S.; Liu, B.Y.; Yong, C.S. Gaussian Process for Non-Linear Displacement TimeSeries Prediction of Landslide. J. China Univ. Geosci. 2007, 18, 212–219. [Google Scholar]
- Su, G.S.; Song, Y.C.; Yan, L.B. A new method for predicting the effect of rock blasting. J. Rock Mech. Eng. 2007, 1, 3509–3514. [Google Scholar]
- Fyfe, C.; Leen, G.; Lai, P.L. Gaussian processes for Canonical Correlation Analysis. Neurocomputing 2008, 71, 3077–3088. [Google Scholar] [CrossRef]
- Liu, K.Y. Intelligent model for time series analysis of nonlinear deformation of slope based on genetic combined kernel function Gaussian process regression algorithm. J. Geotech. Mech. Eng. 2009, 10, 2128–2134. [Google Scholar]
- Liu, K.Y.; Fang, Y.; Liu, B.G. Parameter inversion of elastoplastic model of tunnel engineering based on evolutionary Gaussian process regression algorithm. J. Geotech. Eng. 2011, 6, 884–889. [Google Scholar]
- He, P.; Li, S.C.; Li, L.P.; Zhang, Q.Q.; Xu, Z.H. Tunnel surrounding rock deformation response prediction and dynamic change permission mechanism based on data mining. J. Rock Mech. Eng. 2017, 12, 2940–2953. [Google Scholar]
- Zhang, Y.P.; Li, L.P.; He, P.; Qin, C.S. Large deformation Gaussian process regression prediction model of tunnel surrounding rock and its engineering application. Sci. Technol. Eng. 2018, 1, 122–127. [Google Scholar]
- Dai, S.L.; Lv, Y.L. Rockmass Stability Analysis of YunYang’s Arch Dam Left Shoulder. Adv. Mater. Res. 2012, 518–523, 4405–4408. [Google Scholar] [CrossRef]
- Li, W.; Bai, J.W.; Li, K.X.; Zhang, S.J. Experimental Analysis of Deformation Mechanics and Stability of a Shallow-Buried Large-Span Hard Rock Metro Station. Adv. Civ. Eng. 2020, 2020, 4031306. [Google Scholar] [CrossRef]
- Wang, J.B.; Huo, Q.; Song, Z.P.; Zhang, Y.W. Study on adaptability of primary support arch-cover method for large-span embedded tunnels in the upper-soft lower-hard stratum. Adv. Mech. Eng. 2019, 11, 1687814018825375. [Google Scholar] [CrossRef]
- Liu, T.; Huang, Y.L.; Lei, G. Analysis of the Optimum Support Dismantling Scheme for Shallow Bored Subway Stations in a Soil-Rock Compound Stratum. Mod. Tunn. Technol. 2015, 52, 131–137. [Google Scholar]
- Liu, X.; Jiang, A.; Guo, X.; Lu, H. Effect of Excavation Blasting in the arch-cover method on Adjacent Existing Pipelines in a Subway Station. Appl. Sci. 2022, 12, 1529. [Google Scholar] [CrossRef]
- Guo, X.P.; Jiang, A.N. Study on the stability of a large-span subway station constructed by combining with the shaft and arch-cover method. Tunn. Undergr. Space Technol. 2022, 127, 104582. [Google Scholar] [CrossRef]
- Jiang, A.N. Optimizing generator socket construction schemes of Shuibuya Underground Powerhouse based on intelligent back analysis. Rock Soil Mech. 2008, 29, 1372–1376. [Google Scholar]
- Zhang, Y.; Su, G.S.; Liu, B.C.; Li, T.B. A novel displacement back analysis method considering the displacement loss for underground rock mass engineering. Tunn. Undergr. Space Technol. 2020, 95, 103141. [Google Scholar] [CrossRef]
- Tian, M.L.; Han, L.J.; Meng, Q.B. Nonlinear Regression Analysis for Deep Rock Mass Parameters of the Hoek-Brown Failure Criterion Based on the Differential Evolution. KSCE J. Civ. Eng. 2021, 25, 3160–3171. [Google Scholar] [CrossRef]
- Tian, H.M.; Chen, W.Z.; Yang, D.S.; Dai, Y.H.; Yang, J.P. Application of the orthogonal design method in geotechnical parameter back analysis for underground structures. Bull. Eng. Geol. Environ. 2015, 75, 239–249. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, X.T.; Su, G.S.; Chen, G.Q. Intelligent Back Analysis of Rock Mass Parameters for Large Underground Caverns Under High Earth Stress Based on Edz and Increment Displacement. Chin. J. Rock Mech. Eng. 2007, 26, 2654–2662. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).