Abstract
Unilateral vocal fold polyps can lead to incomplete glottal closure and irregular vocal fold vibration. Depending on polyp size and resulting dysphonia severity, voice therapy or surgery may be recommended. As part of voice therapy, patients may learn how to optimize intrinsic and extrinsic laryngeal muscle use to mitigate benign lesion effects, increase vocal efficiency, and improve voice quality. In this study, we used a low-dimensional mass model with a simulated unilateral vocal fold polyp and varied intra-laryngeal muscle activity to simulate vocal fold vibration across varied conditions. Differing muscle activation has different effects on frequency, periodicity, and intensity. Accordingly, learning how to optimize muscle activity in a unilateral polyp setting may help patients achieve the best possible periodic and most efficiently produced voice in the context of abnormal vocal fold morphology.
1. Introduction
Vocal fold polyps are benign mass lesions arising from phonotrauma [1]. They may be hemorrhagic or gelatinous and are typically unilateral. Microscopically, vocal fold polyps exhibit fibrosis, fibrin deposition, hemorrhage, vascular thrombosis, and dilatation of blood vessels [2]. Ongoing phonotraumatic behavior will result in repetitive injury to the true vocal fold with potential for resulting dysphonia, reduced vocal range, odynophonia, and occasionally risk of scar [1]. In addition, vocal fold polyps have the potential to become cancerous. It is estimated that there will be 12,470 new cases of laryngeal carcinoma and 3820 deaths from laryngeal carcinoma in the USA in 2022. Laryngeal carcinoma is one of the most common forms of head and neck cancer, with an estimated number of 12,370 new cases and 3750 deaths in the USA in 2020 [3]. Accordingly, timely treatment of vocal fold polyps is necessary. Depending on polyp characteristics, patient vocal demands, patient preference, and degree of dysphonia, treatment may include voice therapy and/or surgery [4]. However, this type of surgery has some technical difficulties and may lead to post-operative complications [5,6]. In either case, voice therapy is useful in helping the patient identify less phonotraumatic methods of voice use to increase vocal efficiency, improve vocal quality, decrease stress on the true vocal folds, and decrease probability of recurrence if procedural intervention is pursued. Identifying optimal intra-laryngeal muscle use patterns may be a part of therapy. Computational modeling of vocal fold vibration offers the opportunity to manipulate degree of muscle activity and examine effects on vibratory characteristics and acoustic output. It could be used to better understand pathological vocal fold vibration and potentially guide therapy [7,8].
There are multiple recent studies on pathological vocal fold vibration using vocal fold models. The first low-dimensional mass model of the vocal fold was developed by Ishizaka and Flanagan [9] and later modified by Steinecke and Herzel [10]. Much work has been done to couple various flow models to these two-mass models to better match physiological data. For this study, two aspects of previous models were of particular interest. One was the use of a nonlinear model to study chaotic vibration in the unilateral polyp setting, first proposed by Zhang et al. [11]. Nonlinear dynamic methods can be used to describe disordered voice production when vocal fold vibration is aperiodic. The influence of tension asymmetry on phonation onset, intensity, and fundamental frequency has been experimentally observed and simulated with this nonlinear model by Xue [12]. Mehta [13] used high-speed videoendoscopy and modeling to investigate the phase asymmetry of vibration and found that vibratory asymmetries have no direct relationship with acoustic spectral tilt measures.
The second relevant aspect is intrinsic laryngeal muscle activation during phonation. The intrinsic muscles interconnect the cartilages of the larynx, such as the thyroarytenoid muscle, cricoarytenoid muscle, lateral cricoarytenoid muscle, and posterior cricoarytenoid muscle. Previous studies have shown direct correlations between intrinsic muscle activation and characteristics of sound production [14,15,16]. Chhetri et al. [14] showed the influence of various combinations of thyroarytenoid muscle, lateral cricoarytenoid muscle, and cricothyroid muscle activation on acoustic output in an in vivo canine model. Dewan et al. [15] also used an in vivo canine model to assess possible neuromuscular compensation mechanisms that could potentially be used in the treatment of vocal fold pathology. Azar et al. [16] evaluated combinations of superior and recurrent laryngeal nerve activation to explore fundamental relations between nerve activation and laryngeal muscle activation during phonation.
There are many differences between normal vocal fold and pathological vocal fold vibration. The natural frequencies of the vocal fold entail the vibration of the two lips of vocal fold to the same frequency on phonation [17,18]. It is not clear if such entrainment occurs when a unilateral polyp is present, nor if the whole vocal fold will have the same effect when a vocal polyp is present. For a pathological vocal fold, the natural frequency differs from the normal one. Vocal polyps may affect the vocal fold vibrations and flow dynamics.
Prior studies have focused more on the manipulation of normal mode frequencies, effective mass in vibration, vocal fold length, stiffness, and vocal fold thickness, which are not directly controlled by the speaker [19]. Greater attention to muscle activation may yield new insights into the physiology of disordered voice production. Current modeling guidelines for vocal fold muscle activation are mostly based on normal vibration. Titze [19] described an empirically derived set of rules that converts laryngeal muscle activities into physical quantities and used these rules to investigate a shear mode and two compressional modes of vibration in a self-oscillating model of vibration. Zhang [20] investigated the implication of stiffness on fundamental frequency (F0) and glottal flow rate through a three-dimensional model. Evidence for a direct correlation between muscle activation and vocal fold vibration in this model, though, is still limited.
To better understand the effect of unilateral polyps on vibration, we have concentrated more on muscle activation in a computational pathological vocal fold model. This allows for the study of vocal fold oscillatory characteristics in perceptually and physiologically realistic controlled spaces. Compared to animal models, computational models based on human vocal folds are more customizable and generalizable. We have developed a vocal fold model with a unilateral polyp to simulate irregular vocal fold vibrations. We could also study aerodynamics in this asymmetric configuration, which obeys a set of rules that transform muscle activation into geometrical and viscoelastic parameters of lumped element models. Our pathological model may shed light on the effect of muscle activation on vocal fold vibration to help patients learn how to optimize muscle activity for different phonation situations.
2. Materials and Methods
2.1. Vocal Fold Model with a Unilateral Polyp
The two-mass model is a classic model for vocal fold vibration. The model used here is based on Steinecke and Herzel [18]. Their model regards each vocal fold as two masses that are connected by springs. In our study, we added a unilateral mass representing a polyp to this model, following previous work [11].
Figure 1 shows a schematic of the three-mass model in which the indices a = l, r denote the left and right vocal fold and i, j = 1, 2 are the upper and lower masses or vocal fold lips. xia is the displacement of the mass mi with length di. kia is the stiffness constant, and kca is the coupling stiffness between m1a and m2a. ria is the damping constant. The mass m1a and m2a has length l0 and depth D0. The height of m1a is d1, and d2 is the height of m2a. The height of the vocal fold is d0, d0 = d1 + d2.
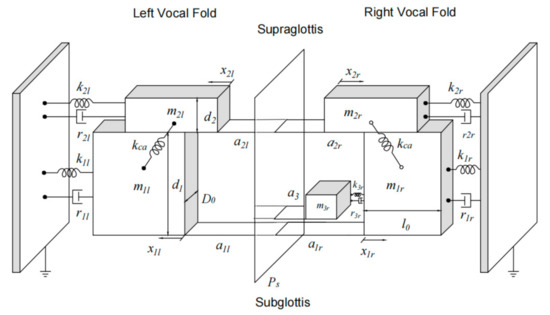
Figure 1.
Schematic of vocal fold model with a polyp. Vertical plane represents midline.
A unilateral vocal polyp is connected with the lower mass m1r of the right vocal fold by the spring k3r and the damper r3r. The vocal polyp has mass m3r, length l3, depth D3, and height d3. x3r is the displacement of the polyp m3r. In this model, the vocal folds and polyp have the same density. Collisions occurs between m1l and m1r, m1l and m3r, and m2l and m2r. cia is the spring constant, cia = 3kia. All masses are only allowed to move in the medio-lateral direction.
Using these parameters, we first began to develop muscle activation rules for the pathological model.
2.2. Development of Rules for Muscle Control
In reality, the value of some parameters will vary with the movement of the laryngeal muscles during phonation, which is called the effective value of vocal fold vibration [21]. For a more realistic simulation, we improved the rules for controlling geometric and elastic parameters with muscle activation proposed by Titze [19] to fit our model. These rules take the place of the physics of deformable bodies for vocal fold posturing. To reduce the number of control parameters, only the cricothyroid muscle activity aCT (ranging from 0.05 to 0.9), the thyroarytenoid muscle activity aTA (same range), and the lateral cricoarytenoid muscle activity aLC (same range) were considered. The reason for setting the different muscle activities in this range is that the muscle cannot actually relax and contract completely. The length of the vocal fold is the primary geometric variable for adjustment of F0, and it changes during phonation. It is therefore important to identify what is meant by effective vocal fold length. Titze [22] showed that the fractional length change (vocal fold strain) due to rotation can be written as
where ε is the longitudinal vocal fold strain, G is a gain factor, R is a torque ratio, and H is the adductory strain factor. The range of ε for human must be higher to achieve a larger pitch range than canines. To obtain a larger maximum elongation, we needed to increase the values of the above parameters (G, R, H) compared to the canine model. For this study, we set G = 0.2, R = 3.0, and H = 0.2, as in a previous study [22]. When a polyp develops on one vocal fold, it can be approximated that the length and tension of the vocal folds remain constant, while the vocal fold linear density ρ increases slightly in the local area around the polyp [21]. In the present model, we treated the entire vocal fold cover as one with the polyp but still follow this formula. Using the above rule, the vocal fold length can be expressed in the form
Vocal fold depth increases with vocal fold shortening during vocal fold vibration. We developed the following rules for thickness:
where Dmuc, standing for depth of mucosa is 0.2 cm, and Dlig, standing for depth of ligament, is 0.2 cm. Thickness is described as
where d0 is the vibrating thickness at resting length. We defined the ratio of the effective vibration parameter to the original parameter as the effective vibration ratio ω. The effective vibration ratio of length ωl, depth ωD and thickness ωd can be written as
In addition to the above parameters, the stresses acting on the vocal fold also change with muscle activation during vibration. The cover layer has only a passive stress and can be expressed as
where σmuc is the mucosa stress, and σlig is the ligament stress. According to previous work [23,24], the passive stress of mucosa and ligament has been modeled with a combination of a linear and an exponential function and matched to vocal fold stress–strain curves. The form of this function can be expressed in the form
σ0 is the stress when ε = 0, ε1 is the strain where the linear portion goes to zero, ε2 is a scale factor for the exponential portion, and ε2 is the strain where the exponential portion begins. The numerical constants used in Equation (7) for mucosa are ε1 = −0.5, ε2 = 0.35, σ0 = 0.5 kPa, σ2 = 30 kPa, C = 4.4; for ligament are ε1 = −0.5, ε2 = 0, σ0 = 0.4 kPa, σ2 = 1.393 kPa, C = 17; and for TA muscle are: ε1 = −0.5, ε2 = −0.05, σ0 = 1.0 kPa, σ2 = 1.5 kPa, C = 6.5. Hence, the effective vibration ratio of cover stress is
where σc0 is stress on the cover when the vocal folds are at rest. The above rules consider the polyp and vocal fold as a whole.
2.3. Effective Parameters of Vocal Fold Vibration
Muscle activation affects the mass and stiffness by changing the above parameters, which have an impact on the vibration [19]. In our low-dimensional model, the mass of the vocal folds can be calculated by
Changes in muscle activation do not affect density of the vocal fold. Therefore, we only consider the effective length, depth, and width of the vibration, such that the effective mass of the vocal fold now become the following:
where mia and m3r on the right side of the equation are the default values of vocal fold mass.
For vocal fold stiffness, the following relationship is given by the definition of fundamental frequencies:
Likewise, for our model, we can similarly write,
where kia and k3r on the right side of the equation are the vocal fold stiffness when no vibration occurs. In addition, the coupling stiffness kca is different from others. According to the mass distribution rule of a previous study [19], the effective coupling stiffness becomes
The default parameters in the deterministic vocal fold models with steady airflow used in Table 1 are considered as common physiological conditions [19,25]. The units of parameters are cm, g, ms, and their corresponding combinations.

Table 1.
Parameters and values of the model.
The damping constant of the vocal folds can be calculated as
where ζ1, ζ2 refer to damping ratios for the viscous resistances r1a and r2a. Based on previous studies [11], we selected the following parameters for the vocal fold polyp: m3r = m1rl3D3/lD0d1, k3r = 0.014, c3r = 3k3r, r3r = r1r(m3rk3r/m1rk1r)0.5, l3 = l0/3, D3 = 0.1D0, d3 = (d1 + d2)/3.
2.4. Equations of Motion for the Three-Mass Model
The differential equations for the pathological model are
and for the equation of the right vocal fold polyp,
The function describing the collision is approximated by
The polyp m3r and the right lower mass m1r are connected by nonlinear spring and the damping, which can be described as
while the effective nonlinear spring forces of the left lower mass m1l can be written as
for which the parameters were set as ηk3 = 100 and ηh3 = 500. There is no coupling or collision effect between the right vocal fold polyp and the upper mass, so T2l = 0 and T2r = 0.
To obtain the glottal airflow, it is necessary to calculate the minimal glottal area, using
and the glottal areas of the lower mass pair m1a and the upper mass pair m2a, using
The area from the midline to mia is aia, and a01 = a02 = 0.05. Similarly, the equation of glottal area for the polyp can be written as:
Ps is the subglottal pressure, and P1 acts on m1a, P2 acts on m2a, and P3 acts on m3r. The volume flow velocity U can be described by the Bernoulli equation as
The effective driving forces F1a acting on m1a, F2a acting on m2a, and F3r acting on m3r can thus be deduced as
The equations in this section give the vibratory equations of the vocal folds coupled with a right vocal polyp, while the vocal fold model with a unilateral polyp is reducible to the normal two-mass model when D3 = 0, l3 = 0, d3 = 0, and Tia = 0.
3. Results and Discussion
3.1. Qualitative Features of Pathological Vocal Fold
The glottal volume flow velocity U of the normal and pathological vocal folds is shown in Figure 2. As can be seen from the figure, the mass block displacement in both normal and pathological vocal fold models vibrates periodically and produces a valley-cut sinusoidal shape for airflow. However, the amplitude of volume flow velocity U decreases when the polyp is present. In the closing phase of the whole cycle, the pathological vocal fold can not close entirely, and the duration of the closed phase is reduced. As we can see, vocal fold polyps have an impact on the quality and intensity of phonation. Hence, the study focused on simulating muscle activations that may reduce the adverse effect of polyps on phonation.
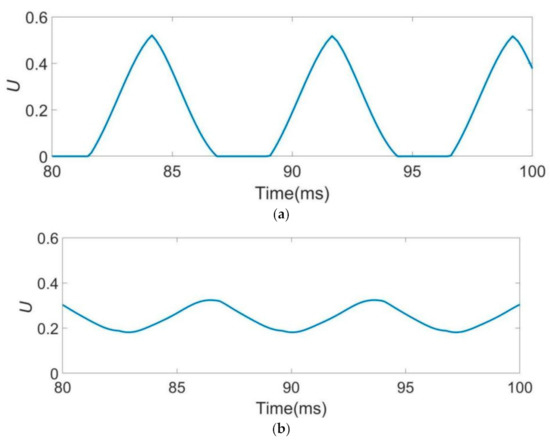
Figure 2.
Glottal volume flow velocity rate. (a) The normal vocal fold. (b) The vocal fold with a unilateral polyp.
Previous work has identified that for aLC > 0.5, the vocal processes are approximated, and for aLC < 0.5, the vocal processes are separated. Oscillation occurs approximately along the constant horizontal line of aLC = 0.5 [19]. Therefore, we fixed aLC at 0.5 to better understand the implication of muscle activation on adduction and abduction. When aCT = 0.25, aTA = 0.25, and aLC = 0.5, the longitudinal strain of the vocal fold ε will be 0, and all laryngeal muscles are activated. Hence, fixing aCT at 0.25 for the study of aTA was seen as the best choice. The same method used for fixing aTA was used for the study of aCT.
Figure 3 shows glottal volume flow velocity waveforms of different cricothyroid muscle activities (aCT). aCT now increases from 0.05 to 0.9 with aTA constant at 0.25 and aLC constant at 0.5. Note that the effect of increasing aCT is an initial increase in fundamental frequency. The average amplitude of the glottal airflow first increases and then decreases with increasing aCT. It can be seen the vocal polyp cannot change the status of the glottal cycle on phonation. However, the figure shows that the vocal folds can maintain a more periodic vibration only when aCT is at a moderate value. When the level of CT muscle activity is too low, there is low stiffness of the vocal fold cover, causing the vocal fold to vibrate with little speed and amplitude. However, when aCT increases, the effect of the polyp on vibration becomes obvious, and there is abnormal glottal airflow. As the stiffness increases with aCT to the maximum of the range, the stabilized waveforms of glottal airflow tend to be a straight line, and vibration is severely impaired.

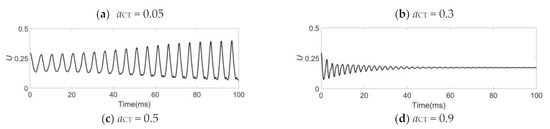
Figure 3.
Glottal volume flow velocity U for a unilateral polyp vocal fold model across differing levels of cricothyroid muscle activity, aCT. In each case, aTA was fixed at 0.25 and aLC was fixed at 0.5.
Figure 4 shows glottal volume flow velocity waveforms for different levels of thyroarytenoid muscle activity (aTA). The waveform is nearly sinusoidal at small values of aTA but decreases in amplitude when aTA increases. The waveforms in Figure 3a and Figure 4d are similar, showing the effect of low stiffness on vocal fold vibration. The fundamental frequency slightly decreases with increasing values of aTA. This supports the function of the thyroarytenoid and cricothyroid muscles in controlling fundamental frequency [21].
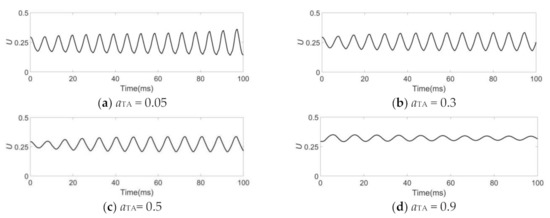
Figure 4.
Glottal volume flow velocity U for a unilateral polyp vocal fold model with different aTA. In each case, aCT was fixed at 0.25 and aLC was fixed at 0.5.
Figure 5 shows glottal volume flow velocity waveforms for different levels of lateral cricoarytenoid muscle activity (aLC). There is a decrease in glottal airflow amplitude with increasing aLC. Unlike for the thyroarytenoid muscle, the glottal airflow waveform is almost sinusoidal when aLC is around 0.5. Irregular vocal fold vibration occurs with increasing or decreasing aLC. Furthermore, there is a glitch in the glottal airflow waveforms for large values of aLC. This indicates that in the vocal fold polyp setting, high levels of lateral cricoarytenoid activity affects voice quality. Of note, increasing aLC can also result in a small decrease in F0.
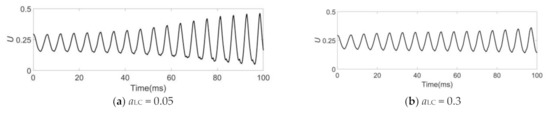

Figure 5.
Glottal volume flow velocity U for a unilateral polyp vocal fold model with different aLC. In each case, aCT was fixed at 0.25 and aTA was fixed at 0.25.
Evaluating the above three sets of waveforms, we obtain an initial understanding of the muscle activation ranges that will optimize voice production in the polyp setting. Cricothyroid activity should be greater than 0 but less than 0.5, and both aTA and aLC should be kept at a moderate value. Under these conditions, periodic vocal fold vibration can occur.
3.2. Glottal Flow and Implications for Phonation
Phonation is essentially an energy-transfer process, transforming aerodynamic energy into acoustic energy. Because the glottal flow is the main determinant of voice production, further studying its properties can help us learn the effect of muscle activation on onset, effort, and quality. Following the experimental method in III.A and referring to the experimental design from Xue [12], we plotted the variation of four airflow parameters affecting sound quality with respect to different levels of muscle activation (Figure 6). Figure 6a shows the root-mean-square fluctuation of the airflow velocity (UA). We defined the intensity of fluctuation in glottal flow rate as UA. The effect of increasing aCT was to obtain an initial increase in UA, followed by a decrease. UA reaches a maximum when aCT ranges from 0.4 to 0.5. In contrast to aCT, glottal flow fluctuation decreases monotonically with aTA and aLC. For small values of aLC, however, UA is always at a high level.
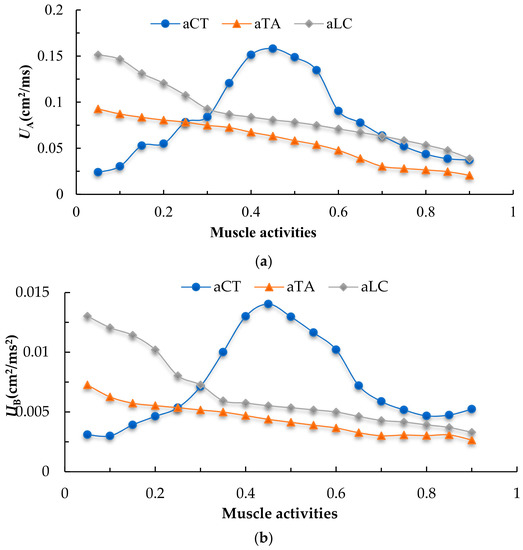
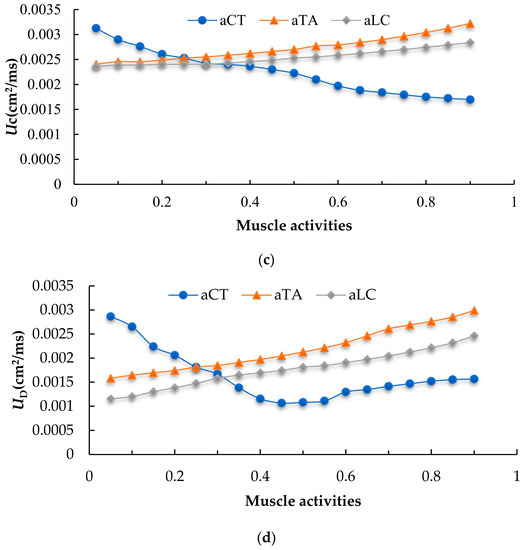
Figure 6.
Comparison of effects of important airflow parameters related to laryngeal muscle activation on voice quality. (a) The fluctuation amplitude of volume flow rate, which is the root mean square of the time shift of glottal flow during the test. (b) The time-rate of change of the volume flow rate, which is the root mean square of the time shift of glottal flow velocity during the test. (c) The mean value of volume flow rate during the test time. (d) The average of minimum volume flow rate over cycles during the test time.
Likewise, we plotted the time rate of glottal flow-rate change, UB, in Figure 6b, which is related to the sound strength of human [12]. This plot shows several important factors that have direct impact on the onset and intensity of vocal fold vibration in phonation (UB). Compared with UA, the behavior of UB is similar, which means that the variation in glottal flow velocity with different muscle activation is approximately the same as the variation in acceleration of change of the airflow. UB also provides an understanding of efforts to improve intensity of voice production. Changes in laryngeal muscle activities, such as increased CT muscle activities and decreased TA and LC muscle activities, will result in an increase in the amplitude of vocal fold vibration, thus increasing intensity of the voice. The cricothyroid muscle plays the primary role in controlling F0. However, in the pathological vocal fold, the process of changing cricothyroid muscle activity to make F0 reach the medium-high frequency is accompanied by irregular glottal airflow (large airflow velocity fluctuations and large airflow acceleration fluctuations). This suggests that stable voice production cannot be obtained in the vocal fold with a unilateral polyp. Thus, humans usually increase subglottal pressure to match the muscle activation to reduce laryngeal muscle fatigue and increase sound intensity. When the value of aCT is large enough to create a high frequency, UA and UB decrease significantly. According to Section 3.1, this is because the stiffness of the vocal fold is high at this point, making it almost impossible for the vocal folds to vibrate effectively. Hence, it is difficult for a patient with a polyp to phonate even with small fluctuations in the amplitude of UA and UB. Similarly, for the thyroarytenoid and lateral cricoarytenoid muscles, low activity leads to unstable sound intensity. The values of UA and UB decrease monotonically with aTA and aLC.
Two figures related to glottal flow rate are shown here that evaluate the effect of muscle activation on sound quality. Figure 6c shows the mean value of volume glottal flow rate (UC) which is indicative of flow impedance. Figure 6d shows the leakage flow rate (UD), which is the average of minimum volume flow rate over cycles, reflective of glottal gap size. This is a method for measuring the leakage of glottal flow during maximal glottic closure. High values of each parameter indicate a breathy voice quality.
Figure 6c shows that the mean flow rate decreases monotonically with aCT and increases monotonically with aTA and aLC, a result that matches clinical results. Stretching the CT muscle leads to elongation of the vocal fold, but stretching the TA muscle or LC muscle leads to contraction of the vocal fold. The elongation and contraction of vocal fold affects the glottal area. The variation of UC is related to vocal fold vibration. Vibration at low frequency often requires high glottal volume flow velocity. The opposite is true at high frequency. This may seem counter-intuitive, but it is difficult for pathological vocal folds to vibrate regularly even if the muscle activity achieves the conditions for producing high-frequency sound. Because of the unilateral polyp, the amplitude of vocal fold vibration is small, and the glottal area has little variation. Increased vocal fold stiffness prevents normal vibration. Figure 6d can be regarded as a supplement to other figures. Leakage flow is not zero, which means that there is incomplete glottal closure in each cycle for the pathological vocal fold. Note that the fluctuation in the amplitude of volume flow rate increases as the minimum volume flow rate decreases. That is, in contrast to normal vocal folds, low leakage flow in pathological vocal folds may not result in a good voice quality. Vibratory periodicity should still be the primary consideration.
3.3. Fundamental Frequency and Related Perturbation Parameters
Other properties of the pathological vocal fold, such as natural frequency, probably have some differences from the normal vocal fold. To determine the effect of differing muscle activation on phonatory frequency and perturbation parameters, we fixed the activity of two muscles at a certain value and varied the value of the other to create plots of frequency and related perturbation parameters versus muscle activity (Figure 7).
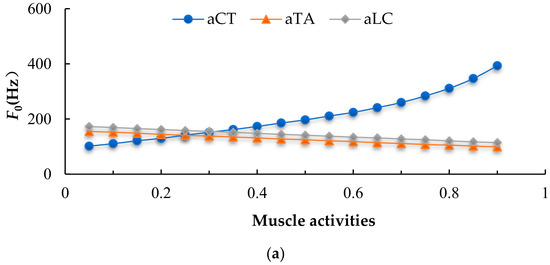
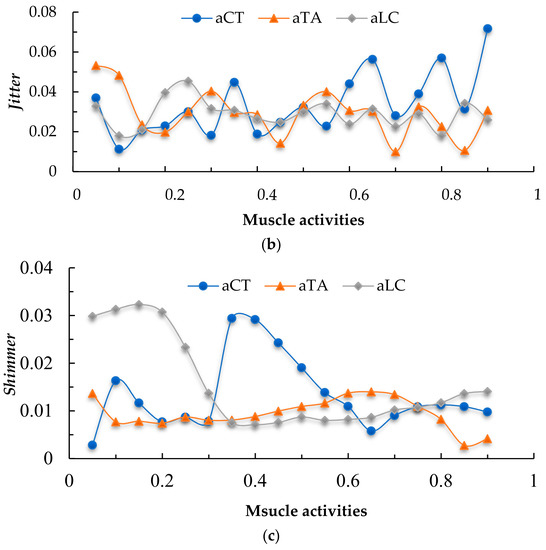
Figure 7.
Effect of CT, TA, LC activity on fundamental frequency and perturbation parameters. (a) Mean fundamental frequency. (b) Mean jitter (variation in frequency). (c) Mean shimmer (variation in amplitude).
Figure 7a shows that the CT muscle is most highly correlated with fundamental frequency. Similar to normal people, increasing CT muscle activity will always increase F0 in people with vocal fold polyps. However, increasing TA and LC muscle activity only causes a decrease in F0. The deformation of the polyp counteracts the increase in stiffness. Activation of the TA and LC muscle under this condition may only shorten the vocal fold and reduce the stiffness. These examples illustrate the antagonistic roles that the CT and adductor muscles play in phonation onset parameters. As pointed out in previous work, these muscle activities could be interpreted as a requirement for stability in the laryngeal framework. When the vocal folds are being tensed, restraining forces may be needed to counteract gross movement of the larynx. In our pathological model, the control range of the vocal fold on frequency may be wider than that seen in the normal physiological situation. The reason is that we amplified the influence of muscle activation on vocal fold vibration. Our model aims to shed light on the effect of muscle activation on frequency to help find adapted muscle activities for different phonation situations. In fact, it should be noted that the actual muscle activation range of polyp vocal folds is much smaller than that of normal vocal folds. Hence, there will be a decrease in the upper frequency range for actual pathological vocal folds.
Variations in frequency (jitter) and amplitude (shimmer) have been commonly used to describe pathological voice quality. For our model, jitter is calculated by the average absolute difference between consecutive periods, divided by the average period, as
where Ti is the extracted period length, and N is the number of periods [26]. The mean value of jitter during phonation is depicted in Figure 7b. Overall, there was not a strong correlation with activity of any muscle. For large values of aCT, the jitter was high, reflective of aperiodic vibration. For small values of aTA, a decrease in aTA will generally cause an increase in jitter.
Shimmer is the cycle-to-cycle variation in amplitude. Similar to jitter, shimmer is measured as the average absolute difference between the amplitudes of consecutive periods, divided by the average amplitude:
where Ai is the extracted amplitude and N is the number of extracted periods [26]. Figure 7c shows the mean value of shimmer on phonation. Shimmer seems to have a strong link with CT and LC activity. The waveform of UA is similar to the waveform for shimmer. In general, increasing aCT will cause an initial increase in shimmer, followed by a decrease. Shimmer is high when aCT ranges from 0.3 to 0.6. When aCT is between 0.3 and 0.4, shimmer is at its maximum. For LC muscle, shimmer increases monotonically when aLC < 0.5. In particular, for aLC < 0.2, the value of shimmer is much higher than at other activity levels.
Figure 7 narrows the range of muscle activation for normal phonation by frequency and perturbation parameters. Similar to the results in the previous section, in addition to the difficulty with high-frequency vibration, patients with a vocal fold polyp should pay attention to increasing their TA and LC muscle activity while decreasing CT muscle activity to produce a voice in a medium-high frequency range. One of the reasons for limited pitch range may be a decreased ability to vary vocal fold length. As shown in the figure, vocal fold vibration is irregular when aCT > 0.4, so CT activity will be restricted to a small range. The results also provide insights into the increase in fundamental frequency in response to effort. For patient with a vocal fold polyp, obtaining a better balance between CT and TA muscle activity is critical. As the results in Figure 6 and Figure 7 show, when the value of aCT is not small, TA muscle activity has little influence on voice quality. Hence, TA muscle activity can be increased appropriately to control F0 while avoiding the generation of high-frequency sound. LC activity should be kept greater than 0.3 even when the pitch is in the low-frequency range.
4. Conclusions
In this paper, a low-dimensional mass model is proposed to study the effects of muscle activation in a unilateral polyp setting. The simulations showed that different combinations of muscle activation have different effects on frequency, quality, and intensity. Based on the experimental results, we can draw conclusions about the optimal degree of muscle activation: aCT should be around 0.3, aLC should be fixed at greater than 0.3, and aTA can assume most values. Model simulations demonstrate that, in a unilateral polyp setting, combined TA and LC muscle activity will produce a more periodic voice at a higher frequency compared to high CT activity alone. The upper frequency range is also limited.
Overall, our computational model produced a substantial amount of significant information about the human vocal fold during phonation. However, the model is still simplistic compared with in vivo vocal fold geometry [27]. Future studies will focus on more realistic three-dimensional models.
Author Contributions
Conceptualization, M.J. and B.L.; methodology, M.J. and B.L.; software, M.J. and B.L.; validation, B.L., J.J. and M.R.H.; formal analysis, B.L.; investigation, M.J., B.L., J.L. and J.F.; resources, B.L.; data curation, M.J.; writing—original draft preparation, M.J. and B.L.; writing—review and editing, M.J., B.L., J.J. and M.R.H.; visualization, M.J.; supervision, B.L.; project administration, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Educational Science Research Project (C2021016).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vasconcelos, D.; Gomes, A.O.C.; Araújo, C.M.T. Vocal Fold Polyps: Literature Review. Int. Arch. Otorhinolaryngol. 2019, 23, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Dikkers, F.G.; Nikkels, P.G.J. Benign lesions of the vocal folds: Histopathology and phonotrauma. Ann. Otol. Rhinol. Laryngol. 1995, 104, 698–703. [Google Scholar] [CrossRef] [PubMed]
- Cancer Stat Facts: Laryngeal Cancer. Available online: https://seer.cancer.gov/statfacts/html/laryn.html (accessed on 1 December 2022).
- Greiss, R.; Rocha, J.; Matida, E. Validation of a finite element for a continuum model of a vocal fold vibration under the influence of a sessile polyp. Can. Acoust. 2015, 43, 13–23. [Google Scholar]
- Mimica, X.; Hanson, M.; Patel, S.G.; McGill, M. Salvagesurgery for recurrent larynx cancer. Head Neck 2019, 41, 3906–3915. [Google Scholar] [CrossRef]
- Tsetsos, N.; Poutoglidis, A.; Vlachtsis, K. Twenty-year experience with salvage total laryngectomy: Lessons learned. J. Laryngol. Otol. 2021, 135, 729–736. [Google Scholar] [CrossRef]
- Vlot, C.; Ogawa, M.; Hosokawa, K.; Iwahashi, T. Investigation of the immediate effects of humming on vocal fold irregularity using electroglottography and high-speed laryngoscopy in patients with organic voice disorders. J. Voice 2017, 31, 48–56. [Google Scholar] [CrossRef]
- Lee, Y.S.; Lee, D.H.; Jeong, G.E.; Kim, J.W. Treatment Efficacy of Voice Therapy for Vocal Fold Polyps and Factors Predictive of Its Efficacy. J. Voice 2017, 31, 120. [Google Scholar] [CrossRef]
- Ishizaka, K.; Flanagan, J.L. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Syst. Tech. J. 1972, 51, 1233–1268. [Google Scholar] [CrossRef]
- Story, B.H.; Titze, I.R. Voice simulation with a body-cover model of the vocal folds. J. Acoust. Soc. Am. 1995, 97, 1249–1260. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J.J. Chaotic vibrations of a vocal fold model with a unilateral polyp. J. Acoust. Soc. Am. 2004, 115, 1266–1269. [Google Scholar] [CrossRef]
- Xue, Q.; Mittal, R.; Zheng, X. A computational study of the effect of vocal-fold asymmetry on phonation. J. Acoust. Soc. Am. 2010, 128, 818–827. [Google Scholar] [CrossRef] [PubMed]
- Mehta, D.D.; Zanartu, M.; Quatieri, T.F. Investigating acoustic correlates of human vocal fold vibratory phase asymmetry through modeling and laryngeal high-speed videoendoscopy. J. Acoust. Soc. Am. 2010, 130, 3999–4009. [Google Scholar] [CrossRef] [PubMed]
- Chhetri, D.K.; Park, S.J. Interactions of subglottal pressure and neuromuscular activation on fundamental frequency and intensity. Laryngoscope 2016, 126, 1123–1130. [Google Scholar] [CrossRef] [PubMed]
- Dewan, K.; Vahabzadeh-Hagh, A.; Soofer, D.; Chhetri, D.K. Neuromuscular Compensation Mechanisms in Vocal Fold Paralysis and Paresis. Laryngoscope 2017, 127, 1633–1638. [Google Scholar] [CrossRef]
- Azar, S.S.; Chhetri, D.K. Phonation Threshold Pressure Revisited: Effects of Intrinsic Laryngeal Muscle Activation. Laryngoscope 2021, 132, 1427–1432. [Google Scholar] [CrossRef]
- Titze, I.R. On the mechanics of vocal-fold vibration. J. Acoust. Soc. Am. 1976, 60, 1366–1380. [Google Scholar] [CrossRef]
- Herzel, H.; Berry, D.; Titze, I.; Steinecke, I. Nonlinear dynamics of the voice: Signal analysis and biomechanical modeling. Chaos 1995, 5, 30–34. [Google Scholar] [CrossRef]
- Titze, I.R.; Story, B.H. Rules for controlling low-dimensional vocal fold models with muscle activation. J. Acoust. Soc. Am. 2002, 112, 1064–1076. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Vocal instabilities in a three-dimensional body-cover phonation model. J. Acoust. Soc. Am. 2019, 143, 1216–1230. [Google Scholar] [CrossRef]
- Titze, I.R. Principles of Voice Production, 2nd ed.; Prentice Hall: Iowa City, ID, USA, 2000; pp. 211–238. [Google Scholar]
- Titze, I.R.; Jiang, J.; Druker, D. Preliminaries to the body cover theory of pitch control. J. Voice 1988, 1, 314–319. [Google Scholar] [CrossRef]
- Alipour-Haghighi, F.; Titze, I.R. Elastic models of vocal fold tissues. J. Acoust. Soc. Am. 1991, 90, 1326–1331. [Google Scholar] [CrossRef] [PubMed]
- Min, Y.; Titze, I.R.; Alipour-Haghighi, F. Stress-strain response of the human vocal ligament. Ann. Otol. Rhinol. Laryngol. 1995, 104, 563–569. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.J.; Zhang, Y.; Stern, J. Modeling of chaotic vibrations in symmetric vocal folds. J. Acoust. Soc. Am. 2001, 110, 2120–2128. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, J.P.; Goncalves, A. Accuracy of jitter and shimmer measurements. Procedia Technol. 2014, 16, 1190–1199. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z. A parametric vocal fold model based on magnetic resonance imaging. J. Acoust. Soc. Am. 2016, 140, 159–165. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).