Abstract
Because of its geometry dependence and loss of physical meaning, the incremental crack resistance curve cannot characterize ductile fractures with large crack extensions and plastic deformations. Therefore, the energy dissipation rate R is employed to overcome these deficiencies, even though specimen size effects still exist. In the study, considering the fractal crack path and concomitant plastic dissipation in the fractal domain, a scale-invariant energy dissipation rate, γp*, is proposed in the context of renormalization group theory. Some experiments in the literature have validated this approach. The fitted fractal energy dissipation rate is independent of the specimen size and initial crack length; moreover, as the specimen size increases, progressive fractality vanishing is found consistently with geometrical multifractality.
1. Introduction
The crack resistance curve is widely applied to characterize irreversible energy dissipation. The ductile crack growth resistance curve is generally presented in the form of fracture mechanics parameters, i.e., path-independent J-integral or crack opening displacement δ versus crack extension Δa—that is, a crack starts to propagate at J = J0 or δ = δ0, then grows stably, and eventually reaches its steady-state value. Typically, the steady-state value is much larger than the initiation value, and primarily comprises the additional irreversible contribution from remote and local plastic energy dissipation in the bulk [1]. Therefore, ductile fracture in metals generally exhibits a rising resistance curve, in contrast to the flat curve of brittle materials.
Extensive research has focused on this problem. Wittmann et al. [2] argued that progressive dilatation of the fracture process zone leads to an increase in crack resistance during crack growth until a specific value corresponding to the fully developed process zone is reached. Size effects may be caused by the deviation of the actual stress from the first singular-term solution, i.e., Hutchinson–Rice–Rosengren (HRR) solution, at a finite distance from the crack front. The higher accuracy of stress with higher-order series expansion as well as the first term of the stress solution can capture a better crack initiation toughness and resistance curve [3,4,5,6]. However, for large plastic energy dissipation and crack extension, the two or three-parameters fracture parameters cannot describe the accumulated energy at a given crack increment and the true “driving force” [7,8]. Despite these drawbacks, the fracture resistance curve remains the most conventional method for the ductile fracture toughness characterization. Moreover, the classical fracture mechanics must suppose that the resistance curve eventually reaches steady values if the cracked body is relatively large compared with the fully developed process zone at the crack tip. Obviously, this postulate does not sufficiently explain some phenomena, particularly regarding crack propagation and its topology.
2. Fractal Aspects and Energy Dissipation Rate in Fracture
Following the pioneering works by Mandelbrot [9,10], the achievements of the fractal approach in fractures are fruitful and effective, especially regarding crack topologies and surfaces in a finite range of scales. Williford [11] proposed a power-law relationship between the J-integral and the crack length increment assuming an invasive fractal crack tip geometry. Gong and Lai [12] further investigated the relationship between the fracture resistance JR curve and fractal fracture surface in alloys. Especially, the fractality of the fracture surface, crack path, and related irreversible energy have been widely recognized in both brittle and ductile materials [13,14,15,16,17,18,19,20,21,22,23,24]. Fractal patterns were experimentally observed by Kleiser and Bocek [13] in metals, where strain localization led to the formation of fractal slip bands. Pioneering investigations into fractal fracture mechanics were performed by Mosolov [14], Goldshtein and Mosolov [15], and Yavari [16]. Alves et al. [17] investigated the stress singularity and path dependence of J-integral on fractal cracks. The classical Griffith’s theory for fractal cracks has led to the conclusion that, because of the nondifferentiable fractal sets, cracking requires infinite surface energy to create an increment of fractal crack extension regardless of the nominal crack growth length [18]. In engineering, there exists upper and lower bounds in the scaling range for all fractal structures: the upper bound is represented by the macroscopic size, whereas the lower bound is related to the internal characteristic length [19,20,21,22,23]. Borodich [24] thus extended Griffith’s criterion to fractal cracks by a fractal measurement of surface energy per unit, and the generalized Griffith’s criterion can be stated locally as
, where ΔUe is the driving force or the strain energy release rate corresponding to the crack increment Δa, and ΔUs is the crack growth resistance. The fractal specific surface energy, γf, is a function of material microstructure ΔmD and fractal dimension D.
Carpinteri and Chiaia [18] suggested an interpretation of crack resistance behavior in terms of a self-similar fracture surface. Accordingly, the nominal fracture resistance is related to the renormalized fracture energy and fractal crack increment. As a result, the energy dissipation rate of smooth cracks is independent of the crack length and remains constant, whereas that of fractal cracks increases with crack propagation. Because of the discrepancy between ideal and natural fractal sets, crack-size scaling energy dissipation is a geometrical multifractal. The effect of fractality on the mechanical properties gradually vanishes as the scale of the crack size increases. Owing to the fractional measurement of physical fractal sets, the corresponding mechanical quantities must consider anomalous physical dimensions to obtain physically universal quantities [19,20,21,22,23]. Current work shows that a physically universal and scale-independent energy dissipation rate can be obtained by considering an anomalous physical dimension in the energy dissipation rate, abandoning the complete similarity of the Euclidean topologies.
Ductile fracture tests following BSI 7448 Part 4 [25] and ASTM E1820 [26] have confirmed that the irreversible energy rate is not only loading configuration–dependent but also intimately related to the crack and specimen size. The path-independent J-integral or crack tip open displacement thus cannot represent the strain energy release rate and becomes a description of accumulated energy at a given crack extension, deviating from the true “driving force” for a propagating crack. Several researchers [7,27,28,29,30] have suggested a more plausible characterization of the local separation energy related to the creation of new surfaces and plastic deformation remote from the crack tip, i.e., the energy dissipation rate, R, which is defined as the rate of all nonrecoverable energy dissipation with regard to the crack increment. A stable crack increment, da, must satisfy the energy balance as
where dw is the energy input rate, and dU is the rate of internal energy dissipation from all causes, including plastic yielding remote from the crack tip. Furthermore, the dissipated work rate dU for the cracked body can be divided into the elastic (recoverable) component wel, Griffith energy, 2γ, and plastic component, wpl [1]:
For ductile fractures involving large-scale yielding, remote and local plasticity both contribute to wpl, and distinguishing between these two irreversible energies is extremely difficult. Therefore, the conventional test method that characterizes the ductile fracture toughness by resistance curves embraces all unrecoverable energy dissipation together, particularly in ductile tearing and deep notch/crack extension, which coincides with the definition of hardening cohesive energy, as shown in Figure 1 [31].
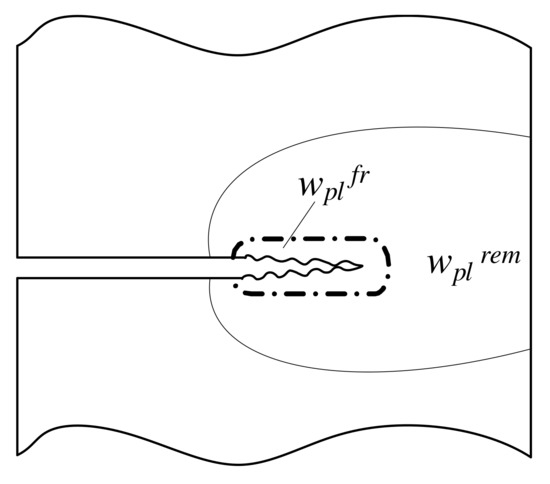
Figure 1.
Different energy dissipation regions: fracture, local plasticity, and remote plasticity.
For a stable crack extension, the energy dissipation rate is physically meaningful, as well as more generally, in contrast to the ambiguous driving force in terms of J or δ. Turner et al. [7,8] proved that R degenerates to G for linear elastic fracture mechanics, to J for nonlinear fracture mechanics, and to the work absorption rate for the elastoplastic material. Accordingly, R is defined as [7]
The dissipation work, Udis, can be determined from the area under the measured load–displacement curve, as indicated in some standards. If the J-integral is used to measure the irreversible fracture energy, using Equations (3) and (4), the following formulation is obtained [32].
where B is the specimen thickness, b0 is the ligament length, and η is the plastic factor [26]. Although the energy dissipation rate R for ductile fracture is more physical than the classical fracture resistance, the geometrical dependency, i.e., in-plane constraint caused by the crack length and loading configuration, still exists [32,33]. Therefore, it is essential to identify geometry-invariant material parameters from R. To obtain a geometrically independent material fracture property, Brocks et al. [32] proposed a four-parameter exponential function to fit the R–Δa curve to explore the transferability of different values of geometric specimen fracture toughness, where the constraint effects on the JR curves have to be parameterized by four fitting parameters. Therefore, the theoretical background of the energy dissipation rate requires further study.
3. Fracture Resistance and Energy Dissipation Rate in Ductile Crack Extension
Carpinteri and Chiaia [18] established the relationship between the structural behavior and crack growth resistance curve using the energy brittleness number, where the ductile-to-brittle transition resulting from size effects can be characterized by the modified J resistance curve. Consequently, a plausible description of the topology of the fracture domain is essential for stable crack growth resistance behaviors. It is assumed that the non-integer fractal dimensions are a proper description of the fracture domains. Owing to the fractional measurability of fractal sets, the mechanical quantities defined in these domains must take non-integer physical dimensions. Meanwhile, unlike the complete similarity in the Euclidean domain, the incomplete similarity can be used to capture the geometry in the fractal domains, i.e., to characterize the energy dissipation rate using the fractal approach. Therefore, a fractal model was developed to calculate the rugged crack length based on the Voss equation [17], where the crack is compared with a self-affine noise in time as follows:
where Δa* is the increment in the rugged crack length, Δa is its horizontal projection, l0 is the unit length or scaling factor, and H is the Hurst exponent, which is usually smaller than one and related to the fractal dimension D through H = I − D (i = 2 or 3). In the present work, it is assumed that Δa* and Δa are the geometrical descriptions of the crack path and its accompanying plastic wake in the fractal and Euclidean domains, respectively.
Considering energy equivalence and fractal crack, the path-independent J-integral can be modified in fractal domains as
where Π is the potential energy of an elastic body. Incorporating Equation (6) into Equation (7), the fractal crack resistance JR per unit thickness is:
Furthermore, Equation (8) can be divided into elastic and plastic (or irreversible) components.
When Δa >> l0, Equation (9) can be simplified as
and the plastic (or irreversible) component can be obtained as
A similar result was obtained by Carpinteri and Chiaia for crack-resistance curves [18]. Based on Equations (5) and (9), the energy dissipation rate, R, can be obtained in the fractal form:
Here, W is the characteristic reference size of the specimen, i.e., the height of beam. Using Equation (10), and in the self-similar limit a* >> a, we obtain:
Because the fractal set is defined in a limit sense corresponding to the observation scale n at approximately zero, Equation (12) can be rewritten as Equation (13) to obtain the scale-independent value of R*:
The expression in the square brackets is indeterminate in classical meaning because, at the infinitesimal scale of observation (n→∞), γp(l0)H−1 tends to be nondifferentiable (l0→0, γp→0) in the form . More specifically, when the scale of observation tending to zero, we can assume that the length l0 is a atom diameter, and γp is the energy to break an atomic bond, and it is worth noting that H is the Hurst’s exponent and less than 1 so than γp(l0)H−1 is mathematically non-soluble. The key to this procedure is to solve the limit in Equation (13) by invoking renormalization group theory, which makes it possible to define finite renormalized physical quantities as the fixed points of the scaling transformations at the cost of abandoning canonical dimensions [18]. Therefore, the nondifferentiable expression in the square brackets of Equation (13) can be reformulated in the fractal domain as
and the energy dissipation rate is
where γp* is referred to as the “fractal energy dissipation rate”, whose anomalous non- integer physical dimensions [Newton][Length]−(2−H) imply that the classical fracture energy dissipation is intermediate between a Euclidean surface and a volume one [18]. The scale-invariant material constant, γp*, is a renormalized physical quantity that characterizes the irreversible process related only to the microstructure. Consistent with Borodich [24] as discussed previously, γp* is a function of the material property γp and fractal measure l0 of the process zone. Experiments on specimens of different sizes show that the monofractal dimension is strictly valid only within a limited scale range, where the fractal dimensions of the supporting domains can be considered constants [19,20,21,22,23]. The monofractal scaling behavior does not adequately reproduce the experimental results. Moreover, the topology of the fracture surfaces appears experimentally multifractal because the presence of an internal microstructural scale l0 and an external macrostructural size results in a progressively decreasing influence of disorder when the scale of observation increases. This geometrical trend implies that the effect of microstructural disorder on the mechanical properties of the material becomes progressively less important for larger specimens. As the specimen size increases, geometrical multifractality connects with the self-affine fractals and progressively vanishes. Because the microstructure of a material is independent of the macroscopic size, the effects of disorder on the mechanical properties are essentially dominated by the ratio between the characteristic material length (grain size and external size) and initial ligament size. The transition between a fractal domain and a homogeneous regime can therefore be emphasized in the scaling power-law exponents of the energy dissipation rate, as verified by subsequent experiments.
4. Experimental Validation
The proposed fractal energy dissipation rate was validated against the relevant experimental data in the literature. The nonlinear best-fitting algorithm of Levenberg and Marquardt [34] was adopted to obtain parameters H and γp*. The experimental load–displacement curves from Zhu and Joyce [35] were reinterpreted using the fractal approach, where the load–loading-line displacement curves are available. The material used for the tests was HY80 steel available in a 27-mm-thick plate. The tensile test results showed that the 0.2% offset yield stress was 630 MPa, and the ultimate tensile stress was 735 MPa. The specimens were subjected to single-edge notched bending, as recommended by ASTM E1820-01 [26], with different initial crack lengths a0. The geometric parameters of the beam were L = 203 mm, W = 50.75 mm, B = 25.375 mm, and slenderness λ = 4:1. The initial crack-length ratios were a0/W = 0.19, 0.40, 0.55, and 0.60. Details are presented in Table 1. Because the calculation of the R–Δa curve requires the correlation between the load and crack extension, the instantaneous crack extension was then determined directly using the normalization method suggested in ASTM E1820-01 Annex 15 [26]. Another series of compact tension tests were performed by Anuschewski et al. [36], where the material was a 20MnMoNi55 steel alloy with different thicknesses. The geometric details are presented in Table 1. In Figure 2, the experimental results for the R–Δa curve from a previous report [36] as well as the fitting curves obtained using Equation (15) are plotted. The determined parameters H and γp* are listed in Table 1. The domain dimension of energy dissipation is denoted by D = 3 − H.

Table 1.
Specimen geometries and fitted results.
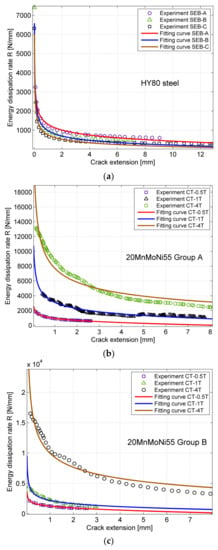
Figure 2.
Fitting results of R(Δa)-curve by the proposed theory for (a) HY80, (b) 20MnMoNi55 Group A, and (c) 20MnMoNi55 Group B.
5. Discussion
During ductile crack growth, massive plastic flow occurs in the vicinity of the crack tip, and the wake is governed by dislocation–dislocation interactions in crystalline materials. Although the actual cell structures depend on various extrinsic and intrinsic parameters, dislocation patterning and its relation to work hardening are common among various materials. Thus, the dislocation pattern plays a critical role in energy dissipation, which can be directly characterized by transmission electron microscopy [37] and indirectly by acoustic emission (AE). Because AE can represent the rapid release of energy from localized sources within materials, e.g., dislocation avalanches and microcrack generation and propagation, AE also provides direct information regarding the existence and location of pressure wave energy emissions [38,39,40,41]. AE results for single ice crystals under plastic deformation showed that the probability density function of signal intensity follows a power-law distribution with an exponent (fractal dimension) in the range of 1.6–2.0 [42]. Dislocation avalanches were also observed spatially with a self-similarity dimension D = 2.5 ± 0.1 [43]. Furthermore, the fractal dimensions D in Table 1 range from 2.5 to 2.8, which is consistent with the experimental results [42,43]. Here, the fractal dimension of the plastic energy dissipation is always greater than 2.5. For ductile fracture, it is believed that the energy dissipated is proportional to the area slipped by dislocation loops with different orientations, i.e., the cellular pattern, the fractal dimension of which is generally greater than 2.5 [42]. This is higher than the fracture surface observation by Carpinteri [20,21,22,23] wherein the limit fractal scaling exponents are equal to 0.5. In this study, the defect size distribution was a power law with a negative exponent D = 2b, which can be interpreted as a fractal dimension of the damage domain. By linking the b-value to the damage fractal dimension D, the evolution of the power-law exponent is captured immediately. In the initial phase, criticality D = 3.0, whereas, when final failure is imminent, the exponent tends to 2.0.
6. Conclusions
The peculiar crack resistance behavior of metallic materials was reinterpreted in terms of the energy dissipation rate and self-similar topology of the fracture domains. The scale-independent fractal energy dissipation rate, γp*, was derived based on renormalization group theory, which provides a novel approach for characterizing ductile fractures. Different specimen geometries in terms of the initial crack ratio and self-similar size were considered using experimental data from the literature, and the obtained γp* remained almost constant for the same material, independent of the specimen size and crack length. The fractal energy dissipation rate, γp*, can be considered as a material parameter to characterize the ductile fracture energy dissipation rate, although more experiments are necessary for further validation.
Author Contributions
Conceptualization, B.G.; methodology, G.L.; validation, Y.Z. (Yunfeng Zhao), G.L. and B.G.; formal analysis, Y.Z. (Yangyang Zhao); investigation, Y.Z. (Yunfeng Zhao); resources, Y.Z. (Yunfeng Zhao) and S.W.; data curation, Y.Z. (Yangyang Zhao); writing—original draft preparation, Y.Z. (Yangyang Zhao); writing—review and editing, B.G. and Y.Z. (Yunfeng Zhao); visualization, Y.Z. (Yunfeng Zhao); supervision, B.G.; project administration, Y.Z. (Yunfeng Zhao) and S.W.; funding acquisition, B.G. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC), Grant No. 52075366. Moreover, the sponsorship guaranteed with basic research funds provided by Politecnico di Torino (Italy) is acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The sponsorship guaranteed with basic research funds provided by Politecnico di Torino (Italy) is acknowledged. GBM gratefully acknowledges the research support provided by the National Natural Science Foundation of China (NSFC) (Grant No. 52075366).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Anderson, T. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wittmann, F.; Mihashi, H.; Nomura, N. Size effect on fracture energy of concrete. Eng. Fract. Mech. 1990, 35, 107–115. [Google Scholar] [CrossRef]
- Betegon, C.; Hancock, J. Two-parameter characterization of elastic-plastic crack-tip fields. Appl. Mech. 1991, 58, 104–110. [Google Scholar] [CrossRef]
- O’dowd, N.; Shih, C.F. Family of crack-tip fields characterized by a triaxiality parameter—I. Structure of fields. J. Mech. Phys. Solids 1991, 39, 989–1015. [Google Scholar] [CrossRef]
- Chao, Y.; Yang, S.; Sutton, M. On the fracture of solids characterized by one or two parameters: Theory and practice. J. Mech. Phys. Solids 1994, 42, 629–647. [Google Scholar] [CrossRef]
- Chao, Y.; Zhu, X. Constraint-modified J− R curves and its application to ductile crack growth. Int. J. Fract. 2000, 106, 135–160. [Google Scholar] [CrossRef]
- Turner, C.; Kolednie, O. A micro and macro approach to the energy dissipation rate model of stable ductile crack growth. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 1089–1107. [Google Scholar] [CrossRef]
- Turner, C.; Kolednik, O. Application of energy dissipation rate arguments to stable crack growth. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 1109–1127. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Passoja, D.; Paullay, A. Fractal character of fractal surfaces of metal. Nature 1986, 320, 429–431. [Google Scholar]
- Mandelbrot, B.; Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Williford, R. Fractal fatigue. Scr. Met. Mater. 1990, 24, 455–460. [Google Scholar] [CrossRef]
- Gong, B.; Lai, Z. Fractal characteristics of J-R resistance curves of Ti-6A1-4V alloys. Eng. Fract. Mech. 1993, 44, 991–995. [Google Scholar]
- Kleiser, T.; Bocek, M. The fractal nature of slip in crystals. Z. Für Met. 1986, 77, 582–587. [Google Scholar]
- Mosolov, A. Mechanics of fractal cracks in brittle solids. EPL (Europhys. Lett.) 1993, 24, 673. [Google Scholar] [CrossRef]
- Goldshtein, R.; Mosolov, A. Fractal cracks. J. Appl. Math. Mech. 1992, 56, 563–571. [Google Scholar] [CrossRef]
- Yavari, A. Generalization of Barenblatt’s cohesive fracture theory for fractal cracks. Fractals 2002, 10, 189–198. [Google Scholar] [CrossRef]
- Alves, L.; Da Silva, R.; Lacerda, L. Fractal modeling of the J–R curve and the influence of the rugged crack growth on the stable elastic–plastic fracture mechanics. Eng. Fract. Mech. 2010, 77, 2451–2466. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B. Crack-resistance behavior as a consequence of self-similar fracture topologies. Int. J. Fract. 1996, 76, 327–340. [Google Scholar] [CrossRef]
- Carpinteri, A. Scaling laws and renormalization groups for strength and toughness of disordered materials. Int. J. Solids Struct. 1994, 31, 291–302. [Google Scholar] [CrossRef]
- Carpinteri, A. Fractal nature of material microstructure and size effects on apparent mechanical properties. Mech. Mater. 1994, 18, 89–101. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Ferro, G. Size effects on nominal tensile strength of concrete structures: Multifractality of material ligaments and dimensional transition from order to disorder. Mater. Struct. 1995, 28, 311–317. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ferro, G. Size effects on tensile fracture properties: A unified explanation based on disorder and fractality of concrete microstructure. Mater. Struct. 1994, 27, 563–571. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B. Multifractal nature of concrete fracture surfaces and size effects on nominal fracture energy. Mater. Struct. 1995, 28, 435–443. [Google Scholar] [CrossRef]
- Borodich, F. Some applications of the fractal parametric-homogeneous functions. Fractals 1994, 2, 311–314. [Google Scholar] [CrossRef]
- BS7448-4; Fracture Mechanics Toughness Test-Part 4: Method for Determination of Fracture Resistance Curve and Initiation Values for Stable Crack Extension in Metallic Materials. BSI: London, UK, 1997.
- E1820-01; Standard Test Measurement for Fracture Toughness. ASTM: West Conshohocken, PA, USA, 2001.
- Sumpter, J. The energy dissipation rate approach to tearing instability. Eng. Fract. Mech. 2004, 71, 17–37. [Google Scholar] [CrossRef]
- Sumpter, J. An alternative view of R curve testing. Eng. Fract. Mech. 1999, 64, 161–176. [Google Scholar] [CrossRef]
- Sumpter, J. Size effects in tearing instability: An analysis based on energy dissipation rate. Eng. Fract. Mech. 2007, 74, 2352–2374. [Google Scholar] [CrossRef]
- Memhard, D.; Brocks, W.; Fricke, S. Characterization of ductile tearing resistance by energy dissipation rate. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 1109–1124. [Google Scholar] [CrossRef]
- Carpinteri, A.; Gong, B.; Corrado, M. Hardening cohesive/overlapping zone model for metallic materials: The size-scale independent constitutive law. Eng. Fract. Mech. 2012, 82, 29–45. [Google Scholar] [CrossRef]
- Brocks, W.; Anuschewski, P. Parametrizing ductile tearing resistance by four parameters. Eng. Fract. Mech. 2004, 71, 127–146. [Google Scholar] [CrossRef]
- Brocks, W.; Anuschewski, P.; Hellmann, D. A concept for scaling J R-curves by plastic constraint factors. Int. J. Fract. 2004, 130, 455–469. [Google Scholar] [CrossRef]
- Milliken, G. Nonlinear Regression Analysis and Its Applications; Taylor & Francis: Abingdon-on-Thames, UK, 1990. [Google Scholar]
- Zhu, X.; Joyce, J. J–Resistance curve testing of HY80 steel using SE (B) specimens and normalization method. Eng. Fract. Mech. 2007, 74, 2263–2281. [Google Scholar] [CrossRef]
- Anuschewski, P.; Brocks, W.; Hellmann, D. Characterisation of Ductile Tearing Resistance by the Energy Dissipation Rate: Effects of Material, Specimen Shape and Size; GKSS Report GKSS-2002/13; GKSS-Forschungszentrum Geesthacht GmbH: Geesthacht, Germany, 2002. [Google Scholar]
- Hähner, P.; Bay, K.; Zaiser, M. Fractal dislocation patterning during plastic deformation. Phys. Rev. Lett. 1998, 81, 2470. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G. Fractal analysis of damage detected in concrete structural elements under loading. Chaos Solitons Fractals 2009, 42, 2047–2056. [Google Scholar] [CrossRef]
- Carpinteri, A. Mechanical Damage and Crack Growth in Concrete: Plastic Collapse to Brittle Fracture; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Carpinteri, A. Decrease of apparent tensile and bending strength with specimen size: Two different explanations based on fracture mechanics. Int. J. Solids Struct. 1989, 25, 407–429. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Puzzi, S. From criticality to final collapse: Evolution of the “b-value” from 1.5 to 1.0. Chaos Solitons Fractals 2009, 41, 843–853. [Google Scholar] [CrossRef]
- Miguel, M.; Vespignani, A.; Zapperi, S.; Weiss, J.; Grasso, J. Intermittent dislocation flow in viscoplastic deformation. Nature 2001, 410, 667–671. [Google Scholar] [CrossRef]
- Weiss, J.; Marsan, D. Three-dimensional mapping of dislocation avalanches: Clustering and space/time coupling. Science 2003, 299, 89–92. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).