An Algorithm of Acoustic Emission Location for Complex Composite Structure
Abstract
1. Introduction
2. Algorithms
2.1. Location Algorithm
2.2. Dijkstra’s Algorithm
- (1)
- A travel time array and a ray source array are defined for each detector. The size of each array is equal to the total number of nodes. The elements in each array and the nodes are in one-to-one correspondence. Each element of the travel time array stores the travel time from the node, where the detector is located, to the corresponding node of the element. Consider that a ray emits from Node A to Node B, and the element of the ray source array corresponding to Node B is used to store the identifier number of Node A. Furthermore, a candidate queue, which is initially empty, is defined to store the identifier numbers of candidate nodes.
- (2)
- Define P as a source node where the detector locates. The element in the travel time array corresponding to Node P is set to zero. Define Q as the current secondary source node. The initial value of the element in the travel time array corresponding to Node Q is equal to TP-Q which is the travel time from Node P to Node Q.
- (3)
- Calculate the travel time from Node P to all the adjacent nodes of Node Q. Let be the ith adjacent node of Node Q, be the travel time from Node P to Node , and be the travel time from Node Q to , then we can obtain = TP-Q + . If is less than the value that has been previously stored in the travel time array, the previously stored value is replaced by . Accordingly, the path source array is also modified, and the identifier numbers of are added to the candidate queue if they are not in the queue.
- (4)
- The calculation ends when the candidate queue is empty. Otherwise, let Q to be the node with the minimum travel time in the candidate queue, then Node Q should be removed from the candidate queue since the path and travel time of Node Q has been determined. Then, go back to the step (3) and continue to calculate.
2.3. Optimization of Dijkstra’s Algorithm
- (1)
- The use of heap sort. It is very popular to add heap sort to Dijkstra’s algorithm [41]. In the original Dijkstra’s algorithm, the candidate queue is in a disordered state, the time complexity for seeking the node of minimum travel time from the candidate queue is , where is the total number of nodes in the candidate queue. If heap sort is used to manage the candidate queue, the time consumption for seeking the node of minimum travel time from the candidate queue includes k times of inserting or adjusting nodes into the heap, and one time of heap reconstruction after removing the minimum value. Specifically, k, which depends on the adjacency radius, is the number of nodes that need to be inserted or adjusted in the candidate queue. Thus, the time complexity is to insert or adjust nodes, and is to rebuild the heap after removing the minimum value. On average, is a big number, but is relatively small, then is much less than . Therefore, we add heap sort into the original Dijkstra’s algorithm to improve the calculation efficiency for seeking nodes of minimum travel time from the candidate queue.
- (2)
- The use of parallel computing. This can largely improve the utilization of multi-cored CPU. Specifically, the nodes in the sample space are assigned to different threads, and a sub-heap is established for each thread. The travel time calculation of adjacent nodes as well as the addition and adjustment of the nodes in candidate queues are implemented by parallel computing. However, the removal of the nodes of minimum travel time from the candidate queue still uses the serial processing.
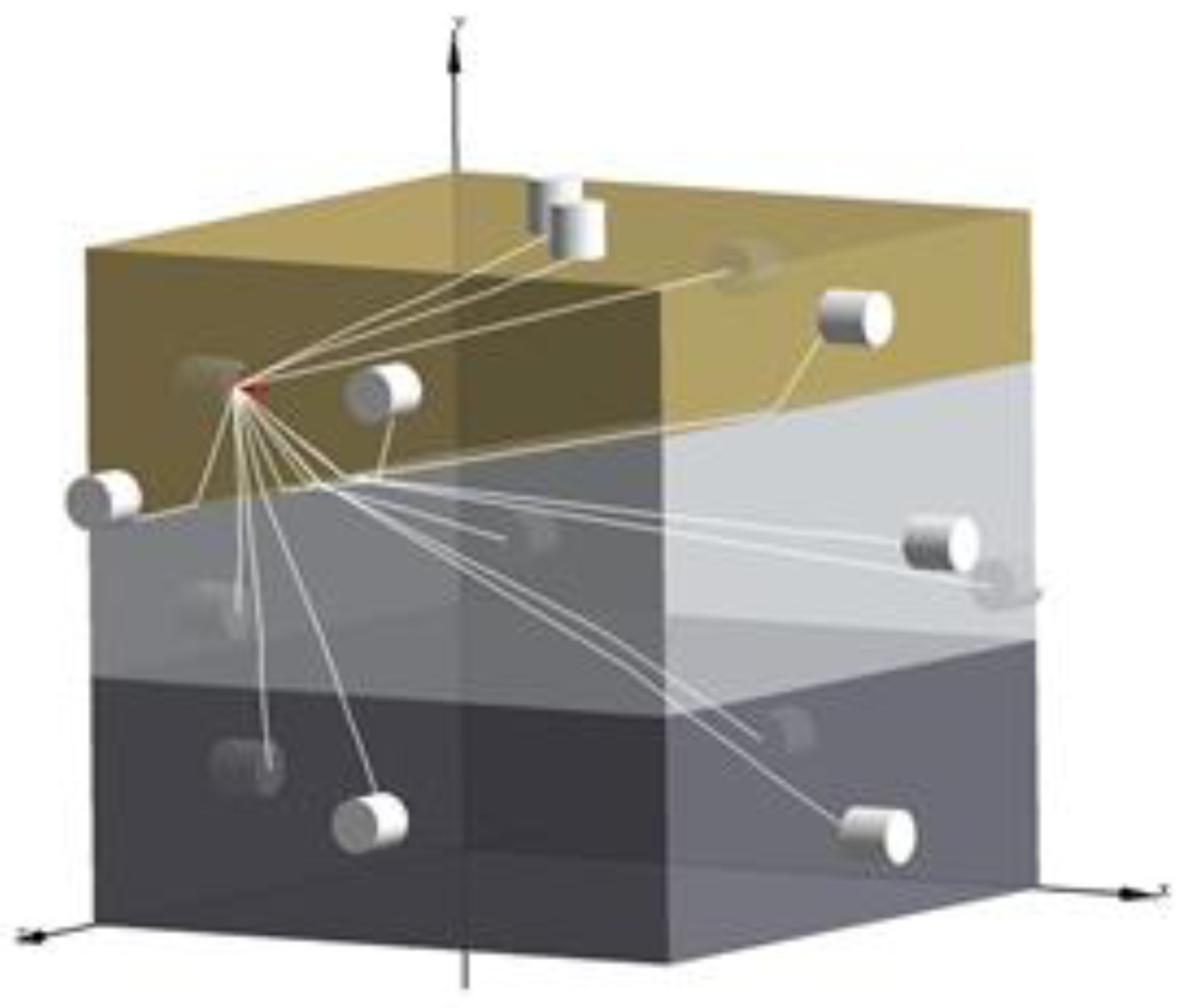
2.4. Construction of 3D Structure Model
2.5. Correction of Travel Time Error for Straight Path Inside a Block
2.6. Efficiency Test of Travel Time Calculation
3. The Algorithm Testing
3.1. Theoretical Verification
3.2. Experimental Verification
4. Application: An Experiment on a Simulated CCS with a Hole
5. Discussion
5.1. Algorithm Optimization
5.2. Limitations of the Algorithm
- (1)
- Only the first arrival wave can be used to obtain the path and travel time by using our algorithm. The first arrival wave may be P wave, head wave, or diffraction wave.
- (2)
- Our algorithm is only suitable for models with step-like change in wave velocity, such as layered model or block model, but not for models with gradual change in wave velocity.
- (3)
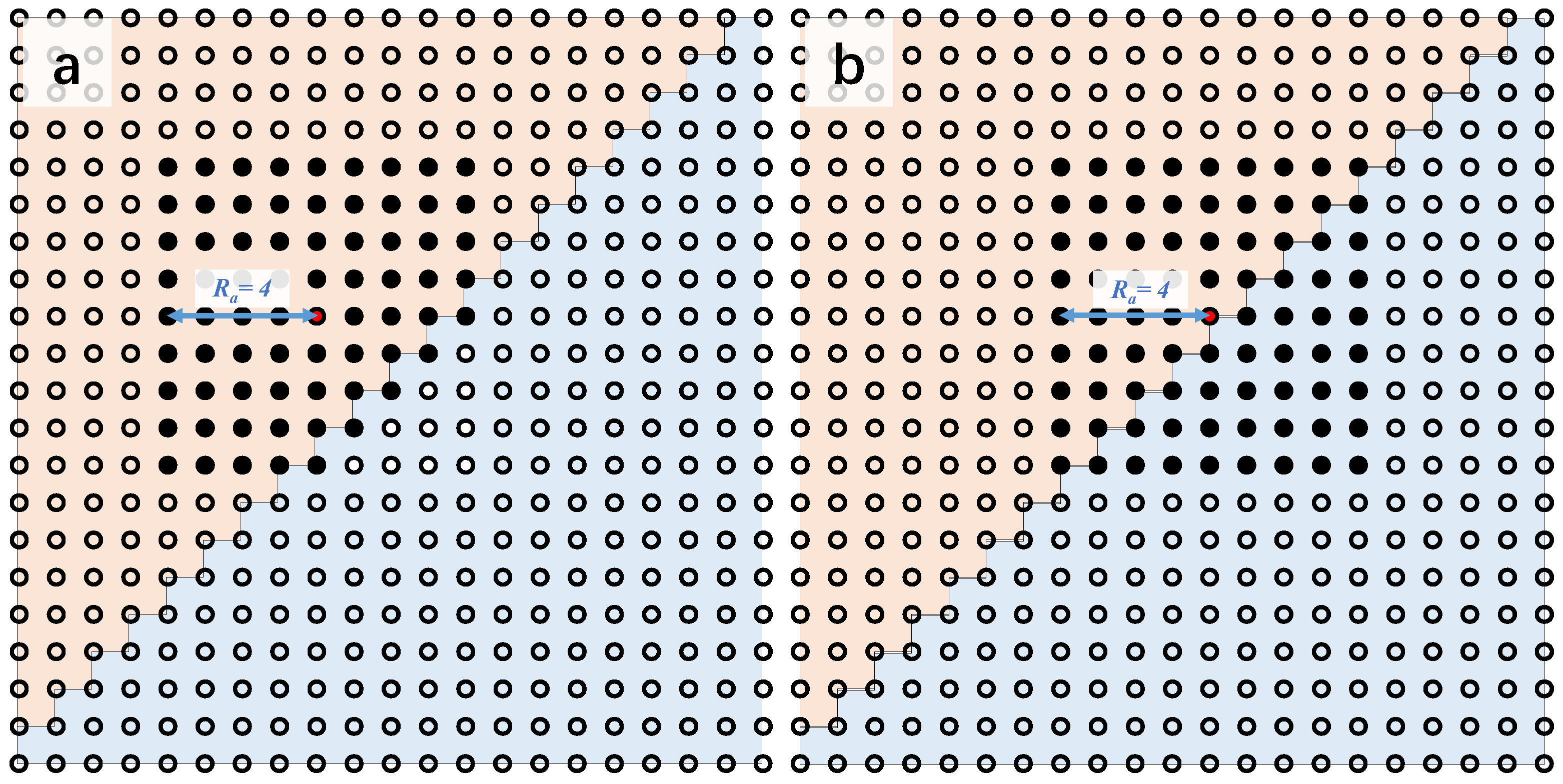
- Our algorithm stipulates that two nodes in the same block are adjacent nodes if the spacing in all directions of , and between the two nodes is less than or equal to the adjacency radius, and that the waves can directly propagate between the adjacent nodes. As a result, an interlayer of the third material between two nodes, which is thinner than the adjacency radius, will be omitted during the calculation so as to guarantee calculation speed. To solve this problem, the material, which contains the thin interlayer, should be cut into two blocks along the two boundaries of the thin interlayer during 3D model meshing.
5.3. Comparison with Moser’s Algorithm
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, K.; Li, D.; He, Z.; Zhou, H.; Li, J. Study on Acoustic Emission Characteristics of Low-Temperature Asphalt Concrete Cracking Damage. Materials 2021, 14, 881. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R. An early-warning method for rock failure based on Hurst exponent in acoustic emission/microseismic activity monitoring. Bull. Eng. Geol. Environ. 2021, 80, 7791–7805. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Wang, W.; Zhao, K.; Ye, Z.; Wang, L. Acoustic Emission Wave Velocity Measurement of Asphalt Mixture by Arbitrary Wave Method. Appl. Sci. 2021, 11, 8505. [Google Scholar] [CrossRef]
- Zhou, Z.; Rui, Y.; Cai, X.; Lan, R.; Cheng, R. A Closed-Form Method of Acoustic Emission Source Location for Velocity-Free System Using Complete TDOA Measurements. Sensors 2020, 20, 3553. [Google Scholar] [CrossRef]
- Zhou, Z.; Rui, Y.; Cai, X.; Cheng, R.; Du, X.; Lu, J. A Weighted Linear Least Squares Location Method of an Acoustic Emission Source without Measuring Wave Velocity. Sensors 2020, 20, 3191. [Google Scholar] [CrossRef]
- Yang, H.-M.; Chen, S.-Y.; Liu, P.-X.; Guo, Y.-S.; Zhuo, Y.-Q.; Qi, W.-B. Experimental study on the changes of ultrasonic coda wave and acoustic emission during rock loading and deformation. Seismol. Geol. 2020, 42, 715–731. [Google Scholar] [CrossRef]
- Wang, C.; Hou, X.; Liao, Z.; Chen, Z.; Lu, Z. Experimental investigation of predicting coal failure using acoustic emission energy and load-unload response ratio theory. J. Appl. Geophys. 2019, 161, 76–83. [Google Scholar] [CrossRef]
- Zhuo, Y.Q.; Liu, P.; Chen, S.; Guo, Y.; Jin, M. Laboratory Observations of Tremor-Like Events Generated During Preslip. Geophys. Res. Lett. 2018, 45, 6926–6934. [Google Scholar] [CrossRef]
- Wang, C.-l. Identification of early-warning key point for rockmass instability using acoustic emission/microseismic activity monitoring. Int. J. Rock Mech. Min. Sci. 2014, 71, 171–175. [Google Scholar] [CrossRef]
- Liu, P.X.; Chen, S.Y.; Guo, Y.S.; Li, P.C. Moment tensor inversion of acoustic emission. Chin. J. Geophys. 2014, 57, 858–866. [Google Scholar] [CrossRef]
- Ma, S.L.; Chen, S.Y.; Liu, P.X.; Hu, X.Y.; Wang, K.Y.; Huang, Y.M. Effect of fault jogs on frictional behavior: An experimental study. Sci. China Ser. D Earth Sci. 2008, 51, 1426–1435. [Google Scholar] [CrossRef]
- Liu, P.-X.; Liu, L.Q.; Chen, S.-Y.; Hu, X.-Y. Software for three-dimensional location of acoustic emission in laboratory. Seismol. Geol. 2007, 29, 674–679. [Google Scholar] [CrossRef]
- Lei, X.; Nishizawa, O.; Kusunose, K.; Cho, A.; Satoh, T. Compressive failure of mudstone samples containing quartz veins using rapid AE monitoring: The role of asperities. Tectonophysics 2000, 328, 329–340. [Google Scholar] [CrossRef]
- Bai, C.-Y.; Greenhalgh, S.A. 3D Local Earthquake Hypocenter Determination with an Irregular Shortest-Path Method. Bull. Seismol. Soc. Am. 2006, 96, 2257–2268. [Google Scholar] [CrossRef]
- Moser, T.J.; Eck, T.V.; Nolet, G. Hypocenter determination in strongly heterogeneous Earth models using the shortest path method. J. Geophys. Res. 1992, 97, 6563–6572. [Google Scholar] [CrossRef]
- Nelson, G.D.; Vidale, J.E. Earthquake locations by 3-D finite-difference travel times. Bull. Seismol. Soc. Am. 1990, 80, 395–410. [Google Scholar] [CrossRef]
- Peng, P.; Wang, L. Targeted location of microseismic events based on a 3D heterogeneous velocity model in underground mining. PLoS ONE 2019, 14, e0212881. [Google Scholar] [CrossRef]
- Tan, Y.; He, C.; Mao, Z. Microseismic velocity model inversion and source location: The use of neighborhood algorithm and master station method. Geophysics 2018, 83, KS49–KS63. [Google Scholar] [CrossRef]
- Nugraha, A.D.; Shiddiqi, H.A.; Widiyantoro, S.; Thurber, C.H.; Pesicek, J.D.; Zhang, H.; Wiyono, S.H.; Ramdhan, M.; Wandono; Irsyam, M. Hypocenter Relocation along the Sunda Arc in Indonesia, Using a 3D Seismic-Velocity Model. Seismol. Res. Lett. 2018, 89, 603–612. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, X. Seismic Moment Tensor Inversion Using 3D Velocity Model and Its Application to the 2013 Lushan Earthquake Sequence. Phys. Chem. Earth Parts A/B/C 2016, 95, 10–18. [Google Scholar] [CrossRef]
- Latorre, D.; Mirabella, F.; Chiaraluce, L.; Trippetta, F.; Lomax, A. Assessment of earthquake locations in 3-D deterministic velocity models: A case study from the Altotiberina Near Fault Observatory (Italy). J. Geophys. Res. Solid Earth 2016, 121, 8113–8135. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, X.; Peng, K. Locating Mine Microseismic Events in a 3D Velocity Model through the Gaussian Beam Reverse-Time Migration Technique. Sensors 2020, 20, 2676. [Google Scholar] [CrossRef] [PubMed]
- Siwek, S. Earth tides and seismic activity in deep coal mining. Int. J. Rock Mech. Min. Sci. 2021, 148, 104972. [Google Scholar] [CrossRef]
- Gupta, H.K. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna, India. Earth-Sci. Rev. 2002, 58, 279–310. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Eaton, D.W.; Ghofrani, H.; Walker, D.; Cheadle, B.A.; Schultz, R.; Shcherbakov, R.; Tiampo, K.F.; Gu, J.; Harrington, R.M.; et al. Hydraulic Fracturing and Seismicity in the Western Canada Sedimentary Basin. Seismol. Res. Lett. 2016, 87, 631–647. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, X.; Ma, S.; Wang, X.; Wan, Y.-G. Induced Earthquakes Before and After Cessation of Long-Term Injections in Rongchang Gas Field. Geophys. Res. Lett. 2020, 47, e2020GL089569. [Google Scholar] [CrossRef]
- Cesca, S.; Stich, D.S.; Grigoli, F.; Vuan, A.; López-Comino, J.A.; Niemz, P.; Blanch, E.; Dahm, T.; Ellsworth, W.L. Seismicity at the Castor gas reservoir driven by pore pressure diffusion and asperities loading. Nat. Commun. 2021, 12, 4783. [Google Scholar] [CrossRef]
- Ellsworth, W.L.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T. Triggering of the Pohang, Korea, Earthquake (Mw 5.5) by enhanced geothermal system stimulation. Seismol. Res. Lett. 2019, 90, 1844–1858. [Google Scholar] [CrossRef]
- Bao, X.; Eaton, D. Fault activation by hydraulic fracturing in western Canada. Science 2016, 354, 1406–1409. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, M.; Chen, Y. Obtaining free USArray data by multi-dimensional seismic reconstruction. Nat. Commun. 2019, 10, 4434. [Google Scholar] [CrossRef]
- Thurber, C.H.; Kissling, E. Advances in Travel-Time Calculations for Three-Dimensional Structures; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Moser, T.J. Shortest path calculation of seismic rays. Geophysics 1991, 56, 59–67. [Google Scholar] [CrossRef]
- Zhang, M.; Cheng, B.; Li, X.; Wang, M. A Fast Algorithm of the Shortest Path Ray Tracing. Chin. J. Geophys. 2006, 49, 1315–1323. [Google Scholar] [CrossRef]
- Li, F.; Xu, T.; Zhang, M.; Wu, Z.; Wu, C.; Zhang, Z.; Teng, J. Seismic traveltime inversion of 3D velocity model with triangulated interfaces. Earthq. Sci. 2014, 27, 127–136. [Google Scholar] [CrossRef][Green Version]
- Zhao, D.; Hasegawa, A.; Horiuchi, S. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. J. Geophys. Res. 1992, 97, 19909–19928. [Google Scholar] [CrossRef]
- Xu, L.S.; Du, H.L.; Yan, C.; Li, C.L. A method for determination of earthquake hypocentroid: Time-reversal imaging technique I—Principle and numerical tests. Chin. J. Geophys. 2013, 56, 1190–1206. [Google Scholar] [CrossRef]
- Larmat, C.; Montagner, J.P.; Fink, M.; Capdeville, Y.; Tourin, A.; Clévédé, E. Time-reversal imaging of seismic sources and application to the great Sumatra earthquake. Geophys. Res. Lett. 2006, 33, L19312. [Google Scholar] [CrossRef]
- Fink, M. Time reversal in acoustics. Contemp. Phys. A Rev. Phys. Assoc. Technol. 1996, 37, 95–109. [Google Scholar] [CrossRef]
- Li-Sheng, X.; Chuan, Y.; Xu, Z.; Chun-Lai, L. A method for determination of earthquake hypocentroid: Time-reversal imaging technique—An examination based on people-made earthquakes. Chin. J. Geophys. 2013, 56, 4009–4027. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connection with graphs. Numer. Math. 1959, 1, 287–290. [Google Scholar] [CrossRef]
- Shaffer, C.A. Data Structures and Algorithm Analysis in C++, 3rd ed.; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
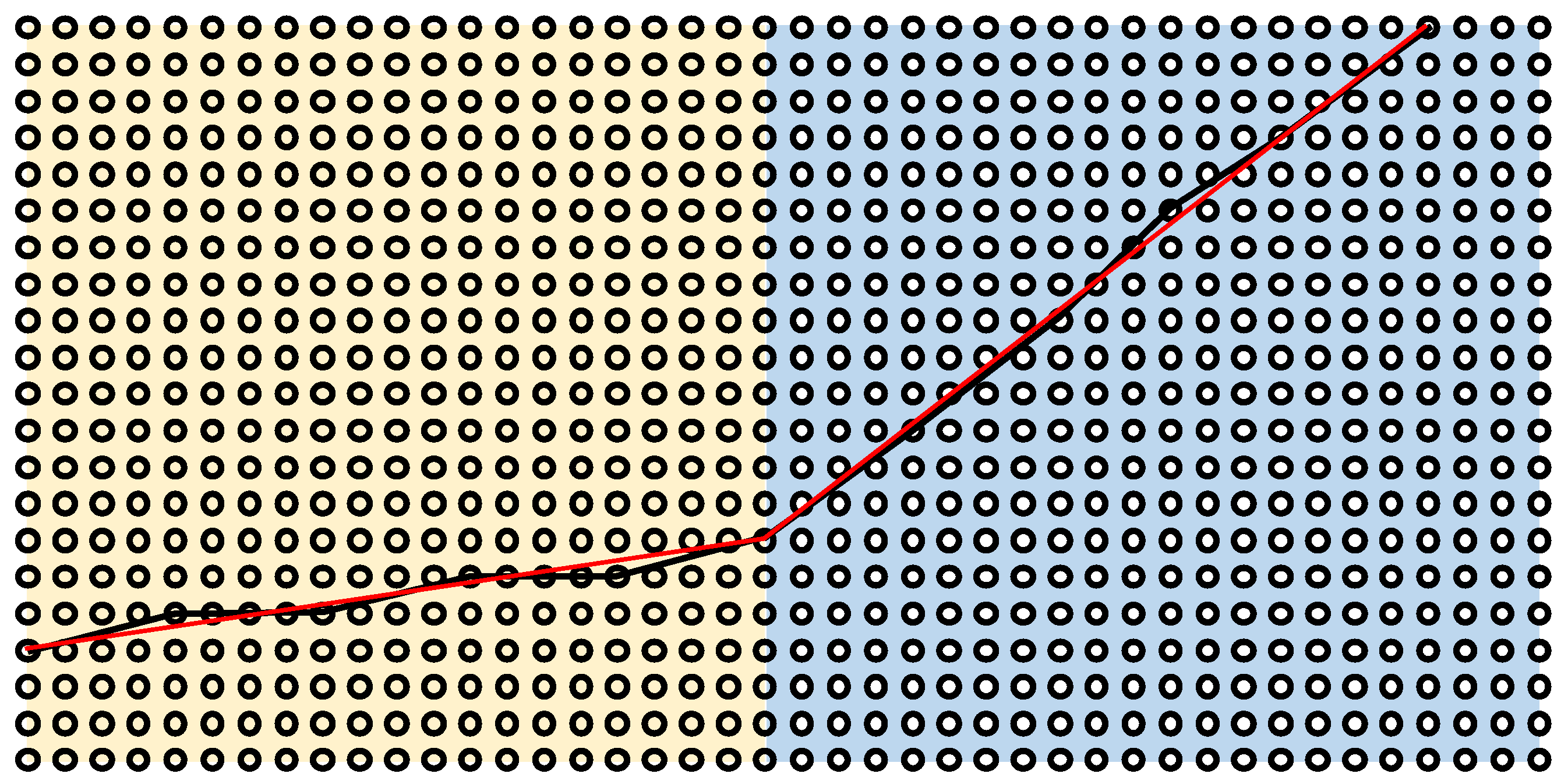




| Adjacency Radius (Cell Number) | Maximum Relative Error |
|---|---|
| 4 | 1.46% |
| 5 | 1.15% |
| 6 | 0.74% |
| 7 | 0.50% |
| 8 | 0.40% |
| 9 | 0.34% |
| 10 | 0.27% |
| Total Nodes n | Time Consumption t (s) | Memory Usage (MB) |
|---|---|---|
| 1,000,000 | 6 | 94 |
| 8,000,000 | 65 | 385 |
| 27,000,000 | 292 | 1169 |
| 64,000,000 | 786 | 2647 |
| 125,000,000 | 1745 | 5126 |
| 216,000,000 | 3139 | 8826 |
| 343,000,000 | 5231 | 13,863 |
| 512,000,000 | 7377 | 20,699 |
| Grid Spacing (mm) | Adjacency Radius (Cell Number) | Path Correction | The Maximum Relative Errors |
|---|---|---|---|
| 2 | 5 | No | 1.43% |
| 2 | 5 | Yes | 1.28% |
| 1 | 5 | No | 1.16% |
| 1 | 5 | Yes | 0.64% |
| 0.5 | 5 | No | 1.16% |
| 0.5 | 5 | Yes | 0.61% |
| 0.5 | 7 | No | 0.50% |
| 0.5 | 7 | Yes | 0.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Guo, Y.; Zhuo, Y.; Qi, W.; Feng, J.; Chen, H.; Chen, S. An Algorithm of Acoustic Emission Location for Complex Composite Structure. Appl. Sci. 2022, 12, 12323. https://doi.org/10.3390/app122312323
Liu P, Guo Y, Zhuo Y, Qi W, Feng J, Chen H, Chen S. An Algorithm of Acoustic Emission Location for Complex Composite Structure. Applied Sciences. 2022; 12(23):12323. https://doi.org/10.3390/app122312323
Chicago/Turabian StyleLiu, Peixun, Yanshuang Guo, Yanqun Zhuo, Wenbo Qi, Jiahui Feng, Hao Chen, and Shunyun Chen. 2022. "An Algorithm of Acoustic Emission Location for Complex Composite Structure" Applied Sciences 12, no. 23: 12323. https://doi.org/10.3390/app122312323
APA StyleLiu, P., Guo, Y., Zhuo, Y., Qi, W., Feng, J., Chen, H., & Chen, S. (2022). An Algorithm of Acoustic Emission Location for Complex Composite Structure. Applied Sciences, 12(23), 12323. https://doi.org/10.3390/app122312323










