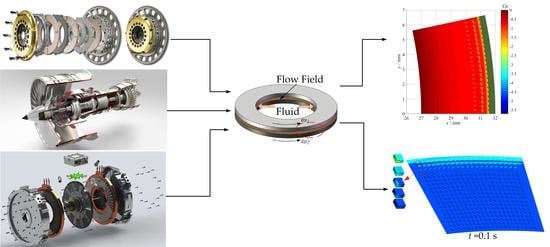
Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System
Abstract
:Featured Application
Abstract
1. Introduction
2. Numerical Analysis
2.1. Cavitation Inception Mechanism
2.1.1. Pressure Coefficient
2.1.2. Critical Pressure of Cavitation Inception
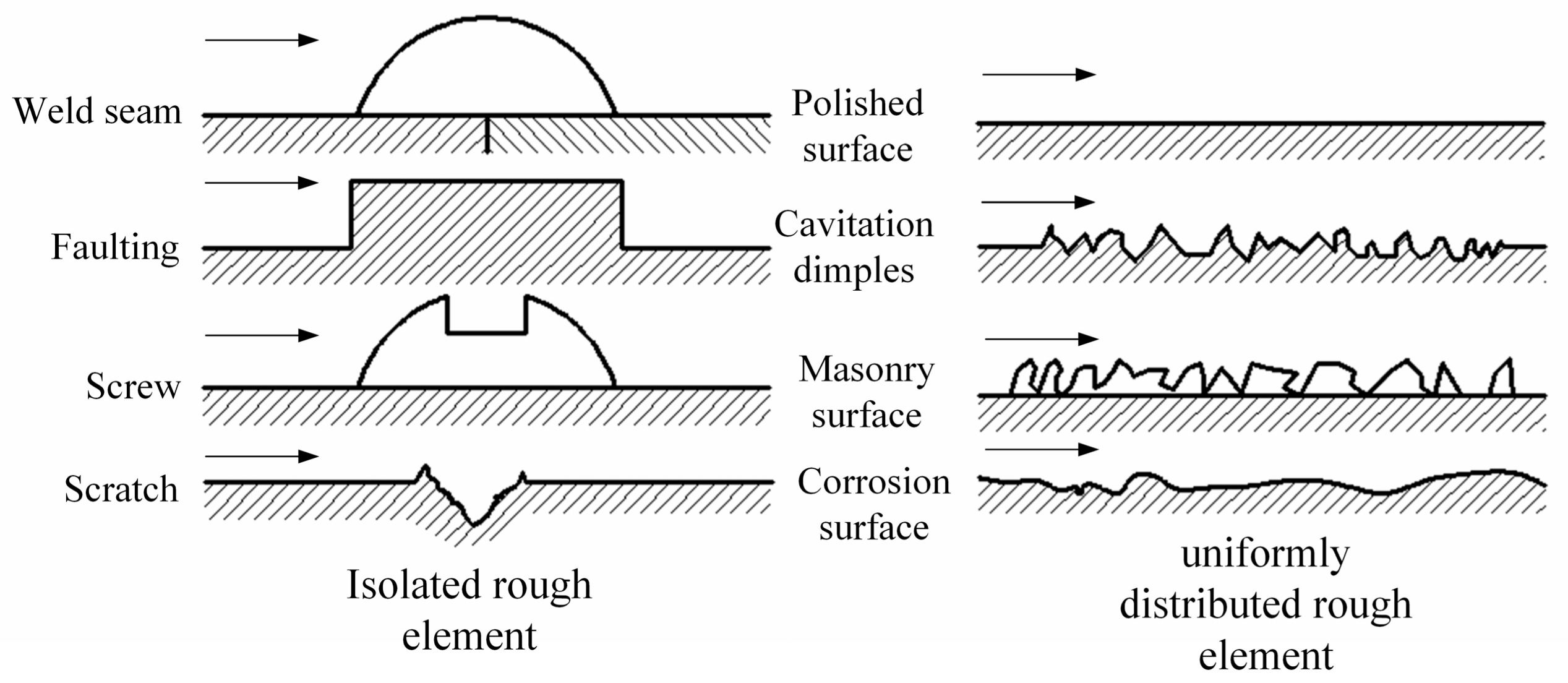
2.1.3. Effect of Surface Structure on Cavitation
2.1.4. Methods for Predicting Cavitation
2.2. Reynolds Equation and Its Dimensionlessification
2.2.1. Reynolds Equation
- (1)
- No relative slippage on the contact surface of fluid oil and friction disk;
- (2)
- The disks are always parallel to each other without bias grinding, the oil film thickness is always greater than 0, and there is no convex peak contact;
- (3)
- Flow field flow is laminar flow;
- (4)
- The effect of volume force and inertia terms are neglected and only the effect of centrifugal terms is considered;
- (5)
- The axial movement of oil is neglected.
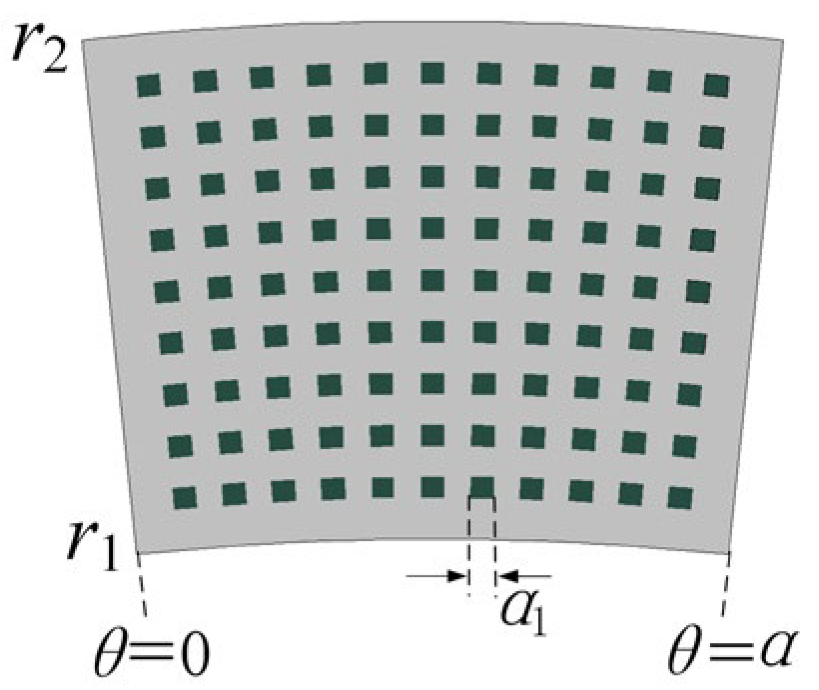
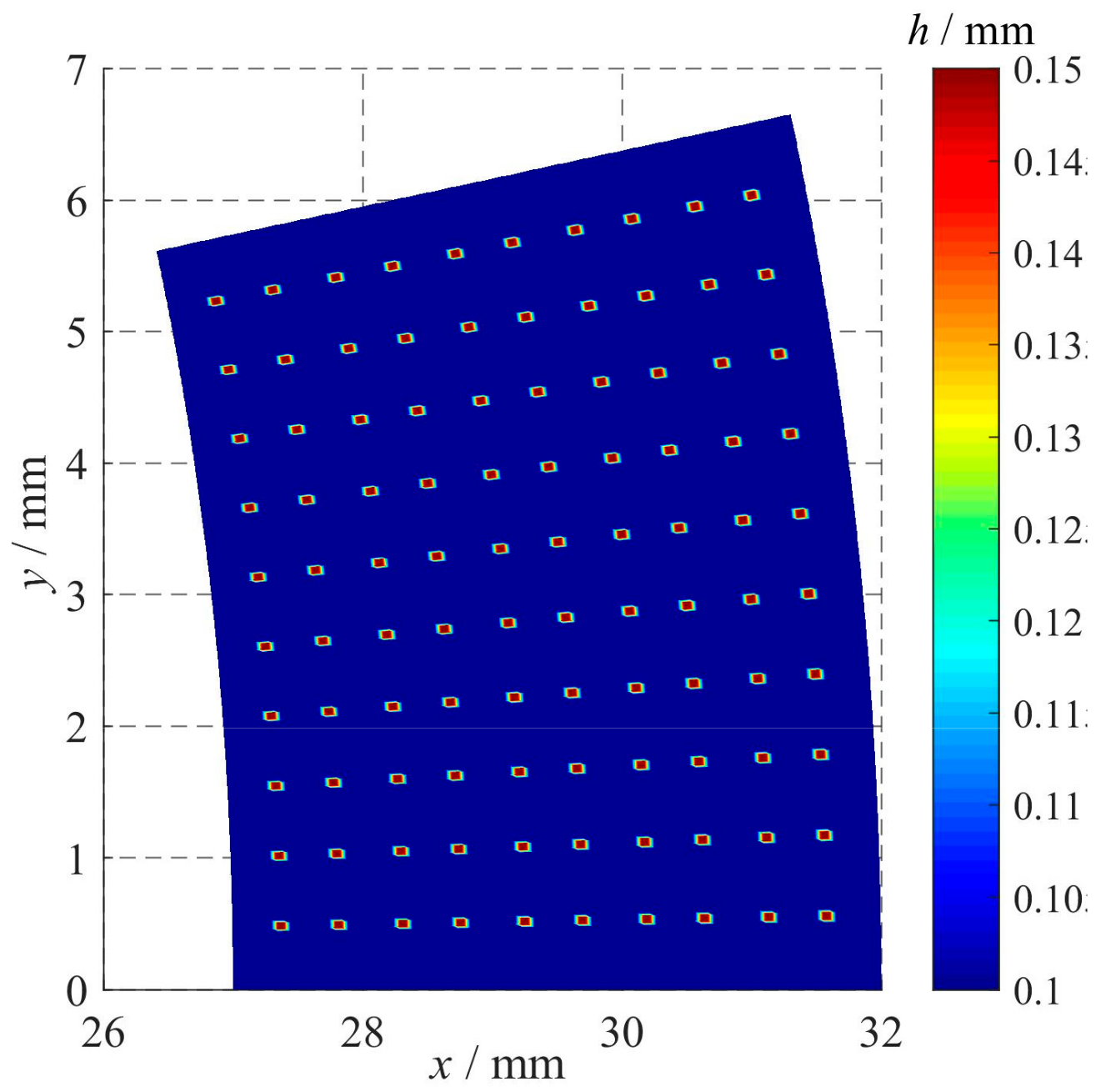
2.2.2. Texture Distribution and Oil Film Thickness
2.3. Reynolds Equation Dimensionlessification
2.4. Results of Numerical Analysis
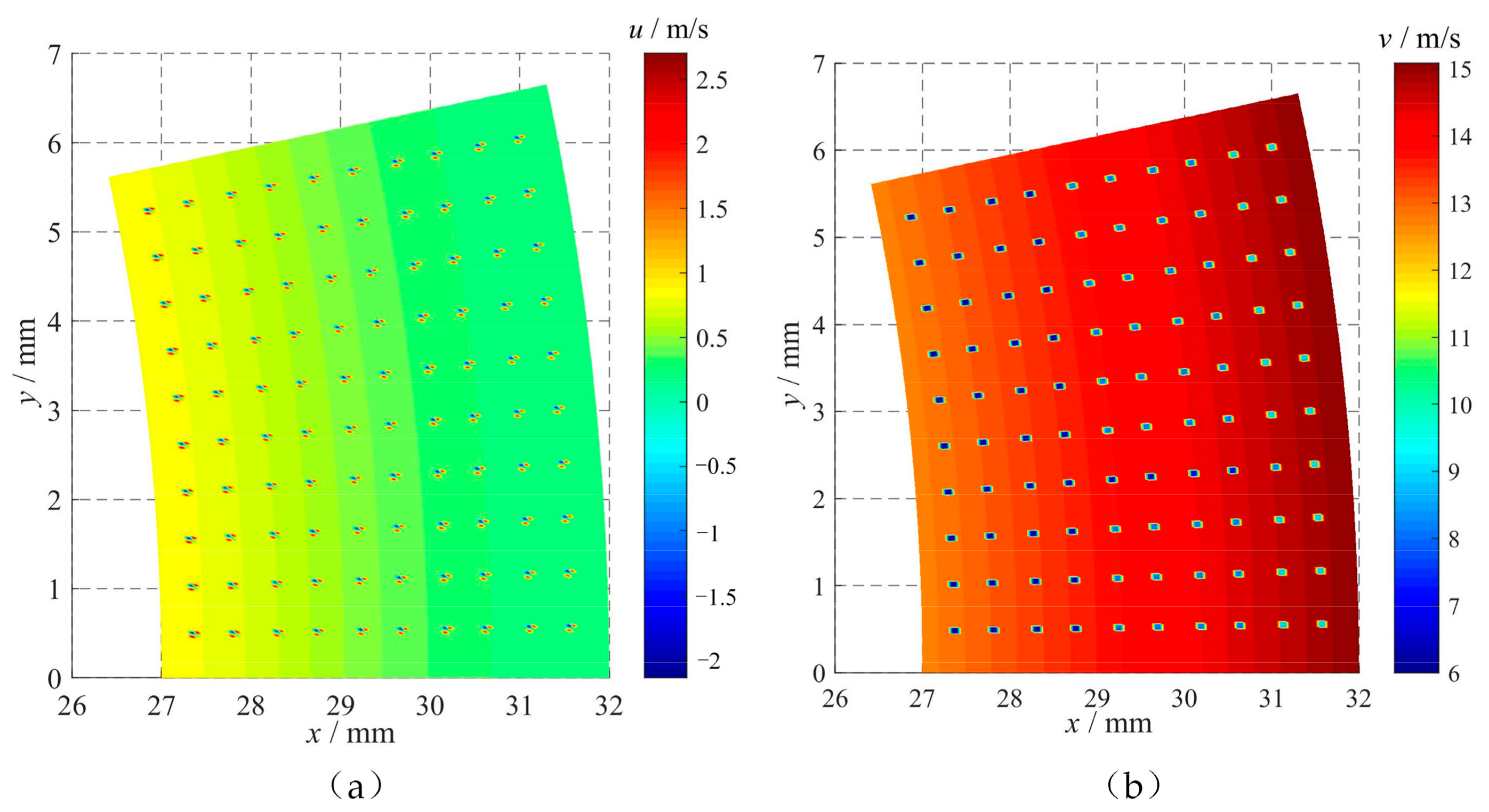
2.4.1. Effect of Cavitation on Oil Film Velocity
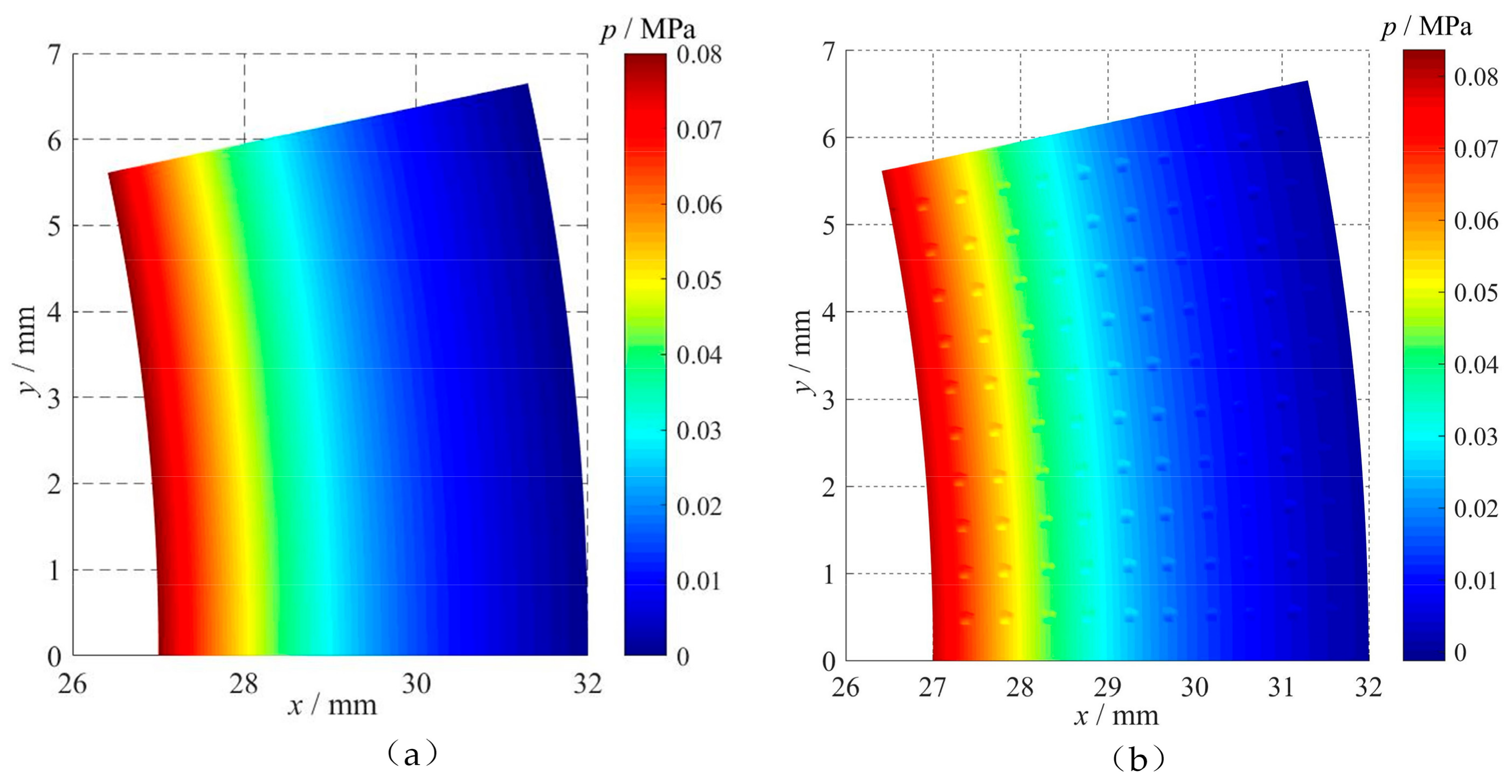
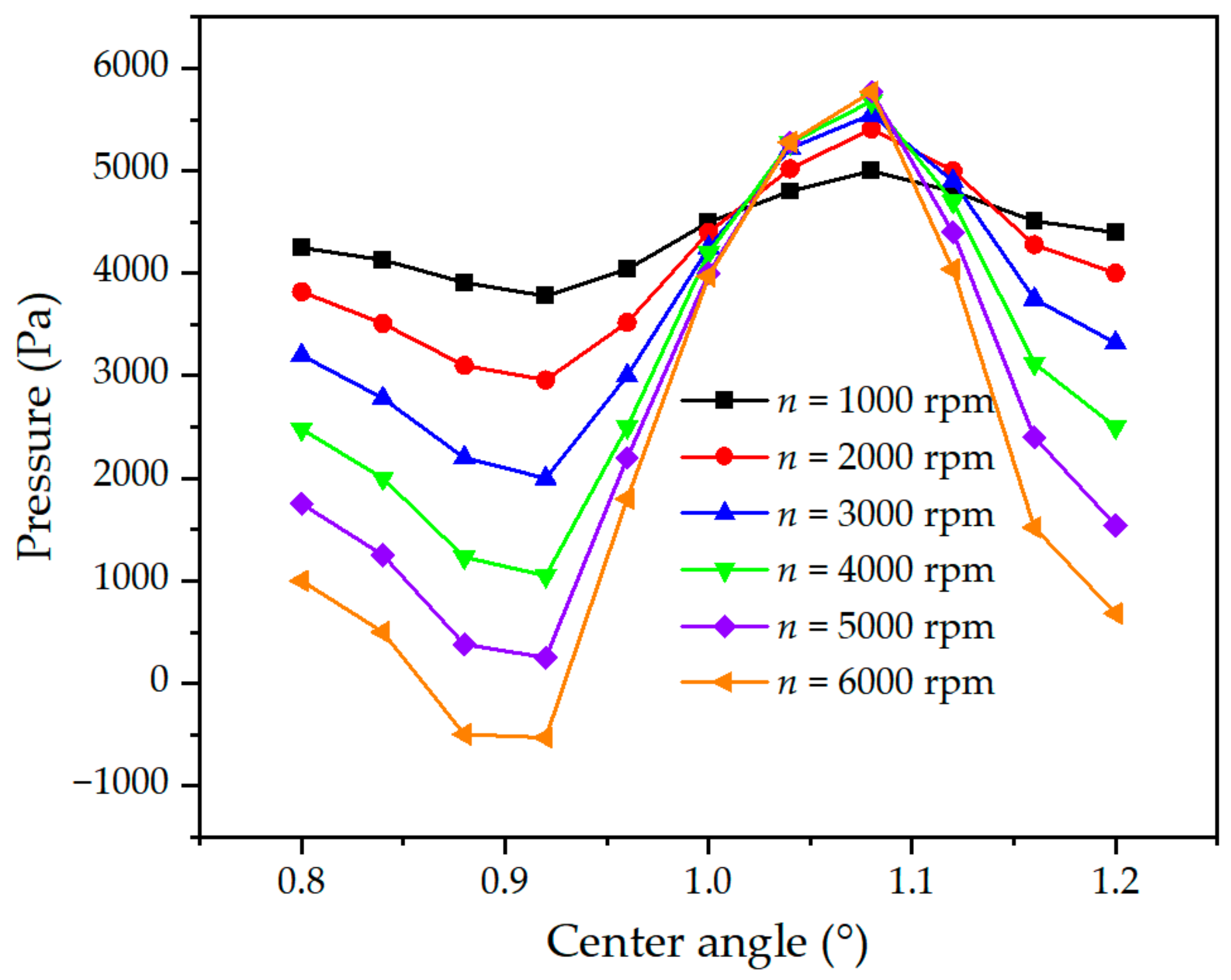
2.4.2. Effect of Cavitation on Oil Film Pressure
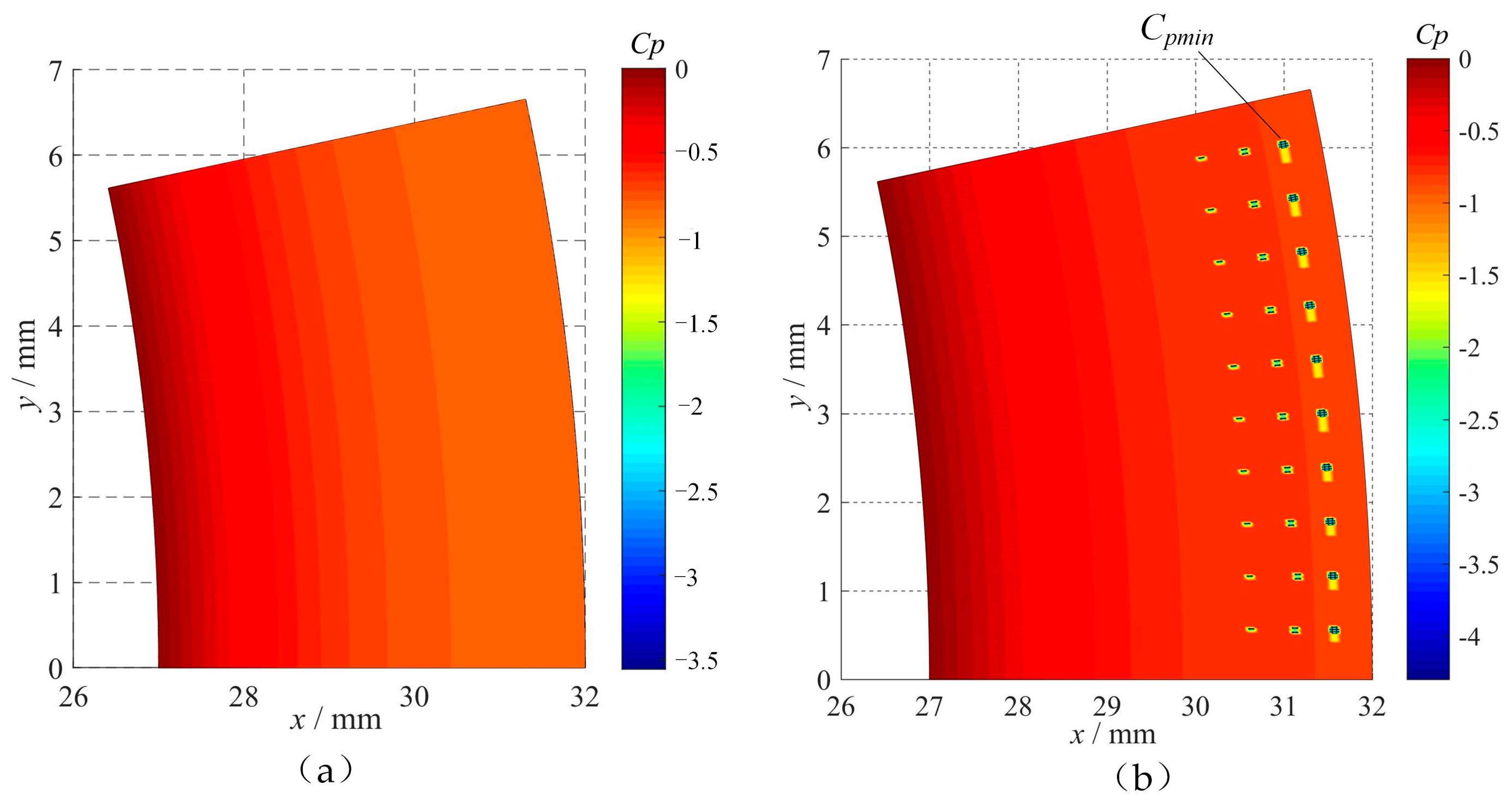
2.4.3. Effect of Cavitation on Pressure Coefficient
3. Simulation Analysis
3.1. CFX Model Analysis
3.1.1. Multiphase Models
3.1.2. Cavitation Models
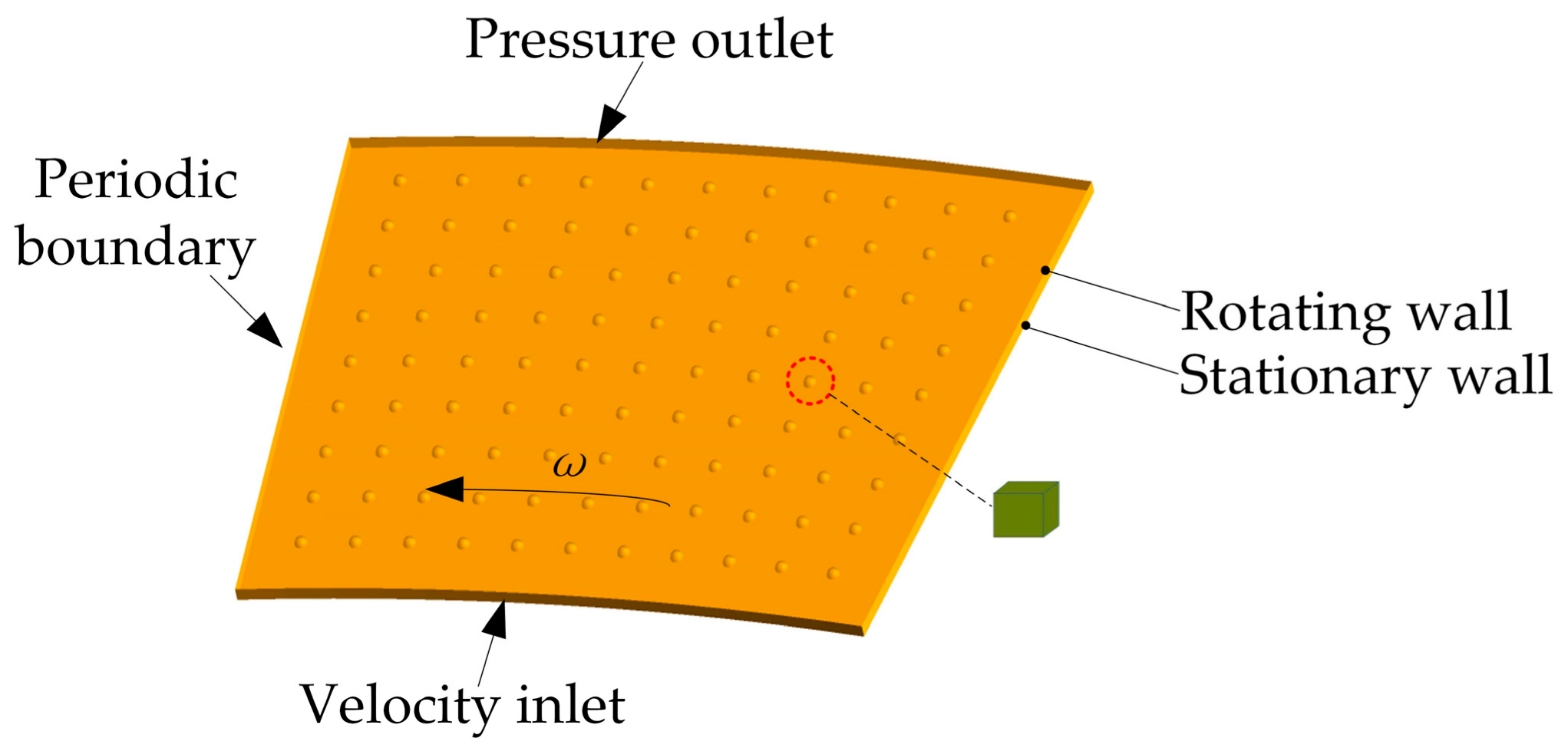
3.2. Mesh Model Analysis
3.3. Results of Simulation Analysis
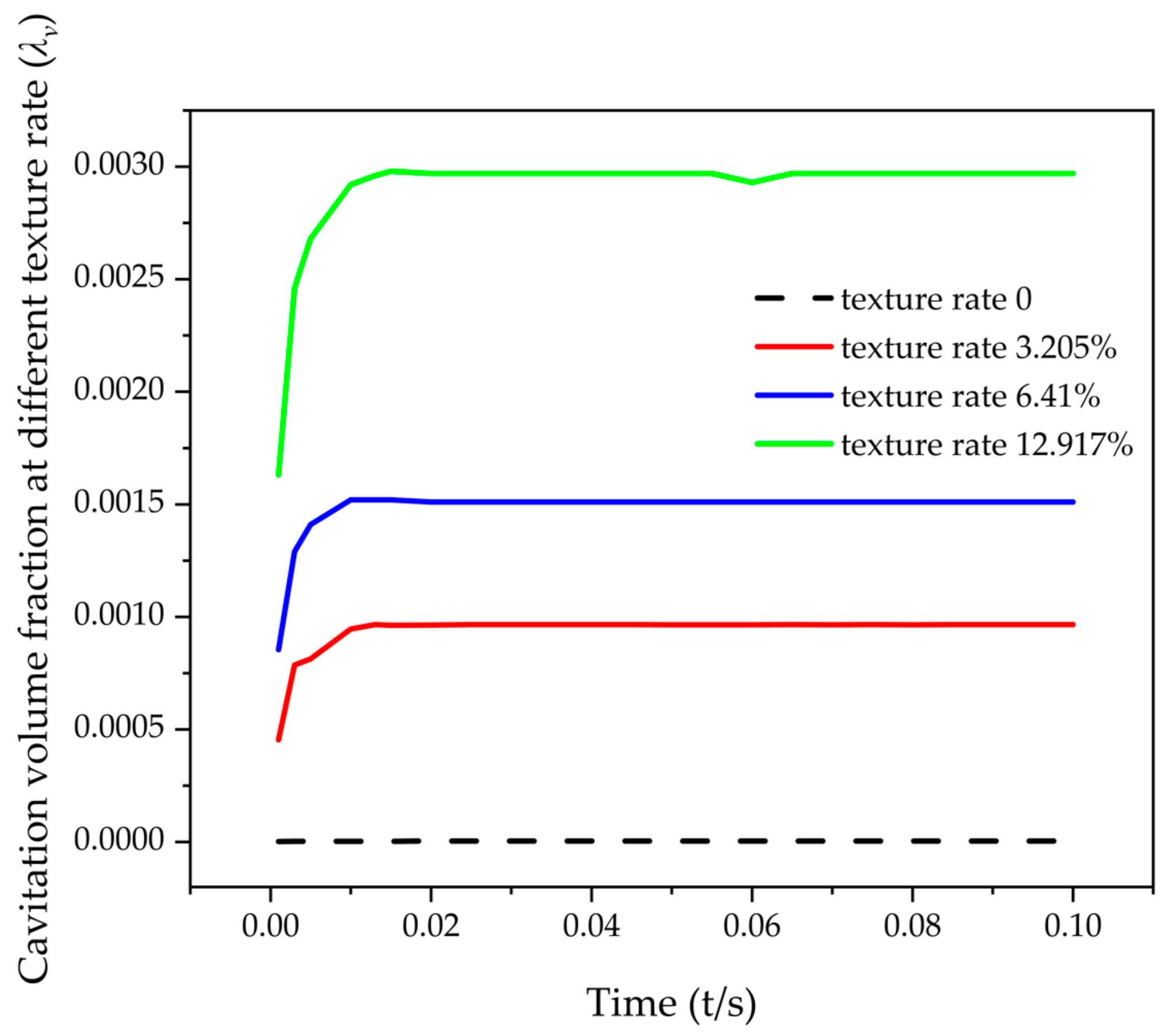
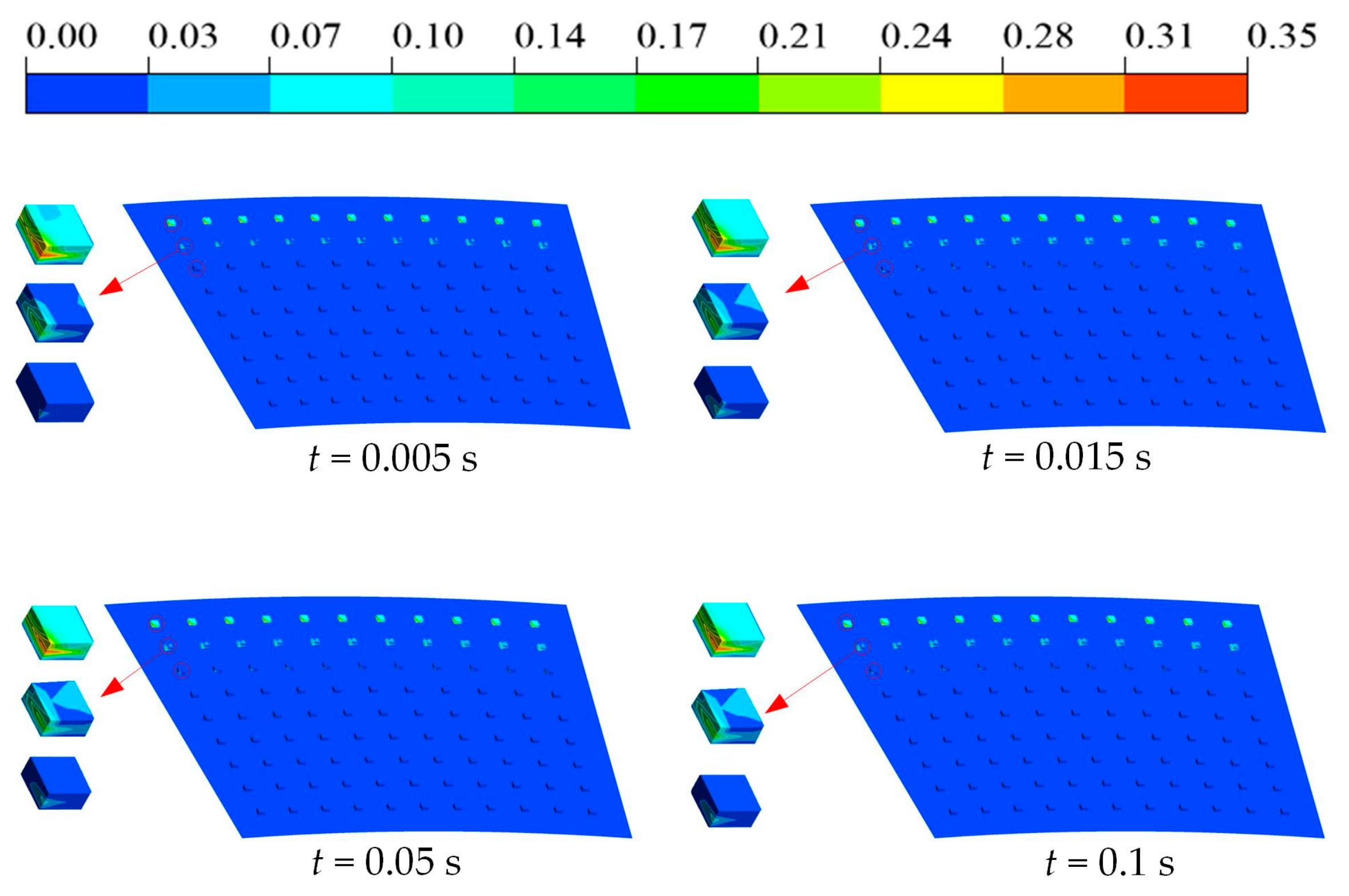
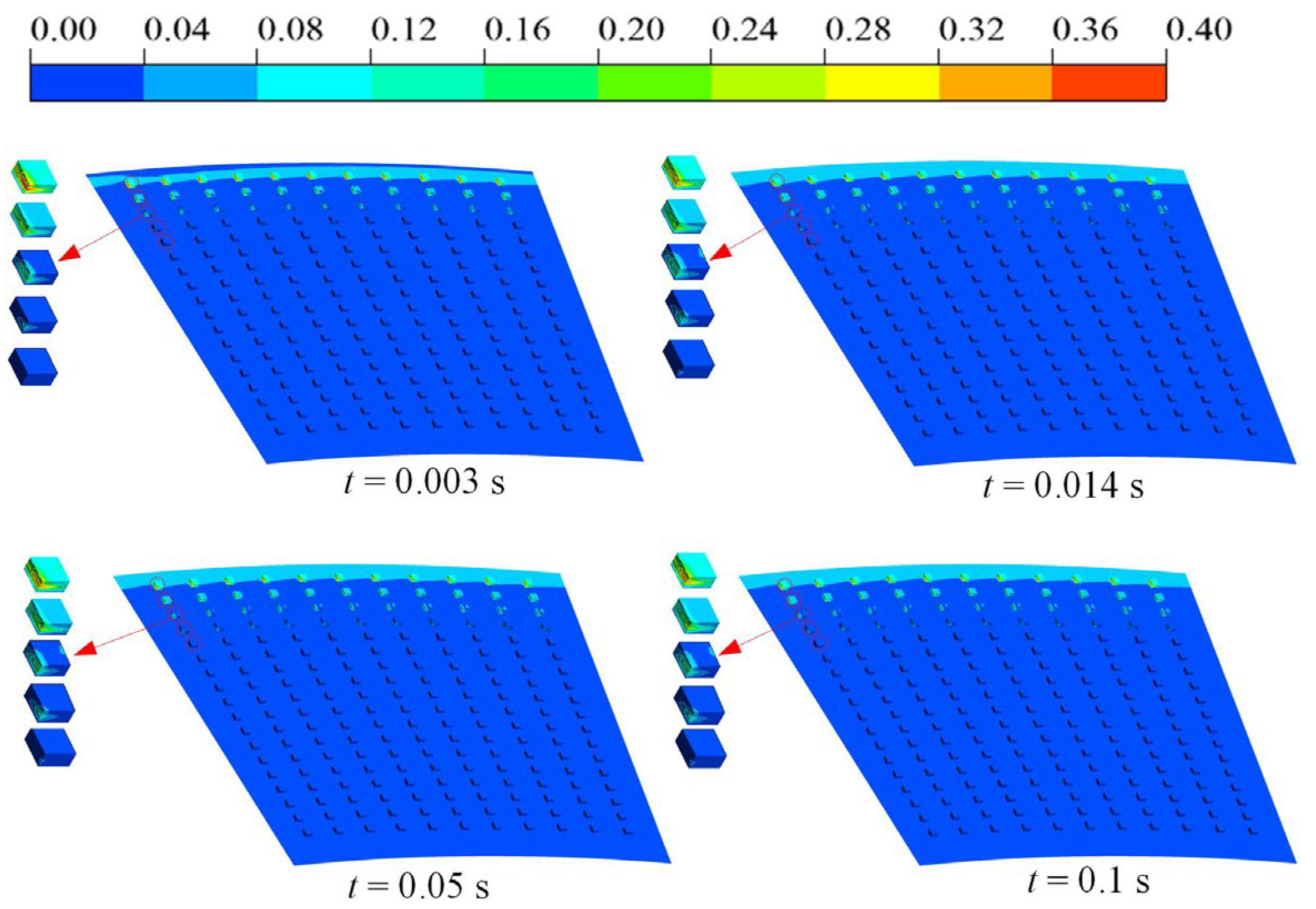
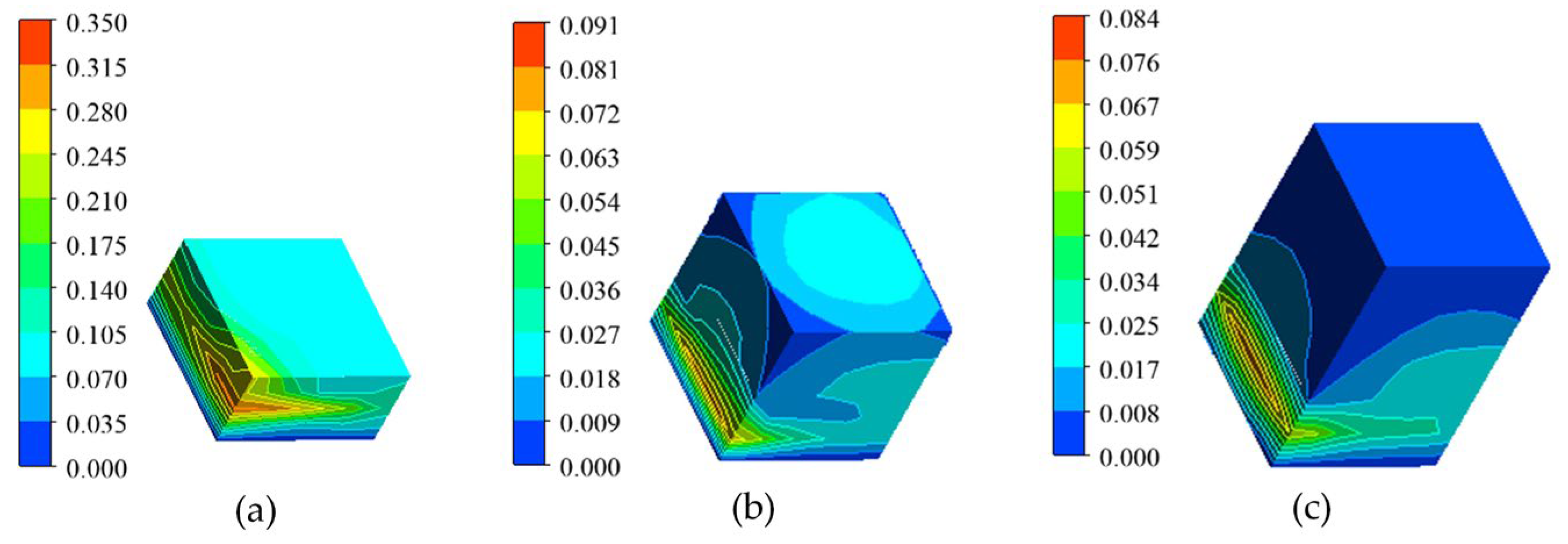
3.3.1. Effect of Texture Rate on Cavitation
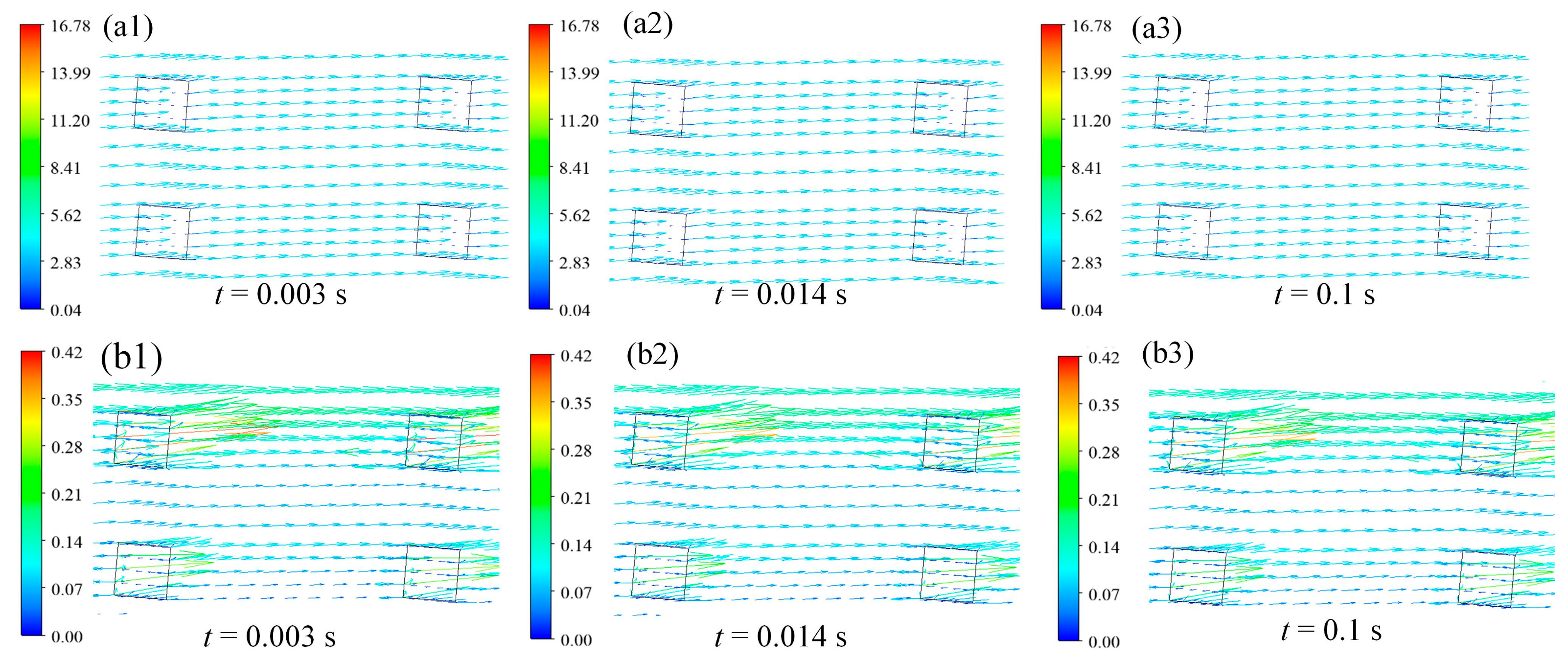
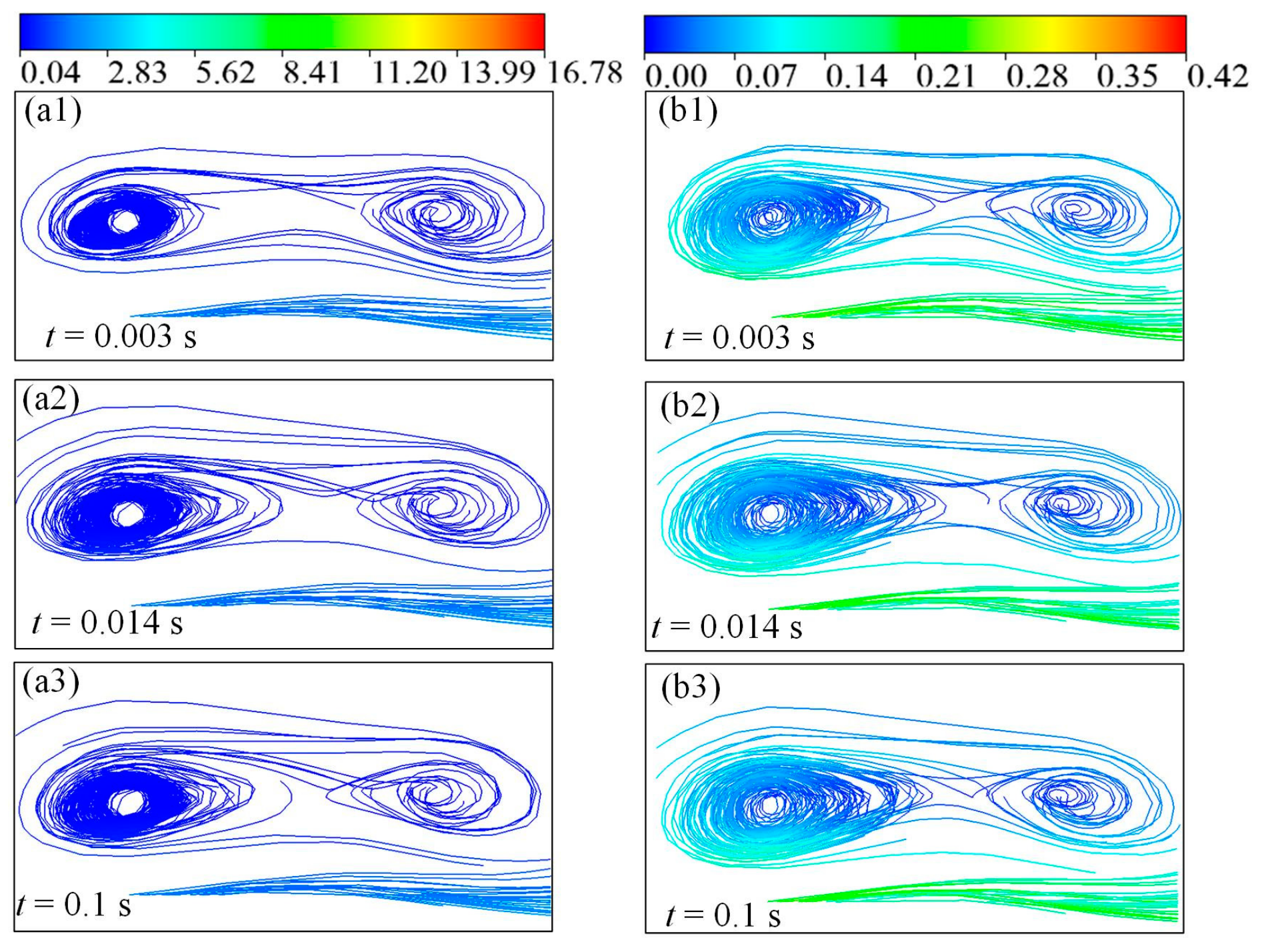
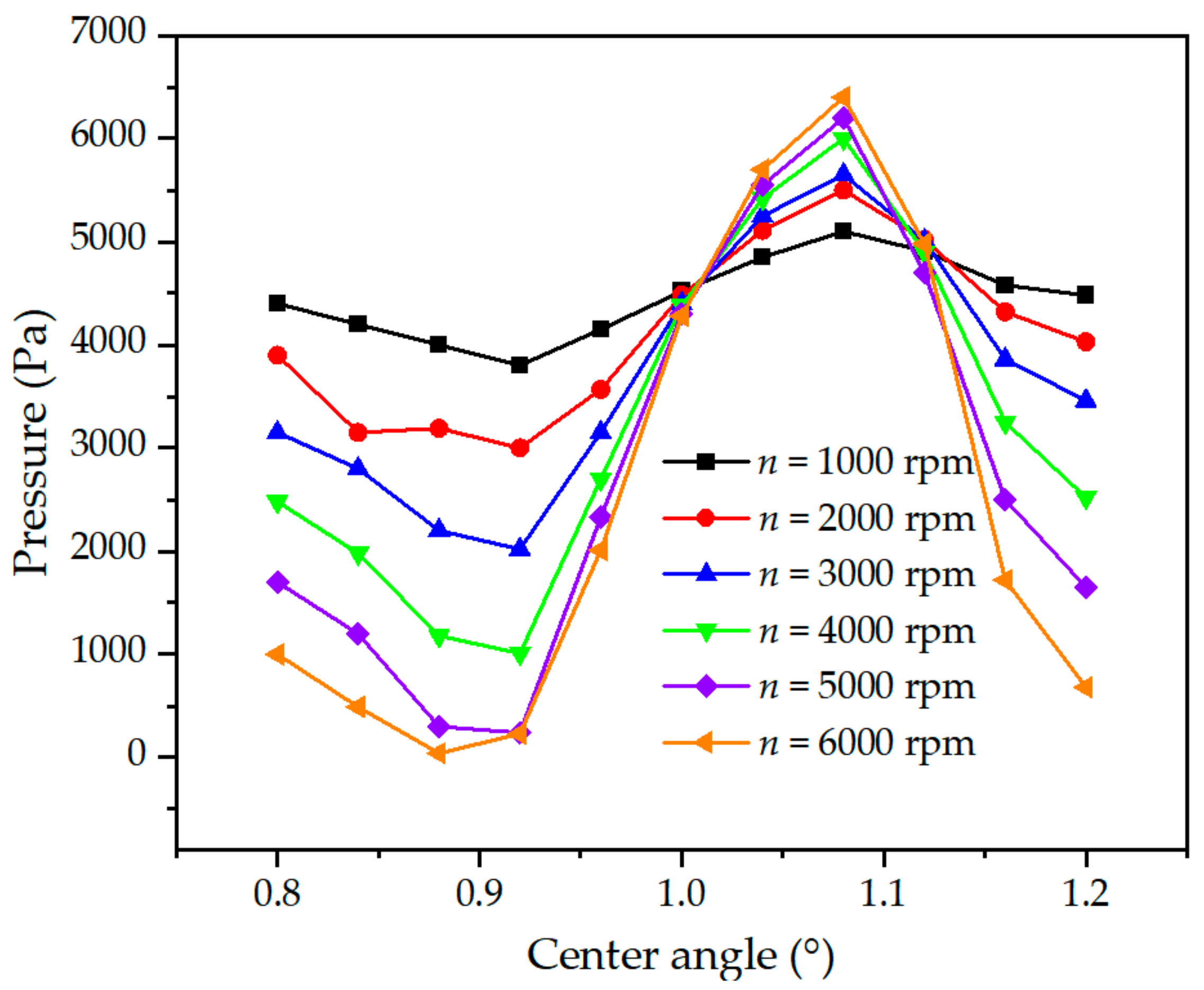
3.3.2. Effect of Cavitation on Velocity
3.3.3. Effect of Texture Depth on Cavitation
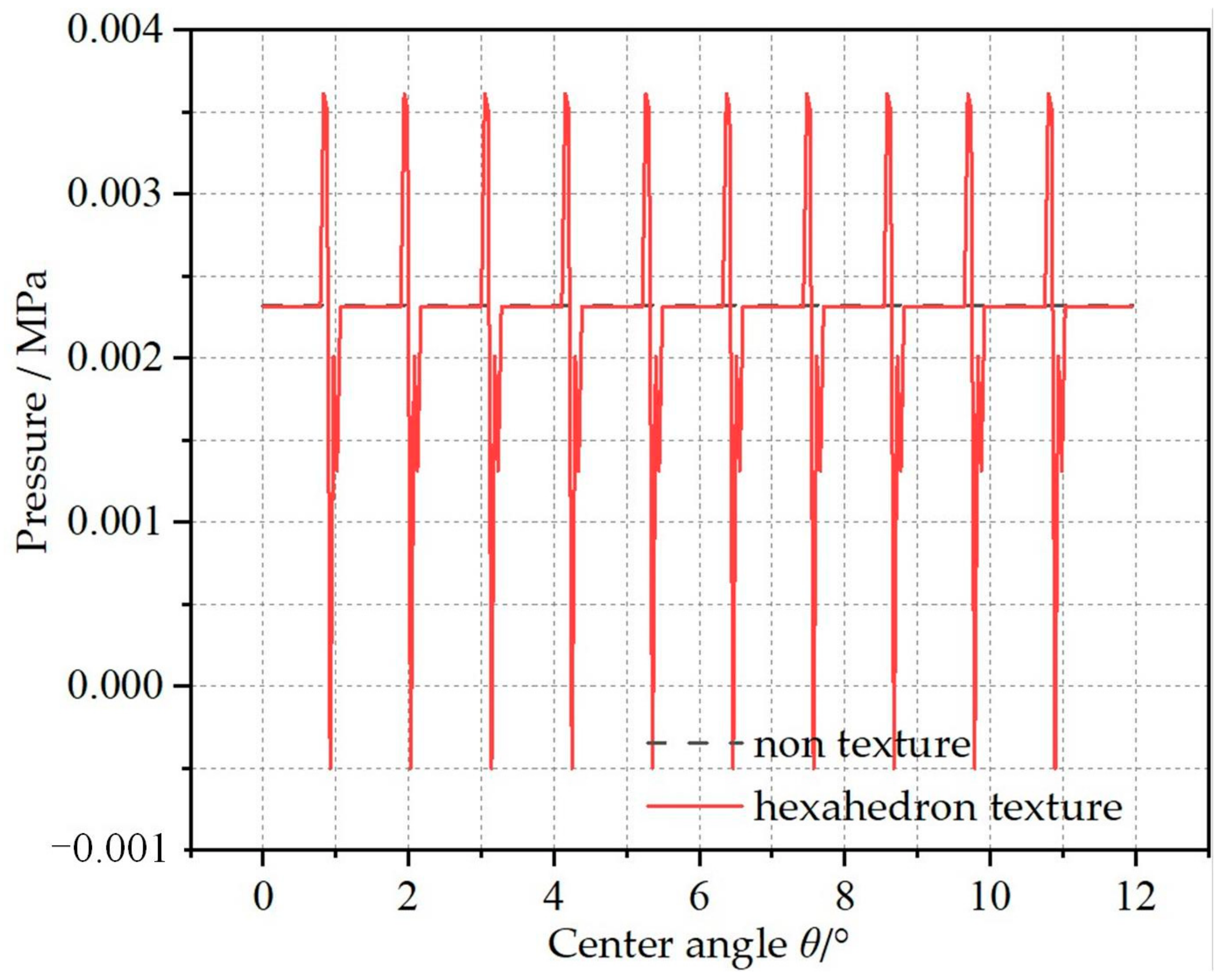
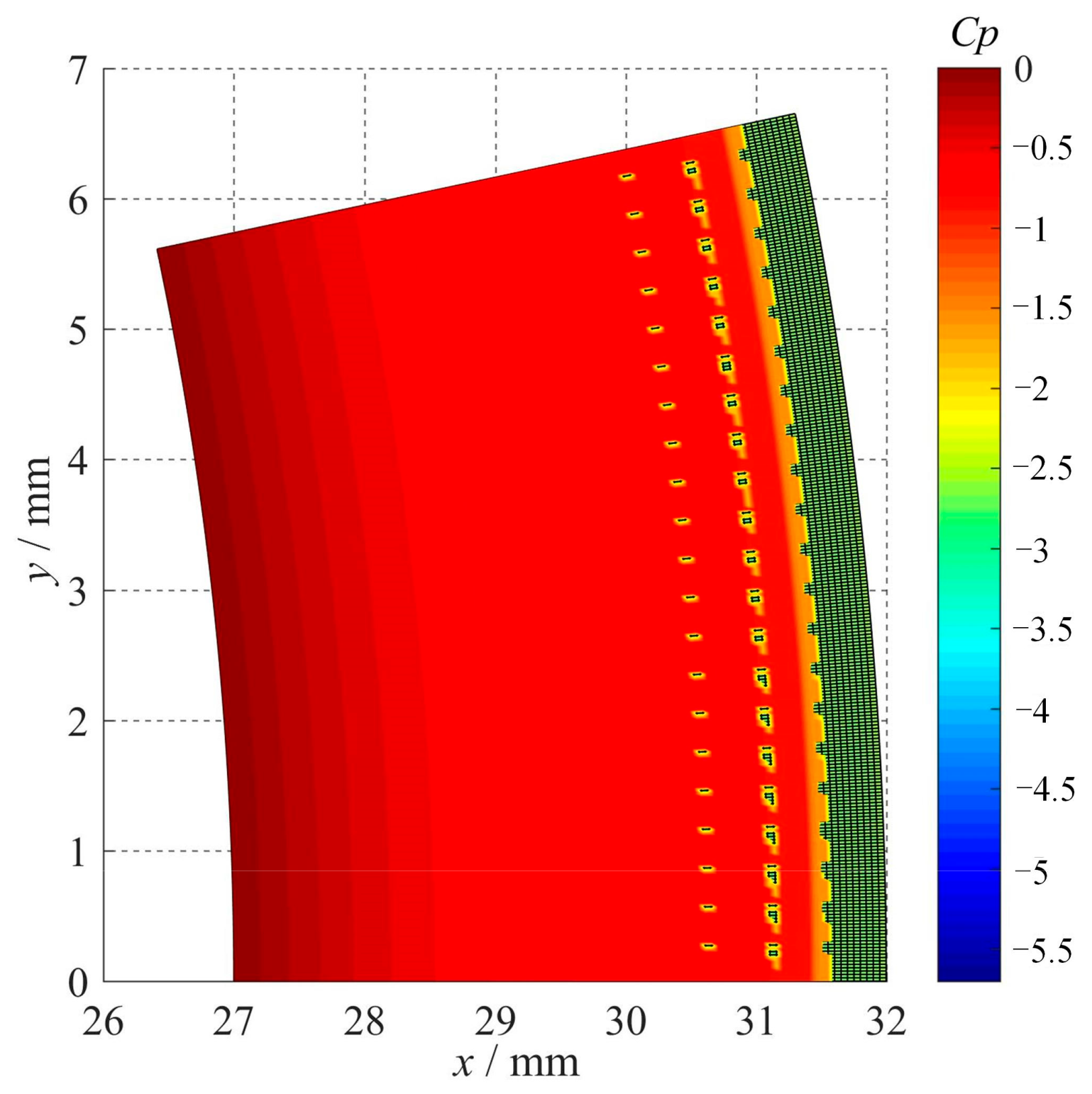
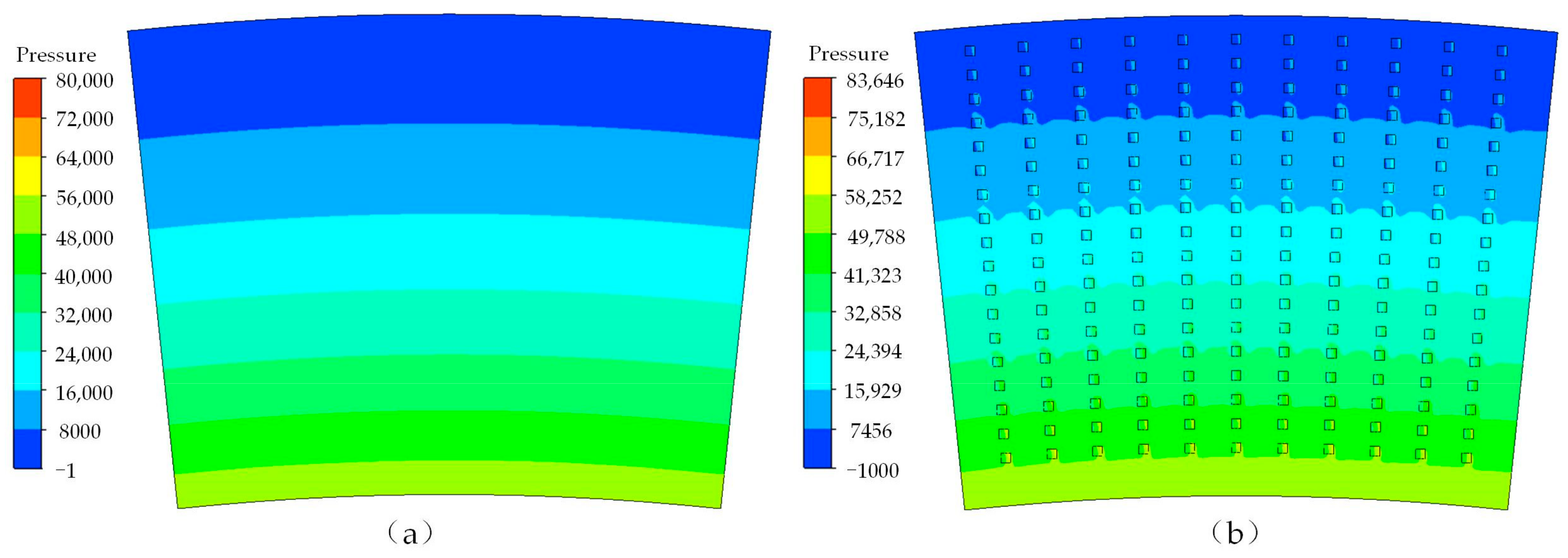
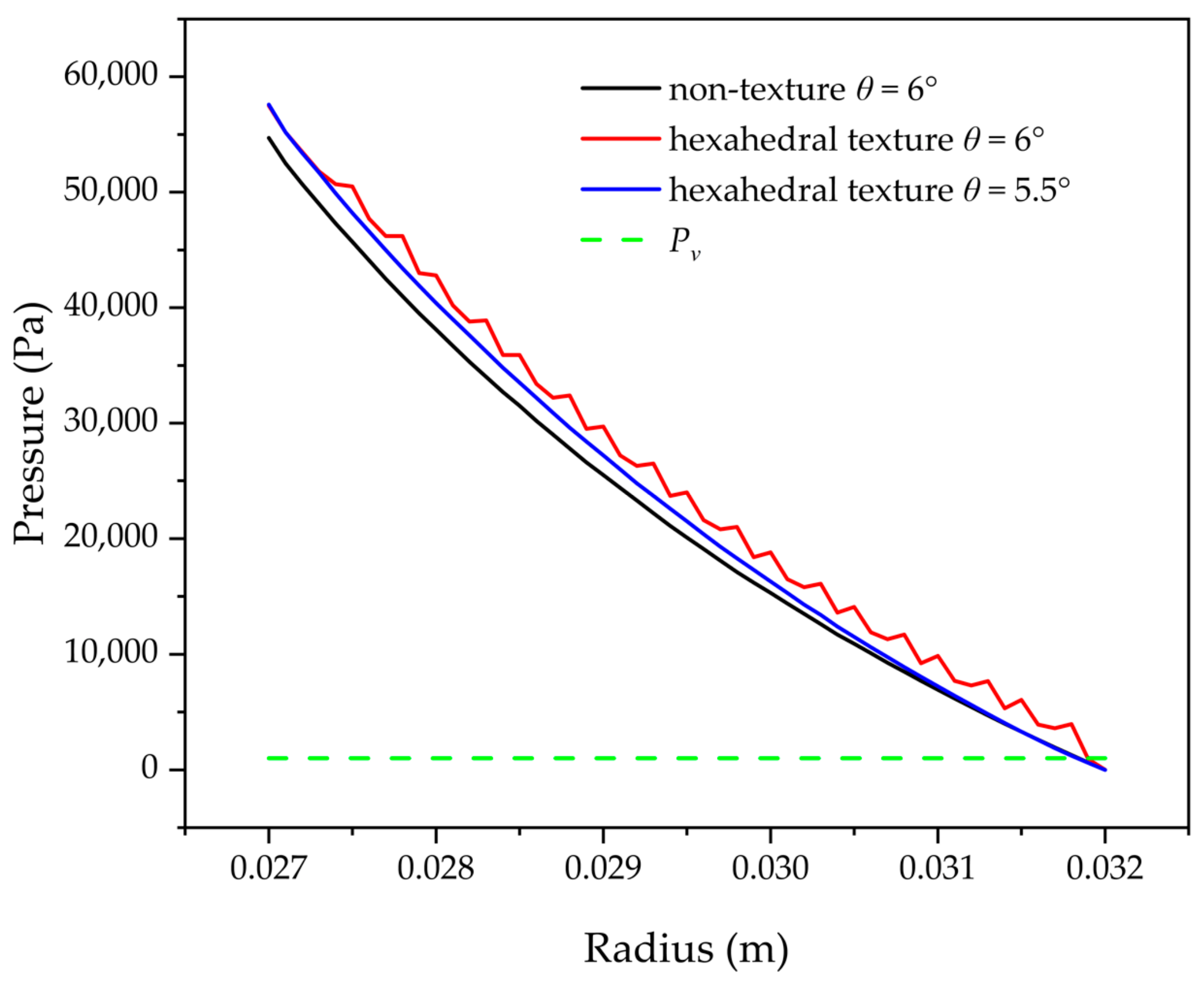
3.3.4. Pressure Analysis in Cavitation Area
4. Experimental Analysis
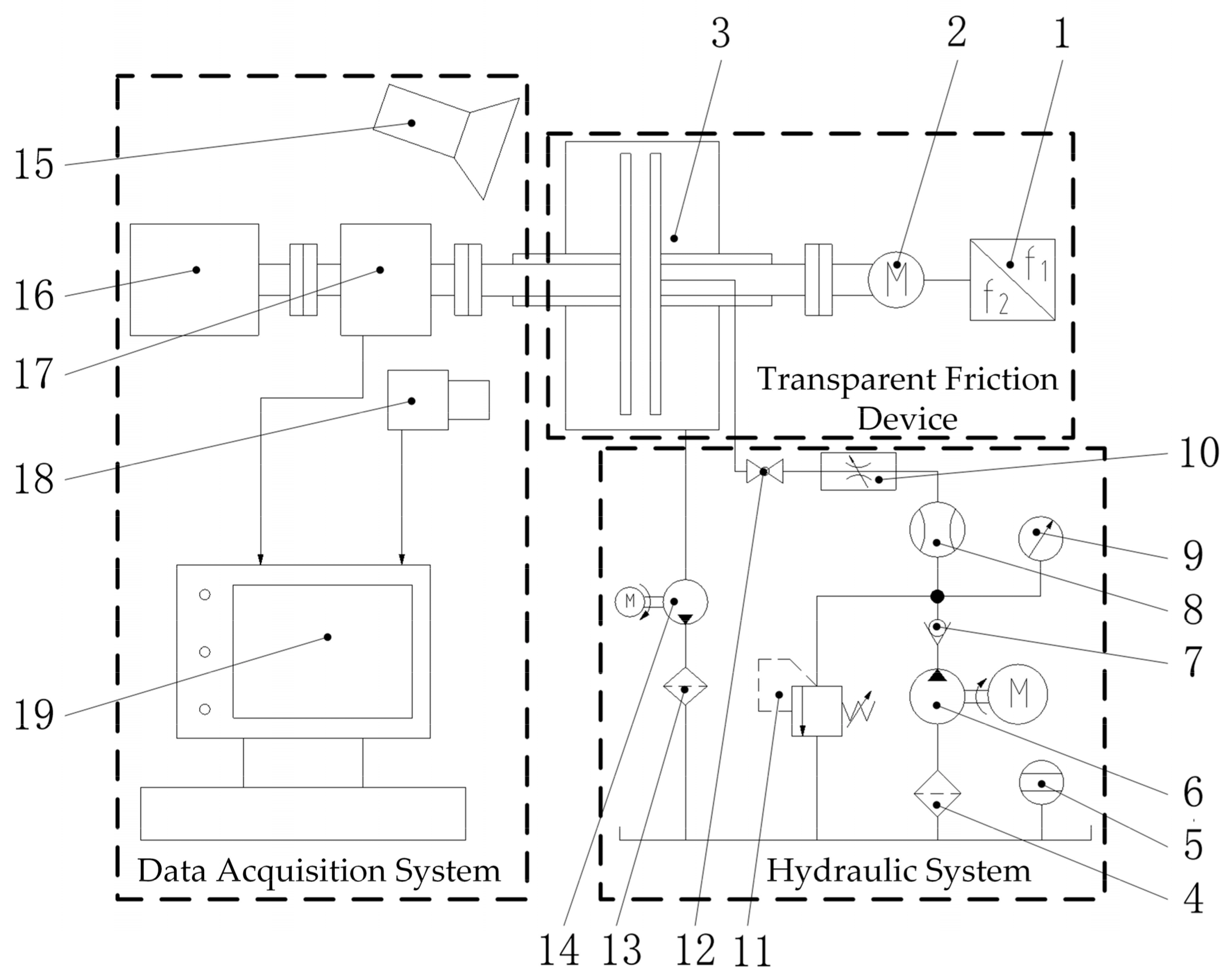
4.1. Experiment Design
4.2. Experiment Results
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karman, T.V. Uber laminare and turbulente reibung. J. Appl. Math. Comp. Mec. 1921, 1, 233–252. [Google Scholar]
- Cochron, W.G. The flow due to a rotating disc. Math. Proc. Camb. 1934, 30, 365–375. [Google Scholar] [CrossRef]
- Bodewadt, U.T. Die Drehstromung fiber festem Grunde. J. Appl. Math. Comp. Mec. 1940, 20, 241–253. [Google Scholar]
- Qian, P.; Pu, C.; Liu, L.; Li, X.; Zhang, B.; Gu, Z.; Meng, D. Development of a new high-precision friction test platform and experimental study of friction characteristics for pneumatic cylinders. Meas. Sci. Technol. 2022, 33, 065001. [Google Scholar] [CrossRef]
- Qian, P.; Pu, C.; Liu, L.; Lv, P.; Ruiz Páez, L.M. A novel pneumatic actuator based on high-frequency longitudinal vibration friction reduction. Sens. Actuat. A-Phys. 2022, 344, 113731. [Google Scholar] [CrossRef]
- Togawa, T.; Takuma, T.; Tanaka, Y. Hydro-disk-type of electrorheological brakes for small mobile robots. Int. J. Hydromechatron. 2021, 4, 99–115. [Google Scholar] [CrossRef]
- Klingl, S.; Lecheler, S.; Pfitzner, M. Absolute and convective stability of flow between closely spaced co-rotating disks with imposed throughflow. Eur. J. Mech. B-Fluid. 2022, 91, 226–232. [Google Scholar] [CrossRef]
- Vijay, N.; Sharma, K. Heat and mass transfer study of ferrofluid flow between co-rotating stretchable disks with geothermal viscosity: HAM analysis. Chin. J. Phys. 2022, 78, 83–95. [Google Scholar] [CrossRef]
- Lin, A.Q.; Liu, G.W.; Yu, X.X.; Chang, R.; Feng, Q. Comprehensive investigations on fluid flow and heat transfer characteristics of a high-speed rotating turbine disk cavity system of aero-engine. Int. Commun. Heat Mass 2022, 136, 106170. [Google Scholar] [CrossRef]
- Shen, C.; Khonsari, M. Effect of dimple’s internal structure on hydrodynamic lubrication. Tribol. Lett. 2013, 52, 415–430. [Google Scholar] [CrossRef]
- Bai, L.; Bai, S. Frictional performance of a textured surface with elliptical dimples: Geometric and distribution effects. Tribol. Trans. 2014, 57, 1122–1128. [Google Scholar] [CrossRef]
- Kant, K.; Pitchumani, R. Fractal textured glass surface for enhanced performance and self-cleaning characteristics of photovoltaic panels. Energ. Convers. Manag. 2022, 270, 116240. [Google Scholar] [CrossRef]
- Gropper, D.; Harvey, T.J.; Wang, L. Numerical analysis and optimization of surface textures for a tilting pad thrust bearing. Tribol. Int. 2018, 124, 134–144. [Google Scholar] [CrossRef]
- Qian, P.; Pu, C.; He, D. A method to improve the motion trajectory tracking accuracy of pneumatic servo system-by exciting longitudinal resonance. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 376. [Google Scholar] [CrossRef]
- Hamilton, D.; Walowit, J.; Allen, C. A theory of lubrication by microirregularities. J. Basic Eng. 1966, 88, 177–185. [Google Scholar] [CrossRef]
- Siripuram, R.B.; Stephens, L.S. Effect of Deterministic Asperity Geometry on Hydrodynamic Lubrication. J. Tribol. 2004, 126, 527–534. [Google Scholar] [CrossRef]
- Yu, H.; Huang, H.; Wang, X. The effect of dimple shapes on friction of parallel surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2011, 225, 693–703. [Google Scholar] [CrossRef]
- Yu, H.; Wang, X.; Fei, Z. Geometric Shape Effects of Surface Texture on the Generation of Hydrodynamic Pressure Between Conformal Contacting Surfaces. Tribol. Lett. 2010, 37, 123–130. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, H. Hydrodynamic lubrication of partial textured sliding journal bearing based on three-dimensional CFD. Ind. Lubr. Tribol. 2016, 68, 106–115. [Google Scholar] [CrossRef]
- Han, J.; Fang, L.; Sun, J. Hydrodynamic Lubrication of Microdimple Textured Surface Using Three-Dimensional CFD. Tribol. Trans. 2010, 53, 860–870. [Google Scholar] [CrossRef]
- Etsion, I.; Burstein, L. A Model for Mechanical Seals with Regular Microsurface Structure. Tribol. Trans. 1996, 39, 677–683. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Fillon, M.; Maspeyrot, P. Effect of textured area on the performances of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 211–219. [Google Scholar] [CrossRef]
- Arif, M.; Kango, S.; Shukla, D.K. Analysis of textured journal bearing with slip boundary condition and pseudoplastic lubricants. Int. J. Mech. Sci. 2022, 228, 107458. [Google Scholar] [CrossRef]
- Arndt, R.E.A.; Holl, J.W.; Bohn, J.C. Influence of surface irregularities on cavitation performance. J. Ship Res. 1979, 23, 157–170. [Google Scholar] [CrossRef]
- Braun, M.J.; Hannon, W.M. Cavitation formation and modelling for fluid film bearings: A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 839–863. [Google Scholar] [CrossRef]
- Shahjada, P.; Faria, M.S.; Masamitsu, K. New development of a gas cavitation model for valuation of drag torque characteristics in disengaged wet clutches. SAE Int. J. Engines 2016, 9, 2016–01-1137. [Google Scholar]
- Shahjada, P.; Faria, M.S.; Masamitsu, K. Multiphase drag modeling for prediction of the drag torque characteristics in disengaged wet clutches. SAE Int. J. Commer. Veh. 2016, 9, 2016–01-1137. [Google Scholar]
- Bulut, D.; Bader, N.; Poll, G. Cavitation and film formation in hydrodynamically lubricated parallel sliders. Tribol. Int. 2021, 162, 107113. [Google Scholar] [CrossRef]
- Ma, D.; Harvey, T.J.; Zhuk, Y.N.; Wellman, R.G.; Wood, R.J.K. Cavitation erosion performance of CVD W/WC coatings. Wear 2020, 452, 203276. [Google Scholar] [CrossRef]
- Jahangir, A.; Ghahramani, B.; Neuhauser, M.; Bourgeois, S.; Bensow, R.E.; Poelma, C. Experimental investigation of cavitation-induced erosion around a surface-mounted bluff body. Wear 2021, 480, 203917. [Google Scholar] [CrossRef]
- Nagalingam, A.P.; Yuvaraj, H.K.; Yeo, S.H. Synergistic effects in hydrodynamic cavitation abrasive finishing for internal surface-finish enhancement of additive-manufactured components. Addit. Manuf. 2020, 33, 101110. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Phan, T.H.; Duy, T.N.; Park, W.G. Unsteady cavitation around submerged and water-exit projectiles under the effect of the free surface: A numerical study. Ocean Eng. 2022, 263, 112368. [Google Scholar] [CrossRef]
- Kadivar, E.; Moctar, O.E.; Skoda, R.; Löschner, U. Experimental study of the control of cavitation-induced erosion created by collapse of single bubbles using a micro structured riblet. Wear 2021, 486, 204087. [Google Scholar] [CrossRef]
- Nowakowska, M.; Łatka, L.; Sokołowski, P.; Szala, M.; Toma, F.L.; Walczak, M. Investigation into microstructure and mechanical properties effects on sliding wear and cavitation erosion of Al2O3-TiO2 coatings sprayed by APS, SPS and S-HVOF. Wear 2022, 508, 204462. [Google Scholar] [CrossRef]
- Pan, S.S.; Peng, X.X. Physical Mechanism of Cavitation; National Defense Industry Press: Beijing, China, 2013; pp. 23–24. ISBN 978-7-118-09513-5. [Google Scholar]
- Ingber, M.S.; Hailey, C.E. Numerical modeling of cavities on axisymmetric bodies at zero and non-zero angle of attack. Int. J. Numer. Methods Fluids 1992, 15, 25–271. [Google Scholar] [CrossRef]
- Pan, S.; Xu, W.; Peng, X.; Xu, J. On the theoretical prediction of cavitation inception. J. Hydrodyn 1992, 1, 74–82. [Google Scholar]
- Watanabe, T.; Oyama, T. Magnetohydrodynamic boundary layer flow over a rotating disk. Z. Angew. Math. Und Mech. 1991, 71, 522–524. [Google Scholar] [CrossRef]
- Meng, Q.R.; Hou, Y.F.; Wang, Y. Finite element analysis of oil film pressure field of liquid viscous drive based on Matlab. Min. Mach. 2007, 9, 121–124. [Google Scholar]
- Liu, S.; Higuchi, J.; Ikohagi, T. Experimental Study of Cavity Flow Behavior on a 2-D Hydrofoil. Bull. JSME 1999, 42, 641–648. [Google Scholar]
- Sun, J.; Chen, L.; Qian, P.; Zhang, B. Oil Cavitation Morphology Analysis of Textured Cylindrical Rotating Friction Pair on Circular-Disk End Faces. Machines 2022, 10, 1036. [Google Scholar] [CrossRef]
- Razzaque, M.M.; Kato, T. Effects of Groove Orientation on Hydrodynamic Behavior of Wet Clutch Coolant Films. J. Tribol. 1999, 121, 56–61. [Google Scholar] [CrossRef]
- Sun, J.; Chen, L.; Zhang, B.; Huang, H.; Qian, P. Cavitation Morphology Study between Hemispherical Textured Rotating Friction Pairs. Lubricants 2022, 10, 249. [Google Scholar] [CrossRef]











| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Inner radius r1 (mm) | 27 | Oil film thickness h0 (mm) | 0.1 |
| Outer radius r2 (mm) | 32 | Texture depth ht (mm) | 0.05 |
| Number of textures N1 | N × M | Inlet pressure p0 (MPa) | 0.08 |
| Radial number N | 10 | Rotational speed ω (rpm) | 6000 |
| Circumferential number M | 10 | Oil viscosity at 30 °C μ (Pa·s) | 0.05 |
| Oil density ρ (kg/m3) | 865 | Oil saturated vapor pressure pv (Pa) | 1000 |
| Parameters | Values |
|---|---|
| Inner radius r1 (mm) | 27 |
| Outer radius r2 (mm) | 32 |
| Center angle θ (°) | 12 |
| Default thickness h0 (mm) | 0.1 |
| Default depth of texture ht (mm) | 0.0564 |
| Scheme | Radial Layer | Circumferential Layer | Axial Layer | Number of Grid Cells | Cavitation Volume Fraction | |
|---|---|---|---|---|---|---|
| Texture Area | Non-Texture Area | |||||
| 1 | 68 | 20 | 100 | 14 | 48,106 | 0.0004345 |
| 2 | 68 | 20 | 100 | 28 | 105,324 | 0.0003432 |
| 3 | 68 | 20 | 100 | 56 | 219,760 | Divergence |
| 4 | 68 | 30 | 120 | 28 | 137,484 | 0.0005012 |
| 5 | 68 | 40 | 160 | 28 | 184,384 | 0.0006212 |
| 6 | 102 | 30 | 120 | 28 | 207,252 | 0.0006417 |
| 7 | 136 | 30 | 120 | 28 | 277,020 | 0.0006419 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Output power | 70% | Laser wavelength | 1064 ± 5 nm |
| Laser processing speed | 500 mm/s | Processing speed | 1000 mm/s |
| Spot diameter | 0.05 mm | Repetition accuracy | ±0.003 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Chen, L.; Huang, H.; Zhang, B.; Qian, P. Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System. Appl. Sci. 2022, 12, 12303. https://doi.org/10.3390/app122312303
Sun J, Chen L, Huang H, Zhang B, Qian P. Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System. Applied Sciences. 2022; 12(23):12303. https://doi.org/10.3390/app122312303
Chicago/Turabian StyleSun, Junyu, Liyu Chen, Hua Huang, Bing Zhang, and Pengfei Qian. 2022. "Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System" Applied Sciences 12, no. 23: 12303. https://doi.org/10.3390/app122312303
APA StyleSun, J., Chen, L., Huang, H., Zhang, B., & Qian, P. (2022). Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System. Applied Sciences, 12(23), 12303. https://doi.org/10.3390/app122312303