Multi-UAV Cooperative Path Planning with Monitoring Privacy Preservation
Abstract
1. Introduction
- Considering monitoring frequency and path privacy, this study shows how to formulate a multi-UAV cooperative persistent monitoring path planning problem with multiple constraints based on the monitoring of overdue time and of monitoring period entropy.
- A multi-group ant colony optimization algorithm, called overdue-aware multiple ant colony optimization (OMACO), is proposed to obtain an optimal flight path for UAV cooperation. The heuristic function and pheromone update method are improved based on the monitoring delay time and overdue time. In addition, a target exclusive mechanism and greedy strategy are proposed for ant node selection.
- Simulation experiments are carried out in complete and incomplete environments to verify the effectiveness and advantages of the designed algorithm. The simulation results show that the algorithm proposed in this paper can effectively improve both the monitoring frequency and the monitoring privacy protection.
2. Multi-UAV Cooperative Persistent Monitoring Path Planning Model
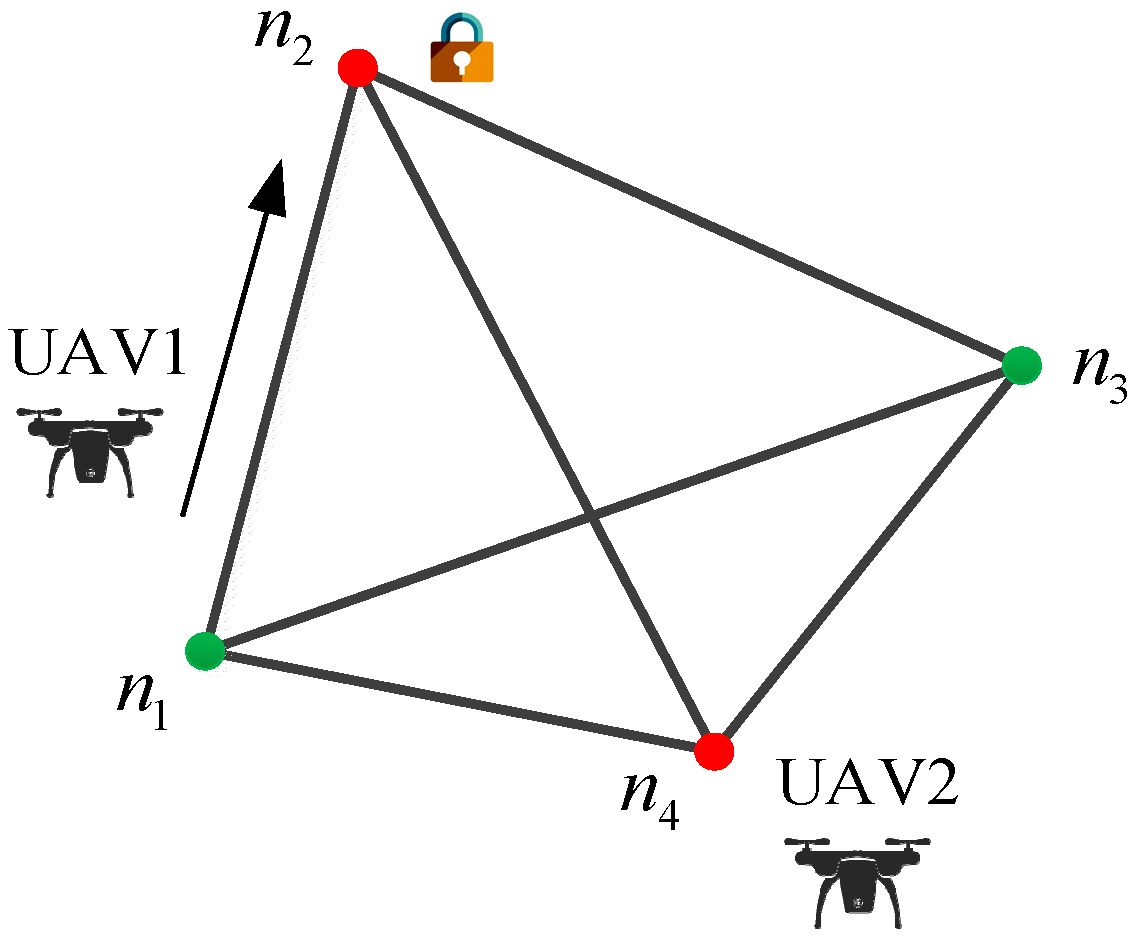
2.1. Problem Description
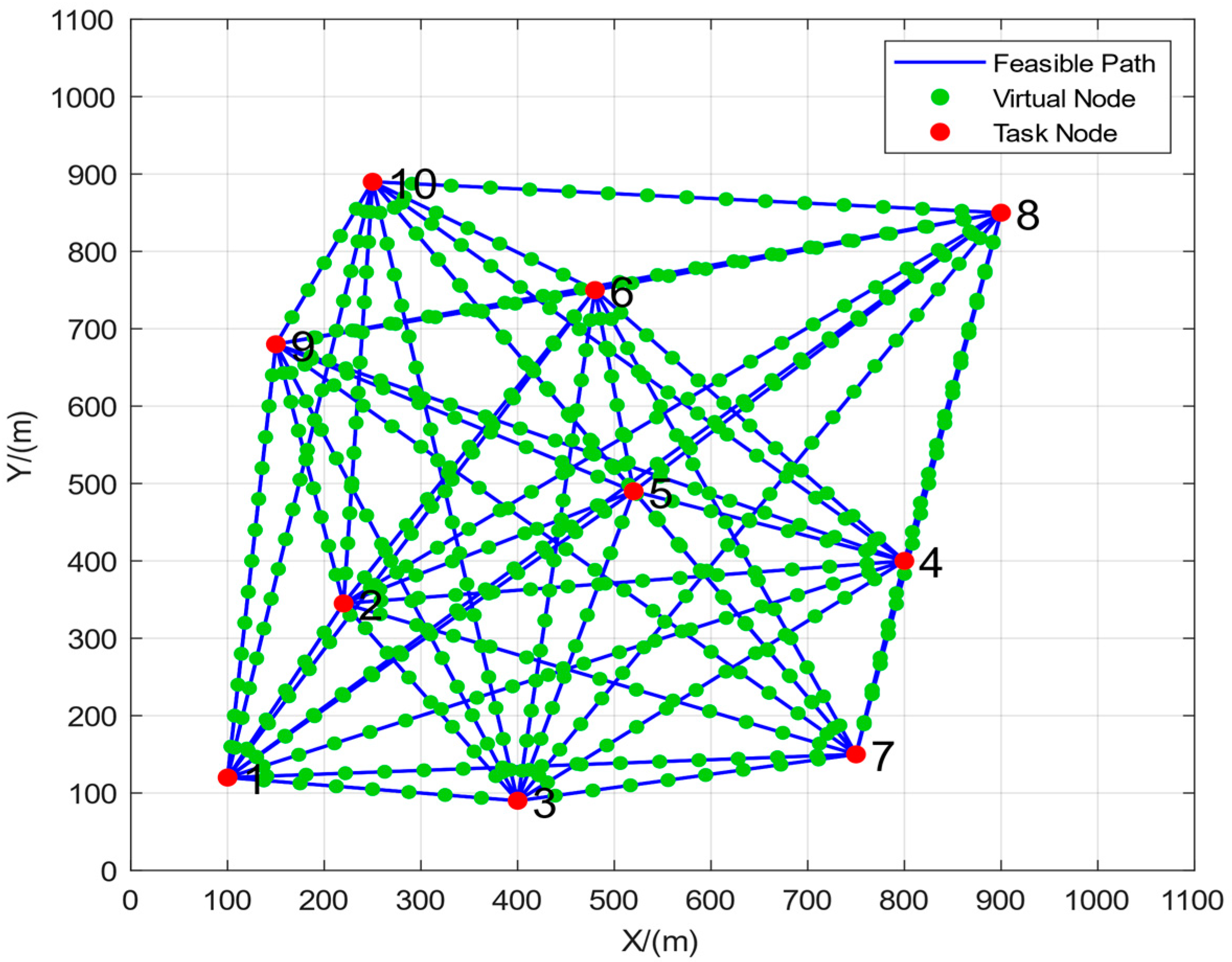
2.2. Discretization of the Graph
2.3. Multi-UAV Collaborative Monitoring Constraints
2.4. UAV Motion Constraints
2.5. The Waiting Time Constraint of the Task Node
2.6. Min–Max Optimization for Multi-UAV Cooperative Monitoring
2.6.1. UAVs Monitoring Overdue Time Evaluation
2.6.2. UAVs Monitoring Path Privacy Criterion
2.6.3. Multi-UAV Persistent Monitoring Path Planning Model
3. Improved Multi-Group Ant Colony Optimization Algorithms Based on Monitoring Overdue Time
- A greedy strategy for node selection is proposed, in which the ant colony heuristic function is modified using the expected period of the task nodes.
- Ant colony pheromone is updated based on monitoring overdue time and monitoring period entropy.
- A target exclusion mechanism is proposed to improve the utilization rate of multi-UAV in cooperative monitoring.
3.1. Heuristic Function Based on Monitoring Expectation Period
3.2. Target Exclusion Mechanism
3.3. Greedy Strategy for Node Selection
3.4. Pheromone Update Based on Monitoring Overdue Time and Monitoring Period Entropy
| Algorithm 1: Overdue-aware multiple ant colony optimization (OMACO). |
| Step 1: Initialization (node quantity N, adjacency matrix A, ant quantity Z, maximum iterations Nc, pheromone importance factor α, heuristic function importance factor β, pheromone volatility factor ρ, pheromone quantity Q, and maximum monitoring horizon K, weight parameter w). Step 2: Discretization of the graph. Step 3: Calculate the target exclusion set O0. Step 4: Calculate the ant transition probability according to (19). Step 5: Select the next node according to the roulette method, and update the node waiting time . Step 6: Update the ant’s taboo table. Step 7: Update the target exclusive flag . Step 8: Calculate the monitoring overdue time and monitoring period entropy according to (11) and (13). Step 9: Update pheromone according to (20) and (21). Step 10: Determine whether the iteration reaches the maximum iterations. If so, the procedure ends; otherwise, go to Step 3. |
4. Simulation Experiments and Discussions
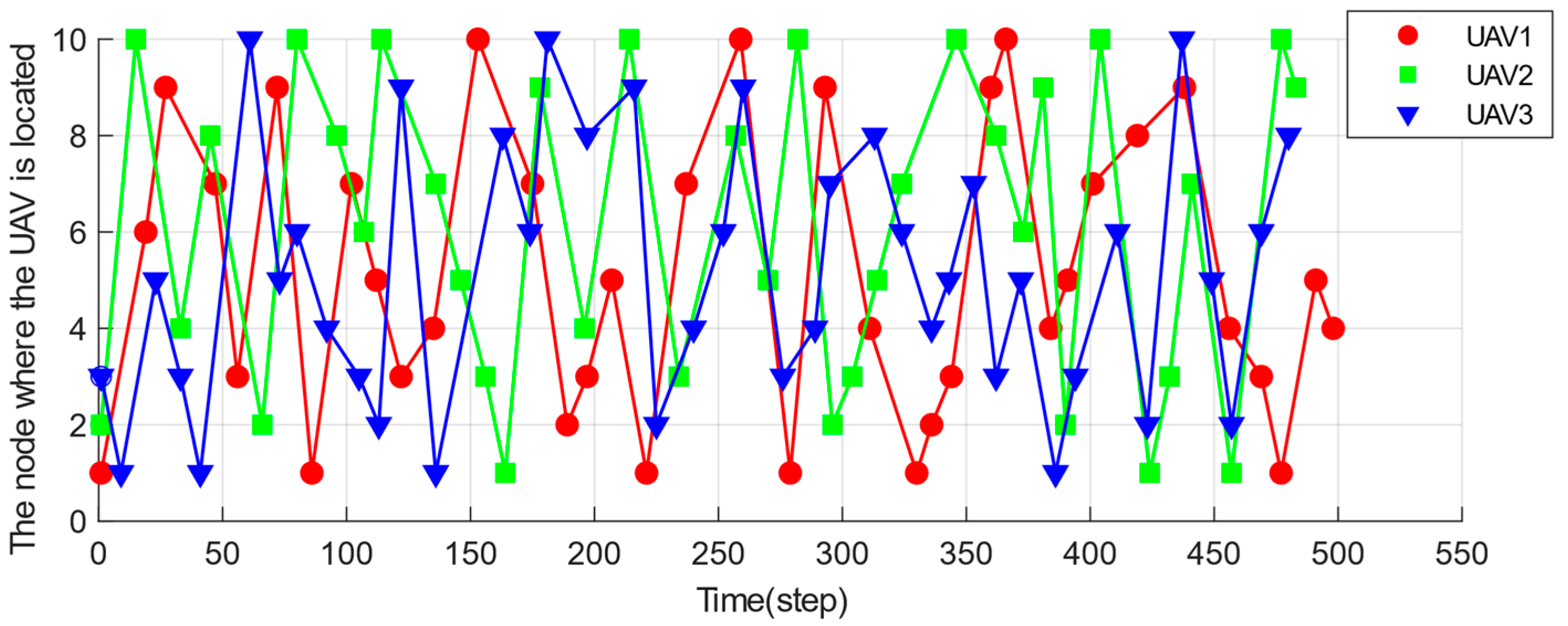
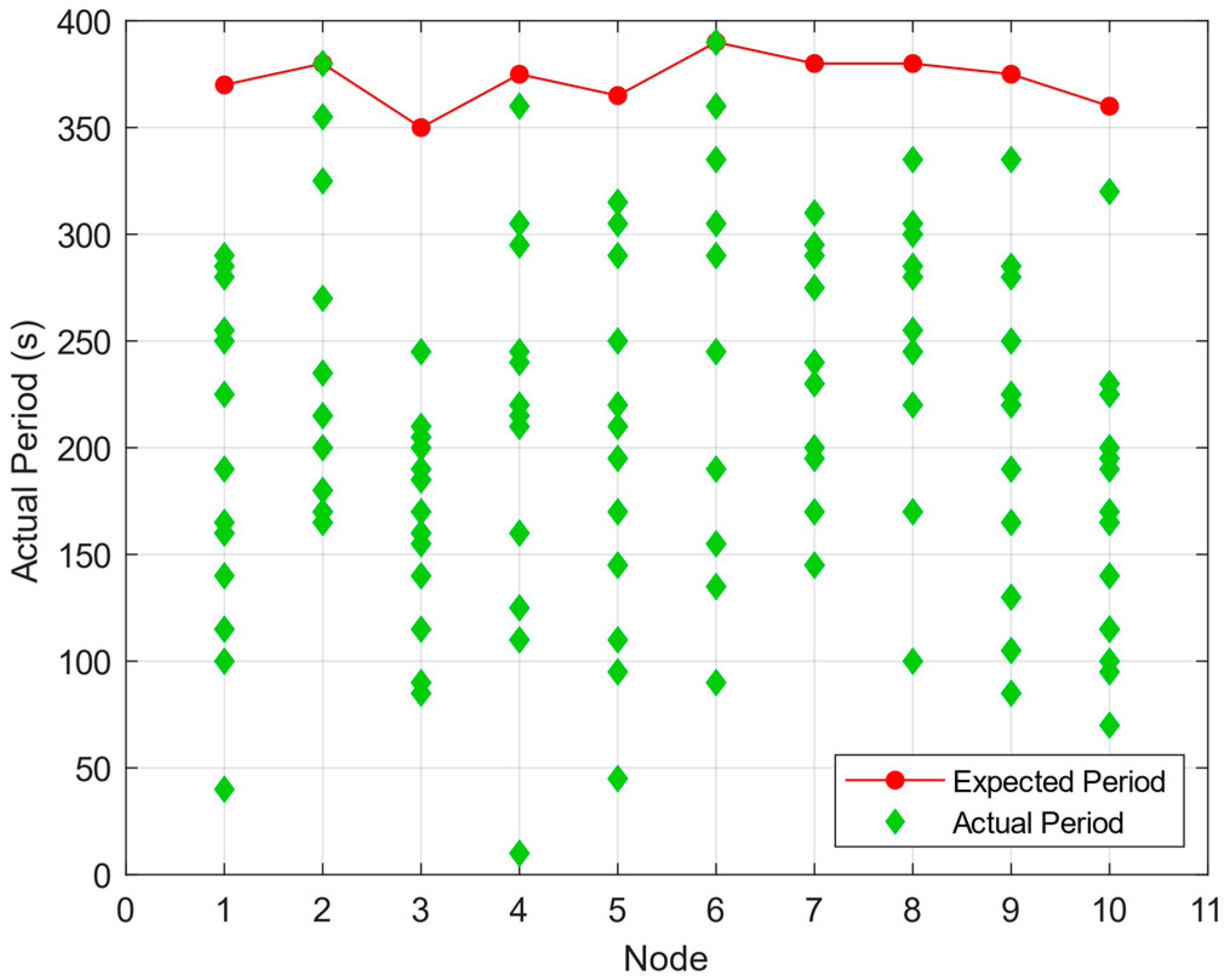
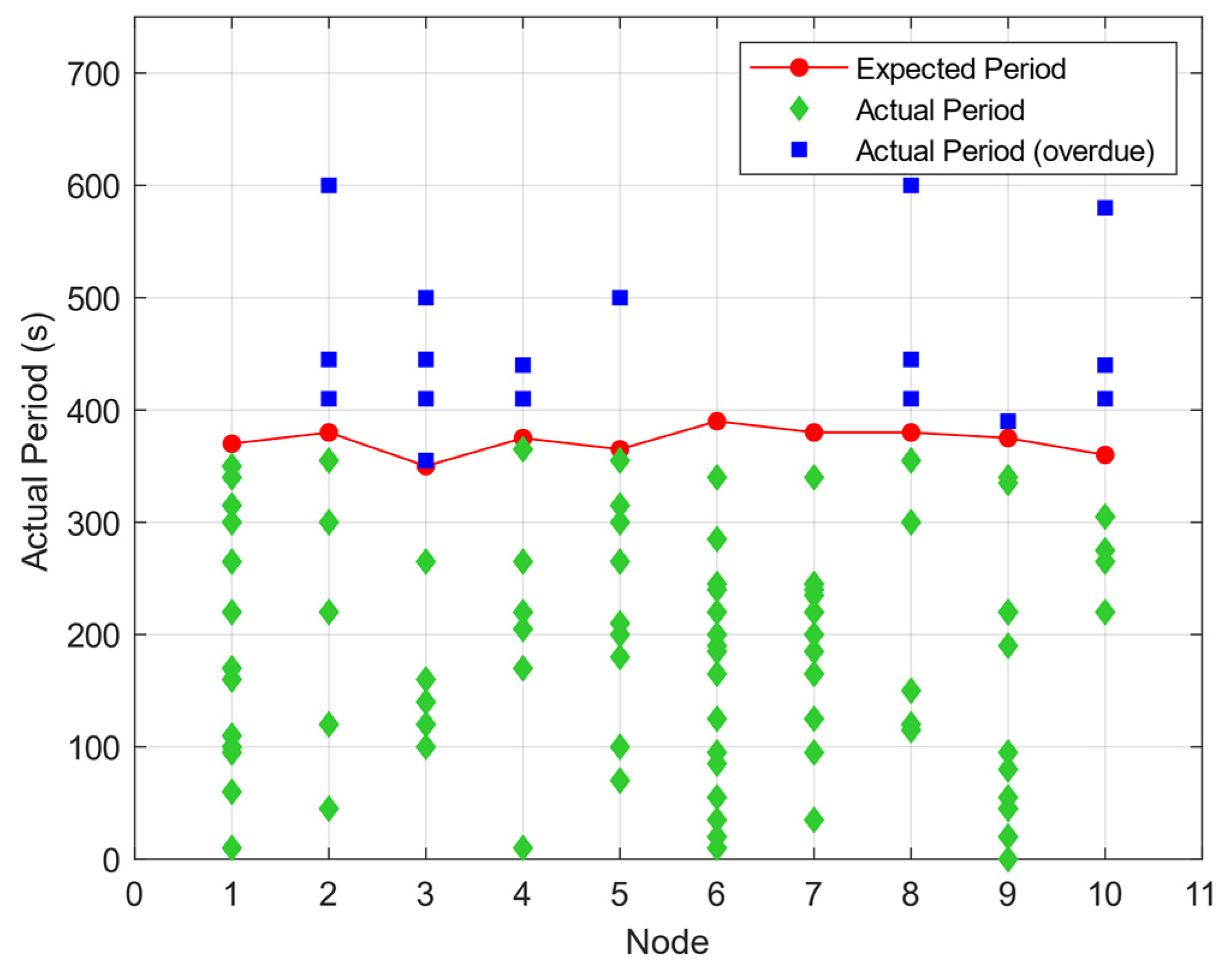
4.1. Algorithm Feasibility Analysis
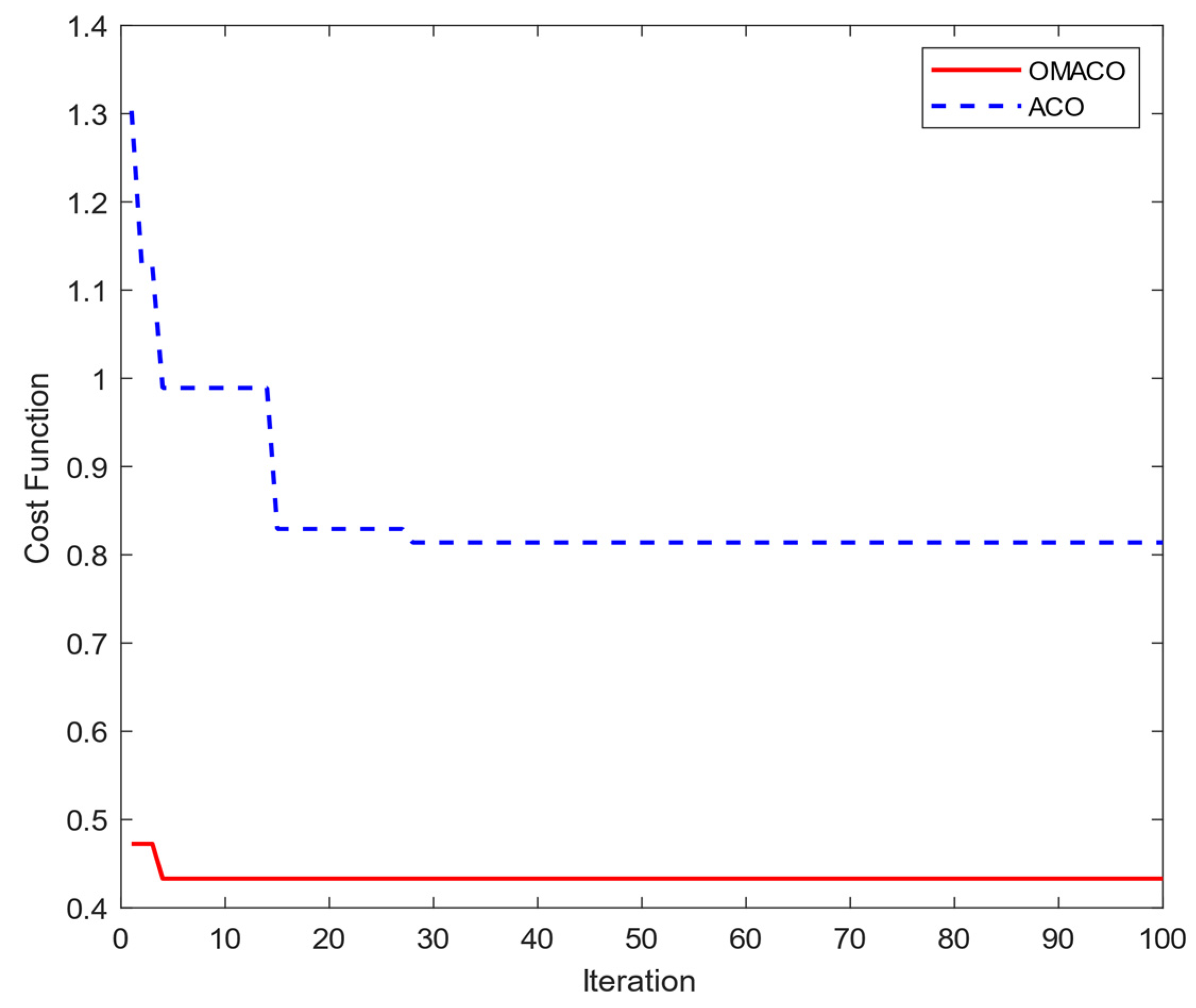
4.2. Comparative Analysis with Traditional ACO
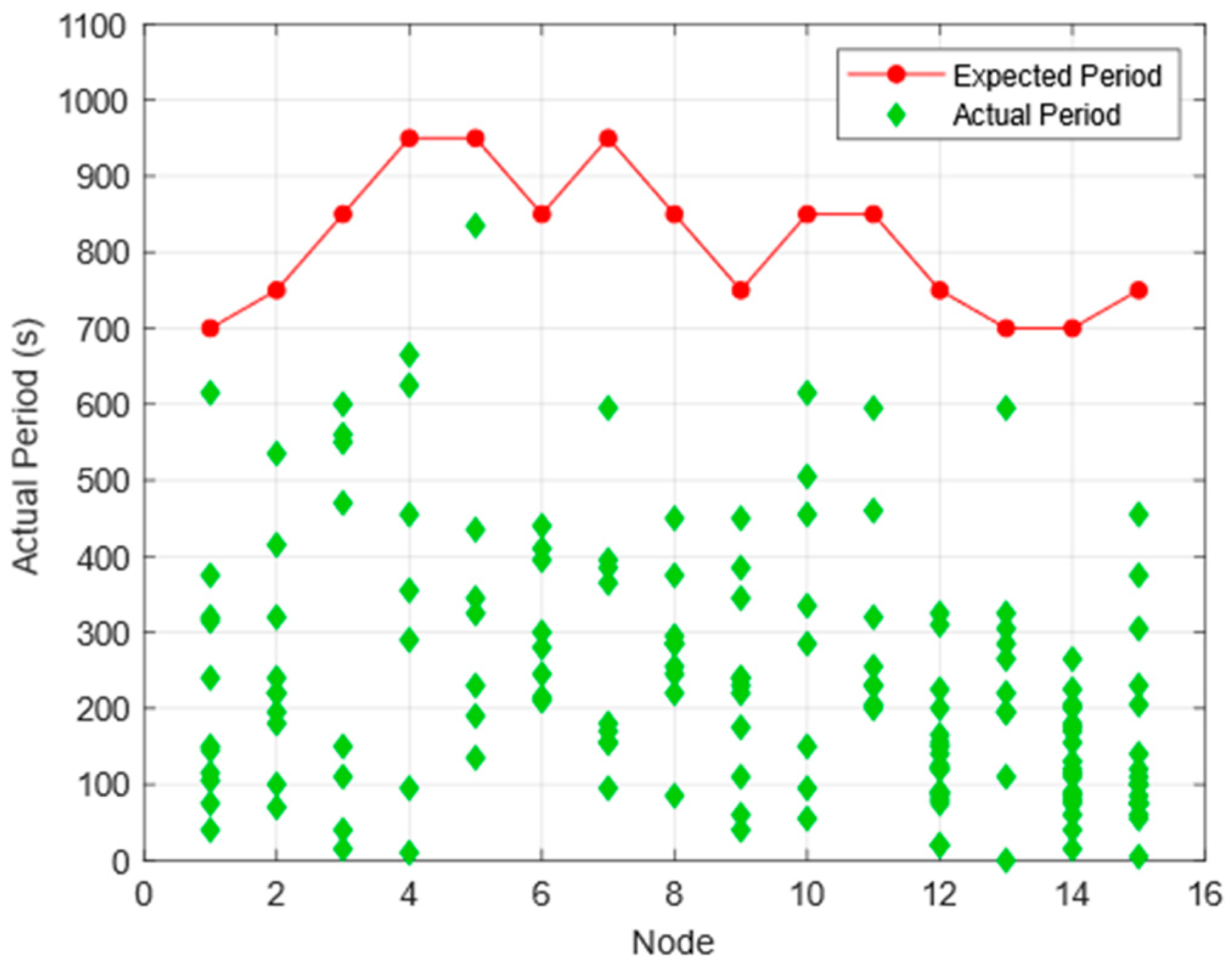
4.3. Algorithm Scalability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cassandras, C.G.; Lin, X.; Ding, X. An optimal control approach to the multi-agent persistent monitoring problem. IEEE Trans. Autom. Control 2012, 58, 947–961. [Google Scholar] [CrossRef]
- Wang, Y.W.; Wei, Y.W.; Liu, X.K.; Zhou, N.; Cassandras, C.G. Optimal persistent monitoring using second-order agents with physical constraints. IEEE Trans. Autom. Control 2018, 64, 3239–3252. [Google Scholar] [CrossRef]
- Smith, S.L.; Rus, D. Multi-robot monitoring in dynamic environments with guaranteed currency of observations. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; IEEE: Manhattan, NY, USA, 2010; pp. 514–521. [Google Scholar]
- Ostertag, M.; Nikolay, A.; Tajana, R. Trajectory planning and optimization for minimizing uncertainty in persistent monitoring applications. J. Intell. Robot. Syst. 2022, 106, 2. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, D. Adversarial ground target tracking using UAVs with input constraints. J. Intell. Robot. Syst. 2012, 65, 521–532. [Google Scholar] [CrossRef]
- Girard, A.R.; Howell, A.S.; Hedrick, J.K. Border patrol and surveillance missions using multiple unmanned air vehicles. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 1, pp. 620–625. [Google Scholar]
- Huang, L.; Qu, H.; Ji, P.; Liu, X.; Fan, Z. A novel coordinated path planning method using k-degree smoothing for multi-UAVs. Appl. Soft Comput. 2016, 48, 182–192. [Google Scholar] [CrossRef]
- Yun, W.J.; Park, S.; Kim, J.; Shin, M.; Jung, S.; Mohaisen, D.A.; Kim, J.H. Cooperative multiagent deep reinforcement learning for reliable surveillance via autonomous multi-UAV control. IEEE Trans. Ind. Inform. 2022, 18, 7086–7096. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, M.; Hao, K.; Hou, E. A survey of multi-robot regular and adversarial patrolling. IEEE/CAA J. Autom. Sin. 2019, 6, 894–903. [Google Scholar] [CrossRef]
- Portugal, D.; Rocha, R. A survey on multi-robot patrolling algorithms. In Proceedings of the Doctoral Conference on Computing, Electrical and Industrial Systems, Costa de Caparica, Portugal, 22–24 February 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 139–146. [Google Scholar]
- Alamdari, S.; Fata, E.; Smith, S.L. Persistent monitoring in discrete environments: Minimizing the maximum weighted latency between observations. Int. J. Robot. Res. 2014, 33, 138–154. [Google Scholar] [CrossRef]
- Elmaliach, Y.; Agmon, N.; Kaminka, G.A. Multi-robot area patrol under frequency constraints. Ann. Math. Artif. Intell. 2009, 57, 293–320. [Google Scholar] [CrossRef]
- Smith, S.L.; Schwager, M.; Rus, D. Persistent robotic tasks: Monitoring and sweeping in changing environments. IEEE Trans. Robot. 2011, 28, 410–426. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Dong, G. Cooperative persistent surveillance on a road network by multi-UGVs with detection ability. IEEE Trans. Ind. Electron. 2022, 69, 11468–11478. [Google Scholar] [CrossRef]
- Kalyanam, K.; Pachter, M.; Casbeer, D. Average reward dynamic programming applied to a persistent visitation and data delivery problem. In Proceedings of the Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 58295, p. V003T39A002. [Google Scholar]
- Kalyanam, K.; Manyam, S.; Von Moll, A.; Casbeer, D.; Pachter, M. Scalable and exact MILP methods for UAV persistent visitation problem. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; IEEE: Manhattan, NY, USA, 2018; pp. 337–342. [Google Scholar]
- Von Moll, A.L.; Casbeer, D.W.; Kalyanam, K.; Manyam, S.G. Genetic algorithm approach for UAV persistent visitation problem. In Proceedings of the Dynamic Systems and Control Conference, Atlanta, GA, USA, 30 September–3 October 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51913, p. V003T36A001. [Google Scholar]
- Scherer, J.; Rinner, B. Multi-UAV surveillance with minimum information idleness and latency constraints. IEEE Robot. Autom. Lett. 2020, 5, 4812–4819. [Google Scholar] [CrossRef]
- Hari, S.K.K.; Rathinam, S.; Darbha, S.; Kalyanam, K.; Manyam, S.G.; Casbeer, D. The generalized persistent monitoring problem. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; IEEE: Manhattan, NY, USA, 2019; pp. 2783–2788. [Google Scholar]
- Lei, Z.; Chen, X.; Chen, X.; Chai, L. Radial coverage strength for optimization of monocular multicamera deployment. IEEE/ASME Trans. Mechatron. 2021, 26, 3221–3231. [Google Scholar] [CrossRef]
- Agmon, N.; Kaminka, G.A.; Kraus, S. Multi-robot adversarial patrolling: Facing a full-knowledge opponent. J. Artif. Intell. Res. 2011, 42, 887–916. [Google Scholar]
- Tao, X.; Lang, N.; Li, H.; Xu, D. Path planning in uncertain environment with moving obstacles using warm start cross entropy. IEEE/ASME Trans. Mechatron. 2021, 27, 800–810. [Google Scholar] [CrossRef]
- George, M.; Jafarpour, S.; Bullo, F. Markov chains with maximum entropy for robotic surveillance. IEEE Trans. Autom. Control 2018, 64, 1566–1580. [Google Scholar] [CrossRef]
- Duan, X.; George, M.; Bullo, F. Markov chains with maximum return time entropy for robotic surveillance. IEEE Trans. Autom. Control 2019, 65, 72–86. [Google Scholar] [CrossRef]
- Basilico, N.; Gatti, N.; Amigoni, F. Patrolling security games: Definition and algorithms for solving large instances with single patroller and single intruder. Artif. Intell. 2012, 184, 78–123. [Google Scholar] [CrossRef]
- Xu, H.; Ford, B.; Fang, F.; Dilkina, B.; Plumptre, A.; Tambe, M.; Driciru, M.; Wanyama, F.; Rwetsiba, A.; Nsubaga, M.; et al. Optimal patrol planning for green security games with black-box attackers. In Proceedings of the International Conference on Decision and Game Theory for Security, Vienna, Austria, 10–13 October 2017; Springer: Cham, Switzerland, 2017; pp. 458–477. [Google Scholar]




| Parameters | Value | Notes |
|---|---|---|
| v | 8 m/s | UAV speed |
| δ | 40 m | interval for discretization |
| Z | 15 | ant quantity |
| c | 5 s | constant |
| Nc | 200 | maximum iteration |
| α | 1.2 | pheromone importance factor |
| β | 4 | heuristic function importance factor |
| ρ | 0.3 | pheromone volatility factor |
| Q | 10 | pheromone quantity |
| K | 500 | monitoring Horizon |
| w | 0.6 | weight parameter |
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ti (s) | 370 | 380 | 350 | 375 | 365 | 390 | 380 | 380 | 375 | 360 |
| Node | Number of Visits | Average of Actual Monitoring Period | ||
|---|---|---|---|---|
| OMACO | ACO | OMACO | ACO | |
| 1 | 12 | 12 | 198.33 | 198.75 |
| 2 | 9 | 7 | 253.33 | 350.00 |
| 3 | 14 | 8 | 167.14 | 278.75 |
| 4 | 11 | 8 | 232.50 | 286.25 |
| 5 | 12 | 9 | 204.17 | 242.22 |
| 6 | 9 | 15 | 260.00 | 165.00 |
| 7 | 10 | 12 | 220.00 | 188.33 |
| 8 | 9 | 7 | 266.11 | 335.00 |
| 9 | 11 | 15 | 219.09 | 166.33 |
| 10 | 14 | 6 | 170.00 | 365.00 * |
| Average | 11.1 | 9.9 | 219.07 | 257.56 |
| OMACO | ACO | |
|---|---|---|
| Iterations | 4 | 28 |
| Minimum Cost | 0.433 | 0.814 |
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ti (s) | 700 | 750 | 1050 | 950 | 950 | 850 | 950 | 850 | 700 | 850 | 850 | 750 | 700 | 700 | 750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shu, Y.; Hu, M.; Zhao, X. Multi-UAV Cooperative Path Planning with Monitoring Privacy Preservation. Appl. Sci. 2022, 12, 12111. https://doi.org/10.3390/app122312111
Chen Y, Shu Y, Hu M, Zhao X. Multi-UAV Cooperative Path Planning with Monitoring Privacy Preservation. Applied Sciences. 2022; 12(23):12111. https://doi.org/10.3390/app122312111
Chicago/Turabian StyleChen, Yang, Yifei Shu, Mian Hu, and Xingang Zhao. 2022. "Multi-UAV Cooperative Path Planning with Monitoring Privacy Preservation" Applied Sciences 12, no. 23: 12111. https://doi.org/10.3390/app122312111
APA StyleChen, Y., Shu, Y., Hu, M., & Zhao, X. (2022). Multi-UAV Cooperative Path Planning with Monitoring Privacy Preservation. Applied Sciences, 12(23), 12111. https://doi.org/10.3390/app122312111









