A Hybrid Multi-Objective Optimization Method and Its Application to Electromagnetic Device Designs
Abstract
1. Introduction
2. Multi-Objective Optimization
2.1. Problem Definition
2.2. Performance Indicators
2.2.1. Convergence Metric
2.2.2. Diversity Metric
2.2.3. Non-Dominated Individual Ratio
3. A Hybrid Multi-Objective Optimization Method
3.1. NSGA-II
| Algorithm 1: NSGA-II |
 |
3.2. MOPSO
| Algorithm 2: MOPSO |
|
Input: N (particle swarm size), K (Archive size) Output: R (Archive) 1 P ← Initialization(N); 2 V ← Initialize the velocity of each particle; 3 R ← Non-dominated-sort(P); //Select the better K individuals from P 4 while termination criterion not fulfilled do 5 Pbest ← Update the individual optimal particle according to P; 6 V ← Compute the velocity of each particle by (8); 7 P′ ← Update P by (7) and (8); 8 P ← R ∪ P′; 9 R ← Select the better K individuals by Non-dominated-sort(P) and adaptive-lattice(P); 10 Gbest ← Update the global optimal particle according to R; 11 return R; |
3.3. Adaptive Operators
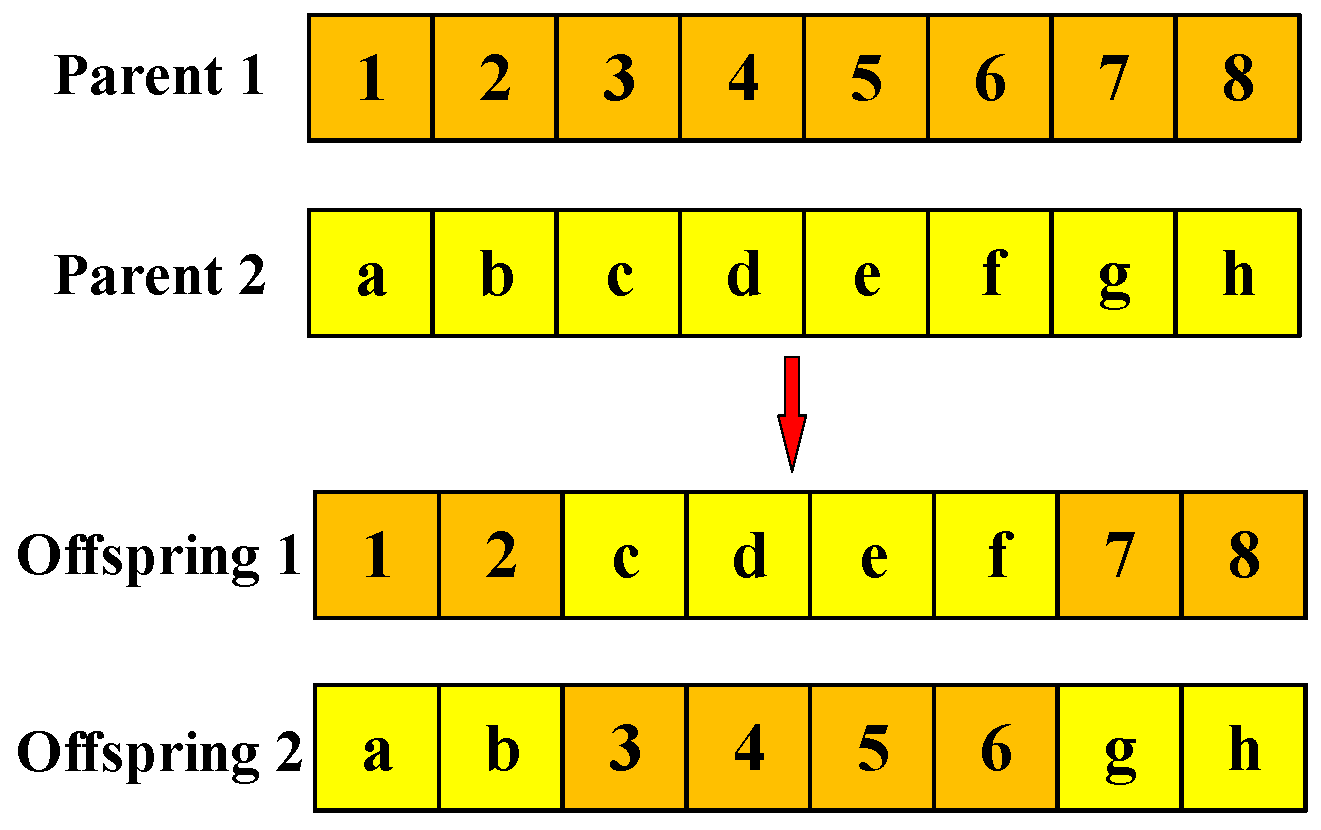
3.3.1. Crossover Operator
3.3.2. Mutation Operator
3.3.3. Selection of the Operators
3.4. Framework of the Hybrid Algorithm
| Algorithm 3: INSGAP |
 |
4. Numerical Examples
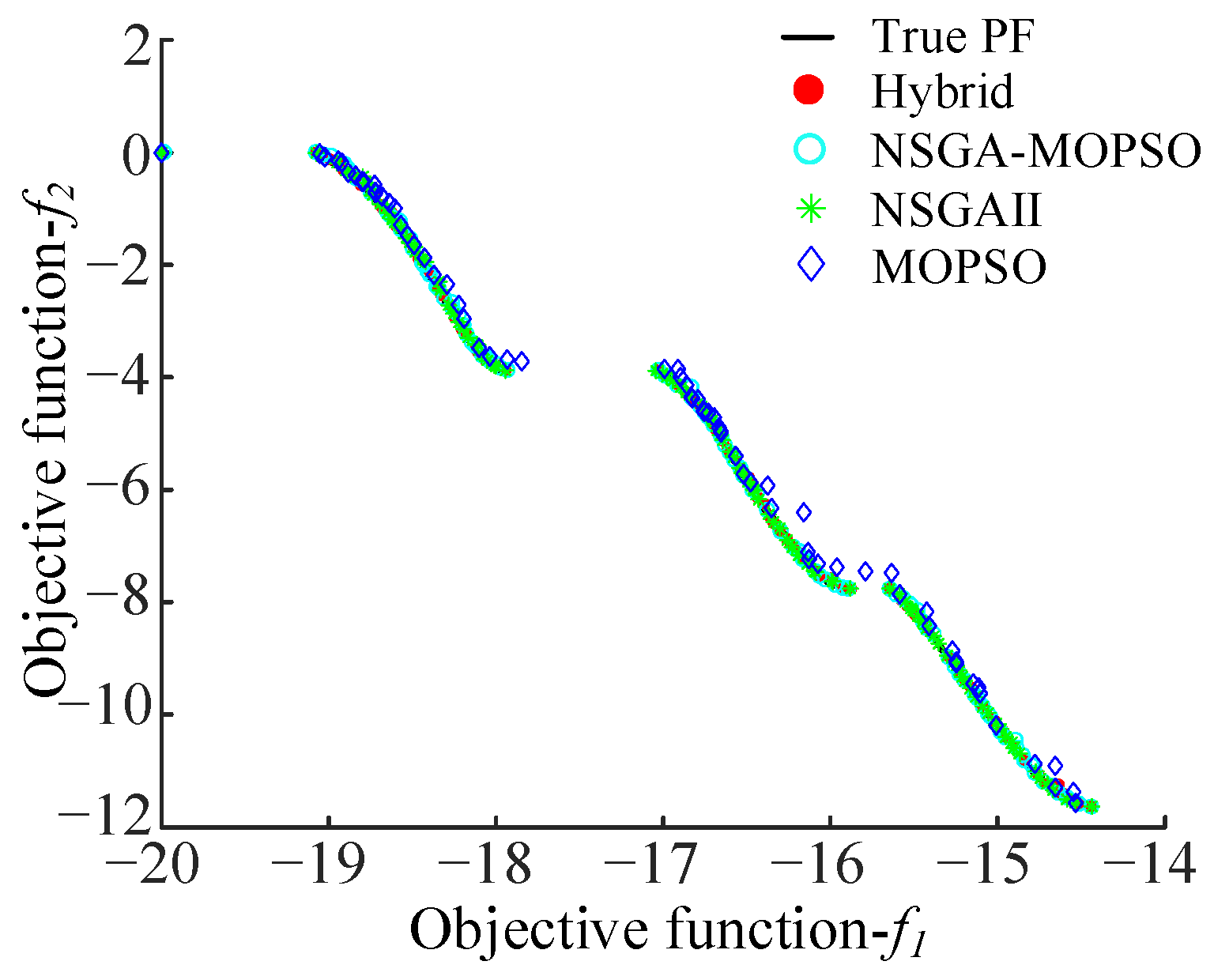
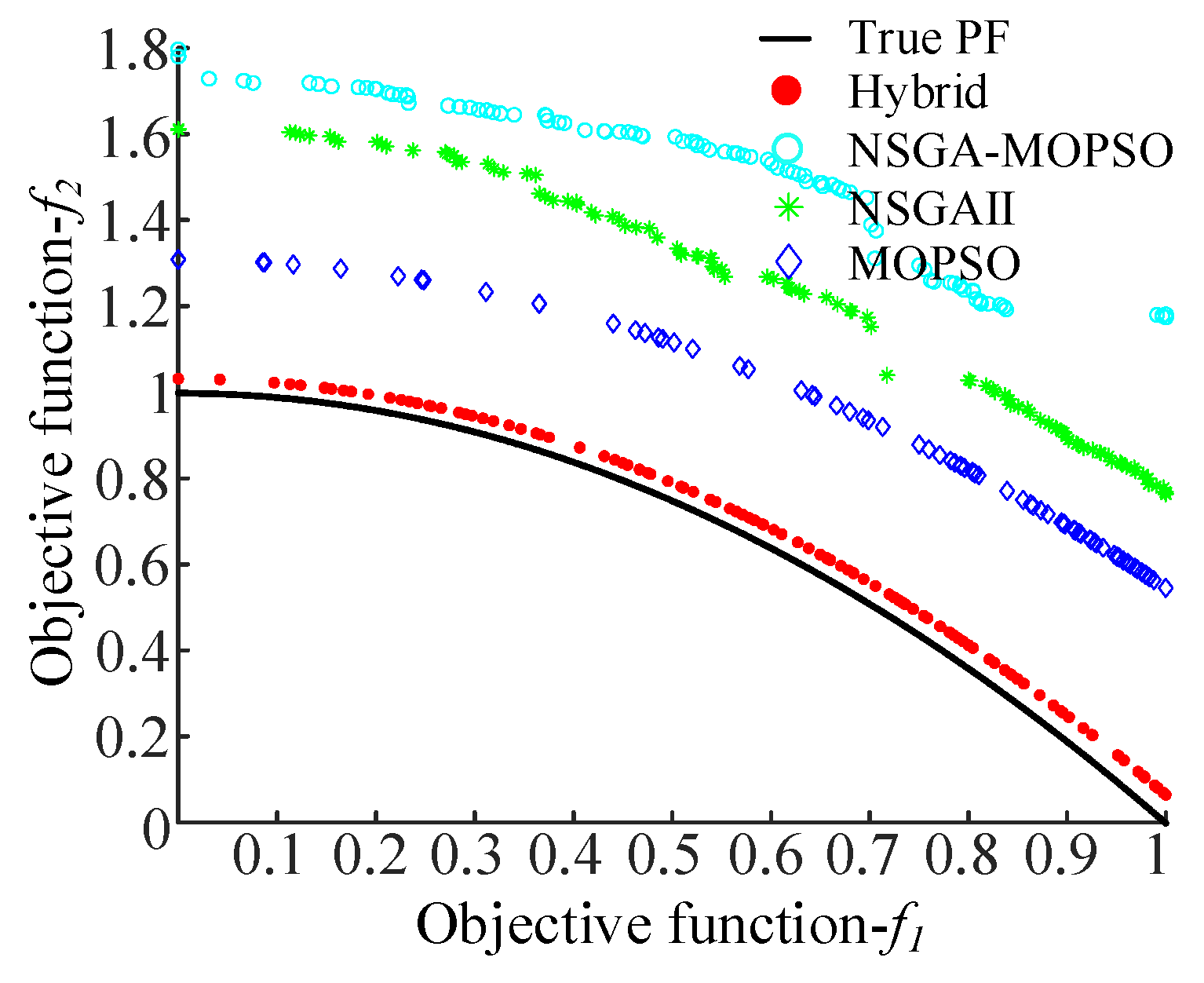
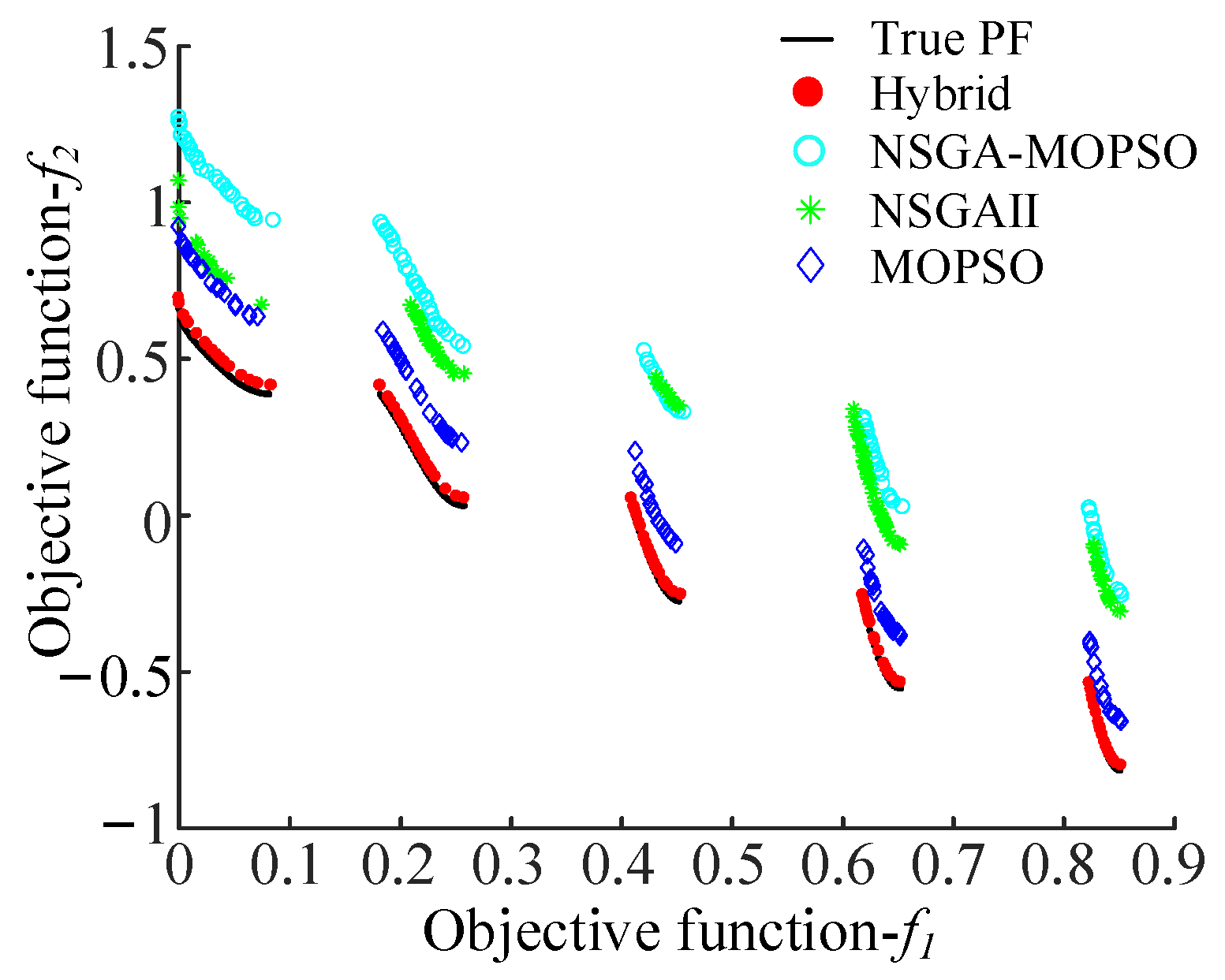
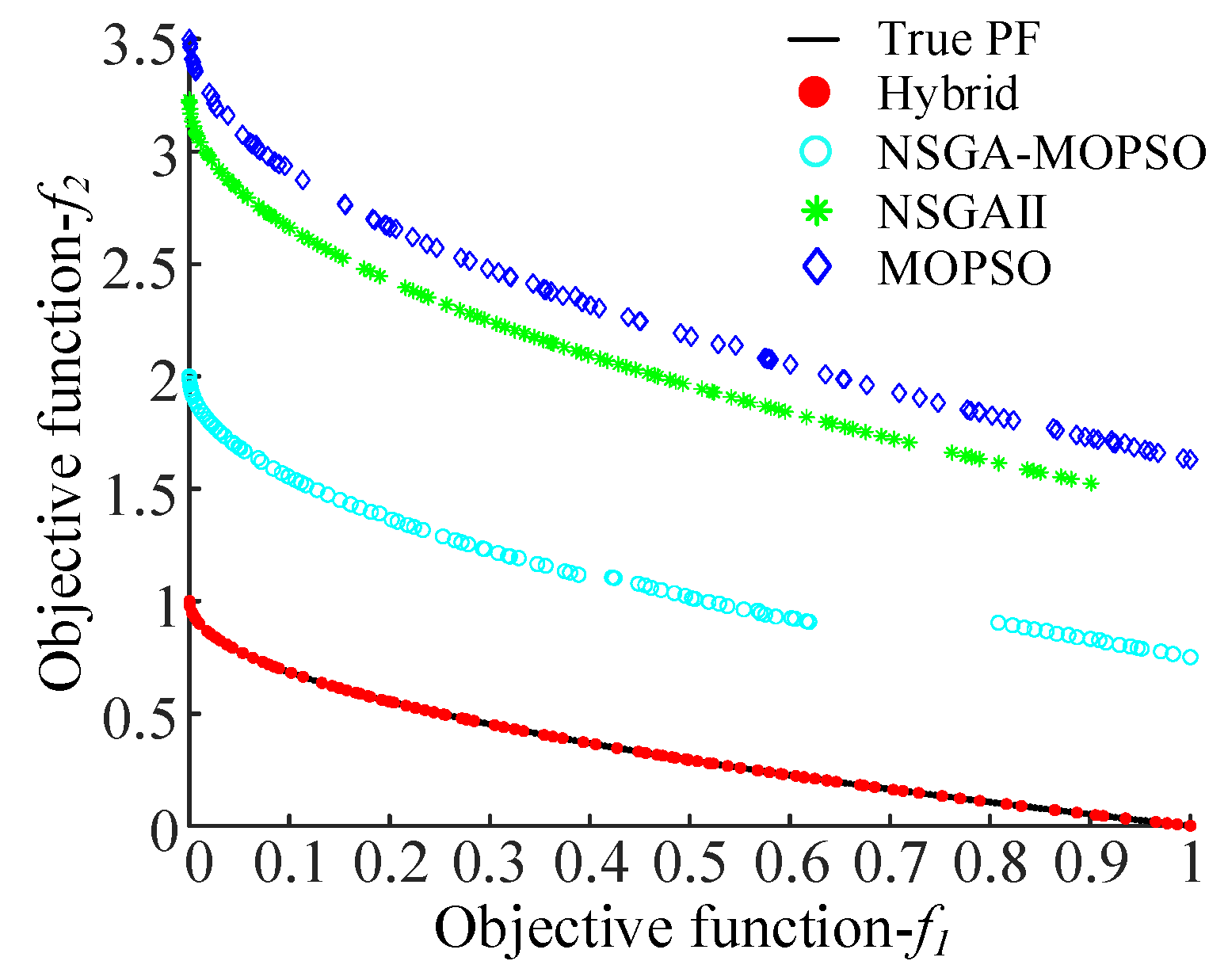
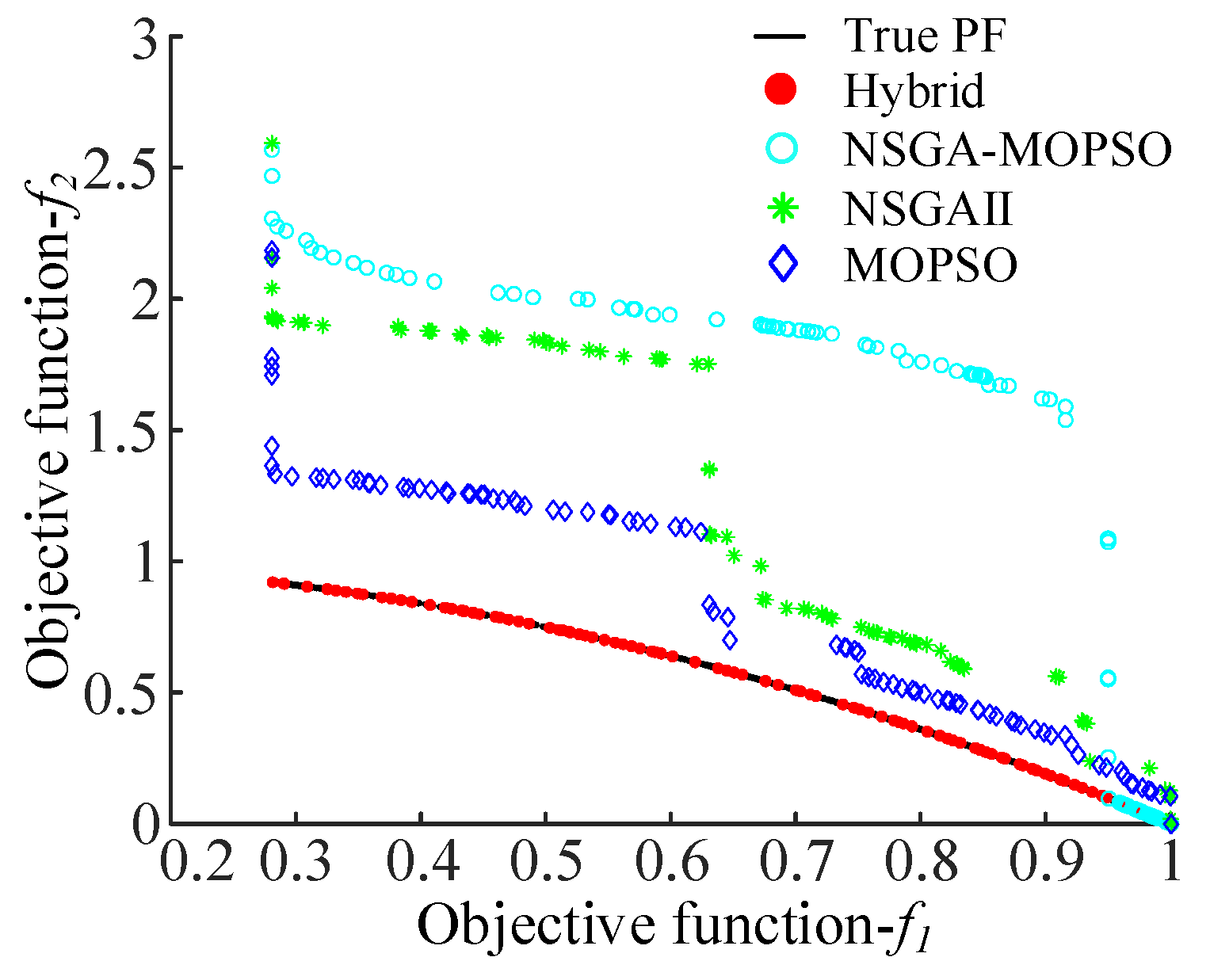
4.1. Performance Validation
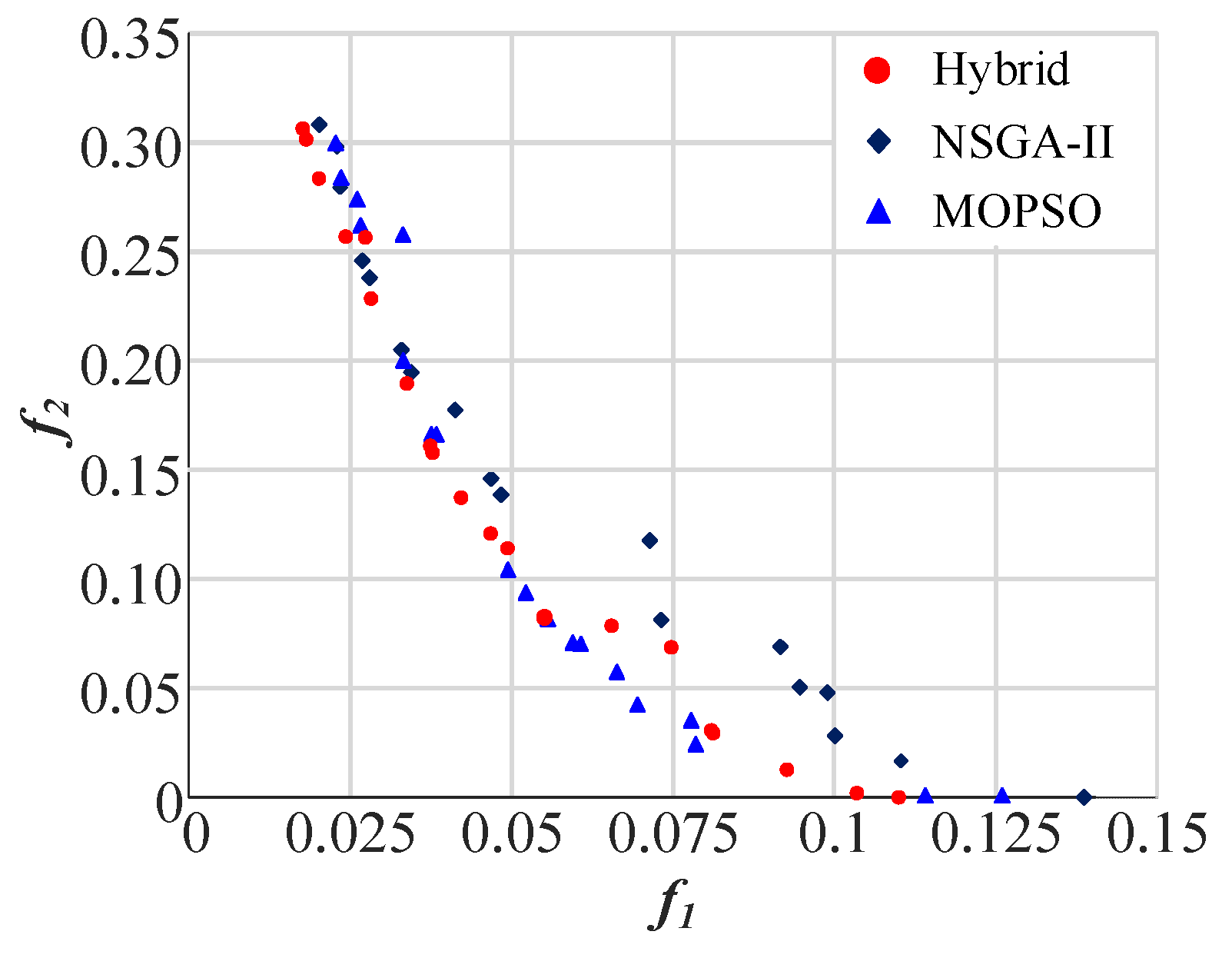
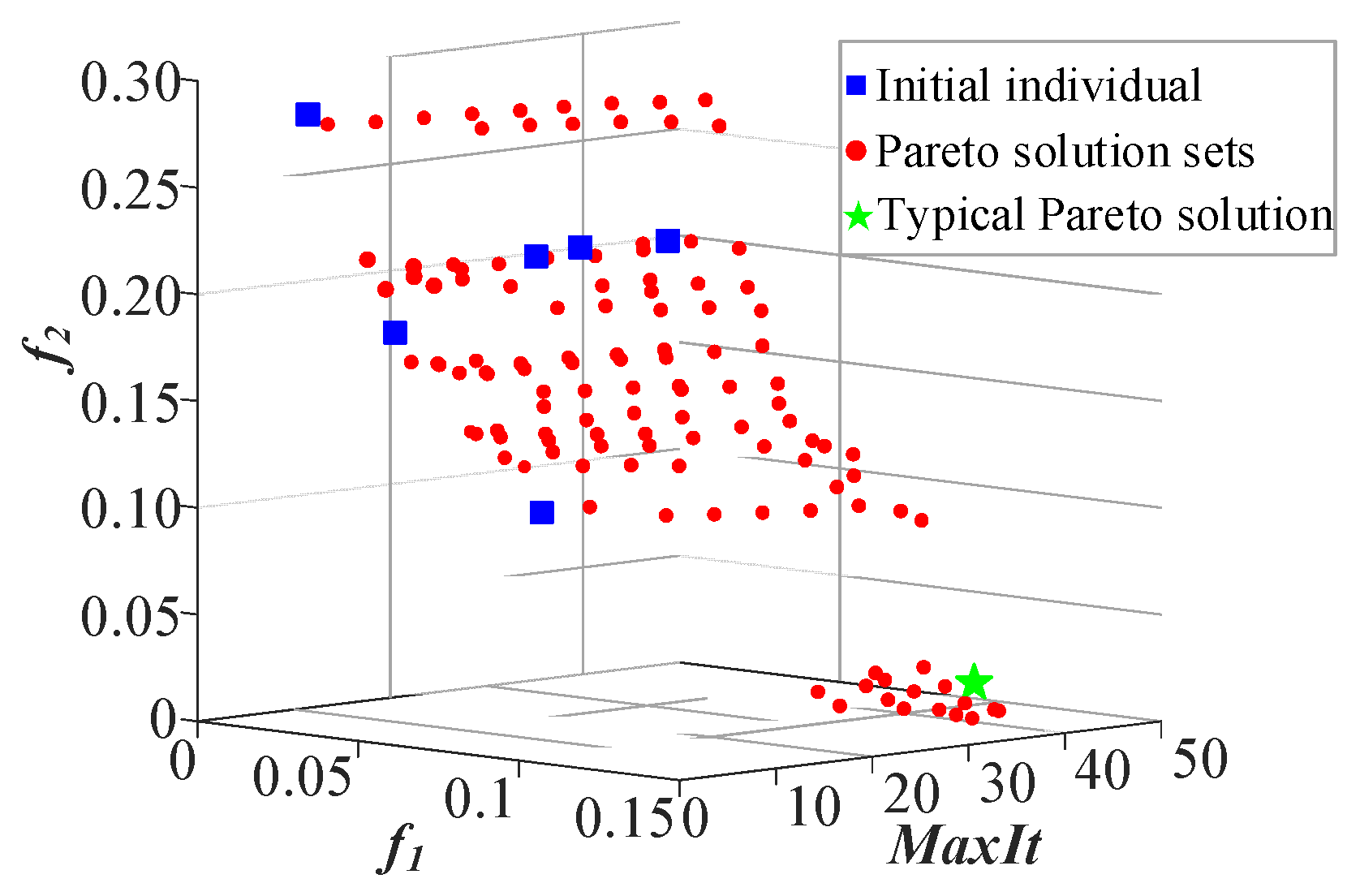
4.2. Multi-Objective Design of a SMES Device
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coello, C.A. An updated survey of GA-based multiobjective optimization techniques. ACM Comput. Surv. (CSUR) 2000, 32, 109–143. [Google Scholar] [CrossRef]
- Palmeri, R.; Bevacqua, M.; Morabito, A.; Isernia, T. Design of artificial-material-based antennas using inverse scattering techniques. IEEE Trans. Antennas Propag. 2018, 66, 7076–7090. [Google Scholar] [CrossRef]
- Palmeri, R.; Isernia, T. Inverse design of artificial materials based lens antennas through the scattering matrix method. Electronics 2020, 9, 559. [Google Scholar] [CrossRef]
- Palmeri, T.I.R. Inverse design of EBG waveguides through scattering matrices. EPJ Appl. Metamaterials 2020, 7, 10. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Systematic design of photonic crystal structures using topology optimization: Low-loss waveguide bends. Appl. Phys. Lett. 2004, 84, 2022–2024. [Google Scholar] [CrossRef]
- Callewaert, F.; Velev, V.; Kumar, P.; Sahakian, A.V.; Aydin, K. Inverse-designed broadband all-dielectric electromagnetic metadevices. Sci. Rep. 2018, 8, 1358. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.; Xu, X.; Huang, Z. Optimal design of magnetically suspended high-speed rotor in turbo-molecular pump. Vacuum 2021, 193, 110510. [Google Scholar] [CrossRef]
- Heydarianasl, M.; Rahmat, M.F. Design optimization of electrostatic sensor electrodes via MOPSO. Measurement 2020, 152, 107288. [Google Scholar] [CrossRef]
- Niu, B.; Wang, D.; Pan, P. Multi-objective optimal design of permanent magnet eddy current retarder based on NSGA-II algorithm. Energy Rep. 2022, 8, 1448–1456. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G.; Xu, S. Bi-objective green supply chain network design under disruption risk through an extended NSGA-II algorithm. Clean. Logist. Supply Chain 2022, 3, 100025. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, Z.; Zhang, K.; Tang, X.; Huang, S. Statistical modeling and multi-objective optimization of road geopolymer grouting material via RSM and MOPSO. Constr. Build. Mater. 2021, 271, 121534. [Google Scholar] [CrossRef]
- Zhao, W.; Luan, Z.; Wang, C. Parameter optimization design of vehicle E-HHPS system based on an improved MOPSO algorithm. Adv. Eng. Softw. 2018, 123, 51–61. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Zhu, Q.; Lin, Q.; Du, Z.; Liang, Z.; Wang, W.; Zhu, Z.; Chen, J.; Huang, P.; Ming, Z. A novel adaptive hybrid crossover operator for multiobjective evolutionary algorithm. Inf. Sci. 2016, 345, 177–198. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Fu, Z.; Liu, S.; Mao, W.; Liu, G.; Jiang, Y.; Li, S. Novel biogeography-based optimization algorithm with hybrid migration and global-best Gaussian mutation. Appl. Math. Model. 2020, 86, 74–91. [Google Scholar] [CrossRef]
- Raj, R.; Mathew, J.; Kannath, S.K.; Rajan, J. Crossover based technique for data augmentation. Comput. Methods Programs Biomed. 2022, 218, 106716. [Google Scholar] [CrossRef]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Gong, W.; Cai, Z.; Ling, C.X.; Li, H. A real-coded biogeography-based optimization with mutation. Appl. Math. Comput. 2010, 216, 2749–2758. [Google Scholar] [CrossRef]
- Stacey, A.; Jancic, M.; Grundy, I. Particle swarm optimization with mutation. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, Australia, 8–12 December 2003; Volume 2, pp. 1425–1430. [Google Scholar]
- Singh, P.; Dwivedi, P.; Kant, V. A hybrid method based on neural network and improved environmental adaptation method using Controlled Gaussian Mutation with real parameter for short-term load forecasting. Energy 2019, 174, 460–477. [Google Scholar] [CrossRef]
- Alotto, P.; Baumgartner, U.; Freschi, F.; Jaindl, M.; Kostinger, A.; Magele, C.; Renhart, W.; Repetto, M. SMES optimization benchmark extended: Introducing Pareto optimal solutions into TEAM22. IEEE Trans. Magn. 2008, 44, 1066–1069. [Google Scholar] [CrossRef]



| Parameter | Hybrid | NSGA-MOPSO | MOPSO | NSGA-II |
|---|---|---|---|---|
| 125 | 125 | 250 | 250 | |
| 100 | 100 | 100 | 100 | |
| 0.9 | 0.9 | — | 0.9 | |
| 0.1 | ||||
| 0.5 | 0.5 | 0.5 | — | |
| 0.1 | 0.1 | 0.1 | — | |
| 20 | 20 | — | 20 | |
| 1 | 1 | 1 | — | |
| 2 | 2 | 2 | — |
| Problem | n | Variable Bounds | Objective Functions | Optimal Solutions | PF Characteristics |
|---|---|---|---|---|---|
| KUR | 3 | [–5, 5] | Ref [12] | nonconvex | |
| ZDT1 | 30 | [0, 1] | convex | ||
| ZDT2 | 30 | [0, 1] | nonconvex | ||
| ZDT3 | 30 | [0, 1] | nonconvex, disconnected | ||
| ZDT4 | 10 | nonconvex | |||
| ZDT6 | 10 | [0, 1] | nonconvex, nonuniformly distributed |
| Hybrid | NSGA-MOPSO | MOPSO | NSGA-II | |||||
|---|---|---|---|---|---|---|---|---|
| E(γ) | σ(γ) | E(γ) | σ(γ) | E(γ) | σ(γ) | E(γ) | σ(γ) | |
| KUR | 0.0137 | 0.0111 | 0.01523 | 0.01248 | 0.0379 | 0.0349 | 0.0143 | 0.0115 |
| ZDT1 | 0.0231 | 0.0114 | 0.05392 | 0.01327 | 0.0213 | 0.0092 | 0.3370 | 0.0940 |
| ZDT2 | 0.2370 | 0.0045 | 0.8526 | 0.06125 | 0.2691 | 0.1213 | 0.6127 | 0.0879 |
| ZDT3 | 0.0171 | 0.0308 | 0.06385 | 0.05269 | 0.0393 | 0.0296 | 0.0557 | 0.0131 |
| ZDT4 | 0.1103 | 0.0092 | 1.4603 | 0.3753 | 2.7106 | 0.4014 | 2.1833 | 0.376 |
| ZDT6 | 0.0979 | 0.0039 | 1.4917 | 0.9526 | 0.7835 | 0.2724 | 0.9325 | 0.9128 |
| Hybrid | NSGA-MOPSO | MOPSO | NSGA-II | |||||
|---|---|---|---|---|---|---|---|---|
| E(∆) | σ(∆) | E(∆) | σ(∆) | E(∆) | σ(∆) | E(∆) | σ(∆) | |
| KUR | 0.5103 | 0.0216 | 0.5019 | 0.02983 | 0.7230 | 0.0249 | 0.4996 | 0.0326 |
| ZDT1 | 0.4831 | 0.0436 | 0.5173 | 0.107 | 0.9513 | 0.1455 | 0.6499 | 0.0557 |
| ZDT2 | 0.5073 | 0.0427 | 1.02 | 0.1157 | 0.9181 | 0.1130 | 0.8497 | 0.1626 |
| ZDT3 | 0.6182 | 0.0257 | 0.6623 | 0.03448 | 0.8655 | 0.0350 | 0.7647 | 0.0407 |
| ZDT4 | 0.4512 | 0.0488 | 0.8297 | 0.07222 | 1.2481 | 0.3920 | 0.7906 | 0.0416 |
| ZDT6 | 0.4590 | 0.1278 | 1.1983 | 0.1032 | 0.9143 | 0.1424 | 1.3307 | 0.1083 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Li, Y.; Yang, S. A Hybrid Multi-Objective Optimization Method and Its Application to Electromagnetic Device Designs. Appl. Sci. 2022, 12, 12110. https://doi.org/10.3390/app122312110
Xie Z, Li Y, Yang S. A Hybrid Multi-Objective Optimization Method and Its Application to Electromagnetic Device Designs. Applied Sciences. 2022; 12(23):12110. https://doi.org/10.3390/app122312110
Chicago/Turabian StyleXie, Zhengwei, Yilun Li, and Shiyou Yang. 2022. "A Hybrid Multi-Objective Optimization Method and Its Application to Electromagnetic Device Designs" Applied Sciences 12, no. 23: 12110. https://doi.org/10.3390/app122312110
APA StyleXie, Z., Li, Y., & Yang, S. (2022). A Hybrid Multi-Objective Optimization Method and Its Application to Electromagnetic Device Designs. Applied Sciences, 12(23), 12110. https://doi.org/10.3390/app122312110






