Discovering Irregularities from Computer Networks by Topological Mapping
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
3.1. Objectives
3.2. Significance
3.3. Method
4. Experimental Results
4.1. Main Results
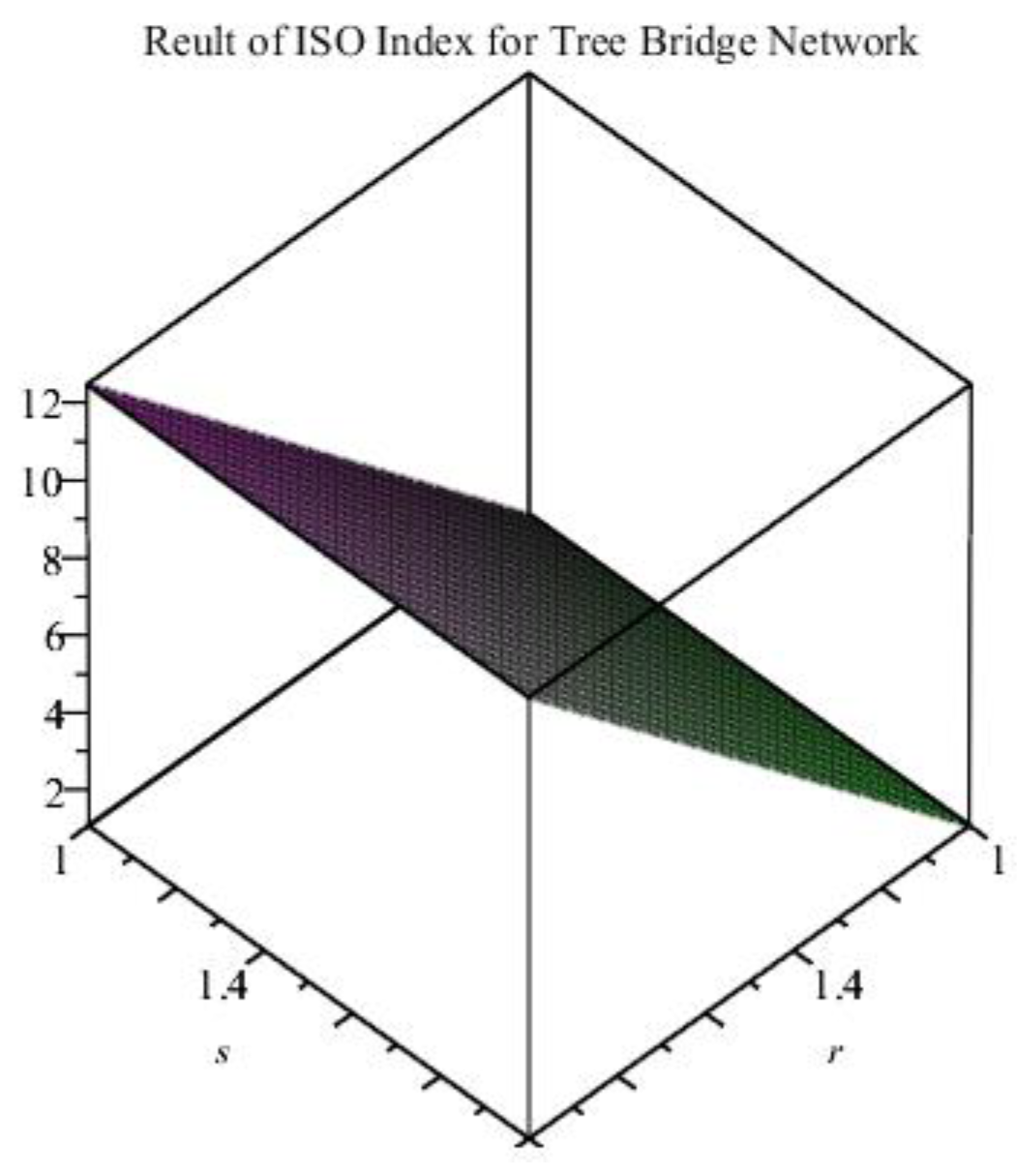
4.1.1. Bridge Graph Gr (Ps, v) over Path
4.1.2. Theorem 1
4.2. Main Results
4.2.1. Bridge Graph Gr (Cs, v) over Cycle
4.2.2. Theorem 2
4.3. Main Results
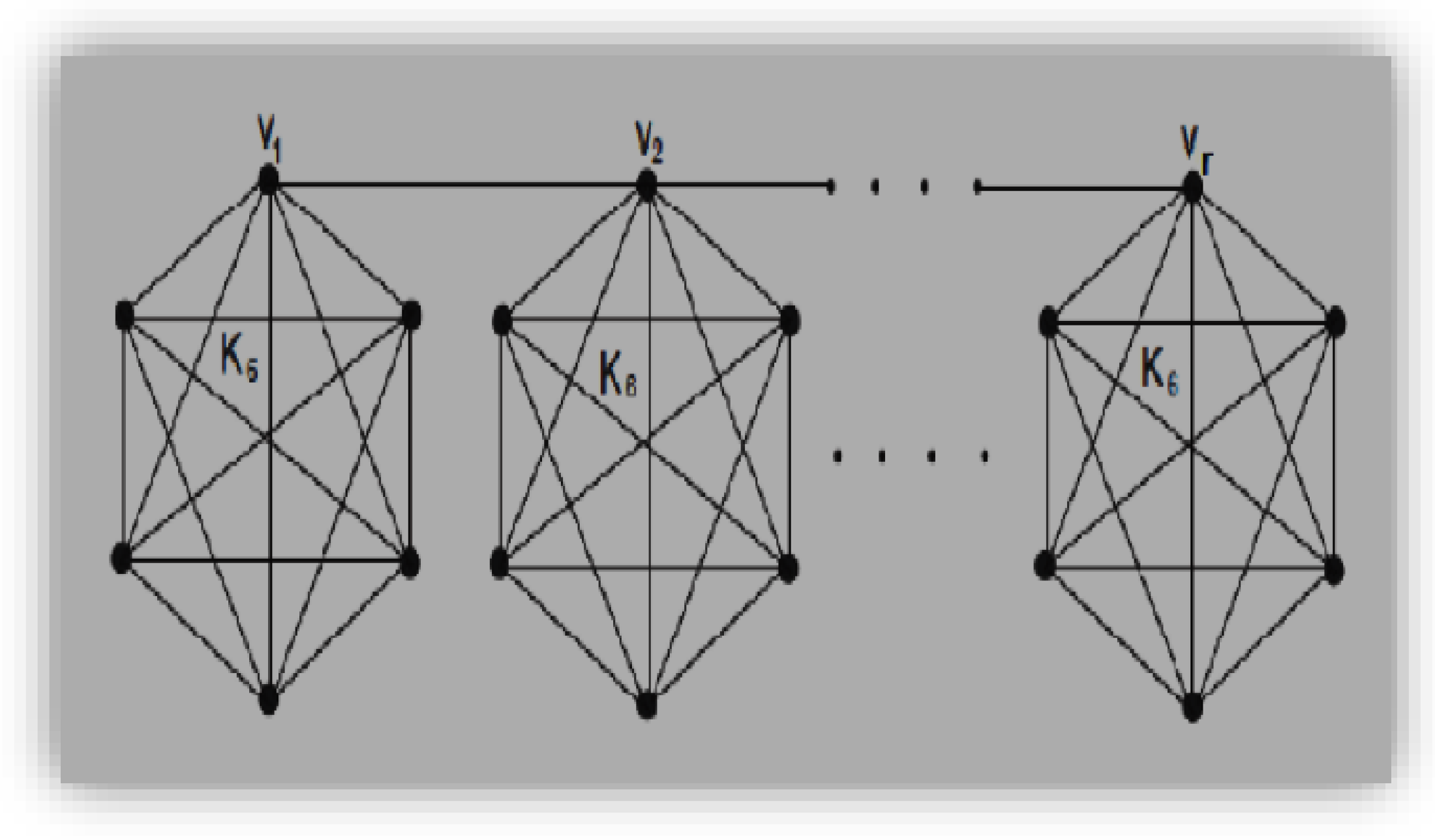
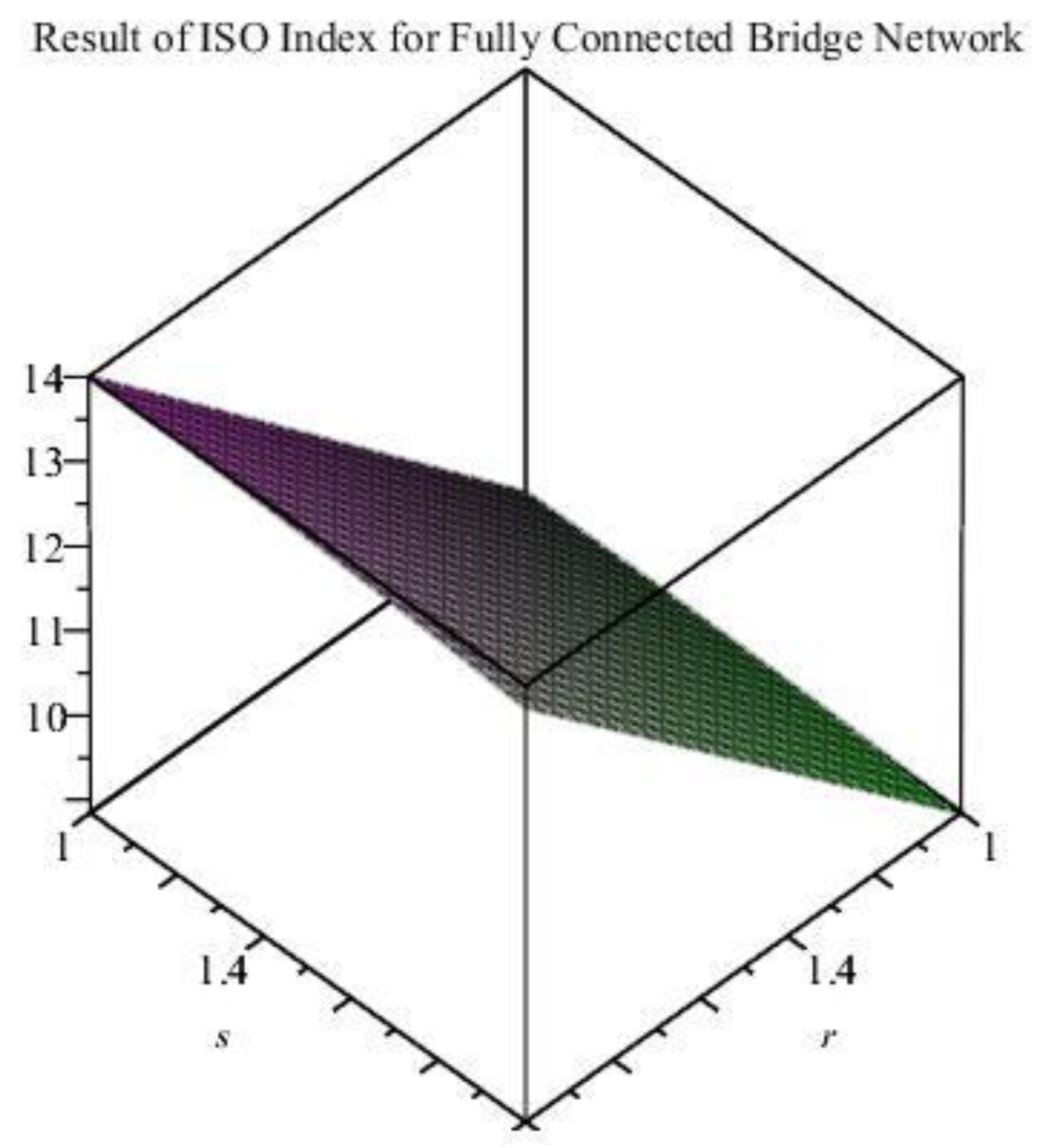
4.3.1. Bridge Graph Gr (Ks, v) over Complete Graph
4.3.2. Theorem 3
4.4. Main Results of Honeycomb Network
4.4.1. Honeycomb Graph
4.4.2. Theorem 4
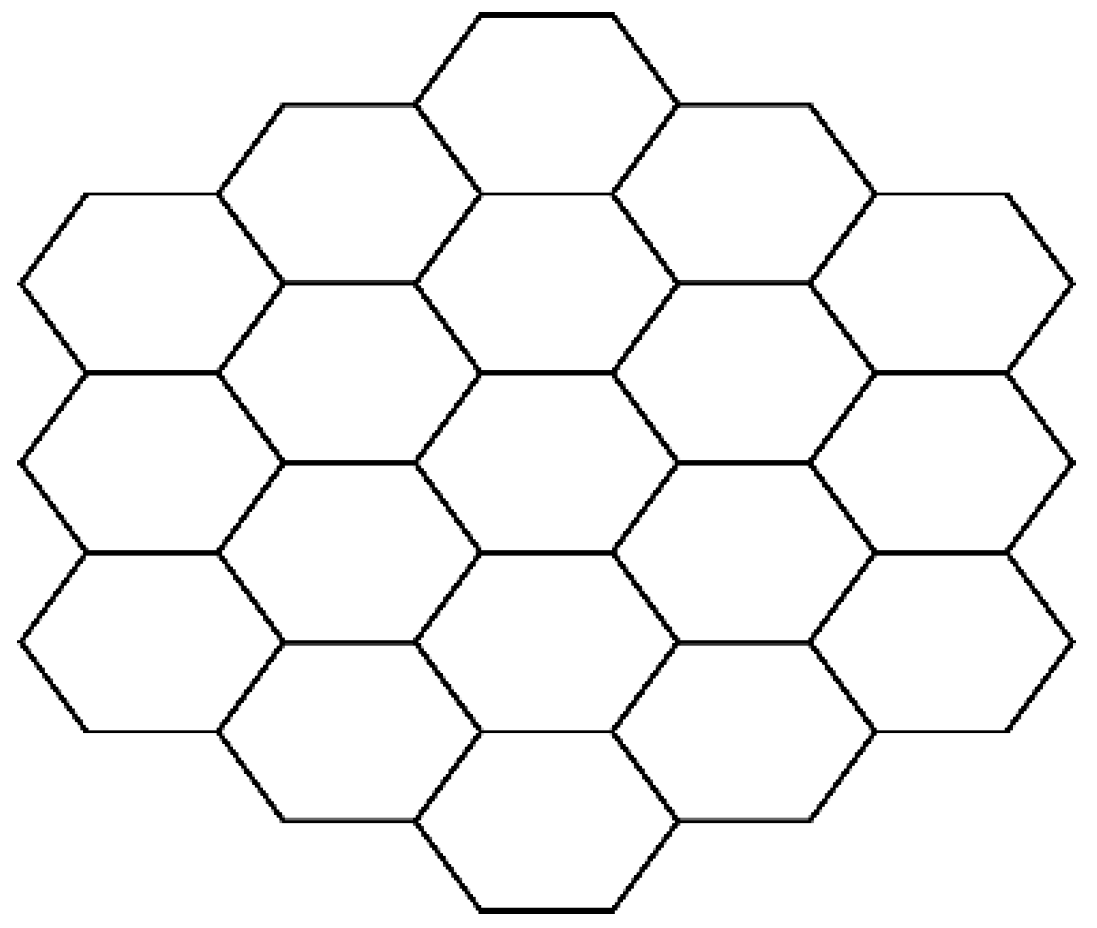
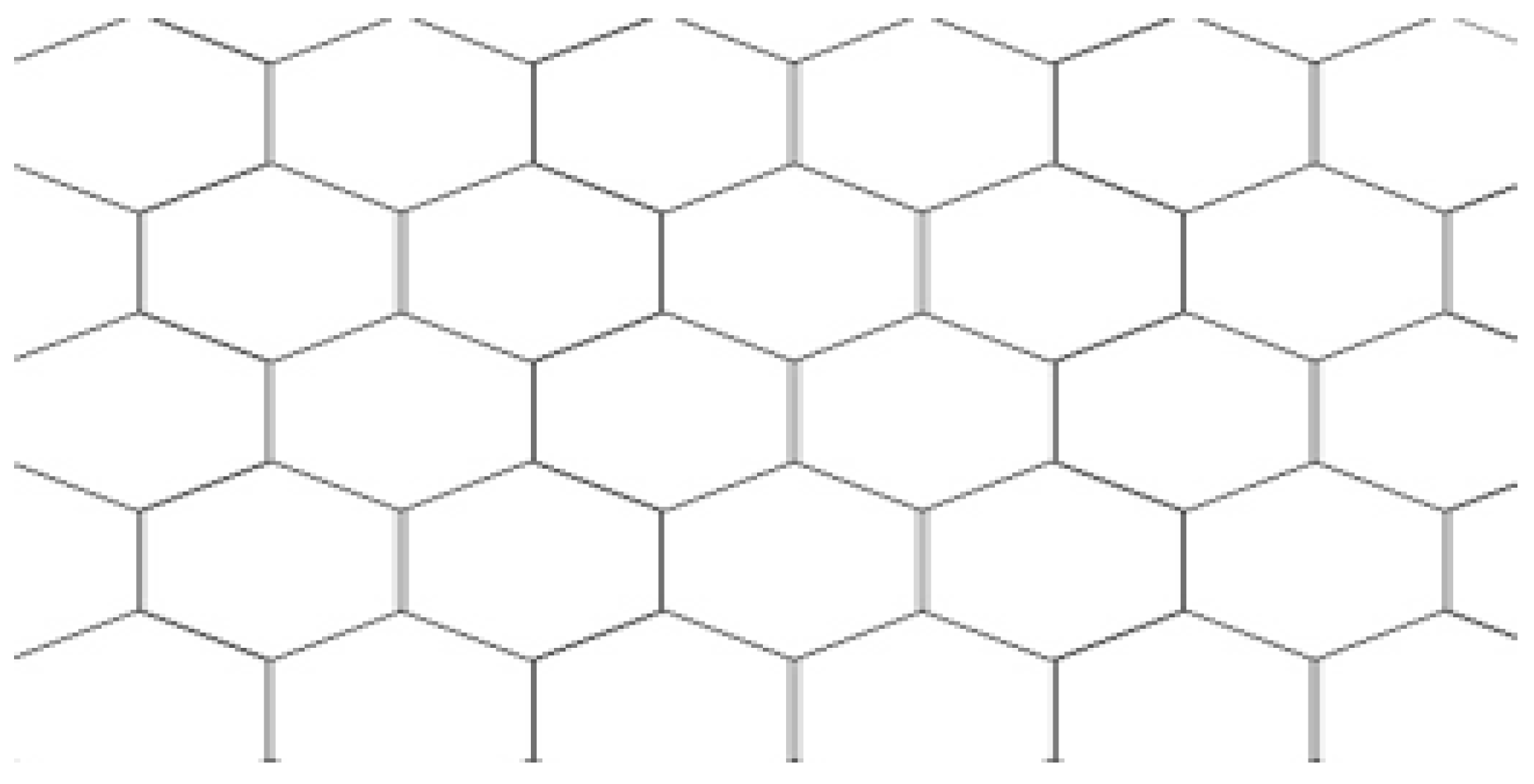
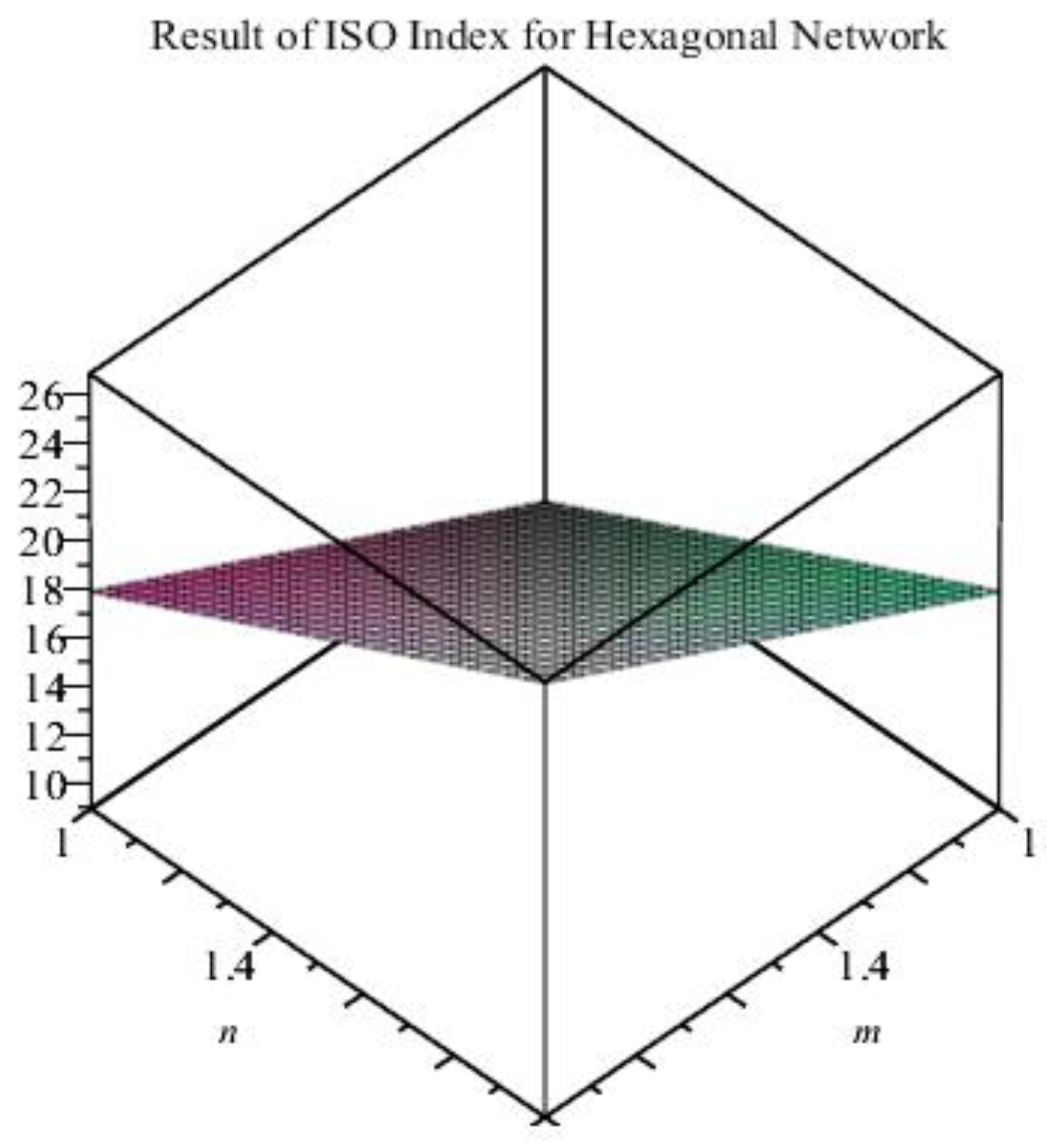
4.5. Main Results of Regular Hexagonal Cell Network
4.5.1. Regular Hexagonal Cells Network
4.5.2. Theorem 5
4.6. Main Results
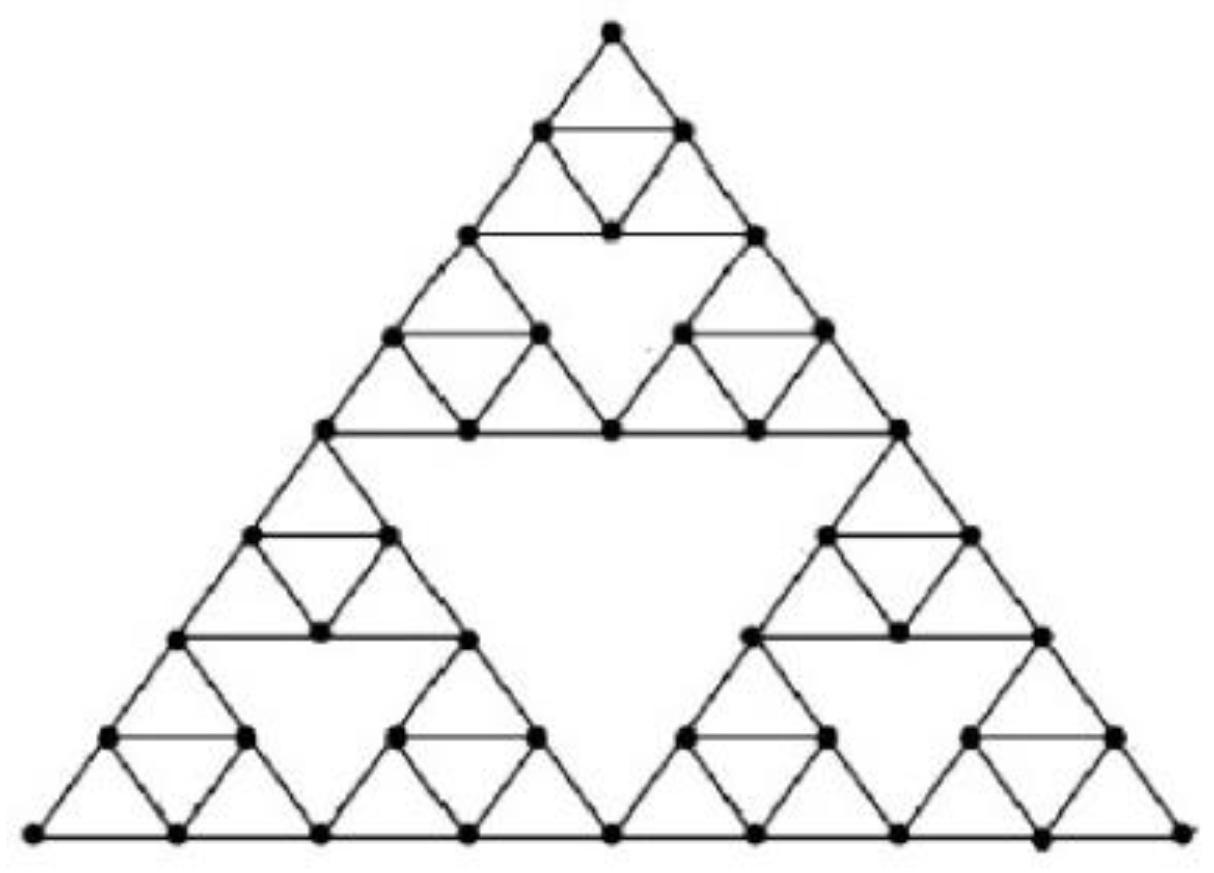
4.6.1. Sierpinski Network Graph
4.6.2. Theorem 6
4.7. Main Results
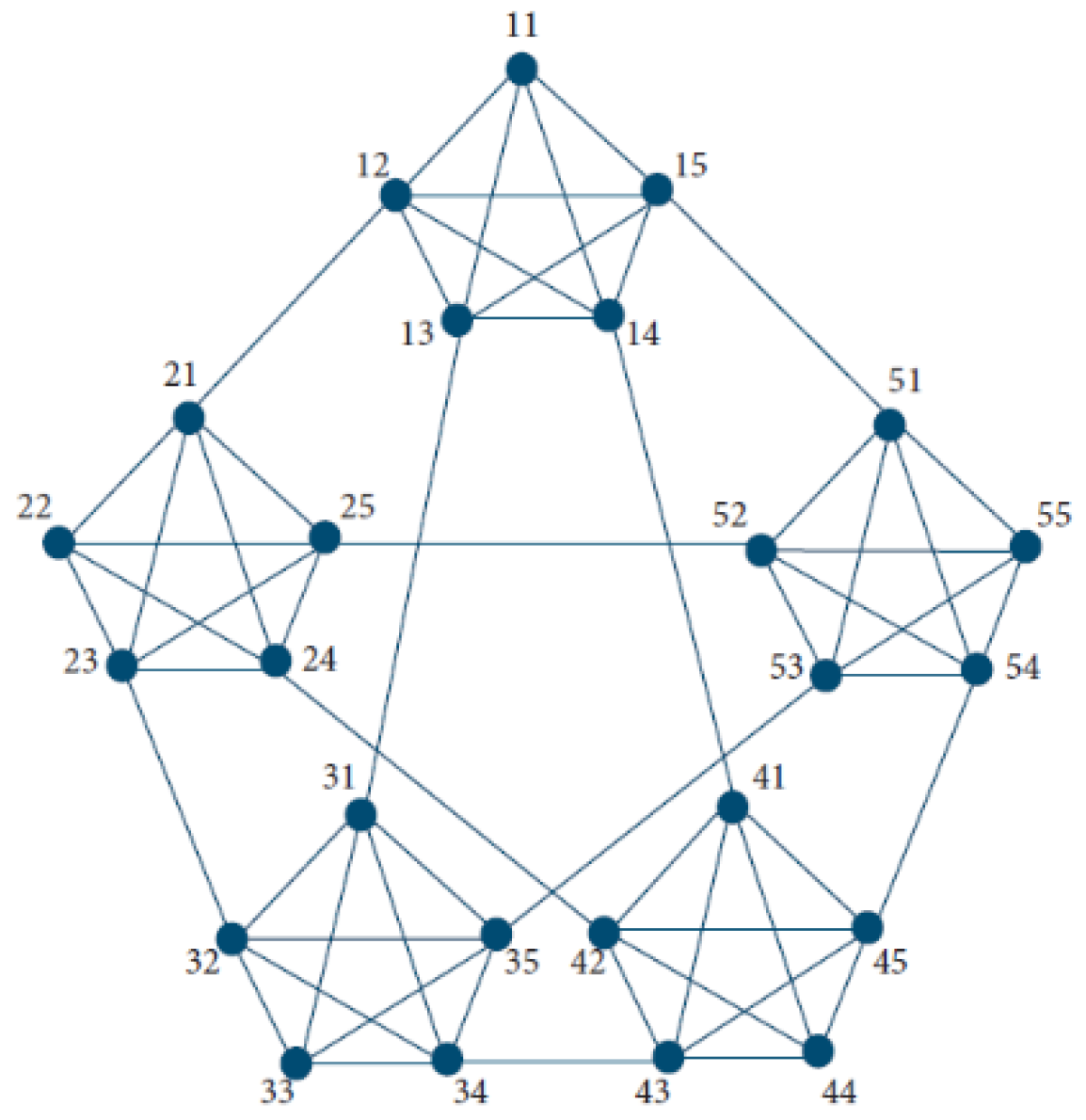
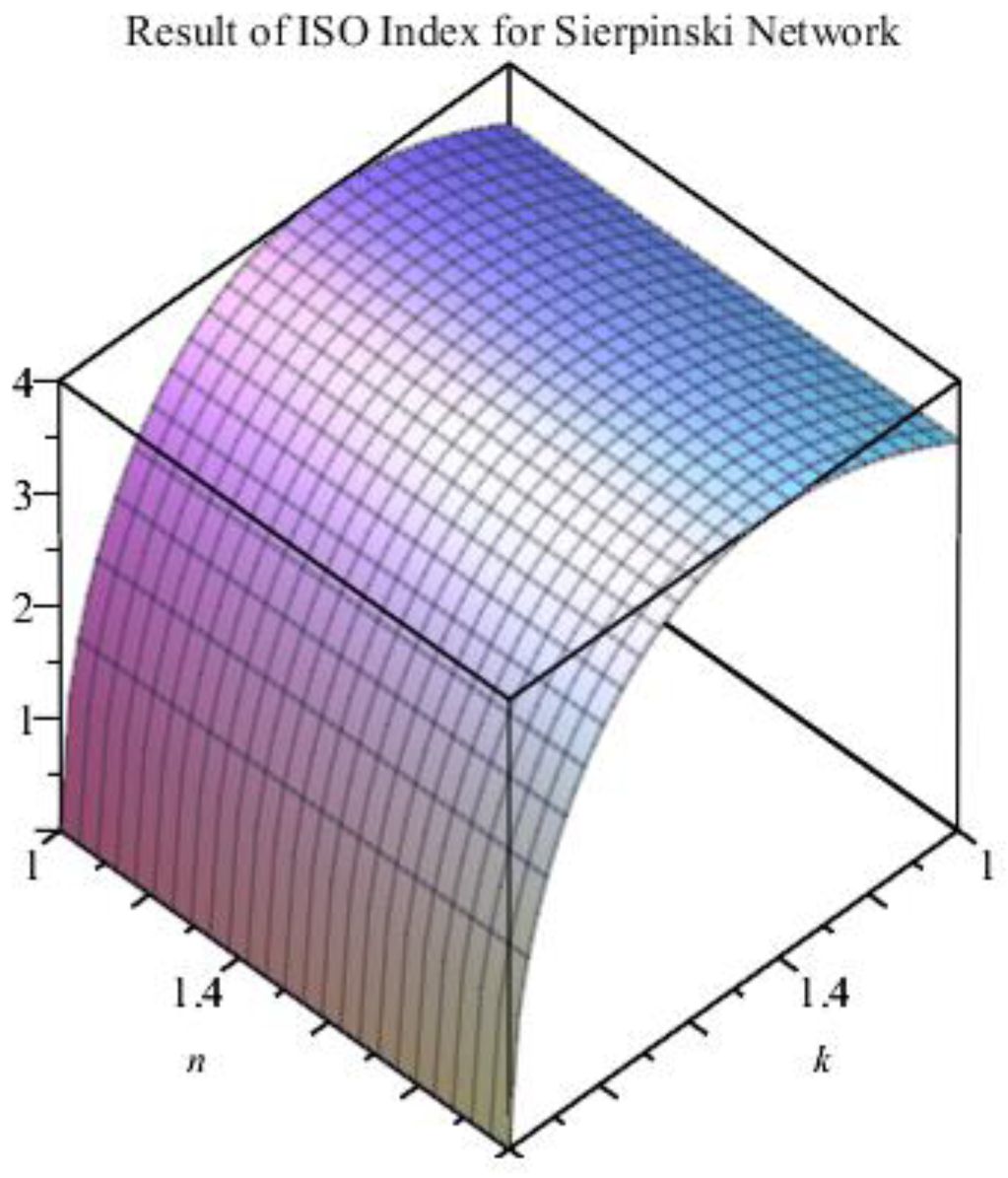
4.7.1. Sierpinski Network S(n, k)
4.7.2. Theorem 7
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mansour, T.; Schork, M. The Vertex PI Index and Szeged Index of Bridge Graphs. Discret. Appl. Math. 2009, 157, 1600–1606. [Google Scholar] [CrossRef]
- Khalaf, A.J.M.; Farhan, M.; Siddiqui, M.; Farahani, M. On Degree Based Topological Indices of Bridge Graphs [547]. J. Discret. Math. Sci. Cryptogr. 2020, 23, 1139–1156. [Google Scholar] [CrossRef]
- Imran, M.; Sabeel-e-Hafi; Gao, W.; Reza Farahani, M. On Topological Properties of Sierpinski Networks. Chaos Solitons Fractals 2017, 98, 199–204. [Google Scholar] [CrossRef]
- Abbas, S.; Raza, Z.; Siddiqui, N.; Khan, F.; Whangbo, T. Edge Metric Dimension of Honeycomb and Hexagonal Networks for IoT. Comput. Mater. Contin. 2022, 2022, 023003. [Google Scholar] [CrossRef]
- Ahmad, M.; Javaid, M.; Bonyah, E.; Saeed, M. Comparative Analysis of Subdivided Hex-Derived Networks Using Structural Descriptors. J. Chem. 2022, 2022, e6502473. [Google Scholar] [CrossRef]
- Gutman, I. Some Basic Properties of Sombor Indices. Open J. Discret. Appl. Math. 2021, 4, 1–3. [Google Scholar] [CrossRef]
- Kulli, V. Contraharmonic quadratic index of certain nanostar dendrimers. Int. J. Math. 2022, 13, 1–7. [Google Scholar]
- Khalid, H.; Muhammad, I.; Abaid, U.; Muhammad, A.; Ahmed, A.; Adel, B.; Khalid, A. K-Banhatti Sombor Invariants of Certain Computer Networks. Comput. Mater. Contin. 2022, 73, 15. [Google Scholar]
- Zhong, J.F.; Rauf, A.; Naeem, M.; Rahman, J.; Aslam, A. Quantitative Structure-Property Relationships (QSPR) of Valency Based Topological Indices with Covid-19 Drugs and Application. Arab. J. Chem. 2021, 14, 103240. [Google Scholar] [CrossRef]
- Kiralj, R.; Ferreira, M. Basic validation procedures for regression models in QSAR and QSPR studies: Theory and application. J. Braz. Chem. Soc. 2021, 20, 770–787. [Google Scholar] [CrossRef]
- Yousaf, S.; Bhatti, A.A.; Ali, A. On Total Irregularity Index of Trees with given Number of Segments or Branching Vertices. Chaos Solitons Fractals 2022, 157, 111925. [Google Scholar] [CrossRef]
- Valle, M.E.; Francisco, S.; Granero, M.A.; Velasco-Forero, S. Irregularity Index for Vector-Valued Morphological Operators. J. Math. Imaging Vis. 2022, 1, 1007. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Shahzadi, Z.; Kang, S.M. Some Invariants of Circulant Graphs. Symmetry 2016, 8, 134. [Google Scholar] [CrossRef]
- Virk, A.U.R.; Rehman, M.A.; Nazeer, W. New Definition of Atomic Bond Connectivity Index to Overcome Deficiency of Structure Sensitivity and Abruptness in Existing Definition. Sci. Inq. Rev. 2019, 3, 01–20. [Google Scholar] [CrossRef]
- Hashmi, M.; Chaudhry, F.; Khalaf, A.J.M.; Farahani, M. Investigation of Dendrimer Structures by Means of Reverse Atomic Bond Connectivity Index. J. Discret. Math. Sci. Cryptogr. 2021, 24, 473–485. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Virk, A.U.R.; Nazeer, W.; Rehman, M.A.; Kang, S.M. On the Multiplicative Degree-Based Topological Indices of Silicon-Carbon Si2C3-I[p,q] and Si2C3-II[p,q]. Symmetry 2018, 10, 320. [Google Scholar] [CrossRef]
- Virk, A.U.R. Multiplicative shingali and kanabour indices for bismuth tri-iodide. J. Prime Res. Math. 2020, 16, 80–88. [Google Scholar]
- Alsheekhhussain, Z.; Réti, T.; Ali, A. Weighted Graph Irregularity Indices Defined on the Vertex Set of a Graph. J. Math. 2022, 2022, e7834080. [Google Scholar] [CrossRef]
- Alrasheed, W.A.; Owayda, A.M.; Hajeer, M.Y.; Khattab, T.Z.; Almahdi, W.H. Validity and Reliability of Intraoral and Plaster Models’ Photographs in the Assessment of Little’s Irregularity Index, Tooth Size-Arch Length Discrepancy, and Bolton’s Analysis. Cureus 2022, 14, 23067. [Google Scholar] [CrossRef] [PubMed]
- Yousaf, S.; Bhatti, A.A. Maximum Total Irregularity Index of Some Families of Graph with Maximum Degree n − 1. Asian-Eur. J. Math. 2022, 15, 2250069. [Google Scholar] [CrossRef]
- Zhang, Q.; Munir, M.M.; Ahmad, H.; Liu, J.-B. Irregularity Molecular Descriptors of Cerium Oxide CeO2 Based on Mathematical Model and Calculation. Arab. J. Chem. 2022, 15, 103567. [Google Scholar] [CrossRef]
- Geneson, J.; Tsai, S.-F. Peripherality in Networks: Theory and Applications. J. Math. Chem. 2022, 60, 1021–1079. [Google Scholar] [CrossRef]
- Yurttaş Güneş, A.; Togan, M.; Demirci, M.; Cangül, İ.N. Inverse Problem for Albertson Irregularity Index. TWMS J. Appl. Eng. Math. 2022, 12, 662. [Google Scholar]
- Hamid, K.; Iqbal, M.; Arif, E.; Mahmood, Y.; Khan, A.; Kama, N.; Azmi, A.; Ikram, A. K-Banhatti Invariants Empowered Topological Investigation of Bridge Networks. Comput. Mater. Contin. 2022, 73, 5423–5440. [Google Scholar] [CrossRef]
- Radanliev, P.; De Roure, D. New and emerging forms of data and technologies: Literature and bibliometric review. Multimedia Tools Appl. 2022, 1–25. [Google Scholar] [CrossRef]
- Hamid, K.; Iqbal, M.W.; Ashraf, M.U.; Gardezi, A.A.; Ahmad, S.; Alqahtani, M.; Shafiq, M. Intelligent systems and photovoltaic cells empowered topologically by sudoku networks. Comput. Mater. Contin. 2023, 74, 4221–4238. [Google Scholar] [CrossRef]
- Alghamdi, A.M.; Hamid, K.; Iqbal, M.; Ashraf, U.; Alshahrani, A.; Alshamrani, A. Topological evaluation of certain computer networks by contraharmonic-quadratic indices. Comput. Mater. Contin. 2023, 74, 3795–3810. [Google Scholar] [CrossRef]
- Wan, B.-F.; Zhou, Z.-W.; Xu, Y.; Zhang, H.-F. A Theoretical Proposal for a Refractive Index and Angle Sensor Based on One-Dimensional Photonic Crystals. IEEE Sens. J. 2021, 21, 331–338. [Google Scholar] [CrossRef]
- Hamid, K.; Iqbal, M.w.; Muhammad, H.; Fuzail, Z.; Nazir, Z. Topological Analysis Empowered Bridge Network Variants by Dharwad Indices. Jilin Daxue Xuebao (Gongcheng Jishuban)/J. Jilin Univ. (Eng. Technol. Ed.) 2022, 41, 53–67. [Google Scholar]





| Sr. No. | Title of Research Paper | Year | Networks Solved | Invariants Used | Results |
|---|---|---|---|---|---|
| 1 | Topological Properties Of Degree-Based Invariants Via M-Polynomial Approach | 2022 | Hexagonal Networks | Zagreb Indices, Randi’C, Product Connectivity Gourava Index and their Forms | Give valuable information about the molecular structure or network and applications in QSPR & QSAR. |
| 2 | Contraharmonic Quadratic Index Of Certain Nanostar Dendrimers | 2022 | Dendrimer Nanostars | Contraharmonic-Quadratic Index and Quadratic-Contraharmonic Index | computed the CQ index for some standard graphs |
| 3 | Some Results On The Sombor Indices of Graphs | 2021 | Degree-Regular Graph/Network | The Sombor Index, The Reduced Sombor Index and the Average Sombor Index | Establishing inequalities related to the aforementioned three graph invariants and proving a recently proposed conjecture concerning the sombor index |
| 4 | Some Basic Properties of Sombor Indices | 2021 | Regular Graph or Network | Vertex-Degree-Based (VDB) Molecular Structure Descriptors (Sombor Index and its Reduced Form) | Any reduced VDB index can be viewed as a reduced sombor-type index |
| 5 | Analysis Of Dendrimer Generation By Sombor Indices | 2021 | Dendrimers Generation Networks | Sombor Index and Reduced Sombor Index | Computed sombor indices for phosphorus-containing dendrimers & types of dendrimers. |
| 6 | Sombor Index of Some Nanostructures | 2021 | Nanostructures | Sombor Index | Computed explicit formulae for sombor index of 2D-lattice, nanotube, and nanotorus |
| 7 | Polynomials And General Degree-Based Topological Indices of Generalized Sierpinski Networks | 2021 | Sierpinski Networks | Connectivity Polynomials Such As m-Polynomial, Zagreb Polynomials, Forgotten Polynomial, (A, Β)-Zagreb Index and Several Other General Indices | These facts can be Physicochemical properties of the molecules modeled on the S(k, n) networks can be forecasted using the results. |
| 8 | The Calculations of Topological Indices on Certain Networks | 2021 | Hexagonal Networks | ABC Index, AZI Index, GA Index, The Multiplicative Version Of Ordinary First Zagreb Index, The Second Multiplicative Zagreb Index, and Zagreb Index | Calculating the correlation index provides potential help for scholars to study networks characteristics better. for further work, if the corresponding networks are replaced by other networks |
| 9 | Discovering Irregularities from Computer Networks by Topological Mapping | 2022 | Bridge Networs, Hexagonal Networks, Honeycomb Networks and Sierpinski Networks | Irregularity Sombor Index | Finding Sharp upper bounds, lower bounds and irregularities |
| ε | ε(du, dv) | de | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(1, 2) | 1 | ε(1, 1) | R |
| ε2 | ε(2, 2) | 2 | ε(2, 2) | 3r + 2 |
| ε3 | ε(2, 3) | 3 | ε(2, 3) | R |
| ε4 | ε(3, 3) | 4 | ε(3, 4) | r − 3 |
| ε | ε(du, dv) | de | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(2, 2) | 2 | ε(2, 2) | rs − 2r |
| ε2 | ε(2, 3) | 3 | ε(2, 3) | 4 |
| ε3 | ε(2, 4) | 4 | ε(2, 4) | 2r − 4 |
| ε4 | ε(3, 4) | 5 | ε(3, 5) | 2 |
| ε5 | ε(4, 4) | 6 | ε(4, 6) | r − 3 |
| ε | ε(du, dv) | De | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(4, 5) | 7 | ε(4, 7) | 2 |
| ε2 | ε(4, S−1) | S + 1 | ε(4, s+1) | 2 |
| ε3 | ε(5, 5) | 8 | ε(5, 8) | r − 2 |
| ε4 | ε(5, S−1) | S + 2 | ε(5, s+2) | r − 2 |
| ε5 | ε(S−1, S−1) | 2s − 4 | ε(s−1, 2s−4) | [rs(r − 1) − 2(r + 1)]/2 |
| Ε | ε(du, dv) | de | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(5, 5) | 8 | ε(5, 8) | 6 |
| ε2 | ε(5, 7) | 10 | ε(5,10) | 12(n − 1) |
| ε3 | ε(7, 9) | 14 | ε(7, 14) | 6(n − 1) |
| ε4 | ε(9, 9) | 16 | ε(9, 16) | 9n2 − 21n + 12 |
| Ε | ε(du, dv) | de | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(2, 2) | 2 | ε(2, 2) | 2n + 4 |
| ε2 | ε(2, 3) | 3 | ε(2, 3) | 4m + 4n + 4 |
| ε3 | ε(3,3) | 4 | ε(3, 4) | 6 mn + m − 5n − 4 |
| Ε | ε(du, dv) | De | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(2, 4) | 4 | ε(2, 4) | 6 |
| ε2 | ε(4, 4) | 6 | ε(4, 6) | 3n − 6 |
| ε | ε(du, dv) | De | ε(du, de) | Recurrence |
|---|---|---|---|---|
| ε1 | ε(2, k) | k | ε(2, k) | 2k |
| ε2 | ε(3, 3) | 4 | ε(3, 4) | (kn+1 − 5k)/2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamid, K.; Waseem Iqbal, M.; Abbas, Q.; Arif, M.; Brezulianu, A.; Geman, O. Discovering Irregularities from Computer Networks by Topological Mapping. Appl. Sci. 2022, 12, 12051. https://doi.org/10.3390/app122312051
Hamid K, Waseem Iqbal M, Abbas Q, Arif M, Brezulianu A, Geman O. Discovering Irregularities from Computer Networks by Topological Mapping. Applied Sciences. 2022; 12(23):12051. https://doi.org/10.3390/app122312051
Chicago/Turabian StyleHamid, Khalid, Muhammad Waseem Iqbal, Qaiser Abbas, Muhammad Arif, Adrian Brezulianu, and Oana Geman. 2022. "Discovering Irregularities from Computer Networks by Topological Mapping" Applied Sciences 12, no. 23: 12051. https://doi.org/10.3390/app122312051
APA StyleHamid, K., Waseem Iqbal, M., Abbas, Q., Arif, M., Brezulianu, A., & Geman, O. (2022). Discovering Irregularities from Computer Networks by Topological Mapping. Applied Sciences, 12(23), 12051. https://doi.org/10.3390/app122312051








