Fault-Tolerant Control of Multi-Joint Robot Based on Fractional-Order Sliding Mode
Abstract
1. Introduction
2. Related Works
3. Fractional-Order Sliding Mode Controller Design
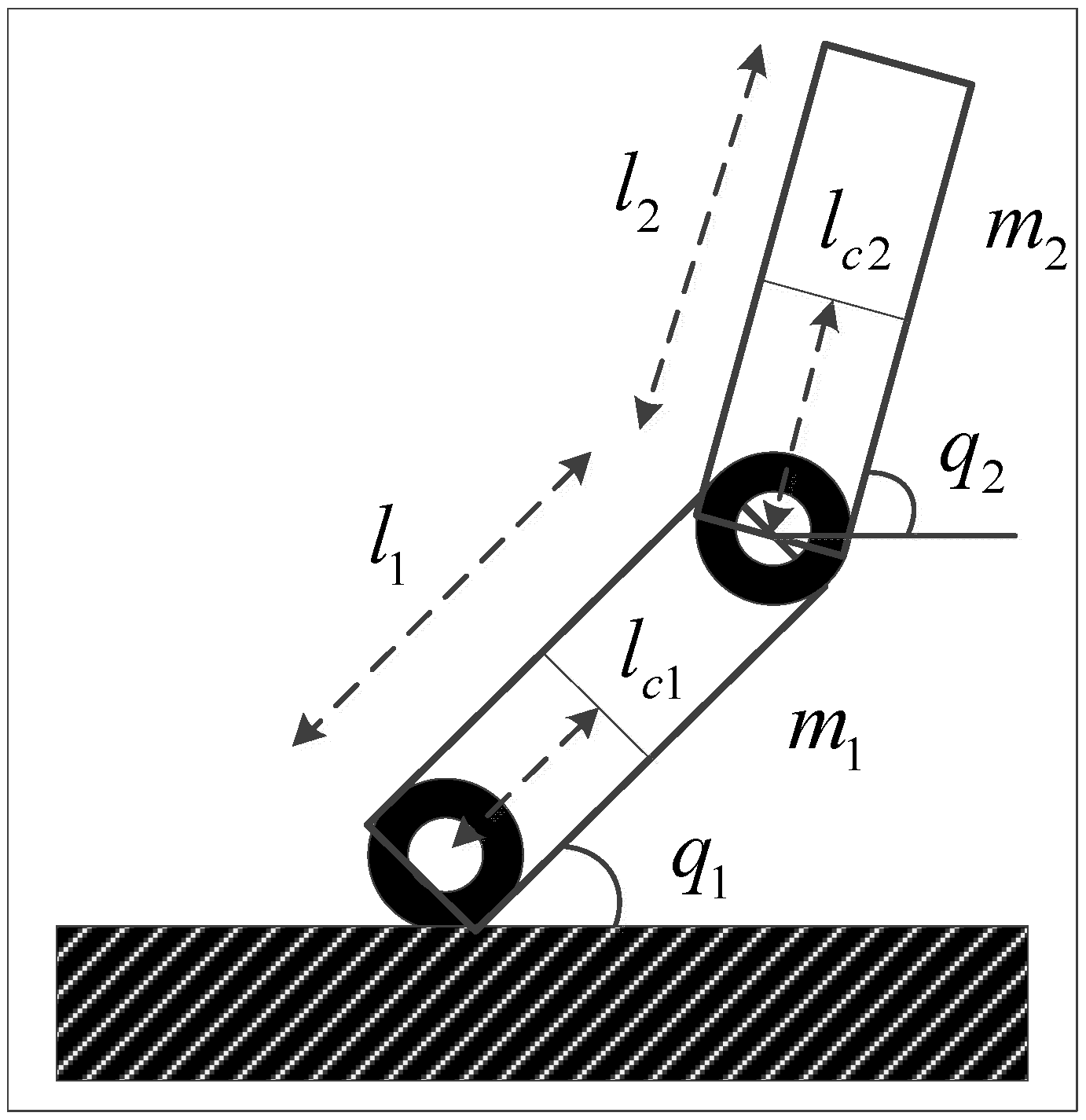
3.1. Multi-Joint Robot Model
3.2. Design of Fractional-Order Sliding Mode Controller for Multi-Joint Robots
3.3. Proof of Stability
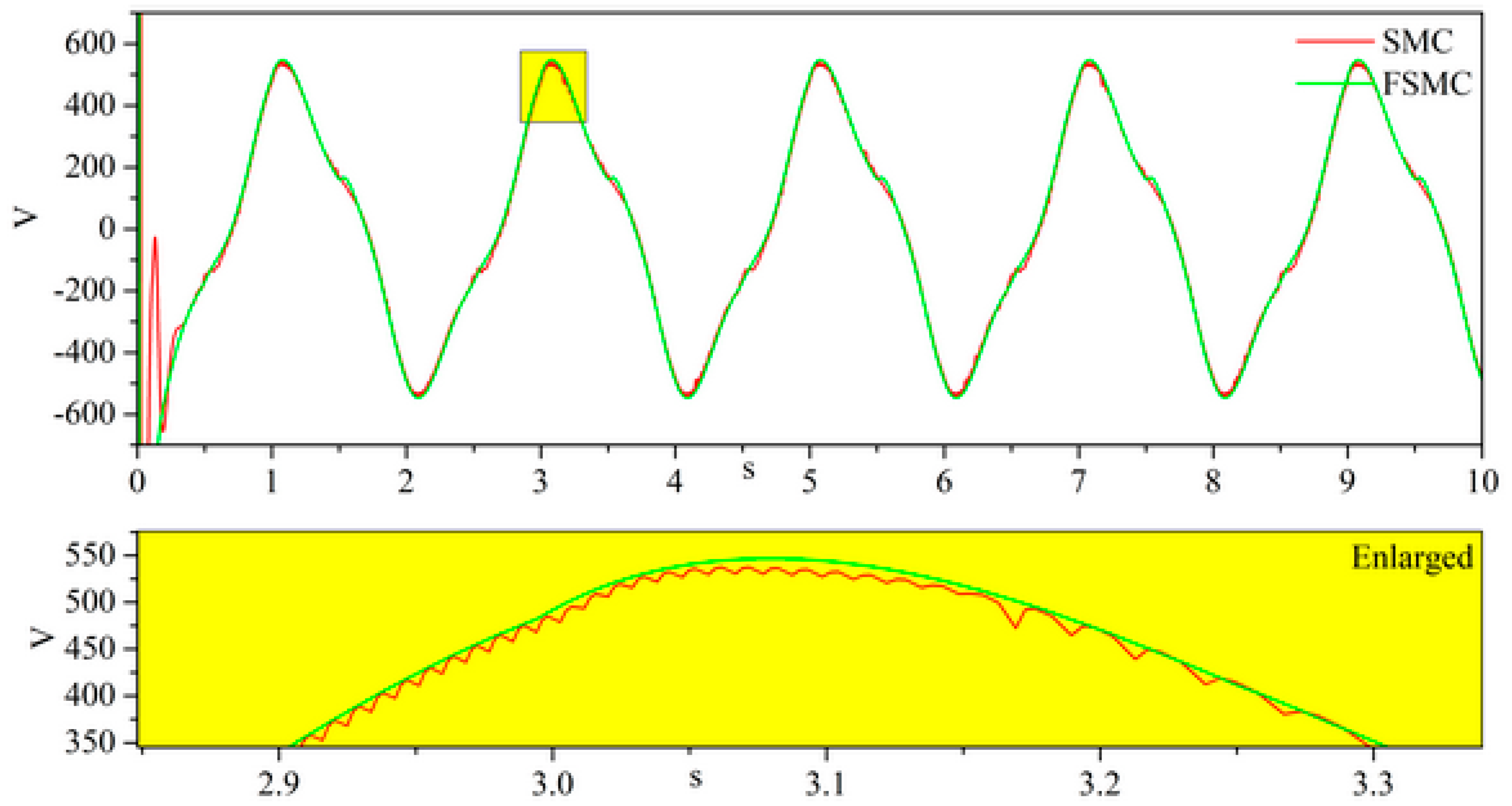
4. Simulation and Experimental Results
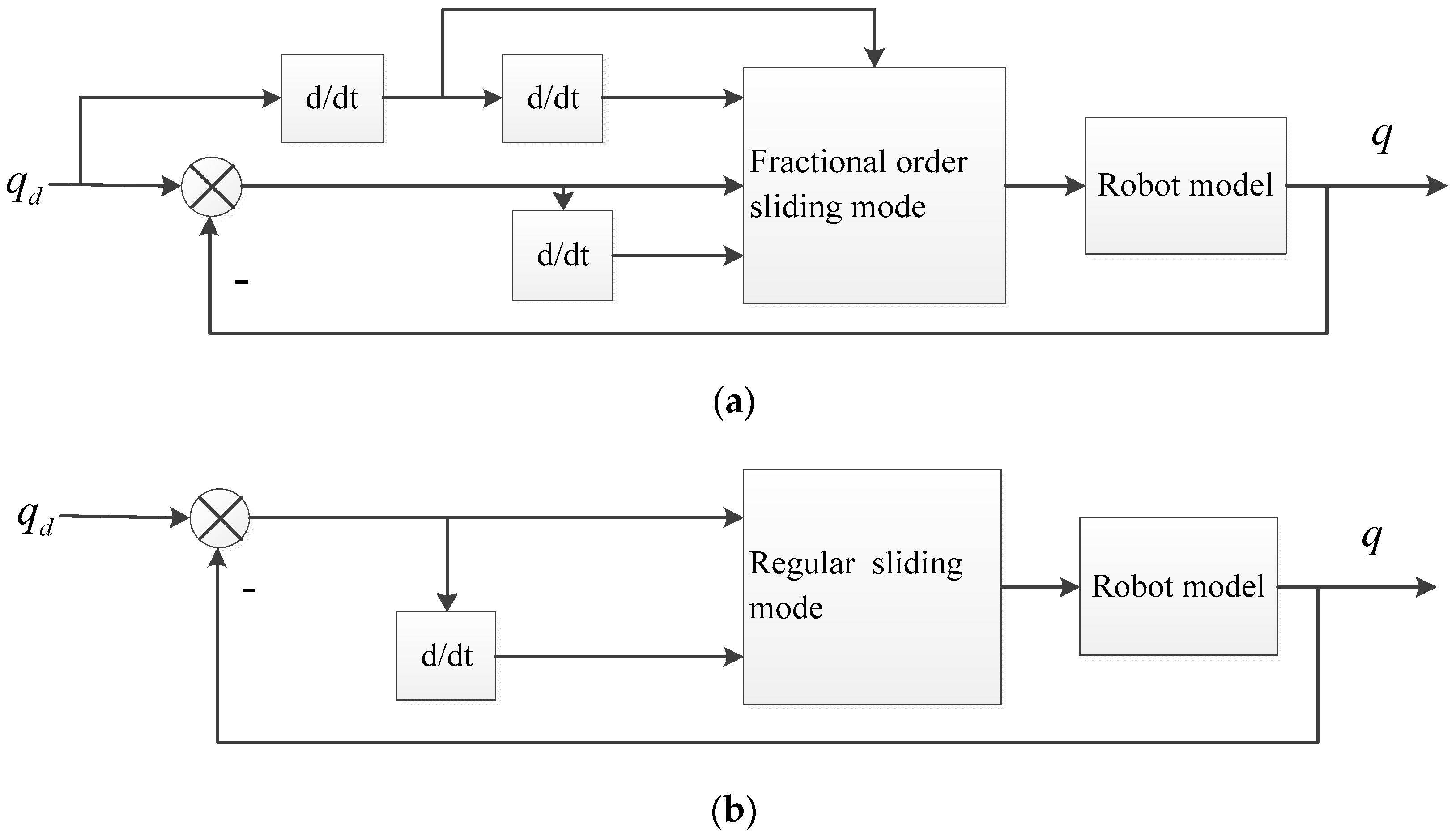
4.1. Control Block
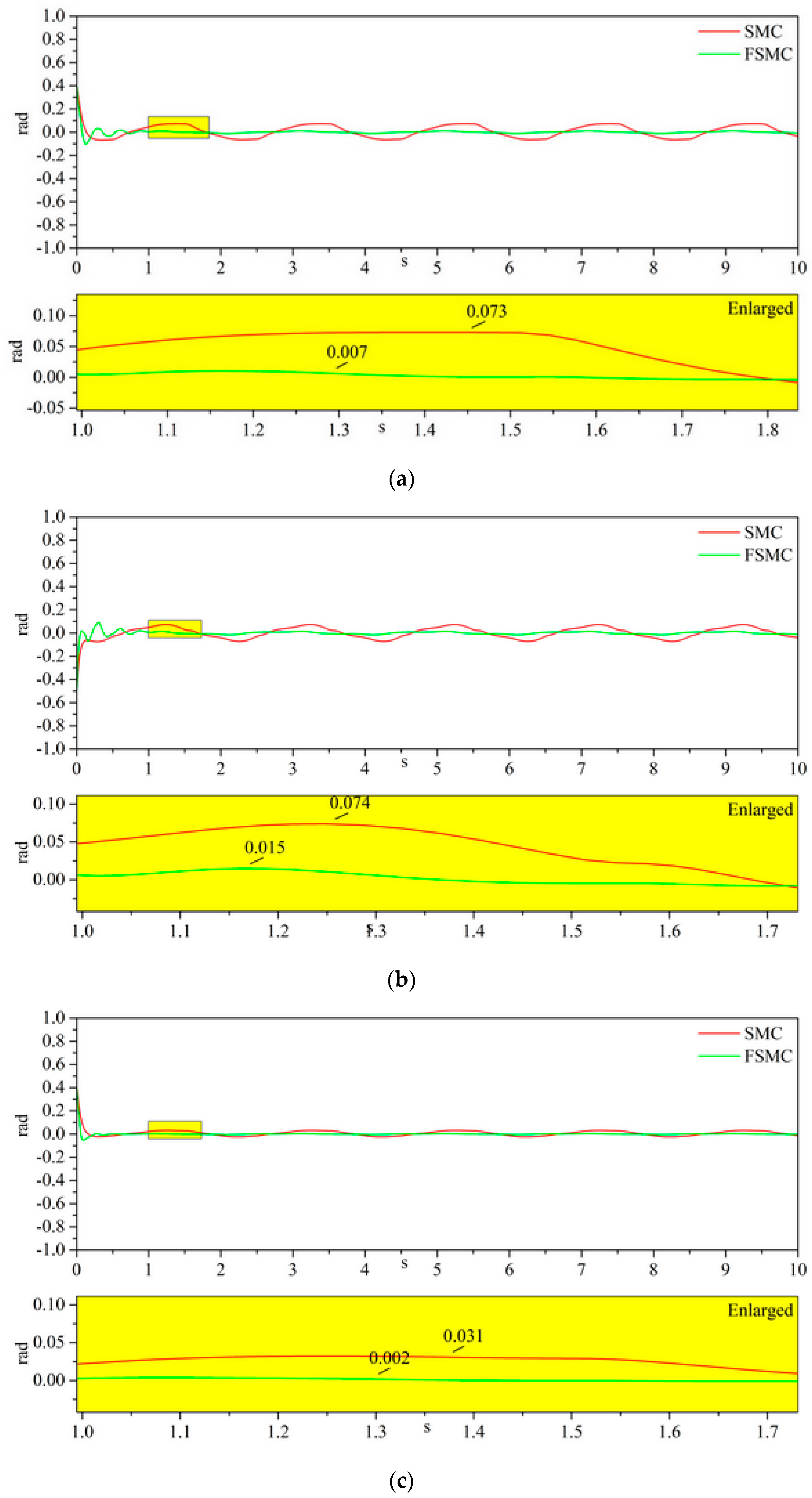
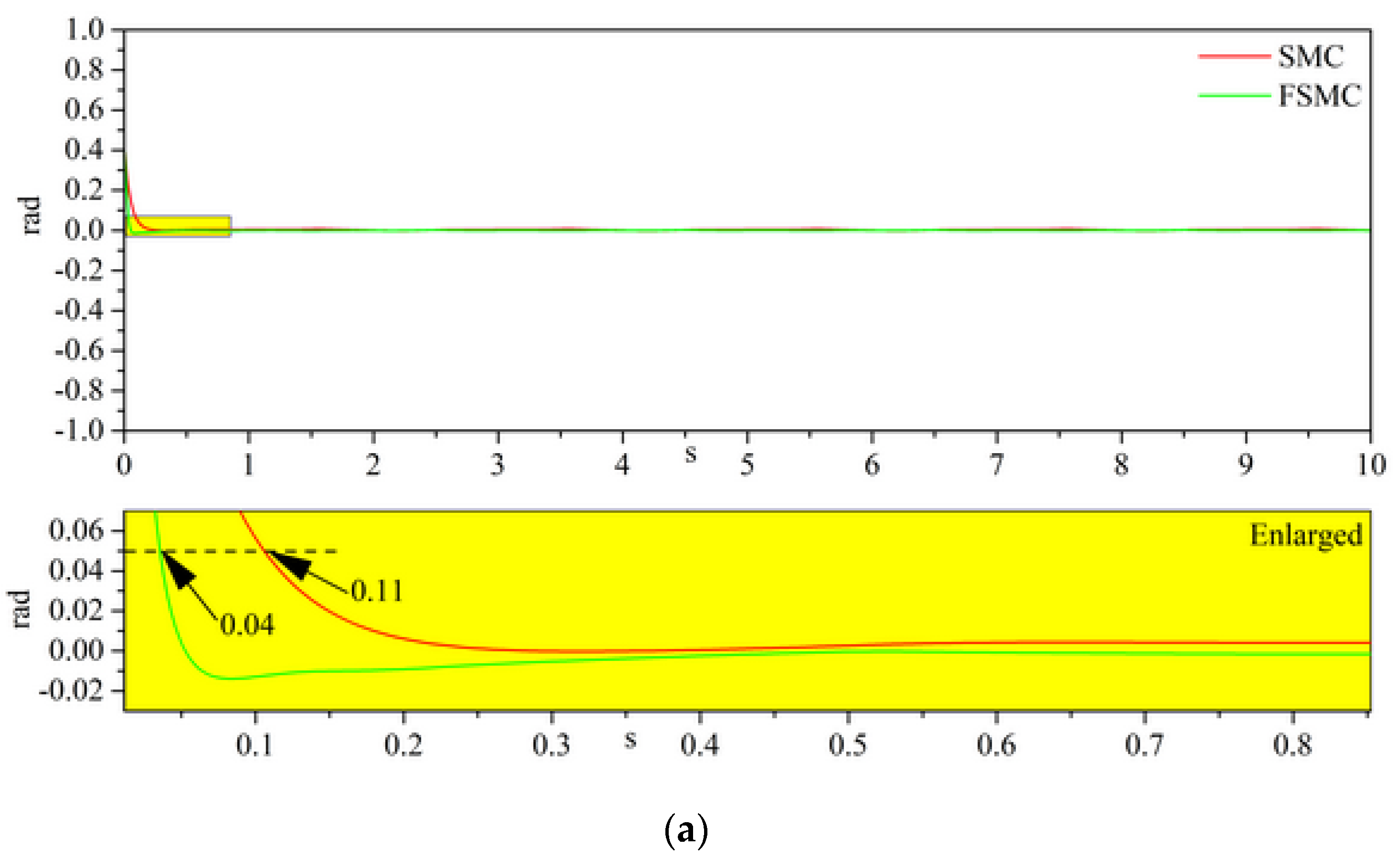
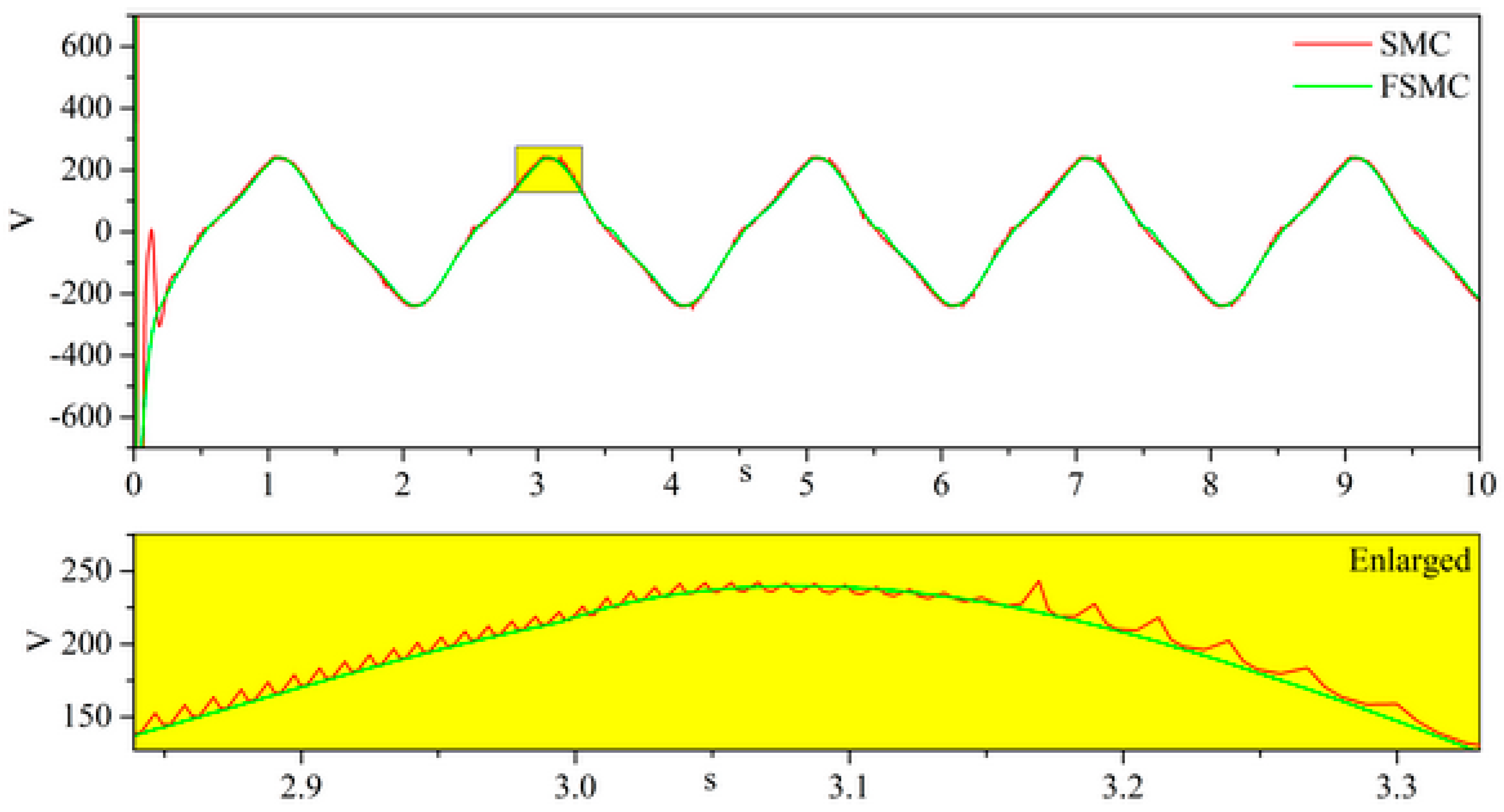
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.H. Multi-Axis Force-Torque Sensors for Measuring Zero-Moment Point in Humanoid Robots: A Review. IEEE Sens. J. 2020, 20, 1126–1141. [Google Scholar] [CrossRef]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Urrea, C.; Kern, J. Fault-Tolerant Controllers in Robotic Manipulators. Performance Evaluations. IEEE Lat. Am. Trans. 2013, 11, 1318–1324. [Google Scholar] [CrossRef]
- Sanket, N.J.; Singh, C.D.; Ganguly, K.; Fermüller, C.; Aloimonos, Y. GapFlyt: Active Vision Based Minimalist Structure-Less Gap Detection for Quadrotor Flight. IEEE Robot. Autom. Lett. 2018, 3, 2799–2806. [Google Scholar] [CrossRef]
- Khalastchi, E.; Kalech, M. Fault Detection and Diagnosis in Multi-Robot Systems: A Survey. Sensors 2019, 19, 4019. [Google Scholar] [CrossRef]
- Shi, C.; Yang, G.; Li, X. Data-Based Fault-Tolerant Consensus Control for Uncertain Multiagent Systems Via Weighted Edge Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 2548–2558. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Su, C.; Deng, J.; Zhang, W. Vision-Based Model Predictive Control for Steering of a Nonholonomic Mobile Robot. IEEE Trans. Control. Syst. Technol. 2016, 24, 553–564. [Google Scholar] [CrossRef]
- Yang, C.; Chen, C.; He, W.; Cui, R.; Li, Z. Robot Learning System Based on Adaptive Neural Control and Dynamic Movement Primitives. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 777–787. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Jin, L. Kinematic control of redundant manipulators using neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2243–2254. [Google Scholar] [CrossRef]
- Wei, H.; Dong, Y. Adaptive Fuzzy Neural Network Control for Constrained Robot Using Impedance Learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1174–1186. [Google Scholar]
- Yang, C.; Peng, G.; Cheng, L.; Na, J.; Li, Z. Force Sensorless Admittance Control for Teleoperation of Uncertain Robot Manipulator Using Neural Networks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3282–3292. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Miao, J.; Na, J.; Zhao, Z.; Yang, C. Composite-Learning-Based Adaptive Neural Control for Dual-Arm Robots with Relative Motion. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1010–1021. [Google Scholar] [CrossRef] [PubMed]
- Bugeja, M.K.; Fabri, S.G.; Camilleri, L. Dual Adaptive Dynamic Control of Mobile Robots Using Neural Networks. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 39, 129–141. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Hughes, J.; Georgopoulou, A.; Clemens, F.; Iida, F. Using Redundant and Disjoint Time-Variant Soft Robotic Sensors for Accurate Static State Estimation. IEEE Robot. Autom. Lett. 2021, 6, 2099–2105. [Google Scholar] [CrossRef]
- Ferrell, C. Failure recognition and fault tolerance of an autonomous robot. Adapt. Behav. 1994, 2, 375–398. [Google Scholar] [CrossRef]
- Wang, H.; Daley, S. Actuator fault diagnosis: An adaptive observerbased technique. IEEE Trans. Automat. Contr. 1996, 41, 1073–1078. [Google Scholar] [CrossRef]
- Tao, G.; Ma, X.; Joshi, S.M. Adaptive state feedback control of systems with actuator failures. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 4, pp. 2669–2673. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H.; Tang, D.; Hou, Y.; Wang, Y. Adaptive Fixed-Time Fault-Tolerant Tracking Control and Its Application for Robot Manipulators. IEEE Trans. Ind. Electron. 2022, 69, 2956–2966. [Google Scholar] [CrossRef]
- Inoue, D.; Ito, Y.; Yoshida, H. Optimal Transport-Based Coverage Control for Swarm Robot Systems: Generalization of the Voronoi Tessellation-Based Method. IEEE Control. Syst. Lett. 2021, 5, 1483–1488. [Google Scholar] [CrossRef]
- Ratner, E.; Bajcsy, A.; Fong, T.; Tomlin, C.J.; Dragan, A.D. Efficient Dynamics Estimation with Adaptive Model Sets. IEEE Robot. Autom. Lett. 2021, 6, 2373–2380. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Cocquempot, V.; Najjar, M.E.B.E.; Jiang, B. Adaptive Compensation of Multiple Actuator Faults for Two Physically Linked 2WD Robots. IEEE Trans. Robot. 2018, 34, 248–255. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.-G. Distributed Adaptive Event-Triggered Fault-Tolerant Synchronization for Multiagent Systems. IEEE Trans. Ind. Electron. 2021, 68, 1537–1547. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Cai, Y.; Han, J. Adaptive Fuzzy Fault-Tolerant Tracking Control for Partially Unknown Systems with Actuator Faults via Integral Reinforcement Learning Method. IEEE Trans. Fuzzy Syst. 2019, 27, 1986–1998. [Google Scholar] [CrossRef]
- Prakash, R.; Behera, L.; Mohan, S.; Jagannathan, S. Dual-Loop Optimal Control of a Robot Manipulator and Its Application in Warehouse Automation. IEEE Trans. Autom. Sci. Eng. 2022, 19, 262–279. [Google Scholar] [CrossRef]
- Peng, H.J.; Fei, L.F.; Liu, J.G. A symplectic instantaneous optimal control for robot trajectory tracking with differential-algebraic equation models. IEEE Trans. Ind. Electron. 2019, 67, 3819–3829. [Google Scholar] [CrossRef]
- Medina, J.R.; Hirche, S. Considering Uncertainty in Optimal Robot Control Through High-Order Cost Statistics. IEEE Trans. Robot. 2018, 34, 1068–1081. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, J.; Li, H.; Huang, Q. Stable Parking Control of a Robot Astronaut in a Space Station Based on Human Dynamics. IEEE Trans. Robot. 2019, 36, 399–413. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Kong, H.; Ke, F. Model Predictive Tracking Control of Nonholonomic Mobile Robots with Coupled Input Constraints and Unknown Dynamics. IEEE Trans. Ind. Inform. 2018, 15, 3196–3205. [Google Scholar] [CrossRef]
- Liao, J.; Chen, Z.; Yao, B. Model-Based Coordinated Control of Four-Wheel Independently Driven Skid Steer Mobile Robot with Wheel–Ground Interaction and Wheel Dynamics. IEEE Trans. Ind. Inform. 2019, 15, 1742–1752. [Google Scholar] [CrossRef]
- Khadem, M.; O’Neill, J.; Mitros, Z.; da Cruz, L.; Bergeles, C. Autonomous Steering of Concentric Tube Robots via Nonlinear Model Predictive Control. IEEE Trans. Robot. 2020, 36, 1595–1602. [Google Scholar] [CrossRef]
- Thieffry, M.; Kruszewski, A.; Duriez, C.; Guerra, T. Control Design for Soft Robots Based on Reduced-Order Model. IEEE Robot. Autom. Lett. 2019, 4, 25–32. [Google Scholar] [CrossRef]
- Ziquan, Y.; Youmin, Z.; Bin, J. PID-type fault-tolerant prescribed performance control of fixed-wing UAV. J. Syst. Eng. Electron. 2021, 32, 1053–1061. [Google Scholar] [CrossRef]
- Van, M.; Mavrovouniotis, M.; Ge, S.S. An Adaptive Backstepping Nonsingular Fast Terminal Sliding Mode Control for Robust Fault Tolerant Control of Robot Manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1448–1458. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H. A Novel Fault-Tolerant Control Method for Robot Manipulators Based on Non-Singular Fast Terminal Sliding Mode Control and Disturbance Observer. IEEE Access 2020, 8, 109388–109400. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Robust Fault-Tolerant Control for a Class of Second-Order Nonlinear Systems Using an Adaptive Third-Order Sliding Mode Control. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 221–228. [Google Scholar] [CrossRef]
- Wang, H.; Pan, Y.; Li, S.; Yu, H. Robust Sliding Mode Control for Robots Driven by Compliant Actuators. IEEE Trans. Control. Syst. Technol. 2018, 27, 1259–1266. [Google Scholar] [CrossRef]
- Nguyen, V.-C.; Vo, A.-T.; Kang, H.-J. A Finite-Time Fault-Tolerant Control Using Non-Singular Fast Terminal Sliding Mode Control and Third-Order Sliding Mode Observer for Robotic Manipulators. IEEE Access 2021, 9, 31225–31235. [Google Scholar] [CrossRef]
- Nair, R.R.; Karki, H.; Shukla, A.; Jamshidi, M. Fault-Tolerant Formation Control of Nonholonomic Robots Using Fast Adaptive Gain Nonsingular Terminal Sliding Mode Control. IEEE Syst. J. 2018, 13, 1006–1017. [Google Scholar] [CrossRef]
- Mujumdar, A.; Tamhane, B.; Kurode, S. Observer-Based Sliding Mode Control for a Class of Noncommensurate Fractional-Order Systems. IEEE/ASME Trans. Mechatron. 2015, 20, 2504–2512. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, J.; Mi, X.; Khan, M.W. Fractional Order Sliding Mode Based Direct Power Control of Grid-Connected DFIG. IEEE Trans. Power Syst. 2017, 33, 3087–3096. [Google Scholar] [CrossRef]
- Momeni, D. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 367–377. [Google Scholar]
- Dinh, T.X.; Thien, T.D.; Anh, T.H.V.; Ahn, K.K. Disturbance Observer Based Finite Time Trajectory Tracking Control for a 3 DOF Hydraulic Manipulator Including Actuator Dynamics. IEEE Access 2018, 6, 36798–36809. [Google Scholar] [CrossRef]

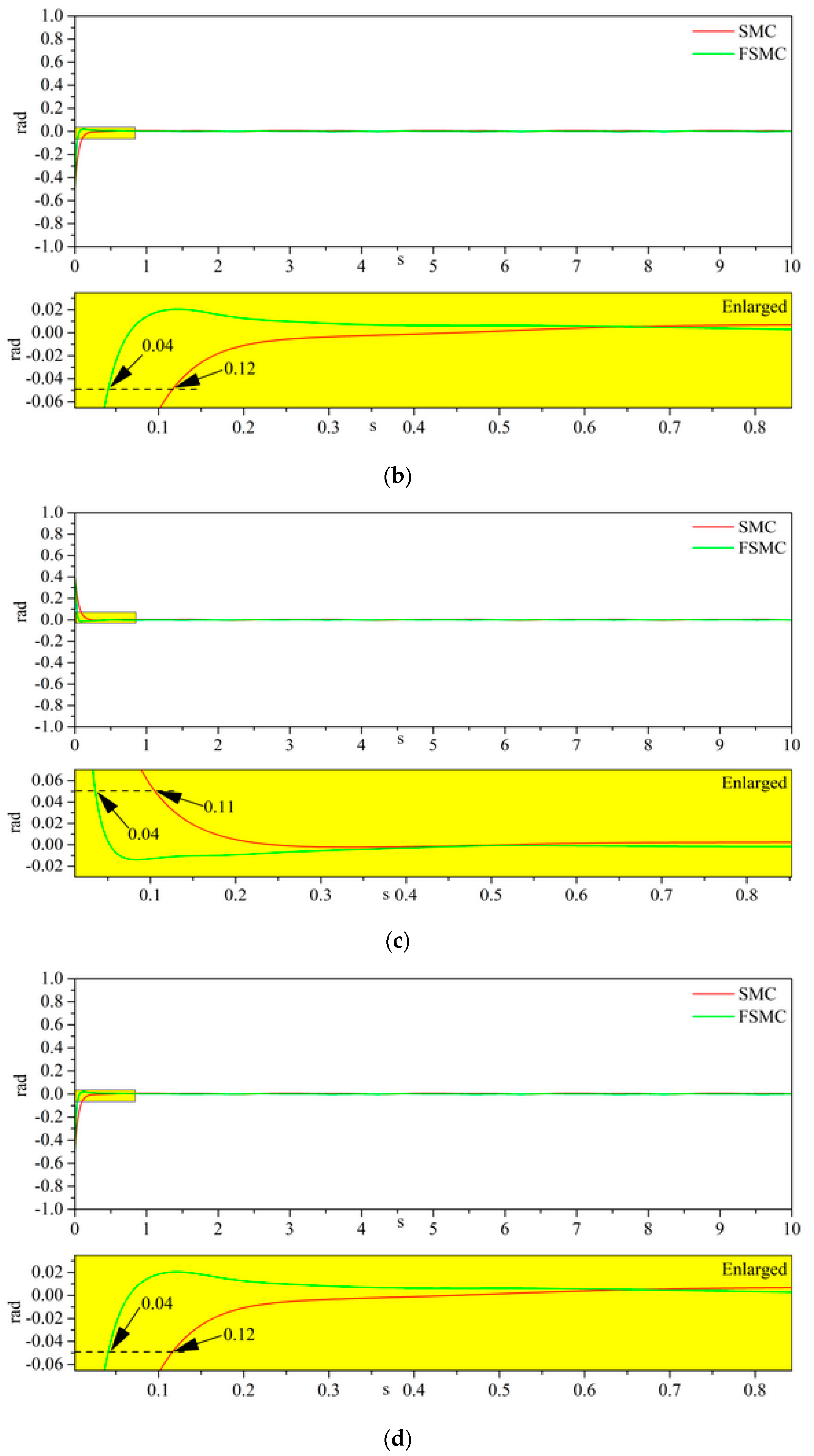
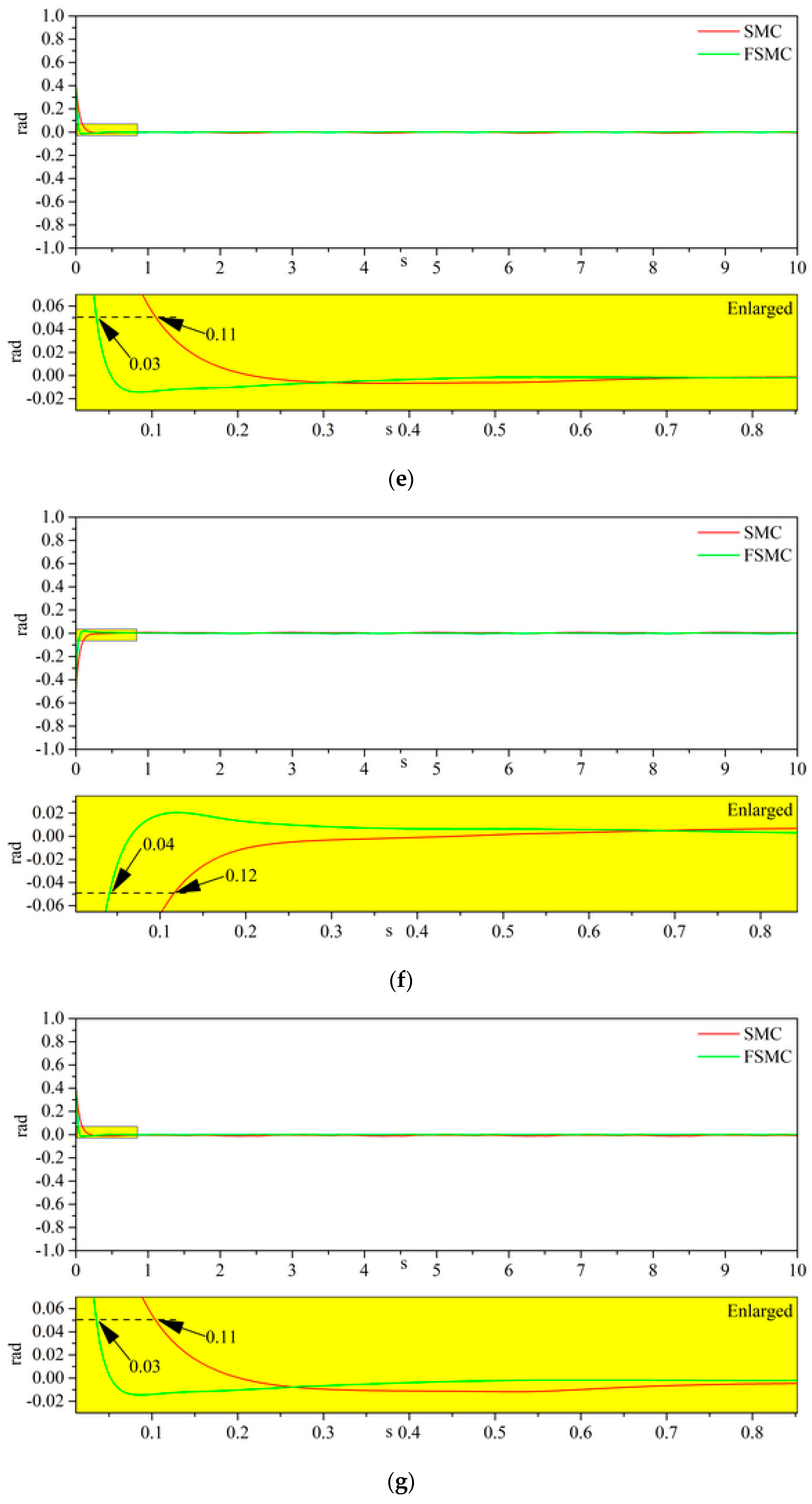
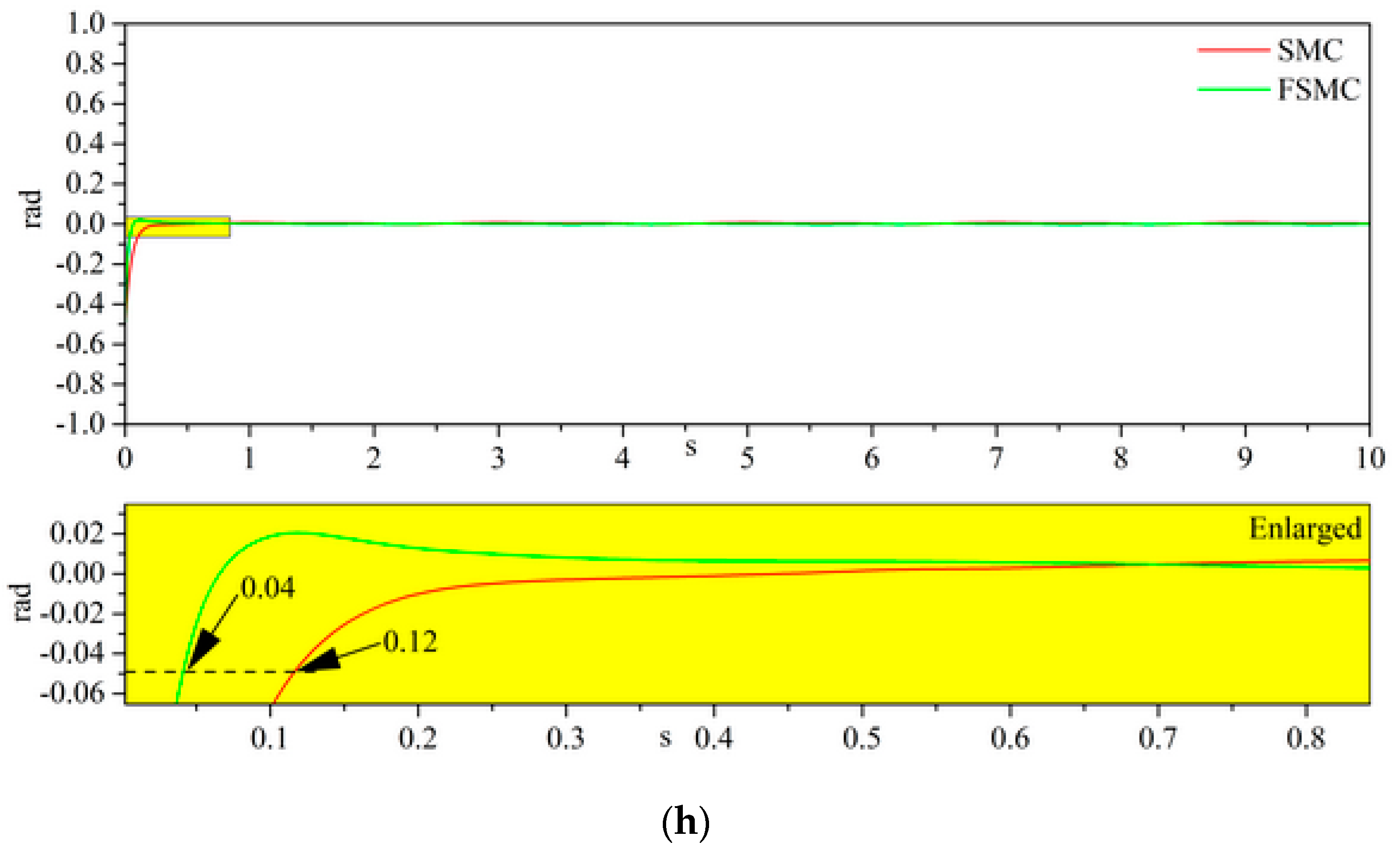

| CGF 60% | CGF 40% | CGF 20% | ||
|---|---|---|---|---|
| SMC | Joint1 | 0.073 | 0.031 | 0.017 |
| Joint2 | 0.074 | 0.033 | 0.018 | |
| FSMC | Joint1 | 0.007 | 0.002 | 0.001 |
| Joint2 | 0.015 | 0.006 | 0.001 | |
| SMC | Joint1 | 0.11 | 0.11 | 0.11 | 0.11 |
| Joint2 | 0.12 | 0.12 | 0.12 | 0.12 | |
| FSMC | Joint1 | 0.04 | 0.04 | 0.03 | 0.03 |
| Joint2 | 0.04 | 0.04 | 0.04 | 0.04 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Qu, L.; Peng, K. Fault-Tolerant Control of Multi-Joint Robot Based on Fractional-Order Sliding Mode. Appl. Sci. 2022, 12, 11908. https://doi.org/10.3390/app122311908
Pan J, Qu L, Peng K. Fault-Tolerant Control of Multi-Joint Robot Based on Fractional-Order Sliding Mode. Applied Sciences. 2022; 12(23):11908. https://doi.org/10.3390/app122311908
Chicago/Turabian StylePan, Jinghui, Lili Qu, and Kaixiang Peng. 2022. "Fault-Tolerant Control of Multi-Joint Robot Based on Fractional-Order Sliding Mode" Applied Sciences 12, no. 23: 11908. https://doi.org/10.3390/app122311908
APA StylePan, J., Qu, L., & Peng, K. (2022). Fault-Tolerant Control of Multi-Joint Robot Based on Fractional-Order Sliding Mode. Applied Sciences, 12(23), 11908. https://doi.org/10.3390/app122311908






