Abstract
In this paper, the main aim is to study and predict macro elastic mechanical parameters of fiber-reinforced composite laminates by combining micro-mechanical analysis models and the non-probabilistic set theory. It deals with uncertain input parameters existing in quantification models as interval variables. Here, several kinds of micro-mechanical mathematical models are introduced, and the parameter vertex solution theorem and the Monte Carlo simulation method can be used to perform uncertainty quantification of macro elastic properties for composites. In order to take the correlations between macro elastic properties into consideration, the obtained limited sample points or experimental data are utilized on the basis of the grey mathematical modeling theory, where correlated uncertain macro parameters can be treated as a closed and bounded convex polyhedral model. It can give out a clear analytical description for feasible domains of correlated macro elastic properties in the process of uncertainty quantification. Finally, two numerical examples are carried out to account for the validity and feasibility of the proposed quantification method. The results show that the proposed method can become a powerful and meaningful supplement for uncertainty quantification of composite laminates and provide data support for further uncertainty propagation analysis.
1. Introduction
Owing to their excellent mechanical properties, such as high specific strength, high specific stiffness and their potential for ‘tailor-made’ designs, advanced fiber-reinforced composite laminates are widely applied in the fields of aviation and aerospace, etc. Furthermore, the accurate prediction and evaluation on mechanical properties is very important and essential for structural responses, safety evaluation and the optimization design of composites. Here, as a kind of multiphase material, their mechanical performance parameters have some relationships with micro- and meso-structures [1,2]. They may depend on fibers and matrix. As a result, many models are provided to study the effects of microstructures on many phenomena including mechanical performance quantification [3,4,5], damage evolution [6,7] and failure prediction [8,9], etc.
However, it should be noted that micro- and meso-parameters in those models always show great dispersions or uncertainties owing to the inherent randomness of basic constituent materials including the fibers and matrix, and complicated multi-stage manufacturing processes [10,11], such as the volume fractions of matrix and fibers, lack or excess amounts of resins in plies, voids and porosity of the matrix and inadequate bonding between the fibers and matrix [12,13,14,15], etc. For example, a new method is proposed to generate random distributions of fibers in the transverse cross-section of fiber-reinforced composites with a high fiber volume fraction for the sake of micro-mechanical analysis [10]. A probabilistic strength model is utilized for unidirectional composites with fibers in hexagonal arrays, where uncertainties in Young’s modulus of fibers and matrix, fiber reference strength, fiber volume fraction and shear yield stress are taken into consideration [12]. In addition, a methodology is presented to evaluate the effects of microscopic manufacturing defects including fiber misalignment, waviness and volume fraction on mechanical performance [14]. An RVE-based micro-mechanical elastic damage model is presented to predict the effective elastic moduli in fiber-reinforced composites considering fiber size dependency [16]. In other words, uncertainties in composite materials can be built up from a constituent level (micro-scale), ply level (meso-scale) or a component level (macro-level) [17,18,19]. As a result, macro-mechanical parameters are also uncertain as functions of micro-mechanical parameters, and they have a significant influence on structural responses made from composite materials. Furthermore, how to carry out uncertainty quantification of macro-elastic mechanical parameters for composite laminates from a micro-scale perspective has become a valuable and important hot topic [20,21,22]. It will play an important role in the risk and reliability assessment of structures made up of composites, such as aircrafts, reusable launch vehicles and other high-risk applications.
Generally speaking, the macro-elastic mechanical parameters of composite laminates can be predicted by theoretical analysis [23,24] or measured by mechanical properties experiments [25,26]. For example, a series–parallel mixture model is proposed to predict the overall property of particle-reinforced composites with more than two phases [27]. A micro-mechanics-based strength theory is addressed to estimate the ultimate strength of fiber-reinforced composites by Huang [28]. On the basis of this study, a critical reliability evaluation of fiber-reinforced composite materials is carried out by taking good advantages of micro- and macro-mechanical analysis [29]. In addition, a method for the probabilistic failure analysis of laminated composite plates with random system parameters subjected to transverse loads is presented, where the statistics of the baseline random variables can be obtained from experiments [30]. A robust and efficient inverse stochastic method based on the non-sampling generalized polynomial chaos method is presented for identifying uncertain elastic parameters from experimental modal data [31]. That is to say, there have already been many successful studies on quantifying mechanical behaviors of composite laminates. However, it should be noted that these research studies are mainly focused on probabilistic thoughts, where available experimental data points should be sufficient or probability density functions of uncertain input parameters can be precisely modeled or known [32,33]. In any case, many studies which report the variability in experimental observations from material characterization testing reveal clearly the need for the development of probabilistic models for characterizing these uncertainties.
However, in practice, the available experimental points or sample points are always limited or insufficient. Consequently, making good use of limited experimental points to quantify the uncertain elastic parameters of composites shows great advantages, where uncertain multi-dimensional parameters of composites can be dealt with as independent or dependent interval variables, or convex-set variables. In this aspect, there also exists some important work concentrating on non-probabilistic uncertainty quantification analyses [34,35,36]. For example, in the literature [37], spatially-stochastic macroscopic material properties are characterized for heterogeneous composite fabrics from limited-size macro-scale experimental measurements. The author has taken good advantages of the smallest ellipsoid and the smallest hyper-rectangle to quantify elastic moduli with some limited experimental points and, further, the uncertainty propagation in vibration and buckling problems of composite shells is studied [38]. In addition, a novel non-probabilistic quantification approach based on grey mathematical theory is developed in order to perform uncertainty quantification of correlated elastic mechanical properties for composite laminates by virtue of some limited experimental points [39], where the validity of experimental points is proved. However, from the point of micro-mechanical analysis, the research on predicting elastic mechanical parameters on the basis of micro-mechanical quantification models and theoretical analysis is rare.
In view of this idea, the main contribution of this paper is to carry out uncertainty quantification of macro elastic mechanical parameters for fiber-reinforced composite laminates on the basis of micro- and macro-mechanical analysis. Here, by virtue of non-probabilistic thoughts, as input variables, material elastic performance parameters of constituents, model parameters and volume fractions are treated as uncertain interval variables in this paper. The remainder of this paper is organized in detail as follows. Firstly, in Section 2, several kinds of deterministic micro- and macro-mechanical analysis models are introduced, where analytical formulas of relationships can be explicitly established between uncertain input parameters at the micro scale and elastic mechanical parameters at the macro scale. In Section 3, by taking uncertain input parameters into account at the micro scale, uncertainty quantification of multi-dimensional elastic parameters of composites can be implemented, where uncertain variables are dealt with as independent interval variables based on non-probabilistic thoughts. Furthermore, considering correlations between any two elastic mechanical parameters, a closed and bounded convex polyhedral model is proposed via some simulated sample points or experimental data points in Section 4. Dependent uncertain macro parameters can be described by some linear inequalities constraints formulations and the non-probabilistic correlation coefficients can be evaluated. Then, in Section 5, two numerical examples are carried out for the sake of accounting for the validity and feasibility of the proposed quantification method, where the results between theoretical analysis and experiments are studied and compared. Finally, some conclusions are drawn in Section 6. The results show that the proposed method can be a powerful and available tool for uncertainty quantification of composites. It can provide theoretical references and data support for further uncertainty response analysis and reliability evaluation.
2. Micro- and Macro-Mechanical Analysis Models for Fiber-Reinforced Composites
As fiber-reinforced composite laminates are widely applied in the fields of aerospace and aviation, their mechanical performance prediction is very important and meaningful. In this section, several kinds of micro-mechanical mathematical models will be introduced to model elastic mechanical properties of fiber-reinforced composites. As is known to all, a composite laminate is a stack of layers of unidirectional fiber-reinforced laminae, which are generally made of fibers and a matrix, which are two different constituent materials. Properties of composite laminates depend on the properties of the constituent materials, distributions, ply orientations and other material parameters. As the basic unit of composite material mechanics, consider a typical unidirectional fiber-reinforced composite lamina as shown in Figure 1, where a coordinate system is used with the 1-axis aligned parallel to the axis of the fibers and the 2–3 plane is transversely isotropic. The 3-axis denotes the thickness direction.
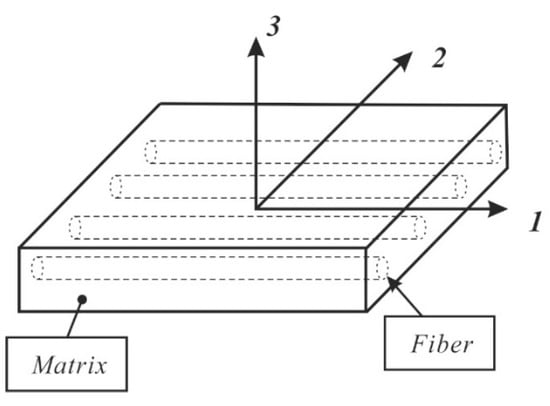
Figure 1.
Sketch map of a typical fiber-reinforced composite lamina [39].
According to the theory of composite materials mechanics, one can make good use of the micro-mechanical analysis method to predict macro elastic mechanical parameters of composite laminates, where the fibers can be transversely isotropic and the matrix material is considered to be isotropic. As a result, the fiber-reinforced composite lamina can be viewed as an orthotropic anisotropic material having three material principal axes coinciding with those of the fibers, which have four independent elastic mechanical parameters including and . Here, is the longitudinal tension modulus and is the transverse tension modulus. is the Poisson’s ratio and is the shear modulus. The micro-scale quantification analysis models can mainly consist of the series model and the parallel model [40], whose sketch maps are as shown in Figure 2. As the series model says, the following quantification formulas can be obtained as
where the analytical relationships between material properties of composite micro constitutes and macro elastic mechanical parameters can be established. The symbols f and m separately represent the fibers and matrix. and are Young’s tension moduli in the longitudinal and in-plane transverse orientations of fibers, respectively. and are the volume fractions of the fibers and matrix, respectively. and are Poisson’s ratios of the fibers and matrix, respectively. and are shear moduli of the fibers and matrix, respectively. When the void volume fraction is taken into account [41,42], one can also obtain the following formula as:
in which is the void volume fraction. On the other hand, as the parallel model says, the following quantification formulas can be obtained as:
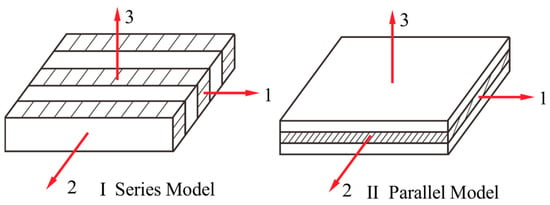
Figure 2.
Sketch maps of the series model and parallel model for the lamina.
For the sake of predicting macro elastic mechanical properties of composite laminates more precisely, some researchers suggest combining the series model with the parallel model [27]. The corresponding formulas can be achieved as
Here, the superscripts I and II represent the series model and parallel model, respectively. It introduces a contact coefficient C to characterize macro elastic mechanical properties of composite laminates. When , it will denote the series model. Instead, when , it will denote the parallel model. The empirical formula for the contact coefficient C can be also studied.
Additionally, a typical quantification model derived by Huang [28] is given below.
where are functions of material properties for constituents including the fibers and matrix. They can be calculated through the following formulas.
Additionally, the compliance matrixes of the fiber and matrix materials are listed as
Therefore, as a conclusion, macro elastic mechanical parameters of the composite lamina can be viewed as functions of the material properties of constituents. Furthermore, when micro input parameters, including elastic mechanical properties of constituents, volume fractions and model parameters, are dealt with as uncertain parameters, macro elastic mechanical parameters of composites are also uncertain. One can make use of some statistical or non-statistical methods to quantify them from the perspective of theoretical analysis or experimental studies. As a result, the uncertainty quantification of composites will play an important role in the structural response analysis of composite laminates.
3. Uncertainty Quantification of Macro Elastic Parameters Based on Non-Probabilistic Thought
In Section 2, we have introduced some deterministic micro- and macro-mechanical analysis models for macro elastic constants including and of composite laminates, where the relationships between macro elastic parameters and micro input parameters of constituents or the explicit functions are established at the micro scale. However, it should be noted that these micro input parameters are uncertain owing to their inherent dispersions and complicated fabricating processes. As a consequence, the following formula can be obtained mathematically as:
where y is the macro elastic mechanical parameters of composites including and b is the uncertain micro input vector including material properties of constituents, volume fractions and model parameters, etc. is the analytical formula or explicit function originating from different quantification models. Generally speaking, the uncertain vector b can be treated as probabilistic random variables [21,29], whose probability density distributions have been given or are known. Here, in order to guarantee that uncertainty quantification of macro elastic parameters for composites is convinced and correct, probability distributions must be precisely modeled. However, in practice, it is always difficult to obtain sufficient sample points. In particular, when available data is limited or insufficient so that uncertain input micro parameters are not appropriately represented with probability distributions, those non-statistic quantification methods will be better choices. Typically, on the basis of non-probabilistic thoughts, uncertain input vector b can be treated as interval variables, namely:
or the component form
Here, only lower and upper bounds of uncertain input parameters should be known. and are the corresponding lower and upper bounds, respectively. is the i-th component of the vector. and are the lower and upper bounds, respectively. m is the number of uncertain input parameters at the micro scale. According to the theory of interval mathematics, the formula (10) can be rewritten as the following interval form as:
where the interval nominal value is and the interval radius is . Furthermore, one can take the use of interval arithmetic operations to carry out non-probabilistic uncertainty quantification by combining with micro- and macro-mechanical analysis models. Here, the interval arithmetic operations of two interval numbers and can be expressed as
with i, j = 1, 2, …, m. As a result, the lower and upper bounds of macro elastic mechanical parameters can be calculated. However, it should be noted that a natural interval expansion of functions may occur. That is to say, the obtained interval will be overlarge. Therefore, one can take good advantage of the parameter vertex solution theorem to precisely calculate the lower and upper bounds of macro elastic mechanical parameters. In other words, one can obtain that:
where is the uncertain micro input parameter vector including all the vertices. Here, for the m-dimensional interval variables, there exist vertices, in which
The parameter vertex solution theorem can provide an exact solution for macro elastic parameters of composites because of the monotonic functions. However, the two aforementioned methods cannot take the correlations between any two uncertain mechanical properties into account. Furthermore, one can make use of the Monte Carlo simulation (MCS) method to carry out uncertainty quantification of macro elastic parameters, where a lot of sample points in feasible domains of interval variables are generated. The MCS method refers to the procedure of assigning a value to an independent interval variable in a chosen quantification model and dependent output variables can be observed and modeled. As a result, the distributed domains of macro elastic mechanical parameters for composites can be obtained and the correlations between elastic parameters can be predicted. The procedure of the MCS method is as follows:
- (i)
- Based on non-probabilistic thoughts, make use of the computer and sampling techniques to generate and select sample points of the independent input variables, such as constituent elastic properties, fiber and void volume ratios and model parameters.
- (ii)
- Calculate dependent output variables including macro elastic mechanical properties and by using the chosen quantification model.
- (iii)
- Replicate the experiment and each time adopt a new set of input parameters.
- (iv)
- Take good advantage of appropriate analysis methods to calculate characteristic parameters and distributions of the macro elastic properties of composite laminates.
4. Convex Polyhedral Modeling of Multi-Dimensional Elastic Parameters Based on Grey Mathematical Theory
In Section 3, we have proposed three kinds of analysis methods to perform uncertainty quantification for macro elastic parameters of composites from the perspective of micro–macro scale on the basis of non-probabilistic thoughts, where uncertain micro input parameters are treated as independent interval variables. Although these methods can give an exact prediction for the intervals of elastic mechanical parameters or evaluate correlations between any two of them, they cannot give a clear boundary or outline for dependent macro elastic parameters of composites. Therefore, in this section one will carry out uncertainty quantification of dependent elastic mechanical parameters based on some finite sample points or experimental data by virtue of grey mathematical theory. Not only can make full use of the obtained available information to determine and evaluate uncertainty characteristic information, but it can also take the correlations between uncertain parameters into account and give an appropriate geometry description for macro elastic mechanical properties of composite laminates. Here, uncertain multi-dimensional elastic parameters are dealt with as uncertain-but-bounded variables or modeled as a closed and bounded convex polyhedral model. It can be described analytically by some linear inequalities constraints by virtue of some sample points or experimental points.
According to grey mathematical theory, for the sake of carrying out uncertainty quantification of elastic properties for composites, the obtained sample points or experimental points should be validated and they can be quantified in a fixed interval. Then, for any two uncertain macro elastic mechanical parameters and , the dependent uncertain-but-bounded parameters x or the combination sequence should satisfy the following linear inequalities constraints as:
where is the grey identification coefficient, which is nearly unaffected by the distribution type of measurement values and can be calculated by the grey evaluation model [43]; is the number of uncertainties. In addition, according to the Chebycheff’s inequity [44] and some statistical analysis methods [45], the quantified parameter K can be calculated, which is practically set to 3. and are nominal values or mean values of uncertain macro elastic mechanical parameters, which can be calculated as:
Further, the macro elastic mechanical parameter of composites should be in the following estimated interval as:
is the standard deviation of an uncertain parameter. is the polar angle, which represents different quantification directions. N is the number of obtained sample points. is the maximum difference between the mean-value accumulated sequence and the accumulated data sequence, namely:
Certainly, the Formula (19) can be rewritten as the following formula as:
As a result, it can be easily seen that the Formula (23) is a set of linear inequalities, which can be expressed as a convex polyhedral model.
where is the dimensional coefficient matrix. M is the number of linear inequalities constraints and is the n-dimensional macro uncertain mechanical parameter vector of composites. That is to say,
Furthermore, the uncertain-but-bounded macro elastic mechanical parameters x can be represented as:
where are the extreme points of the convex polyhedral model and L is the number of all extreme points. is the corresponding coefficient. Further, the correlation coefficient between any two elastic parameters can be evaluated as [39]:
Here, and are auto uncertainties of uncertain elastic parameters and , respectively. is the mutual uncertainty between them. Subsequently, the quantified macro elastic mechanical parameters of composites can be used for structural response analysis and reliability evaluations of fiber-reinforced composite laminates in further work.
The flowchart of the proposed method is shown in Figure 3. The whole process of the proposed method includes three parts; namely, the micro- and macro-mechanical, non-probabilistic interval propagation by MCS and the prediction of macro-mechanical parameters.
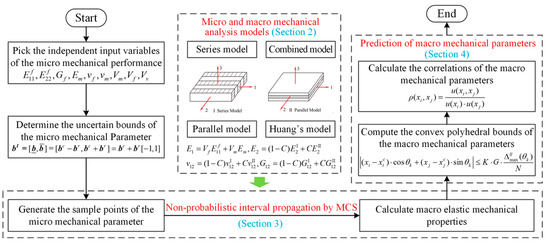
Figure 3.
The flowchart of the proposed method.
5. Numerical Examples
In order to account for the feasibility and validity of the proposed non-probabilistic uncertainty quantification method for composite laminates, two numerical examples are carried out in this section on the basis of micro and macro scales. One is the uncertainty quantification of macro elastic mechanical parameters for graphite–fiber/epoxy–matrix fiber-reinforced composites at the lamina level, where the proposed method is compared with the reference [29] based on the probabilistic thought. The other is the uncertainty quantification of T300/QY8911 composite laminated plates at the component level, where some experimental data points are taken good advantage of.
5.1. Uncertainty Quantification for Elastic Parameters of Graphite—Fiber/Epoxy–Matrix Fiber-Reinforced Laminae
In this section, firstly, the uncertainty quantification of the graphite–fiber/epoxy–matrix fiber-reinforced lamina is considered [29]. It is generally acknowledged that obtaining the statistical information for micro-scale modeling is a challenging task because of complex manufacturing processes and experimental constraints. As a result, uncertain input parameters at the micro scale are treated as independent interval variables, whose uncertain information are listed in Table 1. Uncertain information can consist of the nominal values, stand deviations and lower and upper bounds of uncertain parameters.

Table 1.
Uncertain information at the micro scale for graphite–fiber/epoxy–matrix lamina.
For the sake of carrying out the uncertainty quantification of macro elastic mechanical properties for the lamina, the series model formulated as (1), the parallel model as (3), the combined model as (4) and Huang’s model as (6) are adopted, where the results of reference [29] are listed for comparisons. The corresponding quantification results are listed in Table 2, where the nominal values and variation coefficients under different quantification models are included. Herein, the values before the symbol ‘/’ are nominal values and the values after the symbol ‘/’ are variation coefficients.

Table 2.
The quantification results under different models.
Through making comparisons between the results under different quantification models, it can be easily seen that the quantified results of the longitudinal tension modulus for different models are absolutely the same. However, the quantified results for the transverse tension modulus , the Poisson’s ratio and the gear modulus are different whereas the results under the combined model and Huang’s model are approximately identical. As a result, we will take good advantage of the two kinds of models to be used for further study. Furthermore, by comparing the results under Huang’s model in this paper based on non-probabilistic thoughts and the reference [29] by Shaw based on probabilistic idea, it can be concluded that the nominal values are closely the same, but the non-probabilistic variation coefficients are bigger than the probabilistic ones. That is to say, the dispersions of uncertain macro elastic properties on the basis of non-probabilistic thoughts will be larger. Subsequently, the correlations between any two macro elastic mechanical parameters are evaluated, where the results are listed in Table 3.

Table 3.
The correlation coefficients between any two macro elastic parameters.
By comparing the correlation coefficients listed in Table 3, it can be found that the results obtained by the non-probabilistic Huang’s model can achieve the same correlation relationships as the probabilistic Huang’s model referenced by Shaw [29] and the values are almost identical. Here, the symbol ‘+’ denotes the positive correlation and the symbol ‘−’ denotes the negative correlation. However, for the non-probabilistic combined quantification model, the results show that the correlation relationships between any two macro elastic parameters are closely identical, except that the correlation relationship between the transverse tension modulus and the Poisson’s ratio is contrary to Huang’s model. As a result, we will make good use of some simulated sample points obtained by the non-probabilistic Huang’s model to model macro-mechanical parameters as a closed and bounded convex polyhedral model, which can be plotted in Figure 4. Here, the blue boundary line is the convex polyhedral model based on the developed grey mathematical theory via some sample points. The red solid points are simulated sample points by Monte Carlo simulation methods through the non-probabilistic Huang’s model and the number of simulated points is 30,000. It is easily found that almost all simulated points can be enveloped in the convex polyhedral model and the enveloping rate can be up to 99.9%. In other words, the proposed quantification method on the basis of grey mathematical theory and the micro–macro analysis model can give a very credible and reasonable evaluation domain for macro elastic mechanical parameters of composites. It can be a powerful and efficient tool for uncertainty quantification of composite laminates.
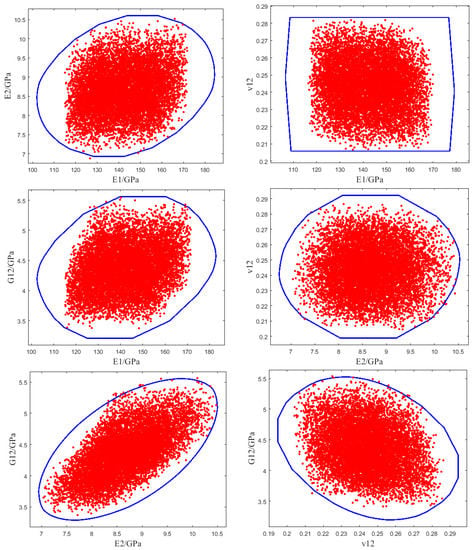
Figure 4.
Convex polyhedral models of macro elastic mechanical parameters for composites.
5.2. Uncertainty Quantification for Elastic Parameters of T300/QY8911 Laminates
In this section, we will consider the uncertainty quantification of composite laminates at the component scale. In general, as a suitable material for the component design, the desired composite laminate is created by stacking plies in specific directions. The integration of ply or lamina properties to yield laminate properties is called the laminate theory. Here, the laminate variables such as ply orientations and stacking sequences can be designed to produce a composite laminate with desired material properties. In this section, the elastic mechanical parameter, namely the longitudinal tension modulus of composite laminated plates, whose material is T300/QY8911, will be quantified by virtue of the proposed non-probabilistic quantification method, and the Huang’s model is adopted. The stacking sequence of composite laminates is . The corresponding uncertain input key parameters at the micro scale are listed in Table 4. Uncertain information can consist of the nominal values, lower bounds and upper bounds of uncertain parameters.

Table 4.
Uncertain information at the micro scale for T300/QY8911 laminates.
One can take use of the non-probabilistic Huang’s model to obtain macro elastic mechanical properties of the composite lamina. Furthermore, the off-axis engineering elastic constants of the laminate can be calculated by the normal-axis engineering constants as:
where and . is the corresponding axis-off angle. In order to carry out the uncertainty quantification by virtue of experimental results, the static mechanical performance experiments of laminates are implemented for comparison, with the sketch map of the test specimens plotted in Figure 5. The measured 39 experimental points are listed in Table 5, which can be calculated by:
where is the load increment of the load–strain curve and is the corresponding strain increment. t is the width of the test specimen and h is the thickness.
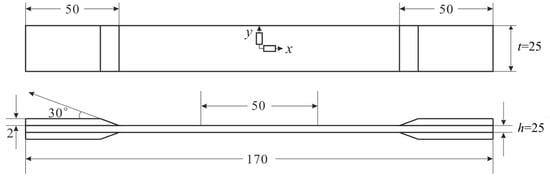
Figure 5.
The sketch map of test specimens for T300/QY8911 composite laminates (mm).

Table 5.
Experimental points of longitudinal tension modulus.
Based on these experimental data points, the statistical methods can be utilized to characterize the longitudinal tension modulus as normal variables, and the observed significance level of the Anderson–Darling statistics test is calculated to ensure that the conclusion that the experimental data are submitted to normal distribution is true. Here, the Anderson–Darling test statistic is:
in which is the standard normal accumulated distribution function. The corresponding observation significance level is:
where:
Through calculations, the observation significance level for longitudinal tension modulus is . As a consequence, characterizing as a normal random variable is reasonable. Furthermore, by making use of the proposed non-probabilistic quantification method and the aforementioned uncertainty quantification approach with experimental points, two kinds of probability distribution plots are plotted in Figure 6, where the black points are the experimental data and the red line is the fitted probability distribution plot. The blue line is the probability distribution plot via the proposed non-probabilistic method on the basis of micro-macro-mechanical analysis.
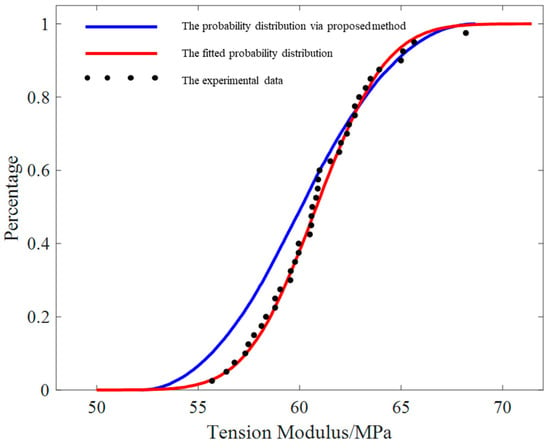
Figure 6.
Probability distribution plots of tension modulus of T300/QY8911 laminates.
By utilizing the proposed non-probabilistic quantification method, the obtained nominal value and standard deviation are 60.16 MPa and 3.06 MPa, respectively. The mean value and standard deviation by virtue of experimental data are 60.83 MPa and 2.72 MPa, respectively. That is to say, the proposed method can achieve a very approximate identical result to experimental studies, but the quantified dispersion may be larger. In addition, the simulated minimum and maximum values by the proposed method are 52.12 MPa and 68.65 MPa, which can cover the minimum and maximum values by the experiments, namely 55.68 MPa and 68.19 MPa. As a conclusion, one is able to think that the proposed non-probabilistic method can play an important role in uncertain quantification of composite laminates, which can lead to a relatively believable and rational result.
6. Conclusions
Owing to special structural formats and excellent mechanical properties, composite laminated structures are widely applied in the fields of aviation and aerospace. Furthermore, uncertainty quantification of elastic mechanical properties for composites is very important and meaningful for composite structural response analysis and optimization design.
In this paper, in order to implement the uncertainty quantification of fiber-reinforced composite laminates, a novel non-probabilistic uncertainty quantification method is proposed to predict macro elastic mechanical parameters of composites based on micro and macro scale mechanical analysis theory. Here, uncertain input parameters at the micro scale are dealt with as independent interval variables by virtue of non-probabilistic thoughts, and the obtained macro elastic properties will be dependent on each other. In addition, dependent macro parameters can be represented by a closed and bounded convex polyhedral model and described by some linear inequalities constraints. Finally, for the sake of accounting for the feasibility and validity of the proposed method, two numerical examples are carried out. The results show that the proposed method can play an important role in the uncertainty quantification of composites when the experimental study is difficult or expensive. Furthermore, it can be a powerful and efficient supplement for the uncertainty quantification of macro elastic mechanical parameters and provide data support for further response analysis and the reliability evaluation of composite structures.
Author Contributions
Conceptualization, J.H.; Methodology, X.W.; Data curation, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China: 12072006, 11872089, 12132001 and 52192632; Civil Products Research of Central Organization Department: 19K512-643; Defense Industrial Technology Development Program: JCKY2019203A003, JCKY2019205A006; Program of State Key Laboratory of Ocean Engineering: GKZD010083.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (Nos. 12072006, 11872089, 12072007, 12132001 and 52192632) and the Defense Industrial Technology Development Program (Nos. JCKY2019203A003, JCKY2019205A006 and JCKY2019209C004). In addition, the authors thank the reviewers for their valuable and constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Toledo MW, E.; Nallim, L.G.; Luccioni, B.M. A micro-macro mechanical approach for composite laminates. Mech. Mater. 2008, 40, 885–906. [Google Scholar] [CrossRef]
- Naskar, S.; Mukhopadhyay, T.; Sriramula, S.; Adhikari, S. Stochastic natural frequency analysis of damaged thin-walled laminated composite beams with uncertainty in micromechanical properties. Compos. Struct. 2017, 160, 312–334. [Google Scholar] [CrossRef]
- Bostanabad, R.; Liang, B.; Gao, J.; Liu, W.K.; Cao, J.; Zeng, D.; Su, X.; Xu, H.; Li, Y.; Chen, W. Uncertainty quantification in multiscale simulation of woven fiber composites. Comput. Methods Appl. Mech. Eng. 2018, 338, 506–532. [Google Scholar] [CrossRef]
- Arteiro, A.; Catalanotti, G.; Melro, A.R.; Linde, P.; Camanho, P.P. Micro-mechanical analysis of the effect of ply thickness on the transverse compressive strength of polymer composites. Compos. Part A 2015, 79, 127–137. [Google Scholar] [CrossRef]
- Drathi, M.R.; Ghosh, A. Multiscale modeling of polymer-matrix composites. Comput. Mater. Sci. 2015, 99, 62–66. [Google Scholar] [CrossRef]
- Abdelal, G.F.; Caceres, A.; Barbero, E.J. A micro-mechanics damage approach for fatigue of composite materials. Compos. Struct. 2002, 56, 413–422. [Google Scholar] [CrossRef]
- Qian, C.; Westphal, T.; Nijssen, R.P.L. Micro-mechanical fatigue modeling of unidirectional glass fibre reinforced polymer composites. Comput. Mater. Sci. 2013, 69, 62–72. [Google Scholar] [CrossRef]
- Li, W.; Cai, H.; Li, C.; Wang, K.; Fang, L. Micro-mechanics of failure for fatigue strength prediction of bolted joint structures of carbon fiber reinforced polymer composite. Compos. Struct. 2015, 124, 345–356. [Google Scholar] [CrossRef]
- Sun, Z.G.; Zhao, L.; Chen, L.; Song, Y.D. Research on failure criterion of composite based on unified macro- and micro-mechanical model. Chin. J. Aeronaut. 2013, 26, 122–129. [Google Scholar] [CrossRef]
- Weng, J.M.; Wen, W.D.; Cui, H.T.; Chen, B. Micromechanical analysis of composites with fibers distributed randomly over the transverse cross-section. Acta Astronaut. 2018, 147, 133–180. [Google Scholar] [CrossRef]
- Mehrez, L.; Doostan, A.; Moens, D.; Vandepitte, D. Stochastic identification of composite material properties from limited experimental databases, Part II: Uncertainty modeling. Mech. Syst. Signal Process. 2012, 27, 484–498. [Google Scholar] [CrossRef]
- Khiat, M.A.; Sereir, Z.; Chateauneuf, A. Uncertainties of unidirectional composite strength under tensile loading and variation of environmental condition. Theor. Appl. Fract. Mech. 2011, 56, 169–179. [Google Scholar] [CrossRef]
- Somoh, G.K.; Toumi, R.B.; Renard, J.; Monin, M. Statistical approach of elastic properties of continuous fiber composite. Compos. Struct. 2015, 119, 287–297. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Gosling, P.D. Influence of stochastic variations in manufacturing defects on the mechanical performance of textile composites. Compos. Struct. 2018, 194, 226–239. [Google Scholar] [CrossRef]
- Lau, K.T.; Hung, P.Y.; Zhu, M.H.; Hui, D. Properties of natural fibre composites for structural engineering applications. Compos. Part B 2018, 136, 222–233. [Google Scholar] [CrossRef]
- Kim, B.R.; Lee, H.K. An RVE-based micromechanical analysis of fiber-reinforced composites considering fiber size dependency. Compos. Struct. 2009, 90, 418–427. [Google Scholar] [CrossRef]
- Potter, K.; Khan, B.; Wisnom, M.; Bell, T.; Stevens, J. Variability, fibre waviness and misalignment in the delamination of the properties of composite materials and structures. Compos. Part A 2008, 39, 1343–1354. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Gosling, P.D.; Ullah, Z.; Pearce, C.J. Exploiting the benefits of multi-scale analysis in reliability analysis for composite structures. Compos. Struct. 2016, 155, 197–212. [Google Scholar] [CrossRef]
- Sriramula, S.; Chryssanthopoulos, M.K. Quantification of uncertainty modeling in stochastic analysis of FRP composites. Compos. Part A 2009, 40, 1673–1684. [Google Scholar] [CrossRef]
- Mustafa, G.; Suleman, A.; Crawford, C. Probabilistic micromechanical analysis of composite material stiffness properties for a wind turbine blade. Compos. Struct. 2015, 131, 905–916. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Rafiee, R.; Zhuang, X.; Lahmer, T.; Rabczuk, T. Uncertainty quantification for multiscale modeling of polymer nanocomposites with correlated parameters. Compos. Part B 2015, 68, 446–464. [Google Scholar] [CrossRef]
- Komeili, M.; Milani, A.S. The effect of meso-level uncertainties on the mechanical response of woven fabric composites under axial loading. Comput. Struct. 2012, 90–91, 163–171. [Google Scholar] [CrossRef]
- Li, L.X.; Wang, T.J. A unified approach to predict overall properties of composite materials. Mater. Charact. 2005, 54, 49–62. [Google Scholar] [CrossRef]
- Shi, W.J.; Hu, W.P.; Zhang, M.; Meng, Q.C. A damage mechanics model for fatigue life prediction of fiber-reinforced polymer composite lamina. Acta Mech. Solida Sin. 2011, 24, 399–410. [Google Scholar] [CrossRef]
- Sasikumar, P.; Suresh, R.; Vijayaghosh, P.K.; Gupta, S. Experimental characterisation of random field models for CFRP composite panels. Compos. Struct. 2015, 120, 451–471. [Google Scholar] [CrossRef]
- Sriramula, S.; Chryssanthopoulos, M.K. An experimental characterisation of spatial variability in GFRP composite panels. Struct. Saf. 2013, 42, 1–11. [Google Scholar] [CrossRef]
- Tan, J.F.; Jia, Y.J.; Li, L.X. A series-parallel mixture model to predict the overall property of particle reinforced composites. Compos. Struct. 2016, 150, 219–225. [Google Scholar] [CrossRef]
- Huang, Z.M. Micromechanical prediction of ultimate strength of transversely isotropic fibrous composite. Int. J. Solids Struct. 2001, 38, 4147–4172. [Google Scholar] [CrossRef]
- Shaw, A.; Sriramula, S.; Gosling, P.D.; Chryssanthopoulos, M.K. A reliability evaluation of fiber reinforced composite materials based on probabilistic micro and macro mechanical analysis. Compos. Part B Eng. 2010, 41, 446–453. [Google Scholar] [CrossRef]
- Lin, S.C.; Kam, T.Y. Probabilistic failure analysis of transversely loaded laminated composite plates using first-order second moment method. J. Eng. Mech. 2000, 126, 812–820. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marburg, S. Identification of composite uncertain material parameters from experimental modal data. Probabilistic Eng. Mech. 2014, 37, 148–153. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Silani, M.; Lahmer, T.; Zhuang, X.; Rabczuk, T. A unified framework for stochastic predictions of mechanical properties of polymeric nanocomposites. Comput. Mater. Sci. 2015, 96, 520–535. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Zhuang, X.; He, P.; Rabczuk, T. Fracture toughness of polymeric particle nanocomposites: Evaluation of models performance using Bayesian method. Compos. Sci. Technol. 2016, 126, 122–129. [Google Scholar] [CrossRef]
- Qiu, Z.P. Convex models and interval analysis method to predict the effect of uncertain-but-bounded parameters on the buckling of composite structures. Comput. Methods Appl. Mech. Eng. 2005, 19, 2175–2189. [Google Scholar] [CrossRef]
- Wang, X.J.; Wang, L. Uncertainty quantification and propagation analysis of structures based on measurement data. Math. Comput. Model. 2011, 54, 2725–2735. [Google Scholar] [CrossRef]
- Wang, X.J.; Wang, L.; Qiu, Z.P. A feasible implementation procedure for interval analysis method from measurement data. Appl. Math. Model. 2014, 38, 2377–2397. [Google Scholar] [CrossRef]
- Mehrez, L.; Moens, D.; Vandepitte, D. Stochastic identification of composite material properties from limited experimental databases, Part I: Experimental database construction. Mech. Syst. Signal Process. 2012, 27, 471–483. [Google Scholar] [CrossRef]
- Wang, X.J.; Elishakoff, I.; Qiu, Z.P.; Kou, C.H. Hybrid theoretical, experimental and numerical study of vibration and buckling of composite shells with scatter in elastic moduli. Int. J. Solids Struct. 2009, 46, 2539–2546. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Wang, L.; Shi, Q.; Li, Y. Uncertainty quantification of multi-dimensional parameters for composite laminates based on grey mathematical theory. Appl. Math. Model. 2018, 55, 299–313. [Google Scholar] [CrossRef]
- Munde, Y.S.; Ingle, R.B. Theoretical modeling and experimental verification of mechanical properties of natural fiber reinforced thermoplastics. Procedia Technol. 2015, 19, 320–326. [Google Scholar] [CrossRef]
- Mesogitis, T.S.; Skordos, A.A.; Long, A.C. Uncertainty in the manufacturing of fibrous thermosetting composites: A review. Compos. Part A 2014, 57, 67–75. [Google Scholar] [CrossRef]
- Facca, A.G.; Kortschot, M.T.; Yan, N. Predicting the elastic modulus of natural fiber reinforced thermoplastics. Compos. Part A 2006, 37, 1660–1671. [Google Scholar] [CrossRef]
- Han, L.F.; Tang, W.Y.; Liu, Y.M.; Wang, J.; Fu, C.F. Evaluation of measurement uncertainty based on grey system theory for small samples from an unknown distribution. Sci. China Technol. Sci. 2013, 56, 1517–1524. [Google Scholar] [CrossRef]
- Qiu, Z.P.; Wang, X.J. Comparison of dynamic response of structures with uncertain-but- bounded parameters using non-probabilistic interval analysis method and probabilistic approach. Int. J. Solids Struct. 2003, 40, 5423–5439. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Alvarez, D.A.; Paredes, J.A. Interval reliability analysis under the specification of statistical information on the input variables. Struct. Saf. 2017, 65, 35–48. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).