Study on Permeability Stress-Sensitivity in Seepage-Geomechanical Coupling of Fractured Deep Tight Sandstone Gas Reservoirs
Abstract
1. Introduction
2. Experiments
2.1. Sample Preparation
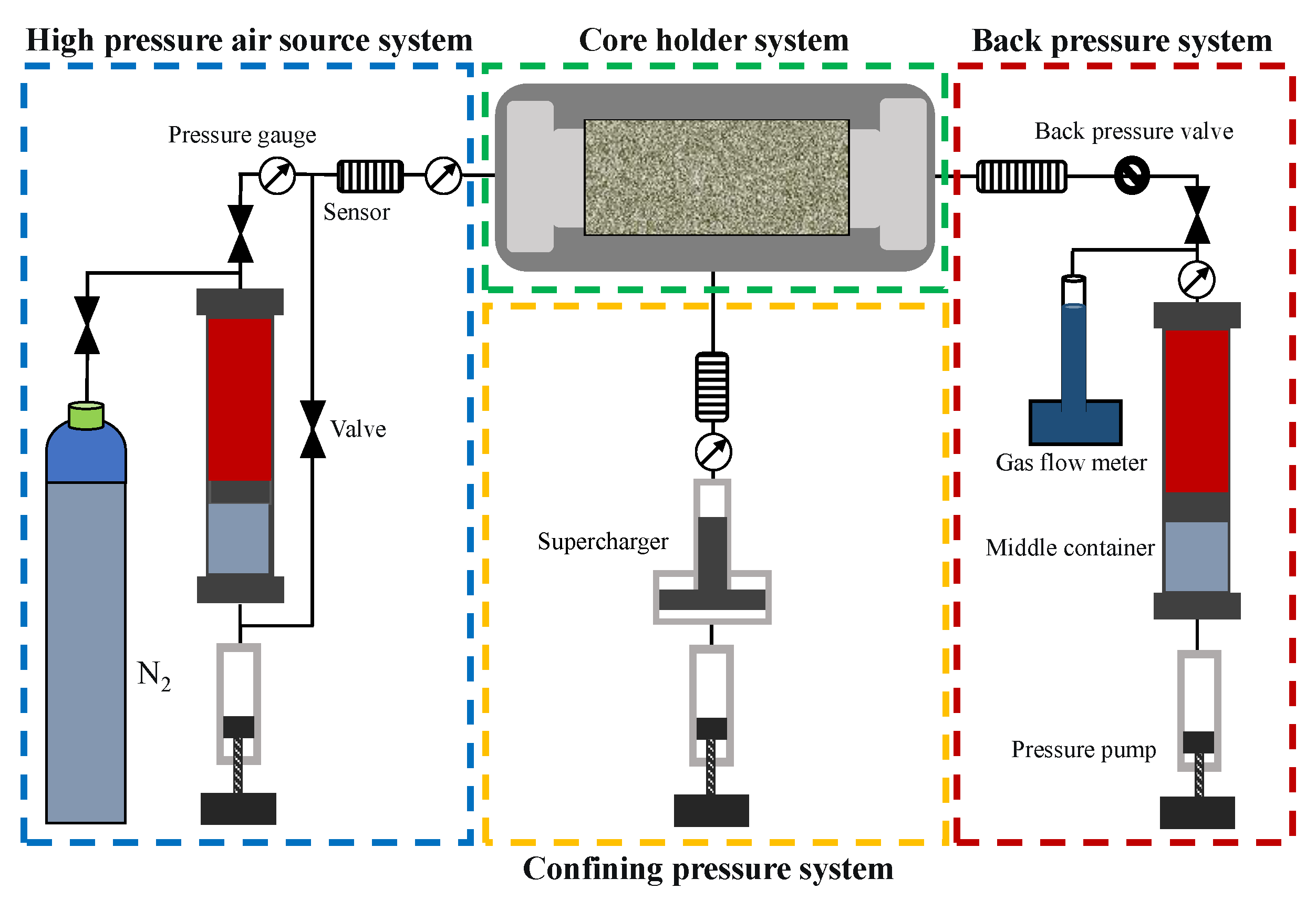
2.2. Experimental Set-Up and Scheme
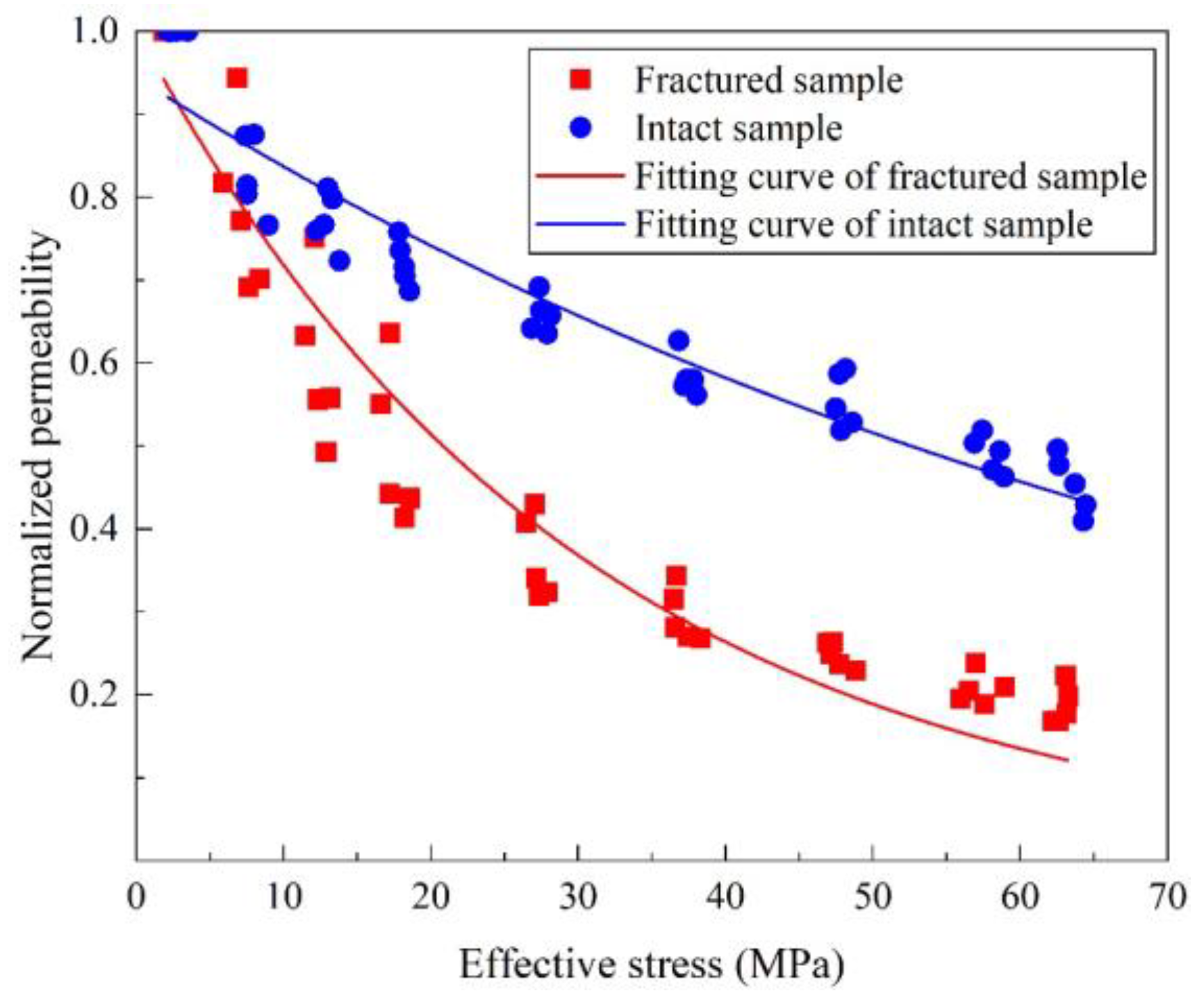
2.3. Experimental Results and Analysis
3. Numerical Simulation of Tight Sandstone Gas Reservoirs
3.1. Governing and Constitutive Equations
3.1.1. Mathematical Model of Seepage Field
3.1.2. Mathematical Model of Stress Field
3.2. Modeling Process
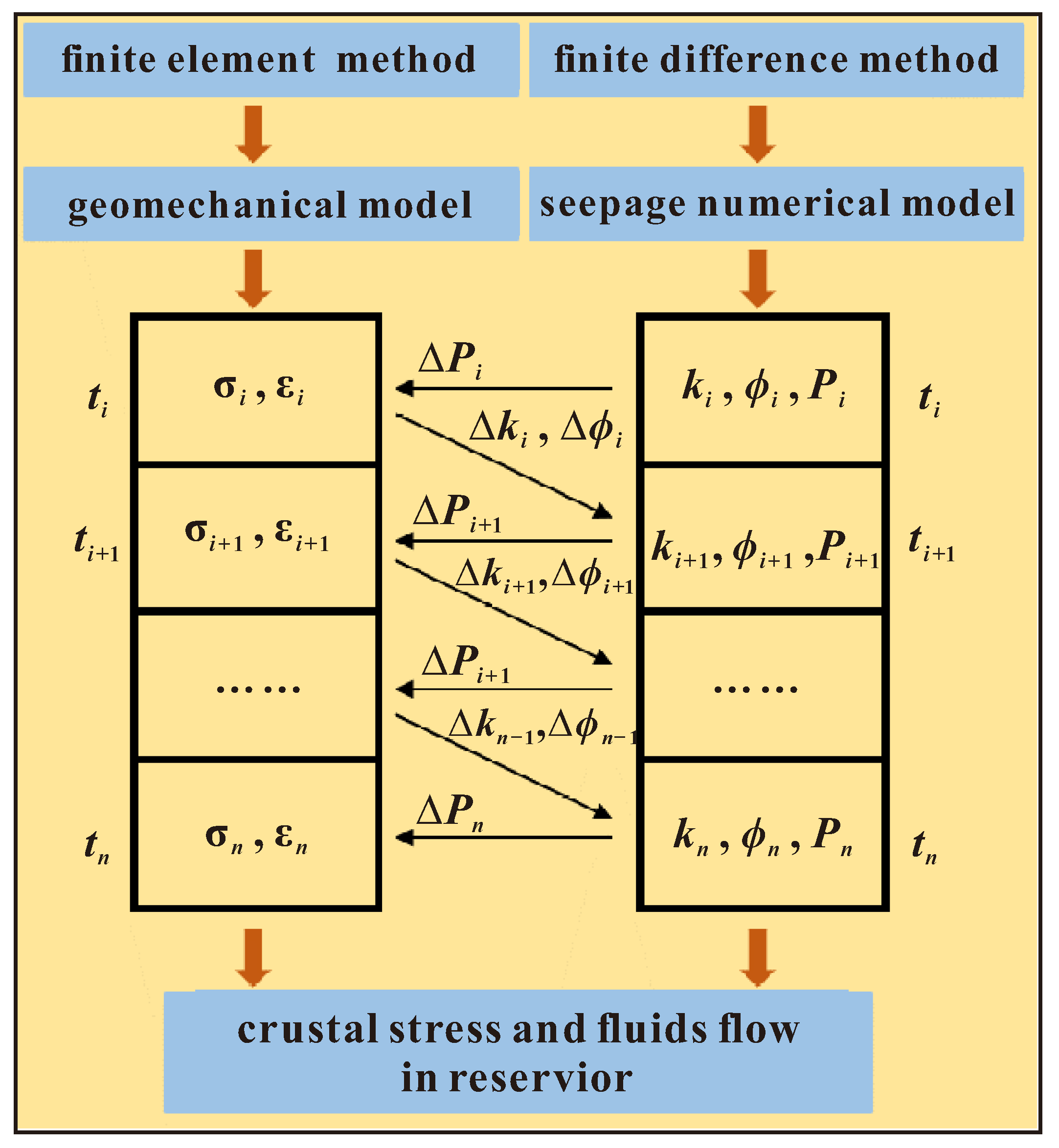
3.2.1. Numerical Simulation Coupling Procedure
3.2.2. Seepage Numerical Model
3.2.3. Geomechanical Model
4. Simulation Results and Discussion
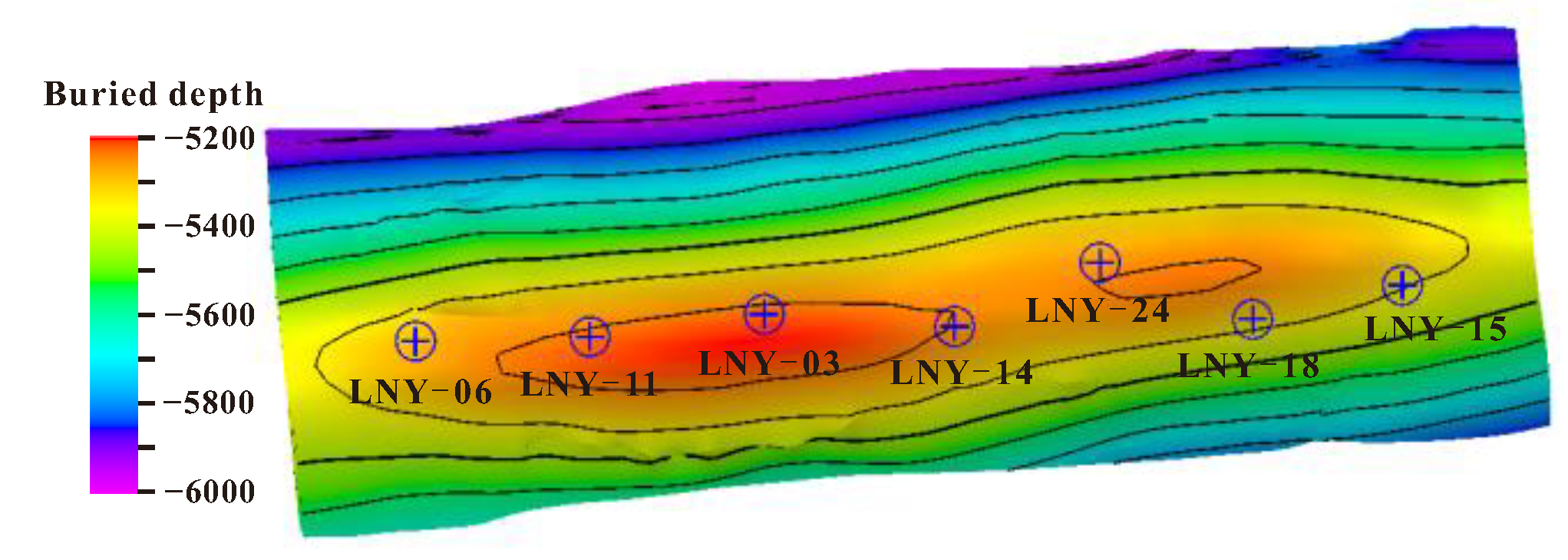
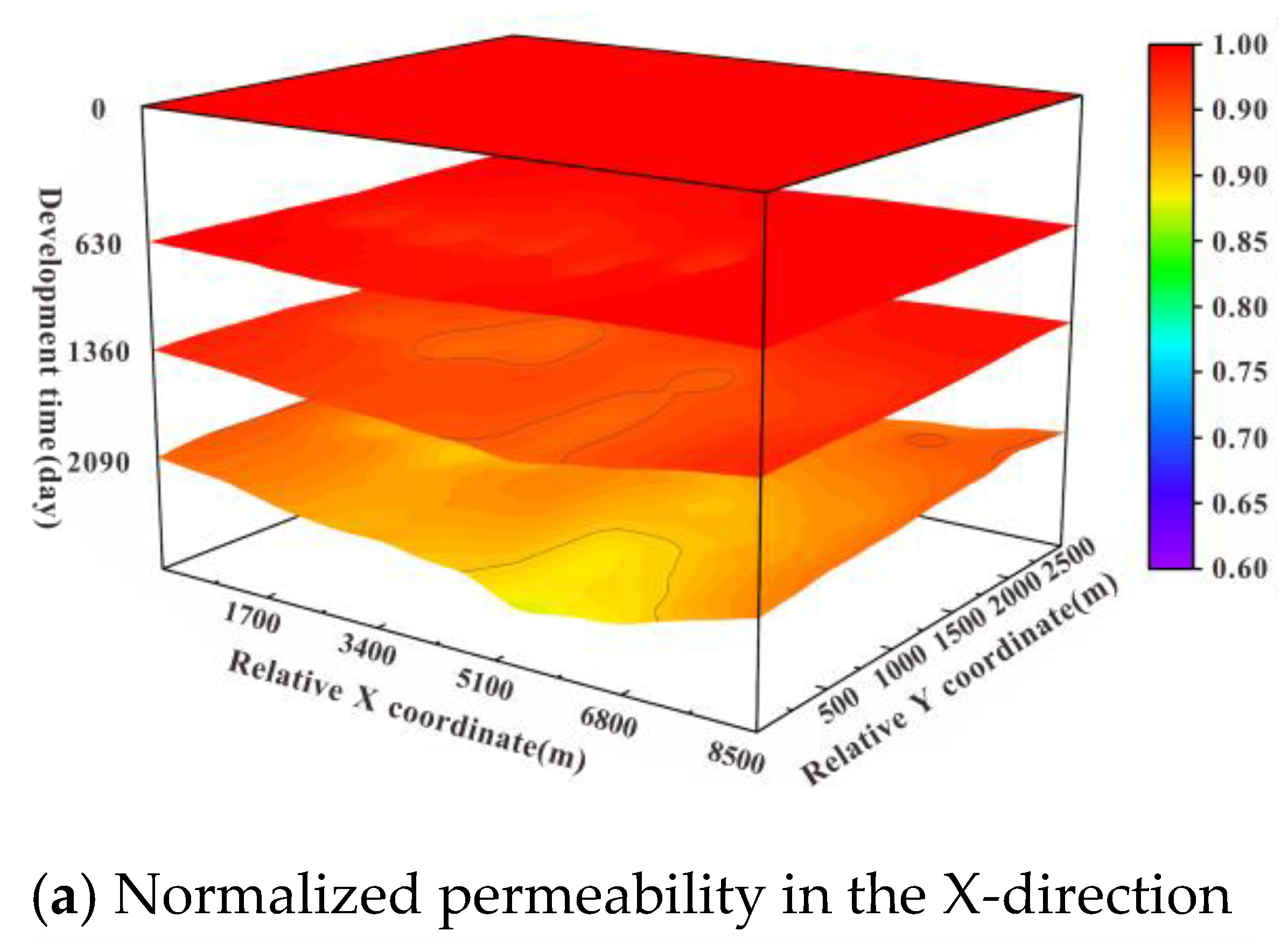
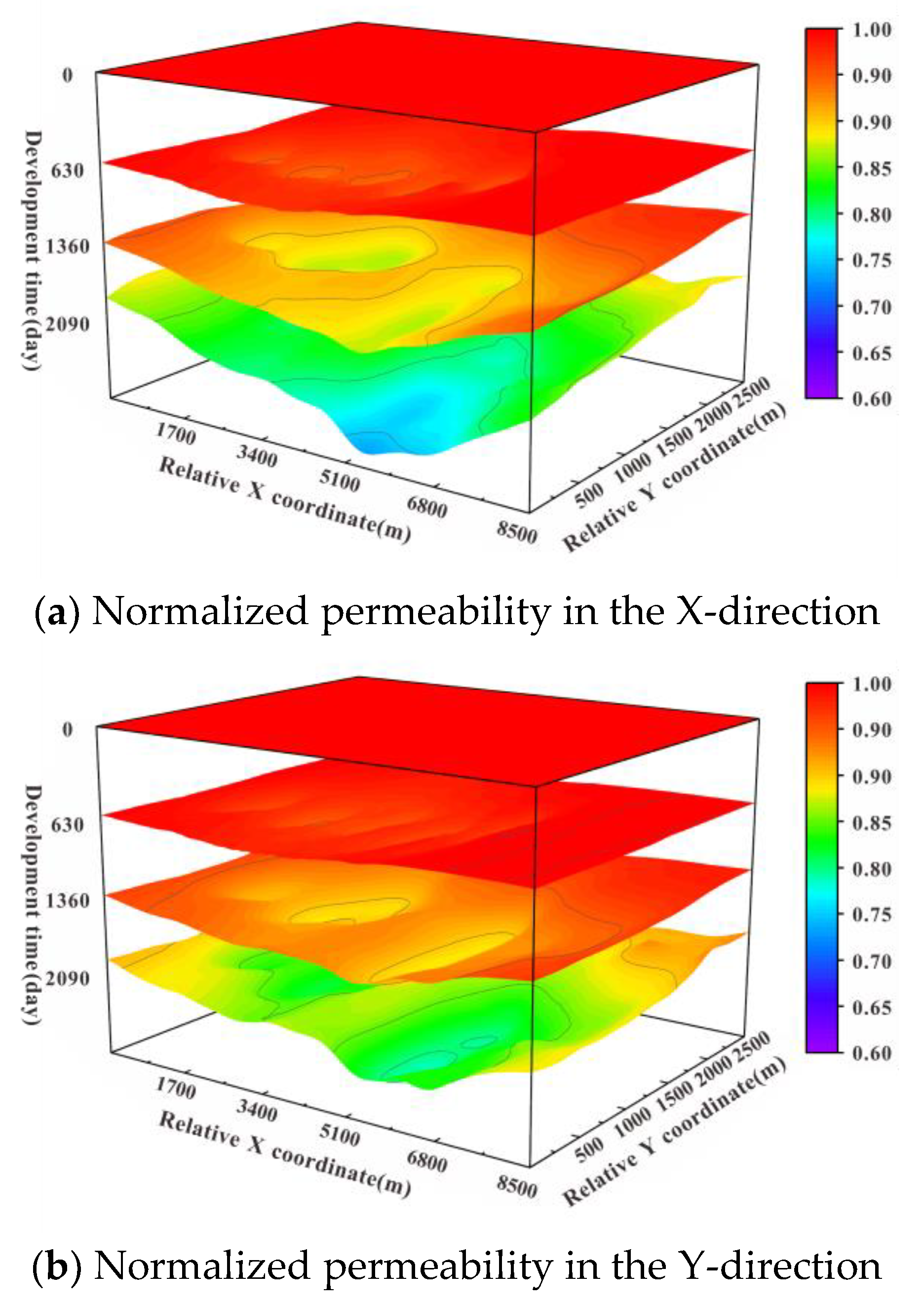
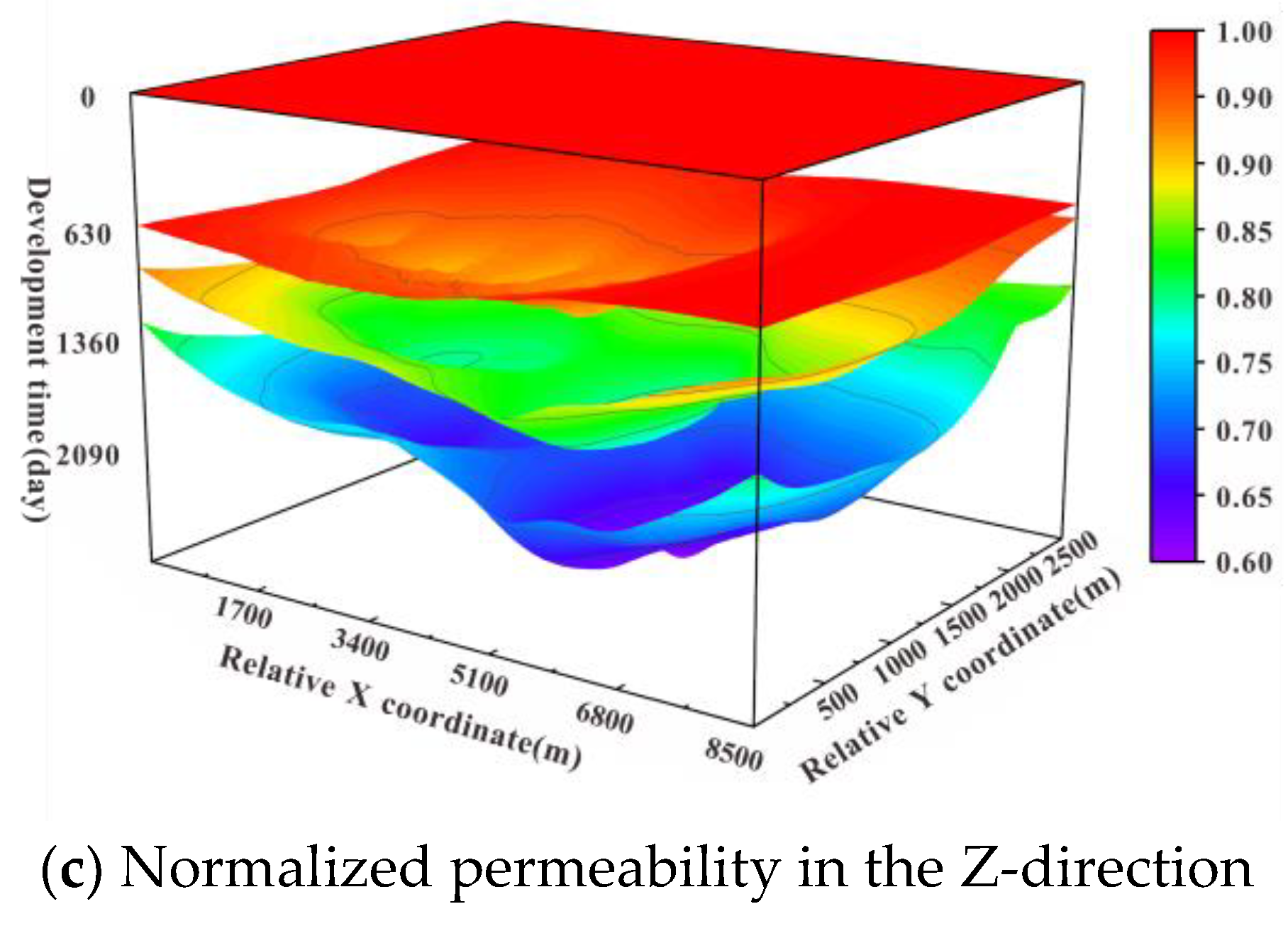
4.1. Evolution Results of Seepage-Geomechanical Field
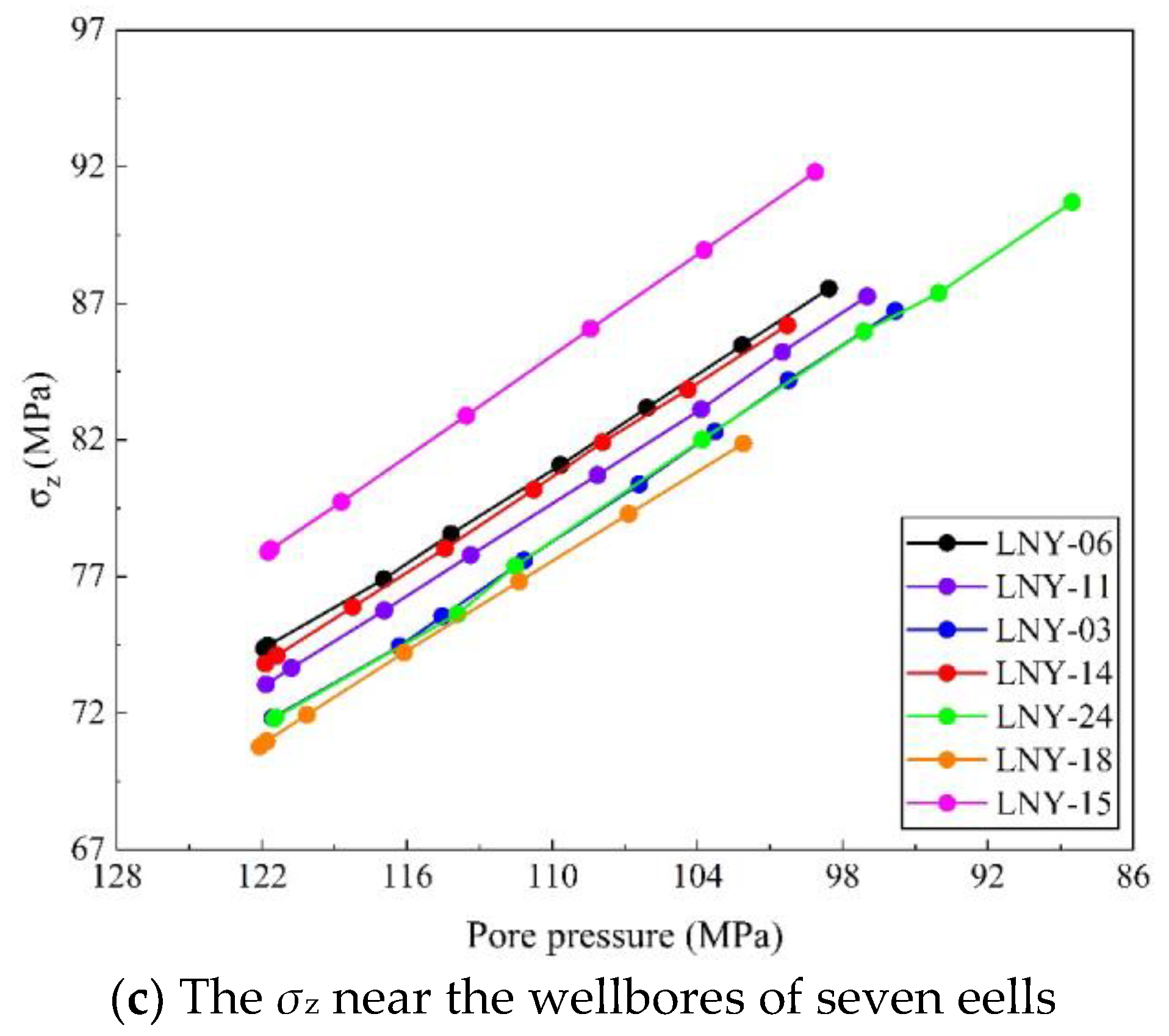
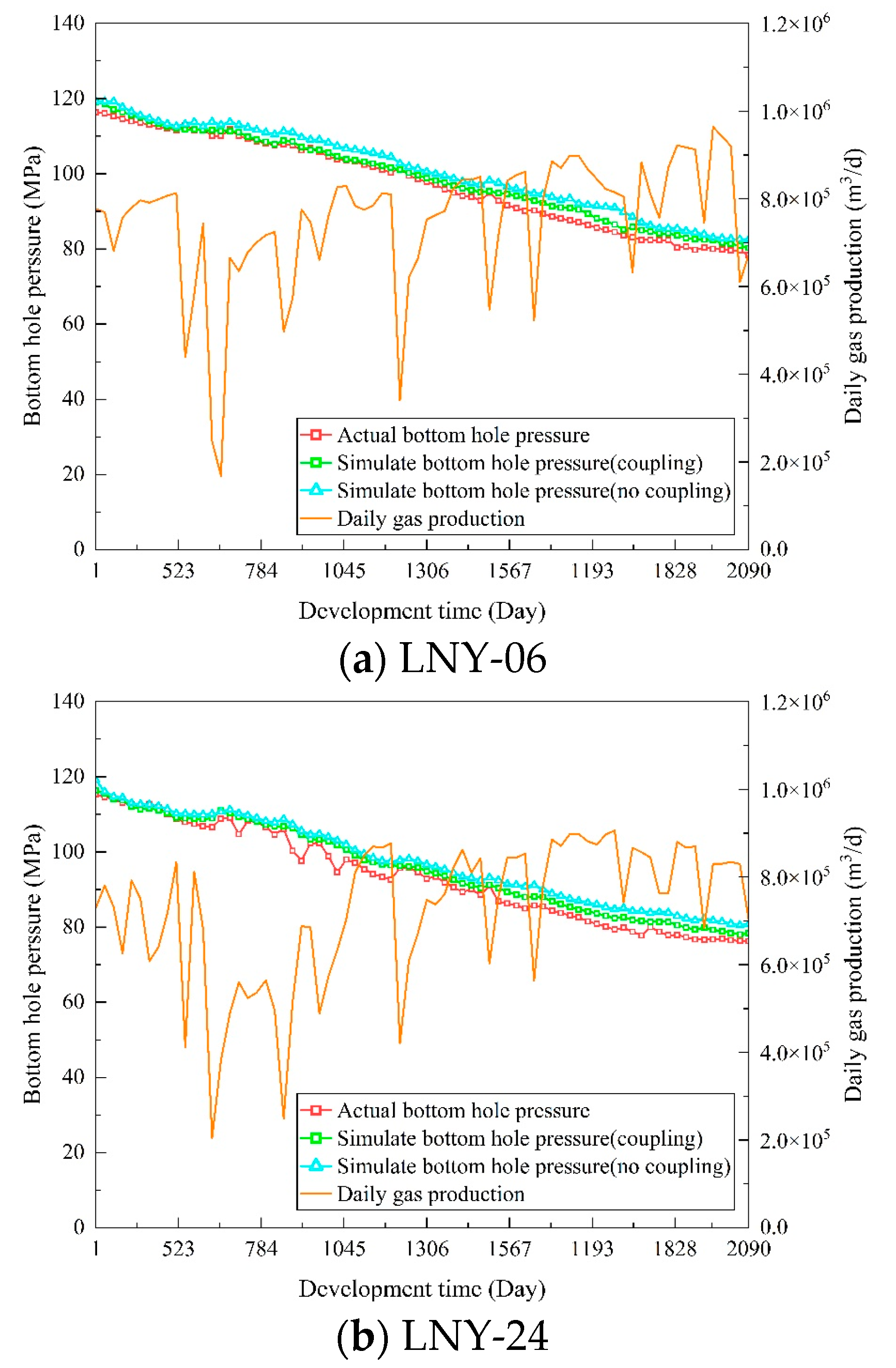
4.2. Analysis of Permeability Stress-Sensitivity Simulation Results
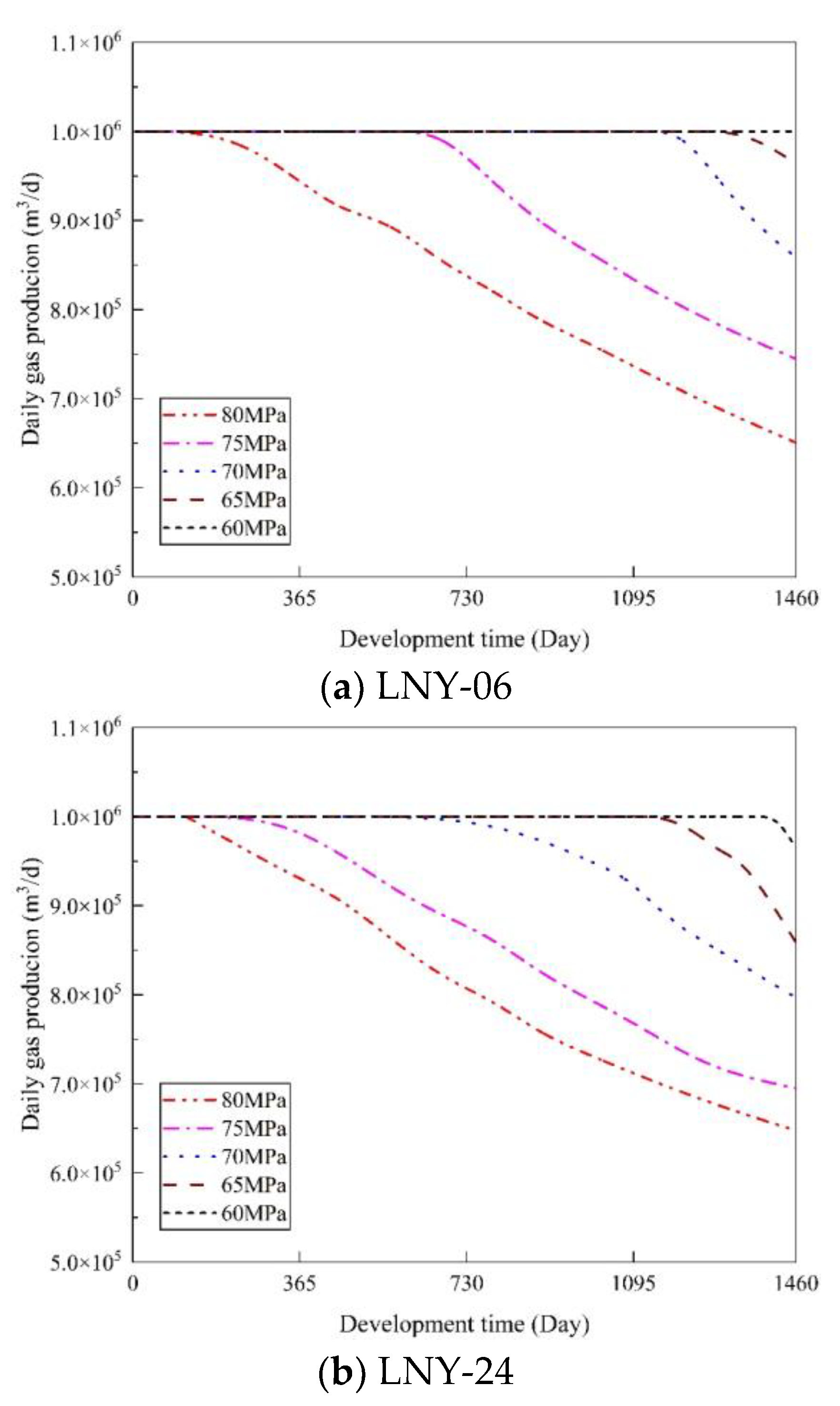
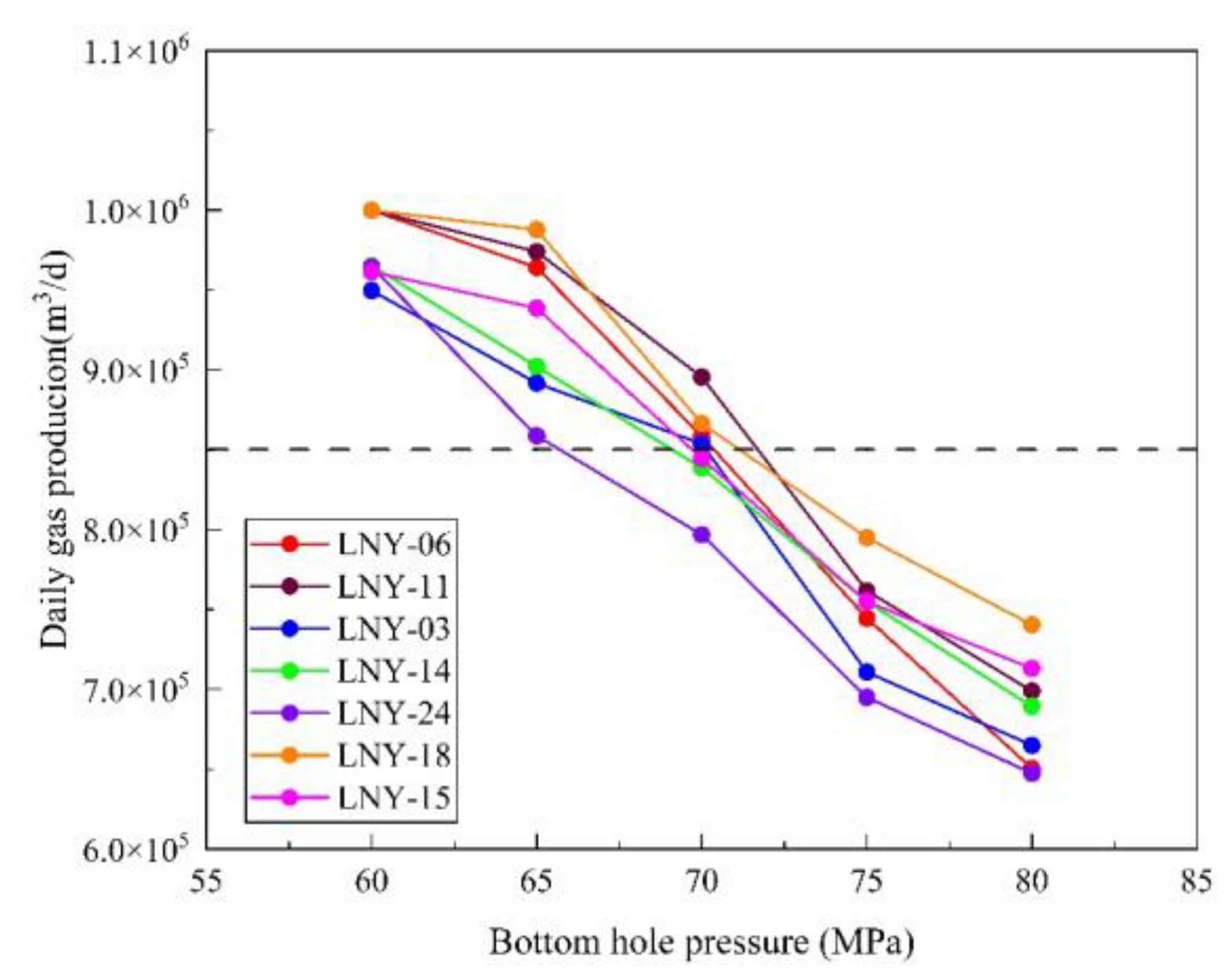
4.3. Optimization Scheme for Gas Reservoir Development
5. Conclusions
- (1)
- When the effective stress increased from 0 to 65 MPa, the permeability of the natural sample with fractures decreased by 81.28%, and the permeability of the intact core sample decreased by 54.67%. The permeability stress-sensitivity of natural fractures is stronger than that of the matrix, which had a dominant influence on permeability;
- (2)
- The reservoir heterogeneity can have an impact on the permeability variation, which is manifested by different changes in three-dimensional permeability. The vertical permeability decreases are the most pronounced. The permeability of the fractured zone and the matrix decreased by about 40% and 16%, respectively;
- (3)
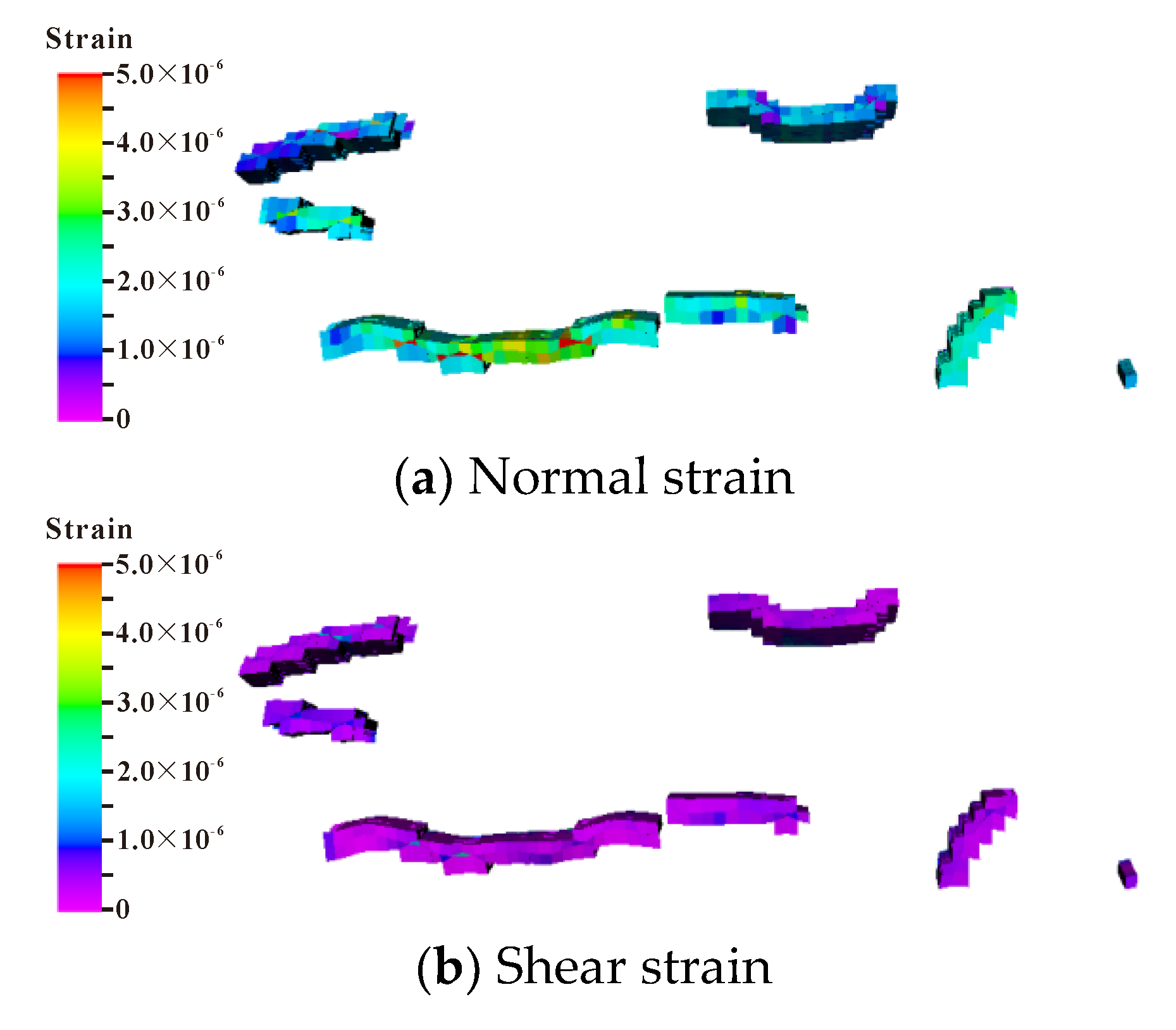
- When the pore pressure near the well decreased from 120 to 85 MPa, the effective stress increased by 5~10 MPa, 4~9 MPa and 11~19 MPa in the three dimensions of X, Y and vertical, respectively. Only elastic deformation occurs in natural fractures and faults, and the normal strain is greater than the shear strain;
- (4)
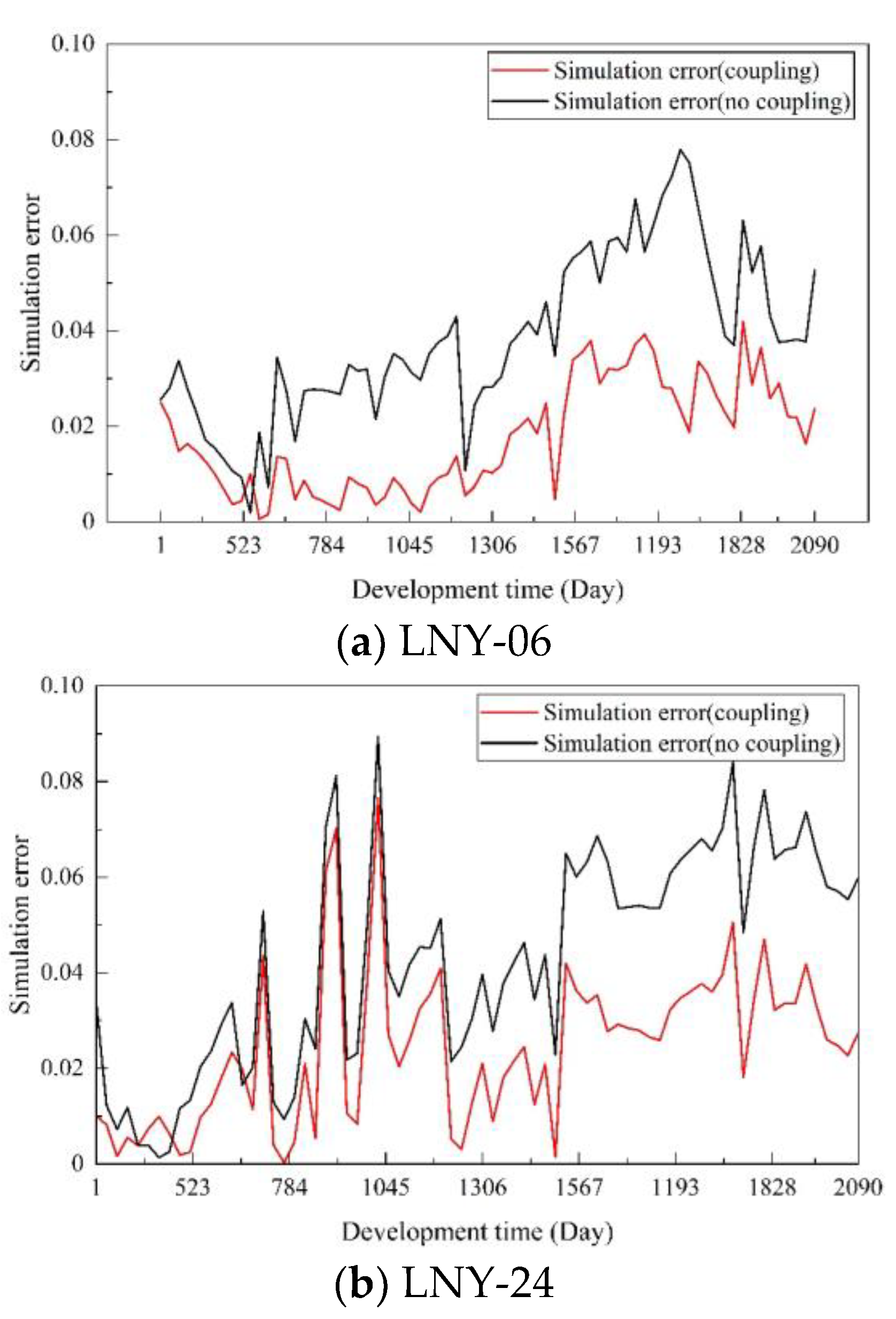
- The mean square error between the historical gas production results and the simulation results considering permeability stress-sensitivity was 2.22, while it was 4.01 without considering permeability stress-sensitivity. The coupled seepage-geomechanical model with permeability stress-sensitivity was more accurate in historical gas production fitting;
- (5)
- According to the numerical simulation and production conditions, three production optimization schemes were determined for the seven wells, including maintaining the state without adjustments, slight depressurization in the well and a combination of depressurization and observation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.Y.; Zhao, S.; Lin, A.D.; Liu, F.; Li, L.; Dai, X.D. Analysis on World Energy Supply & Demand in 2019—Based on BP Statistical Review of World Energy (2020). Nat. Gas Oil. 2020, 38, 122–130. [Google Scholar]
- Dai, J.X.; Ni, Y.Y.; Wu, X.Q. Tight Gas in China and its Significance in Exploration and Exploitation. Pet. Explor. Dev. 2012, 39, 257–264. [Google Scholar] [CrossRef]
- Song, R.; Wang, Y.; Tang, Y.; Peng, J.J.; Liu, J.J.; Yang, C.H. 3D Printing of Natural Sandstone at Pore Scale and Comparative Analysis on Micro-Structure and Single/Two-Phase Flow Properties. Energy 2022, 261, 125226. [Google Scholar] [CrossRef]
- Li, B.; Xu, N.W.; Dai, F.; Zhang, G.L.; Xiao, P.W. Dynamic Analysis of Rock Mass Deformation in Large Underground Caverns Considering Microseismic Data. Int. J. Rock Mech. Min. Sci. 2019, 122, 104078. [Google Scholar] [CrossRef]
- Li1, B.; Ding, Q.F.; Xu, N.W.; Dai, F.; Xu, Y.; Qu, H.L. Characteristics of Microseismic B-value Associated with Rock Mass Large Deformation in Underground Powerhouse Caverns at Different Stress Levels. J. Cent. South Univ. 2022, 29, 693–711. [Google Scholar]
- McLatchie, A.S.; Hemstock, R.A.; Young, J.W. The Effective Compressibility of Reservoirs Rock and Its Effects on Permeability. J. Pet. Technol. 1958, 10, 49–51. [Google Scholar] [CrossRef]
- Liu, J.J.; Liu, X.G.; Hu, Y.R.; Zhang, Z.S. Study of Fluid-Solid Coupling Flow in Low Permeablable Oil Reservoirs. Chin. J. Rock Mech. Eng. 2002, 21, 88–92. [Google Scholar]
- Zhu, J.Z.; Lei, M.; Ren, L.L.; Wang, X.Q.; Xu, G.H.; Huang, W.A. Sensitivity Evaluation and Mechanism of Tight Sandstone Gas Reservoirs Under High Temperature and High Pressure: A Case Study of Tight Gas Reservoirs in B Zone. Fault-Block Oil Gas Field 2017, 24, 222–225. [Google Scholar]
- Yang, Z.M.; Feng, C.; Liu, X.W.; Zhu, D.W.; Teng, Q. Experimental Study of Stress-dependent Sensitivity in Ultra-low Permeability Sandstone Planar Model. Sci. Technol. Rev. 2013, 31, 29–33. [Google Scholar]
- Jiao, C.Y.; He, S.L.; Xie, Q.; Gu, D.H.; Zhu, H.Y.; Sun, L.; Liu, H.X. An Experimental Study on Stress-dependent Sensitivity of Ultra-low Permeability Sandstone Reservoirs. Acta Pet. Sin. 2011, 32, 489–494. [Google Scholar]
- Yang, C.P.; Gao, S.S.; Liu, G.D.; Xiong, W.; Hu, Z.M.; Ye, L.Y.; Yang, R.F. The Research Status and Progress on Percolation Mechanism of Tight Gas Resvervoir. Sci. Technol. Eng. 2012, 12, 8606–8613. [Google Scholar]
- Chalmers, G.R.L.; Ross, D.J.K.; Bustin, R.M. Geological Controls on Matrix Permeability of Devonian Gas Shales in the Horn River and Liard Basins, Northeastern British Columbia, Canada. Int. J. Coal Geol. 2012, 103, 120–131. [Google Scholar] [CrossRef]
- Xiao, W.L.; Li, T.; Li, M.; Zhao, J.Z.; Zheng, L.L.; Li, L. Evaluation of the stress-sensitivity in Tight Reservoirs. Pet. Explor. Dev. 2016, 43, 107–114. [Google Scholar] [CrossRef]
- Dong, J.J.; Hsu, J.Y.; Wu, W.J.; Shimamoto, T.; Hung, J.H.; Yeh, E.C.; Wu, Y.H.; Sone, H. Stress-dependence of the Permeability and Porosity of Sandstone and Shale from TCDP Hole-A. Int. J. Rock Mech. Min. Sci. 2010, 47, 1141–1157. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Liu, J.J.; Liu, Y.C.; Shi, D.; Zhang, B.H. Experimental Investigation on the Stress-Dependent Permeability of Intact and Fractured Shale. Geofluids 2020, 2020, 8897911. [Google Scholar] [CrossRef]
- Zhang, X.L.; Liu, J.J.; Song, J.C. Optimization Algorithm of Effective Stress Coefficient for Permeability. Energies 2021, 14, 8345. [Google Scholar] [CrossRef]
- Fan, X.P.; Xu, X.R. Experimental and Mechanism Research About Permeability Damage with the Change of Stress. Pet. Explor. Dev. 2002, 29, 117–119. [Google Scholar]
- Yang, Z.P.; Wu, Z.W.; Li, Y.H.; Heng, Y.; Lu, T.Y. Effect of Connate Water on stress-sensitivity of Tight Gas Reservoirs. Energy Sources Part A-Recovery Util. Environ. Eff. 2021, 43, 1227–1241. [Google Scholar]
- Luo, R.L. Queries to the Viewpoint Low Permeability Reservoirs Have Not the Characteristics of Strong stress-sensitivity. Oil Drill. Prod. Technol. 2006, 28, 78–80. [Google Scholar]
- Li, C.L.; Zhang, X.L. Misunderstandings of Low Permeability Reservoirs. J. Southwest Pet. Univ. 2009, 31, 177–180,221. [Google Scholar]
- Song, R.; Sun, S.Y.; Liu, J.J.; Yang, C.H. Pore Scale Modeling on Dissociation and Transportation of Methane Hydrate in Porous Sediments. Energy 2021, 237, 121630. [Google Scholar] [CrossRef]
- Song, R.; Liu, J.J.; Yang, C.H.; Sun, S.Y. Study on the multiphase heat and mass transfer mechanism in the dissociation of methane hydrate in reconstructed real-shape porous sediments. Energy 2022, 254, 124421. [Google Scholar] [CrossRef]
- Ghafouri, H.R.; Lewis, R.W. A Finite Element Double Porosity Model for Heterogeneous Deformable Porous Media. Int. J. Numer. Anal. Methods Geomech. 1996, 20, 831–844. [Google Scholar] [CrossRef]
- Wei, Z.J.; Zhang, D.X. Coupled Fluid-Flow and Geomechanics for Triple-Porosity/Dual-Permeability Modeling of Coalbed Methane Recovery. Int. J. Rock Mech. Min. Sci. 2010, 47, 1242–1253. [Google Scholar] [CrossRef]
- Noorishad, J.; Mehran, M. An Upstream Finite-Element Method for Solution of Transient Transport-Equation in Fractured Porous-Media. Water Resour. Res. 1982, 18, 588–596. [Google Scholar] [CrossRef]
- Yang, H.J.; Li, Y.; Tang, Y.G.; Lei, G.L.; Zhou, P.; Zhou, L.; Xu, A.M.; Huan, Z.P.; Zhu, W.H.; Chen, W.L.; et al. Accumulation Conditions, Key Exploration and Development Technologies for Keshen Gas Field in Tarim Basin. Acta Pet. Sin. 2021, 42, 399–414. [Google Scholar] [CrossRef]
- Li, M.; Xiao, W.L. Experimental Study on Permeability-Effective-Stress Law in Low-Permeability Sandstone Reservoirs. Chin. J. Rock Mech. Eng. 2008, 27, 3535–3540. [Google Scholar]
- Xiao, W.L.; Bernabe, Y.; Evans, B.; Mok, U.; Zhao, J.Z.; Ren, X.Y.; Chen, M. Klinkenberg Effect and Effective Pressure for Gas Permeability of Tight Sandstones. J. Geophys. Res.-Solid Earth 2019, 124, 1412–1429. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Tian, J.; Yang, T.H.; Tang, C.A. Coupled Thermal-hydraulic-mechanical Model During Rock Damage and its Preliminary Application. Rock Soil Mech. 2009, 30, 3851–3857. [Google Scholar]
- Pei, G.H.; Song, J.C.; Zhang, X.L. Numerical Simulation of Temporal and Spatial Evolution of Stress Field in Unconsolidated Sandstone Oil Reservoirs. In Journal of Physics: Conference Series, Proceedings of the 2021 5th International Conference on Electrical, Automation and Mechanical Engineering (EAME 2021), Guangzhou, China, 17–18 September 2021; IOP Publishing: Bristol, UK, 2021; Volume 2095, p. 2095. [Google Scholar]
- Liu, J.J.; Zhang, S.Z.; Liu, X.G.; Hu, Y.R. Theory and Simulation of Fluid-Solid Coupling Flow Through Low Permeability Fractured Oil Reservoirs. Theor. Appl. Mech. 2002, 34, 779–784. [Google Scholar]
- Jiang, T.W.; Zhang, H.; Xu, K.; Wang, Z.M.; Wang, H.Y. Reservoirs Geomechanical Characteristics and the Influence on Development in Keshen Gas Field. J. Southwest Pet. Univ. 2020, 42, 1–12. [Google Scholar]
- Wang, K.; Zhang, R.H.; Wang, J.P.; Sun, X.W.; Yang, X.J. Distribution and Origin of Tectonic Fractures in Ultra-deep Tight Sandstone Reservoirs: A Case Study of Keshen Gas Field, Kuqa Foreland Thrust Belt, Tarim Basin. Oil Gas Geol. 2021, 42, 338–353. [Google Scholar]
- Zhu, H.Y.; Song, Y.J.; Lei, Z.D.; Tang, X.H. 4D-stress Evolution of Tight Sandstone Reservoirs During Horizontal Wells Injection and Production: A Case Study of Yuan 284 Block, Ordos Basin, NW China. Pet. Explor. Dev. 2022, 49, 136–147. [Google Scholar] [CrossRef]
- Samier, P.; Onaisi, A.; de Gennaro, S. A Practical Iterative Scheme for Coupling Geomechanics with Reservoirs Simulation. SPE Reserv. Eval. Eng. 2008, 11, 892–901. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.K. The Structured Gridding Implications for Upscaling Model Discrete Fracture Networks (DFN) Using Corrected Oda’s Method. J. Pet. Sci. Eng. 2017, 153, 70–80. [Google Scholar] [CrossRef]
- Wei, H.B.; Zhu, H.L.; Li, H.S.; Shi, S.M.; Gan, S.L.; Zhai, Z.W. The Study of the Reservoirs Inter-architecture Structure and Remaining Oil in the Eastern Part of Sabei II District. Rud.-Geol.-Naft. Zbornik. 2019, 34, 13–20. [Google Scholar] [CrossRef]
- Feng, Y.C.; Gray, K.E. A Fracture-mechanics-based Model for Wellbore Strengthening Applications. J. Nat. Gas Sci. Eng. 2016, 29, 392–400. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Tang, X.H.; Liu, Q.Y.; Liu, S.J.; Zhang, B.H.; Jiang, S.; McLennan, J.D. Permeability Stress-sensitivity in 4D Flow-geomechanical Coupling of Shouyang CBM Reservoirs, Qinshui Basin, China. Fuel 2018, 232, 817–832. [Google Scholar] [CrossRef]
- Chrisangelo, A.U.; Maduabuchi, I.P.; Ma, X.L.; Obunwa, U.J. Application of Machine Learning Models in Predicting Initial Gas Production Rate from Tight Gas Reservoirs. Rud.-Geol.-Naft. Zbornikl. 2019, 34, 29–40. [Google Scholar]


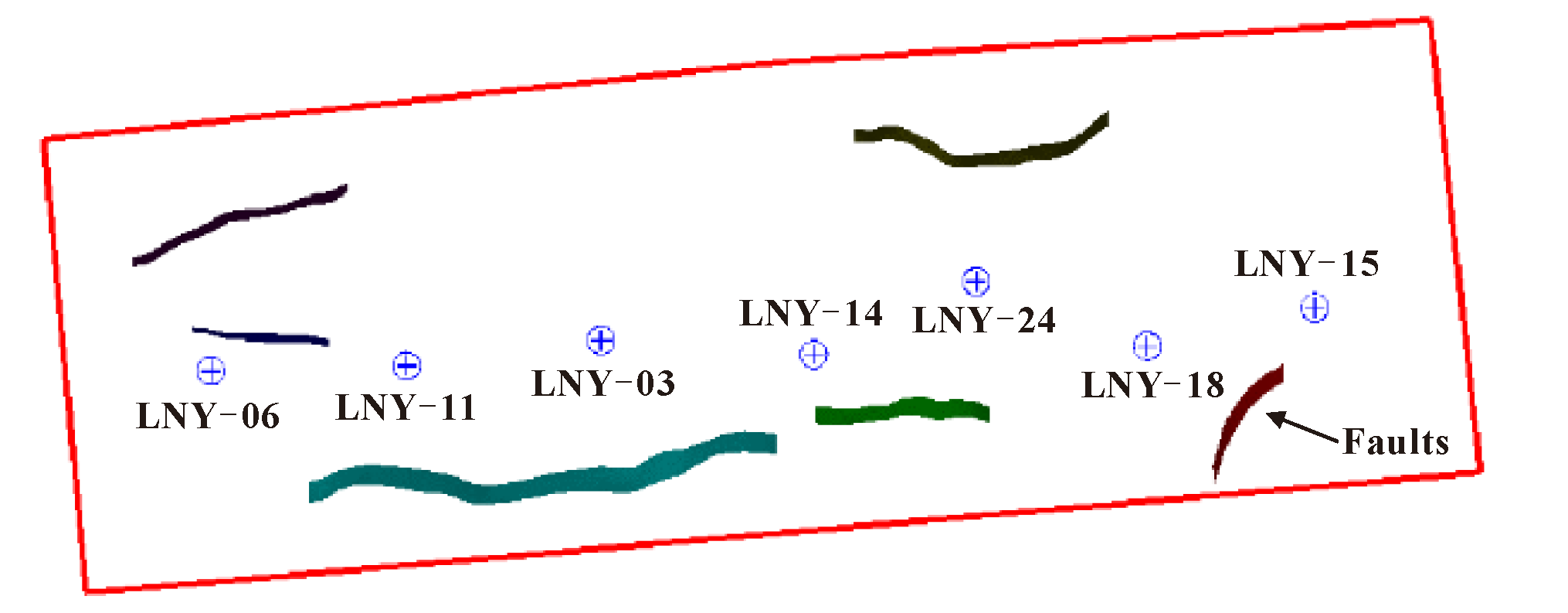

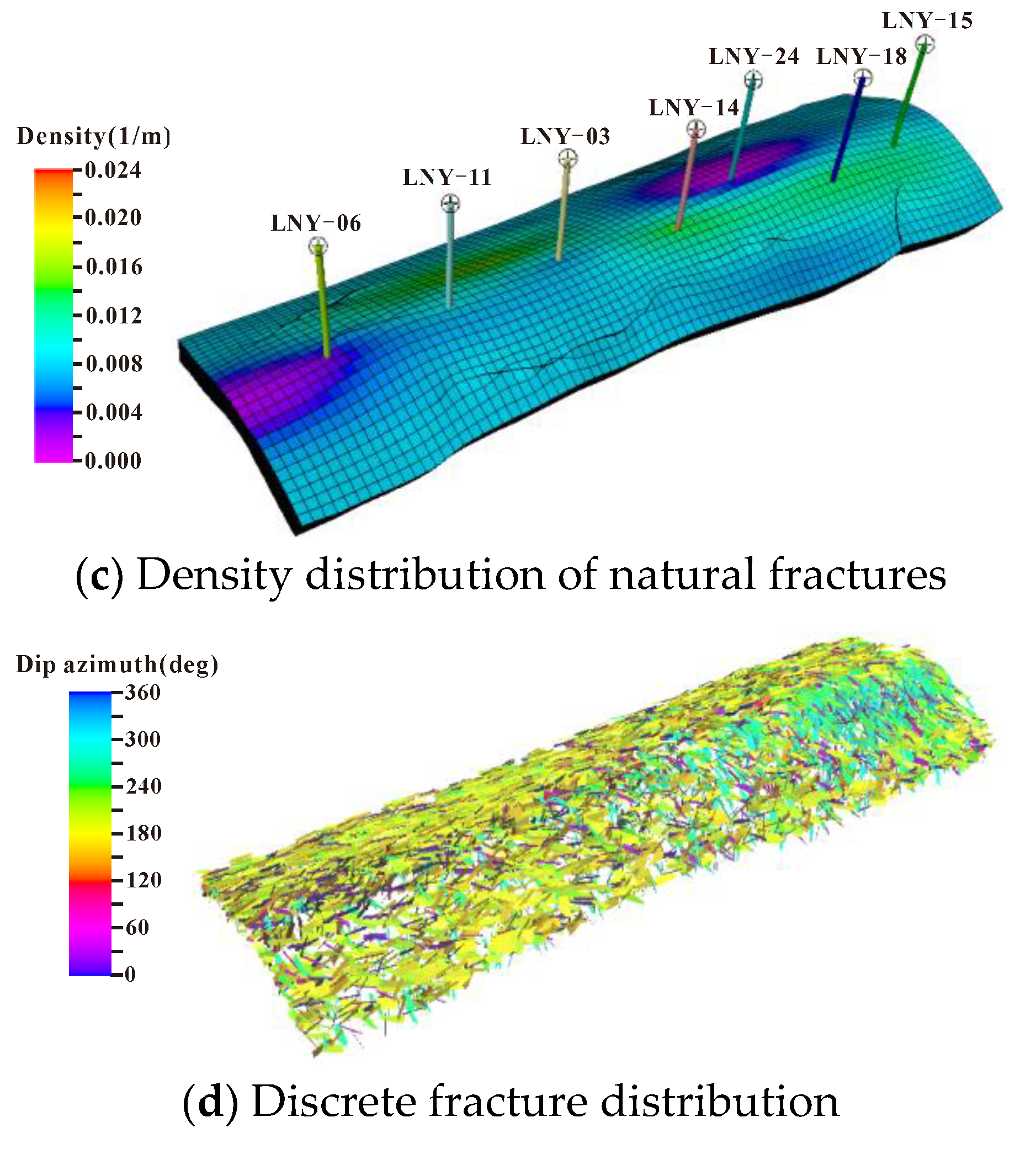
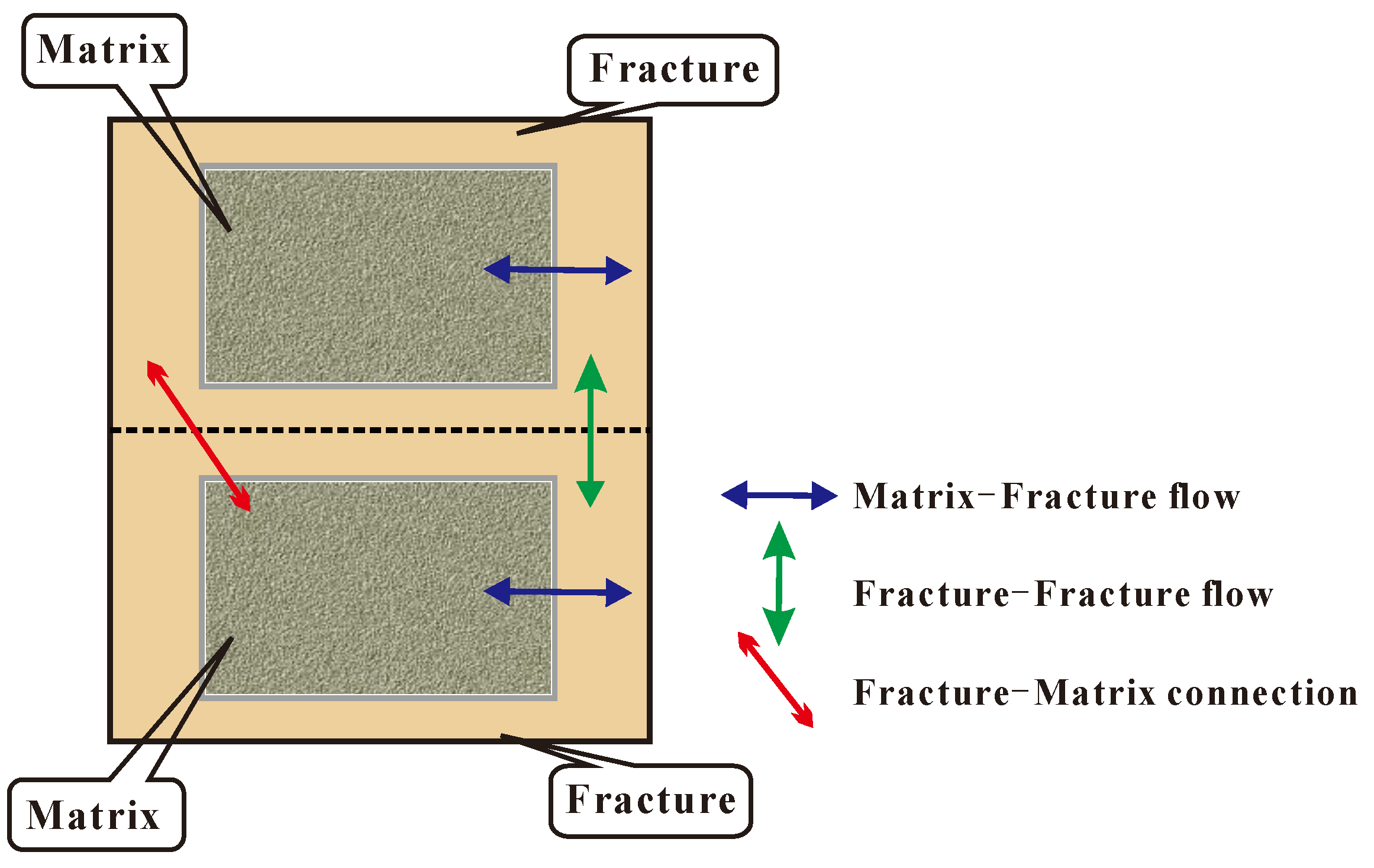

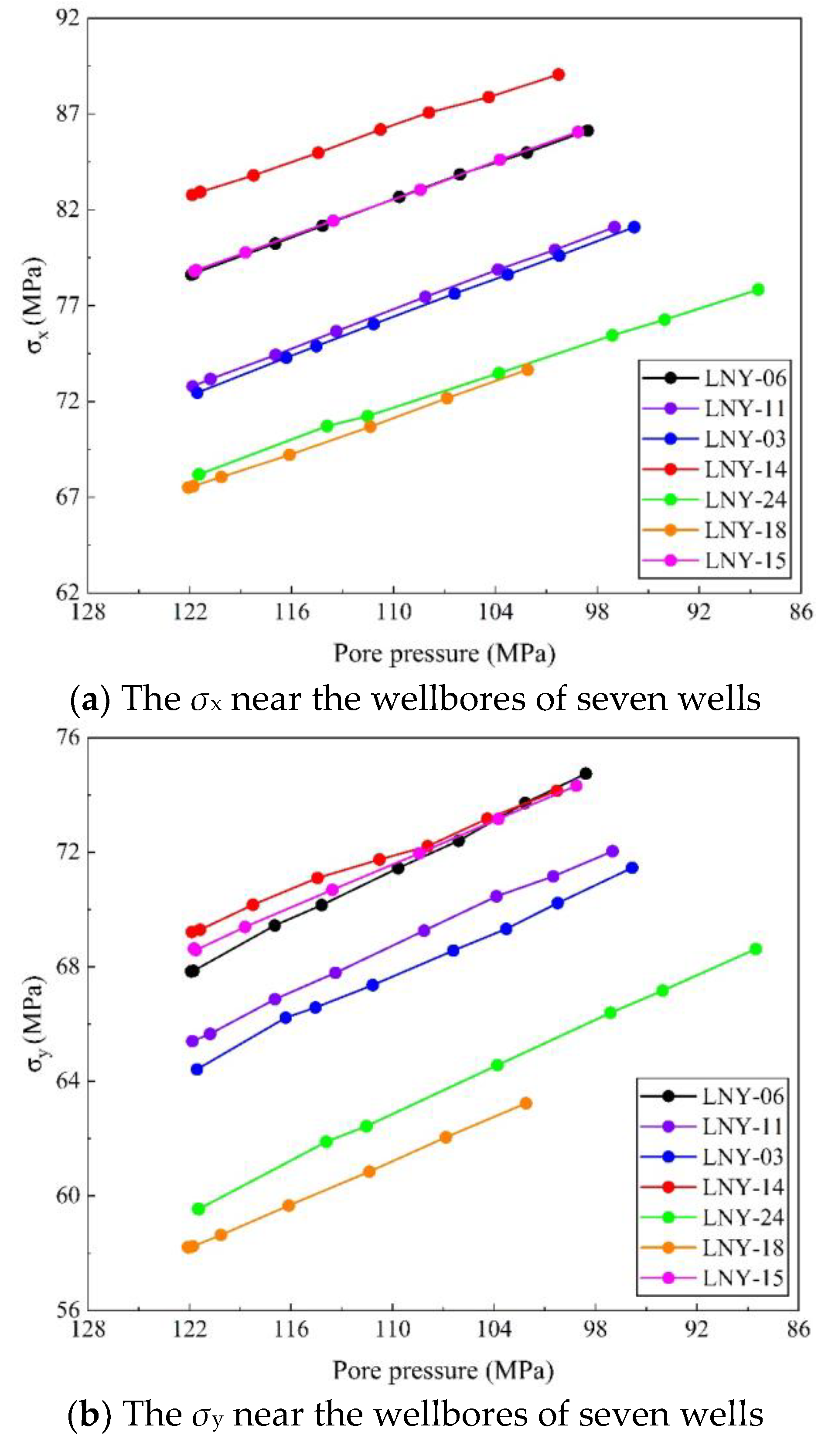




| No. | Depth (cm) | Weight (g) | Length (cm) | Diameter (cm) | Porosity (%) | Permeability (mD) |
|---|---|---|---|---|---|---|
| A1 | 6786.29 | 64.79 | 5.042 | 2.500 | 1.468 | 0.047 |
| A2 | 6703.50 | 62.48 | 5.045 | 2.500 | 4.575 | 0.028 |
| A3 | 6707.43 | 64.24 | 5.048 | 2.500 | — | 0.036 |
| A4 | 6706.61 | 62.29 | 5.045 | 2.504 | 4.606 | 0.033 |
| A5 | 7001.91 | 56.71 | 4.433 | 2.500 | 1.594 | 0.023 |
| B1 | 6778.62 | 64.38 | 5.063 | 2.502 | 2.558 | 0.095 |
| B2 | 6783.92 | 66.10 | 5.063 | 2.516 | — | 3.454 |
| B3 | 6706.61 | 62.41 | 5.054 | 2.499 | — | 0.622 |
| B4 | 6878.80 | 62.49 | 5.055 | 2.500 | 4.198 | 0.087 |
| B5 | 7363.07 | 64.21 | 5.030 | 2.500 | — | 0.113 |
| Parameters | Value |
|---|---|
| Gas phase density under standard conditions (kg/m3) | 0.6972 |
| Water phase density under standard conditions (kg/m3) | 1020.30 |
| Viscosity of water phase under standard conditions (cP) | 0.20 |
| Volume coefficient of water phase | 1.0622 |
| Compression coefficient of water phase | 0.4596 × 10−3 |
| Parameters | Over Burden | Under Burden | Side Burden | Plate | Reservoirs |
|---|---|---|---|---|---|
| Young’s modulus (GPa) | 15 | 36 | 32 | 36 | 17~35 |
| Poisson’s ratio | 0.25 | 0.22 | 0.27 | 0.2 | 0.24~0.3 |
| Density (g/cm3) | 2.65 | 2.52 | 2.6 | 2.52 | 2.46~2.68 |
| Porosity (%) | 4 | 2 | 4 | 1 | 1.5~6.0 |
| Compressive strength (MPa) | 105 | 120 | 110 | 125 | 80~110 |
| Tensile strength (MPa) | 35 | 45 | 42 | 15 | 41~45 |
| Friction Angle (°) | 7.5 | 9.5 | 9.5 | 12 | 6.5~10 |
| Cohesive force (MPa) | 20 | 24 | 24 | 24 | 18~24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Liu, J.; Song, R.; Song, Y. Study on Permeability Stress-Sensitivity in Seepage-Geomechanical Coupling of Fractured Deep Tight Sandstone Gas Reservoirs. Appl. Sci. 2022, 12, 11672. https://doi.org/10.3390/app122211672
Song J, Liu J, Song R, Song Y. Study on Permeability Stress-Sensitivity in Seepage-Geomechanical Coupling of Fractured Deep Tight Sandstone Gas Reservoirs. Applied Sciences. 2022; 12(22):11672. https://doi.org/10.3390/app122211672
Chicago/Turabian StyleSong, Jiecheng, Jianjun Liu, Rui Song, and Yujia Song. 2022. "Study on Permeability Stress-Sensitivity in Seepage-Geomechanical Coupling of Fractured Deep Tight Sandstone Gas Reservoirs" Applied Sciences 12, no. 22: 11672. https://doi.org/10.3390/app122211672
APA StyleSong, J., Liu, J., Song, R., & Song, Y. (2022). Study on Permeability Stress-Sensitivity in Seepage-Geomechanical Coupling of Fractured Deep Tight Sandstone Gas Reservoirs. Applied Sciences, 12(22), 11672. https://doi.org/10.3390/app122211672








