Assessment of Cranial Deformation Indices by Automatic Smartphone-Based Photogrammetric Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. PhotoMeDAS Modelling
2.2. Ground Truth
2.3. Model Comparison
2.4. Uncertainty Propagation
3. Results
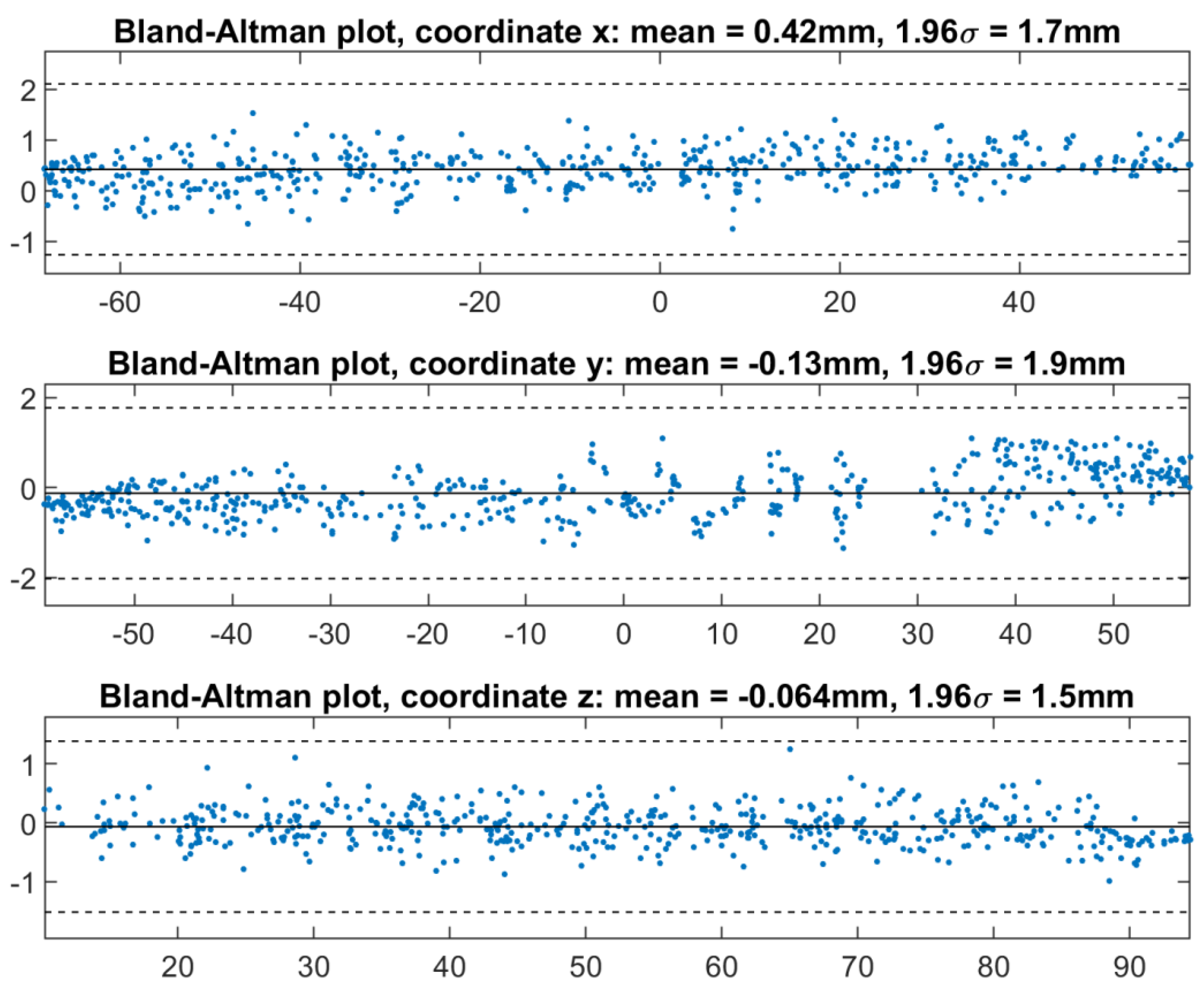
3.1. Accuracy Assessment
3.2. Three-Dimensional Transformation Assessment
3.2.1. Without Scale Correction
3.2.2. With Scale Correction
3.3. Uncertainty Propagation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ballardini, E.; Sisti, M.; Basaglia, N.; Benedetto, M.; Baldan, A.; Borgna-Pignatti, C.; Garani, G. Prevalence and characteristics of positional plagiocephaly in healthy full-term infants at 8–12 weeks of life. Eur. J. Pediatr. 2018, 177, 1547–1554. [Google Scholar] [CrossRef]
- Khormi, Y.; Chiu, M.; Goodluck Tyndall, R.; Mortenson, P.; Smith, D.; Steinbok, P. Safety and efficacy of independent allied healthcare professionals in the assessment and management of plagiocephaly patients. Child’s Nerv. Syst. 2020, 36, 373–377. [Google Scholar] [CrossRef]
- Martiniuk, A.L.C.; Vujovich-Dunn, C.; Park, M.; Yu, W.; Lucas, B.R. Plagiocephaly and developmental delay: A systematic review. J. Dev. Behav. Pediatr. 2017, 38, 67–78. [Google Scholar] [CrossRef]
- Collett, B.R.; Wallace, E.R.; Kartin, D.; Cunningham, M.L.; Speltz, M.L. Cognitive outcomes and positional plagiocephaly. Pediatrics 2019, 143, e20182373. [Google Scholar] [CrossRef] [PubMed]
- Siegenthaler, M.H. Methods to diagnose, classify, and monitor infantile deformational plagiocephaly and brachycephaly: A narrative review. J. Chiropr. Med. 2015, 14, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Wilbrand, J.F.; Wilbrand, M.; Pons-Kuehnemann, J.; Blecher, J.C.; Christophis, P.; Howaldt, H.P.; Schaaf, H. Value and reliability of anthropometric measurements of cranial deformity in early childhood. J. Cranio-Maxillofac. Surg. 2011, 39, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Caple, J.M.; Stephan, C.N.; Gregory, L.S.; MacGregor, D.M. Effect of head position on facial soft tissue depth measurements obtained using computed tomography. J. Forensic Sci. 2016, 61, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Munn, L.; Stephan, C.N. Changes in face topography from supine-to-upright position—And soft tissue correction values for craniofacial identification. Forensic Sci. Int. 2018, 289, 40–50. [Google Scholar] [CrossRef]
- Meulstee, J.W.; Verhamme, L.M.; Borstlap, W.A.; van der Heijden, F.; de Jong, G.A.; Xi, T.; Bergé, S.J.; Delye, H.; Maal, T.J.J. A new method for three-dimensional evaluation of the cranial shape and the automatic identification of craniosynostosis using 3D stereophotogrammetry. Int. J. Oral Maxillofac. Surg. 2017, 46, 819–826. [Google Scholar] [CrossRef]
- Dörhage, K.W.W.; Wiltfang, J.; von Grabe, V.; Sonntag, A.; Becker, S.T.; Beck-Broichsitter, B.E. Effect of head orthoses on skull deformities in positional plagiocephaly: Evaluation of a 3-dimensional approach. J. Cranio-Maxillofac. Surg. 2018, 46, 953–957. [Google Scholar] [CrossRef]
- Barbero-García, I.; Lerma, J.L.; Mora-Navarro, G. Fully automatic smartphone-based photogrammetric 3D modelling of infant’s heads for cranial deformation analysis. ISPRS J. Photogramm. Remote Sens. 2020, 166, 268–277. [Google Scholar] [CrossRef]
- Barbero-García, I.; Pierdicca, R.; Paolanti, M.; Felicetti, A.; Lerma, J.L. Combining machine learning and close-range photogrammetry for infant’s head 3D measurement: A smartphone-based solution. Measurement 2021, 182, 109686. [Google Scholar] [CrossRef]
- Grieb, J.; Barbero-García, I.; Lerma, J.L. Spherical harmonics to quantify cranial asymmetry in deformational plagiocephal. Sci. Rep. 2022, 12, 167. [Google Scholar] [CrossRef]
- Potenziani, M.; Callieri, M.; Dellepiane, M.; Corsini, M.; Ponchio, F.; Scopigno, R. 3DHOP: 3D Heritage Online Presenter. Comput. Graph. 2015, 52, 129–141. [Google Scholar] [CrossRef]
- Boutsi, A.M.; Ioannidis, C.; Soile, S. An Integrated Approach to 3D Web Visualization of Cultural Heritage Heterogeneous Datasets. Remote Sens. 2019, 11, 2508. [Google Scholar] [CrossRef]
- Pindrik, J.; Molenda, J.; Uribe-Cardenas, R.; Dorafshar, A.H.; Ahn, E.S. Normative ranges of anthropometric cranial indices and metopic suture closure during infancy. J. Neurosurg. Pediatr. 2016, 18, 667–673. [Google Scholar] [CrossRef] [PubMed]
- Skolnick, G.B.; Naidoo, S.D.; Nguyen, D.C.; Patel, K.B.; Woo, A.S. Comparison of direct and digital measures of cranial vault asymmetry for assessment of plagiocephaly. J. Craniofac. Surg. 2015, 26, 1900–1903. [Google Scholar] [CrossRef]
- Thompson, A.; Southon, N.; Fern, F.; Stupfler, G.; Leach, R. Efficient empirical determination of maximum permissible error in coordinate metrology. Meas. Sci. Technol. 2021, 32, 105013. [Google Scholar] [CrossRef]
- Bortoluzzi, G.; Ligi, M. DIGMAP: A computer program for accurate acquisition by digitizer of geographical coordinates from conformal projections. Comput. Geosci. 1986, 12, 175–197. [Google Scholar] [CrossRef]
- Hu, P.; Yang, B. Visual perception driven 3D building structure representation from airborne laser scanning point cloud. Virtual Real. Intell. Hardw. 2020, 2, 261–275. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Liu, S.C.; Li, Q.Z. An advanced multiple outlier detection algorithm for 3D similarity datum transformation. Measurement 2020, 163, 107945. [Google Scholar] [CrossRef]
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Bland, J.M. Measurement in medicine: The analysis of method comparison studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Barbero-García, I.; Lerma, J.L.; Marqués-Mateu, Á.; Miranda, P. Low-cost smartphone-based photogrammetry for the analysis of cranial deformation in infants. World Neurosurg. 2017, 102, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Alho, E.J.L.; Rondinoni, C.; Furokawa, F.O.; Monaco, B.A. Computer-assisted craniometric evaluation for diagnosis and follow-up of craniofacial asymmetries: SymMetric v. 1.0. Child’s Nerv. Syst. 2020, 36, 1255–1261. [Google Scholar] [CrossRef] [PubMed]
- Wilbrand, J.F.; Szczukowski, A.; Blecher, J.C.; Pons-Kuehnemann, J.; Christophis, P.; Howaldt, H.P.; Schaaf, H. Objectification of cranial vault correction for craniosynostosis by three-dimensional photography. J. Cranio-Maxillofac. Surg. 2012, 40, 726–730. [Google Scholar] [CrossRef]
- Ayoub, A.; de Freitas Silva, L.; Mossey, P.; Al-Rudainy, D.; Marques de Mattos, A.; Garcia Júnior, I.R.; Quigley, A.; Ju, X. The characterisation of the craniofacial morphology of infants born with Zika virus, Innovative approach for public health surveillance and broad clinical applications. Front. Med. 2021, 8, 612596. [Google Scholar] [CrossRef] [PubMed]
- Freudlsperger, C.; Steinmacher, S.; Bächli, H.; Somlo, E.; Hoffmann, J.; Engel, M. Metopic synostosis: Measuring intracranial volume change following fronto-orbital advancement using three-dimensional photogrammetry. J. Cranio-Maxillofac. Surg. 2015, 43, 593–598. [Google Scholar] [CrossRef] [PubMed]
- Schaaf, H.; Malik, C.Y.; Streckbein, P.; Pons-Kuehnemann, J.; Howaldt, H.P.; Wilbrand, J.F. Three-dimensional photographic analysis of outcome after helmet treatment of a nonsynostotic cranial deformity. J. Craniofac Surg. 2010, 21, 1677–1682. [Google Scholar] [CrossRef]
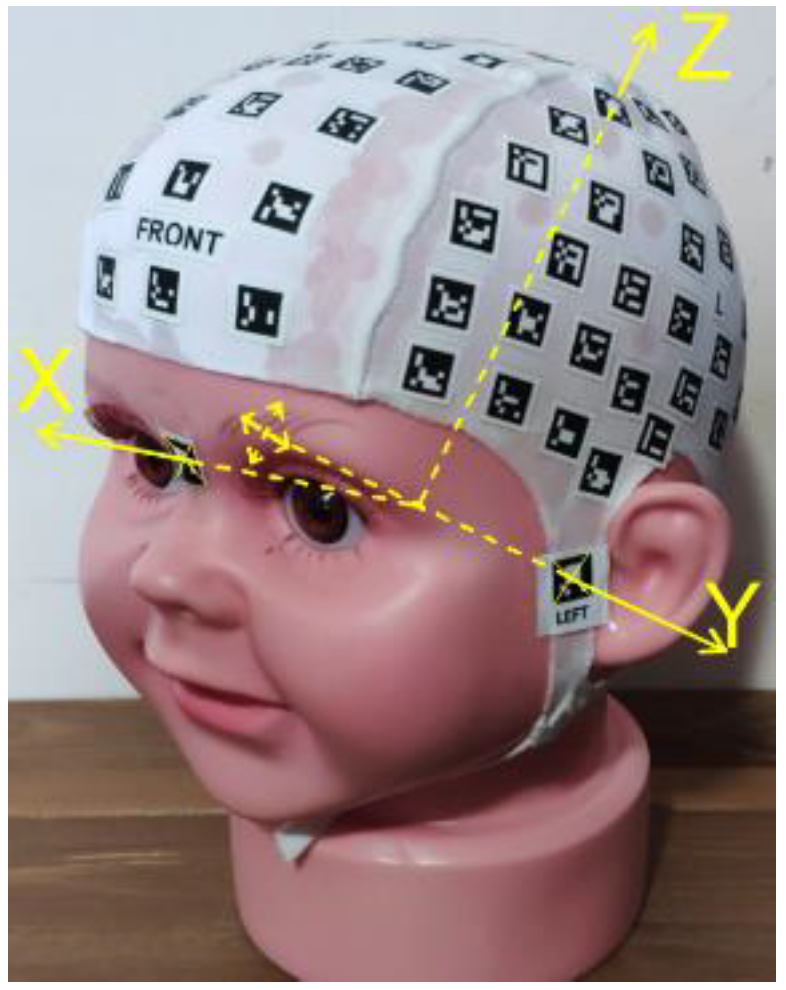

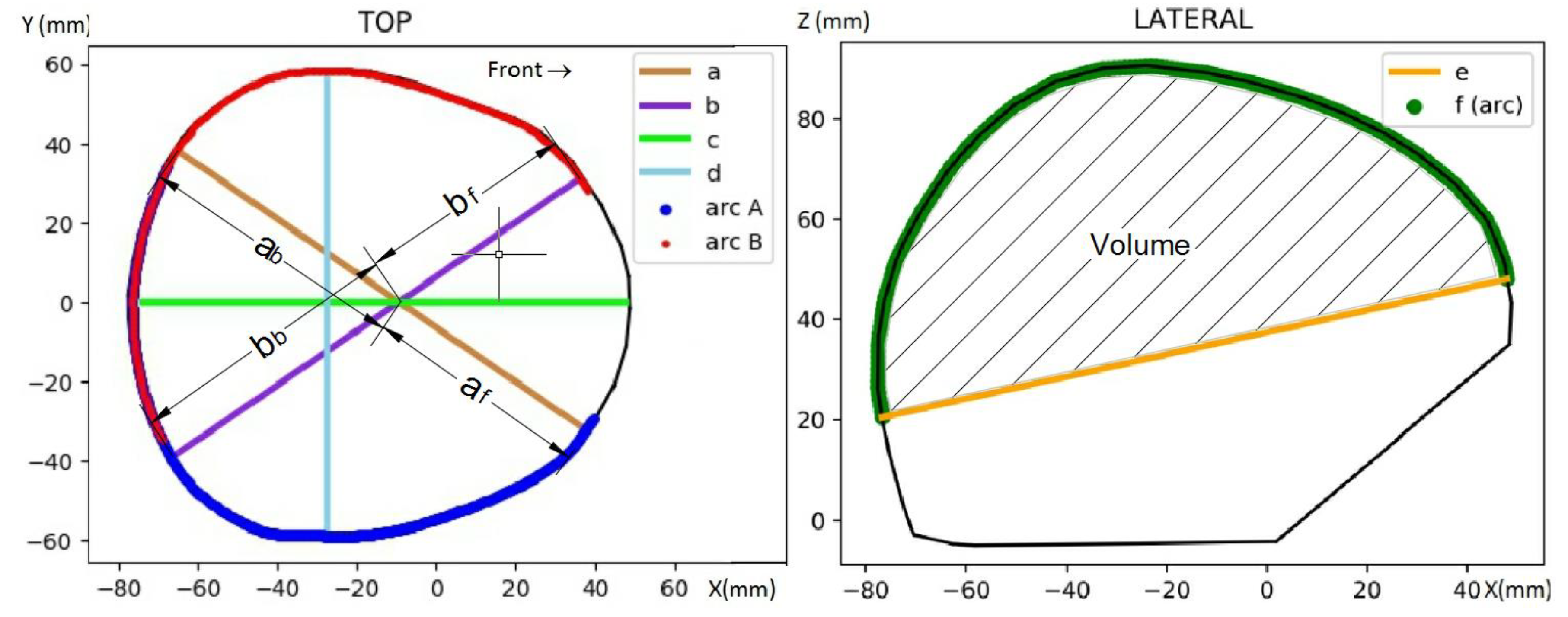
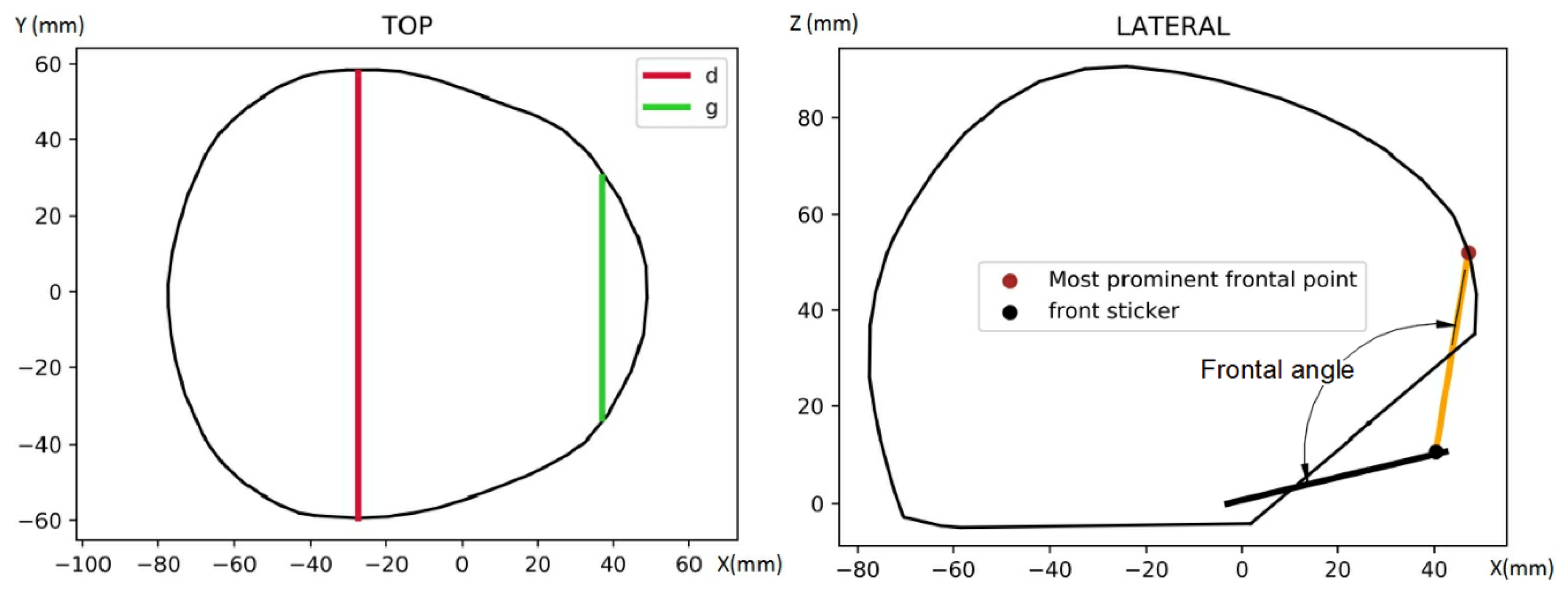



| Parameter or Index | Symbol | Formula or Explanation | |
|---|---|---|---|
| Cranial perimeter | CP | ||
| Pseudo-cranial volume | CV | Volume above the maximum CP | |
| Maximum cranial width | d | ||
| Maximum longitudinal distance | c | ||
| a value | a | Distance between right-frontal bone and left-occipital bone | |
| b value | b | Distance between left-frontal bone and right-occipital bone | |
| af value | af | Frontal part of a | |
| bf value | bf | Frontal part of b | |
| ab value | ab | Back part of a | |
| bb value | bb | Back part of b | |
| Asymmetry index | AI | (1) | |
| Asymmetry index, front | AIf | (2) | |
| Asymmetry index, back | AIb | (3) | |
| Oblique Cranial Length Ratio | OCLR | (4) | |
| Perimeter30 | Perimeter30 | (5) | |
| Cephalic index | CI | (6) | |
| Towering index | TI | (7) | |
| Metopic index | MI | (8) | |
| Frontal angle | FA | ||
| Global | Global | Mean right hemisphere minus left hemisphere | |
| Parameter | Similarity Transformation | Scale Transformation | ||
|---|---|---|---|---|
| Mean | Std. Deviation | Mean | Std. Deviation | |
| X translation (mm) | 0.50 | 0.30 | ||
| Y translation (mm) | 0.00 | 0.31 | ||
| Z translation (mm) | −0.27 | 0.17 | ||
| Differential scale | −0.0065 (0.9935) | 0.0039 | −0.0096 (0.9904) | 0.0043 |
| Rotation in X (deg) | −0.07 | 0.32 | ||
| Rotation in Y (deg) | 0.03 | 0.66 | ||
| Rotation in Z (deg) | −0.36 | 0.66 | ||
| Cranial Parameter or Index | Value | Uncertainty (Meas. Accuracy 0.5 mm) | Uncertainty (Meas. Accuracy 0.75 mm) | Uncertainty (Meas. Accuracy 1.0 mm) | Uncertainty (Meas. Accuracy 1.5 mm) | Uncertainty from the 54 Measured Models |
|---|---|---|---|---|---|---|
| CV (mL) | 464 | 10 | 14 | 19 | 29 | 25.8 |
| CP (mm) | 390 | 2 | 3 | 4 | 7 | 2.0 |
| DPaP (mm) | 106.4 | 0.7 | 1.1 | 1.4 | 2.1 | 0.8 |
| d (mm) | 117.1 | 0.7 | 1.1 | 1.4 | 2.1 | 0.7 |
| c (mm) | 121.3 | 0.7 | 1.1 | 1.4 | 2.1 | 0.8 |
| a (mm) | 146.2 | 0.7 | 1.1 | 1.4 | 2.1 | 1.9 |
| b (mm) | 146.3 | 0.7 | 1.1 | 1.4 | 2.1 | 1.8 |
| af (mm) | 67.3 | 0.6 | 0.9 | 1.2 | 1.8 | 1.1 |
| bf (mm) | 65.9 | 0.6 | 0.9 | 1.2 | 1.8 | 1.2 |
| ab (mm) | 78.9 | 0.6 | 0.9 | 1.2 | 1.8 | 1.0 |
| bb (mm) | 80.4 | 0.6 | 0.9 | 1.2 | 1.8 | 0.8 |
| AI (mm) | 0 | 1.0 | 1.5 | 2.0 | 3.0 | 0.5 |
| AIf (mm) | 1 | 0.9 | 1.3 | 1.7 | 2.6 | 0.5 |
| AIb (mm) | −2 | 0.9 | 1.3 | 1.7 | 2.6 | 0.5 |
| Perimeter30 (mm) | 3 | 1.6 | 2.4 | 3.1 | 4.7 | 1.2 |
| FA (deg) | 114.4 | 1.4 | 2.1 | 2.8 | 4.2 | 1.1 |
| Global (mm) | 2.1 | 0.7 | 1.1 | 1.4 | 2.1 | 0.2 |
| Cranial Parameter or Index | Value | Uncertainty (Meas. Accuracy 0.5 mm) | Uncertainty (Meas. Accuracy 0.75 mm) | Uncertainty (Meas. Accuracy 1.0 mm) | Uncertainty (Meas. Accuracy 1.5 mm) | Uncertainty from the 54 Measured Models |
|---|---|---|---|---|---|---|
| OCLR (%) | 100 | 0.7 | 1.0 | 1.4 | 2.0 | 0.3 |
| CI (%) | 97 | 0.7 | 1.1 | 1.4 | 2.1 | 0.7 |
| TI (%) | 68 | 0.5 | 0.8 | 1.1 | 1.6 | 1.4 |
| MI (%) | 54 | 0.7 | 1.0 | 1.4 | 2.0 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baselga, S.; Mora-Navarro, G.; Lerma, J.L. Assessment of Cranial Deformation Indices by Automatic Smartphone-Based Photogrammetric Modelling. Appl. Sci. 2022, 12, 11499. https://doi.org/10.3390/app122211499
Baselga S, Mora-Navarro G, Lerma JL. Assessment of Cranial Deformation Indices by Automatic Smartphone-Based Photogrammetric Modelling. Applied Sciences. 2022; 12(22):11499. https://doi.org/10.3390/app122211499
Chicago/Turabian StyleBaselga, Sergio, Gaspar Mora-Navarro, and José Luis Lerma. 2022. "Assessment of Cranial Deformation Indices by Automatic Smartphone-Based Photogrammetric Modelling" Applied Sciences 12, no. 22: 11499. https://doi.org/10.3390/app122211499
APA StyleBaselga, S., Mora-Navarro, G., & Lerma, J. L. (2022). Assessment of Cranial Deformation Indices by Automatic Smartphone-Based Photogrammetric Modelling. Applied Sciences, 12(22), 11499. https://doi.org/10.3390/app122211499








