Identity-Based and Leakage-Resilient Broadcast Encryption Scheme for Cloud Storage Service

Abstract

Cloud storage services are an important application of cloud computing. An increasing number of data owners store their data on cloud platforms. Since cloud platforms are far away from users, data security and privacy protection are very important issues that need to be addressed. Identity-based broadcast encryption (IBBE) is an important method to provide security and privacy protection for cloud storage services. Because the side channel attacks may lead to the disclosure of the key information of the cryptographic system, which will damage the security of the system, this paper provides an identity-based broadcast encryption with leakage resilience by state partition (LR-SP-IBBE). By using a binary extractor to compensate for the loss in entropy of the symmetric key caused by side-channel attacks, the proposed scheme randomizes the encapsulated symmetric key. Furthermore, using a state partition technique, we split the private key into two parts, and the corresponding decryption was divided into two stages. Through the double-system encryption skill, the security and leakage-resilience were proved in the composite order group model.

1. Introduction

Cloud storage services are closely related to people’s daily production and life [1,2]. In the Internet environment, people will use cloud storage services more or less. Privacy protection is an important feature of cloud data security. Privacy protection refers to the security of user identity and data privacy. At present, privacy protection has attracted more and more attention and has become a key bottleneck for the further development of the cloud. More effective protection technologies in the cloud environment include identity-based cryptosystems [3,4], attribute-based cryptosystems [5,6,7], etc. In view of security issues, cloud server providers should only allow legitimate users to access and manipulate data.

Unfortunately, side-channel attacks [8,9,10,11,12,13] have been discovered in recent years. Through some characteristic information such as the algorithm execution time and power loss, attackers can reveal some important information of the cryptographic system, even secret information such as private keys. Thus, side-channel attacks can lead to the insecurity of the cryptographic system. As a very important type of encryption system, the identity-based broadcast encryption (IBBE) system received great attention, and many achievements of IBBE emerged. However, there are few broadcast encryption schemes that can resist side-channel attacks. This paper presents a security model of a leakage-resilient broadcast encryption scheme for cloud storage services and proposes a specific broadcast encryption scheme that can resist side-channel attacks. The safety proof and an analysis of the leakage resilience are given.

2. Related Works

In this section, we first introduce the research status of anonymous broadcast encryption. Then, the research progress of identity-based encryption with leakage resilience is introduced. Finally, our motivations and contributions are explained.

2.1. Anonymous Broadcast Encryption

For broadcast encryption (BE) schemes, the sender may send an encrypted message to many users. In a BE scheme, broadcasters usually encrypt messages by combining the public identity of the receiver and system parameters to reveal the identity of the receiver to the public and thus attract attention to user privacy. Most identity-based broadcast encryption schemes have no anonymity, so the attackers may obtain some information about those identities from that ciphertext. Fortunately, some anonymous broadcast encryption schemes have been constructed.

Libert B, et al. [14] provided the definition of anonymous BE (ANOBE) and two general constructions of ANOBE. Their first scheme came from a public key encryption (PKE) scheme. Their second scheme came from an IBE scheme whose security is weak.

The paper [15] presented the idea of an anonymous IBBE (AIBBE) on a server and proposed a concrete scheme with random oracle by pairing. Both the encryption and decryption operations were relatively easy. However, their scheme was secure against the chosen plaintext attack.

Li X, et al. [16] provided an effective anonymous IBBE scheme by a prime order bilinear group in which no attacker could obtain the receivers’ identity from the given ciphertext. Their scheme has a fixed ciphertext size. They proved the security through the assumption of an asymmetric decision bilinear Diffie Hellman exponent (DBDHE) in the standard model.

Ren Y, et al. [17] proposed a completely anonymous IBBE construction using asymmetric bilinear groups. The construction achieved adaptive security and had no random oracle. Any attacker could not obtain the receivers’ identity from the given ciphertext. Each receiver was an anonymous receiver to other receivers. Only the broadcaster knew all the receivers. This scheme could achieve both semantic security and receiver anonymity. Mandal M [18] pointed out that the construction in Ren Y, et al. [17] did not provide the security requirements of message indistinguishability for broadcast encryption. In addition, Mandal M made some improvements to the scheme and constructed a secure and anonymous IBBE.

The reference [19] proposed the first IBBE scheme that achieved both confidentiality and complete anonymity using standard assumptions. The scheme also provided two other required features. One was full collusion resistance; that is to say, even if all external recipients colluded, they could not obtain information in the plaintext. The other was statelessness; that is to say, when a user joined or left the system, other users of the system did not need to update the private key.

The authors of [20] provided a novel AIBBE and proved that their scheme had security against the chosen ciphertext attacks (CCAs) using a random oracle. Based on a comparison with the other four schemes, their scheme was the most effective one.

The reference [21] put forward a general AIBBE that provided confidentiality of information and anonymity of users against CCA. The lengths of the public key and private key were fixed. The decryption calculation was independent of the number of receivers. Therefore, regardless of the perspective, this construction was suitable for the information management system of a smart city.

Zhou Y, et al. [22] designed an updatable identity-based hash proof system (IB-HPS). They updated the private key and added some new random values to one new private key. The new private key had the same distribution as the old one. By using an updatable IB-HPS, they provided a general continual leakage-resilient IBE under a random oracle model.

The reference [23] constructed a receiver-anonymous BE for ciphertext-policy attribute-based encryption (CP-ABBE) that could protect the access structure and the description of the broadcast set related to the ciphertext. The scheme realized complete security and a constant size of the ciphertext.

Ming Y, et al. [24] presented a new anonymous IBBE scheme using asymmetric bilinear pairing. With the help of the dual pairing vector space, they proved the security using the double system encryption method.

Chen L, et al. [25] provided an effective anonymous IBBE construction and applied it to a cloud storage service. In their scheme, the ciphertext length, public parameter length, and user’s private key length were fixed.

The paper [26] put forward an IBBE that was appropriate in open networks. For their scheme, although any sender could send the encrypted information to the target users, the authorized receivers could retrieve the encrypted message. Compared with other constructions of the open network of the IBBE scheme, the decryption key of the scheme was shorter and computation and transmission costs were low.

Chen L, et al. [27] provided the concept for a personalized message BE based on anonymous certificates (ANON-CBBE-PM). They also provided an ANON-CBBE-PM construction.

Mandal M, et al. [28] introduced a BE with personalized messages (BEPM) paradigm. In addition to its adaptive security, their construction could withstand indistinguishable selective plaintext attacks without using random oracle models. Their construction had a fixed ciphertext size and was very ideal for lightweight devices.

The paper [29] presented an IBBE that could simultaneously achieve confidentiality and outsider anonymity under the difficulty of the learning with error (LWE) problem. Their encryption and decryption algorithms were more efficient.

2.2. Leakage Resilience of IBE

According to the ability of side-channel attacks, the leakage-resilient model is divided into the bounded-leakage case and continuous-leakage case. As for the bounded leakage case [30], the leakage amount of the secret information of the system cannot exceed a given limit. As for the continuous-leakage case [31], its private key is usually updated, and the life cycle of the cryptographic mechanism is divided into multiple time cycles by performing corresponding operations (such as key update). In each time cycle, the adversary can obtain some related context for one private key and the exposed amount for this same secret value cannot exceed the leakage parameters set by the system, but the entire execution process can have an unlimited amount of leakage. The continuous-leakage model is closer to the application requirements of the real environment.

Cryptographic researchers have done some research on the leakage resilience of some cryptosystems such as the PKE cryptosystem [32], identity-based cryptographic mechanism [33,34,35], attribute-based cryptographic mechanism [36,37], key exchange protocol [38], and signature [39]. Research on leakage resilience of cryptographic mechanisms is a hot topic in cryptography research.

At present, leakage-resilient achievements mainly occur in identity-based cryptosystems.

The work [40] proposed the first identity-based encryption (IBE) construction with leakage resilience and provided the security proof without a random oracle. Alwen J. [41] proposed an IB-HPS and provided an encryption scheme against bounded-leakage attacks under IB-HPS. Li et al. [42] designed an IBE against bounded-leak attacks. Li et al. applied hash proof technology to a variant scheme of Gentry’s IBE with CCA security and constructed a new and effective leakage-resilient IBE. The reference [43] put forward a leakage-resilient IBE by using the global hash structure. Their construction was implemented through the deterministic linear Diffie–Hellman assumption under the relative-leakage model using a random oracle. The reference [44] provided an IBE with leakage resilience with leakage parameters that were not limited by the length of the message to be encrypted. Chen et al. [45] provided several specific examples of IB-HPS.

The paper [46] pointed out that the IBE against continuous side-channel attacks had stronger practicability. In the continual-leakage-resilient circumstances, the system refreshed the private key and erased the old key periodically. In this process, the public key was unchanged. The leakage of this model only existed between key refreshes. Specifically, the leakage between two consecutive refreshes was limited, but the overall amount of leakage was unlimited. In the case that the hardware did not leak information and in the continuous-leakage model, Zhou et al. [47] proposed an IBE against continual-leakage attacks without a random oracle. Zhang et al. [48] provided a secure big data storage system that was able to resist continuous key leakage. The paper [49] pointed out that blockchain technology could be used to solve the problem of data-tampering prevention in a decentralized environment. The paper [50] provided a comprehensive review of the latest research progress on resilient and dependable management approaches. They provided seven classifications, systematically analyzed the advantages and disadvantages of the schemes, and pointed out the schemes that could be further studied.

Because the leakage circumstances for different application environments are different, the actual application requirements of different environments in reality cannot be met with a constant leakage boundary. To dynamically set the leakage boundary of an IBE mechanism according to the requirements of the application environment, the authors of [51] designed a leakage-resilient IBE mechanism with flexible changes in the leakage boundary. The upper leakage limit of the IBE mechanism could be controlled by changing the corresponding initialization parameters, which effectively achieved the on-demand design goal of the leakage limit; that is to say, the mechanism could improve the leakage-resilience ability of the mechanism by increasing the length of one private key without changing the public parameter.

2.3. Our Motivations and Contributions

Zhang et al. [52] designed a novel leakage-resilient hierarchical IBE mechanism to provide anonymity protection for recipients. Zhang et al. [53] constructed a hierarchical IBE with anonymity against leakage attacks and provided the application scenario of the scheme. The work [54] proposed an anonymous IBE using a dual-system technique. Their construction was implemented with the aid of the composite order bilinear group and was secure in the fully adaptive identity model. Sun et al. [55] designed a completely secure leakage-resilient IBE mechanism with a wildcard key derivation function. Because no anonymous IBBE against leakage attacks had been put forward, this paper constructed an anonymous IBBE scheme against side-channel attacks.

A secret sharing scheme proposed by Xiong et al. [56] could resist persistent side-channel attacks and mainly benefited from the state partitioning technology. Since then, state partitioning technology has been widely used to construct some cryptographic systems with special performance. Liu et al. [57] ensured the security of their scheme for simultaneous continuous state partition exposure and tampering attacks with the help of general reference strings, nonextensible code, and other technologies.

Fanio et al. [58] divided their code into two parts. By using the refresh process based on state partitioning, the nonextensible code could resist persistent leakage attacks. For some schemes based on state partitioning, the state is usually divided into two parts, but there are also four and eight parts [59,60].

Since the dual-system technology [61] was introduced as the security proof, a lot of work has been carried out along this main line. In the dual-system technology, the key and ciphertext appear in two states: normal and semifunctional. Normal ciphertext is correctly decrypted by any key, but semifunctional ciphertext is not correctly decrypted by the semifunctional key. The orthogonality of subgroup elements can be fully utilized to carry effective information and hide invalid information. The references [37,39,46] proved the leakage-resilient security of some schemes through dual-system encryption technology.

Among the anonymous broadcast encryption schemes, there is no leakage-resilient encryption scheme at present. On the basis of [62], this paper provides an anonymous broadcast encryption scheme against continual side-channel attacks.

We used the following two figures to illustrate the differences between this scheme and the original scheme in [62]. Figure 1 shows the encryption and decryption system of the scheme in [62]. Figure 2 shows the encryption and decryption system of our scheme. There were two main technical differences. The first was the use of extractors. The second was the use of state partitioning technology, which divided the decryption step into two stages. CSP denotes the cloud server provider. The encryption algorithm and decryption algorithm will be specified in Section 4.

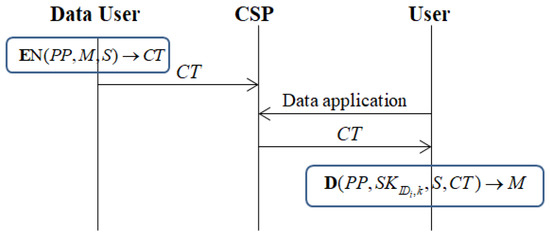
Figure 1. The encryption and decryption system of the scheme in [62].

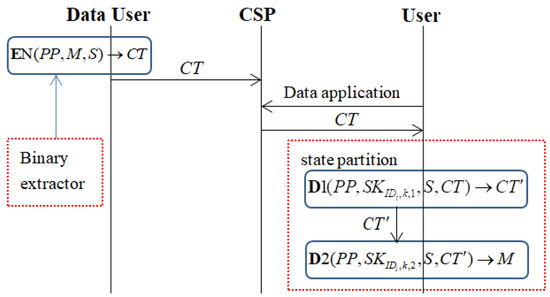
Figure 2. The encryption and decryption system of our scheme.

First, we divided a private key into two states through the state partitioning technology. The private key had a fixed size, which was an important index to be considered in the broadcast encryption scheme. This was different from some current leakage-resilient encryption schemes. Some current encryption schemes obtain certain entropy through lengthening of the private key. This private key has sufficient redundancy to ensure that the security of the private key can be maintained in case of leakage in side-channel attacks.

Secondly, because the key for encrypting the plaintext was the encapsulated symmetric key, the symmetric key was subject to leakage-resilient processing through the extractor technology. Thus, the symmetric key could resist side-channel attacks, and the relative leakage ratio for the private key could almost reach 1.

Thirdly, the scheme given in this paper was anonymous. The presented scheme could effectively provide privacy protection for the receiver. In the IBBE scheme, the anonymity of users was related to its privacy protection.

Figure 3 shows the system structure of our anonymous IBBE against leakage attacks. There were three roles in the system: private key generator (PKG), cloud server provider (CSP), and user. Users were divided into data owners and data users. The private key generation center produced the private key and public key for every user. The data owner encrypted one piece of information according to the identity of some selected users and then transmitted the ciphertext to the CSP. The authorized users correctly decrypted the ciphertext that was downloaded from the CSP, while unauthorized users were not able to decrypt the ciphertext. In addition, onlookers could not obtain some identity information about the users from the ciphertext.

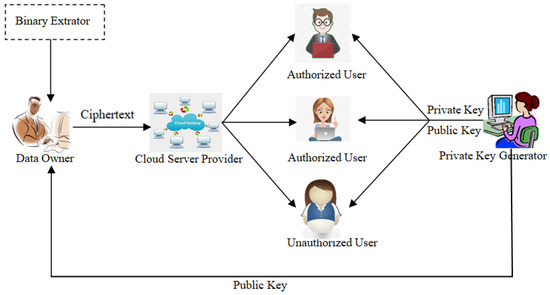
Figure 3. The entire structure of our anonymous IBBE scheme against leakage attack.

3. Preliminary Knowledge

This section provides the basic concepts that are used in this paper such as bilinear mapping, binary extractor, etc. In addition, this section also lists several basic assumptions that had to be used in the safety proof of our scheme.

3.1. Bilinear Map

Definition 1.

Let$G_1$and$G_2$denote two different multiplicative cyclic groups. Let$g$denote a generator for$G_1$and let the bilinear map $e:G_1\times G_1\to G_2$satisfy the next three conditions:

(a) 

Computability: $\forall u,v\in G_1$,$e(u,v)$can be computed effectively.

(b) 

Nondegeneration: $e(g,g)\ne 1_{G_2}$.

(c) 

Bilinearity: $\forall u,v\in G_1$and$a,b\in Z^{*}$;$e(u^a,v^b)=e{(u,v)}^{ab}$.

3.2. Minimum Entropy

Definition 2.

The statistical distance of a random variable $V$and another variable $D$is expressed as $StD=\frac{1}{2}{\displaystyle {\sum }_{\omega \in {\Omega }}\left|\mathrm{Pr}(V=\omega )-\mathrm{Pr}(D=\omega )\right|}$.

Definition 3.

The minimum entropy of one variable $V$is expressed by $H_{\infty }(V)$$=-Log({\max }_v\mathrm{Pr}([V=v]))$; this is a measure of the uncertainty of this variable. The conditional mean minimum entropy for one variable $V$with respect to $D$is expressed by ${\tilde{H}}_{\infty }(V\left|D\right.)=-Log(E_{d\leftarrow D}[{\max }_v\mathrm{Pr}[V=v\left|D=d\right.]])$, which is the measure of uncertainty of the variable $V$under the condition that $D$exists.

Conclusion 1

([63]). If $V$,$D$, and $I$ are three random variables and $D$ has $2^{\lambda }$ values, ${\tilde{H}}_{\infty }(V\left|(D,I)\right.)\ge {\tilde{H}}_{\infty }(V\left|I\right.)-\lambda$.

3.3. Binary Extractor

Definition 4.

A binary function $Ext:{\{0,1\}}^{\mu }\times {\{0,1\}}^{\nu }\to {\{0,1\}}^{\gamma }$is called a $(k,\epsilon )$strong extractor [64] if the following clause holds: $E$ is the uniform distribution over ${\{0,1\}}^{\mu }$; $S$ is the uniform distribution over ${\{0,1\}}^{\nu }$; and as long as $V\in {\{0,1\}}^{\mu }$ and $H_{\infty }(V)>k$, there is $StD((Ext(V,S),S),(E,S))\le \epsilon$ ($\epsilon$ can be ignored).

3.4. General Subgroup Decision Hypothesis

The paper [65] introduced the concept of a bilinear group with a composite order. We used $\mathrm{\Theta }$ to represent a bilinear group generation algorithm for the composite order. $\mathrm{\Theta }$ inputs safety parameters $\zeta$ and outputs the formalization of the bilinear group with the composite order $\mathrm{\Phi }=\{N=q_1{q}_2{q}_3,G_1,G_2,e\}$, where $q_1$, $q_2$, and $q_3$ are three different primes that are $\upsilon$ bits in length (that is to say, ${\log }_2^{q_1}={\log }_2^{q_2}$$={\log }_2^{q_3}=\upsilon$). $G_1$ is a cyclic group with order $N=q_1{q}_2{q}_3$, as is $G_2$. $e$:$G_1\times G_1\to G_2$ is one bilinear map. $\upsilon$ is determined by the safety parameter.

$G_{q_1},G_{q_2}$, and $G_{q_3}$ are used to represent subgroups of order $q_1$, $q_2$, and $q_3$, respectively. The subgroups of order $q_1{q}_2$ in the group $G_1$ are represented by $G_{q_1{q}_2}$. If an element $W$ is expressed by the product of a member of $G_{q_1}$ and a member of $G_{q_2}$, these two parts are called the $G_{q_1}$ part of $W$ and the $G_{q_2}$ part of $W$. Assuming $x_i\in G_{q_i}$ and $x_j\in G_{q_j}$($i\ne j$), we obtain $e(x_i,x_j)$ = 1. So, $G_{q_i}$ and $G_{q_j}$ are orthogonal. For example, this shows how $G_{q_j}$ and $G_{q_2}$ are orthogonal. Suppose $g$ can generate $G_1$, $g^{q_1{q}_2}$ can generate $G_{q_3}$, $g^{q_1{q}_3}$ can generate $G_{q_2}$, and $g^{q_2{q}_3}$ can generate $G_{q_1}$. It can then be obtained that $e(x_1,x_2)$ $=e(g^{q_2{q}_3{a}_1},g^{q_1{q}_3{a}_2})$$=e(g^{a_1},g^{q_3{a}_2}){ }^{q_1{q}_1{q}_3}=1$. Therefore, $G_{q_1}$ and $G_{q_2}$ are orthogonal.

The following three hypotheses given in references [61,66,67] will be used in our proof. For $i\in \{1,2,3\}$, it was assumed that $g_i$ is the generator of $G_{q_i}$.

Hypothesis 1.

Consider that the algorithm $\mathrm{\Theta }$generates a bilinear group with composite order. Given the following distribution:

$$\mathrm{\Phi }=\{N=q_1{q}_2{q}_3,G_1,G_2,e\}\stackrel{R}{\leftarrow }\mathrm{\Theta },g_1\stackrel{R}{\leftarrow }{G}_{q_1},A_3\stackrel{R}{\leftarrow }{G}_{q_3}, W=(\mathrm{\Phi },g_1,A_3)$$

Any attack does not distinguish between $T_1\stackrel{R}{\leftarrow }{G}_{q_1{q}_2}$and $T_2\stackrel{R}{\leftarrow }{G}_{q_1}$.

The advantage that the adversary destroys Hypothesis 1 is expressed by $A{D}_{\mathcal{A}}^1(\zeta )=|\mathrm{P}[\mathcal{A}(W,T_1)=1]-\mathrm{P}[\mathcal{A}(W,T_2)=1]|$.

If it is negligible for every PPT adversary, Hypothesis 1 is said to be true.

Hypothesis 2.

Consider that the algorithm $\mathrm{\Theta }$generates a bilinear group with composite order. Given the following distribution:

$$\begin{gathered} \mathrm{\Phi }=\{N=q_1{q}_2{q}_3,G_1,G_2,e\}\stackrel{R}{\leftarrow }\mathrm{\Theta },g_1,A_1\stackrel{R}{\leftarrow }{G}_{q_1},A_2,B_2\stackrel{R}{\leftarrow }{G}_{q_2},A_3,B_3\stackrel{R}{\leftarrow }{G}_{q_3}, \\ W=(\mathrm{\Phi },g_1,A_1{A}_2,A_3,B_2{B}_3) \end{gathered}$$

Any attack does not distinguish between $T_1\stackrel{R}{\leftarrow }{G}_1$and$T_2\stackrel{R}{\leftarrow }{G}_{q_1{q}_3}$

The advantage that the adversary destroys Hypothesis 2 is expressed by $A{D}_{\mathcal{A}}^2(\zeta )=|\mathrm{P}[\mathcal{A}(W,T_1)=1]-\mathrm{P}[\mathcal{A}(W,T_2)=1]|$.

If it is negligible for every PPT adversary, Hypothesis 2 is said to be true.

Hypothesis 3.

Consider that the algorithm $\mathrm{\Theta }$generates a bilinear group with composite order. Given the following distribution:

$$\begin{gathered} \mathrm{\Phi }=\{N=q_1{q}_2{q}_3,G_1,G_2,e\}\stackrel{R}{\leftarrow }\mathrm{\Theta },\hspace{0.33em}\hspace{0.33em}\alpha ,s\stackrel{R}{\leftarrow }{Z}_N,g_1\stackrel{R}{\leftarrow }{G}_{q_1},A_2,B_2,U_2\stackrel{R}{\leftarrow }{G}_{q_2},A_3\stackrel{R}{\leftarrow }{G}_{q_3}, \\ W=(\mathrm{\Phi },g_1,g_1^{\alpha }{A}_2,A_3,g_1^s{B}_2,U_2) \end{gathered}$$

Any attack does not distinguish between $T_1\stackrel{R}{\leftarrow }e{(g_1,g_1)}^{\alpha s}$and $T_2\stackrel{R}{\leftarrow }{G}_2$

The advantage that the adversary destroys Hypothesis 3 is expressed by $A{D}_{\mathcal{A}}^3(\zeta )=|\mathrm{P}[\mathcal{A}(W,T_1)=1]-\mathrm{P}[\mathcal{A}(W,T_2)=1]|$.

If it is negligible for every PPT adversary, Hypothesis 3 is said to be true.

4. Syntax about LR-SP-IBBE

This section provides the formal description and security semantics of identity-based broadcast encryption with leakage resilience by state partition (LR-SP-IBBE).

Figure 4 gives the relations of the algorithms; the specific algorithms will be detailed in Section 4.1.

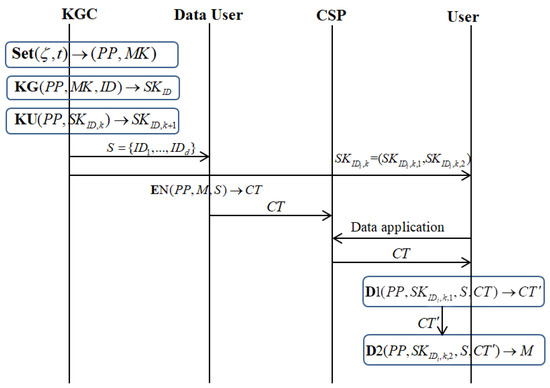
Figure 4. The relations of the algorithms of the proposed scheme.

4.1. Formalization of LR-SP-IBBE

Based on the work in [62,68], the formal definition of LR-SP-IBBE is given below. The LR-SP-IBBE was composed of the following algorithms:

Initialization.$Set(\zeta ,t)\to (PP,MK)$. This inputs the security parameters $\zeta$ and the upper bound $t$ of users. The algorithm produces the public parameter $PP$ and the master private key $MK$. $PP$ is open to all users. $MK$ is kept as a secret.

Private key generation.$KG(PP,MK,ID)\to S{K}_{ID}$. The algorithm inputs the public parameters $PP$, the master private key $MK$, and one user’s identity $ID$. It generates one private key: $S{K}_{ID}= (S{K}_{ID,0,1},S{K}_{ID,0,2})$.

Private key update.$KU(PP,S{K}_{ID,k})\to S{K}_{ID,k+1}$. This inputs $S{K}_{ID,k}$ and $PP$ and outputs the updated private key $S{K}_{ID,k+1}$.

Encryption. $E\mathrm{N}(PP,M,S)\to CT$. This takes $PP$ and one identity set $S=\{I{D}_1,\dots ,I{D}_d\}$ ($d\le t$) as the input and outputs $(Hd,K)$, where $Hd$ is the headers and $K$ is a symmetric key that is used to encrypt the plaintext $M$. If the broadcaster is about to send the ciphertext corresponding to the plaintext $M$, they encrypts $M$ with $K$, which generates the ciphertext $CM$ and broadcasts $(CM,Hd,S)$.

Decryption1.$D1(PP,S{K}_{I{D}_i,k,1},S,CT)\to C{T}^{\prime }$. This inputs $PP$, private keys $S{K}_{I{D}_i,k,1}$, user identity sets $S$, and ciphertext $CT$. First, it divides $CT$ into $(CM,Hd)$. If $I{D}_i\in S$, the algorithm calculates the part plaintext $C{T}^{\prime }$ of $CT$.

Decryption2.$D2(PP,S{K}_{I{D}_i,k,2},S,C{T}^{\prime })\to M$. This inputs $PP$, private keys $S{K}_{I{D}_i,k,2}$, user identity sets $S$, and ciphertext $C{T}^{\prime }$. First, it divides $CT$ into $(CM,Hd)$. If $I{D}_i\in S$, the algorithm uses $Hd$ to calculate the symmetric key $K$. Then, the plaintext message is recovered by $C{T}^{\prime }$.

Semifunctional private key generation. $KSF(PP,MK,ID)\to \widetilde{S{K}_{ID}}$. The algorithm inputs $PP$, $MK$, and one identity $ID$. It generates the semifunctional private key $\widetilde{S{K}_{ID}}$.

Semifunctional encryption. $ESF(PP,M,S)\to \widetilde{CT}$. This inputs $PP$, $S$, and $M$. It gains the semifunctional ciphertext $\widetilde{CT}$.

The first three algorithms were run by the key generation center (KGC), and the other algorithms were run by the user. The last two algorithms were only used for the security proof.

4.2. Security Descriptions for LR-SP-IBBE

The security for the LR-SP-IBBE scheme could be achieved through an interactive game that was executed by one challenger $\mathcal{B}$ and one adversary $\mathcal{A}$. This scheme obtained the security against the chosen ciphertext attack.

The security for LR-SP-IBBE was described through the game ${\mathrm{GM}}_{\mathrm{R}}$. In ${\mathrm{GM}}_{\mathrm{R}}$, the challenger maintained a table, $\mathcal{L}=\left\{\right(\mathcal{H},\mathcal{I},\mathcal{K},\mathcal{SK},\mathcal{LK}\left)\right\}$, where $\mathcal{H}$, $\mathcal{I}$, $\mathcal{K}$, $\mathcal{S}\mathcal{K}$, and $\mathcal{L}\mathcal{K}$ are the handles’ space, identities’ space, symmetric keys’ space, private keys’ space, and the leakage amount’s space, respectively. Assume $\mathcal{H}=\mathbb{N}$ and $\mathcal{LK}=\mathbb{N}$.

${\mathrm{GM}}_{\mathrm{R}}$:

Initialization: By running the initialization algorithm, the challenger produced the public parameters $PP$ and the master private key $MK$. $\mathcal{B}$ gives $PP$ to $\mathcal{A}$, then $\mathcal{B}$ keeps $MK$ in secret.

Stage 1: the adversary conducted the following inquires.

$\mathcal{O}\mathit{-Create}(ID)$. Given one identity $ID$, $\mathcal{B}$ searched for the item corresponding to $ID$ in the list $\mathcal{L}$. In the event that the corresponding item was found in the list $\mathcal{L}$, the challenger ended the operation. Otherwise, $\mathcal{B}$ obtained one private key $S{K}_{ID}$ by running the private key generation algorithm and updated $h\leftarrow h+1$. The challenger put $(h,ID,K,S{K}_{ID},0)$ in $\mathcal{L}$.

$\mathcal{O}\mathit{-Leak}(ID)$. Given the identity $I{D}_i$, $\mathcal{A}$ chose one arbitrary leak function $f(\cdot )$. $f(\cdot )$ input the symmetric key. $\mathcal{B}$ sent the outcome of $f(\cdot )$ to the adversary $\mathcal{A}$. The limitation was that the output could not extend a bound. The information obtained from the output of this leakage function was related to the one encapsulated symmetric key $K$.

Specifically, $\mathcal{B}$ sought an item for the handle $h$ in the table $\mathcal{L}$ provided that $(h,ID,K,S{K}_{ID},L)$ was found. $\mathcal{B}$ determined whether $L+|f(K)|\le L_K$ or not, where $L_K$ is the maximum value that allowed private key disclosure. If $L+|f(K)|\le L_K$, the challenger sent $f(K)$ to $\mathcal{A}$ and updated $(h,ID,K,S{K}_{ID},L)$ with $(h,ID,K,S{K}_{ID},L+|f(K)|)$. Otherwise, the challenger would output ⊥.

$\mathcal{O}\mathit{-Reveal}(h)$. $\mathcal{A}$ inquired about one private key of the handle $h$. $\mathcal{B}$ looked for an item corresponding to the handle $h$ in the table $\mathcal{L}$. In the event that $(h,ID,K,S{K}_{ID},L)$ was found, $\mathcal{B}$ gave $S{K}_{ID}$ to the adversary.

$\mathcal{O}\mathit{-KeyU}$. $\mathcal{A}$ inquired about the updating of the private key corresponding to the handle $h$. $\mathcal{B}$ looked for one item corresponding to the handle $h$ in $\mathcal{L}$. Provided that $(h,ID,K,S{K}_{ID},L)$ was found, $\mathcal{B}$ ran the updating algorithm to obtain the new private key $\widehat{S{K}_{ID}}$. The challenger then gave $\mathcal{A}$ the new private key $\widehat{S{K}_{ID}}$ and updated $(h,ID,K,\widehat{S{K}_{ID}},0)$ to $(h,ID,K,S{K}_{ID},L)$.

$\mathcal{O}\mathit{-D}1$. The adversary inquired about the plaintext of $(ID,CT)$, and the challenger looked up the list $\mathcal{L}$ and found the private key $S{K}_{ID}$. $\mathcal{B}$ invoked the decryption algorithm $D1(PP,S{K}_{I{D}_i,k,1},S,CT)\to C{T}^{\prime }$. If $I{D}_i\in S$, the challenger calculated the part of plaintext $C{T}^{\prime }$ and sent it to $\mathcal{A}$.

$\mathcal{O}\mathit{-D}2$. $\mathcal{A}$ inquired about the plaintext of $(ID,CT)$, and the challenger looked up the list $\mathcal{L}$ and found the private key $S{K}_{ID}$. $\mathcal{B}$ invoked the decryption algorithm $D2(PP,S{K}_{I{D}_i,k,2},S,C{T}^{\prime })\to M$. First, it divided $CT$ into $(CM,Hd)$. If $I{D}_i\in S$, the challenger used $Hd$ to calculate the symmetric key $K$. Then, the plaintext message $M$ was recovered by $K$ and was sent to $\mathcal{A}$.

Challenge.$\mathcal{A}$ offered the message $M_0$ and $M_1$ with an equal length. $\mathcal{B}$ randomly selected $\beta \leftarrow \{0,1\}$. Then, $\mathcal{B}$ input the public parameters $PP$ and user set $S^{*}=\{I{D}_1^{*},\dots ,I{D}_d^{*}\}$ ($d\le t$) and output $(H{d}^{*},K^{*})$. The challenger obtained $C{M}^{*}$ by encrypting $M_{\beta }$ with $K^{*}$. The ciphertext was $C{T}^{*}=(C{M}^{*},H{d}^{*})$. The challenger broadcasted $(C{M}^{*},H{d}^{*},S^{*})$.

Stage 2.$\mathcal{A}$ could ask for $\mathcal{O}\mathit{-Create}$, $\mathcal{O}\mathit{-Reveal}$, $\mathcal{O}\mathit{-D}1$, and $\mathcal{O}\mathit{-D}1$. The basic limitations were the same as those in Stage 1. Other restrictions were that the adversary could not inquire about $ID\in S^{*}$ and $Hd=H{d}^{\ast }$. In addition, a leakage inquiry was not allowed, Because if it were allowed, $\mathcal{A}$ could win the game in an ordinary way.

Guess. $\mathcal{A}$ provided a conjecture ${\beta }^{\prime }\in \{0,1\}$. If ${\beta }^{\prime }=\beta$, $\mathcal{A}$ wins ${\mathrm{GM}}_{\mathrm{R}}$. The advantage of winning the game ${\mathrm{GM}}_{\mathrm{R}}$ was defined as $A{D}_{\mathcal{A}}(L_K)=\left|\mathrm{P}[{\beta }^{\prime }=\beta ]-\frac{1}{2}\right|$.

Supposing every adversary only achieved negligible advantages in the game ${\mathrm{GM}}_{\mathrm{R}}$, our LR-SP-IBBE scheme had leakage-resilience.

5. Specific Construction of LR-SP-IBBE

We used $\mathrm{\Theta }$ to represent a bilinear group generation algorithm for the composite order. $\mathrm{\Theta }$ input safety parameters $\zeta$ and output the formalization of the bilinear group with the composite order $\mathrm{\Phi }=\{N=q_1{q}_2{q}_3,G_1,G_2,e\}$, where $q_1$, $q_2$, and $q_3$ are three different primes with a $\upsilon$ bit length (that is to say, ${\log }_2^{q_1}={\log }_2^{q_2}$$={\log }_2^{q_3}=\upsilon$). $G_1$ was a cyclic group with order $N=q_1{q}_2{q}_3$, as was $G_2$. $e$:$G_1\times G_1\to G_2$ is one bilinear map. $\upsilon$ was determined by the safety parameter.

It was assumed that any identity information was a member of $Z_N$ and any message was a member of $G_2$. Suppose that $g_1,g_2$, and $g_3$ are the generators of the subgroups $G_{q_1},G_{q_2}$, and $G_{q_3}$. The first subgroup $G_{q_1}$ carried some primary information for the plaintext and every user’s private key. $G_{q_2}$ offered the semifunctionality that was used in the security proof. $G_{q_3}$ randomized the private key.

Initialization.$t$ was used to represent the maximum number of users. It randomly selected $g_1,h_1\in G_{q_1},$$g_3\in G_{q_3}$,$u_1,\dots ,u_t\in G_{q_1}$, and $\alpha \in Z_N$. It selected a $(k,\epsilon )$ strong binary extractor $Ext:G_2\times Z_N\to G_2$.

The public parameter was $PP=\{N,Ext,g_1,g_3,h_1,u_1,\dots ,u_t,e{(g_1,g_1)}^{\alpha }\}$.

The master private key was $MK=\left\{\alpha \right\}$.

Private key generation. For an identity $I{D}_i\in S$ where $S=(I{D}_1,\dots ,I{D}_d)$, ($d\le t$) is the target users. The algorithm input $PP$, $MK$, and one user’s identity $I{D}_i$. It randomly selected $a_1,a_2,\dots ,a_d,b\in Z_N$, ${\beta }_{i,0},{\gamma }_{i,0}\in Z_N$, $r_i\in Z_N$$(i=\{1,\dots ,d\})$, and $R_i,Q_i,{R^{\prime }}_i,{Q^{\prime }}_i\in G_{p_3}$. It set $u_1=g_1^{a_1},\dots ,u_d=g_1^{a_d},h_1=g_1^b$ and generated the private key $S{K}_{I{D}_i,0} =(S{K}_{I{D}_i,0,1},S{K}_{I{D}_i,0,2})$, where $S{K}_{I{D}_i,0,1}=(g_1^{r_i}{R}_i{g}_1^{{\beta }_{i,0}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i}{Q}_i{g}_1^{{\gamma }_{i,0}})$ and $S{K}_{I{D}_i,0,2}=(R_i^{\prime }{g}_1^{-{\beta }_{i,0}},Q_i^{\prime }{g}_1^{-{\gamma }_{i,0}})$.

Private key update. This input $PP$ and $S{K}_{I{D}_i,k}$ and produced one new private key $S{K}_{I{D}_i,k+1}$. For $S{K}_{I{D}_i,k} =(S{K}_{I{D}_i,k,1},S{K}_{I{D}_i,k,2})$, where $S{K}_{I{D}_i,k,1} =(S{K}_{I{D}_i,k,1}^1,S{K}_{I{D}_i,k,1}^2) =(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i}{Q}_1{g}_1^{{\gamma }_{i,k}})$ and $S{K}_{I{D}_i,k,2}= (S{K}_{I{D}_i,k,2}^1,S{K}_{I{D}_i,k,2}^2)=({R^{\prime }}_1{g}_1^{-{\beta }_{i,k}},{Q^{\prime }}_1{g}_1^{-{\gamma }_{i,k}})$, it randomly selected ${\beta }_{i,k+1},{\lambda }_{i,k+1}\in Z_N$ and generated one new private key $S{K}_{I{D}_i,k+1}= (S{K}_{I{D}_i,k+1,1},S{K}_{I{D}_i,k+1,2})$, where $\begin{array}{l}S{K}_{I{D}_i,k+1,1}=(S{K}_{I{D}_i,k,1}^1{g}_1^{{\beta }_{i,k+1}},S{K}_{I{D}_i,k,1}^2{g}_1^{{\gamma }_{i,k+1}})=(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}}{g}_1^{{\beta }_{i,k+1}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{Q}_1{g}_1^{{\gamma }_{i,k}}{g}_1^{{\gamma }_{i,k+1}})\\ =(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}+{\beta }_{i,k+1}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{Q}_1{g}_1^{{\gamma }_{i,k}+{\gamma }_{i,k+1}})\end{array}$ and $S{K}_{I{D}_i,k+1,2}=(S{K}_{I{D}_i,k,2}^1{g}_1^{-{\beta }_{i,k+1}},S{K}_{I{D}_i,k,2}^2{g}_1^{-{\gamma }_{i,k+1}})= (R_1^{\prime }{g}_1^{-{\beta }_{i,k}-{\beta }_{i,k+1}},Q_1^{\prime }{g}_1^{-{\gamma }_{i,k}-{\gamma }_{i,k+1}})$.

Since ${\beta }_{i,k+1},{\lambda }_{i,k+1}\in Z_N$ were all random, ${\beta }_{i,k}+{\beta }_{i,k+1}$ and ${\gamma }_{i,k}+{\gamma }_{i,k+1}$ were also random. The private keys $S{K}_{I{D}_i,k+1}$ and $S{K}_{I{D}_i,k}$ had the same distribution. Without losing generality, the original $S{K}_{I{D}_i}$ was used for convenience.

Encryption. This took the message $M$ and an identity set $S=(I{D}_1,\dots ,I{D}_d)$ of the receivers as input. It randomly selected $s,r\in Z_N$ and $Z,Z^{\prime }\in G_{p_2}$. Then, it calculated the ciphertext $\begin{array}{l}CT=(CM,Hd)=(CM,C_1,C_2,C_3)\\ =(M\oplus Ext(e(g_1,g_1{)}^{\alpha s},r),(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^{s}Z,g_1^s{Z}^{\prime }},r)\end{array}$.

The symmetric encryption key was $e(g_1,g_1{)}^{\alpha s}$. $CT$ was sent to the receivers.

Decryption1. If one receiver $I{D}_i$ belongs to $S$, it split $CT$ into two parts $(CM,Hd)$. This receiver ran the decryption algorithm $D1(PP,S{K}_{I{D}_i,k,1},S,CT)\to C{T}^{\prime }$. This receiver calculated the part of the plaintext $C{T}^{\prime }$ using $Hd$.

First, the receiver used $S{K}_{I{D}_{i,k,1}}$ to compute $C{T}^{\prime }=(CM,C_1,C_2,C_3,{C^{\prime }}_1,{C^{\prime }}_2)$, where $C_1^{\prime }=e(S{K}_{I{D}_i,k,1}^1,C_1)=e(g_1^{r_i}{R}_1{g}_1^{{\beta }_i{,}_1+\dots +{\beta }_{i,k}},(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^{s}Z})$ and $C_2^{\prime }=e(S{K}_{I{D}_i,k,1}^2,C_2)=e(g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i}{Q}_1{g}_1^{{\gamma }_{i,1}+\dots +{\gamma }_{i,k}},g_1^s{Z}^{\prime })$.

Decryption2.$D2(PP,S{K}_{I{D}_i,k,2},S,C{T}^{\prime })\to M$. This receiver input $PP$, private key $S{K}_{I{D}_i,k,2}$, identity sets $S$, and ciphertexts $C{T}^{\prime }$. Suppose $I{D}_i\in S$; this receiver first calculated $K$. The plaintext message was recovered by decrypting $C{T}^{\prime }$ using $K$.

First, it used $S{K}_{I{D}_i,k,2}$ to compute:

$$\begin{array}{l}{C}_1^{\prime }e(S{K}_{I{D}_i,k,2}^1,C_1)=e(S{K}_{I{D}_i,k,1}^1,C_1)e(S{K}_{I{D}_i,k,2}^1,C_1)\\ =e(g_1^{r_i}{R}_1{R^{\prime }}_1{g}_1^{{\beta }_1+\dots +{\beta }_k}{g}_1^{-{\beta }_1-\dots -{\beta }_k},(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^{s}Z})=e(g_1^{r_i},(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^s})\end{array}$$

$$\begin{array}{l}{C}_2^{\prime }.e(S{K}_{I{D}_i,k,1}^2,C_2)=e(S{K}_{I{D}_i,k,1}^2,C_2)2.e(S{K}_{I{D}_i,k,2}^2,C_2)\\ =e(g_1^{\alpha }(h{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{Q}_1{Q^{\prime }}_1{g}_1^{{\gamma }_1+\dots +{\gamma }_k}{g}_1^{-{\gamma }_1-\dots -{\gamma }_k},g_1^s{Z}^{\prime })=e(g_1^{\alpha }(h{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i,g_1^s)\end{array}$$

$$\begin{array}{l}M=C_0\oplus Ext(\frac{{C^{\prime }}_2.e(S{K}_{I{D}_i,k,1}^2,C_2)}{{C^{\prime }}_{1}e(S{K}_{I{D}_i,k,2}^1,C_1)},C_3)\\ =M\oplus Ext(e(g_1,g_1{)}^{\alpha s},r)\oplus Ext(\frac{e(g_1^{\alpha }(h{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i},g_1^s)}{e(g_1^{r_i},(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^s})},r)=M\end{array}$$

Semifunctional private key generation. For the private keys $S{K}_{I{D}_i,k}= (S{K}_{I{D}_i,k,1},S{K}_{I{D}_i,k,2})$, where $S{K}_{I{D}_i,k,1}= (S{K}_{I{D}_i,k,1}^1,S{K}_{I{D}_i,k,1}^2) =(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{Q}_1{g}_1^{{\gamma }_{i,k}})$ and $S{K}_{I{D}_i,k,2}= (S{K}_{I{D}_i,k,2}^1,S{K}_{I{D}_i,k,2}^2) =({R^{\prime }}_1{g}_1^{-{\beta }_{i,k}},{Q^{\prime }}_1{g}_1^{-{\gamma }_{i,k}})$, it randomly selected ${\xi }_1,{\xi }_2,{\zeta }_1,{\zeta }_2\in Z_N$ and generated the semifunctional private key $\widetilde{S{K}_{I{D}_i,k}}=(\widetilde{S{K}_{I{D}_i,k,1}},\widetilde{S{K}_{I{D}_i,k,2}})$, where $\widetilde{S{K}_{I{D}_i,k,1}}=(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}}{g}_2^{{\xi }_1},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i}{Q}_1{g}_1^{{\gamma }_{i,k}}{g}_2^{{\xi }_2})$ and $\widetilde{S{K}_{I{D}_i,k,2}}=(R_1^{\prime }{g}_1^{-{\beta }_{i,k}}{g}_2^{{\zeta }_1},Q_1^{\prime }{g}_1^{-{\gamma }_{i,k}}{g}_2^{{\zeta }_2})$.

Semifunctional encryption. By revoking the normal encryption algorithm, it gained the general ciphertext $CT=(CM,Hd)=(CM,C_1,C_2,C_3)=(M\oplus Ext(e(g_1,g_1{)}^{\alpha s},r),(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^{s}Z,g_1^s{Z}^{\prime }},r)$.

Then, it randomly selected ${\rho }_2,{\rho }_3\in Z_N$ and generated the semifunctional ciphertext $\begin{array}{l}\widetilde{CT}=(CM,Hd)=(CM,\widetilde{C_1},\widetilde{C_2},C_3)\\ =(M\oplus Ext(e(g_1,g_1)\alpha s,r),(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}{)}^{s}Z{g}_2^{{\rho }_2},g_1^s{Z}^{\prime }}{g}_2^{{\rho }_3},r)\end{array}$.

The first three algorithms were run by the key generation center (KGC); the other algorithms were run by the user.

6. Safety Proof

The scheme was safe in the standard model.

Theorem 1.

Considering that the symmetric key has$l$bits leakage, if Hypothesis 1, Hypothesis 2, and Hypothesis 3 hold, the presented LR-SP-IBBE scheme has CCA security under the standard model.

The proof was finished through a number of games. These games were modified versions of the real security game. For the last game, the opponent’s advantage was 0. The first game was a real one. We proved the indiscernibility of any two consecutive games. Therefore, the security of this scheme could be obtained. $p$ indicates the number of private key queries in one game.

The definition of these games is given below:.

${\mathrm{GM}}_{\mathrm{R}}$. This is the real interactive game for LR-SP-IBBE that is played by the challenger and the attacker.

${\mathrm{GM}}_0$. This is very similar to ${\mathrm{GM}}_{\mathrm{R}}$, but the only difference is that in ${\mathrm{GM}}_0$, the challenger generates semifunctional ciphertext.

${\mathrm{GM}}_i$($i\in [1,p]$). The ciphertext appears in a semifunctional form. The previous $i$ private key responses are also semifunctional and the subsequent private key responses are normal. Especially for ${\mathrm{GM}}_p$, all private key responses are semifunctional.

${\mathrm{GM}}_F$.This game is similar to ${\mathrm{GM}}_p$ except that in the game ${\mathrm{GM}}_F$, the broadcaster encrypts a random message and in the game ${\mathrm{GM}}_p$, the broadcaster selects any of the two challenge messages and encrypts it.

Proof. 

We will finish the proof through the games ${\mathrm{GM}}_{\mathrm{R}}$, ${\mathrm{GM}}_i$ ($i\in (0,1,\dots ,p)$), and ${\mathrm{GM}}_F$ and three lemmas. Through these three lemmas, we prove the indiscernibility of these games. In addition, the adversary has no advantage in ${\mathrm{GM}}_F$. In this way, the security proof is finished. □

Table 1 illustrates some differences between the adversary advantages in two consecutive games. Here, we provide the conclusion on these three lemmas. Specific proofs of the three lemmas will be presented later. $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}$ or $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}(L_K)$ was used to indicate the superiority achieved by $\mathcal{A}$ over ${\mathrm{GM}}_{\mathrm{R}}$. We used $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_i}$ or $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_i}(L_K)$ to indicate the superiority achieved by $\mathcal{A}$ over ${\mathrm{GM}}_i$($i\in (0,\dots ,p)$. We used $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}$ or $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)$ to indicate the advantage obtained by $\mathcal{A}$ over ${\mathrm{GM}}_F$.

Table 1. The differences between the adversary’ advantages in two consecutive games.

Two Consecutive Games	The Differences of Adversary’ Advantages	Related Lemmas
${\mathrm{GM}}_{\mathrm{R}}$ and ${\mathrm{GM}}_0$	$|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}|\le \epsilon$	Lemma 1
${\mathrm{GM}}_i$ and ${\mathrm{GM}}_{i-1}$$i\in (1,\dots ,p)$	$|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{i-1}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_i}|\le \epsilon$	Lemma 2
${\mathrm{GM}}_p$ and ${\mathrm{GM}}_F$	$|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}|\le \epsilon$	Lemma 3

From Table 1, we obtain:

$$\begin{array}{l}|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}|\\ =|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}+A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}-\dots -A{D}_{\mathcal{A}}^{{\mathrm{GM}}_i}+A{D}_{\mathcal{A}}^{{\mathrm{GM}}_i}-\cdot \cdot \cdot \\ -A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}+A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}|\\ \le |A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}|+|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_1}|+\dots +|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}|\\ \le (p+2)\epsilon \end{array}$$

So, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}|\le (p+2)\epsilon$. In addition, $A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}\le \epsilon$. We obtain $\left|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}\right|\le (p+2)\epsilon$. Thus, Theorem 1 is completed.

Lemma 1.

Considering that the symmetric key has $l$bits of leakage, if there is an adversary $\mathcal{A}$such that $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}(L_K)|\ge \epsilon$, the challenger can destroy Hypothesis 1 with advantage $2^l\epsilon$

Proof. 

Given the challenger $\mathcal{B}$, an instance $W=(\mathrm{\Phi },g_1,A_3)$, $X,Y\in G_{q_2}$, and the challenge $T$

($T\in G_{q_1{q}_2}$ or $T\in G_{q_1}$), $\mathcal{B}$ and $\mathcal{A}$ interacts as follows:

Initialization. Let $t$ indicate the maximum number of users. $\mathcal{B}$ randomly selects $g_1,h_1\in G_{q_1},$ $g_3\in G_{q_3}$, $a_1,a_2,\dots ,a_t,b\in Z_N$, and $\alpha \in Z_N$. $\mathcal{B}$ sets up $u_1=g_1^{a_1},\dots ,u_t=g_1^{a_t},h_1=g_1^b$. $\mathcal{B}$ selects a $(k,\epsilon )$ strong binary extractor $Ext:G_2\times Z_N\to G_2$.

The public parameters are $PP=\{N,Ext,g_1,g_3,h_1,u_1,\dots ,u_t,e(g_1,g_1)\alpha \}$.

The master private key is $MK=\left\{\alpha \right\}$.

$\mathcal{B}$ sends $PP$ to $\mathcal{A}$.

Stage 1. $\mathcal{A}$ asks for the private key of $I{D}_i\in S$, where $S=(I{D}_1,\dots ,I{D}_d)$($d\le t$) is the set of users who can decrypt the ciphertext. $\mathcal{B}$ randomly selects ${\beta }_{i,0},{\gamma }_{i,0}\in Z_N$ and $r_i\in Z_N$$(i=\{1,\dots ,d\})$ and $r_i,q_i,r_i^{\prime },q_i^{\prime }\in Z_N$. Then, $\mathcal{B}$ generates the private key: $S{K}_{I{D}_i,0}= (S{K}_{I{D}_i,0,1},S{K}_{I{D}_i,0,2})$, where $S{K}_{I{D}_i,0,1}=(g_1^{r_i}{A}_3^{r_i}{g}_1^{{\beta }_{i,0}},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{A}_3^{q_i}{g}_1^{{\gamma }_{i,0}})$ and $S{K}_{I{D}_i,0,2}=(g_1^{-{\beta }_{i,0}}{A}_3^{r_i^{\prime }},g_1^{-{\gamma }_{i,0}}{A}_3^{q_i^{\prime }})$.

$\mathcal{B}$ responds to $\mathcal{A}$ with the private key $SK$.

Challenge. $\mathcal{A}$ gives the challenger $\mathcal{B}$ an identity set $S^{\ast }=\{I{D}_1^{\ast },\dots ,I{D}_d^{\ast }\}$ and two messages $M_0$ and $M_1$ of the same size. $\mathcal{B}$ randomly selects $r\in Z_N$ and $\beta \in \{0,1\}$. Then, $\mathcal{B}$ calculates the ciphertext: $CT=(CM,Hd)=(CM,C_1,C_2,C_3)=(M\oplus Ext(e(g_1,T{)}^{\alpha },r),T^{{\displaystyle \sum _{j=1}^d{a}_{j}I{D}_j}+b}X,TY,r)$.

Stage 2. $\mathcal{A}$ continues to ask for the private key, but it requires that $I{D}_i\notin S^{*}$.

Guess. $\mathcal{A}$ provides a guess ${\beta }^{\prime }$ about $\beta$. If ${\beta }^{\prime }=\beta$, $\mathcal{A}$ wins the game.

Probability analysis. When $T=g_1^z{g}_2^v\in G_{q_1{q}_2}$ ($z$ and $v$ are randomly selected), $\mathcal{B}$ properly simulates the game ${\mathrm{GM}}_0$. When $T=g_1^z\in G_{q_1}$ ($z$ is randomly selected), $\mathcal{B}$ properly simulates the game ${\mathrm{GM}}_{\mathrm{R}}$.

The joint distribution of all variables is represented by symbols $VD$. When there was no leakage, [65] showed that ${\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)\ge lo{g}_2^N$. Thus, the probability that the adversary received the invalid ciphertext in every decryption query was $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)}\le 2^{-lo{g}_2^N}=\frac{1}{3\upsilon }$. When the symmetric key exposed $l$ bits of information, we obtained ${\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))\ge lo{g}_2^N-l$. Thus, the superiority that the adversary obtained in every decryption query was $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))}\le 2^{-(lo{g}_2^N-l)}=\frac{2^l}{N}$.

Therefore, the advantage of solving the difficult Hypothesis 1 using $\mathcal{B}$ is ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. That is to say, if $\mathcal{A}$ could distinguish ${\mathrm{GM}}_{\mathrm{R}}$ and ${\mathrm{GM}}_0$ over advantage $\epsilon$, the challenger $\mathcal{B}$ could destroy Hypothesis 1 with the advantage ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. This contradicts Hypothesis 1. So, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{\mathrm{R}}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_0}(L_K)|\le \epsilon$. □

Lemma 2.

Considering that the symmetric key has$l$bits of leakage, if there is an adversary $\mathcal{A}$such that $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{k-1}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)|\ge \epsilon$($k\in (1,\dots ,p)$), the challenger $\mathcal{B}$destroys Hypothesis 2 with the advantage $2^l\epsilon$.

Proof. 

Given the challenger $\mathcal{B}$, an instance $W=(\mathrm{\Phi },g_1,A_1{A}_2,A_3,B_2{B}_3)$ and $T$ ($T\in G_{q_1{q}_3}$ or $T\in G_1$). $\mathcal{B}$ interacts with $\mathcal{A}$ as follows:

Initialization. Let $t$ indicate the maximum number of users. $\mathcal{B}$ randomly selects $g_1,h_1\in G_{q_1},$ $g_3\in G_{q_3}$, $a_1,a_2,\dots ,a_t,b\in Z_N$, and $\alpha \in Z_N$. $\mathcal{B}$ sets up $u_1=g_1^{a_1},\dots ,u_t=g_1^{a_t},h_1=g_1^b$. $\mathcal{B}$ selects a $(k,\epsilon )$ strong binary extractor $Ext:G_2\times Z_N\to G_2$.

The public parameters are $PP=\{N,Ext,g_1,g_3,h_1,u_1,\dots ,u_t,e(g_1,g_1)\alpha \}$.

The master private key is $MK=\left\{\alpha \right\}$.

$\mathcal{B}$ sends $PP$ to $\mathcal{A}$.

Stage 1. $\mathcal{A}$ makes a private key inquiry for $I{D}_i\in S$, where $S=\{I{D}_1,\dots ,I{D}_d\}$. $\mathcal{B}$ responds in the following three ways:

(1)

For $i<k$, $\mathcal{B}$ responds with the semifunctional key. $\mathcal{B}$ randomly chooses ${\xi }_1,{\xi }_2,{\zeta }_1,{\zeta }_2\in Z_N$ and generates the semifunctional private key: $\widetilde{S{K}_{I{D}_i}}=(\widetilde{S{K}_{I{D}_i,k,1}},\widetilde{S{K}_{I{D}_i,k,2}})$ where $\widetilde{S{K}_{I{D}_i,k,1}}=(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}}{g}_2^{{\xi }_1},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}})r_i{Q}_1{g}_1^{{\gamma }_{i,k}}{g}_2^{{\xi }_2})$ and $\widetilde{S{K}_{I{D}_i,k,2}}=(R_1^{\prime }{g}_1^{-{\beta }_{i,k}}{g}_2^{{\zeta }_1},Q_1^{\prime }{g}_1^{-{\gamma }_{i,k}}{g}_2^{{\zeta }_2})$.

(2)

For $i>k$, $\mathcal{B}$ produces a normal private key in response.

(3)

For $i=k$, $\mathcal{B}$ randomly selects ${\beta }_{i,k},{\gamma }_{i,k}\in Z_N$, $r_i\in Z_N$$(i=\{1,\dots ,d\})$, and $R_i,Q_i,R_i^{\prime },Q_i^{\prime }\in G_{q_3}$. Then, $\mathcal{B}$ generates a private key: $S{K}_{I{D}_i,k}= (S{K}_{I{D}_i,k,1},S{K}_{I{D}_i,k,2})$, where $S{K}_{I{D}_i,k,1}= (S{K}_{I{D}_i,k,1}^1,S{K}_{I{D}_i,k,1}^2)=(T^{r_i}{g}_1^{{\beta }_{i,k}}{R}_1,g_1^{\alpha }(T^{{\displaystyle \sum _{j=1}^d{a}_{j}I{D}_j}+b})r_i{g}_1^{{\gamma }_{i,k}}{Q}_1)$ and $S{K}_{I{D}_i,k,2}= (S{K}_{I{D}_i,k,2}^1,S{K}_{I{D}_i,k,2}^2)=(R_1^{\prime }{g}_1^{-{\beta }_{i,k}},Q_1^{\prime }{g}_1^{-{\gamma }_{i,k}})$.

If $T\in G_{q_1{q}_3}$, this private key has a normal form, $\mathcal{B}$ correctly plays the game ${\mathrm{GM}}_{k-1}$.

If $T\in G_1$, the private key has a semifunctional form, $\mathcal{B}$ correctly plays the game ${\mathrm{GM}}_k$.

Challenge. $\mathcal{A}$ sends one challenge identity group $S^{\ast }=\{I{D}_1^{\ast },\dots ,I{D}_d^{\ast }\}$ and two equal-length challenge messages $M_0$ and $M_1$ to $\mathcal{B}$. $\mathcal{B}$ randomly selects $\beta \in \{0,1\}$ and calculates the ciphertext: $CT=(CM,Hd)=(CM,C_1,C_2,C_3)=(M\oplus Ext(e(g_1,A_1{A}_2{)}^{\alpha },r),(A_1{A}_2{)}^{{\displaystyle \sum _{j=1}^d{a}_{j}I{D}_j}+b},A_1{A}_2,r)$.

Stage 2. $\mathcal{A}$ continues to make a private key inquiry for $I{D}_i$. The condition that needs to be met is $I{D}_i\notin S^{*}$.

Guess. $\mathcal{A}$ outputs the guess ${\beta }^{\prime }$ about $\beta$. If ${\beta }^{\prime }=\beta$, $\mathcal{A}$ wins the game.

Probability analysis. When $T\in G_{q_1{q}_3}$, $\mathcal{B}$ correctly simulates the game ${\mathrm{GM}}_{k-1}$. When $T\in G_1$, $\mathcal{B}$ correctly simulates the game ${\mathrm{GM}}_k$. The joint distribution of all variables is represented by the symbol $VD$. When there is no leakage, the paper [65] shows that ${\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)\ge lo{g}_2^N$. Thus, the probability that the adversary receives the invalid ciphertext in every decryption query is $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)}\le 2^{-lo{g}_2^N}=\frac{1}{3\upsilon }$. When the symmetric key exposes $l$ bits of information, we obtain that ${\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))\ge lo{g}_2^N-l$. Thus, the probability that the adversary receives the invalid ciphertext in every decryption query is $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))}\le 2^{-(lo{g}_2^N-l)}=\frac{2^l}{N}$.

Therefore, the advantage of solving the difficult Hypothesis 2 using $\mathcal{B}$ is ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. That is to say, if $\mathcal{A}$ can distinguish ${\mathrm{GM}}_{k-1}$ and ${\mathrm{GM}}_k$ over advantage $\epsilon$, the challenger can destroy Hypothesis 2 with the advantage ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. This contradicts Hypothesis 2. So, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{k-1}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)|\le \epsilon$.

By the same token, for $i=k$ to $i=p$, we obtain $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{k+1}}(L_K)|\le \epsilon$,…, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{p-1}}(L_K)|\le \epsilon$. Therefore,

$$\begin{array}{l}|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)|\\ =|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{k+1}}(L_K)+\dots +A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{p-1}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)|\\ \le |A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{k+1}}(L_K)|+\dots +|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_{p-1}}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)|\\ \le (p-k)\epsilon \end{array}$$

In addition, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)|\le \epsilon$ (the proof will be given in Lemma 3). In this way, we can obtain:

$$\begin{array}{l}A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)\\ =|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)+A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)|\\ \le |A{D}_{\mathcal{A}}^{{\mathrm{GM}}_k}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)|+|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)|\\ \le (p-k+1)\epsilon \end{array}$$

This indicates that the advantage of $\mathcal{A}$ can be ignored in ${\mathrm{GM}}_k$. Lemma 2 is proved. □

Lemma 3.

Considering that the symmetric key has $l$bits of leakage, if there is an adversary $\mathcal{A}$such that $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)|\ge \epsilon$, the challenger $\mathcal{B}$destroys Hypothesis 3 with the advantage $2^l\epsilon$.

Proof. 

Given the challenger $\mathcal{B}$, an instance $W=(\mathrm{\Phi },g_1,g_1^{\alpha }{A}_2,A_3,g_1^s{B}_2,U_2)$ and a challenge item $T$ ($T=e(g_1,g_1{)}^{\alpha s}$ or $T\in G_2$). $\mathcal{B}$ interacts with $\mathcal{A}$ as follows.

Initialization. Let $t$ indicate the maximum number of users. $\mathcal{B}$ randomly selects $g_1,h_1\in G_{q_1},$ $g_3\in G_{q_3}$, $a_1,a_2,\dots ,a_t,b\in Z_N$, and $\alpha \in Z_N$. $\mathcal{B}$ sets up $u_1=g_1^{a_1},\dots ,u_t=g_1^{a_t},h_1=g_1^b$. $\mathcal{B}$ selects a $(k,\epsilon )$ strong binary extractor $Ext:G_2\times Z_N\to G_2$.

The public parameters are $PP=\{N,Ext,g_1,g_3,h_1,u_1,\dots ,u_t,e{(g_1,g_1)}^{\alpha }\}$.

The master private key is $MK=\left\{\alpha \right\}$.

$\mathcal{B}$ sends $PP$ to $\mathcal{A}$.

Stage 1. $\mathcal{A}$ asks for the private key of $I{D}_i\in S$, where $S=(I{D}_1,\dots ,I{D}_d)$($d\le t$) is the intended receivers’ collection. $\mathcal{B}$ randomly selects ${\xi }_1,{\xi }_2,{\zeta }_1,{\zeta }_2\in Z_N$. Then, $\mathcal{B}$ generates the semifunctional private key: $\widetilde{S{K}_{I{D}_i}}=(\widetilde{S{K}_{I{D}_i,k,1}},\widetilde{S{K}_{I{D}_i,k,2}})$, where $\widetilde{S{K}_{I{D}_i,k,1}}=(g_1^{r_i}{R}_1{g}_1^{{\beta }_{i,k}}(g_2^u{g}_3^{\varsigma }{)}^{{\xi }_1},g_1^{\alpha }(h_1{\displaystyle \prod _{j=1}^d{u}_j^{I{D}_j}}{)}^{r_i}{Q}_1{g}_1^{{\gamma }_{i,k}}(g_2^u{g}_3^{\varsigma }{)}^{{\xi }_2})$ and $\widetilde{S{K}_{I{D}_i,k,2}}=(R_1^{\prime }{g}_1^{-{\beta }_{i,k}}(g_2^u{g}_3^{\varsigma }{)}^{{\zeta }_1},{Q^{\prime }}_1{g}_1^{-{\gamma }_{i,k}}(g_2^u{g}_3^{\varsigma }{)}^{{\zeta }_2})$.

$\mathcal{B}$ responds to $\mathcal{A}$ with the private key $S{K}_{I{D}_i}$.

Challenge. $\mathcal{A}$ sends one challenge identity group $S^{\ast }=\{I{D}_1^{\ast },\dots ,I{D}_d^{\ast }\}$ and two equal-length challenge messages $M_0$ and $M_1$ to $\mathcal{B}$. $\mathcal{B}$ randomly selects $\beta \in \{0,1\}$ and calculates the ciphertext: $\widetilde{CT}=(CM,Hd)=(CM,\widetilde{C_1},\widetilde{C_2},C_3)=(M\oplus Ext(T,r),(g_1^s{g}_2^u{)}^{{\displaystyle \sum _{j=1}^d{a}_{j}I{D}_j}+b},g_1^s{g}_2^u,r)$.

Stage 2. $\mathcal{A}$ continues to make a private key inquiry for $I{D}_i$. The conditions that need to be met are $I{D}_i\notin S^{*}$.

Guess. $\mathcal{A}$ outputs a guess ${\beta }^{\prime }$ about $\beta$. If ${\beta }^{\prime }=\beta$, $\mathcal{A}$ wins the game.

Probability analysis. If $T=e(g_1,g_1{)}^{\alpha s}$, $\mathcal{B}$ correctly simulates the game ${\mathrm{GM}}_p$. When $T\in G_2$, $\mathcal{B}$ correctly simulates the game ${\mathrm{GM}}_F$. The joint distribution of all variables is represented by the symbol $VD$. When there is no leakage, [69] shows that ${\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)\ge lo{g}_2^N$. Thus, the probability that the adversary receives the invalid ciphertext in every decryption query is $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)}\le 2^{-lo{g}_2^N}=\frac{1}{3\upsilon }$. When the symmetric key exposes $l$ bits of information, we obtain ${\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))\ge lo{g}_2^N-l$. Thus, the probability that the adversary receives the invalid ciphertext in every decryption query is $2^{-{\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))}\le 2^{-(lo{g}_2^N-l)}=\frac{2^l}{N}$.

Therefore, the advantage of solving the difficult Hypothesis 3 using $\mathcal{B}$ is ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. That is to say, if $\mathcal{A}$ can distinguish ${\mathrm{GM}}_p$ and ${\mathrm{GM}}_F$ over advantage $\epsilon$, the challenger can destroy Hypothesis 3 with the advantage ${\epsilon }^{\prime }\ge \frac{2^l}{N}\epsilon$. This contradicts Hypothesis 3. So, $|A{D}_{\mathcal{A}}^{{\mathrm{GM}}_p}(L_K)-A{D}_{\mathcal{A}}^{{\mathrm{GM}}_F}(L_K)|\le \epsilon$. Lemma 3 is proved. □

Theorem 2.

The LR-SP-IBBE scheme has the performance of continuous leakage resilience.

Proof. 

Similar to [35], the given scheme LR-SP-IBBE obtains continuous leakage resilience by refreshing the private key periodically. The update algorithm inputs $S{K}_{ID,k}$ and public parameters $PP$ and achieves one update secret key $S{K}_{ID,k+1}$. In the update procedure, an additional value is added to the random value of the original exponent of one private key. Since the newly added value is randomly selected from $Z_N$, the distribution of this new private key is the same as that of the original one. After the private key update algorithm ran, we obtained one fresh private key. Thus, the proposed scheme had continuous leakage resilience. □

Theorem 3.

The relative leakage rate of the symmetric key of LR-SP-IBBE is$\tau =\left|\mathit{Leak}\right|/[lo{g}_2^N]\approx 1$

Proof. 

When the symmetric key is not disclosed,${\tilde{H}}_{\infty }(\mathcal{A}\left|VD\right.)=lo{g}_2^N$, where $\mathcal{A}$ represents the adversary and $VD$ represents the joint distribution of all variables. The adversary $\mathcal{A}$ can obtain the $l$ bits of information for the symmetric key by a side-channel attack. This indicates that the variable $Leak$ is $l$ bits in length. By means of conclusion 1, ${\tilde{H}}_{\infty }(\mathcal{A}\left|(VD\right.,Leak))\ge {\tilde{H}}_{\infty }(\mathcal{A}\left|View\right.)-l\ge lo{g}_2^N-l$. In this way, if the $(lo{g}_2^N-l,\epsilon )$ extractor is selected, $StD((Ext(K,r),r),(E,r))\le \epsilon$, where $E$ represents a uniform distribution. Thus, when $lo{g}_2^N-l$ is close to zero, the leakage is close to $lo{g}_2^N$. Then, $CM=Ext(K,\hspace{0.33em}r)\oplus M$ and uniform distribution are indistinguishable. Therefore, the relative leakage rate is: $\tau =\left|Leak\right|/({\mathit{log}}_2^N)\approx \hspace{0.33em}({\mathit{log}}_2^N)/({\mathit{log}}_2^N)\approx 1$. □

7. Performance Analysis

We will now provide the comparisons of our scheme and some other classical schemes regarding security and storage efficiency. Table 2 shows the safety comparison. STD stands for standard model, ROM stands for random oracle model, FS stands for full security, GSD stands for general subgroup decision assumption, DBDH means the decisional bilinear Diffie–Hellman assumption, DBDHE indicates the asymmetric DBDH exponent assumption, and n-BDHE indicates the decision n-bilinear Deffie–Hellman exponent problem.

Table 2. Security comparisons of some related schemes.

Schemes	Model	Assumption	Anonymity	Leakage Resilience
[16]	STD	DBDHE	YES	NO
[17]	ROM	DBDH	YES	NO
[19]	ROM	DBDH	YES	NO
[21]	ROM	DBDH	YES	NO
[25]	STD	GSD	YES	NO
[26]	ROM	n-DBDH	NO	NO
[28]	ROM	DBDHE	YES	NO
[29]	STD	LWE	YES	NO
[35]	STD	GSD	NO	YES
[63]	STD	GSD	YES	NO
Ours	STD	GSD	YES	YES

The model column indicates whether the scheme achieved security under the standard model (STD) or the random oracle model (ROM). The assumption column describes the difficult problem assumption on which the scheme depended. Anonymity indicates whether the scheme was anonymous. Leakage-resilience indicates whether the scheme had the feature of resisting private key disclosure. Table 2 shows that our scheme had security, anonymity, and leakage resilience under STD. This is the best security at present.

Table 3 shows the storage efficiency comparisons. $t$ is used to represent the number of all users, $d$ is the number of the intended receivers, $\left|G_T\right|$ represents the length of the elements in group $\left|G_T\right|$ (others are similar), and $n$ is a value that can be changed and is related to the leakage rate.

Table 3. Comparisons of Storage Efficiency.

Schemes	Length of Public Key	Length of Private Key	Length of Ciphertext
[16]	$\left|G_T\right|+t(\left|G_1\right|+\left|G_2\right|)$	$3d\left|G_1\right|$	$\left|G_T\right|+\left|G_1\right|+\left|G_2\right|$
[17]	$\left|G_T\right|+\left|G_1\right|+t\left|G_2\right|$	$d\left|G_2\right|$	$d\left|G_1\right|+\left|G_T\right|$
[19]	$5\left|G_0\right|$	$\left|G_0\right|$	$(1+d)\left|{\mathrm{Z}}_q^{*}\right|+3\left|G_0\right|$
[21]	$3\left|G_0\right|$	$2\left|G_0\right|$	$2d\left|{\mathrm{Z}}_q^{*}\right|+2\left|G_0\right|$
[25]	$2\left|G_1\right|+\left|G_2\right|+\left|H_1\right|$	$3\left|G_1\right|$	$2\left|G_1\right|+\left|G_2\right|$
[26]	$(t+1)(\left|G_1\right|+\left|G_2\right|)$	$(t+1)\left|G_1\right|$	$2\left|G_1\right|+\left|G_2\right|$
[28]	$(2t+1)\left|G_1\right|$	$(t+2)\left|G_1\right|$	$2\left|G_1\right|+\left|G_2\right|$
[29]	$nm\left|Z_q\right|$	$n\left|Z_q\right|$	$2m$
[35]	$(3+t+n)\left|G_1\right|+\left|G_2\right|$	$(n+2)\left|G_1\right|$	$(n+2)\left|G_1\right|+\left|G_2\right|$
[62]	$(3+t)\left|G_1\right|+\left|G_2\right|$	$2\left|G_1\right|$	$2\left|G_1\right|+\left|G_2\right|$
Ours	$(3+t)\left|G_1\right|+\left|G_2\right|$	$4\left|G_1\right|$	$2\left|G_1\right|+\left|G_2\right|$

Table 3 indicates that our scheme had the shortest ciphertext length, like that in [62]. Compared with the same type of schemes [35,62] and based on a composite order group, our scheme also had the shortest public key length. Because the schemes in [19,21] were constructed using a prime order group, their public key was relatively short. In terms of the private key length, our scheme adopted state partitioning technology, so the private key length was twice that of [62], on which ours was based.

8. Conclusions

This paper provided the syntax expression and security formulation of LR-SP-IBBE and proposed an LR-SP-IBBE construction. The proposed construction had continual leakage resilience. Based on the general subgroup decision hypothesis, our proved to be secure under STD. By comparing the efficiency of our proposed scheme and relevant ones, our scheme had a better performance. The relative leakage ratio could almost reach 1. The scheme had the following advantages.

The scheme had a continuous leakage-resilient performance, which can better reflect real application scenarios. In real applications, adversaries generally have a long-term attack capability.

The scheme had a good leakage-resilient performance, and the almost complete disclosure of the encapsulated symmetric key could also ensure the security of the scheme, which benefited from the use of the extractor. The entropy lost by the symmetric key could be supplemented through the extractor so that the symmetric key had enough entropy to continue to maintain confidentiality.

The scheme had anonymity that well protected the privacy of users. Users are very sensitive to privacy. They all want to effectively protect their privacy while also making cloud storage convenient. Therefore, the scheme proposed in this paper is very suitable for applications such as cloud storage services.

In a health diagnosis system, patient data are very large and usually needs to be stored on a cloud platform. In light of personal privacy, the data need to be secure and anonymous. This system is very suitable for such application scenarios.

Generally speaking, the computational efficiency of schemes in prime order groups is better than that in composite order groups. A method for constructing an anonymous broadcast encryption scheme in a prime order group is a subject we will study in the future.