Abstract
The heat transmission properties along the non-magnetized geometries have been numerically obtainedby various researchers. These mechanisms are less interesting in engineering and industrial processes because of excessive heating. According to current studies, the surface is magnetized and the fluid is electrically conductive, which helps to lessen excessive surface heating. The main objective of the current analysis is to numerically compute the temperature-dependent density effect on magnetohydrodynamic convective heat-transfer phenomena of electrical-conductive fluid flow along the vertical magnetized and heated plate placed in a thermally stratified medium. For the purpose of numerical analysis, the theoretical process governing heat and magnetic intensity along a vertical magnetic plate is examined. By using suitable and well-known similarity transformations for integration, the non-linear coupled PDEs for the aforementioned electrical-conductive fluid flow mechanism are changed and subsequently converted into non-similar formulation. The Keller Box method is used to numerically integrate the final non-similar equations. The MATLAB software program plots the transformed algebraic equations graphically and quantitatively. The behavior of the physical quantities such asvelocity graph, magnetic field graph, and temperature plot along with their slopes that arerate of skin friction, the rate of heat transfer, and the rate of magnetic intensity for different parameters included in the flow model. The novelty of the current work is to compute the magneto-thermo analysis of electrically conducting flow along the vertical symmetric heated plate. First, we secure the numerical solution for steady part and then these results are used to find skin friction, heat transfer, and magnetic intensity. In the current work, the fluid becomes electrically conducing due to a magnetized surface which insulates heat during the mechanism and reduces the excessive heating. The results are excellent and accurate because they are satisfied by its given boundary conditions. Additionally, the current problems have a big impact on the production of polymer materials, glass fiber, petroleum, plastic films, polymer sheets, heat exchangers, catalytic reactors, and electronic devices.
1. Introduction and Literature Review
In metallurgy and polymer technology, the heat, magnetic intensity, and momentum transfer in the laminar boundary layer flow on a magnetized heated plate immersed in thermally stratified medium are significant from both a theoretical and practical standpoint. Engineers can benefit greatly from the laws governing heat transfer and magnetohydrodynamics flows in a variety of fields, including heat exchangers, sunspot theory, intercontinental ballistic missiles, interstellar gas motion, liquid metals, cooling of nuclear reactors, plasma confinement, and geophysics and astrophysics. The dynamic study of electrically conducting fluid is known as magnetohydrodynamics, established by Maxwell for electromagnetism. The fundamental idea behind an electrically conducting fluid is that a magnetic field has the potential to cause currents to flow through conductive fluid that is flowing, which in turn exerts forces on the fluid and affects the magnetic field. In literature, most researchers have analyzed the heat transfer characteristics of mixed convection flow along different geometries. However, in current analysis, the aligned magnetic field is used to make a surface magnetized and to reduce the excessive heating along the proposed surface. Some related literature of the current problem is mentioned here to understand the theoretical and numerical points. Furthermore, the current issues have significant implications for the polymer industries, including paper production, glass-fiber production, liquid crystal solidification, petroleum production, production of unusual lubricants, suspension solutions, wire drawing, continuous cooling, fiber spinning, plastic film production, polymer sheet extraction, heat exchangers, petroleum resource recovery, fault zones, catalytic reactors, and the production of electronic devices.
Nima and Ferdows [1] performed multiple solutions of microorganisms across a non-isothermal inclined disk with gyro-tactic particles. Mahanthesh et al. [2] developed an analysis on squeezing flow along a magnetized channel with hall current, heat source, and thermal radiation effects numerically. They found the increasing behavior in concentration and temperature by reducing value of squeezing parameter. Bansood and Ambedkar [3] studied free forced convective boundary layer flow over a semi-infinite plate in a porous medium. They analyzed heat and mass transfer in boundary layer flow region for opposing flow. Hazarika and Ahmed [4] investigated the numerical development of the MHD natural convective nanofluid flow through a vertical cone with heat source effects. They discovered adecreasing behavior of concentration profile when the Brownian motion parameter is raised. The laminar mixed convection flow from a vertical surface was studied by Chaudhry et al. [5]. The melting effects on mixed convection heat and mass transfer in a non-Newtonian nanofluid submerged in a porous medium were carried out by Ram Reddy and Kairi in [6]. They discovered that when the buoyancy ratio grows, the heat transfer coefficient decreases in the entire range of porous geometry. Hussain et al. [7] developed the unsteady convection flow of two phase nanofluid around a cone embedded in porous material numerically. They found that under viscous dissipation impact, the heat transfer rate decreased with maximum viscous heat generation.
The consequences of temperature-dependent density on a steady mixed Newtonian fluid convective flow near to a vertically permeable heated plate in a stratified material has great importance in industries and engineering. In the manufacturing sector, double diffuse free forced convection over vertical bodies is crucial for the development of dependable machinery, nuclear reactors, satellites, and spacecraft. Using convective boundary conditions and induced magnetic field, Mahdy [8] studied the nanofluid including gyro-tactic microorganisms with specified density motile microorganisms for natural convection flow across a vertical flat sheet. They found that as time dilation, heat conduction, and mixed convection parameter increases, the Nusselt number decreases. In order to simulate mixed convection flow of viscous fluid from a vertical cone with the effect of chemical reaction, Pullepu et al. [9] used numerical methods. They discovered that as skin friction increases, the velocity of steady flow is raised. Srinivasacharya and Surender [10] investigated impact of dual stratification on free forced convective boundary layer flow of nanofluid over a vertical shape embedded in a porous media. They obtained a considerable decrease in heat transmission and an increase in mass transfer rates with thermophoresis effect. Ullah et al. [11,12,13,14] elaborated impacts of MHD, velocity slip, reduced gravity, and stratification on oscillatory fluid along a non-conducting circular heated shape numerically. The baffle effects on enclosure filled with nanofluid for convective heat mechanism were analyzed in [15]. The entropy analysis on pseudo plastic flow along circular shape with MHD by using Keller Box scheme was investigated numerically in [16]. Sofiadis [17] numerically analyzed the Reynolds effects on micro polar flow in a channel.
Mehmood et al. [18] performed free forced convection flow in thermally and solutal stratified magneto nanofluid with non uniform heat source. They examined the volume fraction profile of lowered Brownian motion parameter and solute parameter increases. In the presence of internal heat generation, Elbashbeshy et al. [19] investigated the effects of thermal radiation and magnetic field on unsteady mixed convection flow and heat transfer across an exponentially extending surface with suction. They discovered that the radiative heat transfer increased as the thermal radiation parameter rose. Daniel et al. [20] developed a heat energy problem from a nanofluid flow across a stretched sheet with MHD and a chemical reaction. They observed that velocity and temperature profile rise byincrements in the electrical parameter.
The impact of a chemical reaction on the flow of MHD viscoelastic fluid over vertical stretching sheet with heat source effects was described by Jena et al. in [21]. They found that the chemical reaction and Prandtl number increases the rate of heat transfer along the plate. Yasin et al. [22] performed boundary layer flow with free forced convection embedded in thermally stratified porous medium statured by nanofluid numerically. Rawi et al. [23] introduced the influence of copper nanoparticles on Jeffrey fluid of free forced convection flow generated by g-Jitter. Alzahrani et al. [24] developed a third grade hydro magnetic free/forced convection problem for nonmaterial including gyro tactic microorganisms across a stretched surface. The effects of magnetohydrodynamics and velocity-slip on convective flow along the non-conducting geometry were studied by Ullah et al. in [25]. The opposing flow through a vertical cylinder filled with a Darcy porous medium containing gyro tactic microorganisms with double diffusive mixed convection was examined by Alsenafi and Ferdows in [26]. Babu et al. [27] examined the impact of thermal conductivity and variable viscosity on heat and mass transfer of nanofluid along a vertical cone in the presence of a chemical reaction. Variable density effects on hydro magnetic mixed convective non-Newtonian fluid flow over a moving vertical plate were presented by Salem et al. in [28]. Iqbal et al. [29] investigated the forced convective flow along a cone with heat and mass flux model by using implicit finite difference method graphically. Abulnaja et al. [30] performed unsteady free/forced convection flow filled with nanofluid across the straight disc placed in a porous material in the presence of variable surface temperature. Maranna et al. [31] analyzed the mass transpiration phenomena with MHD and radiation effects on viscous fluid past a stretched shape. Mabood et al. [32] performed Jeffrey nanofluid phenomena with entropy and MHD effects along the stretched geometry for various engineering application.
It can be seen that all of the aforementioned investigations deal with a minimum temperature difference between the fluid at the surface and the ambient fluid. However, there are instances where there is a significant temperature difference. The Boussinesq approximation is no longer appropriate in this case (see Kakac and Yenar [33]). To notice these circumstances, the temperature-dependent density function is suggested in [33] for the specific cases where alarge temperature difference occurs. The theoretical mechanism on heat and magnetic intensity along a vertical magnetic plate has been investigated for numerical analysis. Using the idea from previous research [33], the temperature-dependent density effect on magnetohydrodynamic convective heat-transfer phenomena of electrical-conductive fluid flow along the vertical magnetized and heated plate placed in thermally stratified medium was explored numerically. The non-similar equations werenumerically integrated by employing the Keller Box method. The transformed algebraic equations were plotted graphically and numerically on the MATLAB software package. The heat transfer characteristics along the non-magnetized shapes were performed in various previous studies numerically. Due to excessive heating, these mechanisms are less interesting in engineering and industrial processes. In the current analysis, the surface wasmagnetized and the fluid waselectrically conducting which is responsible forreducing excessive heating along the surface. The novelty of the present work is in the analysis of convective heat transfer analysis of viscous fluid flow with temperature dependent density and thermal stratification effects along the vertical symmetric heated plate numerically. First, the velocity, magnetic field, and temperature profiles weresecured and then those profiles used to compute skin friction, heat transfer, and magnetic intensity along the heated plate. The obtained results are in excellent agreement by satisfying the given boundary conditions.
2. Flow Problem and Mathematical Description
The problem is devoted tonumerical solutions of magneto-thermo analysis of convective heat transfer along thermally and magnetized geometry immersed in thermally stratified medium. The extended issue will change into arrangement of partial differential conditions and then transform into ordinary ones using the stream-function forms. The molded problem will be resolved by using FDM method conjunct with the Keller Box method. The numerical result for considered material properties will be depicted in graphical and tabular form.
Consider two dimensional steady and incompressible electrical conducting fluid. In Figure 1, where and are axes along and perpendicular to the vertical magnetized plate immersed in thermally stratified medium, respectively, and are the velocity-fields in and orders, respectively. The is the magnetic field strength, indicates that the magnetic field is exact at the surface, is the temperature, is the free stream temperature, is the thermal conductivity of the fluid, and is the specific heat. The is the fluid density, is the megnatic permeability, is the kinematic fluid viscosity, is the volumetric coefficient of thermal expansion, and gravity acceleration is . The following is how the equations for continuity, momentum, magnetic force, and energy are expressed where high temperature difference arises with temperature dependent density function:
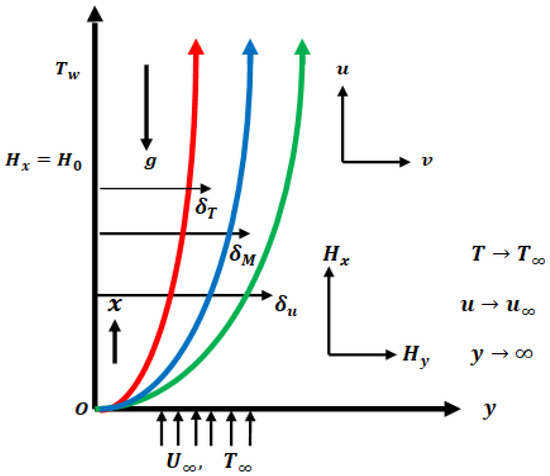
Figure 1.
Coordinate system and flow geometry.
It should be emphasized that the Boussinesq approximation holds true for fluids with of the magnitude of when the temperature differential between the fluid and the surface is of the order of . Consequently, leaving out higher-order terms and expanding Equation (1a) into a Taylor series, the above equation becomes .
The boundary conditions of the present model are,
The proper boundary conditions for the temperature with temperature-dependent density and the thermal stratification components are described above. The Reynolds number is , being the free steam velocity, is the variable temperature, and is ambient variable temperature of the thermally and magnetized heated plate, are positive constants and is the temperature constant along the thermally and magnetizedheated plate.
3. The Similarity Transformation and Stream Function Formulation
The proper dimensionless similarity and stream function to convert PDEs into ODEs are given as:
The stream function and are for magnetic and velocity fields, is dimensilized temperature and similarity parameter is .
The converted form of the ODEs in Equations (1)–(6) by applying the Equations (7) and (8), we have non linear ODEs given below;
where is Prandtl parameter, is magnetic Prandtl parameter, is a magnetic parameter, is the mixed convection parameter, is similarity variable, is dimensionless temperature, is kinematic fluid viscosity, and is stratification number. The transformed boundary conditions in (6) then becomes,
The formula for skin friction is , the formula for the Nusselt number is , and the formula for the magnetic intensity coefficient is . The values of , , and are listed below:
Consequently, the values of magnetic intensity, Nusselt number, and skin friction are provided by,
4. The Solution and Computing Techniques
A suitable stream function formulation is used to convert the linked partial differential equations for the aforementioned model into a set of ordinary differential equations. The iterative Keller Box scheme is used to solve the simplified nonlinear ordinary differential Equations (9)–(11) and boundary conditions in (12). We begin by introducing additional independent variables , and by using Equation (13),
Equations (9)–(12) get simpler to solve in order to get around the problems that they present. Thus, the more simple forms are,
The reduced boundary conditions are
We now consider the segment , with as midpoint given in Equation (23) below;
This is how the central difference form and average form are presented:
and
By applying the above Equations (24)–(29), the governing Equations (14)–(21) become
along with boundary conditions
Applying the below-mentioned iterative Newton–Raphson approach for smooth algorithm;
By ignoring all appearances of powers of greater than the first power, just like in the standard Newton–Raphson method, equations become;
The simplified form of the equations is provided below, again utilizing Equations (35)–(39) in Equations (30)–(33);
The specific boundary conditions that can be met without iteration are recalled. As a result, to ensure that these correct values are maintained across all iterations, we take
5. The Arrangement of Difference Equations in Vector Notation/Matrix
The next essential step is to organize the aforementioned difference equations in matrix form. If it is done wrong, either the matrix solution method fails because there is a singular matrix (determinant = 0) or sub-matrix, or the approach becomes extremely inefficient since there is no discernible structure in the matrix. We have,
6. Analysis and Discussion of Results
The present analysis addresses the temperature-dependent density effect on magnetohydrodynamic convective heat transfer phenomena of electrical-conductive fluid flow along the vertical magnetized and heated plate placed in thermally stratified medium. The non-linear coupled PDE equations for the above fluid flow mechanism are formulated and then converted into non-similar formulation by applying an appropriate and well-known similarity transformation for integration. The final non-similar forms are integrated numerically by employing Keller Box scheme method. The transformed algebraic equations are plotted graphically and numerically on the MATLAB software package. The behavior of physical quantities such as velocity graph, magnetic field graph, and temperature graph along with their slopes, that is skin friction, magnetic intensity, and heat transfer, under the effect of different parameters included in the flow model is discussed. The impact of physical parameters such as Prandtl number , mixed convective parameter , stratification parameter , density number , magnetic-force number , and magnetic Prandtl is interpreted graphically and numerically.
Figure 2a–c are presented for the behavior of velocity graph, temperature plot, and magnetic field for different values of temperature dependent density with some fixed parameters. It was deduced that the velocity profile was enhanced at maximum value of but similar behavior wasnoted for other values of in Figure 2a. This happens because an increasing value of density parameter tends to increase the density variation with temperature, which ultimately increases the buoyancy force. The magnetic field wasincreased at the lower value of but decreased at the maximum value of in Figure 3b. In Figure 3c, the temperature distribution wasincreased at lower value of but decreased at maximum value of . The good variations in each profile werenoted for each value of temperature-density parameter . Hence, as increased, the fluid was under two forces: the first force increased the velocity of the fluid due to increase in the buoyancy forces and the second force decreased the velocity of the fluid due to the decrease in temperature. Figure 3a–c are plotted against the various values of stratification parameter for velocity graph, temperature graph, and magnetic field. It was examined that the velocity profile increased at lower value of but the minimum value wasnoted at the higher value of in Figure 3a. It wasdeduced that the magnetic field wasenhanced at the large value of but decreased at the small value of in Figure 3b. This happens because magnetic diffusion is reduced by increasing the magnetic-Prandtl number which is responsible for above-said phenomena. This behavior of the aforementioned variables supports the physical hypothesis that as the magnetic field grows stronger, more resistance is formed inside the fluid flow domain, which reduces the velocity distribution and improves the temperature profile. The temperature distribution increased at the lower value of but decreased at the maximum value of in Figure 3c. Figure 4a–c depict the behavior of velocity , temperature , and magnetic field for different quantities of with some fixed parameters. It was deduced that the velocity profile wasenhanced at larger but decreased at small value of in Figure 4a. It was examined that the magnetic field increased at lower value of while minimum value wasnoted at higher value of in Figure 4b. It wasalso noted that the temperature distribution increased at lower value of but decreased at maximum value of in Figure 4c. Physically, it was expected because larger values of correspond to stronger buoyancy forces which lead to an increase in the acceleration of fluid flow. Due to conducting phenomena, magnetic effects are strongly observed exactly at the surface, but far from the surface, each value is zero. The good variations in each profile werenoted for each value of mix convection parameter . Figure 5a–c examined the behavior of velocity , temperature , and magnetic field for different quantities of Prandtl number with some fixed parameters. It was shown that the velocity field increased at the highest value of and decreased at in Figure 5a. The magnetic field distribution increased at the lowest value of but minimum value wasnoted at the highest value of in Figure 5b. In Figure 5c, the temperature distribution wasincreased by decreasing the value of but the temperature distribution wasdecreased by increasing the value of . This phenomenon is expected because an increase in Pr tends to increase density variation with temperature which enhances the buoyancy force.The thermal boundary layer thickness wasreduced due to increase in Pr. The prominent thermal slip with good variations are obtained in temperature graph at each value of . The good variations in each profile wereexamined for various values of Prandtl number . Figure 6a–c are demonstrated for velocity , temperature , and magnetic field for different quantities of magnetic Prandtl number with some fixed parameters along the surface of a vertical geometry. In Figure 6a, it wasdeduced that the fluid velocity along the surface wasincreased for the large value of but the minimum value wasobtained at a lower value of with good response. It was deduced that the magnetic graph increased at the large value of but decreased at the small value of in Figure 6b. In Figure 6c, it is depicted that the temperature distribution increased at the small value of but the minimum value wasnoted at the large value of . It wasalso noted that temperature plots are in good form and excellent agreement for the given phenomenon. As the magnetic Prandtl number increased, viscosity of fluid increased and fluid became thicker more and consequently the boundary layer thickness decreased. Figure 7a–c are plotted for velocity, magnetic field, and fluid temperature against the various values of magnetic force parameter with some constant parameters long the surface of the vertical geometry. In Figure 7a, it is deduced that the mixed convection effect in the velocity graph increased at the large value of but minimum value wasobtained at the lower value of by satisfying the given boundary conditions asymptotically. This result was expected because an increase in means enhancement in the Lorentz forces which opposes the flow and velocity of the fluid decreases. In Figure 7b, it wasexamined that the magnetic field profile along the surface wasenhanced at the large value of but the minimum value was obtained at small value of . Thishappens because the magnetic force parameter is the ratio of magnetic energy to kinetic energy, so with the increase in the magnetic force parameter , the magnetic energy is increased, while the kinetic energy is reduced. An excellent and favorable phenomenon is observed in magnetic field graph. In Figure 7c, it is deduced that the temperature profile decreased at the large value of but increased at the small value of . This given mechanism is performed with good agreement.
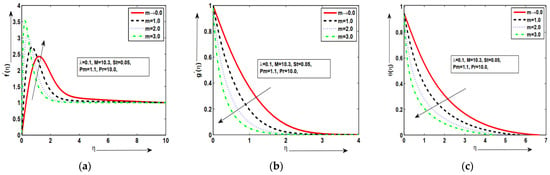
Figure 2.
(a–c) The geometric profiles of , and against .
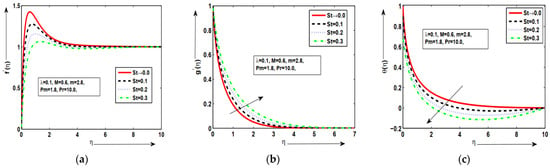
Figure 3.
(a–c) The geometric profiles of , and against .
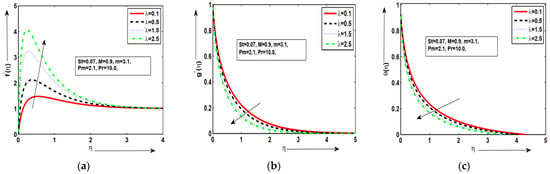
Figure 4.
(a–c) The geometric profiles of , and against .
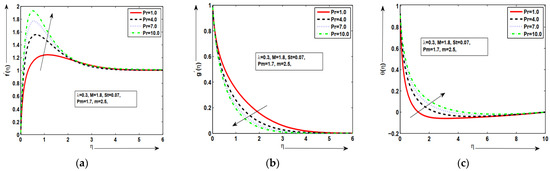
Figure 5.
(a–c) The geometric profiles of , and against .
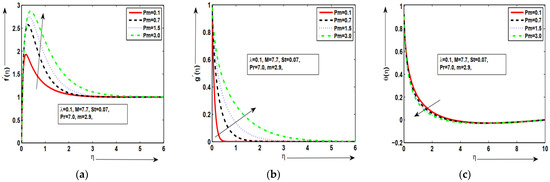
Figure 6.
(a–c) The geometric profiles of and against .
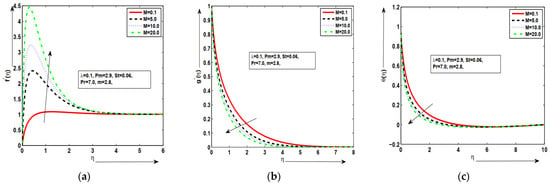
Figure 7.
(a–c) The geometric profiles of , and against .
From Table 1, it is concluded that the skin friction increased at = but the minimum skin friction wasobtained at small = in the presence of buoyancy forces. It should be noted that corresponds to the case of a small temperature difference between the surface and fluid, i.e., the buoyancy approximation becomes valid for this particular case, whereas for a high temperature difference, a considerable enhancement in the numerical values of the skin friction and heat transfer rate wasinspected and can be clearly seen in Table 1. It wasdeduced that the magnetic intensity wasmaximum at larger = but the smaller quantity of magnetic intensity wasexamined at smaller = in the presence of strong magnetic field. This result was expected because an increase in means enhancement in the Lorentz forces which opposes the flow and velocity of the fluid decreases. It was also expected because as magnetic Prandtl number increases, the viscosity of fluid increases and fluid becomes thicker and consequently the boundary layer thickness decreases. It is also depicted that the heat transfer wasincreased at maximum = but the lower quantity of heat transfer is depicted at minimum in the presence of magnetic force . With the increase in value of , the magnetic field became stronger along the surface which is a clear indication that the Lorentz force is more effective in this case. In Table 2, the influence of stratification number with various values along a vertical plate is shown to check the behavior of physical properties of the rate of skin friction, the rate of magnetic intensity, and the rate of heat transfer. From Table 2, it is computed that the skin friction is maximum at smaller value of = but the minimum quantity of skin friction is depicted at a large value of = in the presence of Prandtl number = . Physically, it is possible because thermal conductivity decreases as Pr increases, which has a lower magnitude of frictional forces between the viscous layers. It is depicted that the magnetic intensity is decreased at larger = but the maximum value of magnetic intensity is explored at small = in the presence of = . However, due to the strong buoyancy number which acts like a pressure gradient and dominated over the resistance, skin friction is increased and slight changes in heatand magnetic intensityare noted. It is also mentioned that the heat transfer wasmaximum at the lower value of = but the minimum quantity of heat transfer wasnoticed at larger = in the presence of magnetic Prandtl number = . The reason behind this is that increasing the value of is equivalent to decreasing magnetic diffusivity and consequently the strength of magnetic field becomes loose.

Table 1.
Numerical results for and for for variousvalues of while other parameters are fixed.

Table 2.
Numerical results for and for for various values of while other parameters are fixed.
7. Conclusions
The current physical problem addressed the temperature-dependent density effect on magnetohydrodynamic convective heat-transfer phenomena of electrical-conductive fluid flow along the vertical magnetized and heated plate placed in thermally stratified medium. In previous studies, the heat transfer characteristics along the non-magnetized shapes were performed numerically. Due excessive heating, these mechanisms are less interesting in engineering and industrial processes. To overcome this issue in current analysis, the surface wasmagnetized and fluid waselectrically conducting which is responsible forreducing excessive heating along the surface. The non-linear coupled PDE equations for the above fluid flow mechanism wereformulated and then converted into non-similar formulation by applying an appropriate and well-known similarity transformation for integration. The final non-similar forms werenumerically integrated by employing the Keller Box scheme. The transformed algebraic equations wereplotted graphically and numerically on the MATLAB software package. The main finding of the current analysis wasto compute physical quantities such asvelocity graph, magnetic field graph, and temperature plot along with their slopes that areskin friction, magnetic intensity and heat transfer for different parameters included in the flow model. The comparison of Keller Box analysis wascomputed with previous existing numerical results. Furthermore, the current issues have significant implications for the polymer industries, glass-fiber production, petroleum production, fiber spinning, plastic film production, polymer sheet extraction, heat exchangers, catalytic reactors, and the production of electronic devices. The main findings are given below:
It wasdeduced that the velocity profile increased for maximum temperature-dependent density but similar behavior wasnoted for other values of variable density. This happens because an increasing value of density parameter tends to increase the density variation with temperature, which ultimately increases the buoyancy force.
It wasalso noted that the temperature distribution increased for strong buoyancy forces but decreased for lower buoyancy forces.Physically, it was expected because larger values of correspond to stronger buoyancy forces which leads to increase the acceleration of fluid flow.
It wasexamined that the magnetic field profile along the surface wasenhanced for strong magnetic forces but minimum value wasobtained at lower magnetic forces. Thishappens because the magnetic force parameter is the ratio of magnetic energy to kinetic energy, so with the increase in the magnetic force parameter , the magnetic energy is increased, while the kinetic energy is reduced.
It wascomputed that the skin friction wasmaximum for small thermal stratification but the minimum quantity of skin friction wasdepicted for large stratification in the presence of Prandtl number Pr . Physically, it is possible because thermal conductivity decreases as Pr increases, which has a lower magnitude of frictional forces between the viscous layers.
It wasalso mentioned that the heat transfer is increased for lower stratification, but the minimum quantity of heat transfer is noticed in the presence of magnetic Prandtl number. The reason behind this is that increasing the value of Pm is equivalent to decreasing magnetic diffusivity and consequently the strength of magnetic field becomes loose.
Author Contributions
Conceptualization, Z.U.; Data curation, N.A.; Formal analysis, M.A.; Funding acquisition, N.A.; Methodology, M.J.; Project administration, H.F.A.; Funding acquisition, A.M.A.; Visualization, A.H.; Writing—original draft, Z.U.; Funding acquisition, A.H.; Software, S.M.E.; Writing—review and editing, Z.U.; Funding acquisition, H.F.A.; Validation, A.M.A.; Funding acquisition, S.M.E.; Investigation, M.J.; Methodology, M.A. All authors have contributed in the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourahbint Abdulrahman University researchers supporting project number (PNURSP2022R52) by Aisha M. Alqahtani, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Princess Nourahbint Abdulrahman University researchers supporting project number (PNURSP2022R52), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nima, N.I.; Ferdows, M. Dual Solutions in Mixed Convection Flow Along Non-Isothermal Inclined Cylinder Containing Gyrotactic Microorganism. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 87, 51–63. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Gorla, R.S.R. Mixed convection squeezing three-dimensional flow in a rotating channel filled with nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1460–1485. [Google Scholar] [CrossRef]
- Bansod, V.J.; Ambedkar, B. An integral treatment for combined heat and mass transfer by mixed convection along vertical surface in a saturated porous medium. J. Mech. Eng. Res. 2011, 3, 138–151. [Google Scholar]
- Hazarika, S.; Ahmed, S. Numerical Investigation of Endothermic/Exothermic Reaction in MHD Natural Convective Nano-Fluid Flow over a Vertical Cone with Heat Source/Sink. Walailak J. Sci. Technol. 2021, 18, 22834. [Google Scholar] [CrossRef]
- Chaudhary, K.; Sharma, A.; Jha, A. Laminar mixed convection flow from a vertical surface with induced magnetic field and convective boundary. Int. J. Appl. Mech. Eng. 2018, 23, 307–326. [Google Scholar] [CrossRef]
- Ramreddy, C.; Kairi, R. The effect of melting on mixed convection heat and mass transfer in non-Newtonian nanofluid SATURATEED in porous medium. Front. Heat Mass Transf. 2015, 6, 6. [Google Scholar] [CrossRef]
- Hussain, A.; Haider, Q.; Rehman, A.; Abdussattar, A.; Malik, M.Y. A New Heat Dissipation Model and Convective Two-Phase Nanofluid in Brittle Medium Flow over a Cone. Math. Probl. Eng. 2021, 2021, 6688747. [Google Scholar] [CrossRef]
- Mahdy, A. Free convection flow over a vertical flat plate in nanofluid porous media containing gyrotactic microorganisms with prescribed density motile microorganisms flux. Sci. Technol. Asia 2017, 22, 71–85. [Google Scholar]
- Pullepu, B.; Sambath, P.; Rani, M.S.; Chamkha, A.J.; Viswanathan, K.K. Numerical Solutions of Free Convective Flow from a Vertical Cone with Mass Transfer under the Influence of Chemical Reaction and Heat Generation/Absorption in the Presence of UWT/UWC. J. Appl. Fluid Mech. 2016, 9, 343–356. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Surender, O. Effect of double stratification on mixed convection boundary layer flow of a nanofluid past a vertical plate in a porous medium. Appl. Nanosci. 2014, 5, 29–38. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Rashad, A.M. Magneto-thermo analysis of oscillatory flow around a non-conducting horizontal circular cylinder. J. Therm. Anal. 2020, 142, 1567–1578. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Zia, S.; Ali, I. Surface temperature and freestream velocity oscillation effects on mixed convention slip flow from surface of a horizontal circular cylinder. Therm. Sci. 2020, 24 (Suppl. 1), 13–23. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Zia, S.; Chu, Y.-M.; Khan, I.; Nisar, K.S. Computational analysis of the oscillatory mixed convection flow along a horizontal circular cylinder in thermally stratified medium. Comput. Mater. Contin. 2020, 65, 109–123. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Sarris, I.E.; Karakasidis, T.E. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Appl. Sci. 2022, 12, 5081. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Al-Muhja, B.; Loganathan, K.; Periyasamy, U.; Ali, F.; Sarris, I.E. Analysis of Convection Phenomenon in Enclosure Utilizing Nanofluids with Baffle Effects. Energies 2022, 15, 6615. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Prasad, V.R.; Basha, H.T.; Sarris, I.; Akkurt, N. Keller box simulation of magnetic pseudoplastic nano-polymer coating flow over a circular cylinder with entropy optimisation. Comput. Math. Appl. 2022, 118, 132–158. [Google Scholar] [CrossRef]
- Sofiadis, G.; Sarris, I. Reynolds number effect of the turbulent micropolar channel flow. Phys. Fluids 2022, 34, 075126. [Google Scholar] [CrossRef]
- Mehmood, K.; Hussain, S.; Sagheer, M. Mixed convection flow with non-uniform heat source/sink in a doubly stratified magnetonanofluid. AIP Adv. 2016, 6, 065126. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.; Emam, T.; Abdelgaber, K. Effects of thermal radiation and magnetic field on unsteady mixed convection flow and heat transfer over an exponentially stretching surface with suction in the presence of internal heat generation/absorption. J. Egypt. Math. Soc. 2012, 20, 215–222. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction. J. King Saud Univ. -Sci. 2019, 31, 804–812. [Google Scholar] [CrossRef]
- Jena, S.; Dash, G.; Mishra, S. Chemical reaction effect on MHD viscoelastic fluid flow over a vertical stretching sheet with heat source/sink. Ain Shams Eng. J. 2016, 9, 1205–1213. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Arifin, N.M.; Nazar, R.; Ismail, F.; Pop, I. Mixed convection boundary layer flow embedded in a thermally stratified porous medium saturated by a nanofluid. Adv. Mech. Eng. 2013, 121943. [Google Scholar] [CrossRef]
- Rawi, N.A.; Ilias, M.R.; Jiann, L.Y.; Isa, Z.M.; Shafie, S. The effect of copper nanoparticles on mixed convection flow of jeffrey fluid induced by g-jitter. J. Nanofluids 2018, 7, 156–162. [Google Scholar] [CrossRef]
- Alzahrani, E.O.; Shah, Z.; Dawar, A.; Malebary, S.J. Hydromagnetic mixed convective third grade nanomaterial containing gyrotactic microorganisms toward a horizontal stretched surface. Alex. Eng. J. 2019, 58, 1421–1429. [Google Scholar] [CrossRef]
- Ullah, Z.; Ehsan, M.; Ahmad, H.; Ilyas, A. Combined effects of MHD and slip velocity on oscillatory mixed convective flow around a non-conducting circular cylinder embedded in a porous medium. Case Stud. Therm. Eng. 2022, 38, 102341. [Google Scholar] [CrossRef]
- Alsenafi, A.; Ferdows, M. Dual solution for double-diffusive mixed convection opposing flow through a vertical cylinder saturated in a Darcy porous media containing gyrotactic microorganisms. Sci. Rep. 2021, 11, 19918. [Google Scholar] [CrossRef] [PubMed]
- Babu, S.R.C.; Venkateswarlu, S.; Lakshmi, K.J. Effect of variable viscosity and thermal conductivity on heat and mass transfer flow of nanofluid over a vertical cone with chemical reaction. Int. J. Appl. Eng. Res. 2018, 13, 13989–14002. [Google Scholar]
- Salem, A.M.; El-Aziz, M.A.; Abo-Eldahab, E.M.; Abd-Elfatah, I. Effect of variable density on hydromagnetic mixed convection flow of a non-Newtonian fluid past a moving vertical plate. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1485–1493. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Khan, W.; Mustafa, I.; Ghaffari, A. Numerical study of natural convection flow of nanofluid past a circular cone with Cattaneo–Christov heat and mass flux models. Symmetry 2019, 11, 1363. [Google Scholar] [CrossRef]
- Abualnaja, K.M.; Elgendy, M.S.; Ibrahim, F.S. Unsteady Mixed Convection Flow along Symmetric Wedge with Variable Surface Temperature Embedded in a Porous Medium Saturated with a Nanofluid. J. Appl. Math. Phys. 2021, 09, 101–126. [Google Scholar] [CrossRef]
- Maranna, T.; Sneha, K.N.; Mahabaleshwar, U.S.; Sarris, I.E.; Karakasidis, T.E. An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration. Appl. Sci. 2022, 12, 5466. [Google Scholar] [CrossRef]
- Mabood, F.; Fatunmbi, E.O.; Benos, L.; Sarris, I.E. Entropy Generation in the Magnetohydrodynamic Jeffrey Nanofluid Flow Over a Stretching Sheet with Wide Range of Engineering Application Parameters. Int. J. Appl. Comput. Math. 2022, 8, 98. [Google Scholar] [CrossRef]
- Kakac, S.; Yener, Y.; Pramuanjaroenkij, A. Convective Heat Transfer; CRC Press: Boca Raton, FL, USA, 1995; pp. 312–314, 399. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).