Abstract
This paper addresses the Capacitated Vehicle Routing Problem (CVRP), which is a widely studied optimization problem due to its relevance to the field of transportation, distribution, and logistics. We present a matheuristic method for CVRP that adopts the main idea of the Kernel Search algorithm (KS) based on decomposing the original problem into sub-problems that are easier to solve. Unlike the original scheme of KS, our approach uses the Clarke–Wright savings algorithm to construct a sequence of smaller sub-problems, which are subsequently solved using mathematical programming strategies. The computational experiments performed on a set of benchmark instances showed that the proposed matheuristics achieves good results in acceptable computational time.
1. Introduction
The Capacitated Vehicle Routing Problem (CVRP), which is the focus of the study presented, is a classical operations research problem that can be described as a problem of designing routes for several vehicles traveling from a depot to a set of geographically dispersed customers and then returning back to the depot. The goal is to choose routes to serve all customers at a minimum total transport cost, without exceeding the vehicle capacity.
CVRP falls into the category of NP-hard problems, which are computationally difficult, and no algorithm is known to have solved them in polynomial time. Depending on their size, two main approaches are considered to handle this class of problems. For fairly small-sized instances, researchers usually use exact methods. Exact methods are guaranteed to find an optimal solution, but they have a high time complexity. Therefore, heuristics and particularly metaheuristics are applied to large-scale problems. These methods can obtain good results within shorter execution time. However, they do not guarantee the solution optimality. For a few decades, hybrid algorithms that combine different algorithmic concepts have been successfully applied to a wide range of optimization problems. A special class are matheuristics, where metaheuristics are hybridized with exact methods based on mathematical programming. Since the matheuristics have the advantages of both exact and heuristic methods, they are usually very effective at solving large complex optimization problems.
One of the recently developed matheuristics is Kernel Search (KS). Its strategy is to cleverly divide the solution space into smaller regions and explore them separately to find different feasible solutions. Because the most laborious part of the search relies on an optimization solver, KS is less demanding to implement than other heuristics. The matheuristic method presented in this paper applies the KS general framework to CVRP.
2. Materials and Methods
This part begins with a brief literature review. Then, the definition and mathematical formulation of the CVRP are presented. Finally, the details of the proposed matheuristics are provided.
2.1. Literature Review
CVRP was introduced by Dantzig and Ramser in 1959 [1] under the term of “the truck dispatching problem”, to formulate a real-world problem concerning the distribution of gasoline to service stations. Following this work, many studies have been carried out to solve CVRP, and they proposed various exact and heuristic (approximate) methods. General surveys can be found in [2]. The most successful exact methods are branch-cut-and-price algorithms [3,4,5]. As CVRP is NP-hard, most of the methods developed for this problem are heuristic, metaheuristic and hybrid methods. The state-of-the-art algorithms are the iterated local search with the set partitioning [6], the knowledge-guided local search [7], the fast iterated localized optimization [8], the slack induction by string removals [9], the partial optimization metaheuristic under special intensification conditions [10], and the hybrid adaptive iterated local search with diversification control [11]. The overview and classification of several matheuristic approaches proposed for routing problems are provided in [12].
KS was firstly published by Angelelli et al. [13] as “a heuristic framework for Mixed Integer Linear Programming (MILP) problems with binary variables”, and applied to solve the multi-dimensional knapsack problem [14]. Further applications included several different problems, e.g., the portfolio optimization [15], the capacitated facility location problem [16,17], the index tracking [18] and the Bi-objective index tracking [19], the capacitated p-median problem [20], the multivehicle inventory routing problem [21], or the generalized assignment problem [22]. As far as we know, no literature has reported the application of KS to CVRP so far.
2.2. The Problem Formulation
CVRP is defined on a complete directed graph , where is a set of nodes and is a set of arcs. The node 0 represents the depot for a fleet of p vehicles with the identical capacity Q, and the remaining n nodes represent customers, each with the demand . Every arc is associated with the positive travel cost . We assume that the cost matrix is symmetric, i.e., for all , and it satisfies the triangular inequality, for all . The aim is to determine a minimum-cost set of p routes in order to satisfy the demands of all customers under the following constraints [23]:
- (a)
- Each route starts and ends at the depot,
- (b)
- Each customer is visited exactly once,
- (c)
- The total demand of all customers on any route must not exceed the vehicle capacity.
An illustrative example of a feasible CVRP solution is shown in Figure 1, where 7 customers (their demands are displayed next to the nodes) are served by three vehicles of the capacity 50. The arc labels correspond to travel costs between the nodes, so the total transport cost is 30.

Figure 1.
A feasible CVRP solution.
The following mathematical model is taken from [24]. Two-index binary variables are used as decision variables equal to 1 if arc belongs to the optimal solution and 0 otherwise. Additional continuous variables are defined for all , which model the load in the vehicle after it visits customer i. The mixed linear programming model of the CVRP can be stated as:
- MILP model of the CVRP
The objective function (1), to be minimized, is the total transport cost. The constraints (2)–(5) are the degree constraints for the depot and customers, respectively. The constraints (6) impose both the capacity and connectivity of the feasible routes and also guarantee that sub-tours are avoided. The constraints given in (7) restrict the upper and lower bounds of . Lastly, the obligatory constraints (8) express the binary requirements on the variables.
2.3. Kernel Search
The KS algorithm relies on partitioning the set of decision variables into smaller sub-sets and then solving a restricted version of the problem on those sub-sets. Thanks to the reduction of the solution space, the obtained sub-problem is easier to solve using the MILP solver.
More specifically, KS algorithm runs through two phases: initialization and improvement (Algorithm 1).
In the initialization phase, heuristics searches for the initial feasible solution. The Linear Programming (LP) relaxation of the problem is solved in order to create the initial kernel K that is composed of all variables which take a value greater than zero in the LP optimal solution. Those variables are regarded as promising because they are the most likely to belong to the original MILP optimal solution. The remaining binary variables are sorted in descending order according to their reduced costs in the optimal solution to the LP relaxation: the lower the reduced cost a variable has, the more promising it is. Using this order, they are partitioned into a sequence of sub-sets , called buckets, where the number of buckets has to be predetermined depending on the problem instance. Then the initial feasible solution is found by solving the MILP sub-problem restricted to the initial kernel, denoted by MILP(K).
| Algorithm 1 The KS framework [21] |
Initialization phase
Improvement phase
|
The improvement phase is an iterative phase, where heuristics tries to improve the initial solution: at each iteration i, a new sub-problem MILP() is solved with two additional constraints. The first constraint is that the objective value should be better than or equal to the objective value of the best solution found so far, whereas the second constraint requires that the solution contains at least one variable from the bucket . In the event of this restricted MILP sub-problem being feasible, the current best solution is updated and all variables in bucket with a non-zero value in the solution of MILP() are added to the kernel. When all iterations have been performed, the current best-found solution is returned as the final solution.
The general scheme of the KS framework needs to be adapted to the specific problem. In the next subsection, we describe the modification of KS for CVRP.
Kernel Search for CVRP
KS for CVRP (KS-CVRP) is based on the MILP model (1)–(8). The kernel and sequence of buckets are built considering only variables for all . All the remaining variables and continuous variables are included in each restricted MILP problem.
As explained before, the goal of the initialization phase is to construct the initial kernel and buckets. The original KS algorithm exploits the optimal solution of the continuous (or LP) relaxation of the problem. However, this way is not quite suitable for CVRP. An illustrative example in Figure 2 shows the arcs associated with variables that take the positive value in the optimal solution of the LP relaxation of the problem with 40 nodes and two vehicles (problem instance No. 8). Evidently, LP relaxation does not provide enough information to obtain a feasible initial solution. Hence, we decided on a different approach, utilizing a solution produced by the parameterized Clarke–Wright Savings (CWS) method [25].
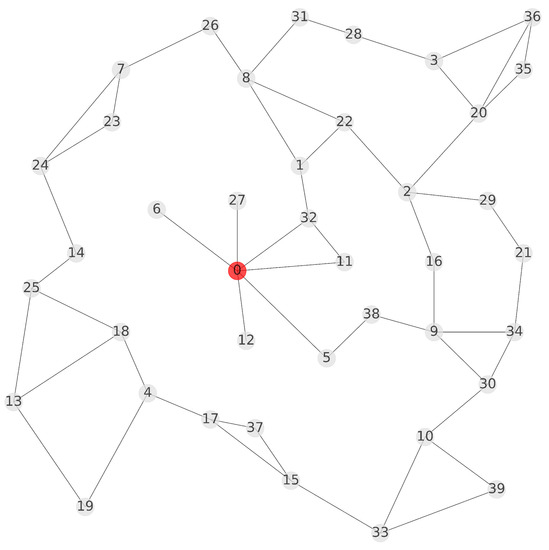
Figure 2.
An optimal solution of the LP relaxation of CVRP (the depot is red).
The CWS algorithm, developed by Clarke and Wright (1964) [26], is probably the most commonly used heuristics to solve CVRP because of its simplicity, speed, and easy implementation. It begins with a solution where every customer is served separately. Linking two routes, one with the arc and another with the arc , results in the cost of
The CWS algorithm iteratively merges pairs of routes maximizing cost savings subject to the merged route feasibility (respecting the capacity restriction). There are two versions of CWS: sequential and parallel. In the sequential version, routes are expanded one at a time, until they are no longer feasible, whereas in the parallel version, several routes are built at the same time. According to [2], the parallel version usually offers better results than the sequential one.
Due to its greedy nature, the CWS heuristics is not the most accurate. In order to achieve solutions with better qualities, the savings Formula (9) has been modified by adding new terms and parameters to it, as follows:
Here, is a route shape parameter [27,28] that controls the relative significance of the distance between two customers, is a weight parameter [29] that takes into account the asymmetry between two merged customers in terms of their distances from the depot, and is a customer demand parameter [25] that prefers customers with larger demands relative to the average demand , i.e., .
To adjust the specific values of these three independent parameters, the authors evaluated 8820 different parameter vectors () by varying , and , respectively, with a step size of 0.1. Later, a genetic algorithm [30], and empirically adjusted greedy heuristics [31] were used as the parameter tuning procedures, which required much shorter computing times. In our implementation, the Taguchi method [32] was applied to set the parameter values for the parameterized CWS algorithm.
The initialization phase of KS-CVRP works as follows: a parameterized CWS method is used to find the initial feasible solution of CVRP, and its value is saved as the initial upper bound . All the variables corresponding to the arcs between customers i and j that belong to the found CWS solution are taken to create the initial kernel K. Variables not present in the kernel are ranked according to a suitable criterion reflecting the variable likelihood to be included in the optimal integer solution. Subsequently, a sequence of buckets with these such ordered variables is created.
Buckets are iteratively explored during the improvement phase. At each iteration a modified MILP sub-problem is solved on the union of the current kernel and the processed bucket . Reminder: we are only seeking such a solution that is better than the current best one, and that uses at least one new item from the current bucket. Figure 3 illustrates the evolution of solution improvement of problem instance No. 8 with 40 nodes, two vehicles, and 11 buckets. Because the original KS (KS-O) did not find an initial feasible solution, the initial value is infinity (in the picture represented by value of 618). This method reached the first feasible solution only in the third iteration. KS-CVRP starts from the initial solution with a value of 464. While KS-O achieved the optimal solution (value of 458) after exploring all buckets, KS-CVRP was enough to explore the first bucket.

Figure 3.
Evolution of solution improvement by different methods.
Regarding the latter constraint, in case of large-sized instances, a time limit must be set to solve each restricted problem. Therefore, some of these problems may not be solved optimally within the specified time. To facilitate computing, we devised an iterative improvement procedure that utilizes the strategy of the Exact Iterative Method for CVRP (EIM-CVRP) [33]. This method is based on so-called k-opt moves, where k edges in the current solution are replaced by a set of k different feasible edges in such a way that a better solution is achieved. Given a feasible solution, EIM-CVRP repeatedly performs k-opt moves that reduce the cost of the current solution, until a solution is reached for which no exchange yields an improvement. The value of k is changed adaptively throughout the search with step as the procedure parameter. The Algorithm 2 summarizes the mentioned procedure adapted to the KS-CVRP in pseudocode.
| Algorithm 2 The iterative improvement procedure |
|
Of course, the procedure can be terminated after a predetermined computational time, or a certain number of iterations without any improvement. If , it means that the found solution improves the current best one and so and are updated. Additionally, the kernel content is extended by adding the newly discovered variables, which have a non-zero value in the solution .
When all buckets have been explored, the recent best-found solution and its value are returned as the final output.
3. Results
Computational experiments were performed on a computer with an Intel i7-5960X, 3.00 GHz processor and 32 GB of RAM. The matheuristics was implemented in Python 3.7, and all optimization problems were solved using the correspondent Python API of the commercial solver Gurobi version 9.1.1.
In our experiments, we used 21 problems taken from set P of benchmark problems from [34], which are publicly available at www.coin-or.org/SYMPHONY/branchandcut/VRP/data/ (accessed on 10 January 2022). The size of problems ranges between 16 and 101 nodes including the depot. All problem instances are very tight capacity constrained, since the proportions of the demand on the capacity (the tightness) are close to 1.0.
To test and analyze the proposed solution method, we have implemented the original KS framework (referred to as KS-O), and two variants of KS-CVRP: basic variant with an initial CWS solution, and its iterative variant with an iterative improvement procedure (denoted as KS-CVRP1 and KS-CVRP2, respectively).
Because the setting of the algorithm parameters influences the trade-off between computational effort and solution quality, numerous preparatory experiments were accomplished on benchmark instances to achieve desired control parameters of the aforementioned implementations of KS, but without a serious statistical evaluation. Tuning an appropriate number of created buckets was especially challenging, as it affects the computational time required for solving the restricted MILP problem. The larger the value is, the greater the number of sub-problems of a smaller size has to be solved. It means that the algorithm works faster, but at the cost of a lower quality result. The experiments indicated that the value of has to be accommodated to each problem instance individually.
Regarding the criterion used to sort the variables in the bucket list, we have considered three different approaches: a non-decreasing order of (Sorting A), a non-increasing order of (Sorting B), and a random order (Sorting C), respectively. The preliminary experiments showed that the best performing criterion was Sorting B.
For each restricted MILP problem, the maximum running time assigned to Gurobi optimizer was set to 1800 s, and the loop of the iterative improvement procedure was stopped after three iterations without any improvement. Below, only the main results of the experiments performed are presented and commented on.
The results reported in Table 1 compare the performance of three variants of KS in terms of computational time. Such analysis could only be done for the small sized instances (), as KS-O requires huge computational times to solve large problems. For each instance, the number of nodes (n) and vehicles (p) are given, as well as the tightness (), and the optimal solution value () known from literature. For all the tested variants, we have assumed the same number of buckets () adapted to the size of the problem instance. The next columns provide the objective values obtained by particular KS variant (), and the computational time in seconds (). This result seems to show that the variant KS-CVRP2 dominates over the average variant KS-CVRP1 which, in turn, outperforms KS-O.

Table 1.
Comparison of computational times.
Table 2 shows a summary of the results obtained by KS-CVRP2, where the following quantities are shown: the instance parameters (n, p, ), the optimal solution value (), the parameters of the CWS algorithm (, , ), the initial solution value (), the number of buckets (), the parameter of the iterative improvement procedure (), the objective value produced by KS-CVRP2 (), the average percentage gap () computed as , and the computational time in seconds ().

Table 2.
Results for KS-CVRP2.
We can observe that the proposed matheuristics KS-CVRP2 achieves very good results in an acceptable amount of time. It was able to solve to optimality all 10 small-sized instances (), and for medium-size instances (), the gaps are within of the optimal solution. The computation time does not exceed 1 h.
Table 3 compares the KS-CVRP2 and the EIM-CVRP in terms of the time consumption to reach the optimal solution. The EIM-CVRP ran under the same conditions as KS-CVRP2, i.e., with a time limit of 1800 s and a stopping criterion of three iterations without any improvement. Additionally, the initial solution and procedure parameter for particular test instances were identical for both methods. As expected, the KS-CVRP2 is quicker than EIM-CVRP. It is because, unlike the KS-CVRP2, the EIM-CVRP explores the whole solution space at each iteration. Figure 4 shows an example of the solution improvement over time by both methods for test instance No. 8.

Table 3.
Comparison of the KS-CVRP2 and the EIM-CVRP.
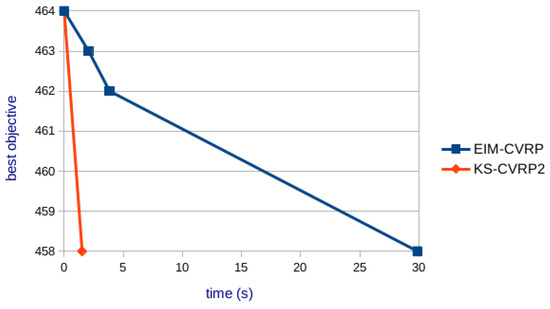
Figure 4.
Time evolution of the solution by different methods.
4. Conclusions
In this paper, we presented the implementation of the matheuristics kernel search to solve the capacitated vehicle routing problem called KS-CVRP. Compared to the original KS framework, a different method has been proposed to construct the kernel and buckets, as well as to carry out the improvement phase so that the time available to find good solutions is used more efficiently. The computational experiments conducted on benchmark instances have shown that KS-CVRP is able to find high quality solutions in reasonable computation times.
The application of the algorithm to other routing problems will be the topic of our future research.
Funding
This research was supported by the Slovak Research and Development Agency under the project APVV-19-0441 “Allocation of limited resources to public service systems with conflicting quality criteria” and by the Scientific Grant Agency of the Ministry of Education of the Slovak Republic and the Slovak Academy of Sciences under the projects VEGA 1/0776/20 “Vehicle routing and scheduling in uncertain conditions” and VEGA 1/0216/21 “Designing of emergency systems with conflicting criteria using tools of artificial intelligence”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used during the current study are publicly available at www.coin-or.org/SYMPHONY/branchandcut/VRP/data/.
Conflicts of Interest
The author declares no conflict of interest.
References
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods and Applications, 2nd ed.; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Pecin, D.; Pessoa, A.; Poggi, M.; Uchoa, E. Improved branch-cut-and-price for capacitated vehicle routing. In Integer Programming and Combinatorial Optimization; Lee, J., Vygen, J., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 393–403. [Google Scholar]
- Pecin, D.; Pessoa, A.; Poggi, M.; Uchoa, E. Improved branch-cut-and-price for capacitated vehicle routing. Math. Program. Comput. 2017, 9, 61–100. [Google Scholar] [CrossRef]
- Pessoa, A.; Sadykov, R.; Uchoa, E.; Vanderbeck, F. A generic exact solver for vehicle routing and related problems. Math. Program. 2017, 183, 483–523. [Google Scholar] [CrossRef]
- Subramanian, A.; Uchoa, E.; Ochi, L.S. A hybrid algorithm for a class of vehicle routing problems. Comput. Oper. Res. 2013, 40, 2519–2531. [Google Scholar] [CrossRef]
- Arnold, F.; Sórensen, K. Knowledge-guided local search for the vehicle routing problem. Comput. Oper. Res. 2019, 105, 32–46. [Google Scholar] [CrossRef]
- Accorsi, L.; Vigo, D. A fast and scalable heuristic for the solution of large-scale capacitated vehicle routing problems. Transp. Sci. 2020, 55, 832–856. [Google Scholar] [CrossRef]
- Christiaens, J.; Vanden Berghe, G. Slack induction by string removals for vehicle routing problems. Transp. Sci. 2020, 54, 417–433. [Google Scholar] [CrossRef]
- Queiroga, E.; Sadykov, R.; Uchoa, E. A POPMUSIC matheuristic for the capacitated vehicle routing problem. Comput. Oper. Res. 2021, 13, 105475. [Google Scholar] [CrossRef]
- Máximo, V.R.; Nascimento, M.C.V. A hybrid adaptive iterated local search with diversi-fication control to the capacitated vehicle routing problem. Eur. J. Oper. 2021, 294, 1108–1119. [Google Scholar] [CrossRef]
- Archetti, C.; Speranza, M.G. A survey on matheuristics for routing problems. EURO J. Comput. Optim. 2014, 2, 223–246. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Speranza, M.G. Kernel Search: A Heuristic Framework for MILP Problems with Binary Variables; Technical Report of the Department of Electronics for Automation; University of Brescia: Brescia, Italy, 2007. [Google Scholar]
- Angelelli, E.; Mansini, R.; Speranza, M.G. Kernel search: A general heuristic for the multi-dimensional knapsack problem. Comput. Oper. Res. 2010, 37, 2017–2026. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Speranza, M.G. Kernel search: A new heuristic framework for portfolio selection. Comput. Optim. Appl. 2012, 51, 345–361. [Google Scholar] [CrossRef]
- Guastaroba, G.; Speranza, M.G. Kernel search for the capacitated facility location problem. J. Heuristics 2012, 18, 877–917. [Google Scholar] [CrossRef]
- Filippi, C.; Guastaroba, G.; Huerta-Muñoz, D.L.; Speranza, M.G. A kernel search heuristic for a fair facility location problem. Comput. Oper. Res. 2021, 132, 105292. [Google Scholar]
- Guastaroba, G.; Speranza, M.G. Kernel search: An application to the index tracking problem. Eur. J. Oper. Res. 2012, 217, 54–68. [Google Scholar] [CrossRef]
- Filippi, C.; Guastaroba, G.; Speranza, M.G. A heuristic framework for the bi-objective enhanced index tracking problem. Omega 2016, 65, 122–137. [Google Scholar] [CrossRef]
- Jánošíková, Ľ. Kernel search for the capacitated p-median problem. In Proceedings of the International Scientific Conference Quantitative Methods in Economics: Multiple Criteria Decision Making XIX, Trenčianske Teplice, Slovakia, 23–25 May 2018; pp. 158–164. [Google Scholar]
- Archetti, C.; Guastaroba, G.; Huerta-Muñoz, D.L.; Speranza, M.G. A kernel search heuristic for the multivehicle inventory routing problem. Int. Trans. Oper. Res. 2021, 28, 2984–3013. [Google Scholar] [CrossRef]
- Maniezzo, V.; Boschetti, M.A.; Stützle, T. Kernel Search. In Matheuristics: Algorithms and Implementations; Springer: Cham, Switzerland, 2021; pp. 189–197. [Google Scholar]
- Laporte, G. What you should know about the vehicle routing problem. Nav. Res. Logist. 2007, 54, 811–819. [Google Scholar] [CrossRef]
- Ordóñez, F.; Sungur, I.; Dessouky, M. A Priori Performance Measures for Arc-Based Formulations of Vehicle Routing Problem. Transp. Res. Rec. 2006, 2032, 53–62. [Google Scholar] [CrossRef]
- Altınel, I.K.; Öncan, T. A new enhancement of the Clarke and Wright savings heuristic for the capacitated vehicle routing problem. J. Oper. Res. Soc. 2005, 56, 954–961. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Gaskell, T.J. Bases for vehicle fleet scheduling. Oper. Res. Q. 1967, 18, 281–295. [Google Scholar] [CrossRef]
- Yellow, P. A computational modification to the savings method of vehicle scheduling. Oper. Res. Q. 1970, 21, 281–283. [Google Scholar] [CrossRef]
- Paessens, H. The savings algorithm for the vehicle routing problem. Eur. J. Oper. Res. 1988, 34, 336–344. [Google Scholar] [CrossRef]
- Battarra, M.; Golden, B.; Vigo, D. Tuning a parametric Clarke-Wright heuristic via a genetic algorithm. J. Oper. Res. Soc. 2008, 59, 1568–1572. [Google Scholar] [CrossRef]
- Corominas, A.; Garcia-Villoria, A.; Pastor, R. Fine-tuning a parametric Clarke and Wright heuristic by means of EAGH (empirically adjusted greedy heuristics). J. Oper. Res. Soc. 2010, 61, 1309–1314. [Google Scholar] [CrossRef]
- Byrne, D.; Taguchi, G. The Taguchi Approach to Parameter Design. Qual. Prog. 1987, 20, 19–26. [Google Scholar]
- Borčinová, Z.; Peško, Š. New exact iterative method for the capacitated vehicle routing problem. Commun. Sci. Lett. Univ. Žilina 2016, 18, 19–21. [Google Scholar]
- Augerat, P.; Belenguer, J.; Benavent, E.; Corbern, A.; Naddef, D.; Rinaldi, G. Computational Results with a Branch and Cut Code for the Capacitated Vehicle Routing Problem; Research Report, 949-M; Université Joseph Fourier: Grenoble, France, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).