Buckling of Composite Structures with Delaminations—Laminates and Functionally Graded Materials
Abstract
1. Introduction
- For predicting the initiation of delamination failure, it is possible to apply analytical or numerical methods (finite element modeling); see, e.g., Ref. [11] combined with the formulation of appropriate strength criteria presented in Appendix A—see Refs. [12,13];
- Contact problems: during the loading or unloading process, the initially opened region of delamination can both grow and/or shrink; however, in the latter case, the strict and concise contact (even frictionless) analysis is required—see, for instance, 1D analysis, 2D analysis and 3D analysis Refs. [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30];
- Different problems in conjunction with the impact/fatigue delamination growth (laminates and FGMs) are also investigated. Several authors use the finite element method and cohesive elements approach to describe various modes of impact/fatigue loading [31,32]. Modeling of impact/fatigue problems and damage propagation in delaminated composite structures are also discussed in Refs. [33,34,35,36,37,38,39,40,41].
- To demonstrate and discuss the formulation of the buckling of laminated and functionally graded structures with 1D and 2D delaminations;
- To compare the results for composite structures made of laminates or functionally graded materials.
2. Kinematic Relations
- ‒
- One-dimensional axisymmetric spherical shells, R1 = R2 = R, where the coordinate variable is eliminated;
- ‒
- Two-dimensional flat rectangular plates, Cartesian rectangular coordinates—R1 , R2 .
3. A Brief Description of Contact Problems Associated with Local Buckling
4. Variational Formulations of Contact Problems with Local Buckling
- ‒
- Hu–Washizu
- ‒
- Hellinger–Reissner
- ‒
- Lagrangewhere σ is the stress tensor, e is the strain tensor and u denotes the components of the displacements. The relation between stresses and strains is described by the linear elastic relation. For laminated composites, the traditional relation takes the classical form presented, e.g., by Jones [60]. For FGMs, the physical relation takes the following form:where:
- ‒
- the Hu–Washizu approach
- ‒
- the Hellinger–Reissner approach
- ‒
- the Lagrange approachwhere λ denotes the Lagrange multiplier.
5. Computational Models
- ‒
- The application of the large displacement (or deformation) option to determine the bifurcation point;
- ‒
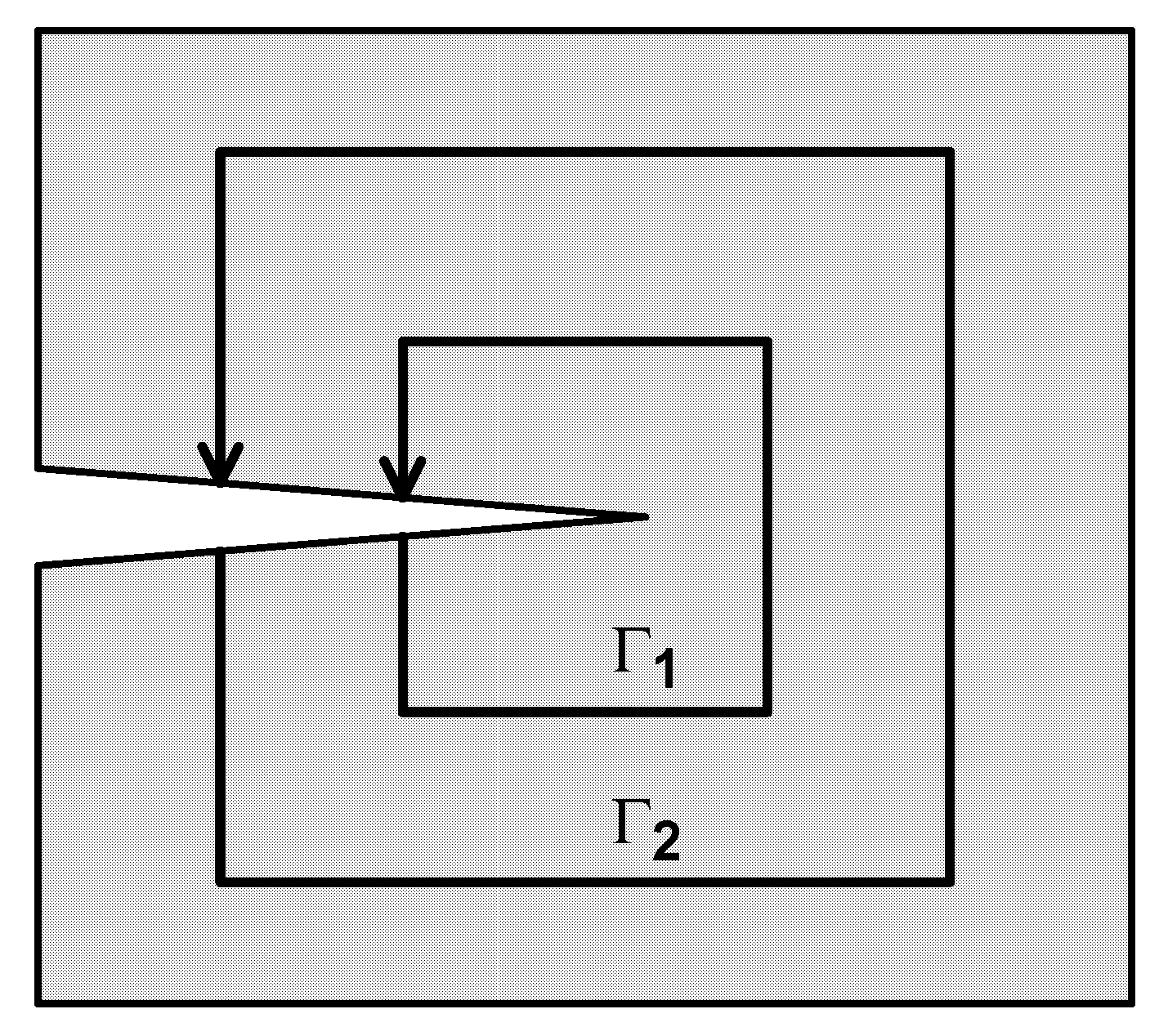
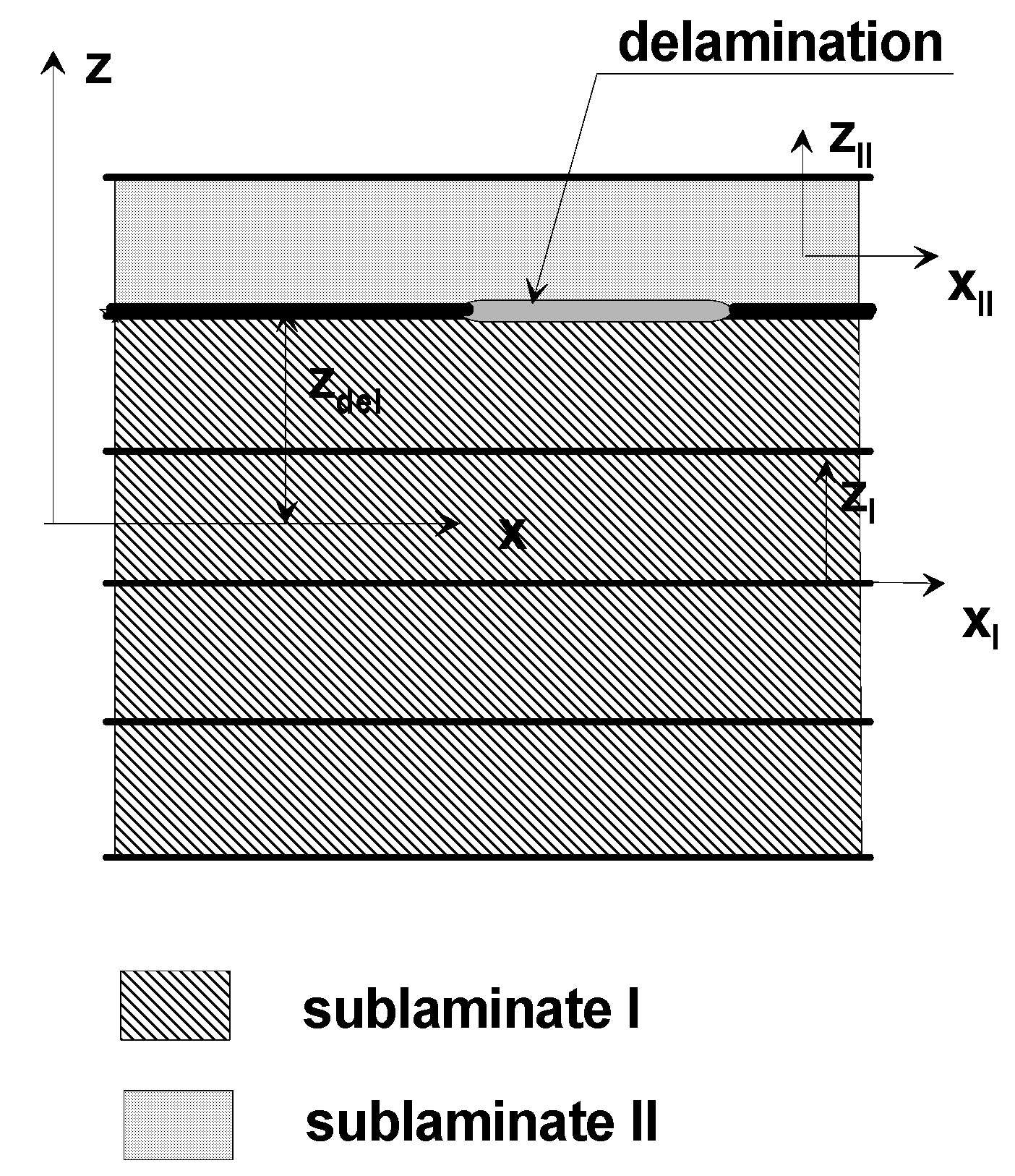
- Structure modeling using 2D or 3D elements is necessary for the analysis of the sub-laminate buckling state, because the classic FEM packages contain only shell elements based on the 3D or first-order transverse shear theory, and as stated previously, in delamination problems, the theories of higher-order shells should be used;
- ‒
- The area where delamination occurs and its surroundings should be discretized using 2D or 3D elements with a triangular base to better approximate, especially at the edge of delamination, the values of the G energy release factors;
- ‒
- Along the thickness of FGMs, the division should include 15 to 20 FE since the material properties vary significantly along the coordinate z—see Equation (10).
6. Three Parametrical Shell Theories
6.1. The Flat Rectangular Plate with An Infinite Width
6.2. Axi-Symmetric Spherical Shells under External Pressure
7. Numerical Examples for Thicker Structures; 2-D Higher-Order or 3-D Approaches
7.1. Axi-Symmetric Shells under External Pressure
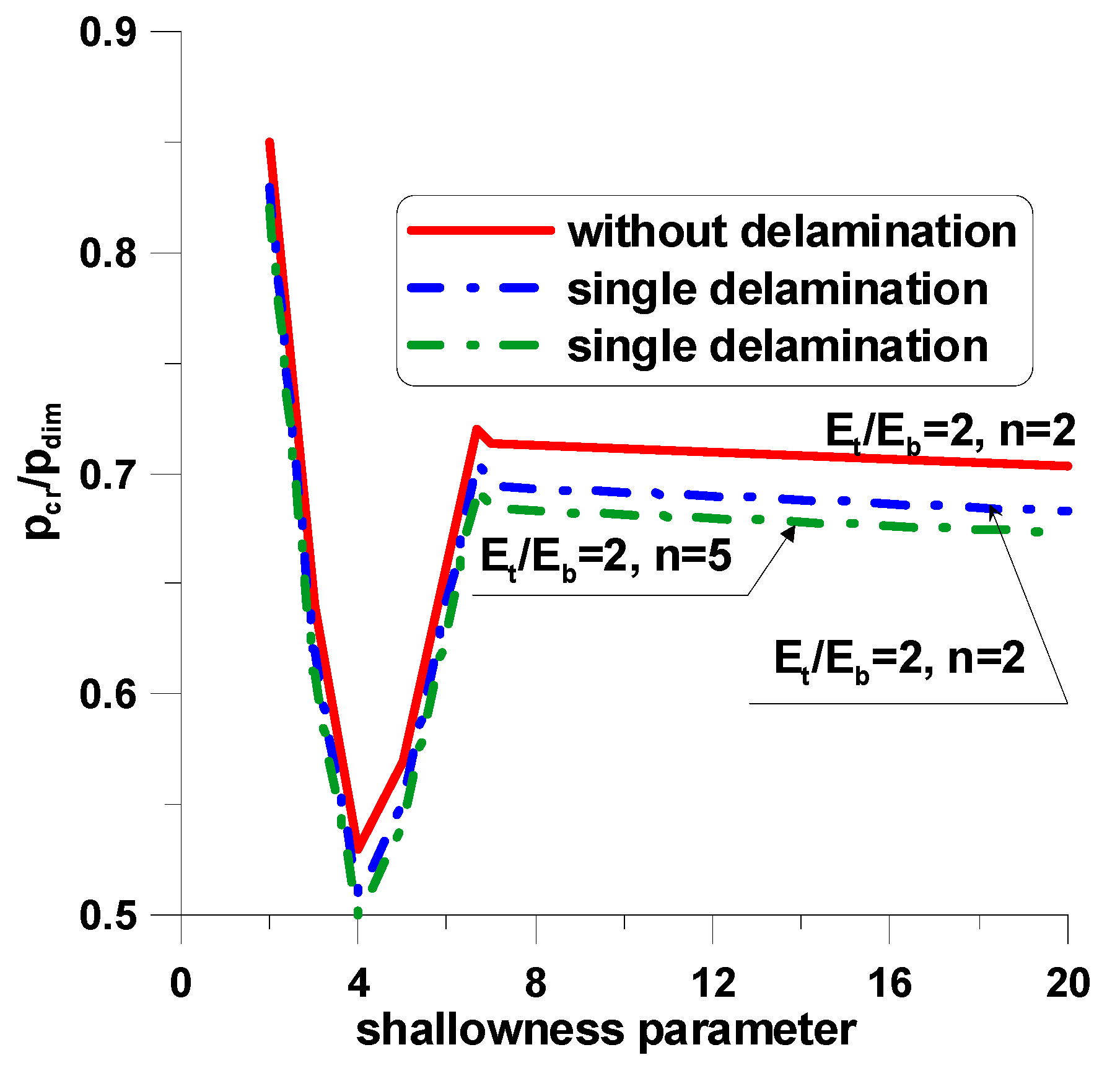
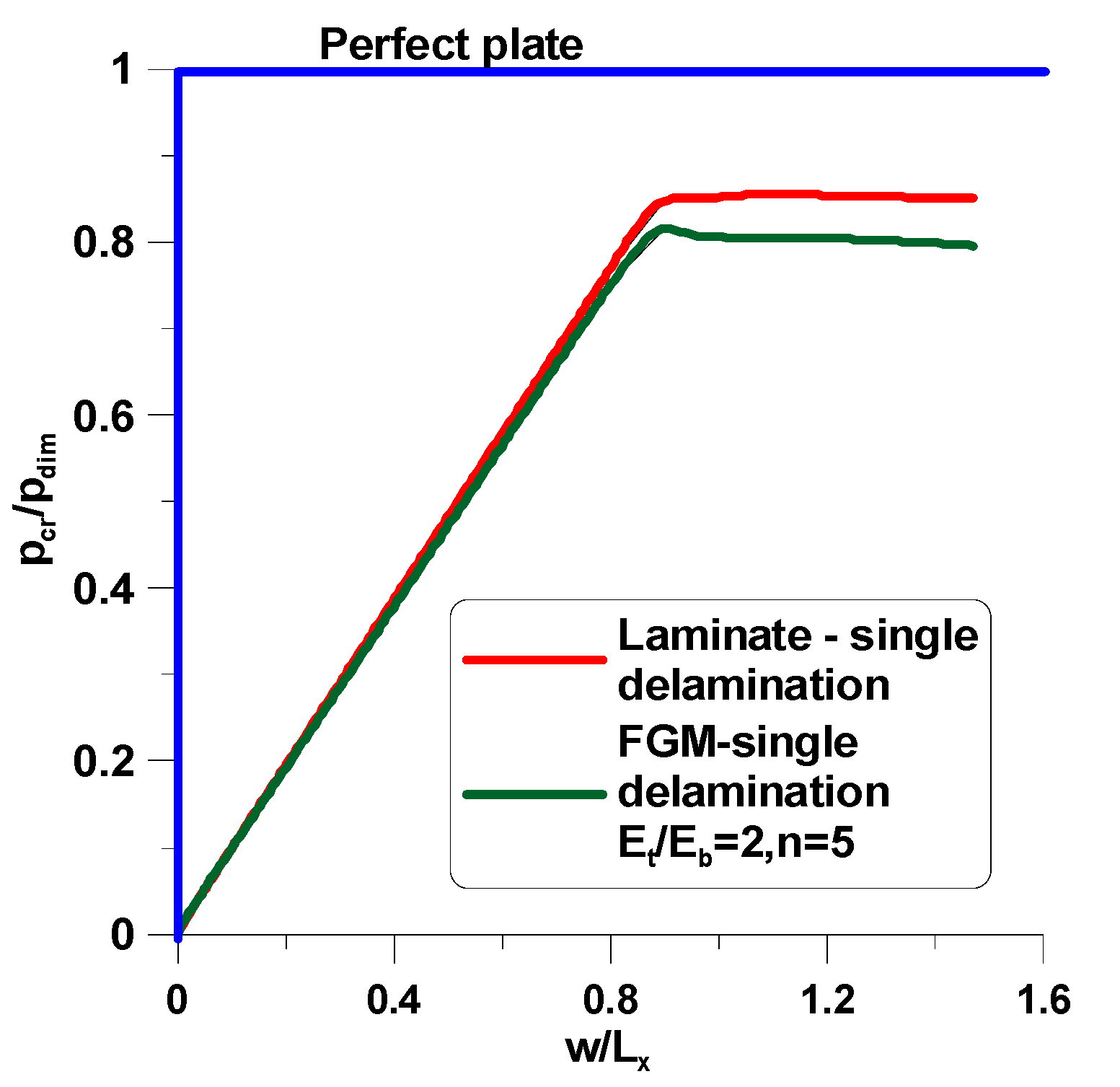
7.2. Compressed Rectangular Plates with a Single Delamination
8. Concluding Remarks and Further Recommendations
- A 2D higher-order method of analysis based on the stretching of the normal to the shell mid-surface is presented herein for obtaining the local buckling loads of structures with unilateral constraints of rectangular plates and axisymmetric spherical shells.
- Applying the general theory of elasticity with tensor analysis, six field equations, which consist of six displacement relations, have been derived and written.
- The energy functionals (variational inequalities) in terms of the physical components of the displacements, Hu–Washizu, Hellinger–Reissner, and Lagrange strain energy J, have been derived.
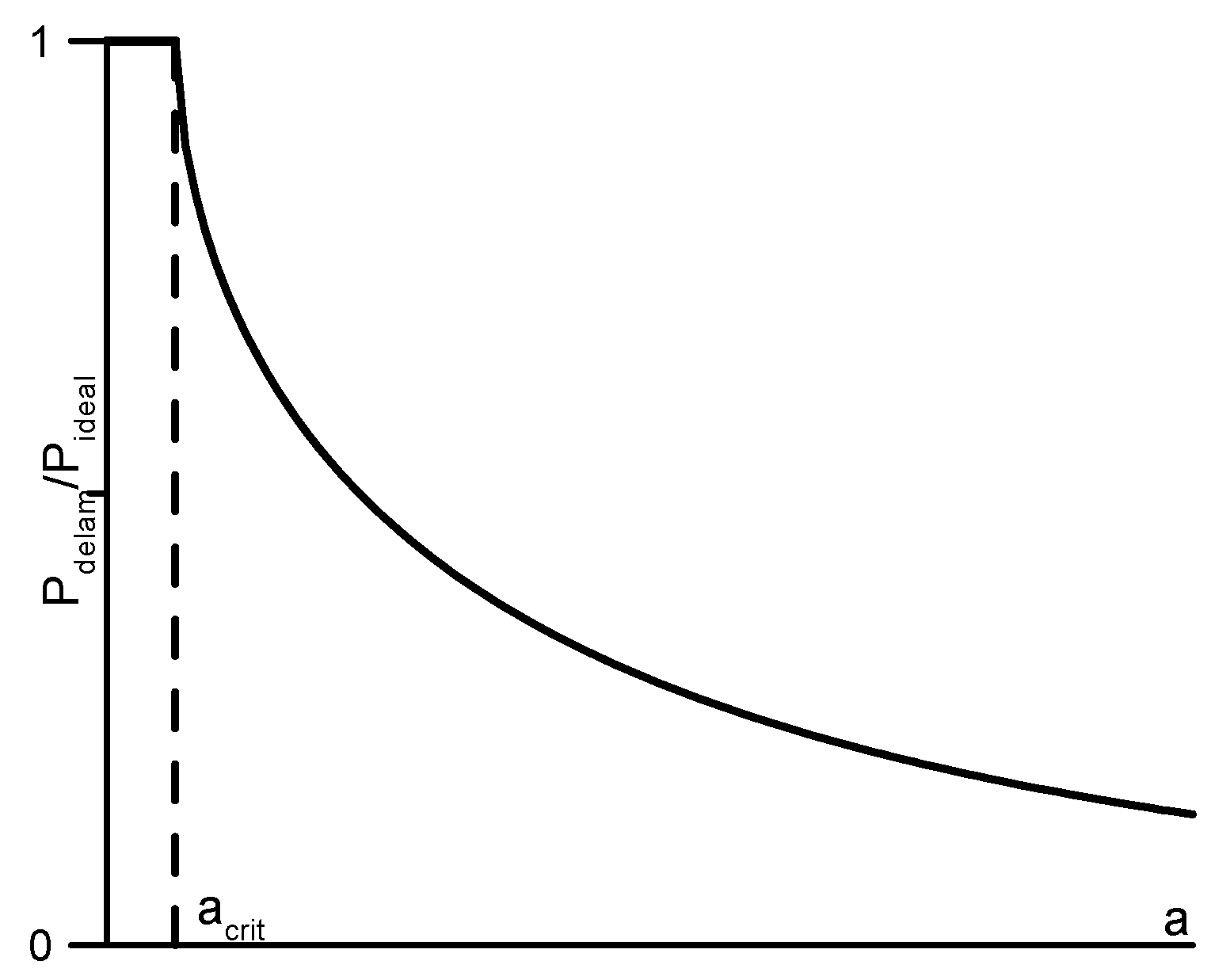
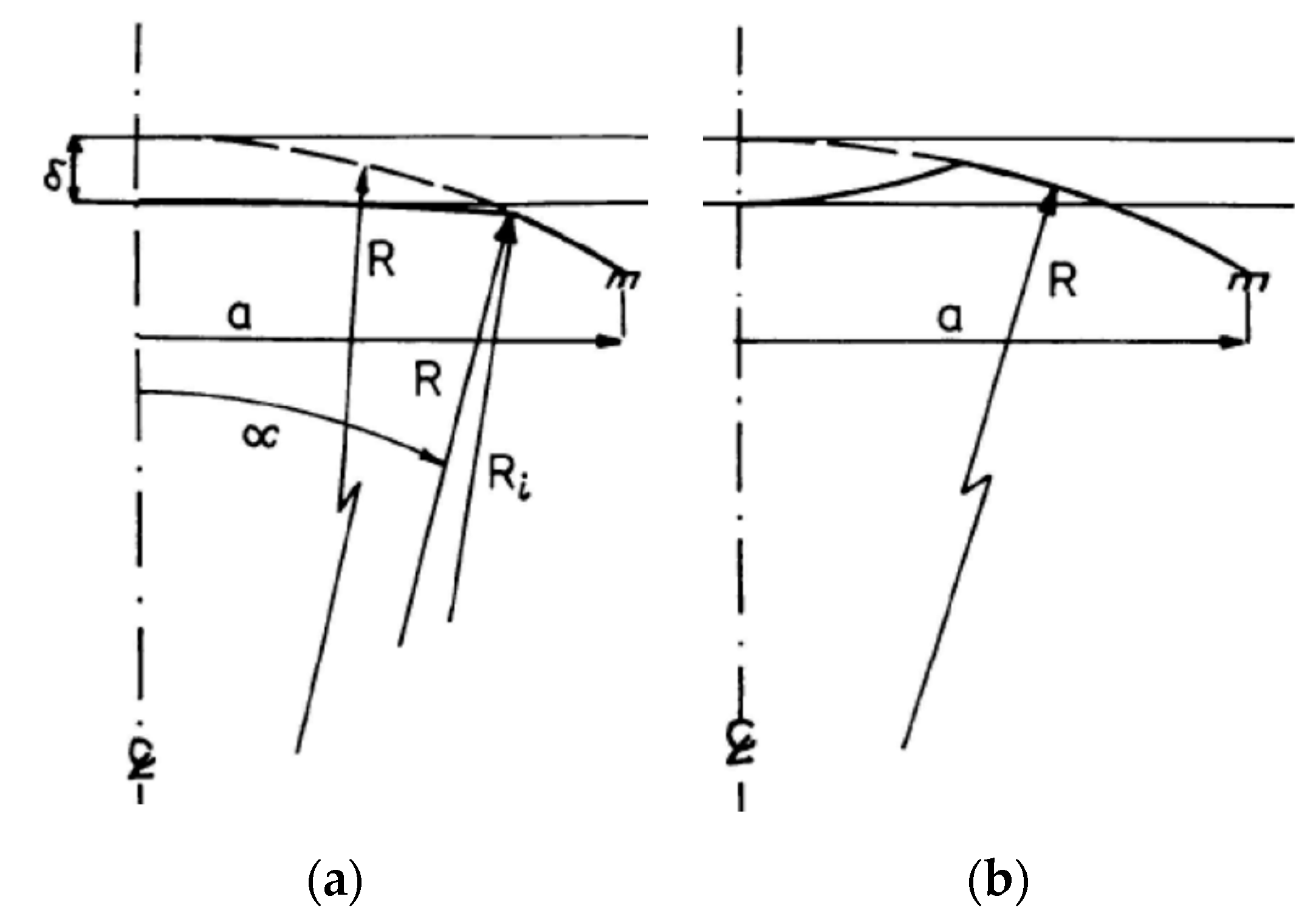
- Delaminations are represented in the form of geometrical imperfections added to normal displacements. They are characterized by a set of geometrical parameters. The parameters are derived as the lower bound of functions of critical load and the parameter of delaminations.
- The numerical solutions can be obtained with the use of analytical solutions (the Rayleigh–Ritz method) or FE analysis.
- The analysis demonstrates that buckling loads with unilateral constraints are reduced for structures made of FGM materials in comparison to laminated structures due to the reduction of bending stiffnesses.
- With increasing computational capabilities, analysts are gradually becoming more able to deal with three-dimensional problems made of unsymmetrical laminated and FG materials.
- The presented analysis can be extended for investigations of plated/shell structures with multiple delaminations.
- The present analysis of buckling characteristics of structures subjected to unilateral constraints shows the necessity of further studies to define the safe lower bounds in the design of laminated and FGM-composed constructions.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin Letters | |
| A | the length of the delamination at the ξ1 direction |
| A | the surface area of the delamination |
| Aγ | the Lame coefficient; γ = 1, 2 |
| B | the length of the delamination at the ξ2 direction |
| D | the length between the edges of spherical shells—Figure 11 and Figure 13 |
| [e] | the matrix representation of the strain components εij |
| E | the Young modulus of FGMs |
| F | the Airy function |
| GI, GII, GIII | the strain energy release rates—see Figure A1 |
| H | the thickness of the structure |
| J | the functional characterizing composite structures as in Equation (6) |
| Jen | the functional characterizing the strain energy |
| Jbbc | the functional characterizing the bilateral boundary conditions |
| Jubc | the functional characterizing the unilateral boundary conditions |
| KI, KII, KIII | the stress intensity factors |
| L | the length of the plate |
| p | pressure |
| q | parameters describing the shapes of geometrical imperfections—see Figure 14 |
| [Q] | the matrix representation of the stiffness matrix |
| RJ | the Rice integral |
| Rγ | the radius of curvature; γ = 1, 2 |
| R | the radius of the spherical shell |
| RJ | the Rice integral |
| RBdel | the parameter of the delamination growrh |
| the 3D displacement components; i = 1, 2, 3 | |
| ui(ξ1, ξ2) | the 2D mid-surface displacement component; i = 1, 2, 3 |
| [u] | the matrix representation of the 2D displacement components ui |
| Vk | the space occupied by the individual k-th layer (or sublaminate) |
| w(ξ1, ξ2) | the 2D normal displacement; it is identical to u3 (ξ1, ξ2) |
| w*(ξ1, ξ2) | the 2D normal displacement of the imperfection (delamination) |
| Greek Letters | |
| ρ | the shallowness parameter (25) |
| δ | the amplitude of the imperfection |
| ξγ | the mid-surface shell curvilinear coordinate; γ = 1, 2 |
| ξ3 | the normal coordinate to the mid-surface; it is identical to z |
| φγ | the rotation of the normal to the mid-surface about the ξγ axe; γ = 1, 2 |
| χi | the parameter characterizing the thickness stretching; i = 1, 2, 3 |
| εij | the 3D strain component; i,j = 1, 2, 3 |
| σij | the 3D stress component; i,j = 1, 2, 3 |
| [σ] | the matrix representation of the stress components σij |
| [σ3] | the matrix representation of the transverse shear stress components σi3; i = 1, 2, 3 |
| ν | the Poisson ratio of FGMs |
| ν12, ν21 | the Poisson ratio of laminates |
| Subscripts | |
| i, j = 1, 2, 3 | |
| γ = 1, 2 | |
| delam | the values of delaminated structures |
| ideal | the values of structures without delamination |
| crit | the critical length of the delamination leading to the decrease of buckling pressures |
| en | the strain energy |
| bbc | the bilateral (equality) boundary conditions |
| ubc | the unilateral (inequality) boundary conditions |
| b | the bottom surface of FGMs |
| t | the top surface of FGFs |
| find | the function of the FGMs distribution (11) |
| n | the power law index |
| dim | dimensionless |
| quasi | the quasiisotropy |
| Superscripts | |
| nonl | means nonlinear terms |
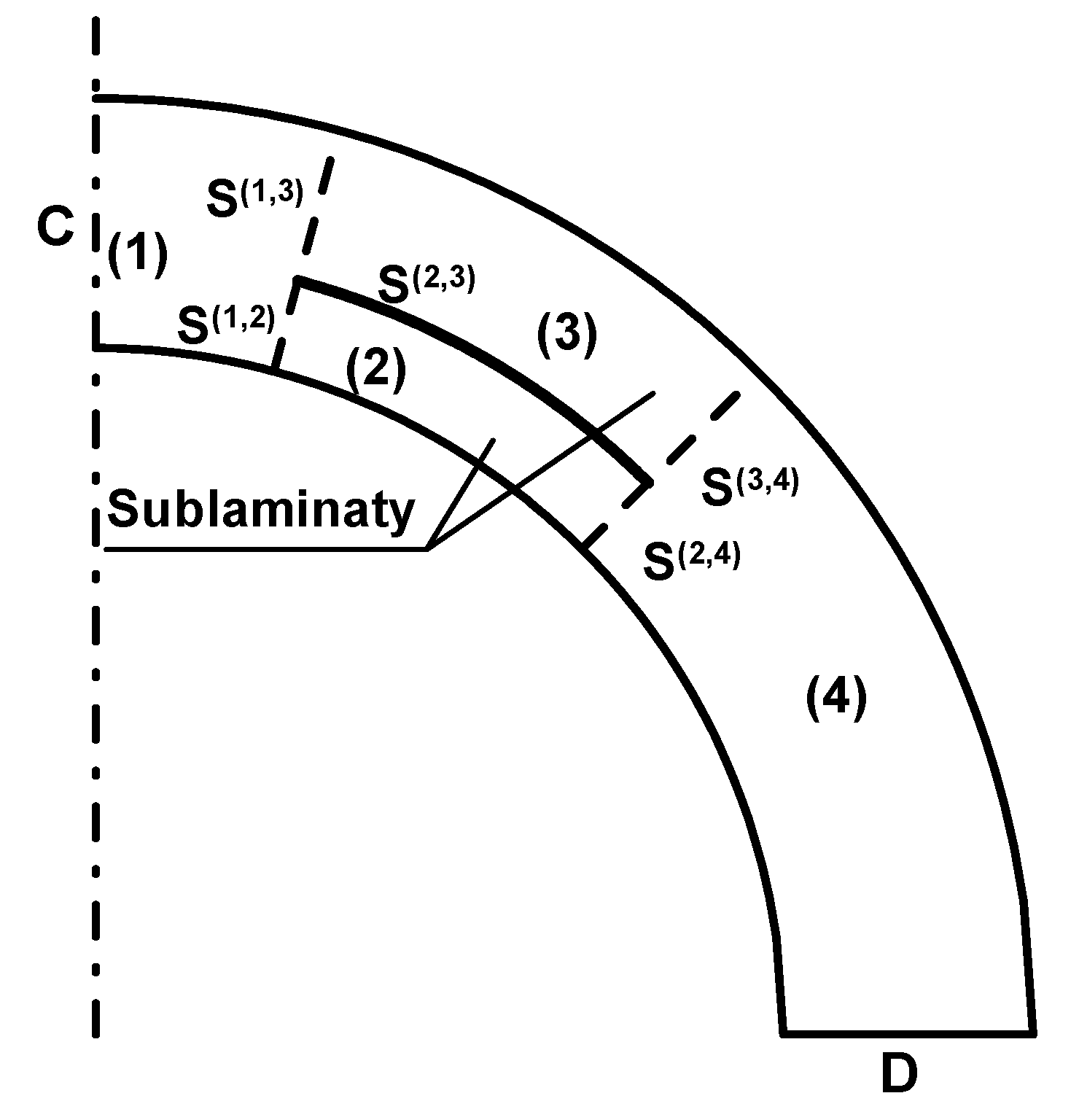
| (k) | the number of sublaminates as in Figure (6)—a single delamination; k = 1, 2, 3, 4 |
| Tr | the transpose matrix |
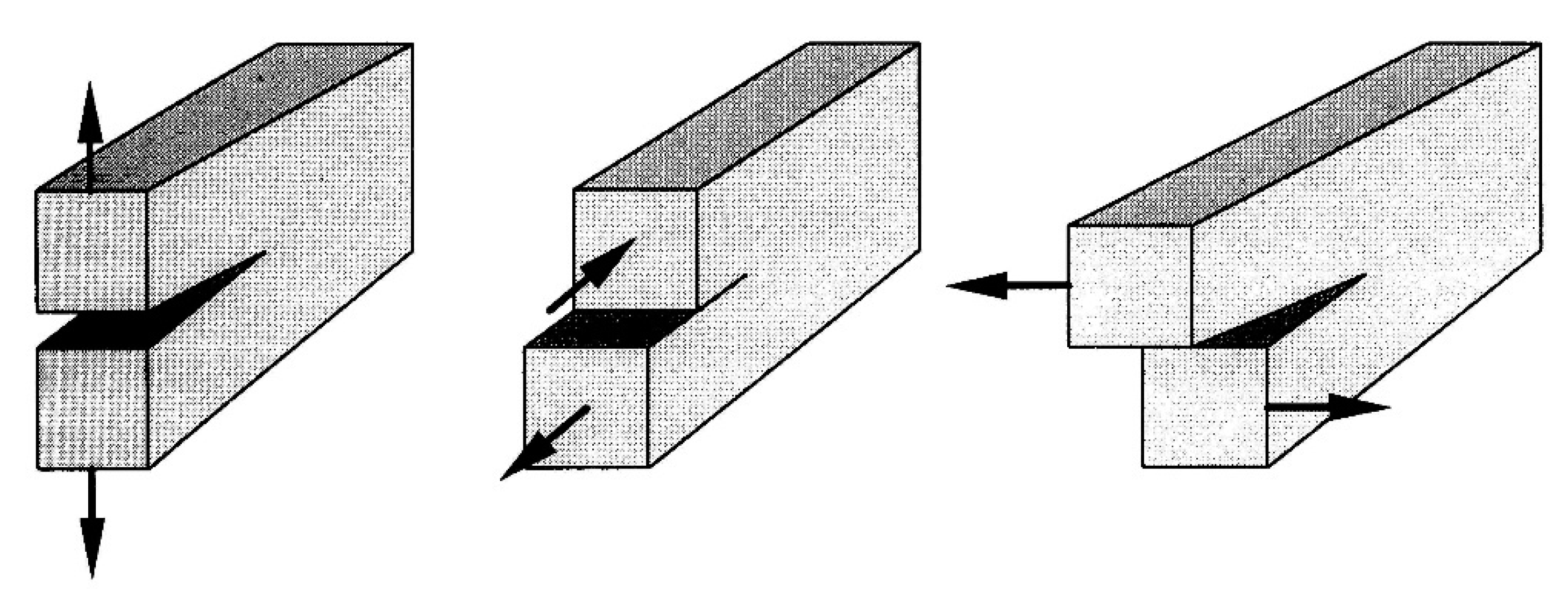
Appendix A. Mean Stresses and Mechanics of Fracture Criteria
Appendix A.1. Mean Stress Criterion
Appendix A.2. Mechanics of Fracture
| Contour I | Contour II | Analytical [76] |
|---|---|---|
| 0.14374 × 10−4 | 0.15189 × 10−4 | 0.15122 × 10−4 |
Appendix A.3. Criterion of Failure and Analysis of the Growth of Delamination
- Determination of the displacement and stress field at each point on the boundaries of individual layers in the laminate.
- Assumption of the existence of an inter-layer gap with a given surface area A (length a).
- Determination of the coefficients of energy release GI, GII, GIII.
- Calculation of the value of the failure index for the RBdel delamination—Formula (A10):
- if RBdel < 1 then delamination is not possible;
- if RBdel = 1, we observe the appearance of delamination at a given point;
- if RBdel > 1, the development of delamination takes place, and it is necessary to redefine the field of displacements and stresses taking into account the increase in delamination.
References
- Bhavar, V.; Kattire, P.; Thakare, S.; Singh, R.K. A review on functionally gradient materials (FGMs) and their applications. IOP Conf Ser Mater. Sci. Eng. 2017, 229, 012021. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rajabi, M.; Ghadiri, M. Functionally graded materials (FGMs): A review of classifications, fabrication methods and their applications. Process. Appl. Ceram. 2021, 15, 319–343. [Google Scholar] [CrossRef]
- Verma, R.K.; Parnagiha, D.; Chopkar, M. A review on fabrication and characteristics of functionally graded aluminum composites fabricated by centrifugal casting method. SN Appl. Sci. 2021, 3, 1–29. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing, and Applications; Springer: Manhattan, NY, USA, 1999. [Google Scholar]
- MitevaMiteva, A.; Bouzekova-Penkova, A. Module for wireless communication in aerospace vehicles. Aerospece Res. Bulg. 2021, 33, 195–209. [Google Scholar] [CrossRef]
- Zhou, W.; Shing, A. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2+Ni) functionally graded bonds. Compos. Part B 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, B. Load distribution in threads of porous metal-ceramic functionally graded composite joints subjected to thermomechanical loading. Compos. Struct. 2015, 134, 680–688. [Google Scholar] [CrossRef]
- Vinh, P.; Tounsi, A. Free vibration analysis of functionally graded doubly curved nanoshells using nonlocal first order shear deformation theory with variable nonlocal parameters. Thin-Walled Struct. 2022, 174, 109084. [Google Scholar] [CrossRef]
- Vinh, P.P.; Chinh, N.V.; Tounsi, A. Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first order shear deformation theory and FEM. Eur. J Mech./A Solids 2022, 96, 104743. [Google Scholar] [CrossRef]
- Muc, A. Non-local approach to free vibrations and buckling problems for cylindrical nano-structures. Comp. Struct. 2020, 250, 112541. [Google Scholar] [CrossRef]
- Składanowska, K.; Sanetra, I.; Muc, A. Analysis of fatigue behaviour of composite structures with circular internal delaminations. Compos. Theory Pract. 2017, 17, 121–125. [Google Scholar]
- Muc, A.; Kędziora, P.; Krawiec, Z. Damage analysis and monitoring of composite materials and structures under cyclic loads. Proc. Eng. 2011, 10, 1315–1320. [Google Scholar] [CrossRef]
- dell’Isola, F.; Della Corte, A.; Battista, A. Generalized Contact Actions. In Encyclopedia of Continuum Mechanics; Altenbach, H., Öchsner, A., Eds.; Springer: Heidelberg, Germany, 2018. [Google Scholar]
- Muc, A. Axisymmetric contact problems for composite pressure vessels. J. Compos. Sci. 2022, 6, 143. [Google Scholar] [CrossRef]
- Karihaloo, B.L.; Stang, H. Buckling-driven delamination growth in composite laminates: Guidelines for assessing the threat posed by interlaminar matrix delamination. Compos. Part B 2008, 39, 386–395. [Google Scholar] [CrossRef]
- Lee, S.Y.; Park, D.Y. Buckling analysis of laminated composite plates containing delaminations using the enhanced assumed strain solid element. Int. J. Solids Struct. 2007, 44, 8006–8027. [Google Scholar] [CrossRef]
- Muc, A. Interlaminar failure & buckling of doubly curved shells. Mech. Compos. Mater. 1995, 31, 330–340. [Google Scholar]
- Ovesy, H.R.; Kharazi, M. Compressional stability behaviour of composite plates with through-the-width and embedded delaminations by using first order shear deformation theory. Comput. Struct. 2011, 89, 1829–1839. [Google Scholar] [CrossRef]
- Pekbey, Y.; Sayman, O. A numerical and experimental investigation of critical buckling load of rectangular laminated composite plates with strip delamination. J. Reinf. Plast. Compos. 2006, 25, 685–697. [Google Scholar] [CrossRef]
- Ricci, A.; Gigliotti, M. A novel numerical delamination growth initiation approach for the preliminary design of damage tolerant composite structures. J. Compos. Mater. 2007, 41, 1939–1960. [Google Scholar] [CrossRef]
- Ricci, A. (Ed.) Damage Growth in Aerospace Composites; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Sekine, H.; Hu, N.; Kouchakzadeh, M.A. Buckling analysis of elliptically delaminated composite laminates with consideration of partial closure of delimitation. J. Compos. Mater. 2000, 34, 551–574. [Google Scholar] [CrossRef]
- Davila, C.G.; Johnson, E.R. Analysis of delamination initiation in postbuckled droppedply laminates. AIAA J. 1993, 31, 721–727. [Google Scholar] [CrossRef]
- Soni, S.R.; Kim, R.Y. Analysis of suppression of free-edge delamination by introducing adhesive layer. In Proceedings of the the Sixth International Conference on Composite Materials and Second European Conference on Composite Materials, London, UK, 13–18 July 1987; pp. 219–230. [Google Scholar]
- Lagace, P.A.; Brewer, J.C. Studies of delamination growth and final failure under tension loading. In Proceedings of the Sixth International Conference on Composite Materials and Second European Conference on Composite Materials, London, UK, 13–18 July 1987; pp. 262–273. [Google Scholar]
- Sallam, S.; Smitses, G.J. Delamination buckling and growth of flat cross-ply laminates. Compos. Struct. 1985, 4, 361–381. [Google Scholar] [CrossRef]
- Lee, J.; Gürdal, Z.; Griffin, O.H. Layer-wise approach for the bifurcation problem in laminated composites with delaminations. AIAA J. 1993, 31, 331–338. [Google Scholar] [CrossRef]
- Chai, H.; Babcock, C.D.; Knauss, W.B. One-dimensional modelling of failure in laminated plates by delamination buckling. Int. J. Solids Struct. 1981, 17, 1069–1083. [Google Scholar] [CrossRef]
- Cochelin, B.; Potier-Ferry, M. A numerical model for buckling and growth of delaminations in composite laminates. Comput. Methods Appl. Mech. Eng. 1991, 89, 361–380. [Google Scholar] [CrossRef]
- Whitcomb, J.D. Analysis of a laminate with a postbuckled embedded delamination, including contact effects. J. Compos. Mater. 1992, 26, 1523–1535. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. A fatigue degradation law for cohesive interface elements—Development and application to composite materials. Int. J. Fatigue 2010, 32, 1774–1787. [Google Scholar] [CrossRef]
- Roe, K.L.; Siegmund, T. An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng. Fract. Mech. 2003, 70, 209–232. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.P.; Dávila, C.G. Simulation of delamination in composites under high-cycle fatigue. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2270–2282. [Google Scholar] [CrossRef]
- Landry, B.; LaPlante, G. Modeling delamination growth in composites under fatigue loadings of varying amplitudes. Compos. Part B Eng. 2012, 43, 533–541. [Google Scholar] [CrossRef]
- Muc, A. Design of composite structures under cyclic loads. Comput. Struct. 2000, 76, 211–218. [Google Scholar] [CrossRef]
- Muc, A. A fuzzy set approach to interlaminar cracks simulation problems. Int. J. Fatigue 2002, 24, 419–427. [Google Scholar] [CrossRef]
- Nikishkov, Y.; Makeev, A.; Seon, G. Progressive fatigue damage simulation method for composites. Int. J. Fatigue 2013, 48, 266–279. [Google Scholar] [CrossRef]
- Nilsson, F.; Asp, L.E.; Sjögren, A. On transition of delamination growth behaviour for compression loaded composite panels. Int. J. Solids Struct. 2001, 38, 8407–8440. [Google Scholar] [CrossRef]
- Paris, P.C.; Gomez, M.P.; Anderson, W.E. A rational analytic theory of fatigue. Trend Eng. 1961, 13, 9–14. [Google Scholar]
- Wu, F.; Yao, W. A fatigue damage model of composite materials. Int. J. Fatigue 2010, 32, 134–138. [Google Scholar] [CrossRef]
- Talreja, R.; Varna, J. (Eds.) Modeling Damage, Fatigue and Failure of Composite Materials; Woodhead Publishing is an imprint of Elseviev: Cambridge, UK, 2016. [Google Scholar]
- Panagiotopoulos, P.D. Inequality Problems in Mechanics and Applications. Convex and Nonconvex Energy Functions; Birkhauser: Boston, MA, USA, 1985. [Google Scholar]
- Muc, A. Theoretical and numerical aspects of contact problems for shells. ZAMP 1984, 35, 890–905. [Google Scholar] [CrossRef]
- Studer, C. Numerics of Unilateral Contacts and Friction, Modeling and Numerical Time Integration in Non-Smooth Dynamics, Lecture. In Notes in Applied and Computational Mechanics, v. 47; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Cao-Rial, M.T.; Rodríguez-Arós, Á. Asymptotic analysis of unilateral contact problems for linearly elastic cshells: Error estimates in the membrane case. Nonlinear Anal. Real World Appl. 2019, 48, 40–53. [Google Scholar] [CrossRef]
- Silveira, R.A.M.; Wellington, L.A.; Pereira, A.P.B. Goncalves Nonlinear analysis of structural elements under unilateral contact constraints by a Ritz type approach. Int. J. Solids Struct. 2008, 45, 2629–2650. [Google Scholar] [CrossRef]
- Hartmann, S.; Brunssen, S.; Ramm, E.; Wohlmuth, B. A primal-dual active set strategy for unilateral non-linear dynamic contact problems of thin-walled structures. In Proceedings of the III European Conference on Computational Mechanics Solids, Structures and CoupledProblems in Engineering, Lisbon, Portugal, 5–8 June 2006. [Google Scholar]
- Wriggers, P.; Wagner, W.; Stein, E. Algorithms for non-linear contact constraints with application to stability problems of rods and shells. Comput. Mech. 1987, 2, 215–230. [Google Scholar] [CrossRef]
- Han, C.-S.; Wriggers, P. On the error indication of shells in unilateral frictionless contact. Comput. Mech. 2002, 28, 169–176. [Google Scholar] [CrossRef]
- Muc, A.; Kubis, S.; Bratek, Ł.; Muc-Wierzgoń, M. Higher-Order Theories for the Buckling and Post-buckling Studies of Shallow Spherical Shells made of Functionally Graded Materials. Compos. Struct. 2022, 219, 11501. [Google Scholar] [CrossRef]
- Gol’denveizer, A.L. Theory of Elastic Thin Shells; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Novozhilov, V.V. The Theory of Thin Shells; Noordhoof Ltd.: Groningen, The Netherlands, 1959. [Google Scholar]
- Muc, A. Mechanics of Fibrous Composites; Wyd.Akad.: Kraków, Poland, 2003. (In Polish) [Google Scholar]
- Akbarov, S.D.; Yahniogliu, N. Delamination buckling of a rectangular orthotropic composite plate containing a band crack. Mech. Compos. Mater. 2010, 46, 721–736. [Google Scholar] [CrossRef]
- Karatas, E.E. Buckling delamination of a rectangular thick orthotropic rectangular plates with an embedded rectangular crack subjected to an axial compressive force. Mech. Compos. Mater. 2019, 55, 935–950. [Google Scholar] [CrossRef]
- Yusuf Arman, Mehmet Zor, Sami Akham, Determination of critical delamination diameter of compressed composite laminated plates under compressed loads. Compos. Sci. Technol. 2006, 66, 2945–2953. [CrossRef]
- Short, G.J.; Guild, F.J.; Pavier, M.J. The effect of the delamination geometry on the compressive failure of composite laminates. Compos. Sci. Technol. 2001, 61, 2075–2086. [Google Scholar]
- Kollner, A. Predicting buckling driven delamination propagation in composite laminates: An analytical modeling approach. Compos. Struct. 2021, 266, 113776. [Google Scholar] [CrossRef]
- Muc, A. Buckling and post-buckling behaviour of imperfect laminated shallow spherical shells under external pressure. In Composite Structures; Springer: Dordrecht, The Netherlands, 1991; pp. 291–306. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; Mc Graw-Hill: London, UK, 1975. [Google Scholar]
- Gu, H.; Chattopadhay, A. Delamination buckling and post-buckling of composite cylindrical shells. AIAA J. 1996, 34, 1279–1286. [Google Scholar] [CrossRef]
- Bazhenov, V.A.; Dinkevich, Y.L. Nonlinear stusdy of deformation and stability of two-layer spherical segments under external pressure with allowance for delaminatiom. Mech. Comp. Mater. 1990, 71–75. [Google Scholar] [CrossRef]
- Bolotin, V.V. Damage and failure of composites by delamination. Mech. Compos. Mater. 1987, 23, 424–432. [Google Scholar] [CrossRef]
- Bolotin, V.V. Mechanics of delaminations in laminate composite structures. Mech. Comp. Mater. 2001, 37, 387–393. [Google Scholar] [CrossRef]
- Kachanov, L.M. Delamination Buckling of Composite Materials; Kluwer Ac. Publ.: Amsterdam, The Netherlands, 1988; pp. 57–87. [Google Scholar]
- Kachanov, L.M. Delamination Buckling; Kluwer Ac. Publ.: Amsterdam, The Netherlands, 1988; pp. 19–56. [Google Scholar]
- Vorontsov, A.N. Delamination failure of Composite Str. Mech. Compos. Mater. 1989, 17, 723–737. [Google Scholar]
- Juhasz, Z. An analytical solution for buckling and vibration of delaminated composite shells. Thin-Walled Struct. 2020, 148, 106563. [Google Scholar] [CrossRef]
- Muc, A. Buckling and post-buckling behaviour of laminated shallow spherical shells subjected to external pressure. Int. J. Non-Linear Mech. 1992, 27, 465–476. [Google Scholar] [CrossRef]
- Muc, A.; Stawiarski, A. Identification of damages in compositemultilayeredcylindricalpanels with delaminations. Compos. Struct. 2012, 94, 1871–1879. [Google Scholar] [CrossRef]
- Muc, A. Description of delaminations in compositemultilayeredstructures - comparison of numerical and experimentalresults for compressedplates. IOP Conf Ser Mater. Sci. Eng. 2020, 744, 012003. [Google Scholar] [CrossRef]
- Whitney, J.M.; Nuismer, R.J. Stress fracture criteria for laminated composites containing stress concentrations. J. Compos. Mater. 1974, 8, 253–265. [Google Scholar] [CrossRef]
- Sih, G.C.; Paris, P.C.; Irwin, G.R. On cracks in rectilinearly anisitropic bodies. Int. J. Fract. 1965, 1, 189–203. [Google Scholar] [CrossRef]
- Irwin, G.R. Fracture in Handbuch der Physik; Springer: Berlin, Germany, 1958; Volume 6, pp. 551–590. [Google Scholar]
- Muc, A.; Kędziora, P. A fuzzy set analysis for a fatigue damage response of composite materials. Compos. Struct. 2001, 54, 283–287. [Google Scholar] [CrossRef]
- Broek, D. The Practical Use of Fracture Mechanics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Kanninen, M.F.; Popelar, C.H. Advanced Fracture Mechanics; Oxford Engng. Sc. Series 15; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Kutlu, Z.; Chang, F.-K. Modeling compression failure of laminated composites containing multiple through-the-width delamination. J. Compos. Mater. 1992, 26, 350–387. [Google Scholar] [CrossRef]





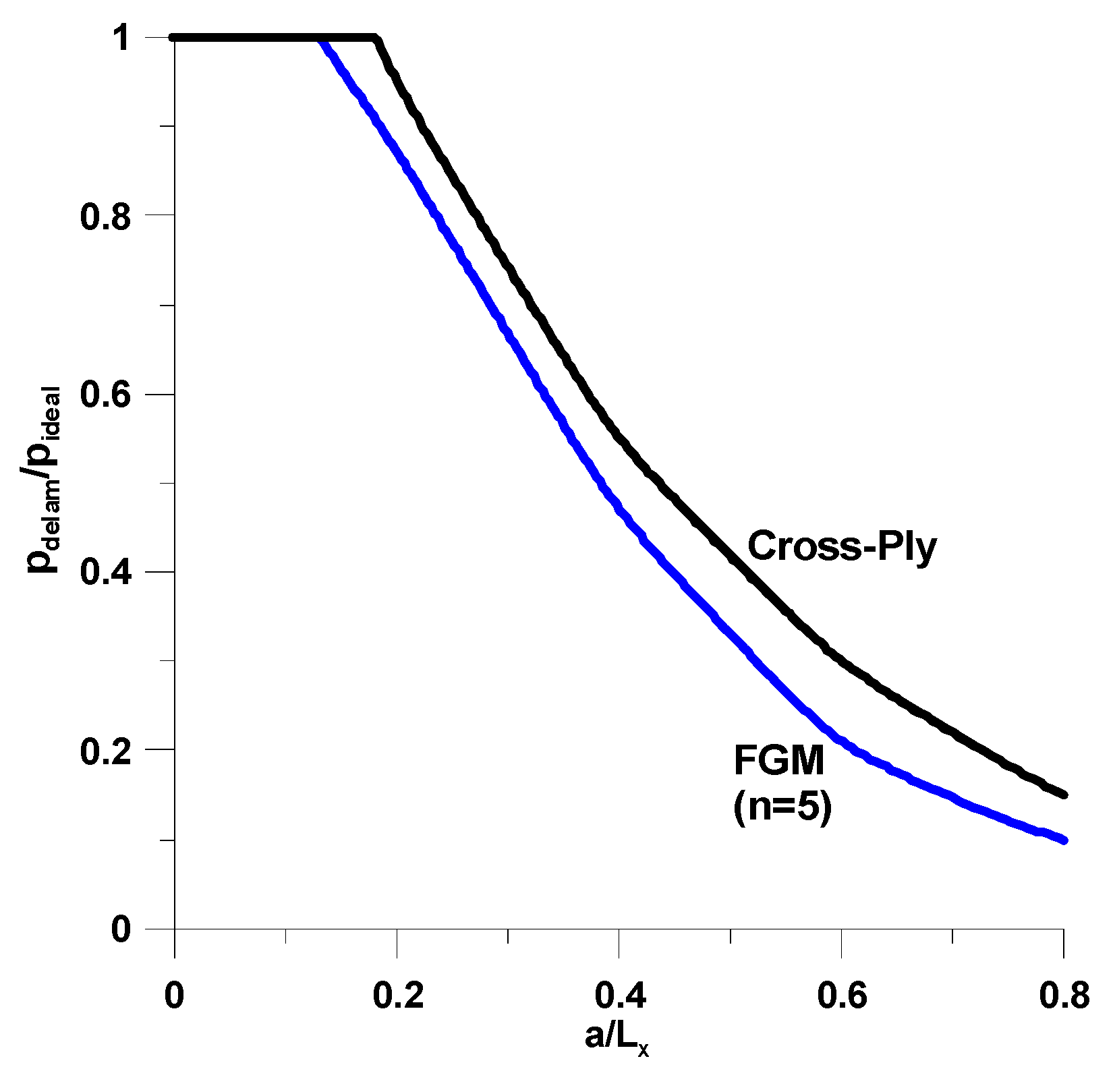


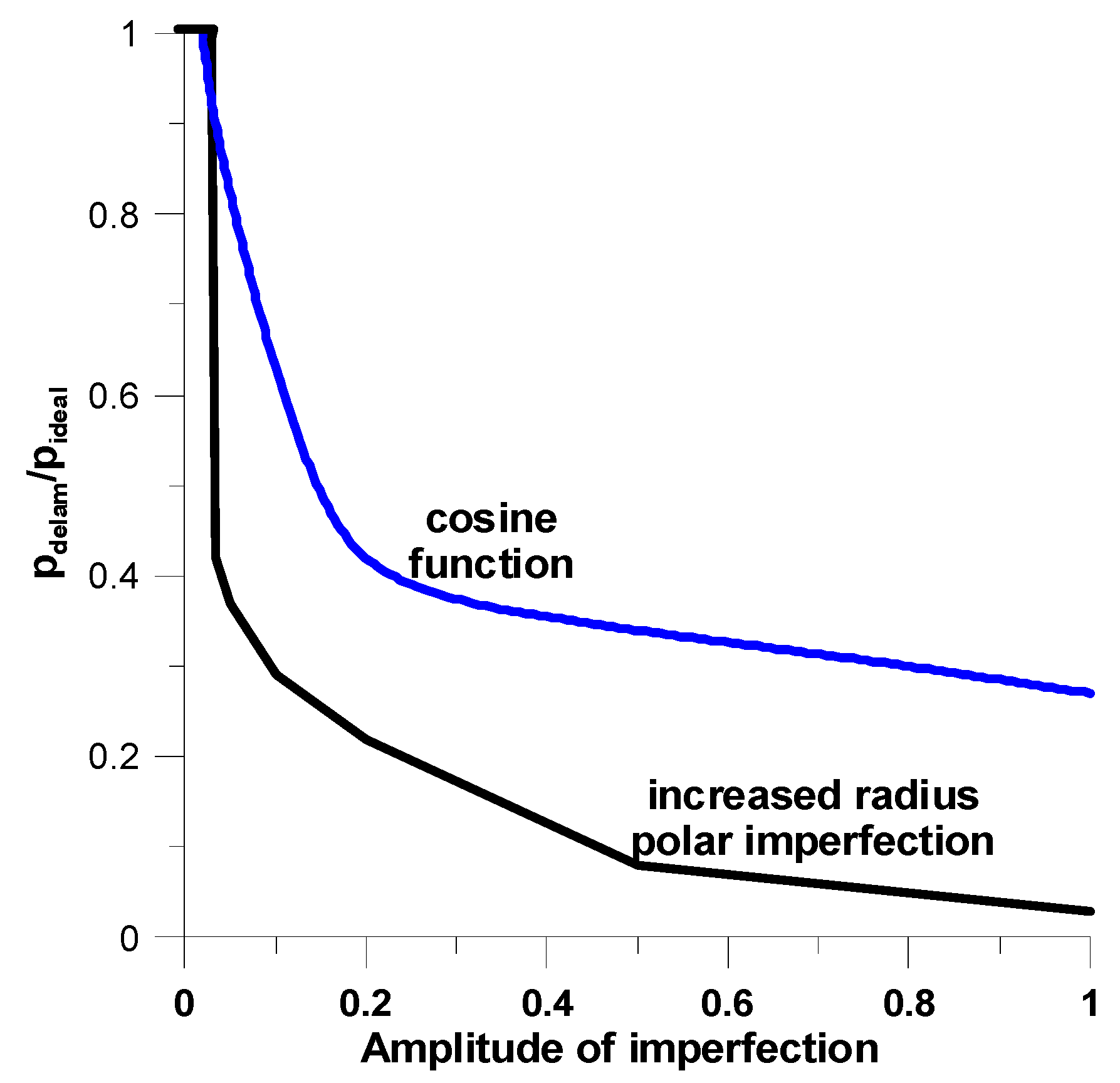
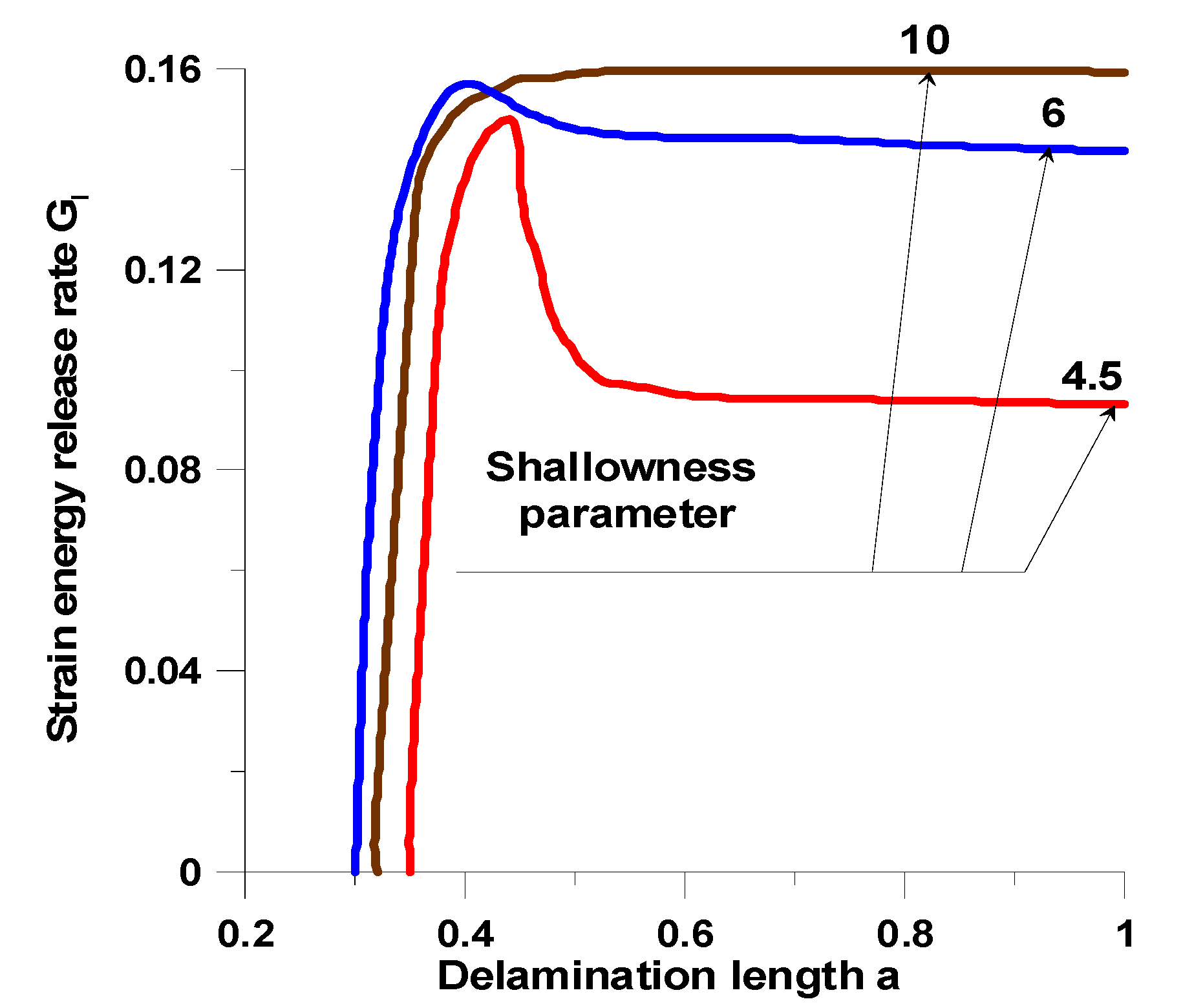
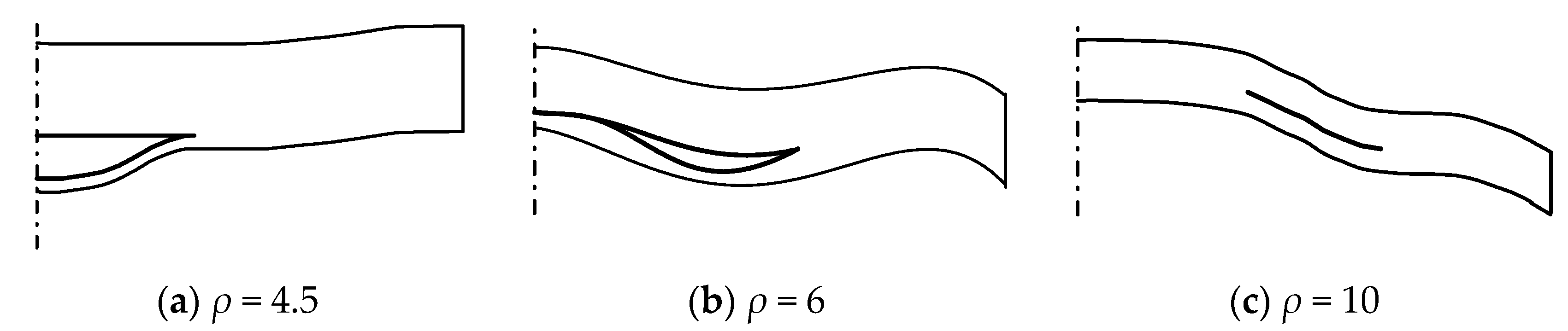
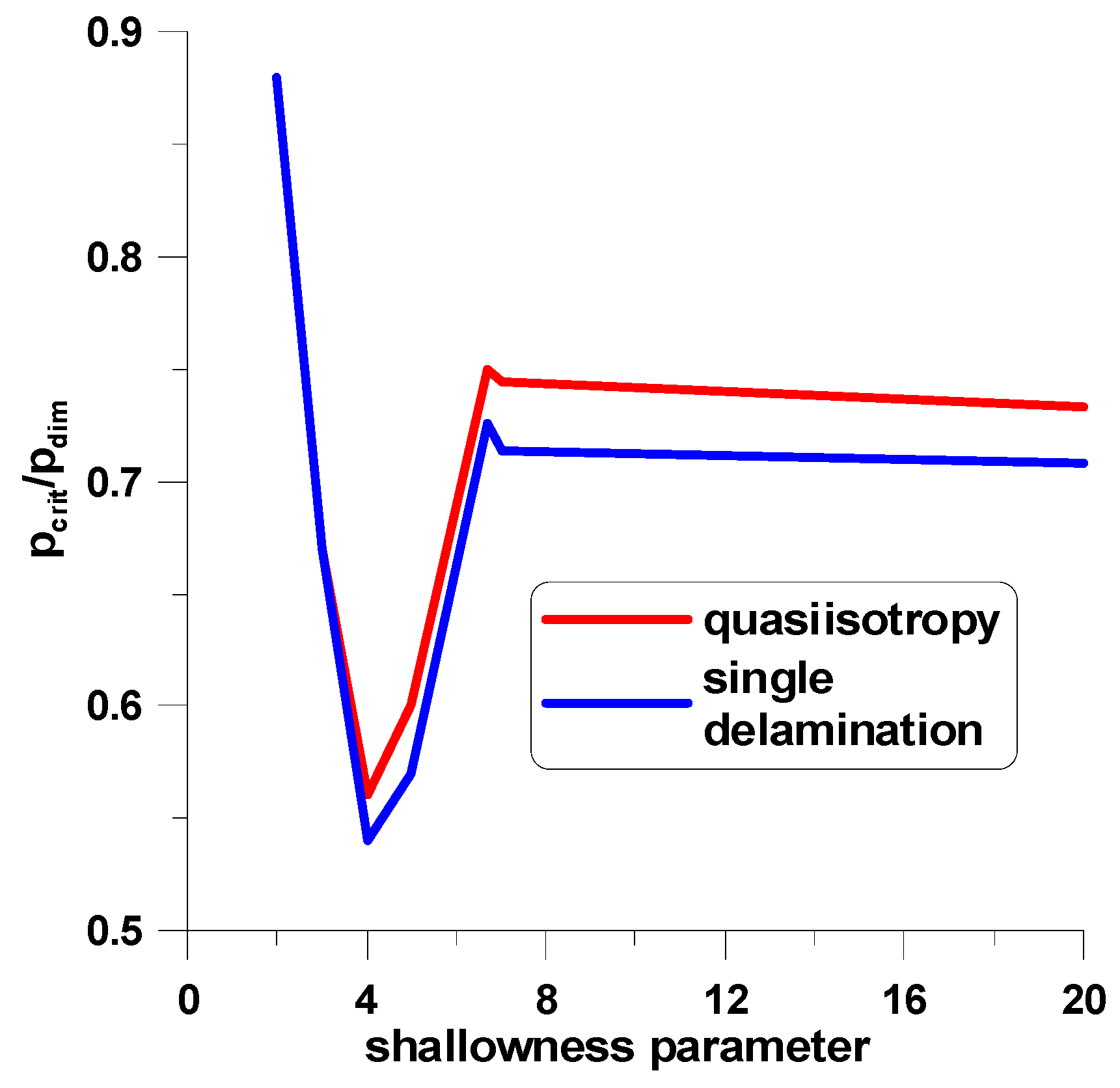
| Unidirectional Composites—See Jones [60] | FGMs—See Equations (10) and (11) | ||
|---|---|---|---|
| E1/E2 = E1/E3 = 20, E1/G13 = 34, E1/G23 = 20 | ν12 = 0.28 | Et/Eb = 5 | ν = 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muc, A. Buckling of Composite Structures with Delaminations—Laminates and Functionally Graded Materials. Appl. Sci. 2022, 12, 11408. https://doi.org/10.3390/app122211408
Muc A. Buckling of Composite Structures with Delaminations—Laminates and Functionally Graded Materials. Applied Sciences. 2022; 12(22):11408. https://doi.org/10.3390/app122211408
Chicago/Turabian StyleMuc, Aleksander. 2022. "Buckling of Composite Structures with Delaminations—Laminates and Functionally Graded Materials" Applied Sciences 12, no. 22: 11408. https://doi.org/10.3390/app122211408
APA StyleMuc, A. (2022). Buckling of Composite Structures with Delaminations—Laminates and Functionally Graded Materials. Applied Sciences, 12(22), 11408. https://doi.org/10.3390/app122211408





