Finding Subsampling Index Sets for Kronecker Product of Unitary Matrices for Incoherent Tight Frames

Abstract

Frames are recognized for their importance in many fields of communications, signal processing, quantum physics, and so on. In this paper, we design an incoherent tight frame by selecting some rows of a matrix that is the Kronecker product of Fourier and unitary matrices. The Kronecker-product-based frame allows its elements to have a small number of phases, regardless of the frame length, which is suitable for low-cost implementation. To obtain the Kronecker-product-based frame with low mutual coherence, we first derive an objective function by transforming the Gram matrix expression to compute the coherence. If the Hadamard matrix is employed as a unitary matrix, the objective function can be computed efficiently with low complexity. Then, we find a subsampling index set for the Kronecker-product-based frame by minimizing the objective function. In simulations, we show that the Kronecker-product-based frames can achieve similar mutual coherence to optimized harmonic frames of a large number of phases. We apply the frames to compressed sensing (CS) as the measurement matrices, where the Kronecker-product-based frames demonstrate reliable performance of sparse signal recovery.

1. Introduction

A frame is a set of vectors in Hilbert space that spans the whole space [1]. The concept of a frame is useful to represent an overcomplete spanning system, which means that a frame has more vectors than the dimension of the space [2]. Frames have been widely applied to various fields of quantum physics/computing [3], communications [4], graph theory [5], algebraic geometry [6], spherical codes [7], and so on.

A frame with incoherent characteristics, where the frame vectors have low similarity to each other, is desired in many applications. The mutual coherence [8] is used as an indicator of how similar each frame vector is to each other. For example, the low mutual coherence of a frame enables sparse signal recovery from incomplete measurements [9] in compressed sensing (CS), accurate target scene recovery in radar sensing [10], low multiple access interference in synchronous code-division multiple access (CDMA) [11], and reliable angular momentum analysis in quantum mechanics [12]. However, the mutual coherence cannot be reduced indefinitely close to 0 when the number of frame vectors N is larger than the frame length m. There exists a theoretical lower bound on mutual coherence, which is called the Welch bound [13]. If all the vectors in a frame have unit norm, and the magnitude of the inner product of each pair meets the Welch bound equality, the frame is called an equiangular tight frame (ETF) [14].

ETFs have been studied for a long time, but they are known to be notoriously difficult to design [15,16,17]. Therefore, a frame with nearly optimal coherence, which is a good alternative to ETF, has been actively studied. A variety of algebraic methods have been exploited in [18,19,20,21,22,23,24,25] to design various incoherent frames with nearly optimal coherence in a constructive way. In addition, there have been numerous algorithmic approaches for obtaining incoherent frames. Alternating projection methods were used in [26,27,28,29], which solved the singular value decomposition (SVD) to minimize the maximum magnitude of the Gram matrix of a frame. To reduce the computational complexity of implementing SVD, the algorithms that optimize the coherence of a frame without solving SVD problems [30,31,32,33] or using only matrix–vector multiplications [34] were proposed. In [35], the authors utilized the discrete stochastic approximation method, using the Kronecker product of two Fourier matrices for near-optimal codebook design under spatially correlated 3D channels. In [7], incoherent tight frames were designed by the distance optimization algorithm for spherical code construction. In [36], incoherent unit-norm frames were designed by the alternating minimization penalty method. In [37], high-dimensional incoherent frames were designed by linear programming exploiting the minorization maximization technique [38]. In [39], the authors optimized the coherence of a dictionary matrix by a greedy algorithm based on a quasi-Newton method [40]. Finally, real/complex-valued, sparse, and harmonic incoherent frames were designed in [41] by using sequential iterative decorrelation convex optimization (SIDCO) or iterative reweighted $l_1$ optimization (IRL1) [42]. Especially, the incoherent harmonic frames were designed by subsampling the indices of the Fourier matrix by solving an $l_1$-optimization problem using IRL1 and exploiting a local search method.

In this paper, we design incoherent tight frames by subsampling rows from the matrices generated by the Kronecker product with unitary and Fourier matrices. In this Kronecker-product-based frame, each frame vector has the elements that have a small number of phases, which allows low implementation complexity. We show that the Gram matrix of the frame is block-wise circulant due to the structure of the Fourier matrix. Using this feature, we derive an objective function that calculates the mutual coherence of the Kronecker-product-based frame equivalently. Furthermore, we show that if the unitary matrix of the frame is closed under column-wise multiplication, such as the Hadamard matrix from the Sylvester’s construction [43], we can calculate the objective function more efficiently with low computational complexity, which is reduced drastically from that of the whole Gram matrix. Finally, an optimization problem is formulated to find subsampling row indices of the Kronecker product using the objective function. We exploit the Algorithm 2 in [41] to solve the optimization problem, which ultimately yields the Kronecker-product-based frames with low mutual coherence.

We conduct extensive simulations to investigate the mutual coherence of the Kronecker-product-based frames for various m and N. We demonstrate that the Kronecker-product-based frames can achieve similar mutual coherence to the optimized harmonic frames [41], although ours have a smaller number of phases. Furthermore, we found two ETFs in dimension $N=64$ and frame length $m=28$, which have 4-phase and 8-phase, respectively. To the best of our knowledge, these ETFs are new ones that have never been reported. Moreover, these ETFs with a small number of phases can be easily generated by the Kronecker product of Fourier and Hadamard matrices, which is suitable for practical applications. Finally, we apply the Kronecker-product-based frame to CS as the measurement matrix to recover sparse signals from incomplete measurements, which demonstrates reliable performance of sparse signal recovery. In conclusion, we show that the Kronecker-product-based frames designed by our novel objective function have low mutual coherence and a small number of phases, which can be a good alternative to optimized harmonic frames in practical applications.

2. Background

2.1. Frame Fundamentals

Definition 1

([1]). A collection of vectors ${\left(f_j\right)}_{j\in J}$ in a Hilbert space $\mathcal{H}$ is called a frame if there exist two constants $0<A\le B<\infty$, such that for all $f\in \mathcal{H}$,

$$A{∥f∥}_2^2\le \sum _{j\in J}{\left|⟨f,f_j⟩\right|}^2\le B{∥f∥}_2^2,$$

(1)

where J is an countable index set [44], $⟨·,·⟩$ denotes inner product, and ${∥·∥}_2$ denotes $l_2$-norm.

In this paper, we consider $\mathcal{H}=\mathbb{R}$ or $\mathcal{H}=\mathbb{C}$. If the frame bounds are $A=B$, the frame is called an A-tight frame and, if the frame bounds are $A=B=1$, the frame is a normalized tight frame. Furthermore, if the frame ${\left(f_j\right)}_{j\in J}$ meets the condition for being a tight frame and if ${∥f_j∥}_2=1,\forall j\in J$, this frame is called a unit-norm tight frame.

Definition 2

([8]). Suppose that a frame ${\left(f_j\right)}_{j\in J}$ has the frame vectors $f_j\in {\mathbb{R}}^m$ or ${\mathbb{C}}^m$ for $\forall j\in J$, where the index set size is $\left|J\right|=N$. Then, the frame ${\left(f_j\right)}_{j\in J}$ is called an equiangular tight frame if it satisfies following conditions.

1. 

${∥f_j∥}_2=1$,

2. 

$|⟨f_j,f_k⟩|=\sqrt{\frac{N-m}{m(N-1)}}$, for $j\ne k$ where $\forall j,k\in J$.

2.2. Mutual Coherence

Suppose that the frame size is $\left|J\right|=N$ and the frame length is m. We can deal with a frame ${\left(f_j\right)}_{j\in J}$ as a matrix that has the frame vectors as its columns, i.e., $\mathbf{A}=[f_1,f_2,\cdots ,f_J]\in {\mathbb{C}}^{m\times N}$. Then, the mutual coherence [8] of $\mathbf{A}$ is given by

$$\mu \left(\mathbf{A}\right)=\underset{1\le i<j\le N}{max}\frac{\left|{\mathbf{a}}_i^H·{\mathbf{a}}_j\right|}{{∥{\mathbf{a}}_i∥}_2{∥{\mathbf{a}}_j∥}_2},$$

(2)

where ${\mathbf{a}}_i$ is the ith column vector of $\mathbf{A}$. The coherence of a frame is bounded by

$$\mu \left(\mathbf{A}\right)\ge \sqrt{\frac{N-m}{m(N-1)}},$$

(3)

which is called the Welch bound [13], and the right-hand side term of (3) is called the Welch bound equality (WBE).

2.3. Kronecker Product

The Kronecker product [45] of $\mathbf{A}\in {\mathbb{C}}^{a\times b}$ and $\mathbf{B}\in {\mathbb{C}}^{c\times d}$ is,

$$\mathbf{A}⨂\mathbf{B}=\left[\begin{array}{ccc}{a}_{1,1}\mathbf{B}& \cdots & a_{1,b}\mathbf{B}\\ ⋮& & \\ a_{a,1}\mathbf{B}& \cdots & a_{a,b}\mathbf{B}\end{array}\right]\in {\mathbb{C}}^{ac\times bd},$$

(4)

where $\mathbf{A}=\left[a_{i,j}\right|1\le i\le a,1\le j\le b]$.

2.4. Other Notations

$\overline{\mathbf{A}}$ and ${\mathbf{A}}^H$ denote the complex conjugate and the conjugate transpose of a matrix $\mathbf{A}$, respectively. ${\mathbf{A}}^T$ denotes the transpose of a matrix $\mathbf{A}$. The support set of a vector $\mathbf{x}=[x_1,\cdots ,x_N]$ is defined by $\mathrm{supp}\left(\mathbf{x}\right)=\left\{i\right|x_i\ne 0\}$. $\mathcal{CN}(\mu ,{\sigma }^2)$ denotes the complex Gaussian distribution with mean $\mu$ and standard deviation $\sigma$. The Fourier matrix ${\mathbf{F}}_q$ is given by ${\mathbf{F}}_q=\left[{\omega }^{(i-1)(j-1)}\right|1\le i,j\le q]$, where $\omega =e^{-2\pi j/q}$. The Hadamard matrix ${\mathbf{H}}_n$ satisfies ${\mathbf{H}}_n·{\mathbf{H}}_n^T=n\mathbf{I}$ [46]. As an example, the Hadamard matrix from Sylvester’s construction [47] is given by

$${\mathbf{H}}_{2n}=\left[\begin{array}{cc}{\mathbf{H}}_n& {\mathbf{H}}_n\\ {\mathbf{H}}_n& -{\mathbf{H}}_n\end{array}\right],$$

(5)

where ${\mathbf{H}}_1=\left[1\right]$ and $\mathbf{I}$ is an $n\times n$ identity matrix. For a matrix $\mathbf{A}\in {\mathbb{C}}^{m\times N},$ the operator $\mathrm{vec}\left(\mathbf{A}\right)$ returns a vector $\mathbf{a}\in {\mathbb{C}}^{mN\times 1}$ by stacking the columns. The operator $\mathrm{circ}\left(\mathbf{a}\right)$ returns a matrix by circularly shifting a input vector $\mathbf{a}={[a_1,\cdots ,a_N]}^T$, i.e.,

$$\mathrm{circ}\left(\mathbf{a}\right)=\left[\begin{array}{ccccc}{a}_1& a_N& a_{N-1}& \cdots & a_2\\ a_2& a_1& a_N& \cdots & a_3\\ a_3& a_2& a_1& \cdots & a_4\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_N& a_{N-1}& a_{N-2}& \cdots & a_1\end{array}\right]\in {\mathbb{C}}^{N\times N}.$$

(6)

The operator $\mathrm{diag}\left(\mathbf{a}\right)$ returns a diagonal matrix that has the vector $\mathbf{a}$ as its diagonal entries. The operator ⨀ denotes a column-wise multiplication operator, i.e.,

$$\mathbf{a}⨀\mathbf{b}={[a_1{b}_1,\cdots ,a_m{b}_m]}^T$$

(7)

where $\mathbf{a}={[a_1,a_2,\cdots ,a_m]}^T\in {\mathbb{C}}^{m\times 1}$ and $\mathbf{b}={[b_1,b_2,\cdots ,b_m]}^T\in {\mathbb{C}}^{m\times 1}$. The operator $\mathcal{M}\left(\mathbf{A}\right)$ returns the maximum magnitude of a matrix $\mathbf{A}$.

3. Problem Formulation for Kronecker-Product-Based Frames

To find a Kronecker-product-based frame with low mutual coherence, we select m rows from an $N\times N$ matrix from the Kronecker product between unitary and Fourier matrices. As a subsampled unitary matrix is equivalent to a tight frame [2], the Kronecker-product-based frame also becomes a tight one.

3.1. Problem Formulation

In this paper, we consider a unitary matrix $\mathbf{U}=\left[u_{i,j}\right|1\le i,j\le p]\in {\mathbb{C}}^{p\times p}$, where $|u_{i,j}|=1$. Let $\mathbf{K}=\mathbf{U}⨂{\mathbf{F}}_q\in {\mathbb{C}}^{N\times N}$, where ${\mathbf{F}}_q\in {\mathbb{C}}^{q\times q}$ is a Fourier matrix. We define a row selection operator ${\mathbf{R}}_{\Omega }\in {\left\{0,1\right\}}^{m\times N}$ to select m rows out of $\mathbf{K}$, where the selected row indices are specified by $\Omega \subset \{1,\cdots ,N\}$ with $|\Omega |=m$. Let ${\mathbf{R}}_{\Omega }=[{\mathbf{R}}_{{\Omega }_1},\cdots ,{\mathbf{R}}_{{\Omega }_p}]$, where ${\mathbf{R}}_{{\Omega }_i}\in {\{0,1\}}^{m\times q}$. Selecting the row indices of $\Omega$ from $\mathbf{K}$, we obtain ${\mathbf{K}}_{\Omega }={\mathbf{R}}_{\Omega }·\mathbf{K}\in {\mathbb{C}}^{m\times N}$, where

$${\mathbf{K}}_{\Omega }=[\sum _{k=1}^p{u}_{k,1}{\mathbf{R}}_{{\Omega }_k}·{\mathbf{F}}_q,\cdots ,\sum _{k=1}^p{u}_{k,i}{\mathbf{R}}_{{\Omega }_k}·{\mathbf{F}}_q,\cdots ,\sum _{k=1}^p{u}_{k,p}{\mathbf{R}}_{{\Omega }_k}·{\mathbf{F}}_q].$$

(8)

The Gram matrix of ${\mathbf{K}}_{\Omega }$ is $\mathbf{G}={\mathbf{K}}_{\Omega }^H·{\mathbf{K}}_{\Omega }={\mathbf{K}}^H·{\mathbf{R}}_{\Omega }^T·{\mathbf{R}}_{\Omega }·\mathbf{K}\in {\mathbb{C}}^{N\times N}$. By definition of (2), the mutual coherence of ${\mathbf{K}}_{\Omega }$ is clearly determined by the maximum magnitude of off-diagonal elements of the Gram matrix $\mathbf{G}$. Therefore, we can formulate a problem to find a subsampling index set $\Omega$ for the Kronecker-product-based frame ${\mathbf{K}}_{\Omega }$ with low mutual coherence by

$$\underset{\Omega \subset \{1,\cdots ,N\}}{min}\mathcal{M}(m^{-1}{\mathbf{K}}^H·{\mathbf{R}}_{\Omega }^T·{\mathbf{R}}_{\Omega }·\mathbf{K}-\mathbf{I}).$$

(9)

3.2. Kronecker Product with Unitary Matrix

In this section, we show that the original problem of (9) can be represented by a new equivalent problem to find a subsampling row index set $\Omega$.

Theorem 1.

Define a binary matrix $\tilde{\mathbf{B}}=[{\tilde{\mathbf{b}}}_1,\cdots ,{\tilde{\mathbf{b}}}_p]\in {\{0,1\}}^{q\times p}$, where $diag\left({\tilde{\mathbf{b}}}_k\right)={\mathbf{R}}_{{\Omega }_k}^T·{\mathbf{R}}_{{\Omega }_k}$. Moreover, define ${\mathbf{U}}_c$ by including distinct column-wise multiplications from all possible pairs of column vectors of $\overline{\mathbf{U}}$ and $\mathbf{U}$, i.e.,

$${\mathbf{U}}_c=[{\mathbf{1}}_p,{\overline{\mathbf{u}}}_1⨀{\mathbf{u}}_2,\cdots ,{\overline{\mathbf{u}}}_i⨀{\mathbf{u}}_j,\cdots ,{\overline{\mathbf{u}}}_{p-1}⨀{\mathbf{u}}_p],$$

(10)

where $1\le i<j\le p$ and ${\mathbf{1}}_p={\{1,\cdots ,1\}}^T$ are all one vector of length p. Then, the problem (9) can be equivalently converted into

$$\underset{\tilde{\mathbf{B}}\in {\{0,1\}}^{q\times p}}{min}\mathcal{M}(m^{-1}{\mathbf{F}}_q^H·\tilde{\mathbf{B}}·{\mathbf{U}}_c-\mathbf{E}),$$

(11)

where all elements of $\mathbf{E}=\left[e_{i,j}\right|1\le i\le q,1\le j\le p]$ are zero except $e_{1,1}=1$.

Proof of Theorem 1. 

For convenience of analysis, we assume that the selected row indices of $\Omega$ are sorted in ascending order. Recall ${\mathbf{R}}_{\Omega }=[{\mathbf{R}}_{{\Omega }_1},\cdots ,{\mathbf{R}}_{{\Omega }_p}]$, where ${\mathbf{R}}_{{\Omega }_i}\in {\{0,1\}}^{m\times q}$. Then, we can write the Gram matrix $\mathbf{G}$ using submatrices ${\mathbf{G}}_{i,j}$, i.e., $\mathbf{G}=\left[{\mathbf{G}}_{i,j}\right|1\le i,j\le p]$, where

$${\mathbf{G}}_{i,j}=\sum _{k=1}^p\sum _{l=1}^p{u}_{l,i}^{*}{u}_{k,j}{\mathbf{F}}_q^H·{\mathbf{R}}_{{\Omega }_l}^T·{\mathbf{R}}_{{\Omega }_k}·{\mathbf{F}}_q.$$

(12)

Since ${\mathbf{R}}_{{\Omega }_l}^T·{\mathbf{R}}_{{\Omega }_k}=\mathbf{0}$ for $l\ne k$ and ${\mathbf{R}}_{{\Omega }_k}^T·{\mathbf{R}}_{{\Omega }_k}=\mathrm{diag}\left({\tilde{\mathbf{b}}}_k\right)$, we have

$${\mathbf{G}}_{i,j}=\sum _{k=1}^p{u}_{k,i}^{*}{u}_{k,j}{\mathbf{F}}_q^H·\mathrm{diag}\left({\tilde{\mathbf{b}}}_k\right)·{\mathbf{F}}_q.$$

(13)

Since ${\mathbf{F}}_q^H·\mathrm{diag}\left({\tilde{\mathbf{b}}}_k\right)·{\mathbf{F}}_q=\mathrm{circ}\left({\mathbf{b}}_k\right)$, where ${\mathbf{b}}_k={\mathbf{F}}_q^H·{\tilde{\mathbf{b}}}_k$, ${\mathbf{G}}_{i,j}$ in (13) becomes

$${\mathbf{G}}_{i,j}=\sum _{k=1}^p{u}_{k,i}^{*}{u}_{k,j}\mathrm{circ}\left({\mathbf{b}}_k\right).$$

(14)

Thanks to the circulant feature of (14), we only need to evaluate the first column vector of each submatrix ${\mathbf{G}}_{i,j}$ for mutual coherence, instead of all the columns. The first column vector of the submatrix ${\mathbf{G}}_{i,j}$ can be written as

$$\sum _{k=1}^p{u}_{k,i}^{*}{u}_{k,j}{\mathbf{b}}_k=\sum _{k=1}^p{u}_{k,i}^{*}{u}_{k,j}{\mathbf{F}}_q^H{\tilde{\mathbf{b}}}_k={\mathbf{F}}_q^H·\tilde{\mathbf{B}}·({\overline{\mathbf{u}}}_i⨀{\mathbf{u}}_j),$$

(15)

where $\tilde{\mathbf{B}}=[{\tilde{\mathbf{b}}}_1,\cdots ,{\tilde{\mathbf{b}}}_p]\in {\{0,1\}}^{q\times p}$. Moreover, we only need to check the submatrices ${\mathbf{G}}_{i,j}$ for $1\le i\le j\le p$, since the Gram matrix $\mathbf{G}$ is symmetric in its magnitude. Note that ${\overline{\mathbf{u}}}_i⨀{\mathbf{u}}_i={\mathbf{1}}_p$ for all i, as each element of $\mathbf{U}$ has unit magnitude. To evaluate the mutual coherence, it is thus sufficient to check the first column vectors of ${\mathbf{G}}_{i,j}$ in (15) only for the column-wise multiplications in ${\mathbf{U}}_c$. As a result, the original problem (9) to find a subsampling index set $\Omega$ can be equivalently represented by (11). □

3.3. Kronecker Product with Special Unitary Matrix

As a special case, we may consider a unitary matrix $\mathbf{U}$ that is closed under column-wise multiplication, i.e., ${\mathbf{U}}_c=\mathbf{U}$. In (10), the matrix ${\mathbf{U}}_c$ has at most $\left(\genfrac{}{}{0pt}{}{p}{2}\right)+1$ distinct columns, which can make the problem (11) computationally expensive for large p. However, if $\mathbf{U}$ is closed under column-wise multiplication, the number of columns of ${\mathbf{U}}_c$ is reduced to p. A typical example of this unitary matrix is the Hadamard matrix generated by Sylvester’s construction [43].

Corollary 1.

Let ${\mathbf{H}}_p\in {\{0,1\}}^{p\times p},p=2^v$ be the Hadamard matrix that is closed under column-wise multiplication. Recall a binary matrix $\tilde{\mathbf{B}}=[{\tilde{\mathbf{b}}}_1,\cdots ,{\tilde{\mathbf{b}}}_p]\in {\{0,1\}}^{q\times p}$ where $diag\left({\tilde{\mathbf{b}}}_k\right)={\mathbf{R}}_{{\Omega }_k}^T·{\mathbf{R}}_{{\Omega }_k}$. Then, the problem of (11) is equivalent to

$$\underset{\tilde{\mathbf{B}}\in {\{0,1\}}^{q\times p}}{min}\mathcal{M}(m^{-1}{\mathbf{F}}_q^H·\tilde{\mathbf{B}}·{\mathbf{H}}_p-\mathbf{E}).$$

(16)

The optimization problem (16) is a non-convex problem that we should solve to find a subsampling index set for the Kronecker-product-based frame with low mutual coherence.

3.4. Computational Complexity of Objective Function

In general, the number of calculations for the objective function of (9) is $O\left(m{N}^2\right)$. The computational complexity of the equivalent objective function (11) is $O\left(N(p^2+plogq)\right)$, which is still quite high. However, if $\mathbf{U}$ is the Hadamard matrix, the computational complexity for the objective function of (16) can be reduced drastically. By exploiting the fast Fourier and Hadamard transform algorithms, we can achieve the computational complexities of $O(pqlogq)$ for multiplication with ${\mathbf{F}}_q$ and $O(pqlogp)$ for multiplication with ${\mathbf{H}}_p$, respectively, where $pq=N$. Therefore, the computational complexity of the objective function in (16) is $O(pqlogq+pqlogp)=O(NlogN)$. As a result, we can compute the objective function of (16) fast and efficiently to find a subsampling index set $\Omega$ by using the features of the Kronecker-product-based frame. The computational complexities of these objective functions are summarized in Table 1.

Table 1. The computational complexities of several objective functions for the frames from Kronecker product, where $N=pq$.

Objective Function	Computational Complexity	Components of Kronecker Product
(9)	$O\left(m{N}^2\right)$	General matrices
(11)	$O\left(N(p^2+plogq)\right)$	Unitary and Fourier matrices
(16)	$O(NlogN)$	Hadamard and Fourier matrices

4. Algorithm for Solving Optimization Problem

In Section 3, we derived a novel objective function that calculates the mutual coherence with lower computational complexity than the typical Gram matrix computation. In this section, we use the Hadamard matrix as a unitary matrix, i.e., $\mathbf{U}={\mathbf{H}}_p$ for the Kronecker product. We use an existing algorithm, Algorithm 2 in [41], to solve the optimization problem (16) to find a subsampling index set for the Kronecker-product-based frame with low mutual coherence. We give a brief sketch of Algorithm 2 in [41], and readers are referred to [41] for more details.

Since the objective function of (16) is non-convex, we relax the binary constraint of $\tilde{\mathbf{B}}$ by finding $\tilde{\mathbf{X}}\in {\mathbb{R}}^{q\times p}$ instead with the elements between 0 and 1, similar to the relaxation of [41]. Then, we begin with an optimization problem, which is based on IRL1 [42], given as

$$\begin{array}{cc}\underset{\tilde{\mathbf{X}}}{min}\mathcal{M}(m^{-1}{\mathbf{F}}_q^H·\tilde{\mathbf{X}}·{\mathbf{H}}_p-{\mathbf{E}}_1)+\lambda {∥\mathrm{diag}\left(\mathbf{w}\right)·\mathrm{vec}(\tilde{\mathbf{X}})∥}_1& \\ & \\ \mathrm{subject}\mathrm{to}{\tilde{x}}_1=1,\sum _{i=2}^N{\tilde{x}}_i=m-1,0\le {\tilde{x}}_i\le 1,{\tilde{x}}_k=0,k\in {\Omega }_0,\end{array}$$

(17)

where $\lambda$ is a regularization parameter and $\mathrm{vec}(\tilde{\mathbf{X}})={[{\tilde{x}}_1,\cdots ,{\tilde{x}}_N]}^T$. To obtain a stable solution of (17), some elements of $\tilde{\mathbf{X}}$ at random positions are fixed to zero. The index set of positions fixed to zero is denoted as ${\Omega }_0\subset \{2,3,\cdots ,N\}$, where $|{\Omega }_0|=⌈\zeta (N-m)⌉$ for $0<\zeta <1$. Moreover, ${\tilde{x}}_1$ is fixed to 1 for a unique solution. In (17), the $l_1$ weight regularization term ${∥\mathrm{diag}\left(\mathbf{w}\right)·\mathrm{vec}\left(\tilde{\mathbf{X}}\right)∥}_1$ promotes the sparsity of $\tilde{\mathbf{X}}$, where $\mathbf{w}={[w_1,\cdots ,w_N]}^T$ with each element used in Algorithm 2 [41], i.e.,

$$w_k={({\tilde{x}}_k+ϵ)}^{-1}.$$

(18)

We solve this optimization problem via CVX [48].

Next, we quantize the solution of (17) to obtain the binary solution $\tilde{\mathbf{B}}$. Let $\mathrm{vec}(\tilde{\mathbf{B}})={[{\tilde{b}}_1,\cdots ,{\tilde{b}}_N]}^T$, where each element is obtained by

$${\tilde{b}}_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{\tilde{x}}_i\ge \delta \hfill \\ 0,\hfill & \mathrm{if}{\tilde{x}}_i<\delta \hfill \end{array}\right.$$

(19)

for $2\le i\le N$, and the support set of $\mathrm{vec}(\tilde{\mathbf{B}})$ is denoted by $\Omega$. Note that $\Omega$ may contain m or more indices with sufficiently small $\delta$ in (19), which requires an additional step to reduce the number of indices to m. As in Step 5 of Algorithm 2 [41], we eliminate some indices iteratively until m indices remain in $\Omega$, where an index $i\in \Omega$ will be eliminated at each iteration if $\Omega \backslash \left\{i\right\}$ causes the lowest increase in mutual coherence. Finally, we conduct a local brute-force search to maximally reduce the mutual coherence of the Kronecker-product-based frame, which updates $\Omega$ by replacing its $\beta$ indices by those in $\{1,\cdots ,N\}\backslash \Omega$. As in the previous step, the mutual coherence is computed by (16) for the local brute-force search. The whole process to find a subsampling index set for the Kronecker-product-based frame is summarized in Figure 1.

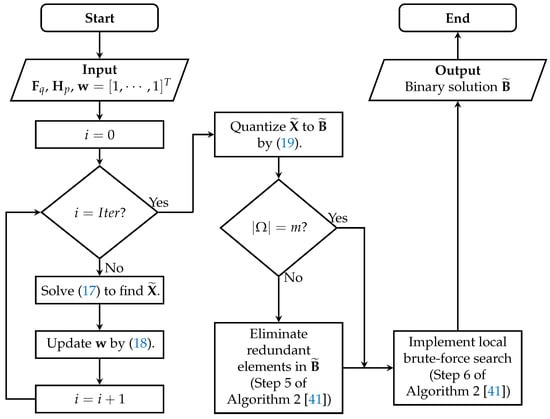
Figure 1. The optimization process for obtaining the Kronecker-product-based frame. In this process, eliminating redundant elements in $\tilde{\mathbf{B}}$ and implementing local brute-force search are carried out by Steps 5 and 6 of Algorithm 2 in [41], respectively.

5. Results

In simulations, we demonstrate the performance of the Kronecker-product-based frames by examining the mutual coherence and evaluating the recovery performance of compressed sensing with the frames.

For the algorithm of Section 4, we set the parameters $\zeta ={10}^{-1}$, $ϵ={10}^{-7}$, $\lambda =m^{-1}$ and $\delta ={10}^{-8}$. We tried the local brute force search to change up to $\beta =3$ indices for $N<128$, $\beta =2$ for $N=128$, and $\beta =1$ otherwise. These parameters are chosen as the same ones as Algorithm 2 [41] that our approach is based on. We set $Iter=30$ for solving the optimization problem of (17) via CVX. We repeated the whole process in Figure 1 10 times and then chose the frame with the lowest mutual coherence at each $(m,N)$. For comparison, the optimized harmonic frames are designed by Algorithm 2 in [41]. As remarked in [41], the optimized Hadamard-based frames are also designed using the same algorithm by exploiting the Hadamard matrix instead of the Fourier matrix. Moreover, random Kronecker-product-based frames, which are labeled by random KP-based frames in each figure, are designed by randomly selecting m rows from $N\times N$ Kronecker product matrix $\mathbf{K}={\mathbf{H}}_p⨂{\mathbf{F}}_q$, where the frames with lowest mutual coherence among 10 random trials are selected. The Kronecker-product-based frame designed by the algorithm of Section 4 is called the optimized Kronecker-product-based frame in this section, which is labeled as optimized KP-based frame in each figure.

5.1. Mutual Coherence

In Figure 2, we show the mutual coherence of the Kronecker-product-based frames with $N=64$ and 256, respectively. The optimized Kronecker-product-based frames have the number of phases $q=4,8,$ and 16, respectively. For $q=4$, the mutual coherence is unstable about the frame length m. However, for $q=16$, the optimized Kronecker-product-based frames show similar mutual coherence with the optimized harmonic frame. This result demonstrates that the optimized Kronecker-product-based frames of a small number of phases $q\ll N$ can perform similarly to the optimized harmonic frames of the number of phases N. This means that the optimized Kronecker-product-based frames are more suitable for practical applications, thanks to the small number of phases. In particular, we found ETFs with the number of phases $q=4$ and $q=8$ in dimension $N=64$ and frame length $m=28$ by the algorithm of Section 4. As far as we know, these have never been reported. As witnessed by Figure 3 in [41], we also observed a small increase in mutual coherence at some m from the optimized Hadamard-based frames, despite the increase in the frame vector length, which is due to the restricted, binary entries of the Hadamard matrix.

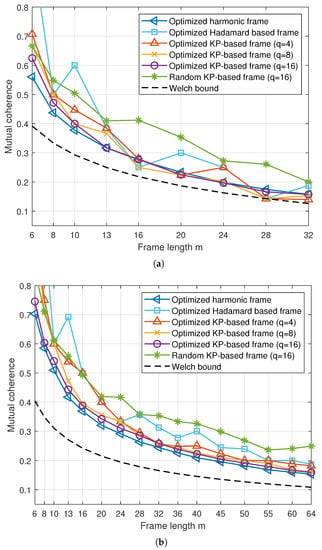
Figure 2. The mutual coherence of various frames over frame length m. (a) $N=64$, (b) $N=256$.

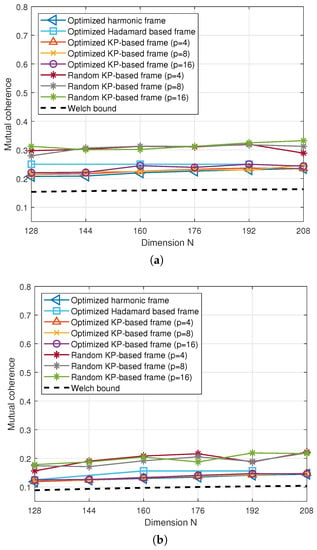
Figure 3. The mutual coherence of various frames over frame dimension N. (a) $m=32$, (b) $m=64$.

In Figure 3, we designed the Kronecker-product-based frames with various dimensions N for fixed frame lengths $m=32$ and 64, respectively, where $p=4,8$ and 16. For the optimized Hadamard-based frames, we examined the mutual coherence for $N=128,160$, and 192, where the Hadamard matrices exist. As $q=N/p$, the number of phases of the Kronecker-product-based frames are p times lower than that of the optimized harmonic frames. We observe that the mutual coherence of the optimized Kronecker-product-based frames is similar to those of the optimized harmonic frames in various N, even if they have significantly lower number of phases. The mutual coherence of optimized Hadamard-based frames is slightly higher than those of the other optimized frames.

5.2. CS Recovery Performance

We apply the optimized Kronecker-product-based frames in CS model to measure sparse signals, where the orthogonal matching pursuit (OMP) [49] is deployed to recover the sparse signals. For a sparse signal $\mathbf{x}$, we select the support set $\mathcal{K}\subset \{1,\cdots ,N\}$ randomly, where $\left|\mathcal{K}\right|=s\ll N$. The non-zero elements are drawn from the complex Gaussian distribution with zero mean and variance 1.

Then, $\mathbf{x}$ is normalized to ${∥\mathbf{x}∥}_2=1$. The linear measurement $\mathbf{y}\in {\mathbb{C}}^{m\times 1}$ is given as

$$\mathbf{y}=\mathbf{A}\mathbf{x}+\mathbf{n},$$

(20)

where $\mathbf{A}\in {\mathbb{C}}^{m\times N}$ is a measurement matrix. The additive white Gaussian noise (AWGN) vector is $\mathbf{n}\sim \mathcal{CN}(\mathbf{0},{\sigma }_N^2\mathbf{I})$. The signal-to-noise ratio (SNR) is defined as $\mathbb{E}({∥\mathbf{A}\mathbf{x}∥}_2^2)/\left(m{\sigma }_N^2\right)$, and we fix the SNR to 15 dB. We assume that the OMP has the prior knowledge of the sparsity s.

We recover $I_s$ = 10,000 signals for sparse recovery performance. We denote the ith original and recovered signal by ${\mathbf{x}}^{\left(i\right)}$ and ${\widehat{\mathbf{x}}}^{\left(i\right)}$, respectively. We also denote the ith original and recovered support set by ${\mathcal{K}}^{\left(i\right)}$ and ${\widehat{\mathcal{K}}}^{\left(i\right)}$, respectively. The mean squared error (MSE) is defined as $I_s^{-1}{\sum }_{i=1}^{I_s}{∥{\mathbf{x}}^{\left(i\right)}-{\widehat{\mathbf{x}}}^{\left(i\right)}∥}_2^2$, and the success rate of support set recovery is defined as $|\mathcal{K}\cap \widehat{\mathcal{K}}|/|\mathcal{K}|$.

In simulations, the CS measurement matrix $\mathbf{A}$ is from the optimized harmonic, optimized Hadamard-based, random Kronecker-product-based, and optimized Kronecker-product-based frames, respectively, where $N=256$ and $m=64$. For random Kronecker-product-based and optimized Kronecker-product-based frames, we set $q=16$. In Figure 4, we show the sparse recovery performance for the four frames in CS. If the sparsity s is small, e.g., $s\le 19$, the optimized harmonic, optimized, and random Kronecker-product-based frames show almost the same performances of success rate and MSE, respectively. Meanwhile, if $s\ge 20$, the success rate and the MSE of random Kronecker-product-based frames becomes worse than those of the optimized Kronecker-product-based and optimized harmonic frames due to their high coherence. Figure 4 reveals that the optimized Hadamard-based frames show the worst performance of success rate and MSE. From the distribution of inner product magnitudes of all possible frame vector pairs, we observed that the optimized Hadamard-based frame has discrete magnitudes of inner products, and many pairs have large magnitudes of inner products, although the largest one is smaller than that of the random Kronecker-product-based frame. Thus, many frame vectors of large inner products are likely to be involved in CS measurement process, which will degrade the CS recovery performance of optimized Hadamard-based frame.

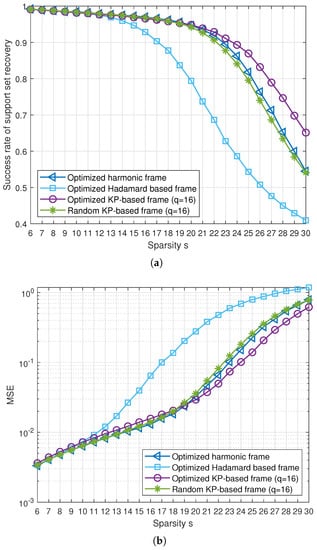
Figure 4. Performance of sparse signal recovery for various frames of $N=256$ and $m=64$. (a) Success rate of support set recovery, (b) mean squared error (MSE).

Moreover, if $s\ge 20$, we observed the optimized Kronecker-product-based frame with $q=16$ achieves better performance of success rate and MSE than the optimized harmonic frame. To investigate this observation, we compare the distributions of the average magnitudes of inner products for randomly selected 30-frame vectors in the optimized harmonic and the optimized Kronecker-product-based frames, respectively. We performed 10,000 random trials of selecting the frame vectors and averaged the inner product magnitudes to sketch the histogram. Figure 5 shows that if 30-frame vectors are selected, the optimized Kronecker-product-based frame tends to have lower inner products on average than the optimized harmonic frame, which implies that OMP will be more likely to detect a support set of 30 non-zero entries in the optimized Kronecker-product-based frame. Because the higher sparsity s requires a larger number of frame vectors to be distinguished, it will be more helpful for CS recovery if the average magnitude of the inner products of a frame is lower. Therefore, Figure 5 demonstrates that the optimized Kronecker-product-based frame is advantageous in high sparsity s.

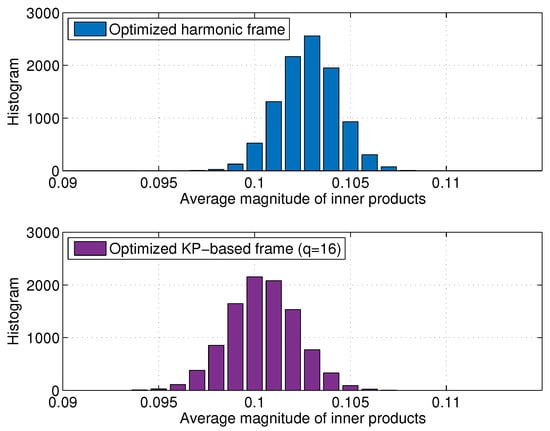
Figure 5. The distribution of average magnitude of inner products for 30-frame vectors randomly selected from the optimized harmonic and Kronecker-product-based frames, where $N=256$ and $m=64$.

6. Conclusions

In this paper, we designed the Kronecker-product-based frame with low mutual coherence and a small number of phases, which is advantageous in practical applications. Utilizing the block-wise circulant feature of the Gram matrix, we derived a novel objective function to optimize the mutual coherence with low computational complexity. To find a subsampling index set for the Kronecker-product-based frame using the objective function, we used Algorithm 2 in [41] by modifying the optimization problem for the Kronecker-product-based frame. Simulation results show that the optimized Kronecker-product-based frames have similar mutual coherence as the optimized harmonic frames, although ours have a smaller number of phases. In particular, we obtained the ETFs in N = 64, m = 28 for $q=4,8$. To the best of our knowledge, these ETFs are new ones that have never been reported. These ETFs with a small number of phases can be easily generated by the Kronecker product of Fourier and Hadamard matrices, which is suitable for practical applications. Finally, we applied the Kronecker-product-based frames for sparse signal recovery in compressed sensing. We demonstrated that the optimized Kronecker-product-based frames achieve similar performances of success rate in support set recovery and MSE of the optimized harmonic frames.

The novelty of our work is to present an efficient objective function to optimize mutual coherence with low complexity for the Kronecker product of Fourier and Hadamard matrices. Furthermore, the algorithmic method for frame design allows us to obtain the frames with arbitrary frame vector length m. In conclusion, the Kronecker-product-based frames designed by a novel objective function can be suitable for practical applications thanks to the low mutual coherence and a small number of phases. Applying our designed frames for real-life applications will remain for future work.