Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area
Abstract
1. Introduction
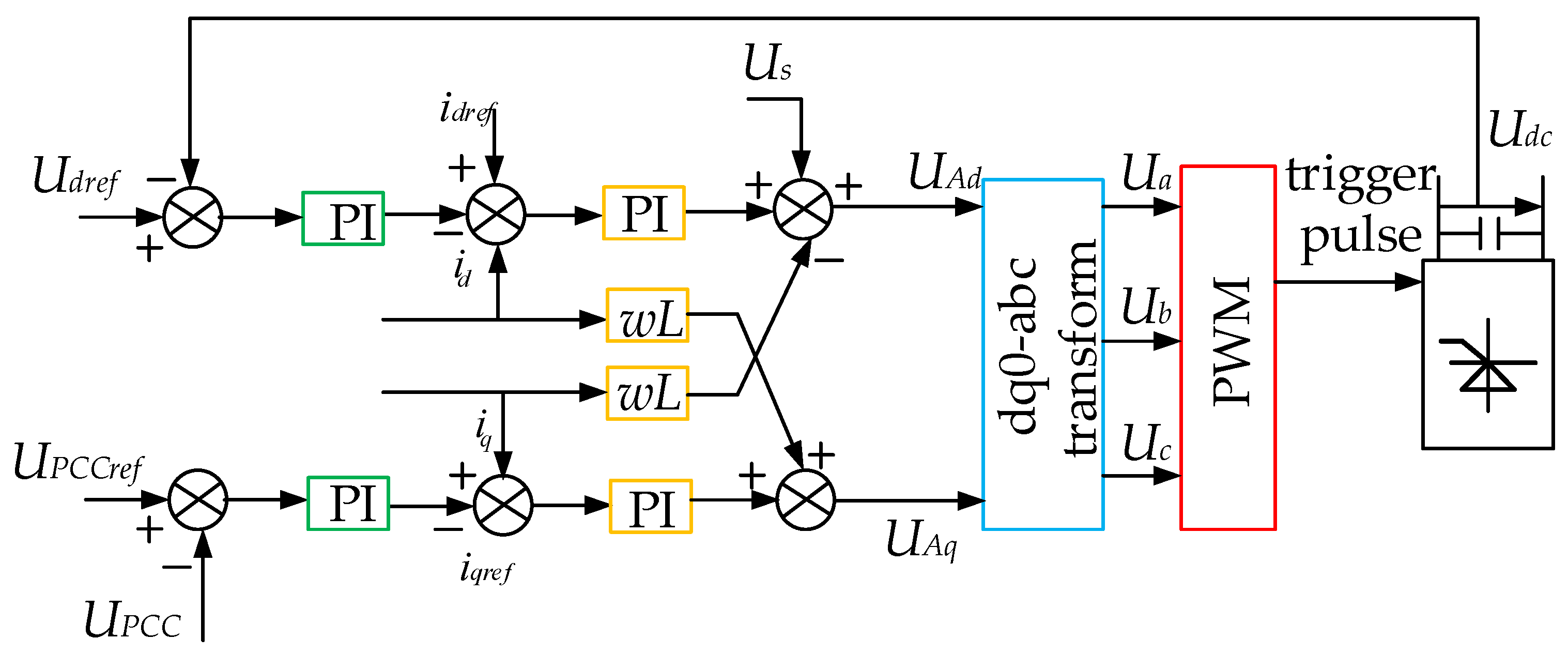
- Using the advantages of fast response and strong economy of the combined reactive power compensation device, a control strategy for the reactive power compensation system based on the wind farm is formulated. This strategy not only avoids the frequent switching of capacitor banks but also guarantees the linear demand of the system for reactive power.
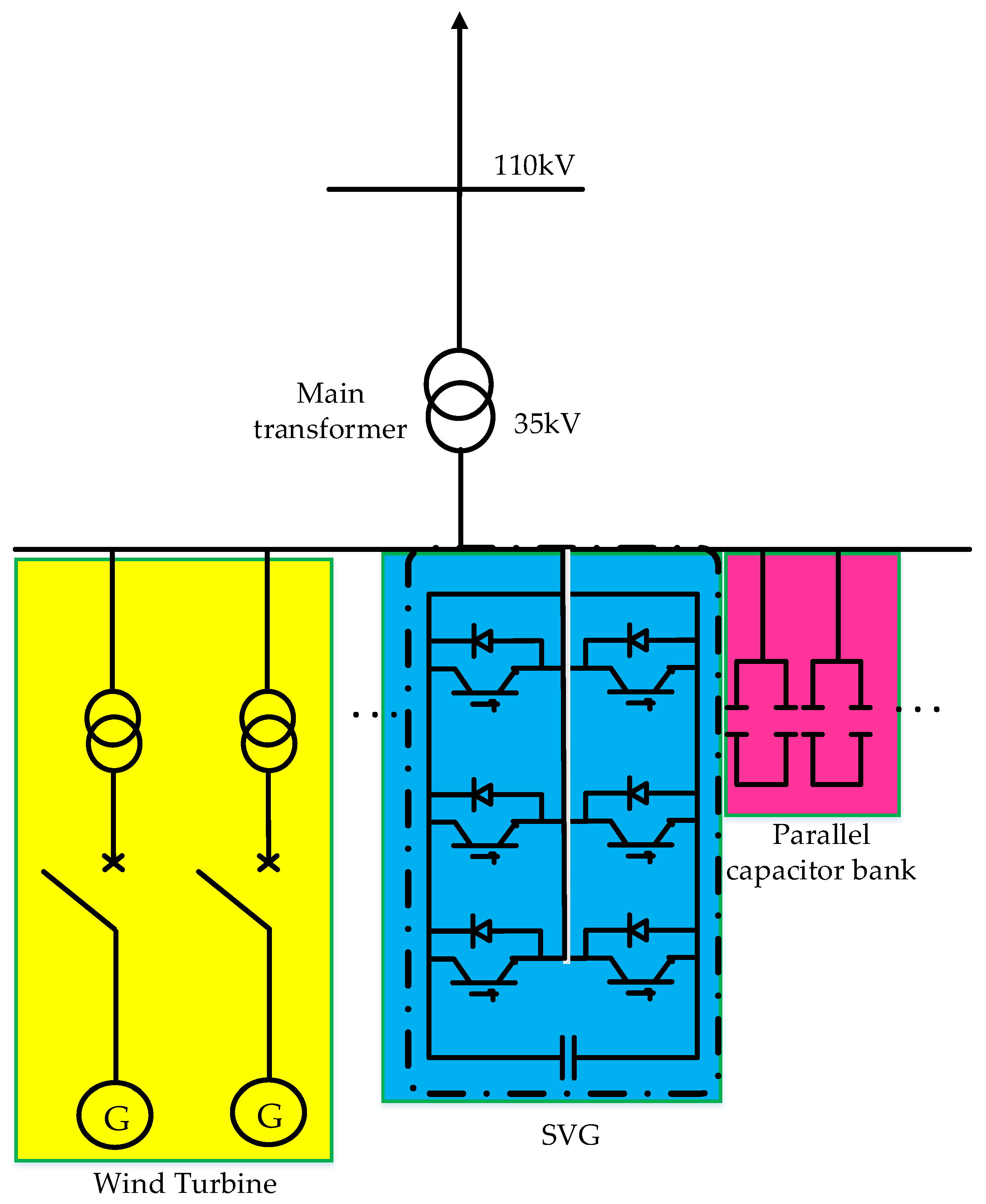
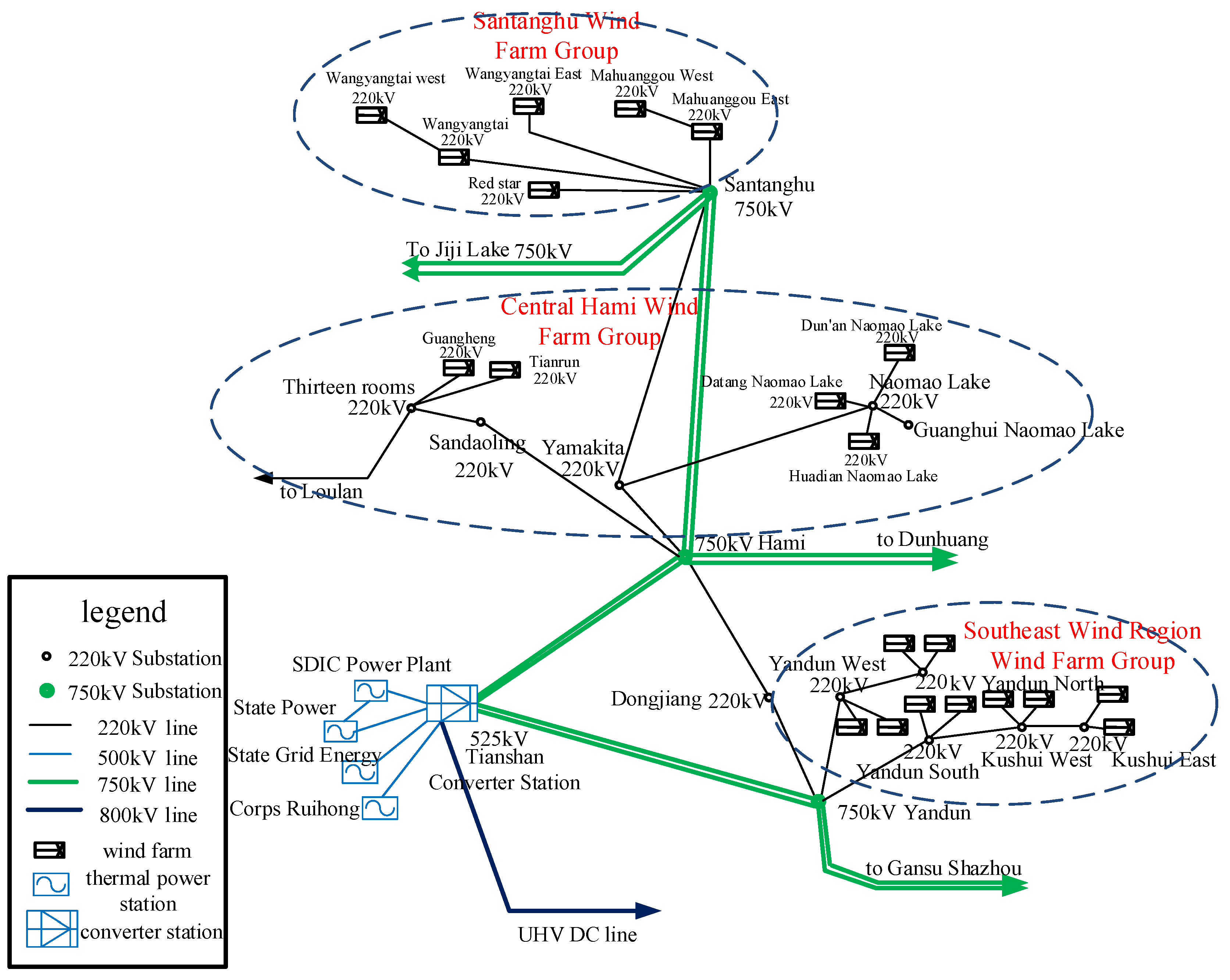
- The active power margin and modal numerical analysis of the wind power gathering area in the Hami area show that the Mahuanggou east wind farm, located in the Santanghu wind area, is the weak node of voltage in this area, so this area is the best place to install reactive power compensation devices.
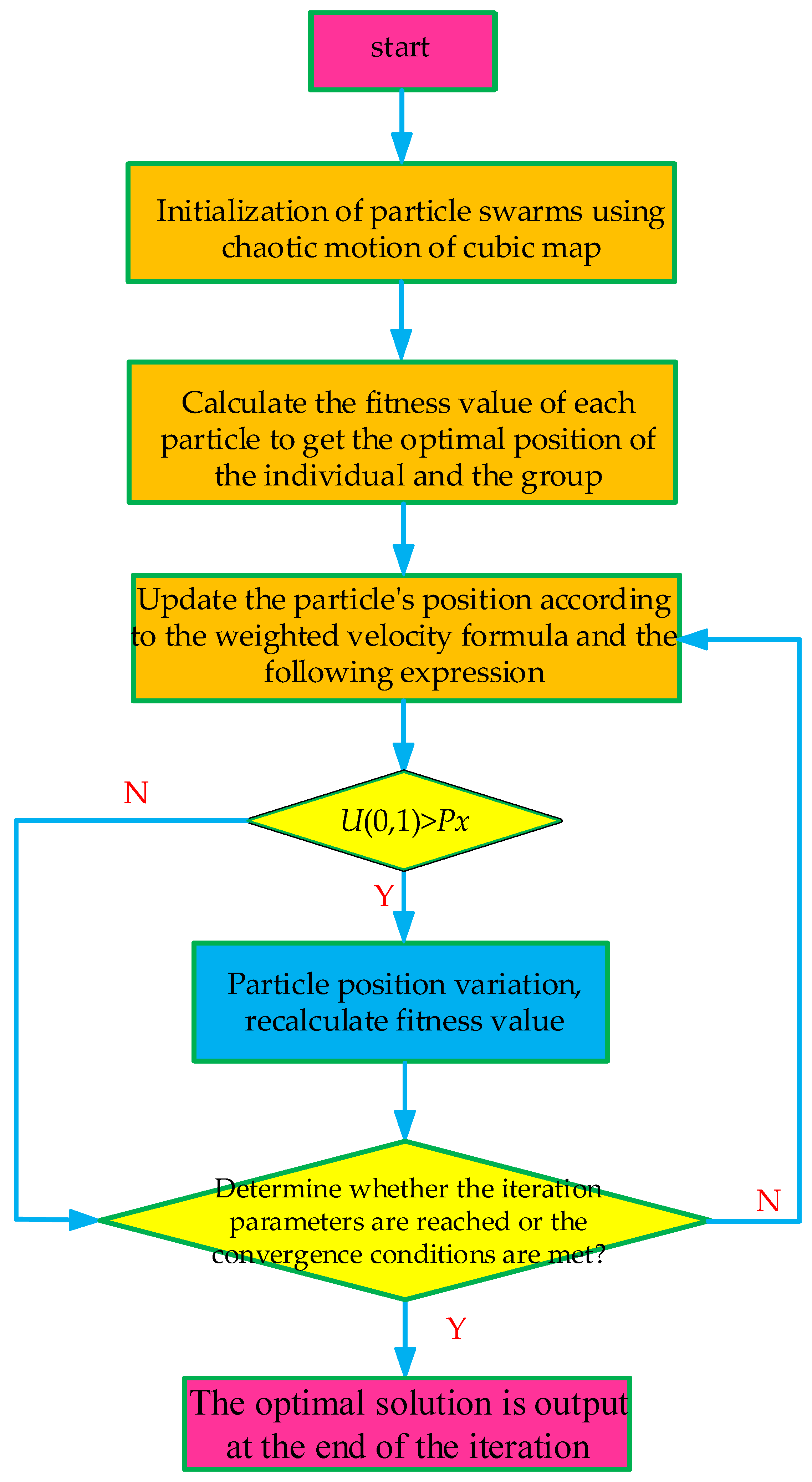
- The improved particle swarm algorithm is used to optimize the capacity of the optimal reactive power compensation device, which ensures the best performance of the compensation device.
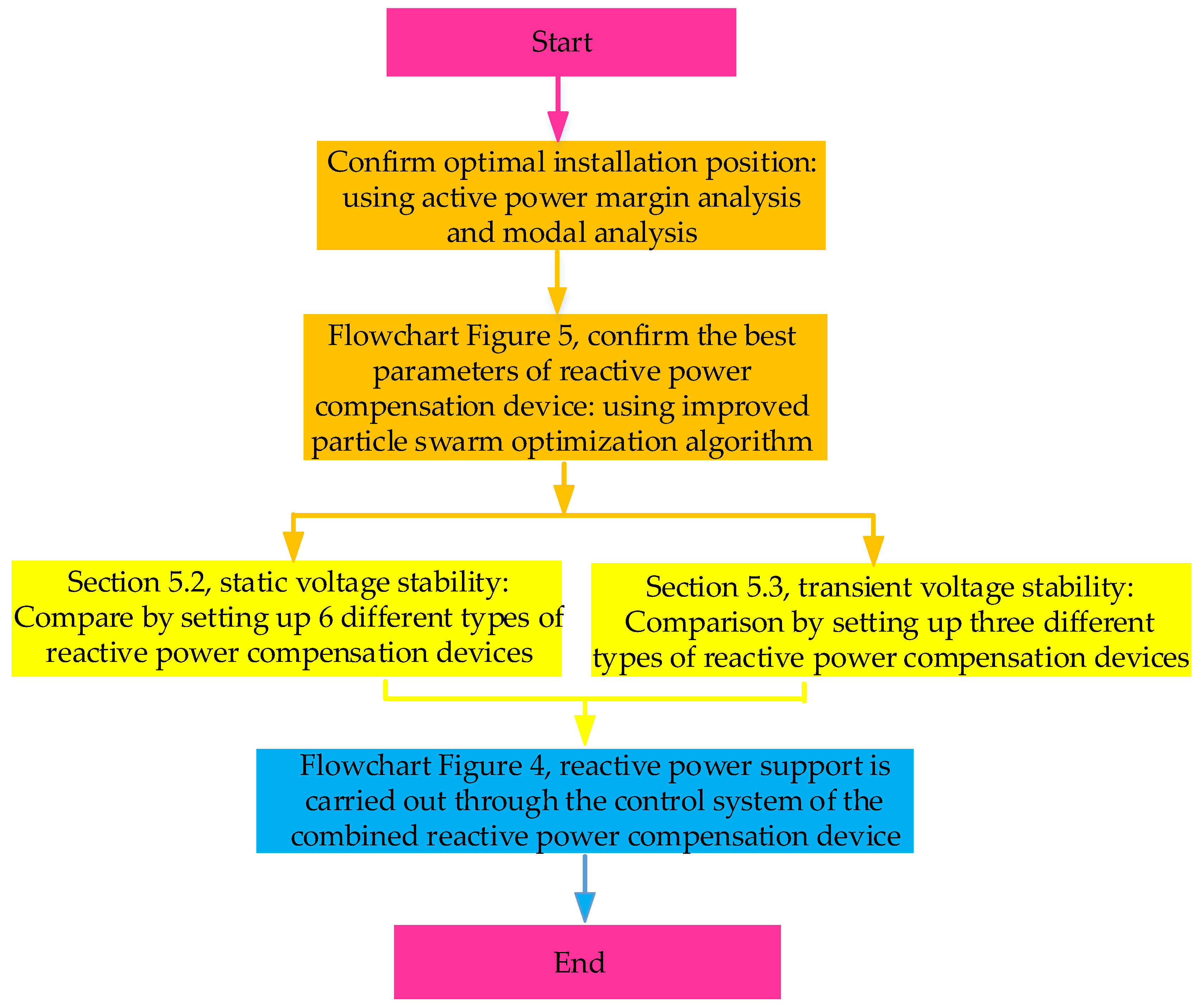
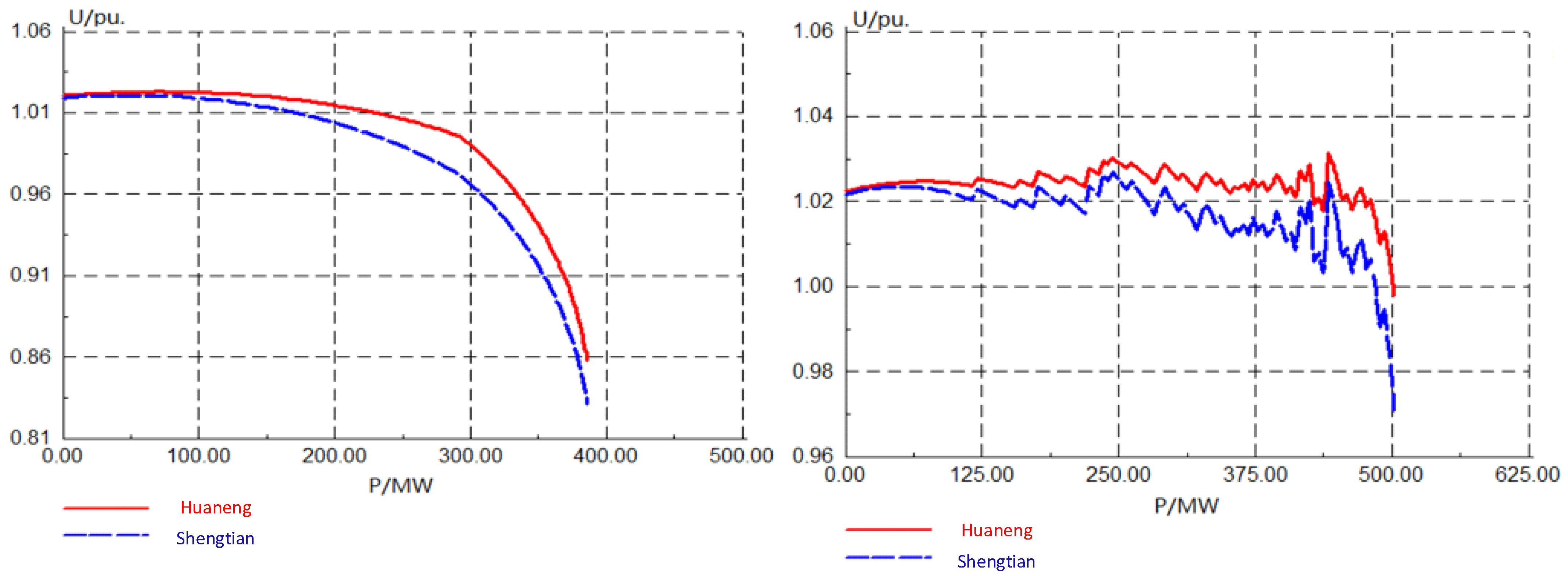
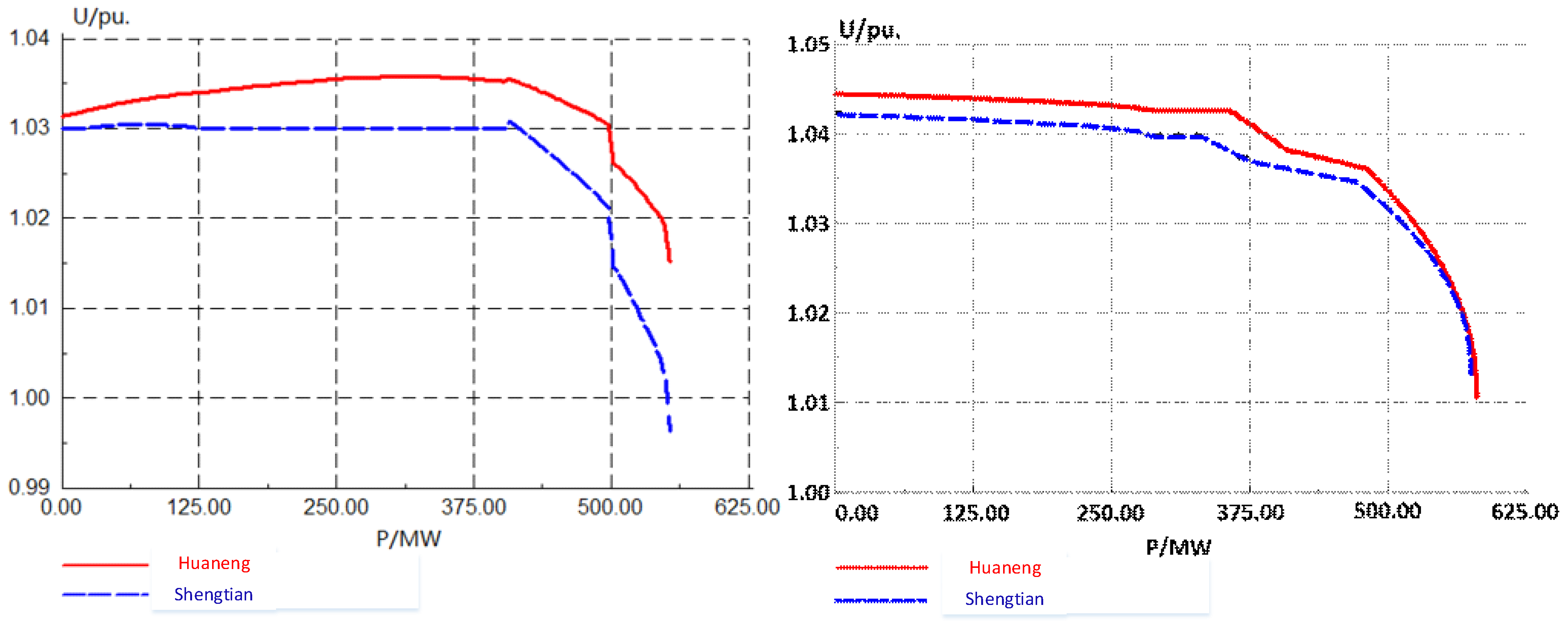
- Using PSCAD simulation software to model the power grid in the Hami area, six different reactive power compensation device configuration programs are set up for static voltage stability simulation verification, as well as three different reactive power compensation device combination programs for transient voltage stability simulation verification.
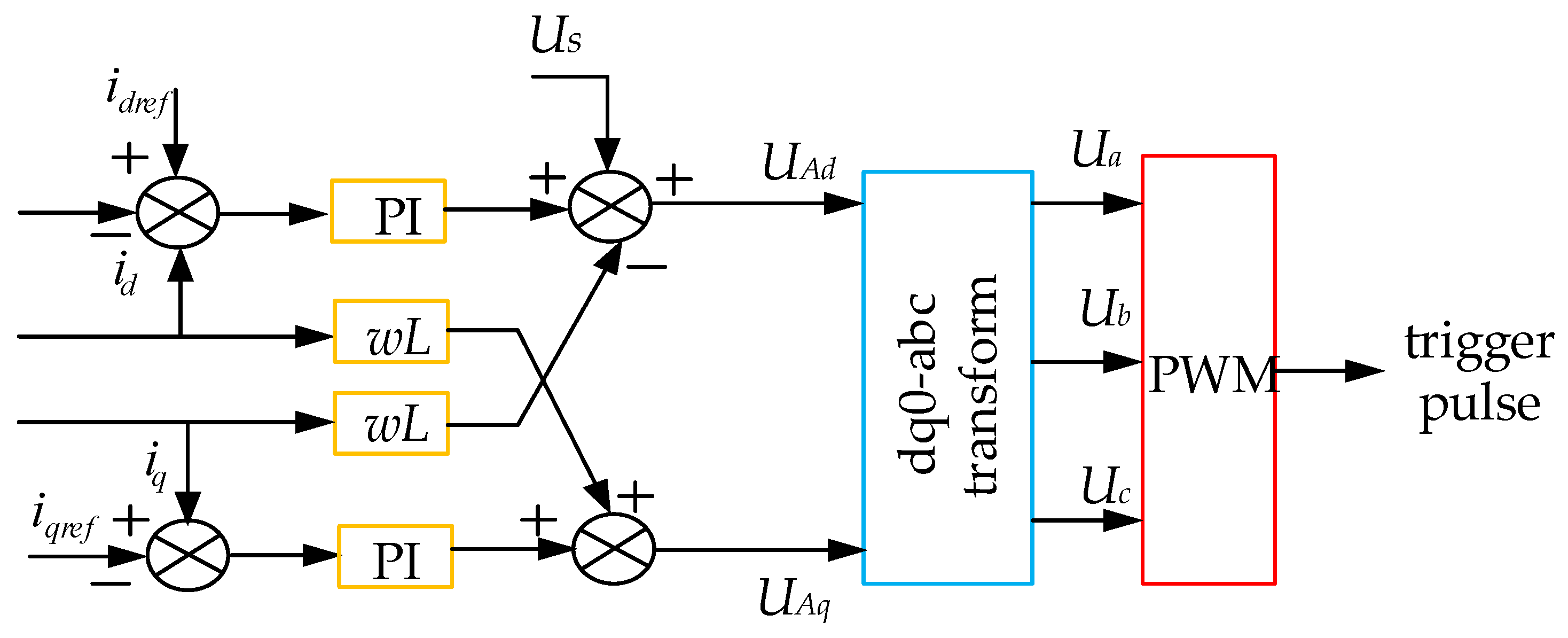
2. Research the Basic Characteristics and Compensation Strategy of SVG
3. Control Strategy of Hybrid Reactive Power Compensation System
4. Parameter Configuration of Reactive Power Compensation System
4.1. Improved Particle Swarm Optimization
4.2. Parameter Optimization of Reactive Power Compensation System
5. Simulation and Verification of Hybrid Reactive Power Compensation Program
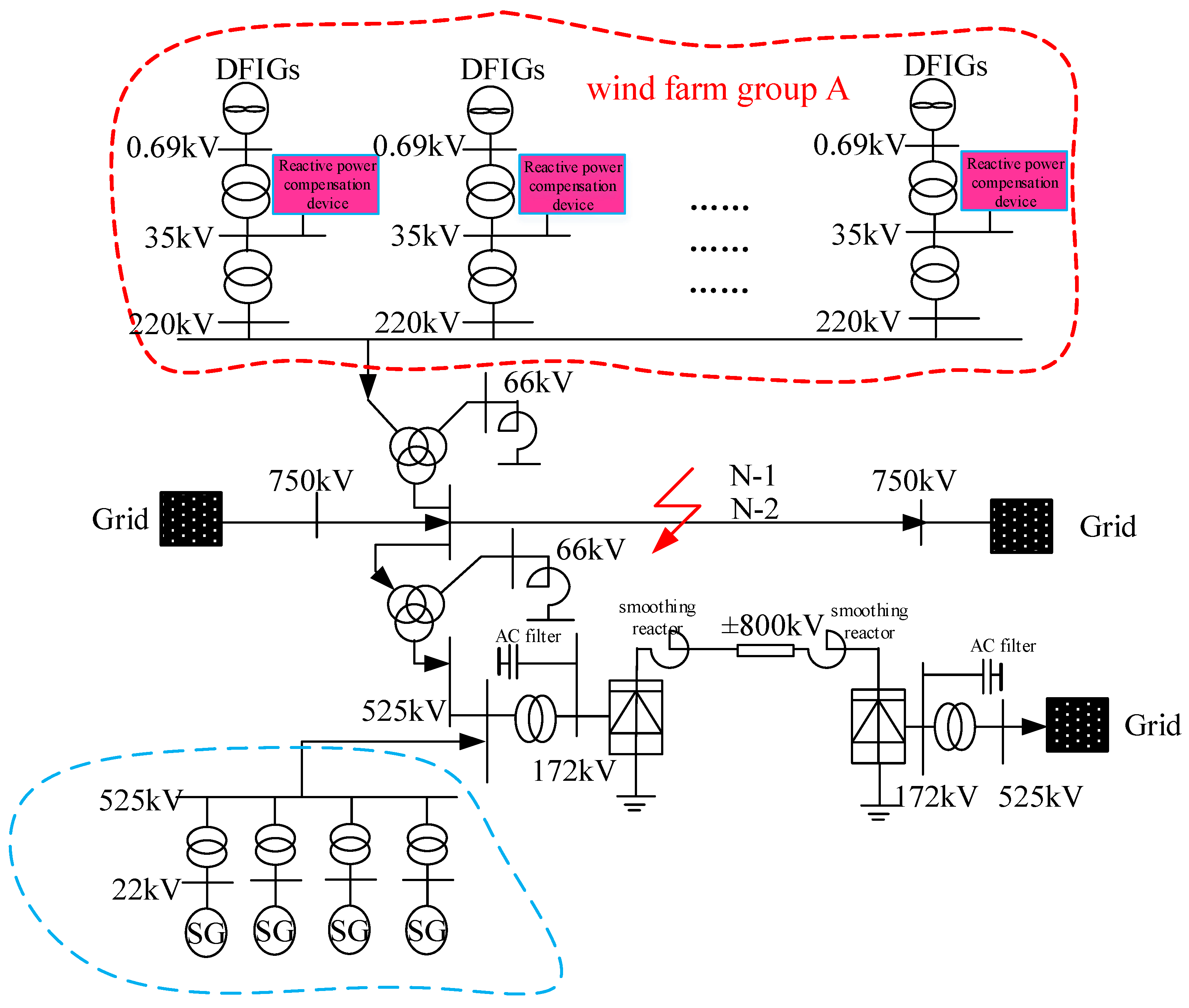
5.1. Analysis of the Best Installation Location
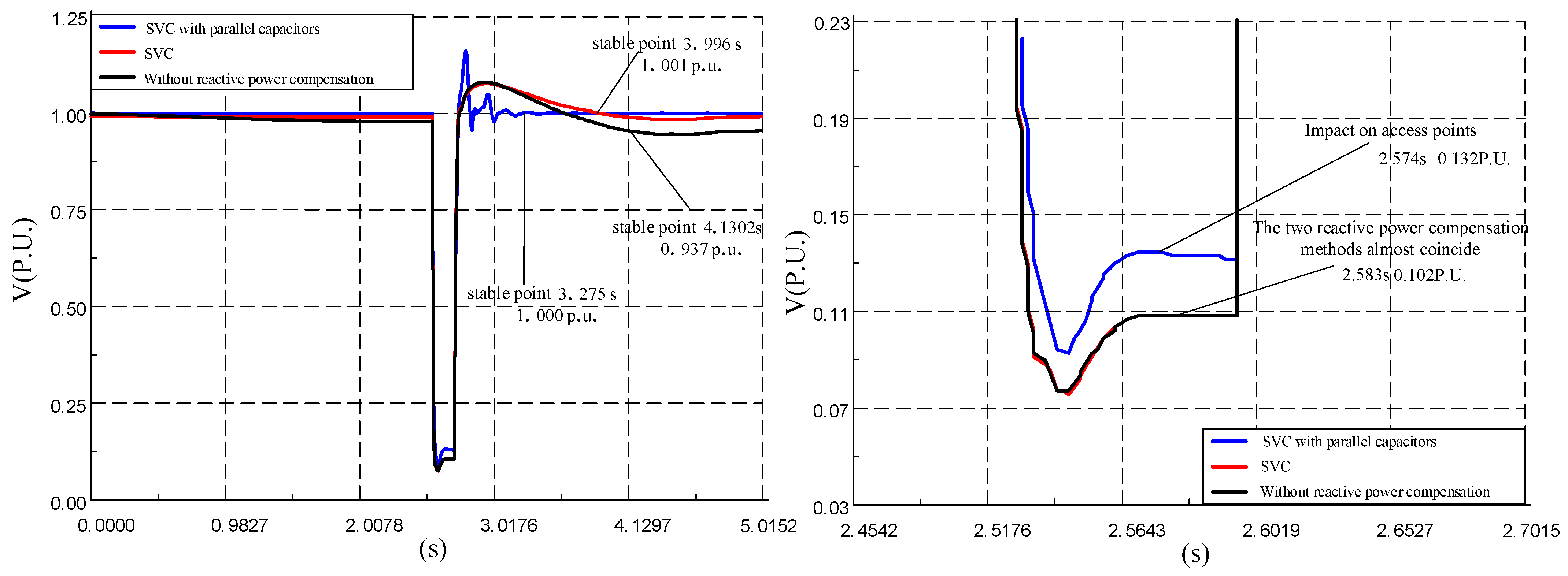
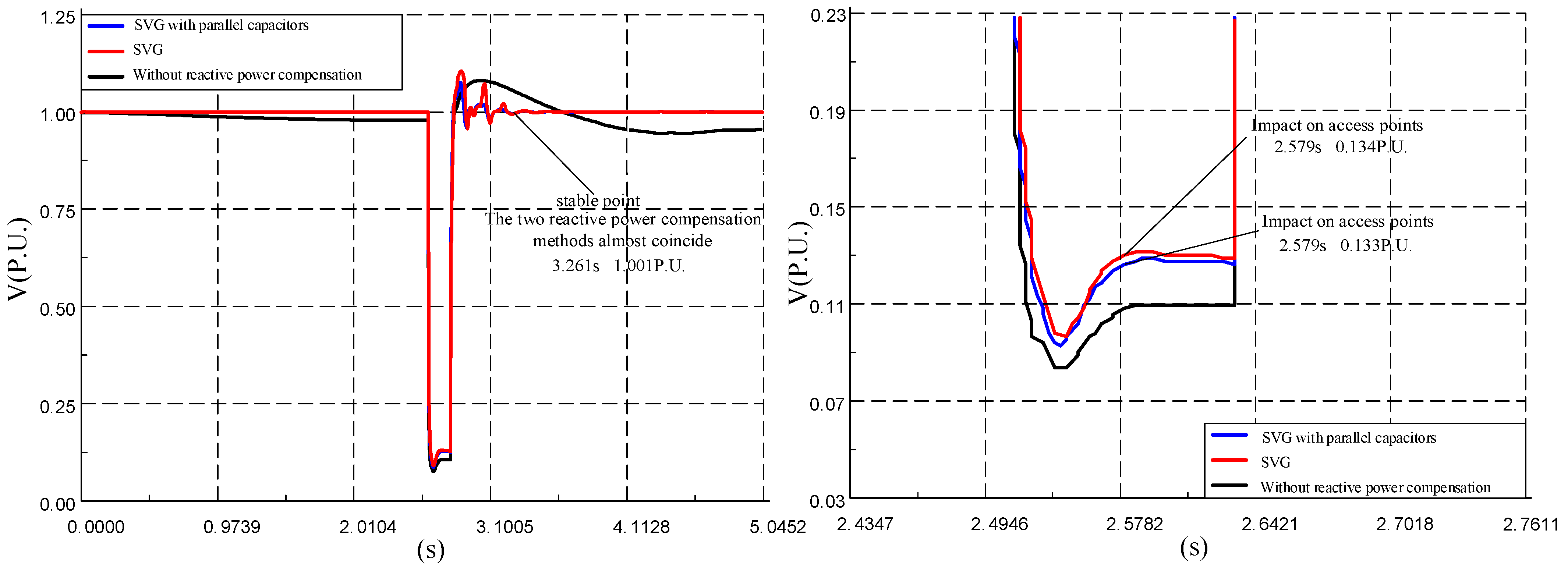
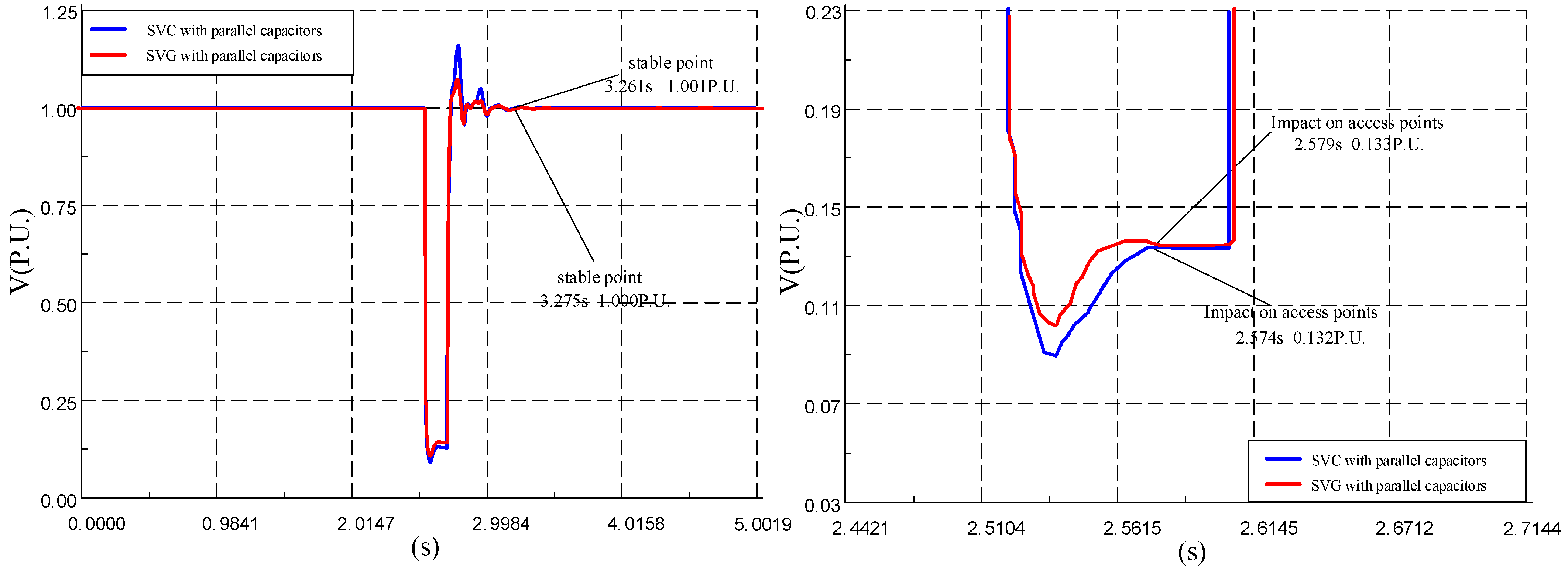
5.2. Static Voltage Stability Simulation Verification
5.3. Transient Voltage Stability Simulation Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, X.C.; Wang, W.Q.; Shi, R.J.; Cheng, Z.J. Hybrid Pluripotent Coupling System with Wind and Photovoltaic-Hydrog Enenergy Storage and the Coal Chemical Industry in Hami, Xinjiang. Renew. Sustain. Energy Rev. 2017, 72, 950–960. [Google Scholar] [CrossRef]
- Xu, L.J.; Fan, X.C.; Wang, W.Q. Renewable and sustainable energy of Xinjiang and development strategy of node areas in the “Silk Road Economic Belt”. Renew. Sustain. Energy Rev. 2017, 79, 274–285. [Google Scholar] [CrossRef]
- Psarros, G.N.; Tsourakis, G.I.; Papathanassiou, S.A. Dimensioning of Reactive Power Compensation in an Autonomous Island System. Appl. Sci. 2022, 12, 2827. [Google Scholar] [CrossRef]
- Chompoo-inwai, C.; Yingvivatanapong, C.; Methaprayoon, K.; Lee, W.J. Reactive Compensation Techniques to Improve Theride-Through Capability of Wind Turbine During Disturbance. IEEE Trans. Ind. Appl. 2005, 41, 666–672. [Google Scholar] [CrossRef]
- Pereira, R.M.M.; Ferreira, C.M.M.; Barbosa, F.P.M. Comparative Study of STATCOM and SVC Performance on Dynami-c Voltage Collapse of an Electric Power System with Wind Generation. IEEE Latin Am. Trans. 2014, 12, 138–145. [Google Scholar] [CrossRef]
- Peng, Y.Z.; Wang, H.Y.; Wang, W.Q. 110 kV Artificial Short-Circuit Test and Result Analysis of Xinjiang Power Grid Wind power base. Autom. Electr. Power Syst. 2020, 44, 226–231. [Google Scholar]
- Zhao, Y.H.; Xia, Y.; Zhou, Q.Y. Coordinated Control Strategy and Configuration Scheme of Reactive Power Compensation Device in DC System of Air-fire baling DC Delivery System. Power Grid Technol. 2016, 40, 2081–2086. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhang, Q.P.; Wang, Y.T. Research on Reactive Power Compensation Measures to Improve the Safety and Stability Level of 750kV Transmission Terminal Power Grid in Xinganqing, Northwest China. Proc. CSEE 2015, 35, 1015–1022. [Google Scholar] [CrossRef]
- Yang, G.; Li, L.; Zhang, X. Numerical and Experimental Analysis of CSR of Transformer Type for Bidirectional Reacti-ve Power Compensation. IEEE Trans. Appl. Supercond. 2016, 26, 5500704. [Google Scholar] [CrossRef]
- Joksimovic, G. Transformer Reactive Power Compensation–Fixed Capacitor Bank Calculation. IEEE Trans. Power Deliv. 2015, 30, 1629–1630. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, N.; Cui, X.; Fu, Z. Research on Reactive Compensation Technology Based on SVC-APF. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, IAEAC, Chongqing, China, 12–14 October 2018; pp. 1547–1551. [Google Scholar] [CrossRef]
- Singh, B.; Niwas, R.; Dube, S.K. Load Leveling and Voltage Control of Permanent Magnet Synchronous Generator-Based DG Set for Standalone Supply System. IEEE Trans. Ind. Inform. 2014, 10, 2034–2043. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Multifunctional Hybrid Structure of SVC and Capacitive Grid-Connected Inverter (SVC//CGCI) for Active Power Injection and Nonactive Power Compensation. IEEE Trans. Ind. Electron. 2019, 66, 1660–1670. [Google Scholar] [CrossRef]
- Wang, L.; Truong, D. Stability Enhancement of a Power System with a PMSG-Based and a DFIG-Based Offshore Wind Farm Using a SVC with an Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Ind. Electron. 2013, 60, 2799–2807. [Google Scholar] [CrossRef]
- He, H.; Lu, Z.; Guo, X.; Shi, C.; Jia, D.; Chen, C.; Guerrero, J.M. Optimized Control Strategy for Photovoltaic Hydrogen Generation System with Particle Swarm Algorithm. Energies 2022, 15, 1472. [Google Scholar] [CrossRef]
- Rather, Z.H.; Chen, Z.; Thøgersen, P.; Lund, P. Dynamic Reactive Power Compensation of Large-Scale Wind Integrated Power System. IEEE Trans. Power Syst. 2015, 30, 2516–2526. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Hybrid Structure of Static Var Compensator and Hybrid Active Power Filter (SVC//HAPF) for Medium-Voltage Heavy Loads Compensation. IEEE Trans. Ind. Electron. 2018, 65, 4432–4442. [Google Scholar] [CrossRef]
- Wang, L.; Lao, K.; Lam, C.; Wong, M. Delta-connected static var compensator (SVC) based hybrid active power filter (SVC-HAPF) and its control method. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 6384–6388. [Google Scholar] [CrossRef]
- Shokouhandeh, H.; Latif, S.; Irshad, S.; Ahmadi Kamarposhti, M.; Colak, I.; Eguchi, K. Optimal Management of Reactive Power Considering Voltage and Location of Control Devices Using Artificial Bee Algorithm. Appl. Sci. 2022, 12, 27. [Google Scholar] [CrossRef]
- Zhang, K.j.; Wang, X.; Bing, H. Research on Reactive Power Compensation Based on Magnetic Saturation Controllable Reactor. IEEE Access 2022, 10, 31377–31384. [Google Scholar] [CrossRef]
- Keskes, S.; Salleem, S.; Chrifi-Alaoui, L.; Ali Kammoun, M.B. Nonlinear Coordinated Passivation Control of Single Ma-chine Infinite Bus Power System with Static Var Compensator. J. Mod. Power Syst. Clean Energy 2021, 9, 1557–1565. [Google Scholar] [CrossRef]
- Ouyang, J.; Li, M.; Zhang, Z.; Tang, T. Multi-Timescale Active and Reactive Power-Coordinated Control of Large-Scale Wind Integrated Power System for Severe Wind Speed Fluctuation. IEEE Access 2019, 7, 51201–51210. [Google Scholar] [CrossRef]
- Ghosh, S.; Isbeih, Y.J.; Bhattarai, R.; Moursi, M.S.E.; El-Saadany, E.F.; Kamalasadan, S. A Dynamic Coordination Control Architecture for Reactive Power Capability Enhancement of the DFIG-Based Wind Power Generation. IEEE Trans. Power Syst. 2020, 35, 3051–3064. [Google Scholar] [CrossRef]
- Hua, Y.Z.; Xie, Q.Q.; Zheng, L.; Cui, J.d.; Shao, L.H.; Hu, W.W. Coordinated Voltage Control Strategy by Optimizing the Limited Regulation Capacity of Air Conditioners. Energies 2022, 15, 3225. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Xue, Y.; Liu, W. Reactive Power Compensation and Optimization Strategy for Grid-Interactive Cascaded Photovoltaic Systems. IEEE Trans. Power Electron. 2015, 30, 188–202. [Google Scholar] [CrossRef]
- Xiao, M.X.; Wang, F.; He, Z.X.; Ouyang, H.L.; Hao, R.Y.F.; Xu, Q.M. Power Control and Fault Ride-Through Capability Analysis of Cascaded Star-Connected SVG under Asymmetrical Voltage Conditions. Energies 2019, 12, 2361. [Google Scholar] [CrossRef]
- Wan, Y.; Murad, M.A.A.; Liu, M.; Milano, F. Voltage Frequency Control Using SVC Devices Coupled with Voltage Dependent Loads. IEEE Trans. Power Syst. 2019, 34, 1589–1597. [Google Scholar] [CrossRef]
- Almohaimeed, S.A.; Abdel-Akher, M. Power Quality Issues and Mitigation for Electric Grids with Wind Power Penetration. Appl. Sci. 2020, 10, 8852. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q.; Wang, F.; Burgos, R. Wind Energy System with Integrated Functions of Active Power Transfer, Reactive Power Compensation, and Voltage Conversion. IEEE Trans. Ind. Electron. 2013, 60, 4512–4524. [Google Scholar] [CrossRef]
- Liu, B.; Wang, M.; Men, J.; Yang, D. Microgrid Trading Game Model Based on Blockchain Technology and Optimized Particle Swarm Algorithm. IEEE Access 2020, 8, 225602–225612. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Wang, X.W.; Yang, J.J. Modified Particle Swarm Optimization with Attention-Based LSTM for Wind Power Prediction. Energies 2022, 15, 4334. [Google Scholar] [CrossRef]
- Javed, M.Y.; Khurshid, I.A.; Asghar, A.B.; Rizvi, S.T.H.; Shahid, K.; Ejsmont, K. An Efficient Estimation of Wind Turbine Output Power Using Neural Networks. Energies 2022, 15, 5210. [Google Scholar] [CrossRef]
- Martinez-Lucas, G.; Sarasua, J.I.; Fernandez-Guillamon, A.; Molina-Garcia, A. Combined hydro-wind frequency control scheme: Modal analysis and isolated power system case example. Renew. Energy 2021, 180, 1056–1072. [Google Scholar] [CrossRef]
- Dorile, P.O.; Jagessar, D.R.; Guardado, L.; McCann, R.A.; Ahanch, M. Grid strength assessment and maximum loadability of a wind-dominated power system through QV modal analysis. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Power Africa 2021, Nairobi, Kenya, 13–27 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Mugnaini, V.; Zanotti Fragonara, L.; Civera, M. A machine learning approach for automatic operational modal analysis. Mech. Syst. Signal Proc. 2022, 170, 108813. [Google Scholar] [CrossRef]


| Month | Active Capacity (MW) | Reactive Capacity (MVar) | Power Factor | Assessment Reward/RMB |
|---|---|---|---|---|
| June | 1252 | 565 | 0.91 | 1247.83 |
| July | 1009 | 462 | 0.91 | 1039.80 |
| August | 1175 | 531 | 0.91 | 1173.31 |
| September | 1444 | 532 | 0.94 | 5727.96 |
| October | 1238 | 368 | 0.96 | 6369.16 |
| November | 1089 | 234 | 0.98 | 5492.54 |
| Area | Active Capacity (MW) | Reactive Capacity (MVar) | Active Power Margin KP (%) |
|---|---|---|---|
| Santanghu wind area | 2582.3 | 1324.5 | 5.7 |
| Southeast wind area | 1791.3 | 3401.2 | 15.8 |
| Central Hami | 521.8 | 1759.6 | 65.4 |
| Wind Area | Wind Farm Bus (220 kV) | Voltage Stability Modal Values/p.u. |
|---|---|---|
| Southeast wind area | Kushui West wind farm | 0.027562346 |
| Kushui East wind farm | 0.025684795 | |
| Yandun South wind farm | 0.021016546 | |
| Yandun West wind farm | 0.020150621 | |
| Yandun North wind farm | 0.016542154 | |
| Central Hami wind area | Naomaohu wind farm | 0.043562145 |
| Guanghui Naomaohu wind farm | 0.040561425 | |
| Shisanjianfang wind farm | 0.045462154 | |
| Santanghu wind area | Red Star wind farm | 0.032456218 |
| Wangyangtai wind farm | 0.027658974 | |
| Wangyangtai east wind farm | 0.028562016 | |
| Wangyangtai west wind farm | 0.027146484 | |
| Mahuanggou west wind farm | 0.015025153 | |
| Mahuanggou east wind farm | 0.014876213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Wang, H.; Zhao, Q.; Nan, D.; Li, W. Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area. Appl. Sci. 2022, 12, 10906. https://doi.org/10.3390/app122110906
Peng Y, Wang H, Zhao Q, Nan D, Li W. Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area. Applied Sciences. 2022; 12(21):10906. https://doi.org/10.3390/app122110906
Chicago/Turabian StylePeng, Yinzhang, Haiyun Wang, Qi Zhao, Dongliang Nan, and Wenxin Li. 2022. "Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area" Applied Sciences 12, no. 21: 10906. https://doi.org/10.3390/app122110906
APA StylePeng, Y., Wang, H., Zhao, Q., Nan, D., & Li, W. (2022). Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area. Applied Sciences, 12(21), 10906. https://doi.org/10.3390/app122110906





