Abstract
As one of the most catastrophic natural disasters worldwide, earthquakes and their effect on structures are very important to structural health monitoring (SHM), particularly for the ones living around the Pacific ring of fire. In this regard, SHM techniques with real-time or online processing can be used to identify states of structures, track modal parameters, provide a warning message about damage, and help post-earthquake reconnaissance and rehabilitation. For instance, a recursive formulation based on subspace identification (SI) has been demonstrated that it is capable to track system changes. In this study, a recursive subspace identification (RSI) algorithm with a fixed window is proposed to investigate the time-varying dynamic characteristics under seismic excitations. Subsequently, some suggestion is described and discussed for practical implementation. For verifying the proposed algorithm, different datasets from full-scale experiments are applied to examine its applicability. In other words, the practicability of implementing RSI in real-time or online has been developed and examined in this paper.
1. Introduction
Structural health monitoring (SHM) is continuously emerging in the field of civil and structural engineering as it is an efficient way to monitor the current state of infrastructure. A well-developed SHM technique can provide useful information about the existence, location, and severity of damage [1], especially during and after a destructive input. For example, as one of the most catastrophic natural disasters worldwide, earthquakes often caused serious damage to structures in a moment. Therefore, the development of real-time or online processing is essential for SHM systems under seismic excitations.
Vibration-based SHM methods are the most common SHM techniques; they are based on the conceptual idea of a modal domain that changes in modal parameters, such as modal frequencies, damping ratios, and mode shapes, are a result of changes in the physical mass, damping, and stiffness properties of the structure [2]. To track the variation and detect the damage, vibration-based SHM methods need to be continuous and autonomous during seismic events for providing timely information and warnings. In the 1990s, Loh et al. introduced least-square estimation (LSE) to detect the changes in structural parameters under seismic excitations [3,4]. For nonlinear hysteretic structural systems, LSE approaches have been employed to identify cumulative damage [5,6]. Later, sequential non-linear LSE (SNLSE) has been developed based on acceleration responses, which is more practical in the field application [7]. Apart from LSE approaches, Hoshiya and Saito first adopted a filtering approach to iteratively identify structural systems [8]. In 2004, Yang et al. extended and used Kalman filter to adaptively track parameter changes [9,10]. Then, Kalman filter approach was applied to nonlinear systems [11,12] and verified via experiments [7,8]. Moreover, other filtering approaches, such as H∞ filter [13] and Monte Carlo filter [14], have been proposed to track parameters over time.
During the past few decades, subspace identification (SI) and its relative approaches have attracted substantial interest in system identification, damage detection, and structural control since they can directly identify the system matrices from input and output data. Several well-known SI algorithms, including CVA (canonical variate analysis) [15], N4SID (numerical algorithms for subspace state space system identification) [16], PAST (projection approximation subspace tracking) [17], and so on, have been developed to identify structural systems and detect structural damage. To accommodate for real-time or online processing, various recursive forms have been proposed using either the matrix inversion lemma [18,19,20,21] or Yang’s criterion [22,23,24,25]. One of the major applications in the field of civil and structural engineering is to extract time-varying dynamic characteristics during seismic excitations. Compared to the LSE and filtering approaches, SI and its relative approaches have stable performance owing to the usage of geometry projection and less limitation on measurement because of the explicit input-output relationship. Consequently, SI based on the recursive formulation has been demonstrated to identify states of structures, track modal parameters, provide a warning message about damage, and help post-earthquake reconnaissance and rehabilitation [26,27,28,29,30].
In this study, a recursive subspace identification (RSI) algorithm originally developed in the field of control and automation is introduced to investigate the time-varying dynamic characteristics under seismic excitations. This algorithm is derived with a fixed window and, compared to the above-mentioned algorithms, the window length can be used to indicate extra time information. In Section 2, SI is first introduced to extract the system matrices and the modal parameters from input and output data. Furthermore, the proposed algorithm is carefully derived as a recursive form of SI to facilitate real-time or online processing. Then, some suggestions for practical implementation is described and discussed using numerical simulation in Section 3. To verify SHM applications based on RSI, two full-scale experiments using shaking tables were conducted and the proposed algorithm is applied to identify the modal parameters reclusively in Section 4. Last of all, brief summary and conclusion are drawn in Section 5 and some future research is illustrated.
2. Recursive Formulation
Considering a linear n degrees of freedom (DOFs) building structure subjected to seismic excitations, the equation of motion can be derived as the discrete-time state-space equations as
where xk is state vector with 2n states; yk is measured output vector with m measurement; uk is input vector with l excitations; wk and vk are the process and measurement noise, respectively; the subscript k denotes k-th step which indicates and ∆t is the sampling interval of measurement; A is linear elastic system matrix; B and D are excitation influence vector; C is output (or observer) matrix. Among those matrices, A and C are particularly important for the application of SHM and need to be frequently identified using SI.
2.1. Subspace Identification (SI)
To develop SI, the state-space equations need to be transformed into “Matrix Input-Output Equations” [31] as
where Yp and Yf are past and future output data Hankel matrices with i rows and j columns (both in samples), respectively.
Similarly, Up and Uf are past and future input data Hankel matrices. As a result, the dimension of Yp and Yf is and the dimension of Up and Uf is . Δi is the reversed extended controllability matrix; Hi and Gi are the lower block triangular Toeplitz matrices. Γi is extended observability matrix which contains information of system matrices (A and C) and is the primary outcome of subspace identification. Details about those matrices can be also found in the literature [31]. So, the problem of identifying the system matrices is identifying the extended observability matrix.
To extract the key matrix, a geometric tool, called projection in the field of linear algebra, is utilized to obtain the extended observability matrix from the matrix input-output equations. Both orthogonal and oblique projections can be used to extract the extended observability matrix and the “Multivariable Output-Error State sPace (MOESP)” is especially efficient for performing the oblique projection [32]. Instead of a series of matrix multiplication, MOESP implements LQ decomposition to the Hankel matrices as
where Ξp denotes an instrumental variable (IV) matrix consisting of both past input and output data Hankel matrices [33].
It is noted that the left-hand side matrix in Equation (9) is suggested to be a square matrix to secure a correct division after the LQ decomposition, meaning that the number of columns, j, has no choice but
where the dimension of L32 is hence specified, . Consequently, is equal to the oblique projection, O, and the column space of L32 is the same with the column space of the extended observability matrix. It is the essence of why the algorithms are named “subspace” identification.
To retrieve the column space of the extended observability matrix, one can take advantage of singular value decomposition (SVD)
where is null space. The extended observability matrix can be obtained as
Furthermore, the discrete-time system matrices (A and C) shown in Equation (1) and Equation (2) can be evaluated as
where denotes Γi without the last m rows, denotes Γi without the first m rows, and the superscript is Moore-Penrose pseudoinverse. Moreover, C can be determined from the first m rows [31].
Finally, the continuous-time system matrices can be computed from discrete-time ones and the modal parameters, such as modal frequencies, damping ratios, and mode shapes, can be successfully estimated. Those modal parameters are one of the most important dynamic features in the application of SHM.
2.2. Recursive Subspace Identification (RSI)
There are several ways to implement SI recursively and they can be roughly divided into two categories. One uses the matrix inversion lemma to update the orthogonal or oblique projection matrix [18,19,20,21] and the other one uses an unconstrained criterion (known as Yang’s criterion) to approximate the projections [22,23,24,25]. Both of them introduce a forgetting factor, which is quite common in the recursive least squares (RLS) algorithm [34,35], to keep fading out the past measurement and updating the newest information of system matrices.
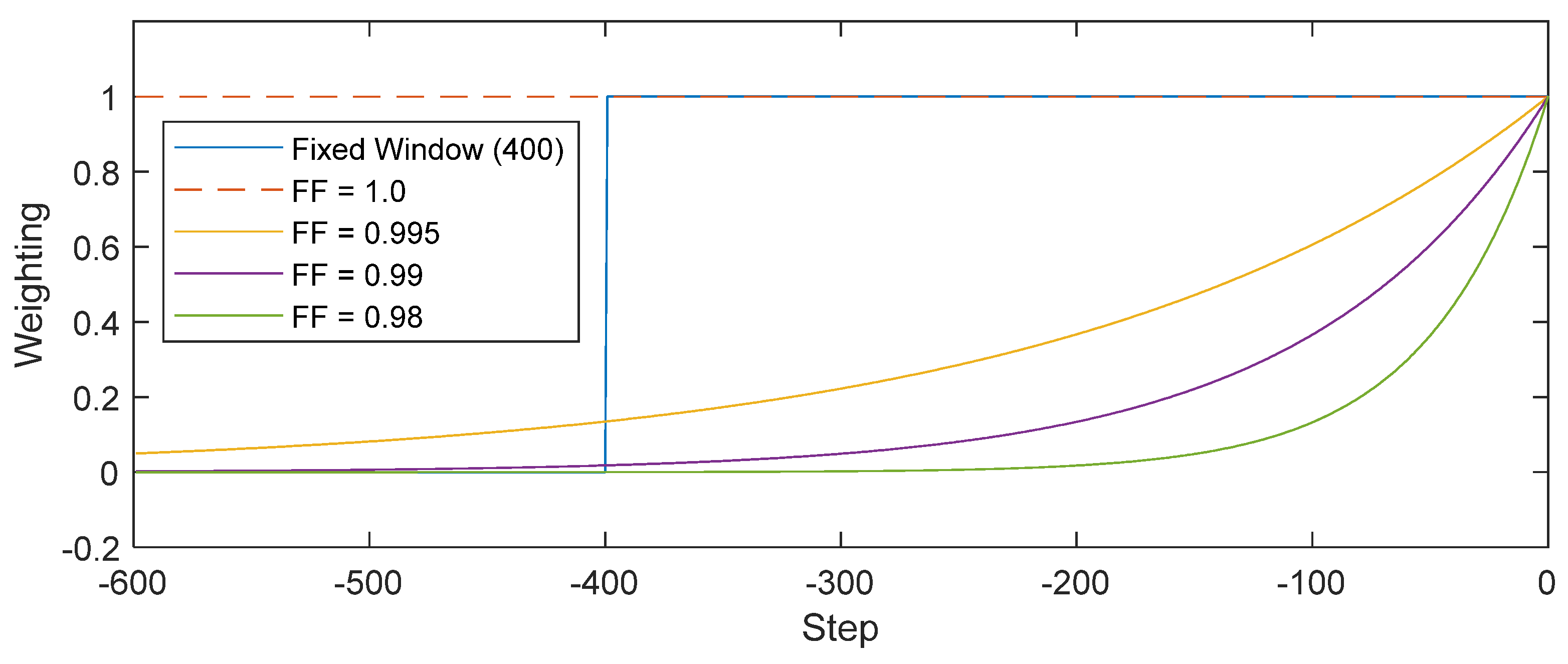
One of the significant results after introducing a forgetting factor is that the weighting of data is exponentially reduced as time goes on. There are pros and cons to using a forgetting factor; undoubtedly, the implementation is very easy, simple, and direct. On the other hand, the forgetting factors produce a time-varying weighting to the past data, as shown in Figure 1. To overcome the problem, constant weighting is preferable, such as a fixed moving window. Kameyama proposed a recursive formulation based on a swap of matrices, called bona fide recursive algorithm [36,37], and brought a moving window with fixed input and output data size, as shown in Figure 1. Definitely, the identified dynamic behaviors appeared only in the current window compared to the other algorithms using forgetting factors.
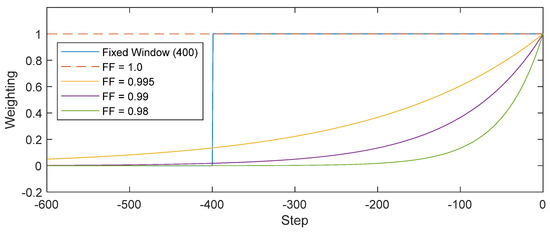
Figure 1.
The weighting of various forgetting factors and fixed window.
The bona fide recursive algorithm is based on MOESP; admittedly, MOESP needs to implement Equation (9) at each step. Given a set of new measurement of input data, uk+1, and output data, yk+1, the vectors , , and can be updated and the following relation holds
Regarding , the equation can be held by and Equation (15) can be further expanded [36,37]. For simplicity, the following five covariance matrices are defined
At next step, these covariance matrices are updated as
Obviously, from Equation (21) to Equation (25), the matrices K0, K1, K2, K3, and K4 are the covariance of input data, output data, and IV.
However, to get the column space of the extended observability matrix, L32 needs to be extracted from Equation (20)
where can be derived from Equations (16)–(18); can be derived from Equations (16), (17) and (19). Therefore, the product of can be constructed as
Consequently, the column space of is the same with the column space of the extended observability matrix.
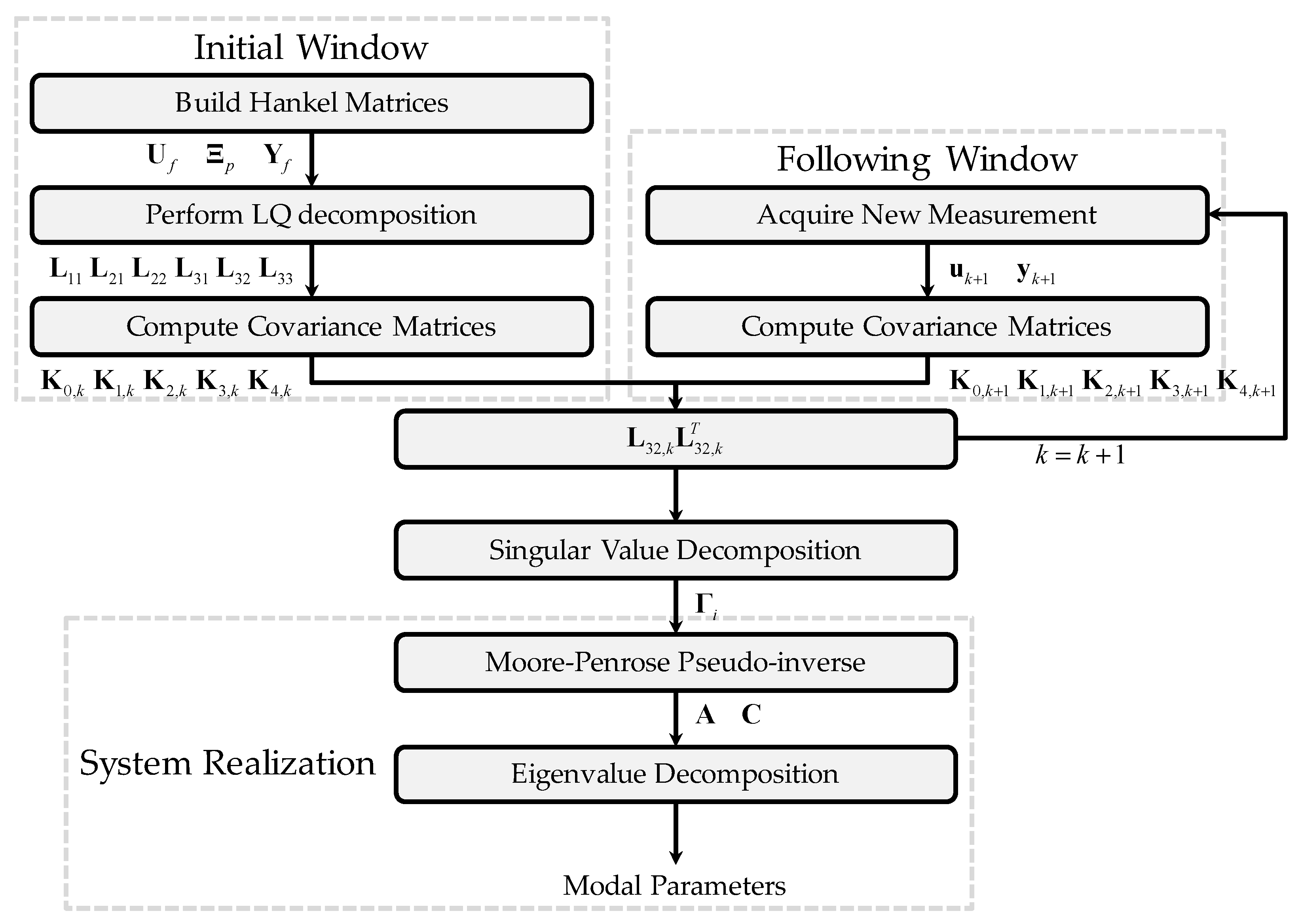
Generally, RSI implementation using the bona fide recursive algorithm consists of four steps, as shown in Figure 2. The first step carries out the initial window and directly uses MOESP with LQ decomposition. Moreover, the five covariance matrices are computed using the equations from Equation (16) to Equation (20). The second step constructs and, afterward, the extended observability matrix can be retrieved using SVD. In the third step, the discrete-time system matrices can be evaluated using Equation (16), the continuous-time system matrices can be computed using Equation (14), and the modal parameters can therefore be estimated. Finally, the new measurement is acquired for the next step and the covariance matrices are updated with those equations from Equation (21) to Equation (25). Then, repeating from the second step to the fourth step produces a close-loop recursion.
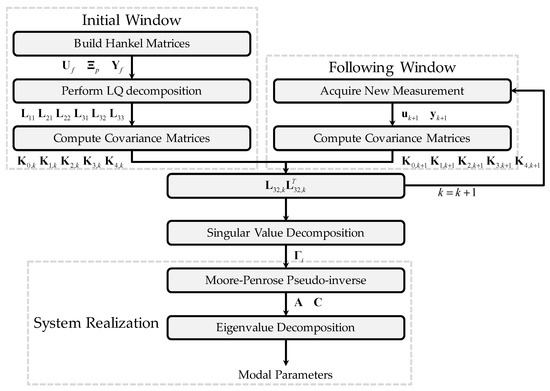
Figure 2.
The flowchart for RSI implementation using bona fide recursive algorithm.
3. Numerical Simulation
Different from the forgetting factor adopted by other algorithms, the proposed algorithm brings a moving window with fixed input and output data size. To demonstrate the effectiveness of the proposed method for seismically excited structures, an 8-story shear-type frame is numerically simulated with a seismic excitation of the El Centro Earthquake (18 May 1940) in the north-south direction. The mass of each story is lumped at the center and assumed to be 10 tons. The stiffness at each story is supposed to be 1200 kN/m. The damping coefficients are calculated via the modal damping and the damping ratio is assumed to be 2% for each mode. Accordingly, the 8 modal frequencies from 1.02 Hz to 10.84 Hz are listed in Table 1. The measurement is assigned to be the 8 acceleration responses of the frame and an additional measurement is the ground acceleration. Although the frame is simulated using a 1 kHz sampling rate, the one in measurement can be variated. All the simulation is done using the software, MATLAB, issued by MathWorks.

Table 1.
The 8 modal frequencies of numerically simulated structure.
3.1. User-Defined Parameter
Before applying SI or RIS, the first and inevitable question is the size of Hankel matrices, such as Uf, Ξp, and Yf. The only user-defined parameter is i because the left-hand side matrix in Equation (9) is a square matrix. Once i is assigned, j can be determined using Equation (11), and the total data size within the current window, lw, called window length, is resolved as
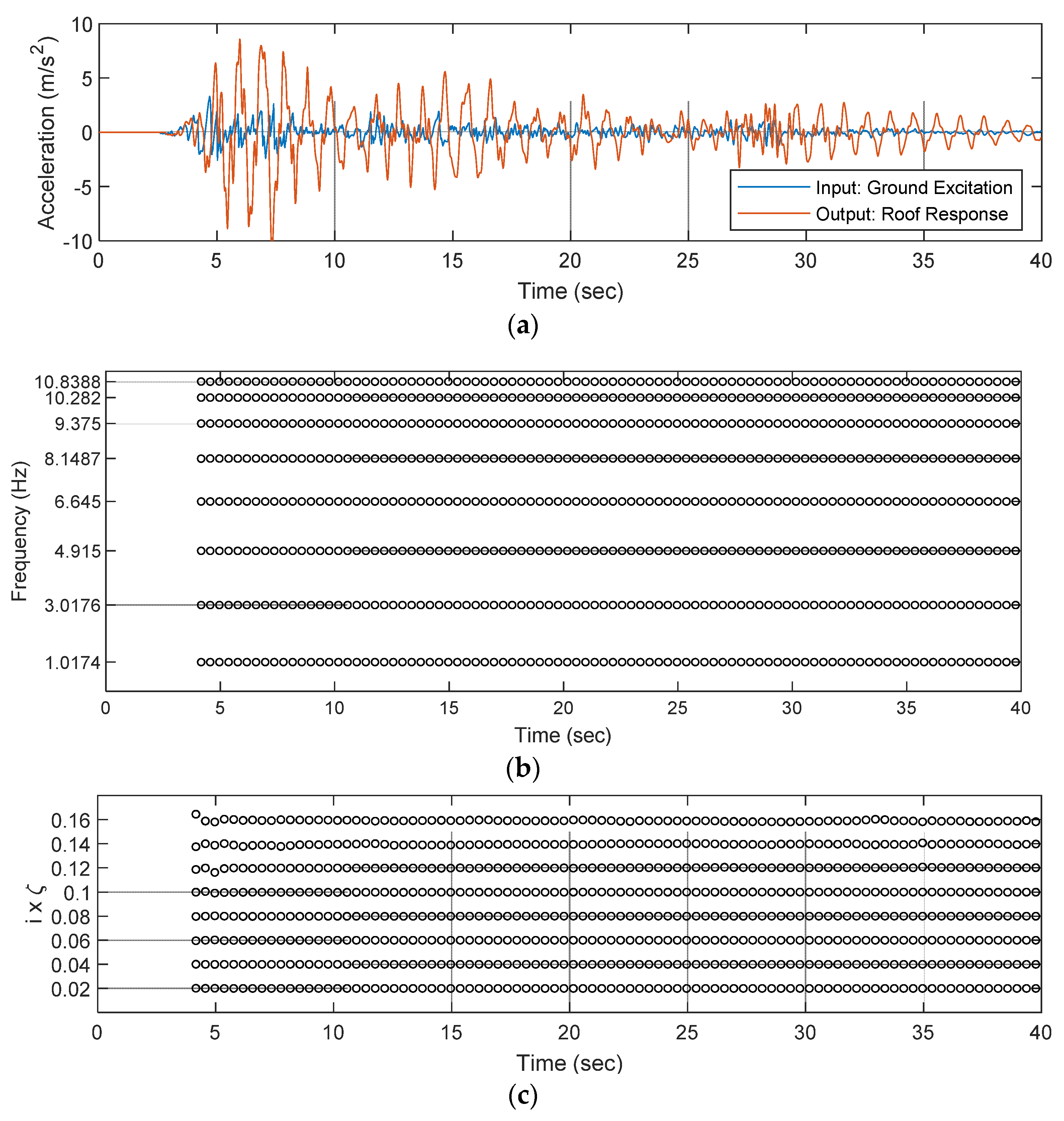
In the field application, the window length is very important since the product of the window length and the sampling interval is the time of providing the first identification result after an earthquake starts. If the window length is longer than the duration of the mainshock, RSI can only identify the modal parameters belonging to the damaged structure. The results may be useless without comparing with the original state. By setting i as 10, the modal parameters identified by RSI are shown in Figure 3.
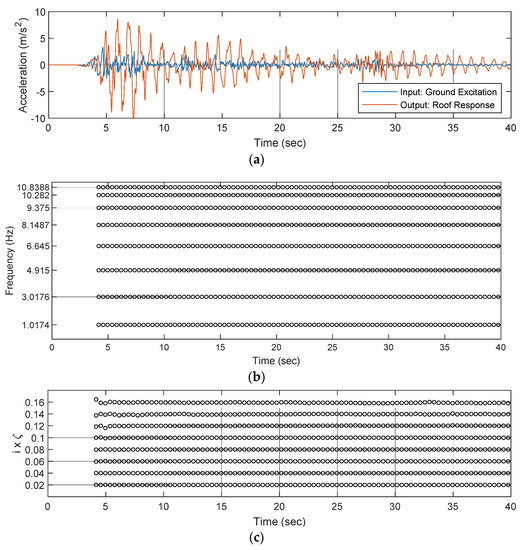
Figure 3.
The identified modal parameters under the seismic excitation. (a) Ground excitation and structural responses; (b) identified frequency over time; (c) identified damping ratio over time.
Obviously, RSI implementation using the bona fide recursive algorithm gives an excellent estimation of the modal parameters. The grids in Figure 3b are drawn according to the 8 modal frequencies listed in Table 1 and, clearly, the different modes can be successfully identified at each step. Note that the identified damping ratios, ζ, in Figure 3c are multiplied by the number of modes to avoid overlap surrounding 0.02 (2%). Therefore, the identified results evenly distributed from 0.02 to 0.16 illustrated that the damping ratios over 8 modes are all 2%. The identified mode shapes are also correct but not shown here due to limited space. Overall, RSI is capable to provide correct modal parameters during the seismic excitation.
As a key parameter, i is crucial to the performance of SI and RSI and some literature gives suggestions about how to decide it [28,29,30]. The concept is that i shall be larger than the half-cycle of the fundamental period and the fundamental period is usually the first modal period of the target structure. Hence, it can be computed by multiplying the Nyquist frequency, Nf (in Hz), and the fundamental period, Tf (in seconds). However, in the above example, i is 25 if the measurement is taken via 50 Hz and the window length is 499, which indicates almost 10 s, for the first identification result. Apparently, the suggested criterion is too conservative and inadequate for the practical implementation of building structures or infrastructures under seismic excitations.
Considering the projection is done by the whole part of the matrix, the criterion shall be taken on the data number rather than the row number of the Hankel matrices. To be specific, the proposed criterion is
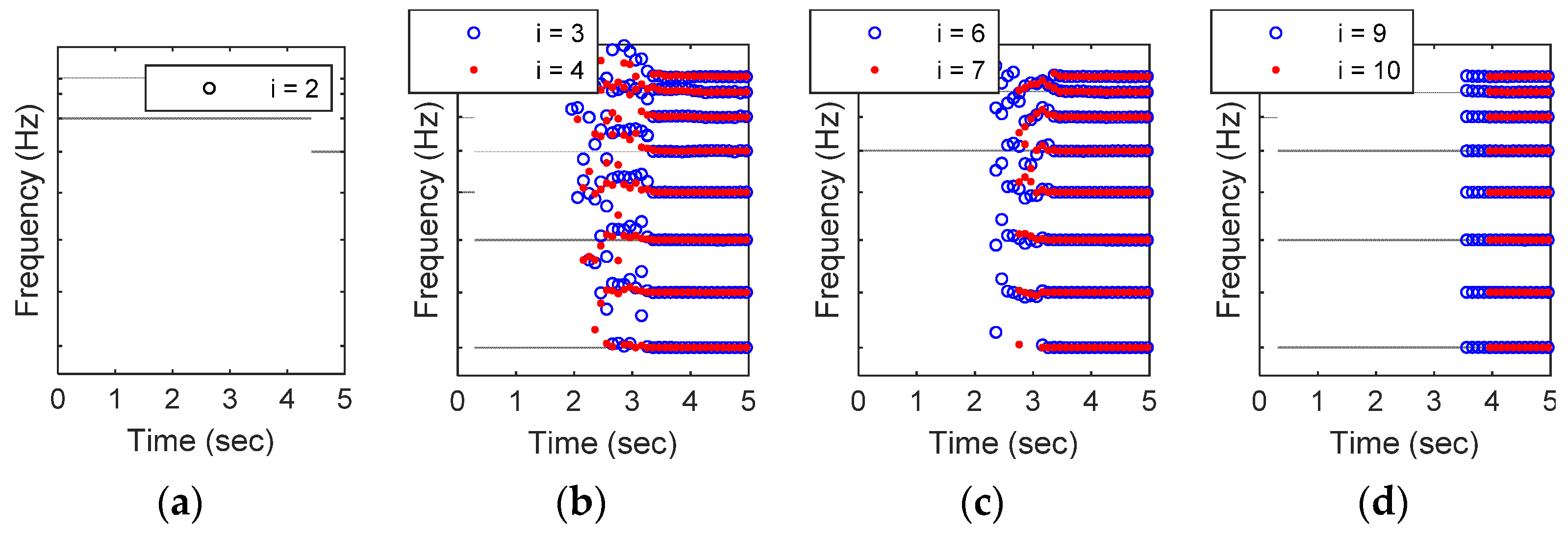
where CE is the extension coefficient. CE shall be at least larger than 1, it can be more than 3 or 4 for stable identified results, and it needs to be further increased while dealing with a noisy measurement. With a 50 Hz measurement, Figure 4 exhibits the identified modal frequencies across various CE. It can be observed that the identification fails when i is equal to 2 () and provide stable results when i is around 9 or 10 (). Moreover, Figure 4b,c indicate that CE still works between 1 and 3 after a few recursive steps. Definitely, the proposed criterion brings a reasonable and effective selection for the practical implementation of RSI on seismically excited structures.
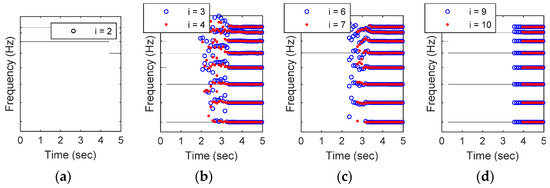
Figure 4.
The identified modal frequencies across various CE ( when , respectively). (a) smallest i; (b) first i group; (c) second i group; (c) third i group.
3.2. Noise Effect
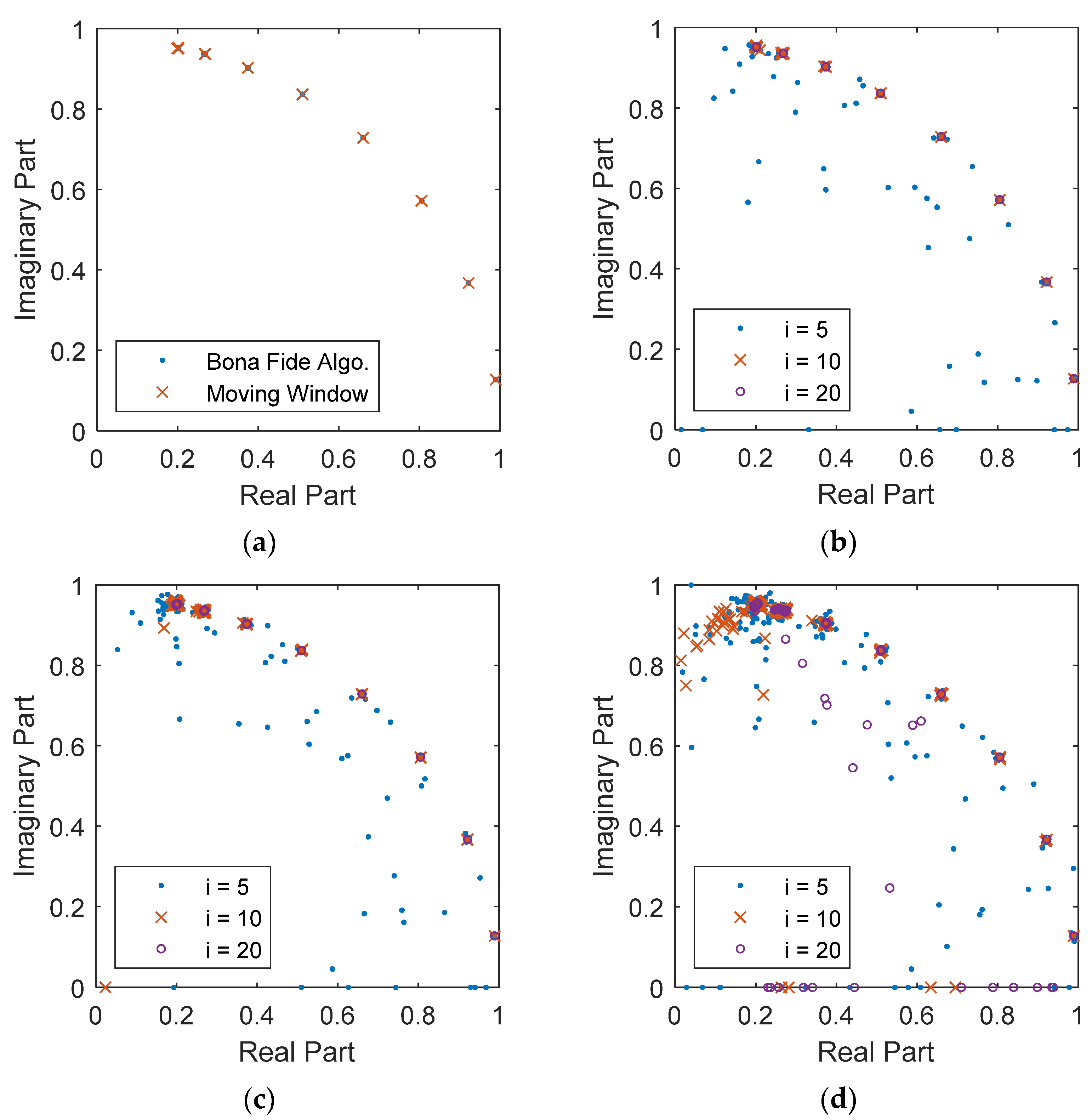
In the field application, the measurement is always perturbed by noise so it is important to examine the performance using noisy measurement. Signal-to-noise ratio (SNR) is commonly used to represent the level of background noise was adopted in this study. By adding different levels of noise into the measurement, the identified system’s poles are displayed in Figure 5. In the noise-free case shown in Figure 5a, both RSI via the bona fide recursive algorithm and SI via the moving window method can extract the identical 8 system’s poles during the seismic excitation. When noise is blended into the measure, spurious poles appear and dramatically increased (in number) as the noise level. It is observed that the spurious poles only come out under the small row number of the Hankel matrices, implying a larger extension coefficient, CE, can somehow deal with the noise problem. However, even an enlarged row number (i = 20) can get rid of the spurious poles if SNR keeps reducing, as shown in Figure 5d.
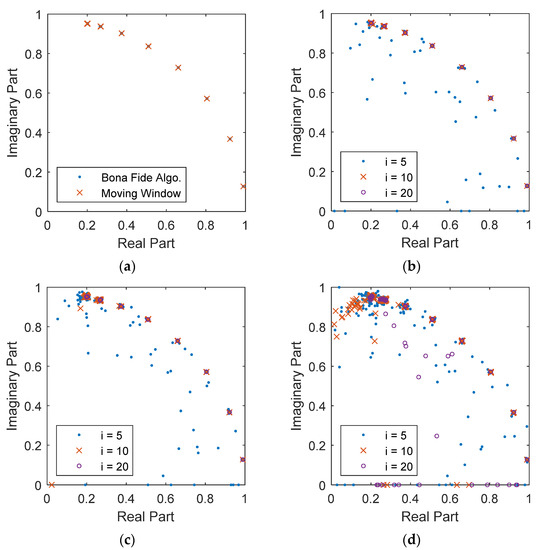
Figure 5.
The identified system poles under different levels of background noise. (a) noise-free (i = 10); (b) low noise (SNR = 30); (c) medium noise (SNR = 25); (d) high noise (SNR = 20).
The modal assurance criterion (MAC) is usually used to discriminate between the spurious poles and the true system’s poles while implementing SI [38,39,40,41]. It is defined as the coherence between two vectors, and , as
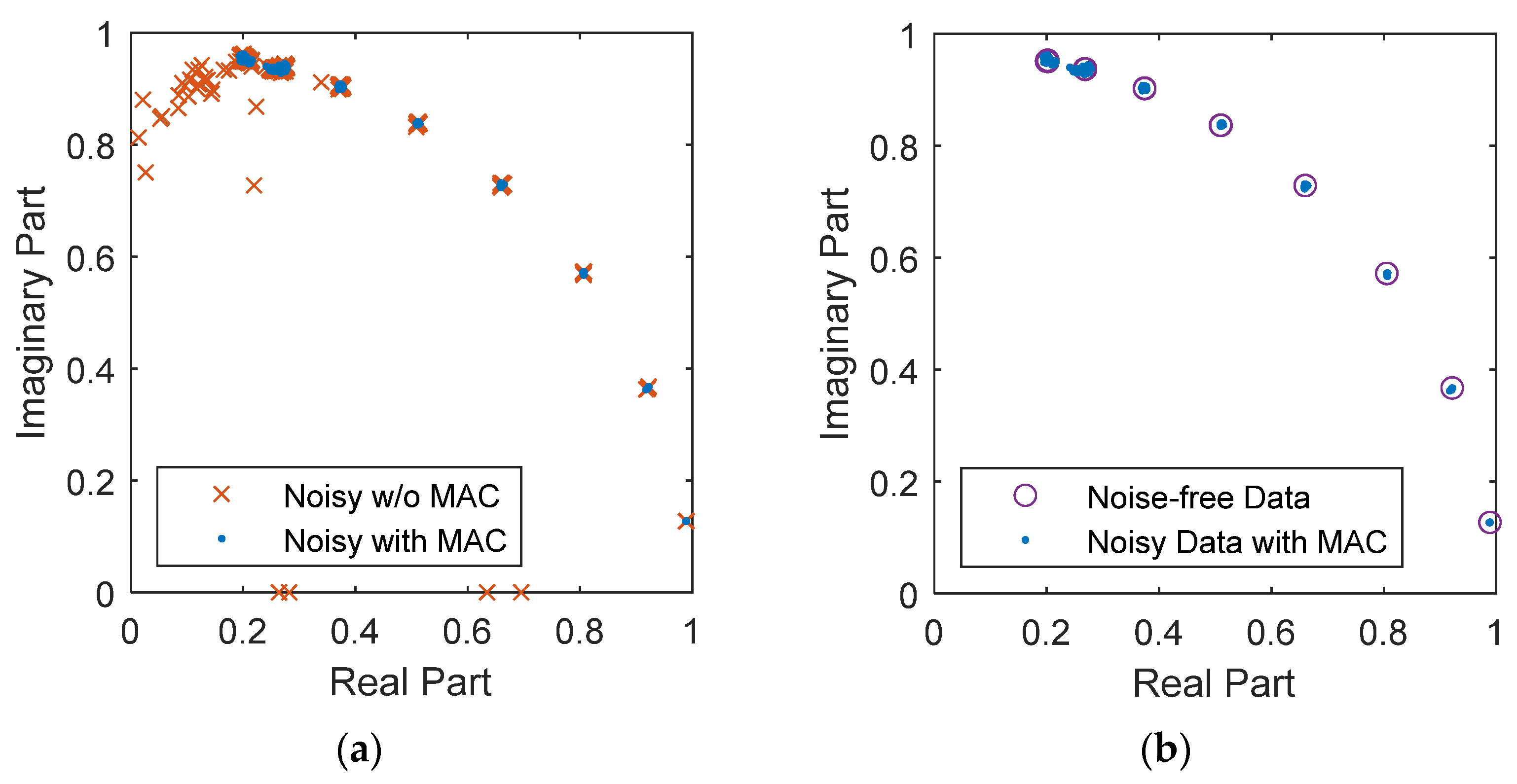
where the superscript H is Hermitian transpose. Generally, those vectors are the mode shapes taken out from a stabilization diagram generated over various values of the user-defined parameters, but RSI uses a consistent value and has no stabilization diagram. In the proposed method, one of the vectors can be the column space of the extended observability matrix and the other one can be the reconstructed column space from the eigenvalues and eigenvectors. Sieving these vectors with MAC and an adequate threshold, CMAC, can remove the spurious modes during the recursive steps. Figure 6 shows the identified system poles with and without MAC criterion under the high noise level. Clearly, all the spurious modes are removed after CMAC is set to 0.98 and the effectiveness of the proposed method is demonstrated.
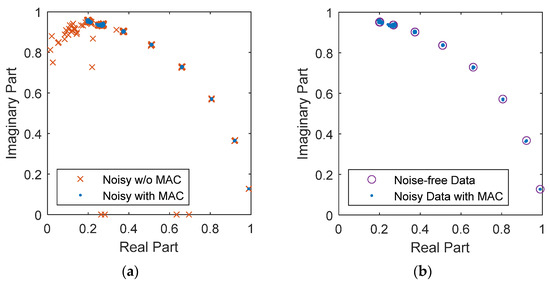
Figure 6.
The identified system poles with and without MAC criterion under high noise level. (a) without MAC criterion; (b) with MAC criterion.
3.3. Computation Time
Time consumption for computation is another issue in the field application; actually, it is even more crucial if SHM systems are designed for a real-time or online application. To ensure the computation time, the frame responses are successively down-sampled to several sampling rates, such as 500, 250, 200, 100, 50, and 40 Hz, as the measurement. Two scenarios, fixed i and fixed CE, are studied and RSI is individually conducted using the same input, output, and parameters in each scenario. Moreover, all the analyses are carried out in the same computer environment for comparison. For the hardware environment, the CPU is Intel(R) Core(TM) i7-6700K and the RAM is 32.0 GB. For the software environment, OS is 64 bit Windows and the platform is MATLAB R2021a [42]. The detailed parameters and the results of computation time are listed in Table 2 and Table 3.

Table 2.
The computation time over various sampling rates and a fixed i.

Table 3.
The computation time over various sampling rates and a fixed α.
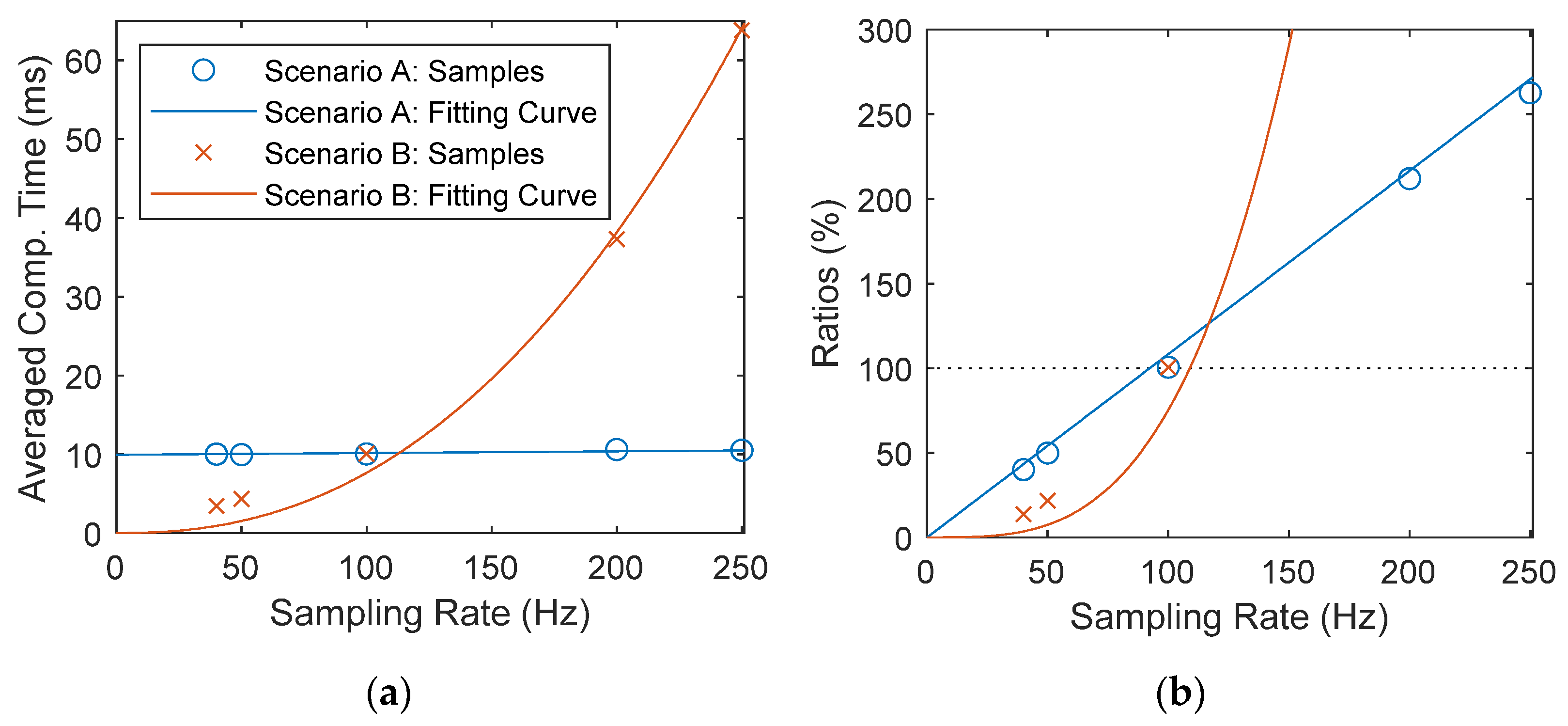
In Table 2, as expected, the averaged computation time, tc, per step is quite similar; however, it exponentially increases if CE is considered in Table 3. Doubtless, too frequent identification may bring no advantage to SHM systems for infrastructures. A ratio is introduced to represent the percentage spent on computation in each step as
The ratios, rc, are shown in Figure 7 and must be smaller than 100% to guarantee real-time or online processing. Figure 7a clearly reveals the exponential increase in the second scenario and the averaged computation time surpasses the result from the fixed i around 112 Hz. Furthermore, according to Figure 7b, the sampling ratio should be smaller than 92 Hz so that the proposed recursive formulation can be finished within each sampling interval. Although the computation time varies with different computer environments, one can conclude that down-sampling processing is generally needed for a real-time or online application. Otherwise, the proposed method may not complete the computation in each step because SHM systems commonly have a sampling rate from 100 Hz to 200 Hz [43,44,45]. One can note that on the other hand, the sampling rate needs to be large enough to see those significant frequencies. In some literature, 50 Hz or 60 Hz is a good suggestion for the sampling rate [46,47,48,49].
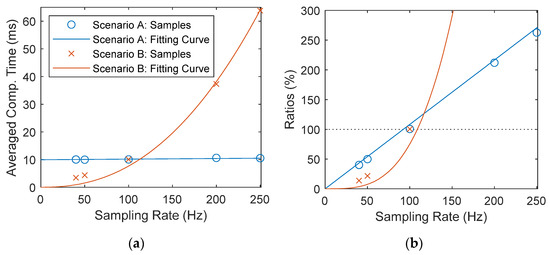
Figure 7.
The averaged computation time and percentage spent on computation in each step. (a) Averaged computation time; (b) ratio in each step.
4. Experimental Validation
The proposed method utilizes the bona fide recursive algorithm with fixed input and output data size to extract the dynamic behaviors. The effectiveness has been demonstrated through a numerically simulated 8-story frame under seismic excitation. Meanwhile, the criterion for selecting the row number of Hankel matrices, the measure for re-moving the spurious modes contaminated by noise, and the down-sampling processing for a real-time or online SHM have been considered and studied with plain suggestions. To further verify the reliability of the proposed method for seismically excited structures, two full-scale specimens are experimentally tested with shaking tables. One is a 3-story steel frame subjected to the El Centro Earthquake (18 May 1940) in the north-south direction. A brace with a special mechanism is designed so that the inter-story stiffness can be reduced during seismic excitations. The other one is a 10-story concrete frame subjected to the Kobe Earthquake (17 January 1995) in three directions. The intensity of excitations is escalated until the peak ground acceleration (PGA) of the original time history. In each experiment, the ground shaking and the structural responses were measured from the accelerometers. Unfortunately, in both experiments RSI was not implemented in real-time because of some technical problems. Instead, the measurement was first recorded and then processed with the bona fide recursive algorithm.
4.1. Experiment of 3-Story Steel Frame
The 3-story specimen is a full-scale steel frame; it was designed and constructed at the National Center for Research on Earthquake Engineering (NCREE) in Taipei, Taiwan. In each story, the specimen is a single bay with 2.15 m by 3.15 m in floor area and 3.0 m in height, as shown in Figure 8. The beams and columns are made by wide flange H-beams (H150 × 150) and each beam-column joint is designed as a bolted connection. Additional mass blocks are located on the floors so that the final weight of each story reaches 6 tons. Then, the 9.0 m height and 18 tons weight specimen are bolted on the shaking table and excited using the pre-specified earthquake. It should be noted that an extra brace is located in the first story. Due to the brace, the approximate stiffness of the first story is 2692 kN/m while the stiffness of the other two stories is 1346 kN/m. As a result, the modes can be identified using the white-noise excitation and the three modal frequencies are 1.23, 3.66, and 5.33 Hz, respectively.

Figure 8.
The photograph of the full-scale specimen and the close-up of the lock-up system.
The extra brace is used to produce the stiffness change and, therefore, to mimic the structural damage. In order to achieve that, a lock-up system is designed to connect the brace and the base floor in the first story, as shown in Figure 8. A trigger is manually held by the technician and can be arbitrarily released during the shaking table test. Once the brace is released (un-connected), the inter-story stiffness is immediately reduced to simulate the abrupt change in stiffness. In the shaking table test, the El Centro earthquake is normalized to 100 gal and then inputted to the actuator system to excite the specimen. Here, the unit, gal, is an acceleration unit (1 gal is equal to 1 cm/s2). The lock-up system is assigned to release the brace around 15 s after the earthquake starts. To confirm the true releasing time, an additional displacement meter is installed on the lock-up system in such a way that the relative displacement between the brace and the base floor can be determined.
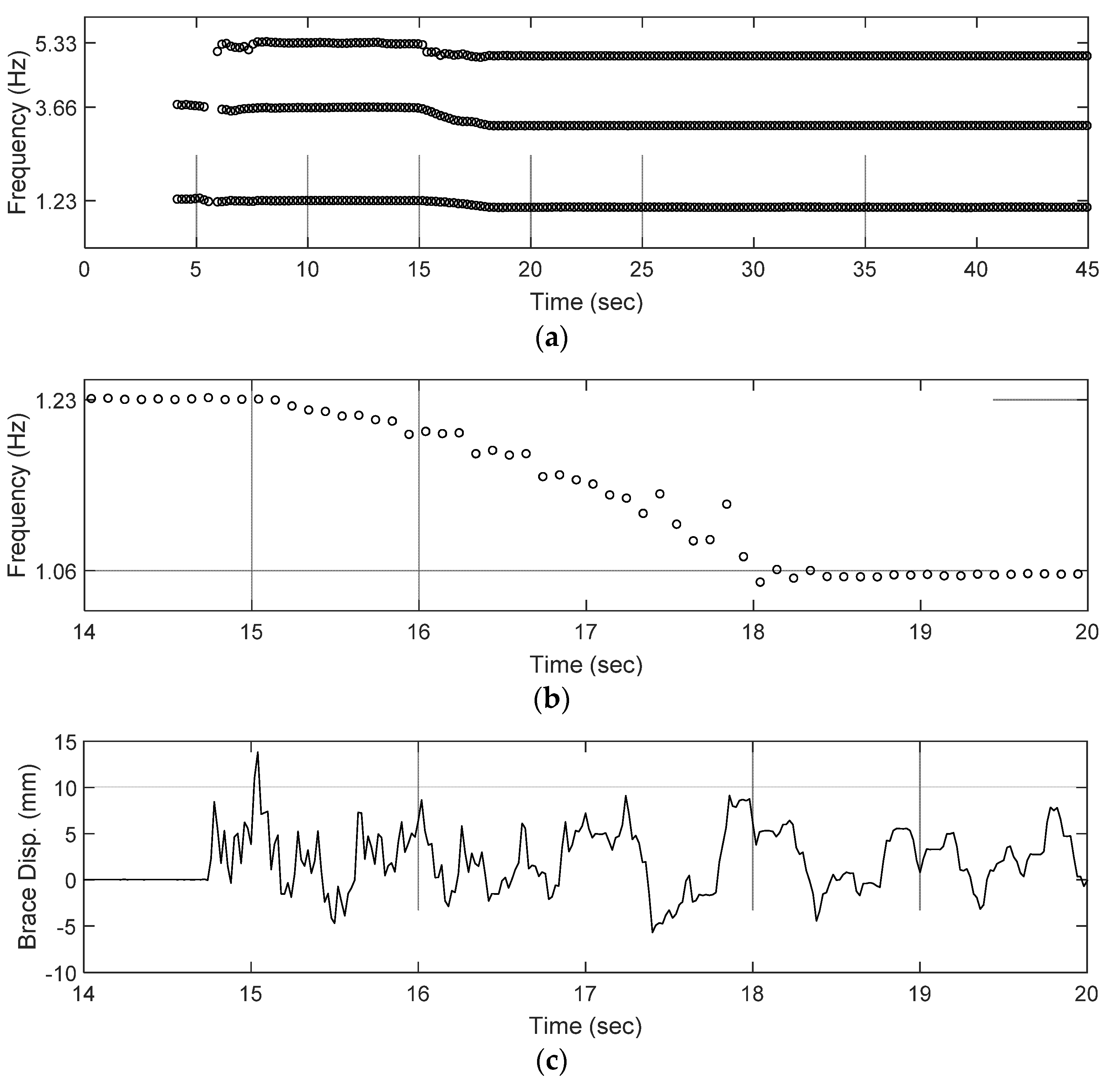
For the application of SHM, RSI implementation using the bona fide recursive algorithm can detect the abrupt change in stiffness at any instant of time. The measurement was taken using a 200 Hz sampling rate in the test and is down-sampled to 50 Hz for efficient computation. Based on the suggestions given in Section 3, the row number of Hankel matrices, i, is set as 20 and the window length, lw, is 199 (3.98 s). The threshold for MAC, CMAC, is set as 0.95 to discriminate between the physical and spurious modes. Hence, the modal parameters identified by RSI and the relative displacement measured by the displacement meter are shown in Figure 9.
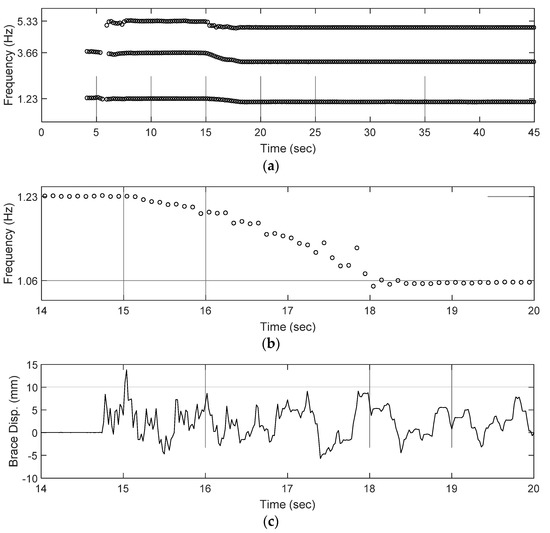
Figure 9.
The identification result of the 3-story frame during the shaking table test. (a) Identified frequency over time (the gray grids indicate the results identified from the white-noise excitaiton); (b) identified frequency (first mode close-up); (c) relative displacement of brace (Lock-up system).
The structural damage represented by the stiffness change can be easily observed as the three modal frequencies are lower after 15 s in Figure 9a. The first mode close-up displays two distinct modal frequencies before 15 s and after 19 s, which points out that the dynamic behaviors of the frame have been changed during these 4 s. Considering the fixed window (produce by the bona fide recursive algorithm) and the window length (3.98 s in this test), the frame probably has a very rapid change at around 15 s. The relative displacement measured by the displacement meter can provide a more definite indicator. In Figure 9c, the brace is firmly locked until 14.74 s, generating no displacement at all. After this instant, the trigger is set and the brace is released with the result that the relative vibration is created between the brace and the base floor.
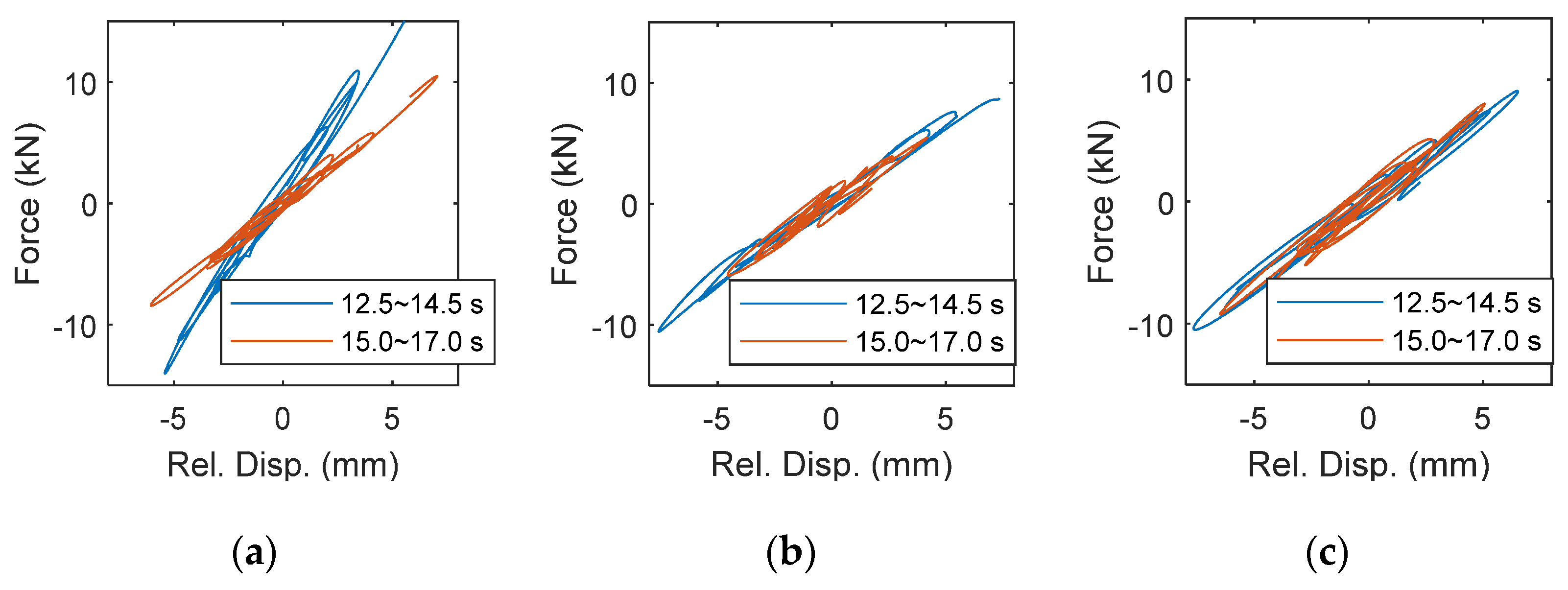
To further confirm the stiffness change produced by the brace and the lock-up system, the hysteresis loop of each story before and after the releasing time is reconstructed using the measurement. Figure 10a–c show the hysteretic behaviors of the first, second, and third stories, respectively. It is noted that the force is reconstructed from the measured acceleration and the floor weights. Unquestionably, the inter-story stiffness in the last two stories is the same before 14.5 s and after 15.0 s, while the one in the first story becomes significantly soft. Moreover, the slope of the hysteresis loop in the first story is similar to the other two after 15.0 s because the inter-story stiffness is supported only by four columns. It can be obviously found that the change of stiffness in the first story can be clearly identified, which is consistent with the original test arrangement. Finally, the computation time for the 46.06 s shaking table test is only 7.94 s, showing the capability for real-time or online processing.
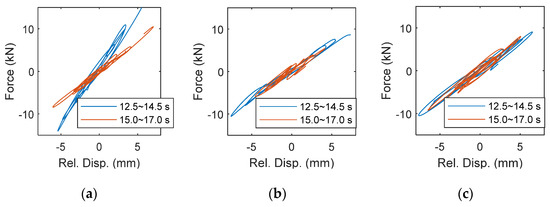
Figure 10.
The hysteresis loop of each story before and after the brace is released. (a) First story; (b) second story; (c) third story.
4.2. Experiment of 10-Story Concrete Frame
The second specimen is a 10-story full-scale reinforced concrete (RC) frame, as shown in Figure 11. It was conducted on the world’s largest three-dimensional (3D) earthquake shaking table test facility, E-Defense, at the National Research Institute for Earth Science and Disaster Resilience (NIED) in Hyogo, Japan. The dimensions of the base are 15.7 and 9.7 m in the longitudinal and transverse directions, respectively. On the standard floors, the dimensions are 13.5 and 9.5 m. The longitudinal direction has 3 spans with 4.0 m each and the transverse direction has 3 spans with 3.1, 1.8, and 3.1 m in each floor. The floor heights are 2.8 m for the first floor, 2.6 m for the second to the fourth floors, 2.55 m for the fifth to the seventh floors, and 2.5 m for the eighth to tenth floors. Considering the base, the total height reaches 27.45 m from the shaking table. Furthermore, the longitudinal direction is a simple frame structure composed of beams and columns, whereas the transverse direction is a frame structure with a multi-story shear wall from the first to the seventh floor.
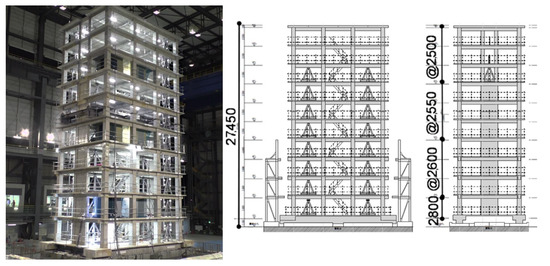
Figure 11.
The photograph and schematic of the full-scale specimen.
Because of some restrictions, the specimen is divided into upper and lower portions. They were constructed separately and steel beams in the sixth floor are designed to facilitate transportation and assembly. The approximate weight of the steam beams is 16 tons and taken into account in the specimen’s design live load. The design load is around 6 tons for the second and the tenth floors and is around 3 tons for other floors. Moreover, the dead load variates from 70 tons to 97 tons for each floor. Consequently, the modes can be identified using the white-noise excitation; the first three modal frequencies in the longitudinal direction are 1.37, 4.05, and 7.31 Hz, and the three in the transverse direction are 1.49, 5.94, and 12.30 Hz, respectively.
The Kobe earthquake is designated as ground excitation in the shaking table test. The excitation is simultaneously applied in three directions and the intensity of excitations is sequentially increased with 10%, 25%, 50%, and 100% PGA of the original time history. Moreover, white-noise excitations are individually applied in each direction before and after seismic excitations to extract the dynamic features. The sampling rate of measurement was 1000 Hz in all the tests and it is down-sampled to 50 Hz before RSI implementation. According to the suggestions, the row number of Hankel matrices, i, is set as 18 and the window length, lw, is 431 (8.62 s). The threshold for MAC, CMAC, is set as 0.95 to discriminate between the physical and spurious modes. Due to limited space, only the identification result in the transverse direction of the 100% PGA’s one is shown here.
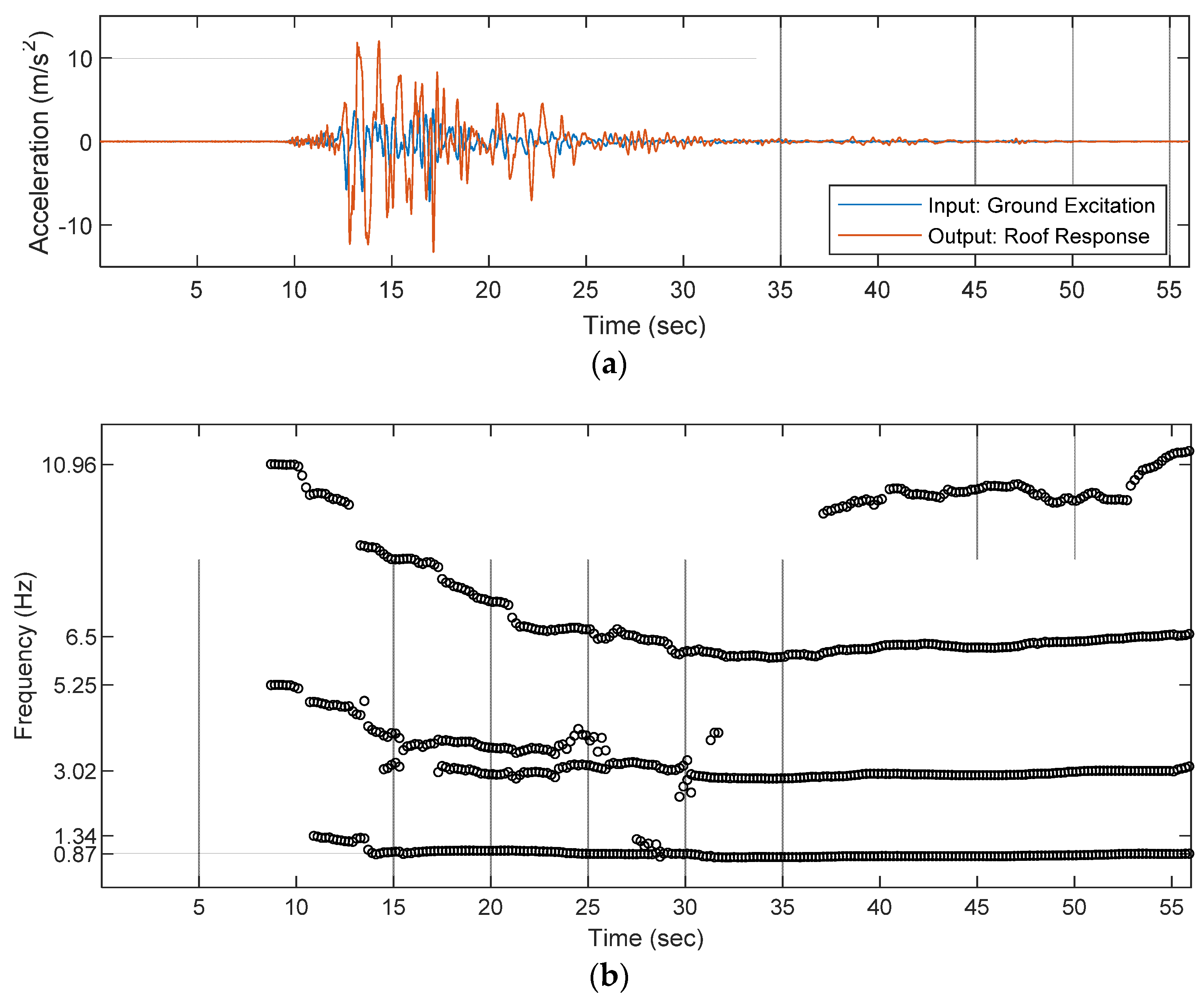
From Figure 12a, 0.761 g was achieved by the shaking table, which is 93.27% of the original time history, and the roof response reaches 1.379 g. It is noted that the specimen has been slightly damaged during the test of 50% PGA, so the first three modal frequencies in the transverse direction were reduced to 1.34, 5.25, and 10.96 Hz, respectively. Subsequently, the modal parameters identified by RSI illustrate severe damage, as shown in Figure 12b. The modal frequencies continuously decrease and, finally, converge to 0.87, 3.02, and 6.5 Hz, respectively. According to the literature, the beam-column joint failure further progressed until the concrete cover spalled and the compression side concrete at the base of the multi-story shear wall has crushed in the transverse direction [50].
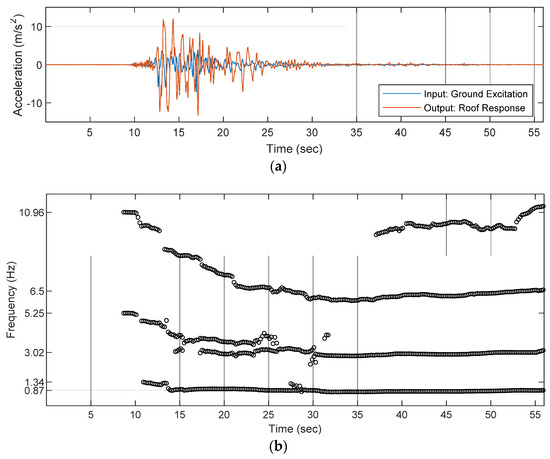
Figure 12.
The identification result of the 10-story RC frame during the shaking table test. (a) Ground excitation and structural responses; (b) identified modal frequencies over time (the gray grids indicate the results identified from the white-noise excitaitons).
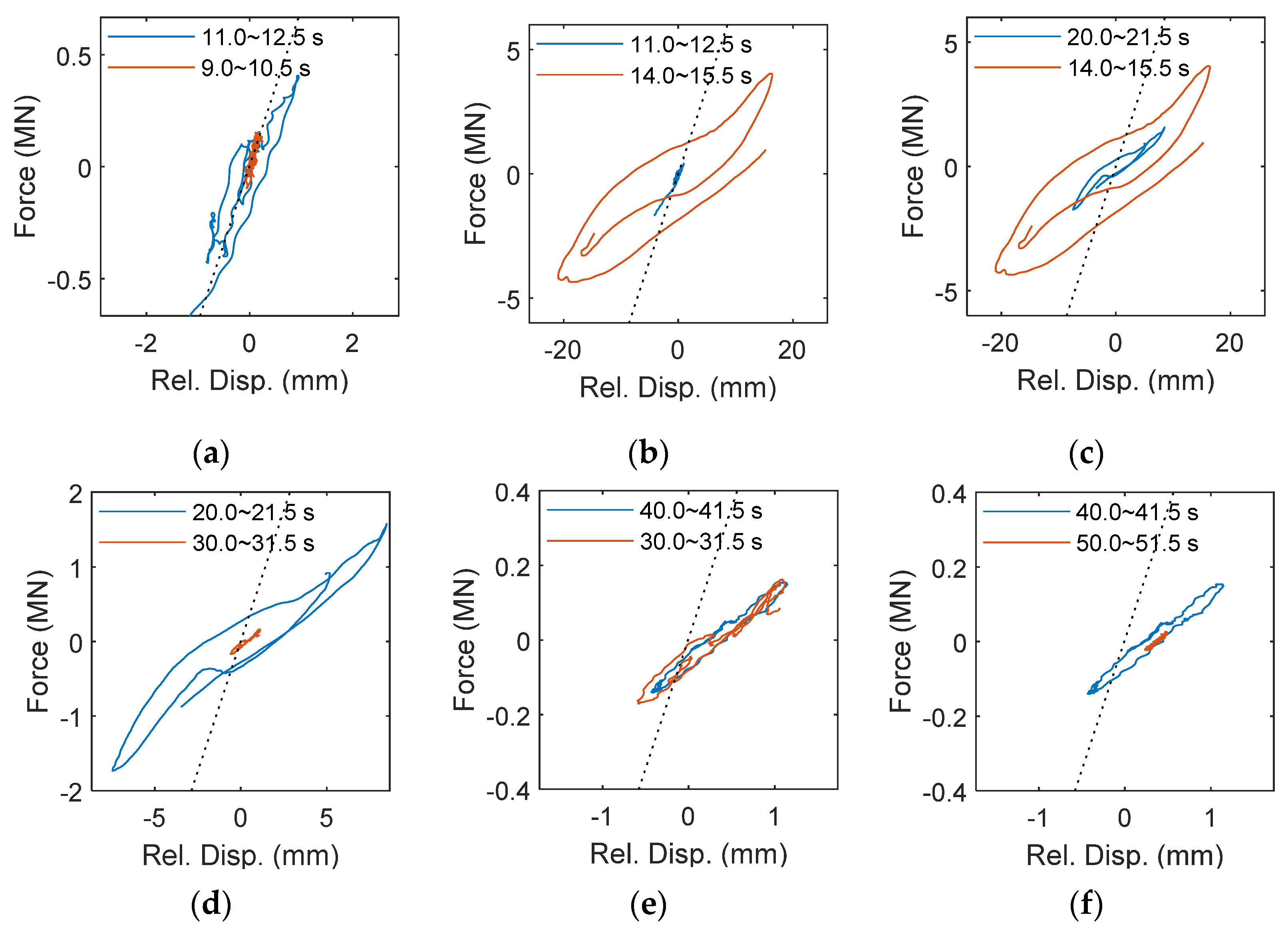
The hysteresis loop of the specimen’s first story during the shaking table test is reconstructed using the measurement to study the nonlinear behaviors produced by the seismic excitation. Figure 13 shows the comparison of hysteretic behaviors of the specimen over time and the dash line represents the initial stiffness fitted around 10 s after an earthquake starts. The stiffness degradation can be clearly observed after 11 s, indicating that the damage is increasing gradually. The RC frame exhibits significant hysteretic and hardening behaviors to dissipate the huge input energy from the earthquake between 14 and 30 s. In consequence, the identified modal frequencies, which describes equivalent ones, have dramatic reduction during the period with the structural nonlinearity. On the other side, the hysteresis loop is similar between 30 and 40 s, as shown in Figure 13e, so that the identified three mods are quite steady. After 50 s, the excitation is about to cease, the hysteretic behaviors are barely seen, and then the identified modal frequencies equivalently gain a small increase. It can be clearly found that the change of modal frequencies obtained from RSI is consistent with the observation of the hysteresis loop in the first story.
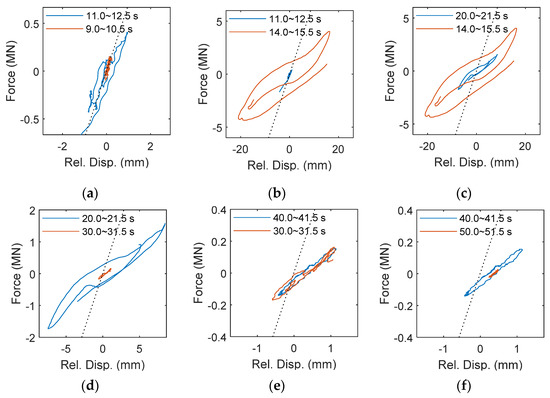
Figure 13.
The hysteresis loop of the 10-story RC frame over time. (a) 9 to 12.5 s; (b) 11 to 15.5 s; (c) 14 to 21.5 s; (d) 20 to 31.5 s; (e) 30 to 41.5 s; (f) 40 to 51.5 s.
5. Conclusions
Continuous system evaluation and autonomous damage assessment under seismic excitations are critical to structural safety evaluation. Generally, the recursive algorithms are exploited to achieve real-time or online processing for SHM. In this study, RSI implementation using the bona fide recursive algorithm is introduced to identify the time-varying dynamic characteristics under the modal domain. To demonstrate and verify the effectiveness for seismically excited structures, both numerical simulation and experimental investigation have been presented and the results are discussed.
In the numerical simulation, the performance of the proposed method is clarified through an 8-story shear-type frame. The only user-defined parameter, i, is suggested to account for the data number rather than the row number of the Hankel matrices. The extension coefficient, CE, brings a reasonable and effective selection for the practical implementation of RSI. For the spurious modes, MAC is taken between the column spaces instead of the stability diagram. The sampling rate shall be reduced for a real-time or online application, but it needs to be larger enough to see those significant frequencies. In the experimental investigation, the capability of the proposed method is verified through two full-scale frames. In the test of the 10-story RC frame, the results show that RSI can track the slow time-varying parameter changes and provide the equivalent modal parameters for the nonlinear behaviors. Next, in the test of the 3-story steel frame, the RSI is capable to detect this kind of sudden damage and estimate the event time by leveraging the fixed window shown in the proposed method.
Overall, the bona fide recursive algorithm is demonstrated and verified in this study. Future works will be focused on the implementation of field application and the long-term performance under the effect of the environment, such as temperature, moisture, and so on.
Author Contributions
Conceptualization, resources, writing, supervision, project administration, and funding acquisition, S.-K.H.; methodology, software, validation, original draft preparation, F.-C.C.; formal analysis, investigation, and data curation, Y.-T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Republic of China (Taiwan), grant number MOST 109-2222-E-005-004-MY2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The experiments were conducted at the National Center for Research on Earthquake Engineering (NCREE) in Taiwan and the National Research Institute for Earth Science and Disaster Resilience (NIED) in Hyogo, Japan. The authors would like to thank all the technical support from NCREE and NIED.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Department of Building Technology and Structural Engineering, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; SAGE Publications: New York, NY, USA, 1996. [Google Scholar]
- Loh, C.H.; Tou, I.C. A system identification approach to the detection of changes in both linear and non-linear structural parameters. Earthq. Eng. Struct. Dyn. 1995, 24, 85–97. [Google Scholar] [CrossRef]
- Loh, C.H.; Lin, H.M. Application of off-line and on-line identification techniques to building seismic response data. Earthq. Eng. Struct. Dyn. 1996, 25, 269–290. [Google Scholar] [CrossRef]
- Lin, J.W.; Betti, R.; Smyth, A.W.; Longman, R.W. On-line identification of non-linear hysteretic structural systems using a variable trace approach. Earthq. Eng. Struct. Dyn. 2001, 30, 1279–1303. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S. On-line identification of non-linear hysteretic structures using an adaptive tracking technique. Int. J. Non-Linear Mech. 2004, 39, 1481–1491. [Google Scholar] [CrossRef]
- Yang, J.N.; Huang, H. Sequential non-linear least-square estimation for damage identification of structures with unknown inputs and unknown outputs. Int. J. Non-Linear Mech. 2007, 42, 789–801. [Google Scholar] [CrossRef]
- Hoshiya, M.; Saito, E. Structural Identification by Extended Kalman Filter. J. Eng. Mech. 1984, 110, 1757–1770. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S.; Huang, H.; Zhou, L. An adaptive extended Kalman filter for structural system and damage identifications. J. Struct. Control. Health Monit. 2006, 13, 849–867. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S.; Zhou, L. Identification of parametric changes for civil engineering structures using an adaptive Kalman filter. In Smart Structures and Materials 2004: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; SPIE: Los Angel, CA, USA, 2004; Volume 5391, pp. 389–399. [Google Scholar]
- Zhou, L.; Wu, S.; Yang, J.N. Experimental study of an adaptive extended Kalman filter for structural damage identification. J. Infrastruct. Syst. 2008, 14, 42–51. [Google Scholar] [CrossRef][Green Version]
- Yin, Q.; Zhou, L.; Mu, T.; Yang, J.N. Experimental study on damage detection of base-isolated structure using an adaptive extended Kalman filter. J. Theor. Appl. Mech. 2013, 51, 1013–1026. [Google Scholar]
- Sato, T.; Qi, K. Adaptive H∞ filter: Its application to structural identification. J. Eng. Mech. 1998, 124, 1233–1240. [Google Scholar] [CrossRef]
- Yoshida, I. Damage detection using Monte Carlo filter based on non-Gaussian noises. In Proceedings of the 8th International Conference on Structural Safety and Reliability, Newport Beach, CA, USA, 17–22 June 2001. [Google Scholar]
- Van Overschee, P.; De Moor, B. Subspace algorithms for the stochastic identification problem. Automatica 1993, 29, 649–660. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. N4SID: Subspace algorithms for the identification of combined deterministic-stochastic systems. Automatica 1994, 30, 75–93. [Google Scholar] [CrossRef]
- Yang, B. Projection approximation subspace tracking. IEEE Trans. Signal Process. 1995, 43, 95–107. [Google Scholar] [CrossRef]
- Oku, H.; Kimura, H. Recursive algorithms of the state-space subspace system identification. Trans. Soc. Instrum. Control Eng. 1999, 35, 800–805. [Google Scholar] [CrossRef][Green Version]
- Oku, H.; Kimura, H. A recursive 4SID from the input-output point of view. Asian J. Control 1999, 1, 258–269. [Google Scholar] [CrossRef]
- Oku, H.; Nijsse, G.; Verhaegen, M.; Verdult, V. Change detection in the dynamics with recursive subspace identification. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 3, pp. 2297–2302. [Google Scholar]
- Tamaoki, M.; Akizuki, K.; Oura, K. Order and parameter estimation of time-varying system by subspace method. Electr. Eng. Jpn. 2006, 157, 57–64. [Google Scholar] [CrossRef]
- Gustafsson, T. Recursive system identification using instrumental variable subspace tracking. IFAC Proc. Vol. 1997, 30, 1579–1584. [Google Scholar] [CrossRef]
- Yu, J.L. A novel subspace tracking using correlation-based projection approximation. Signal Process. 2000, 80, 2517–2525. [Google Scholar] [CrossRef]
- Mercère, G.; Lecoeuche, S.; Vasseur, C. A new recursive method for subspace identification of noisy systems: EIVPM. IFAC Proc. Vol. 2003, 36, 1597–1602. [Google Scholar] [CrossRef]
- Mercère, G.; Bako, L.; Lecœuche, S. Propagator-based methods for recursive subspace model identification. Signal Process. 2008, 88, 468–491. [Google Scholar] [CrossRef]
- Weng, J.H.; Loh, C.H. Recursive subspace identification for on-line tracking of structural modal parameter. Mech. Syst. Signal Process. 2011, 25, 2923–2937. [Google Scholar] [CrossRef]
- Chen, J.D.; Loh, C.H. Tracking modal parameters of building structures from experimental studies and earthquake response measurements. Struct. Health Monit. 2017, 16, 551–567. [Google Scholar] [CrossRef]
- Loh, C.H.; Chen, J.D. Tracking modal parameters from building seismic response data using recursive subspace identification algorithm. Earthq. Eng. Struct. Dyn. 2017, 46, 2163–2183. [Google Scholar] [CrossRef]
- Chen, J.D.; Loh, C.H. Two-stage damage detection algorithms of structure using modal parameters identified from recursive subspace identification. Earthq. Eng. Struct. Dyn. 2018, 47, 573–593. [Google Scholar] [CrossRef]
- Huang, S.K.; Chen, J.D.; Loh, K.J.; Loh, C.H. Discussion of user-defined parameters for recursive subspace identification: Application to seismic response of building structures. Earthq. Eng. Struct. Dyn. 2020, 49, 1738–1757. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Verhaegen, M. Identification of the deterministic part of MIMO state space models given in innovations form from input-output data. Automatica 1994, 30, 61–74. [Google Scholar] [CrossRef]
- Gustafsson, T. Subspace identification using instrumental variable techniques. Automatica 2001, 37, 2005–2010. [Google Scholar] [CrossRef]
- Johnstone, R.M.; Johnson Jr, C.R.; Bitmead, R.R.; Anderson, B.D. Exponential convergence of recursive least squares with exponential forgetting factor. Syst. Control Lett. 1982, 2, 77–82. [Google Scholar] [CrossRef]
- Bittanti, S.; Bolzern, P.; Campi, M. Convergence and exponential convergence of identification algorithms with directional forgetting factor. Automatica 1990, 26, 929–932. [Google Scholar] [CrossRef]
- Kameyama, K.; Ohsumi, A.; Matsuura, Y.; Sawada, K. Recursive 4SID-based identification algorithm with fixed input-output data size. Int. J. Innov. Comput. Inf. Control 2005, 1, 17–33. [Google Scholar]
- Kameyama, K.; Ohsumi, A. Subspace-based prediction of linear time-varying stochastic systems. Automatica 2007, 43, 2009–2021. [Google Scholar] [CrossRef]
- Pappa, R.S. Eigensystem Realization Algorithm User’s Guide for VAX/VMS Computers: Version 931216; (No. NASA-TM-109066), NASA Report; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Döhler, M. Subspace-Based System Identification and Fault Detection: Algorithms for Large Systems and Application to Structural Vibration Analysis. Ph.D. Thesis, Université Rennes 1, Rennes, Germany, 2011. [Google Scholar]
- Liu, Y.C.; Loh, C.H.; Ni, Y.Q. Stochastic subspace identification for output-only modal analysis: Application to super high-rise tower under abnormal loading condition. Earthq. Eng. Struct. Dyn. 2013, 42, 477–498. [Google Scholar] [CrossRef]
- Nord, T.S.; Petersen Ø, W.; Hendrikse, H. Stochastic subspace identification of modal parameters during ice–structure interaction. Philos. Trans. R. Soc. A 2019, 377, 20190030. [Google Scholar] [CrossRef]
- The Math Works, Inc. MATLAB, Version 2021a; The Math Works, Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Chase, J.G.; Begoc, V.; Barroso, L.R. Efficient structural health monitoring for a benchmark structure using adaptive RLS filters. Comput. Struct. 2005, 83, 639–647. [Google Scholar] [CrossRef]
- Ramos, L.F.; Aguilar, R.; Lourenço, P.B.; Moreira, S. Dynamic structural health monitoring of Saint Torcato church. Mech. Syst. Signal Process. 2013, 35, 1–15. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H.; Ou, J. Emerging data technology in structural health monitoring: Compressive sensing technology. J. Civ. Struct. Health Monit. 2014, 4, 77–90. [Google Scholar] [CrossRef]
- Kottapalli, V.A.; Kiremidjian, A.S.; Lynch, J.P.; Carryer, E.D.; Kenny, T.W.; Law, K.H.; Lei, Y. Two-tiered wireless sensor network architecture for structural health monitoring. In Smart Structures and Materials 2003: Smart Systems and Nondestructive Evaluation for Civil Infrastructures; SPIE: Bellingham, WA, USA, 2003; Volume 5057, pp. 8–19. [Google Scholar]
- Wong, K.Y. Instrumentation and health monitoring of cable-supported bridges. Struct. Control Health Monit. 2004, 11, 91–124. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Xia, Y.; Liao, W.Y.; Ko, J.M. Technology innovation in developing the structural health monitoring system for Guangzhou New TV Tower. Struct. Control Health Monit. 2009, 16, 73–98. [Google Scholar] [CrossRef]
- Giles, R.K. Development of a Long-Term, Multimetric Structural Health Monitoring System for a Historic Steel Truss Swing Bridge; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2013. [Google Scholar]
- Tosauchi, Y.; Sato, E.; Fukuyama, K.; Inoue, T.; Kajiwara, K.; Shiohara, H.; Mukai, T. 2015 Three-dimensional Shaking Table Test of a 10-story Reinforced Concrete Building on the E-Defense. In Proceedings of the 16th World Conference on Earthquake, Santiago, Chile, 9–13 January 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).