An Under-Sampling Array Signal Processing Method Based on Improved Hadamard Matrix
Abstract
1. Introduction
2. Array Signal Processing Model Based on Compressive Sensing
2.1. Array Received Signal and Its Sparsity
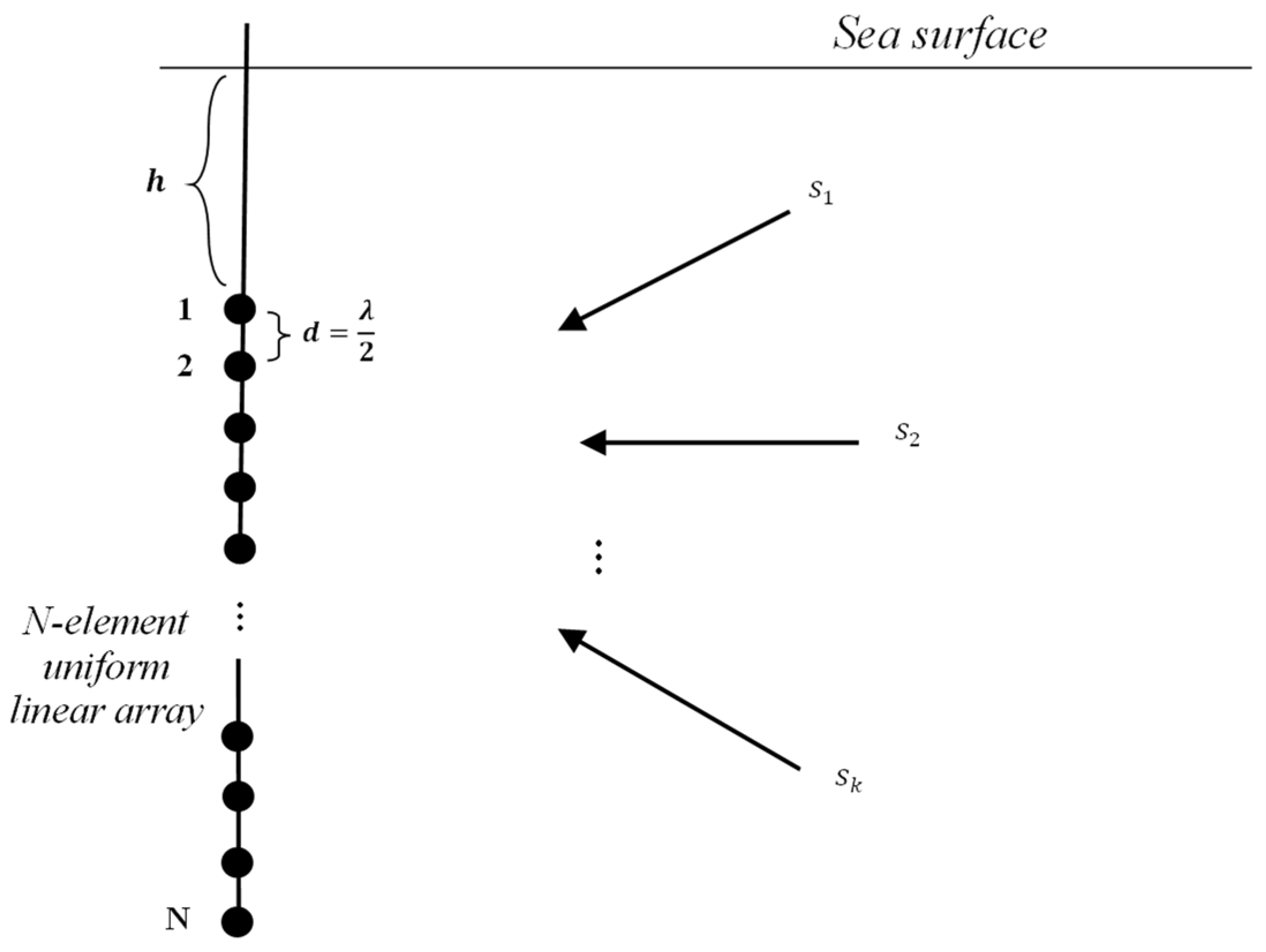
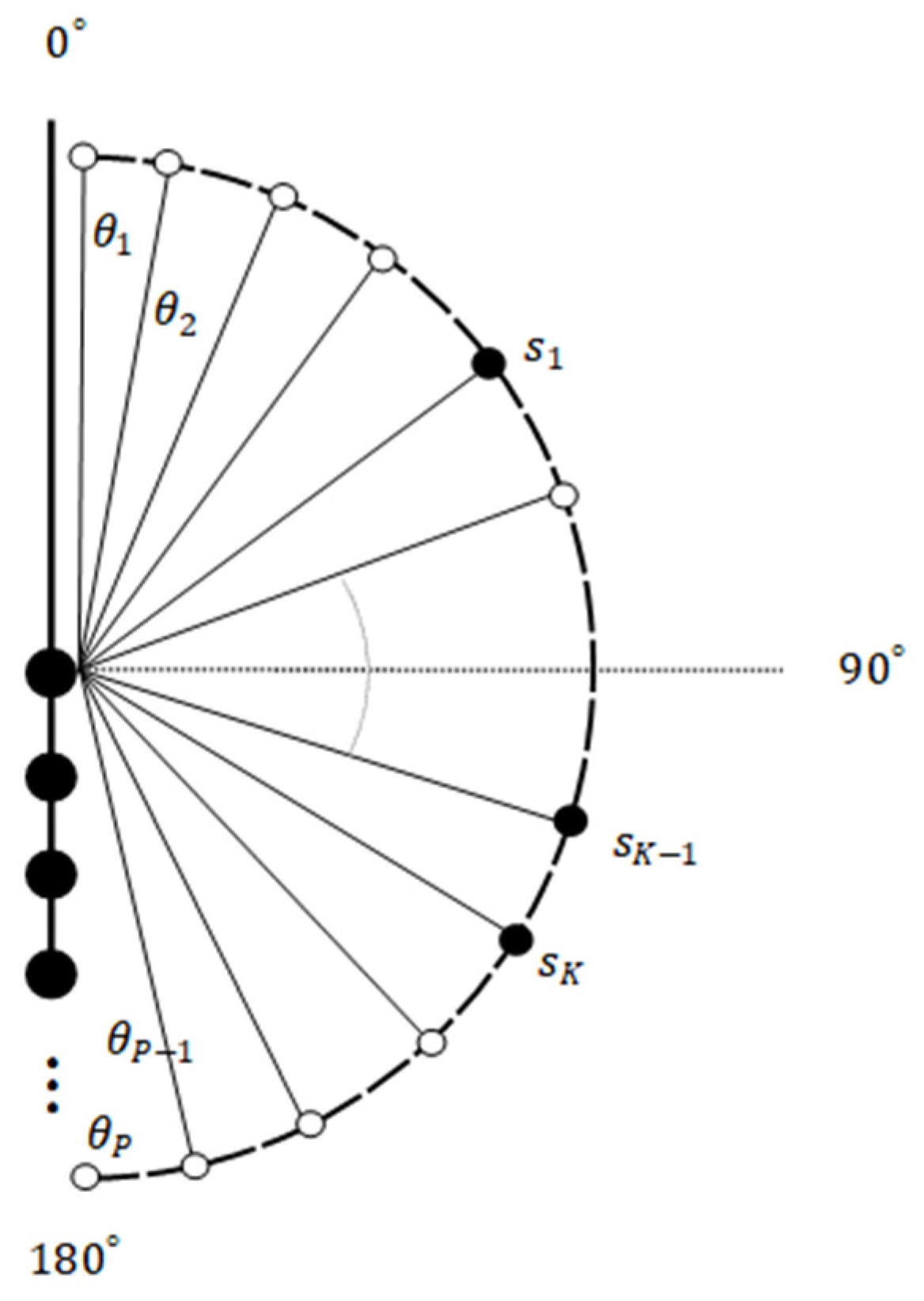
2.1.1. Narrowband Array Received Signal
2.1.2. Wideband Array Received Signal
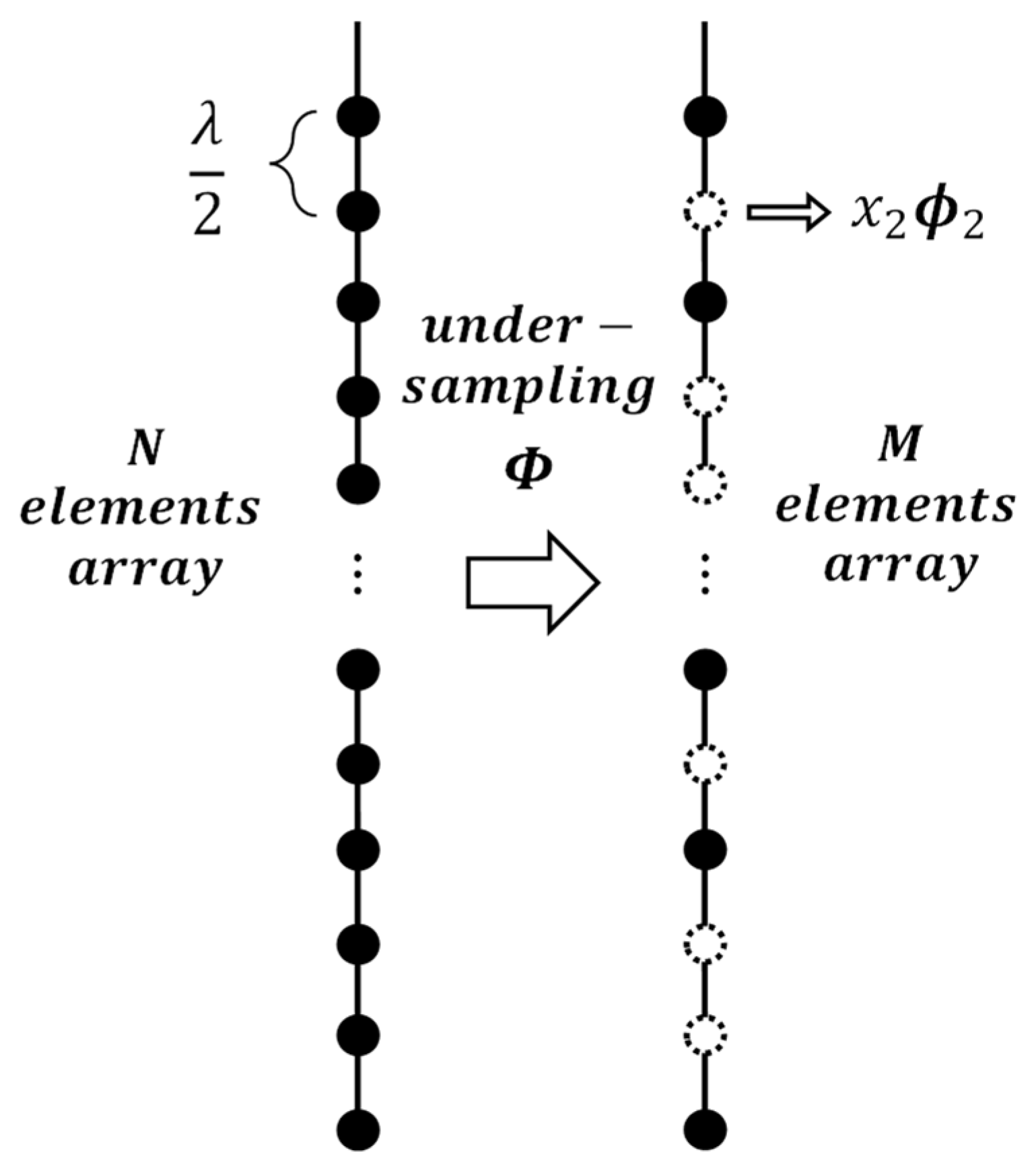
2.2. Compression of The Array Signal
2.3. Reconstruction of The Array Signal and The Direction Estimation
3. Improved Hadamard Matrix
3.1. Hadamard Matrix
3.2. Improved Hadamard Matrix
4. Simulation and Experiments Analysis
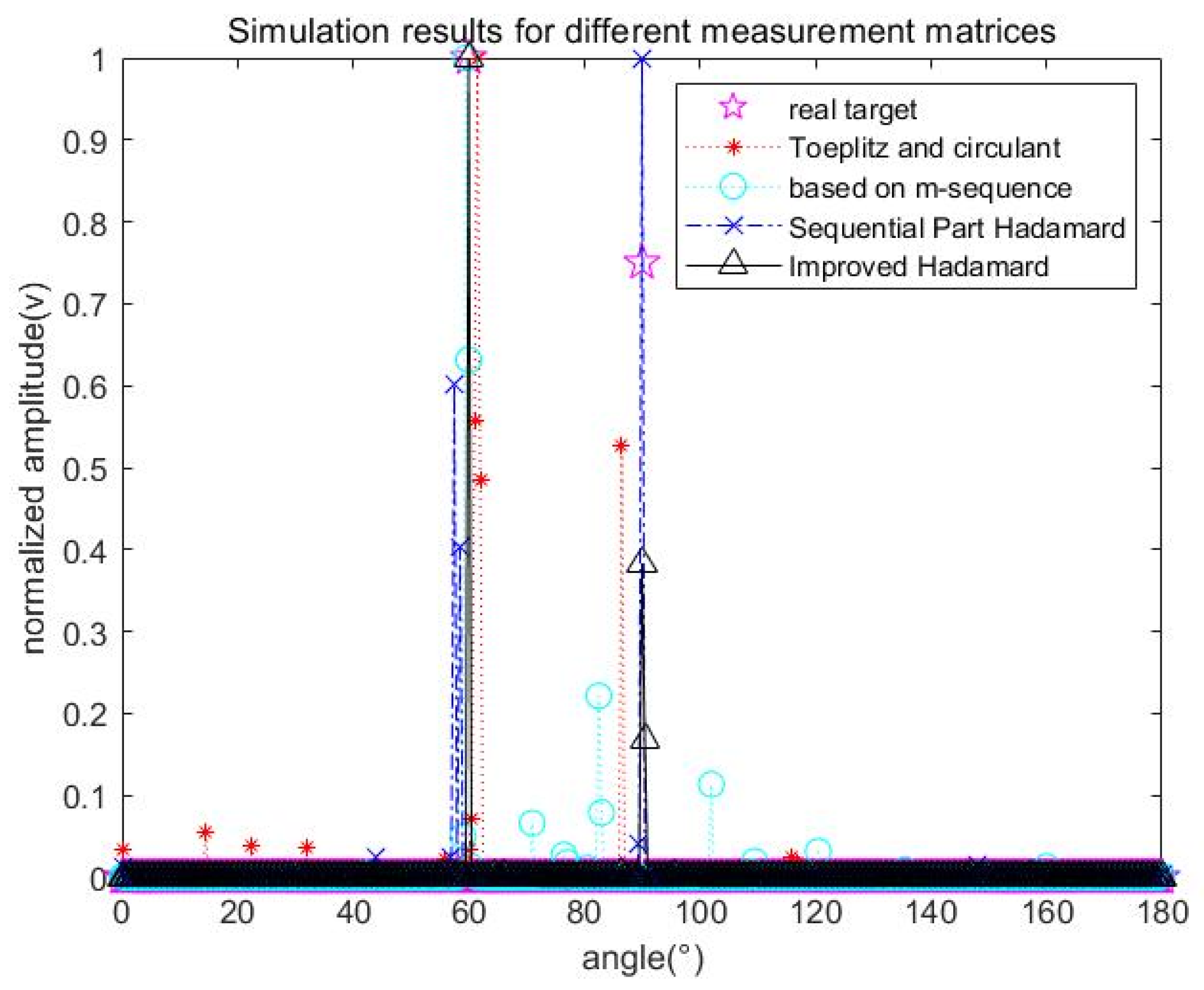
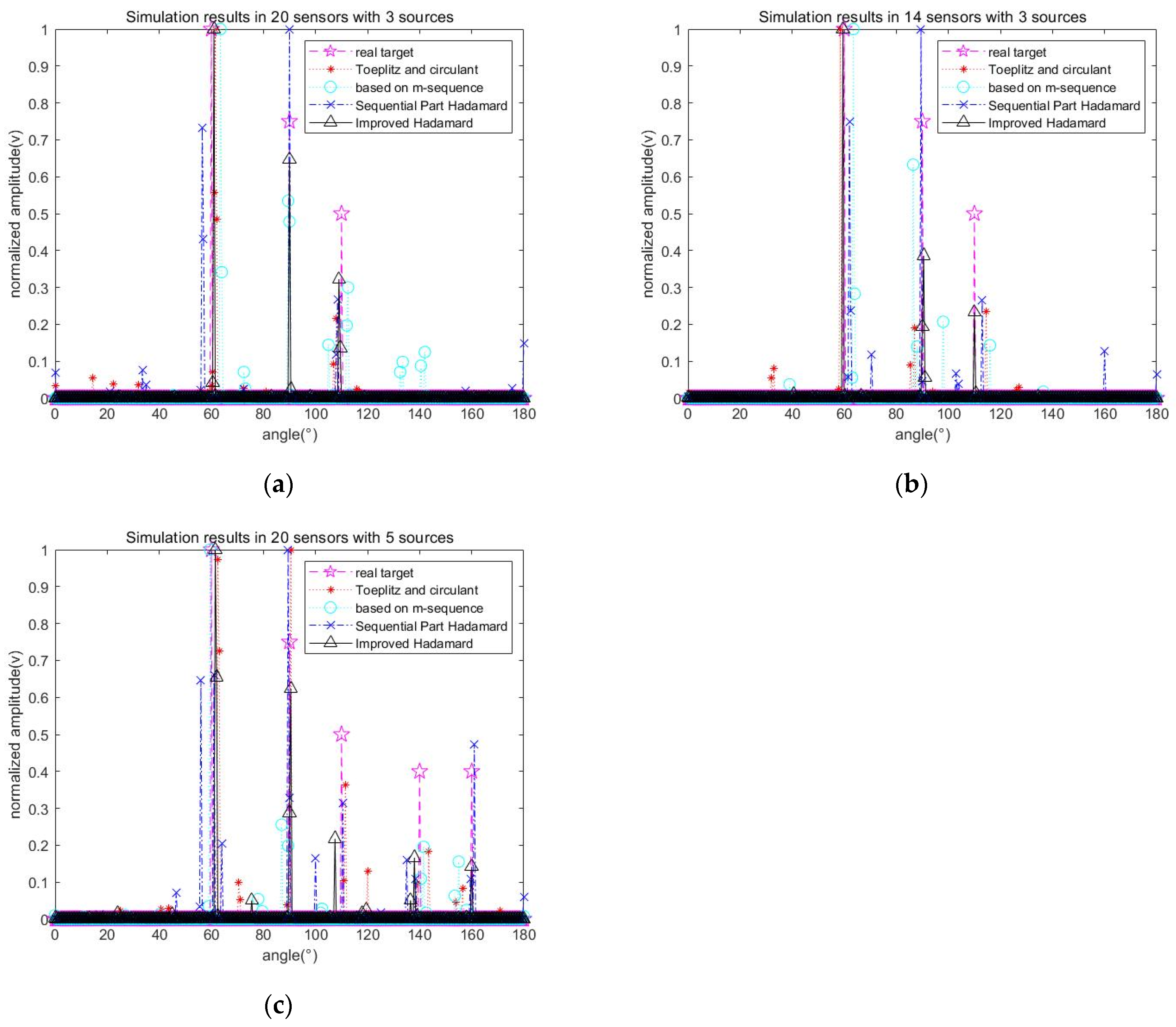
4.1. Validation and Analysis Based on Simulation Signals
4.2. Validation and Analysis Based on Experimental Signals
4.2.1. Test Overview
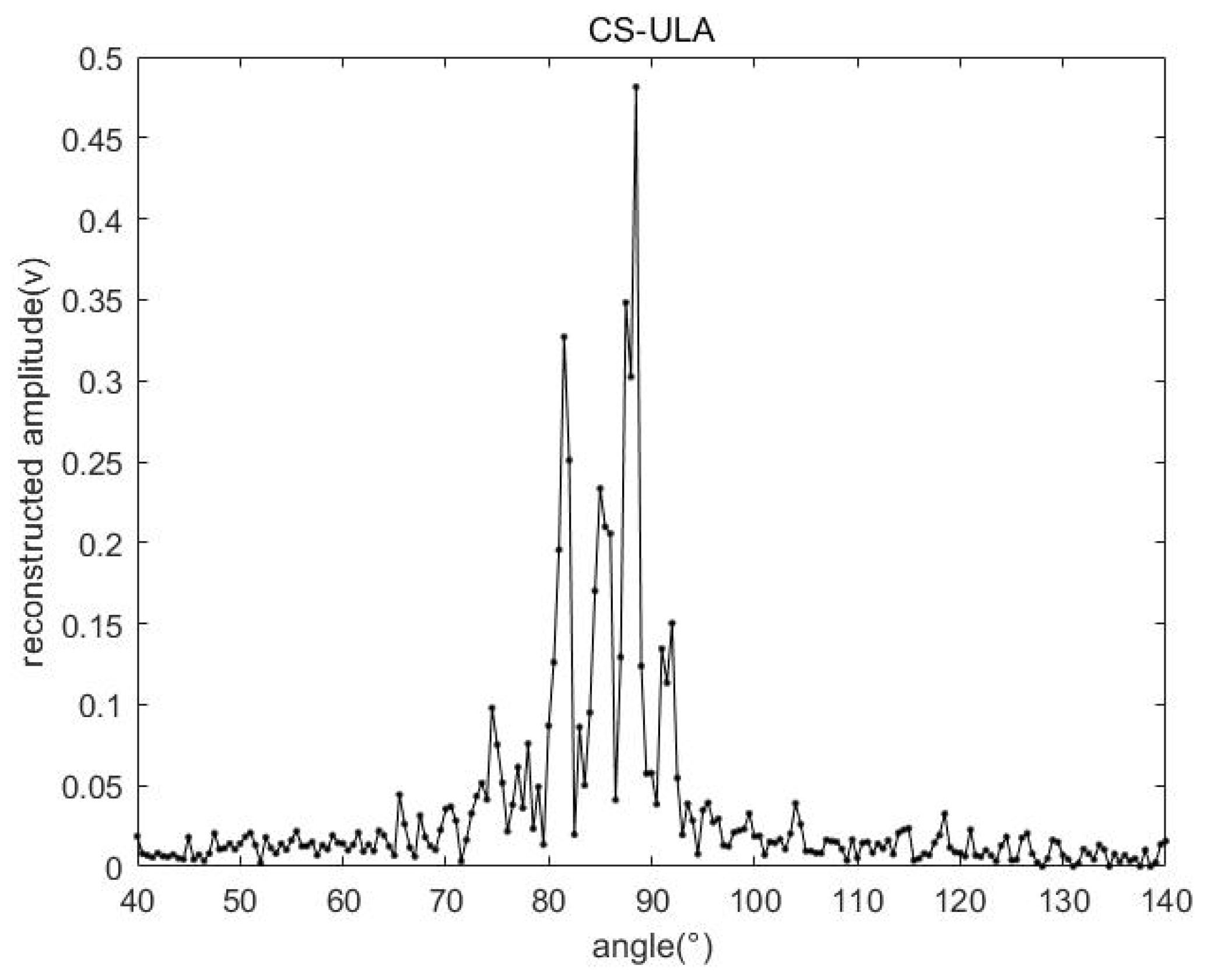
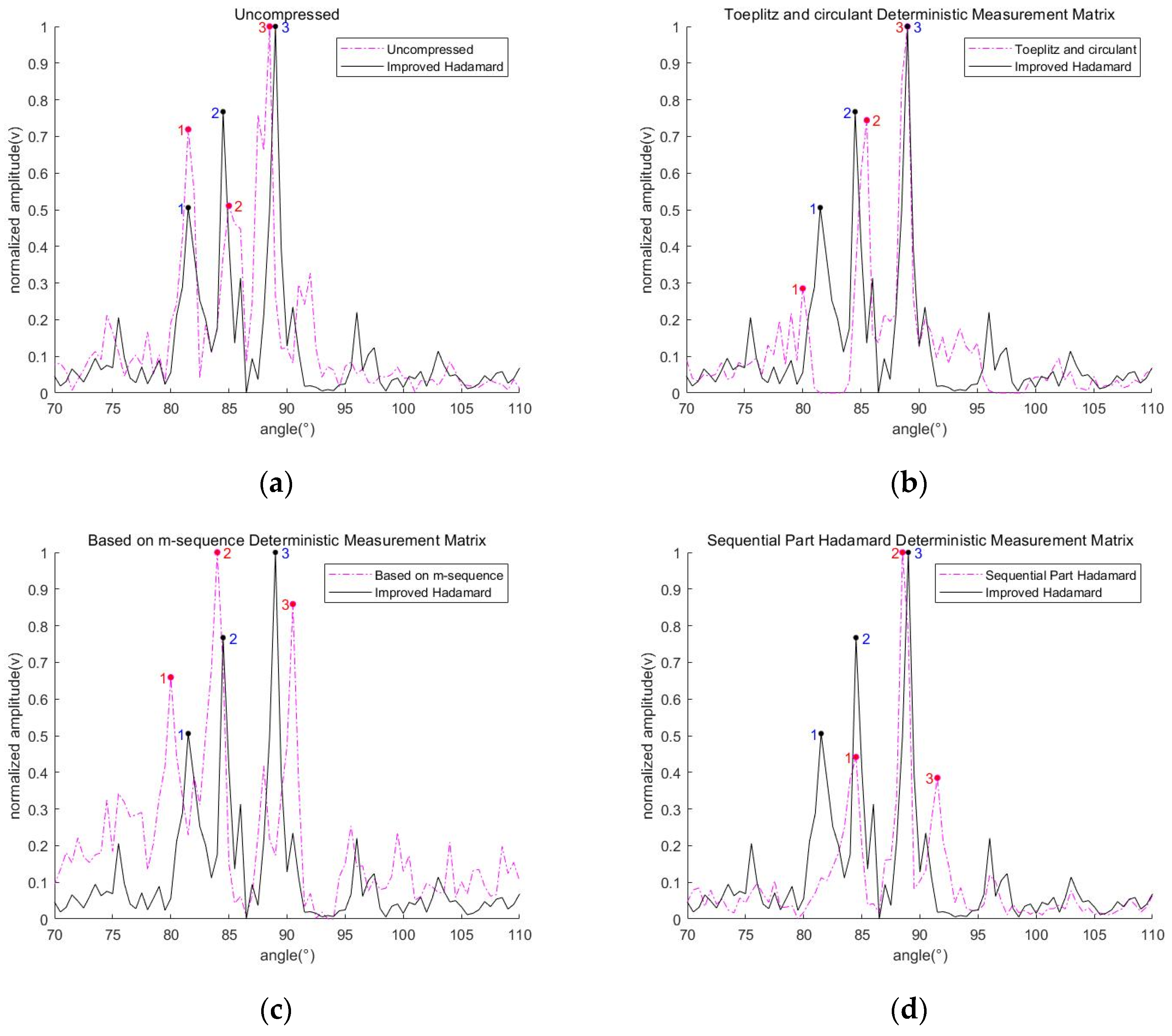
4.2.2. Results and Analysis of The Array Signal Processing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CS | Compressive Sensing |
| DOA | Direction of Arrival |
| CBF | Conventional Beamforming |
| MVDR | Minimum Variance Distortionless Response |
| MUSIC | Multiple Signal Classification |
| ES-DOA | DOA Estimation Based on Eigenspace |
| ESPRIT | Estimation Signal Parameter Via Rotational Invariance Techniques |
| CSA | Compressive Sampling Array |
| CSB | Compressive Sensing Beamforming |
| CSA-ES-DOA | Compressive Sampling Array DOA Estimation Based on Eigenspace |
| ULA | Uniform Linear Array |
| CZ | Compression Zeroing |
| LFM | Linear Frequency Modulation |
| A-OMP | Adaptive Orthogonal Matching Pursuit |
| UUV | Unmanned Underwater Vehicle |
| ISSM | Incoherent Signal Subspace Method |
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Sharma, A.; Mathur, S. Performance analysis of adaptive array signal processing algorithms. IETE Tech. Rev. 2016, 33, 472–491. [Google Scholar] [CrossRef]
- Zhai, W.Q.; Li, J.; Xie, K. Target azimuth estimation in the presence of linear array shape distortion. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015. [Google Scholar]
- Rehacek, J.; Paúr, M.; Stoklasa, B.; Hradil, Z.; Sánchez-Soto, L.L. Optimal measurements for resolution beyond the Rayleigh limit. Opt. Lett. 2017, 42, 231–234. [Google Scholar] [CrossRef] [PubMed]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lv, W.; Shi, Y.; Zhao, R.N.; Xu, D.Z. A novel DOA estimation algorithm based on eigen space. In Proceedings of the 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 16–17 August 2007. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Zhu, Z.; Chi, C.; Zhang, C.H. Spatial-Resampling Wideband Compressive Beamforming. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021. [Google Scholar]
- Hevalier, P.; Albera, L.; Férréol, A.; Comon, P. On the virtual array concept for higher order array processing. IEEE Trans. Signal Process. 2005, 53, 1254–1271. [Google Scholar] [CrossRef]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. DOA Estimation of Quasi-Stationary Signals with Less Sensors Than Sources and Unknown Spatial Noise Covariance: A Khatri–Rao Subspace Approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Hoctor, R.T.; Kassam, S.A. The unifying role of the coarray in aperture synthesis for coherent and incoherent imaging. Proc. IEEE 1990, 78, 735–752. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Sarangi, P.; Hücümenoğlu, M.C.; Pal, P. Single-Snapshot Nested Virtual Array Completion: Necessary and Sufficient Conditions. IEEE Signal Process. Lett. 2022, 29, 1–5. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing with Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Wang, Y.; Leus, G.; Pandharipande, A. Direction estimation using compressive sampling array processing. In Proceedings of the 2009 IEEE/SP 15th Workshop on Statistical Signal Processing(SSP), Cardiff, UK, 31 August–3 September 2009. [Google Scholar]
- Li, G.L.; Huang, G.M. DOA estimation based on compressive sampling array with novel beamforming. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar]
- Li, B.; Zou, Y.X.; Zhu, Y.S. Direction estimation under compressive sensing framework: A review and experimental results. In Proceedings of the 2011 IEEE International Conference on Information and Automation(ICIA), Shenzhen, China, 6–8 June 2011. [Google Scholar]
- Jouny, I. Music DOA estimation with compressive sensing and/or compressive arrays. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011. [Google Scholar]
- Yan, J.; Feng, N.Z.; Shen, Y. Bearing estimation of coherent signals using compressive sampling array. In Proceedings of the 2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Montevideo, Montevideo, Uruguay, 12–15 May 2014. [Google Scholar]
- Dang, K.; Ma, L.H.; Tian, Y.; Zhang, H.W.; Ru, L.; Li, X.B. Construction of the compressive sensing measurement matrix based on m sequences. J. Xidian Univ. 2015, 42, 186–192. [Google Scholar]
- Li, X.L.; Fan, Y.M.; Wu, L.C. Study and construction of a compressed sensing measurement matrix that is easy to implement in hardware. CAAI Trans. Intell. Syst. 2017, 12, 279–285. [Google Scholar]
- Ravelomanantsoa, A.; Rabah, H.; Rouane, A. Compressed Sensing: A Simple Deterministic Measurement Matrix and a Fast Recovery Algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 3405–3413. [Google Scholar] [CrossRef]
- Li, X.B.; Zhao, R.Z.; Hu, S.H. Blocked Polynomial Deterministic Matrix for Compressed Sensing. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010. [Google Scholar]
- Huang, T.; Fan, Y.Z.; Zhu, M. Symmetric Toeplitz-Structured Compressed Sensing Matrices. Sens. Imaging 2013, 16, 7. [Google Scholar] [CrossRef]
- Kang, C.Y.; Zhang, X.H.; Fan, W.T.; Li, J. Suppressing directional interference combining frequency domain blind source separation with beamforming. Acta Acust. 2014, 39, 565–569. [Google Scholar]
- Wei, J.; Yue, F.L.; Li, R.Y.; Wang, W.J.; Gao, D. A particle filter based compressive sensing method for tracking moving wideband sound sources. China Commun. 2018, 15, 197–210. [Google Scholar] [CrossRef]
- Kang, C.Y.; Li, Q.Y.; Jiao, Y.M.; Li, J.; Zhang, X.H. Direction of arrival estimation and signal recovery for underwater target based on compressed sensing. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015. [Google Scholar]

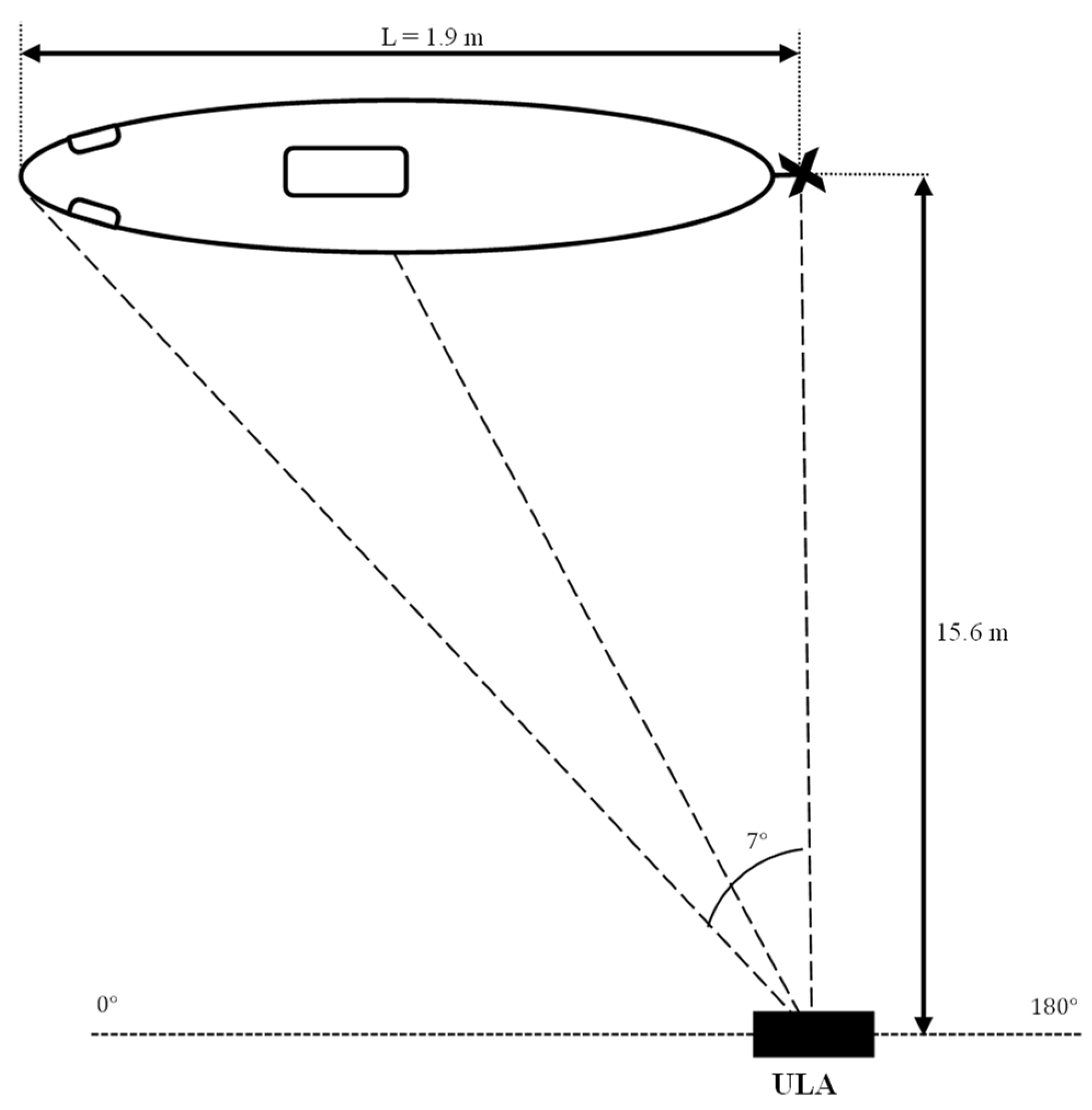


| Parameter | Value |
|---|---|
| Array type | Linear array |
| Sensors number | 27 |
| Underwater speed | 1500 m/s |
| Central frequency | 150 kHz |
| Sampling frequency | 1000 kHz |
| Element spacing | 0.005 m |
| Target angle | [60°, 90°] |
| Target amplitude | [1, 0.75] |
| gridding | [0:0.5:180] |
| Number of sensors after compression | 11 |
| Parameter | Value |
|---|---|
| Sensors number | 2014 |
| Target angle | [60°, 90°, 110°, 140°, 160°] |
| Target amplitude | [1, 0.75, 0.5, 0.4, 0.4] |
| compression ratio | 50% |
| Number of sensors after compression | 10, 7 |
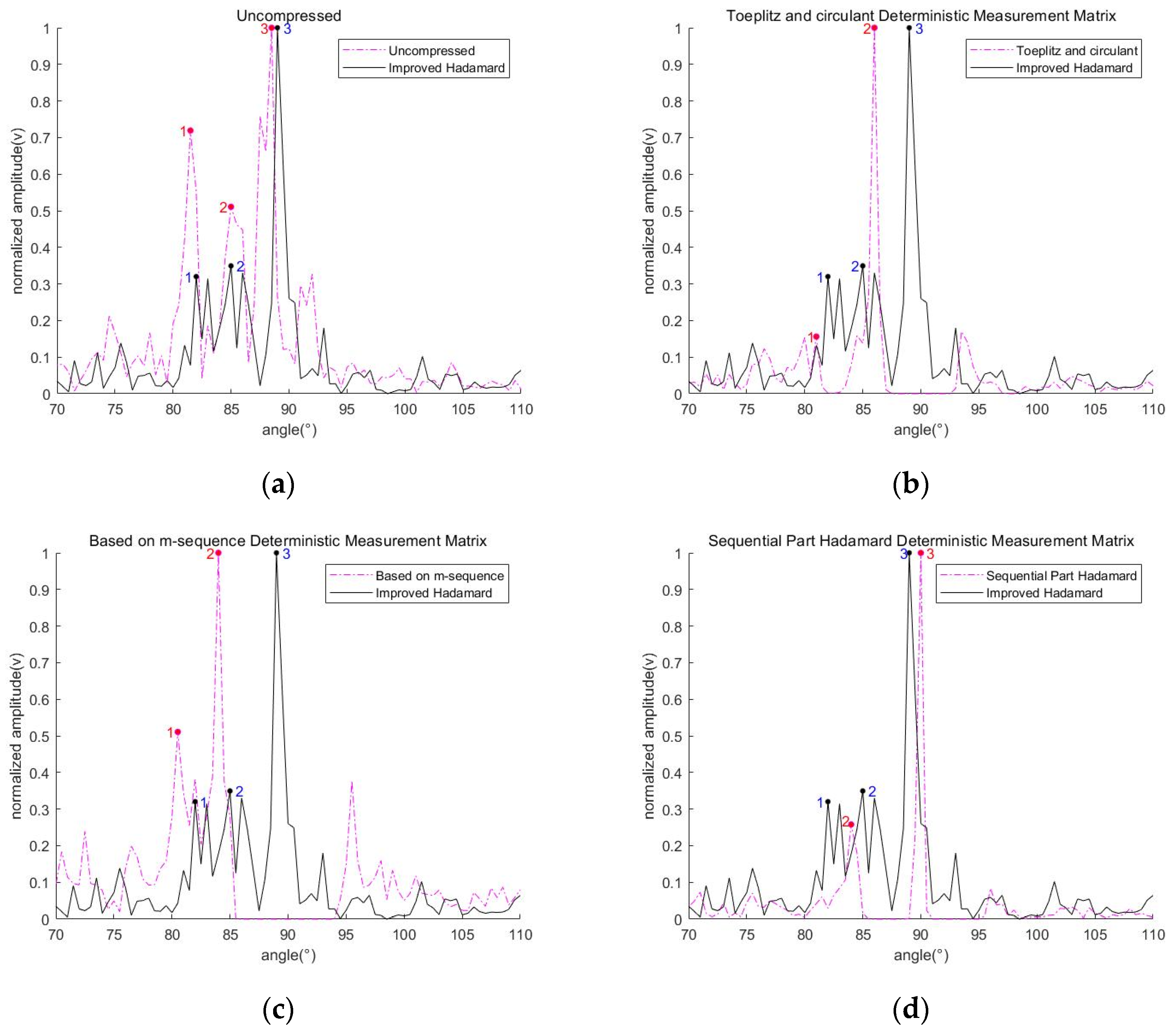
| In 70% Compression Ratio | |||
|---|---|---|---|
| Mark | 1 | 2 | 3 |
| Uncompressed | 81.5° | 85° | 88.5° |
| Improved Hadamard | 81.5° | 84.5° | 89° |
| Toeplitz and circulant | 80° | 85.5° | 89° |
| Based on m-sequence | 80° | 84° | 90.5° |
| Sequential-Part Hadamard | 84.5° | 88.5° | 91.5° |
| In 44% Compression Ratio | |||
|---|---|---|---|
| Mark | 1 | 2 | 3 |
| Uncompressed | 81.5° | 85° | 88.5° |
| Improved Hadamard | 82° | 85° | 89° |
| Toeplitz and circulant | 81° | 86° | - |
| Based on m-sequence | 80.5° | 84° | - |
| Sequential-Part Hadamard | - | 84° | 90° |
| Improved Hadamard | |||
|---|---|---|---|
| Compression Ratio | 1 | 2 | 3 |
| 70% | 81.5° | 85° | 89° |
| 60% | 81.5° | 84.5° | 89° |
| 52% | 82° | 84.5° | 88.5° |
| 44% | 82° | 85° | 89° |
| 41% | 81.5° | 85° | 89° |
| 37% | 82.5° | 84.5° | 89.5° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Ge, Q.; Wen, Y.; Guo, Y.; Li, M. An Under-Sampling Array Signal Processing Method Based on Improved Hadamard Matrix. Appl. Sci. 2022, 12, 10769. https://doi.org/10.3390/app122110769
Sun T, Ge Q, Wen Y, Guo Y, Li M. An Under-Sampling Array Signal Processing Method Based on Improved Hadamard Matrix. Applied Sciences. 2022; 12(21):10769. https://doi.org/10.3390/app122110769
Chicago/Turabian StyleSun, Tongjing, Qidong Ge, Yabin Wen, Yunfei Guo, and Mingda Li. 2022. "An Under-Sampling Array Signal Processing Method Based on Improved Hadamard Matrix" Applied Sciences 12, no. 21: 10769. https://doi.org/10.3390/app122110769
APA StyleSun, T., Ge, Q., Wen, Y., Guo, Y., & Li, M. (2022). An Under-Sampling Array Signal Processing Method Based on Improved Hadamard Matrix. Applied Sciences, 12(21), 10769. https://doi.org/10.3390/app122110769





