An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network
Abstract
1. Introduction
2. Compensation Model and Method
2.1. T-L Model
2.2. Primitive Neural Model
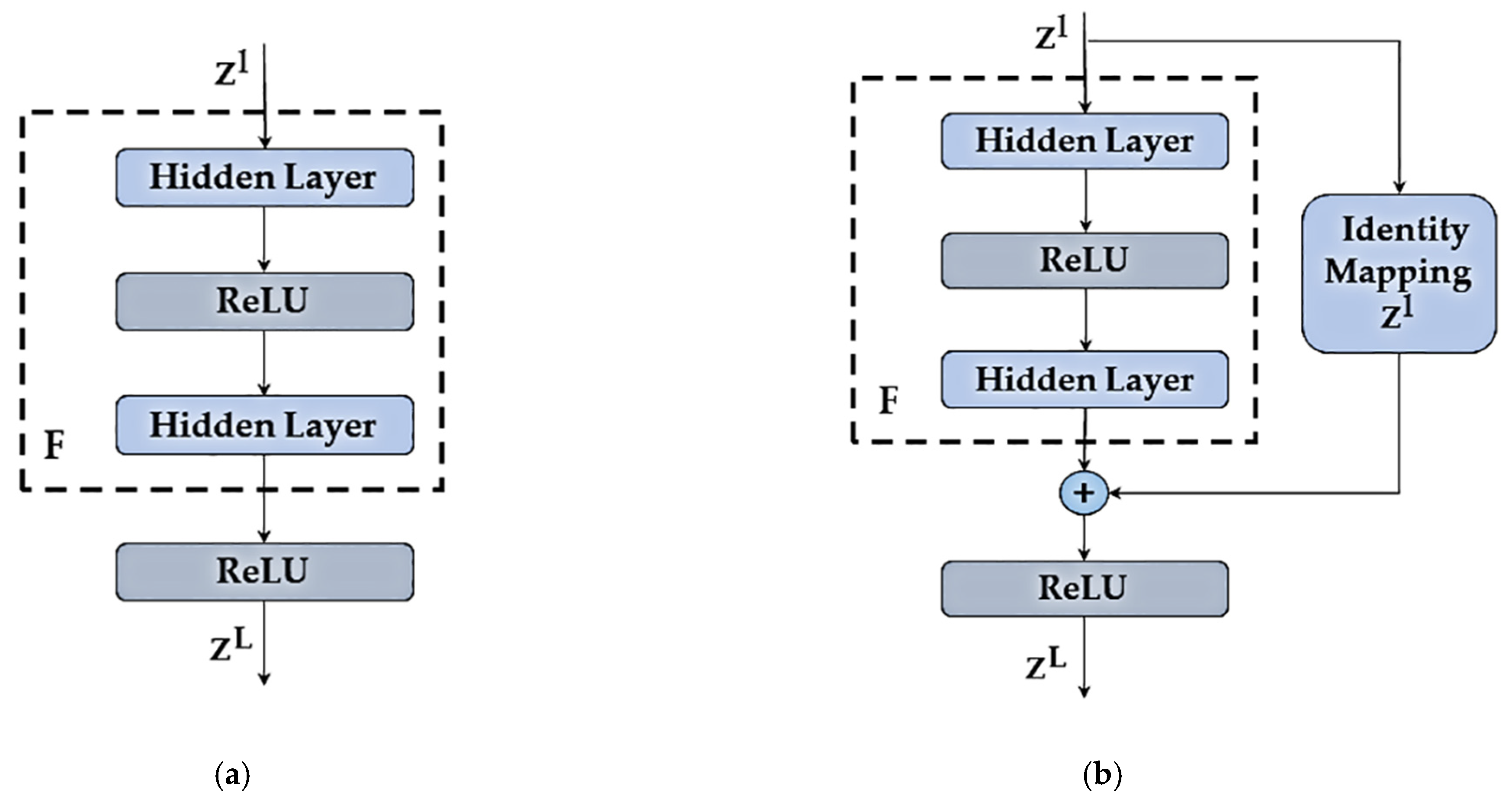
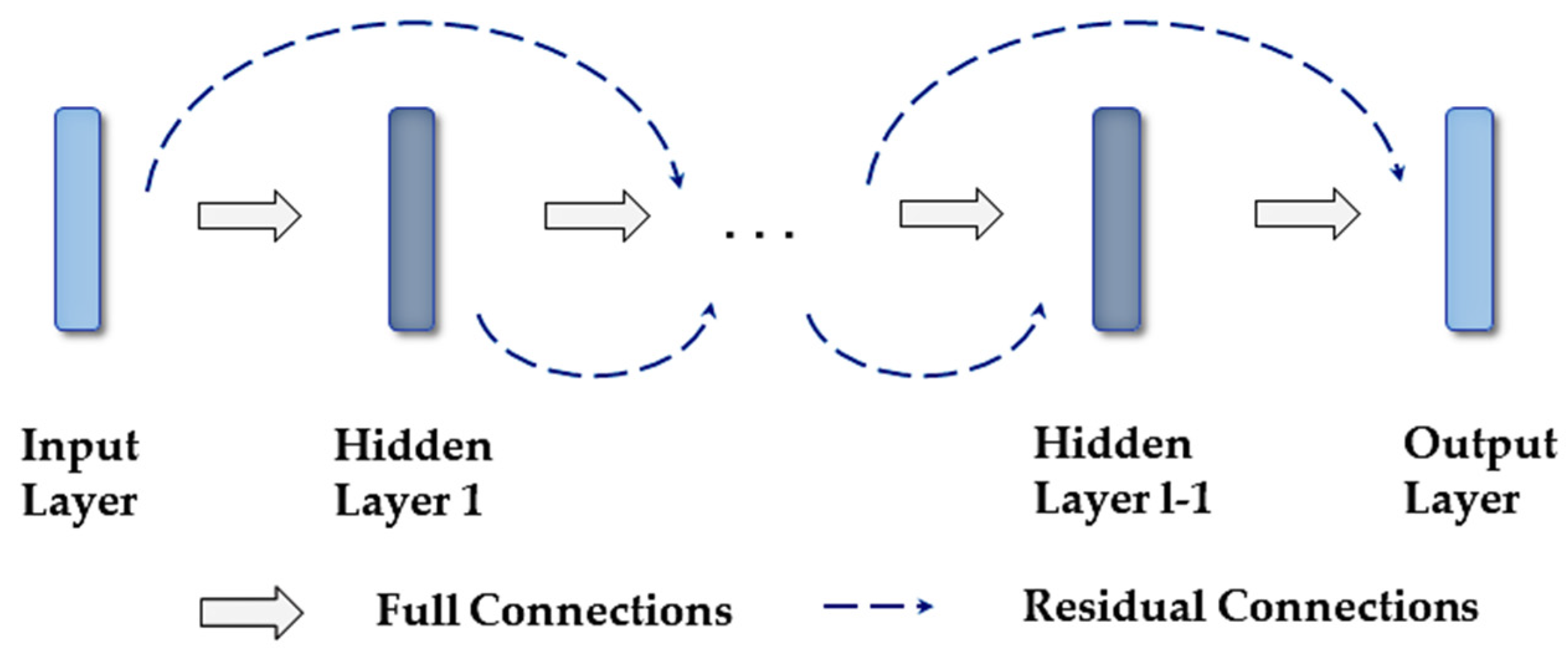
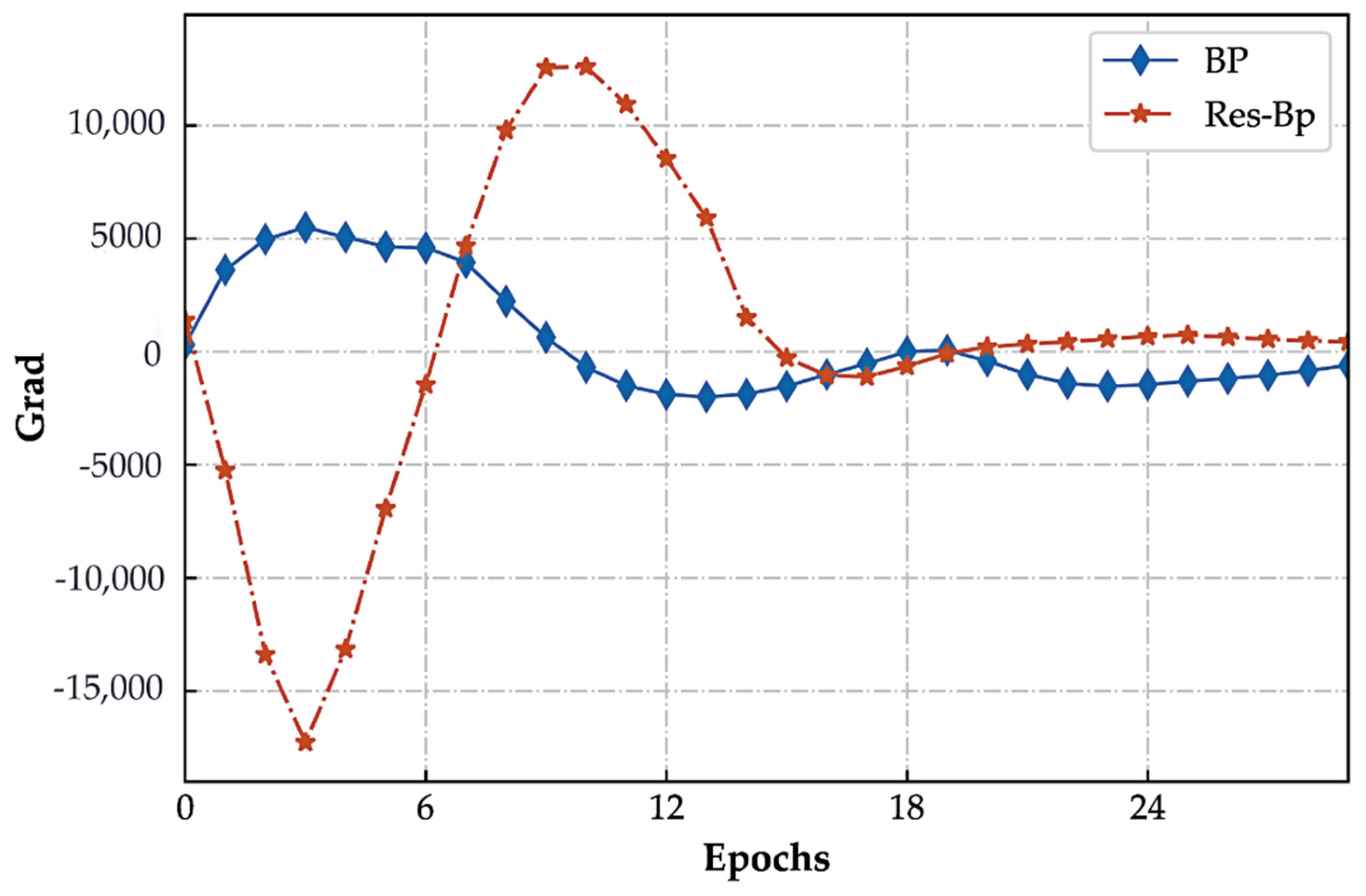
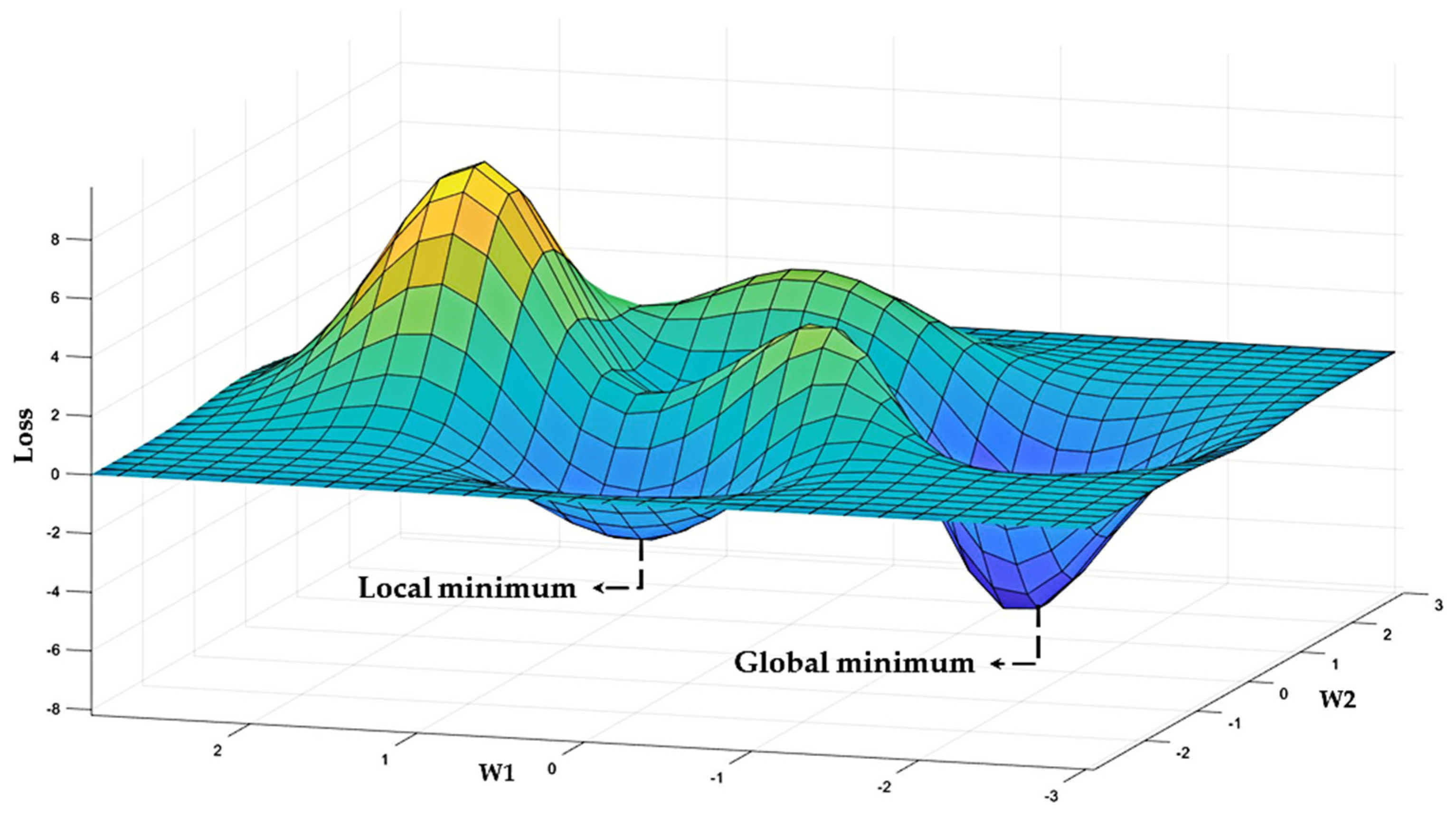
2.3. Res-Bp
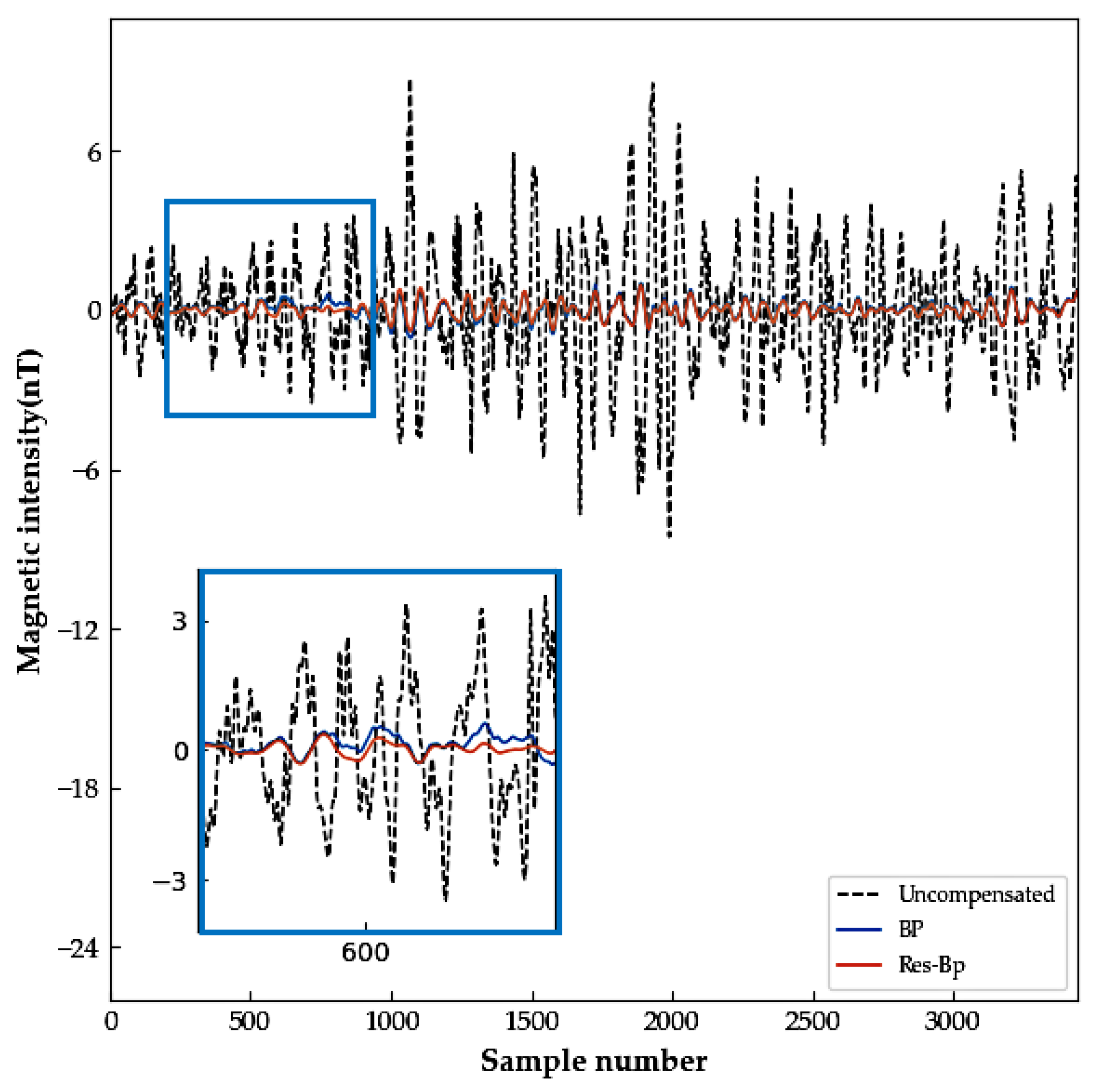
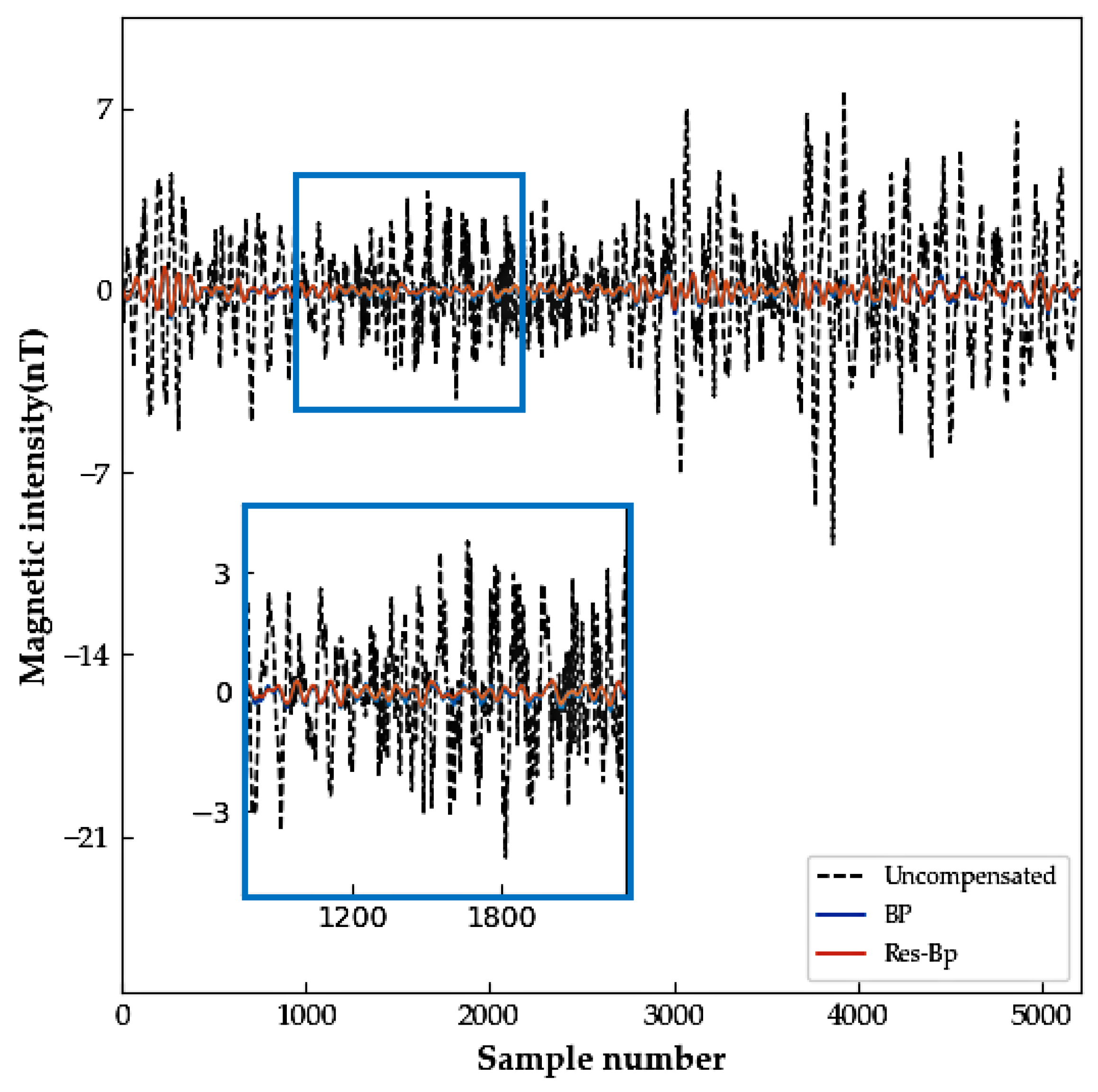
3. Experiment
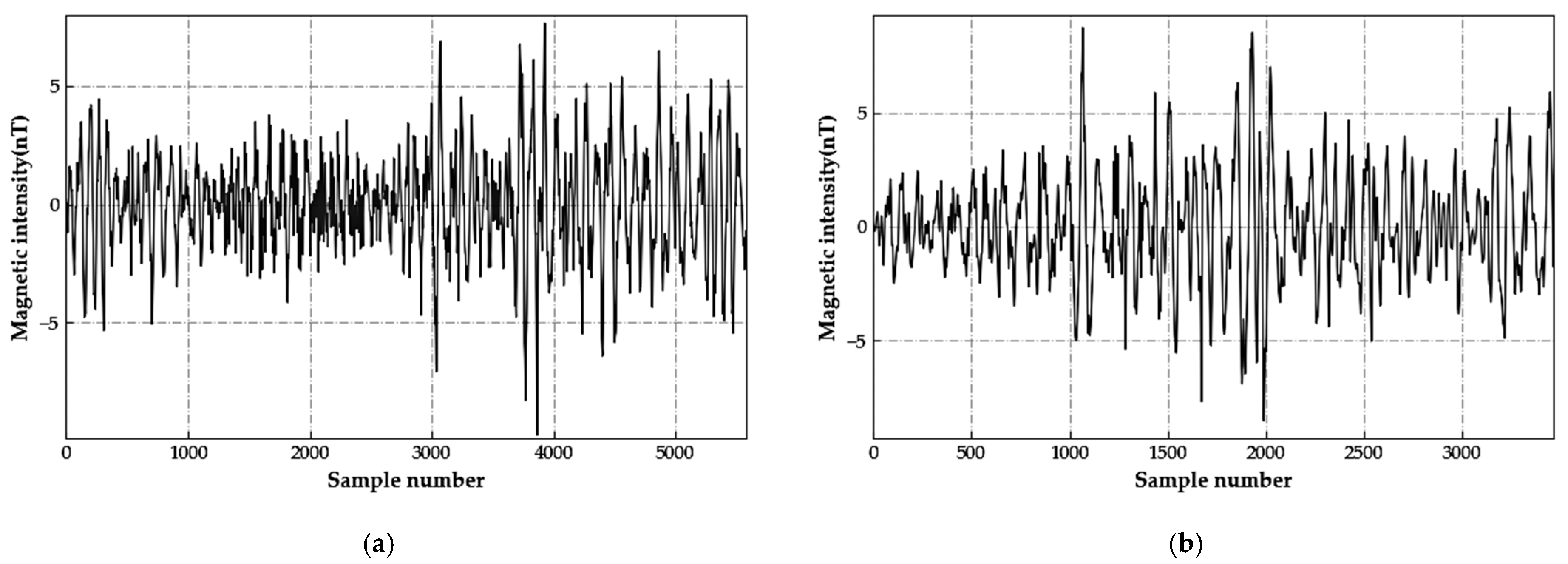
3.1. Compensation Flight
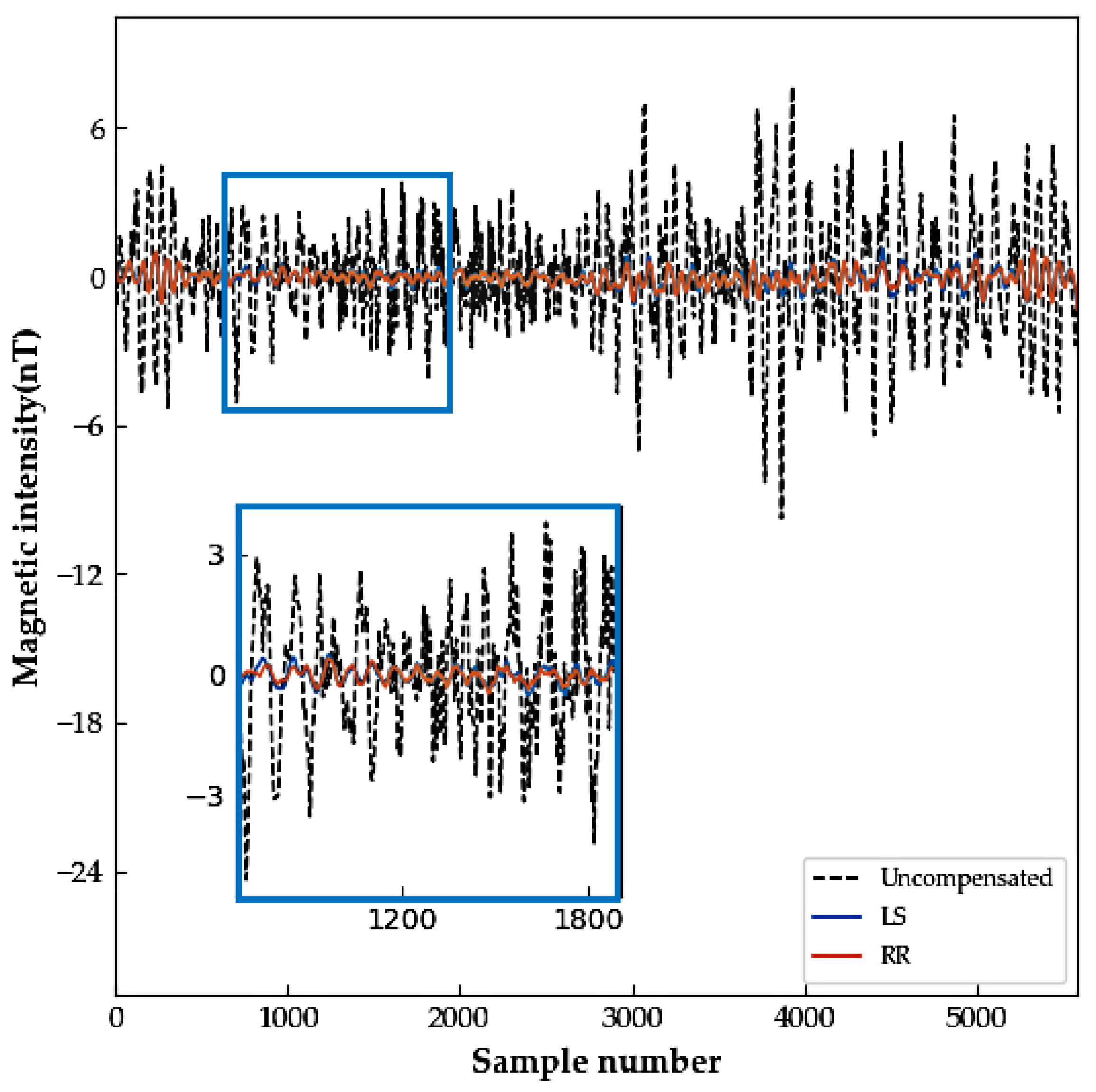
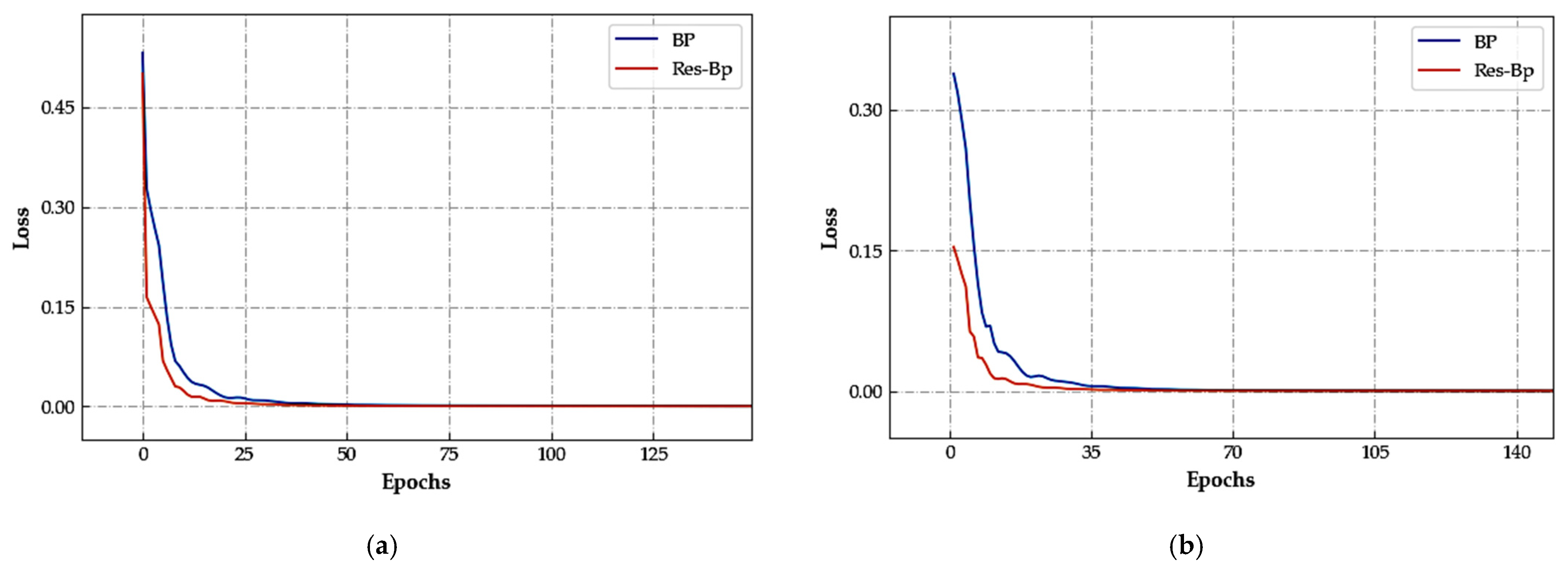
3.2. Compensation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiong, S.Q. Technological innovation and application of aerogeophysical exploration. J. Geomech. 2020, 26, 791–818. [Google Scholar]
- Meng, Q.K.; Zhou, D.W. History and Prospect of aeromagnetic compensation technology at home and abroad. Geophys. Geochem. Explor. 2017, 41, 694–699. [Google Scholar]
- Noriega, G. Aeromagnetic compensation in gradiometry—Performance, model stability, and robustness. IEEE Geosci. Remote Sens. Lett. 2014, 12, 117–121. [Google Scholar] [CrossRef]
- Tolles, W.E.; Lawson, J.D. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instruments Lab. Inc.: Mineola, NY, USA, 1950; p. 201. [Google Scholar]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerospace Navig. Electr. 1961, 3, 95–105. [Google Scholar] [CrossRef]
- Leach, B.W. Aeromagnetic compensation as a linear regression problem. In Information Linkage between Applied Mathematics and Industry II; Academic Press: London, UK, 1980; pp. 139–161. [Google Scholar]
- Wu, P.L.; Zhang, Q.Y. Aeromagnetic compensation algorithm based on principal component analysis. J. Sens. 2018, 2018, 7. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, P.; Jiao, J. A New Improved Algorithm for Aeromagnetic Compensation. IOP Conf. Ser.: Earth Environ. Sci. 2021, 660, 012132. [Google Scholar] [CrossRef]
- Williams, P.M. Aeromagnetic compensation using neural networks. Neural Comput. Appl. 1993, 1, 207–214. [Google Scholar] [CrossRef]
- Zhang, D.K. Analysis of Aeromagnetic Swing Noise and Corresponding Compensation Method. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–10. [Google Scholar] [CrossRef]
- Xu, X.; Huang, L.; Liu, X. DeepMAD: Deep Learning for Magnetic Anomaly Detection and Denoising. IEEE Access 2020, 8, 121257–121266. [Google Scholar] [CrossRef]
- Zhao, X.; Jiao, J. An aeromagnetic compensation algorithm based on a deep autoencoder. IEEE Geosci. Remote Sens. Lett. 2020, 19, 3044999. [Google Scholar]
- Wang, Z. Fault Early Warning of Wind Turbine Generator based on Residual Autoencoder Network. In Proceedings of the 6th International Conference on High Performance Compilation, Computing and Communications, Jilin, China, 23–25 June 2022. [Google Scholar]
- Ma, M.; Zhou, Z.; Cheng, D. A dual estimate method for aeromagnetic compensation. Meas. Sci. Technol. 2017, 28, 115904. [Google Scholar] [CrossRef]
- Yu, P.; Zhao, X.; Jiao, J. An improved neural network method for aeromagnetic compensation. Meas. Sci. Technol. 2021, 32, 045106. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Jiao, J.; Yu, P.; Zhao, X. Real-Time Aeromagnetic Compensation With Compressed and Accelerated Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Jastrzębski, S.; Arpit, D.; Ballas, N. Residual connections encourage iterative inference. arXiv 2017, arXiv:1710.04773. [Google Scholar]
- He, K.; Zhang, X.; Ren, S. Identity mappings in deep residual networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 630–645. [Google Scholar]
- Hardwick, C.D. Important design considerations for inboard airborne magnetic gradiometers. Geophysics 1984, 49, 2004–2018. [Google Scholar] [CrossRef]
- Noriega, G. Performance measures in aeromagnetic compensation. Leading Edge 2011, 30, 1122–1127. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, X.C.; Jiao, J. Fast Processing Method of Aeromagnetic Compensation Basedon Fluxgate Estimation. J. Jilin Univ. (Earth Sci. Ed.) 2019, 49, 857–864. [Google Scholar]
- Li, J.J.; Zhang, J.T. Study on the determinacy of the determinate coefficient of regression model. Stat. Decision Making 2005, 11, 19–20. [Google Scholar]


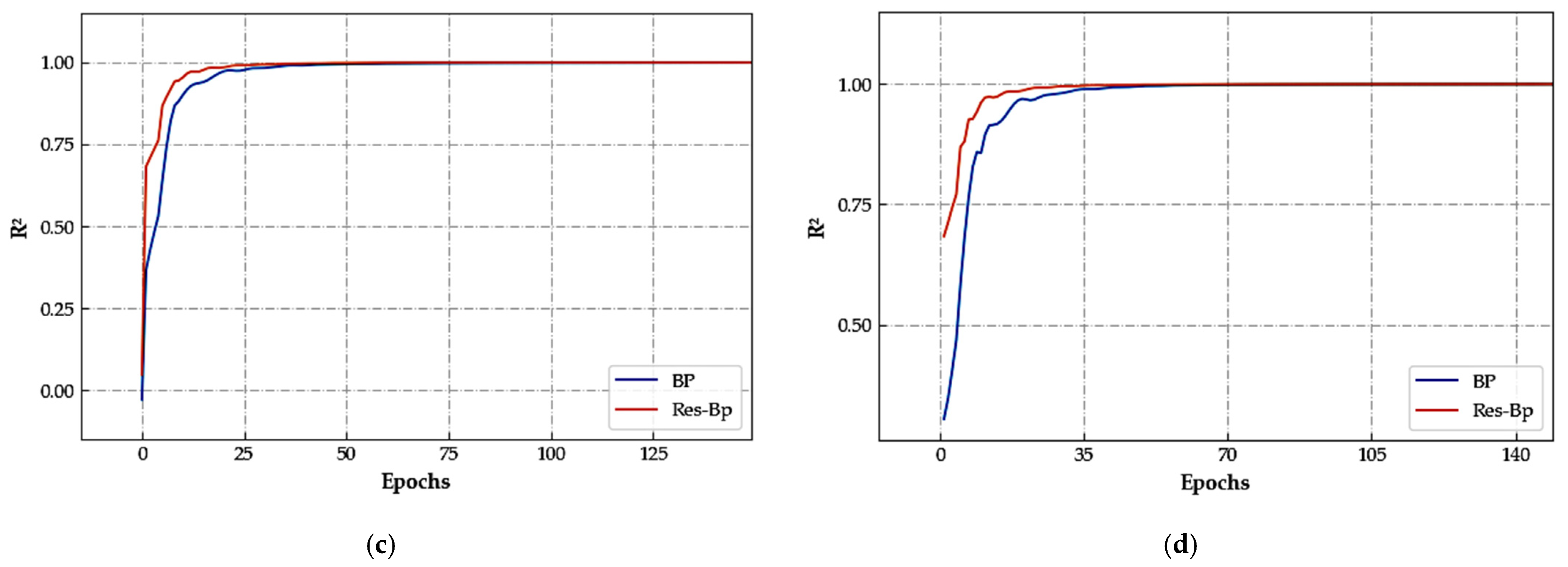
| Test Set | Training Set | Method | STDu | STDc | IR |
|---|---|---|---|---|---|
| Flight A | Flight B | LS | 2.171 | 0.355 | 6.115 |
| RR | 0.324 | 6.701 |
| Test Set | Training Set | Method | STDu | STDc | IR |
|---|---|---|---|---|---|
| Flight B | Flight A | BP | 2.334 | 0.294 | 7.939 |
| Res-Bp | 0.260 | 8.977 | |||
| Flight A | Flight B | BP | 2.112 | 0.285 | 7.411 |
| Res-Bp | 0.266 | 7.940 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Bi, F.; Jiao, J.; Zhao, X.; Zhou, S.; Su, Z. An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Appl. Sci. 2022, 12, 10759. https://doi.org/10.3390/app122110759
Yu P, Bi F, Jiao J, Zhao X, Zhou S, Su Z. An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Applied Sciences. 2022; 12(21):10759. https://doi.org/10.3390/app122110759
Chicago/Turabian StyleYu, Ping, Fengyi Bi, Jian Jiao, Xiao Zhao, Shuai Zhou, and Zhenning Su. 2022. "An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network" Applied Sciences 12, no. 21: 10759. https://doi.org/10.3390/app122110759
APA StyleYu, P., Bi, F., Jiao, J., Zhao, X., Zhou, S., & Su, Z. (2022). An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Applied Sciences, 12(21), 10759. https://doi.org/10.3390/app122110759







