Variation Mechanism and Prediction of Soil–Water Characteristic Curve Parameters of Low-Liquid-Limit Silty Clay under Freeze–Thaw Cycles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. F–T Cycle Test Method
2.3. Matric Suction Test Method
2.4. Electron Microscopic Scanning Test Method
3. Results and Discussion
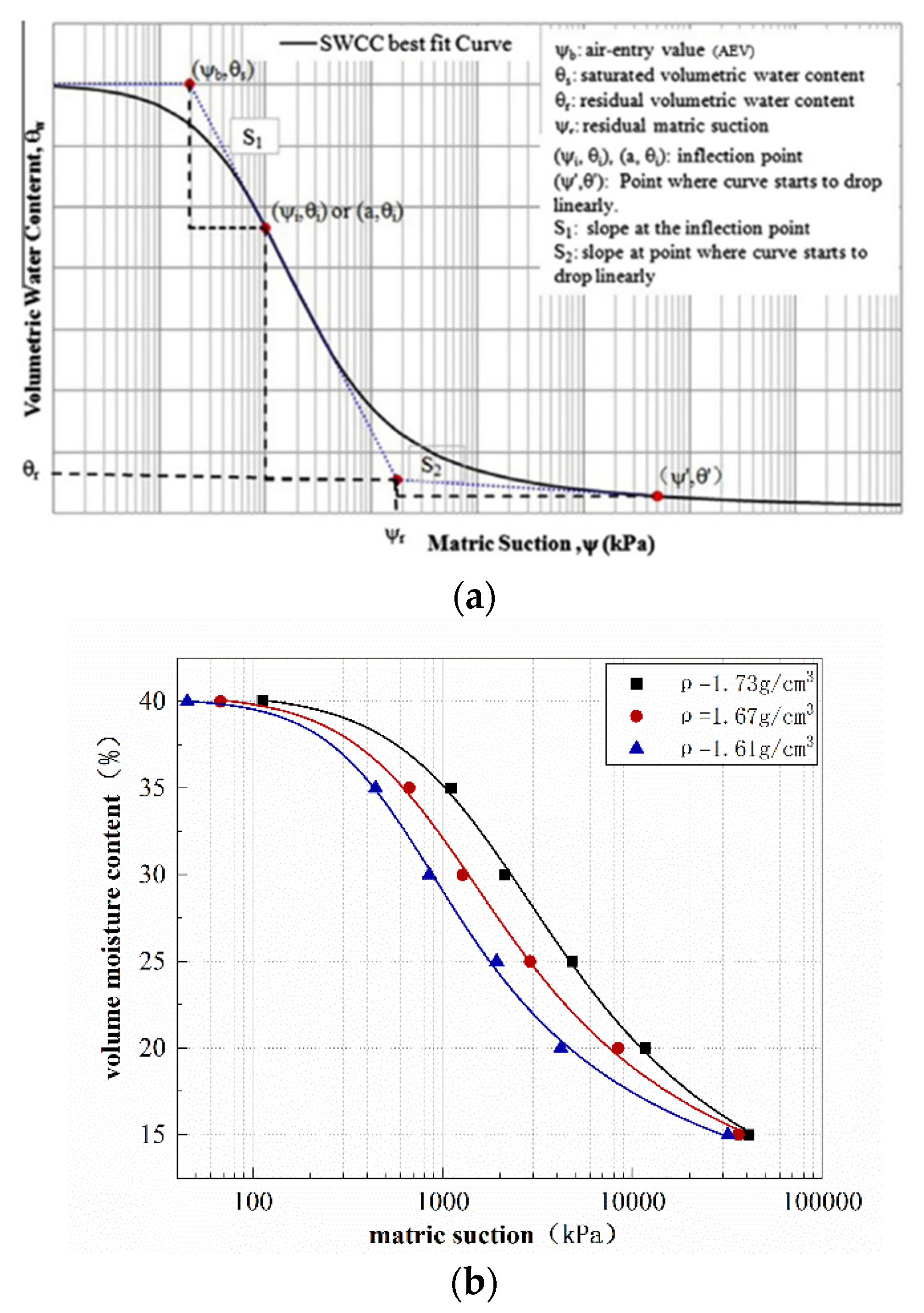
3.1. Effect of F–T Cycles on SWCC for Three Dry Densities
3.2. Effect of F–T Cycles on the Microstructure of Soil Samples
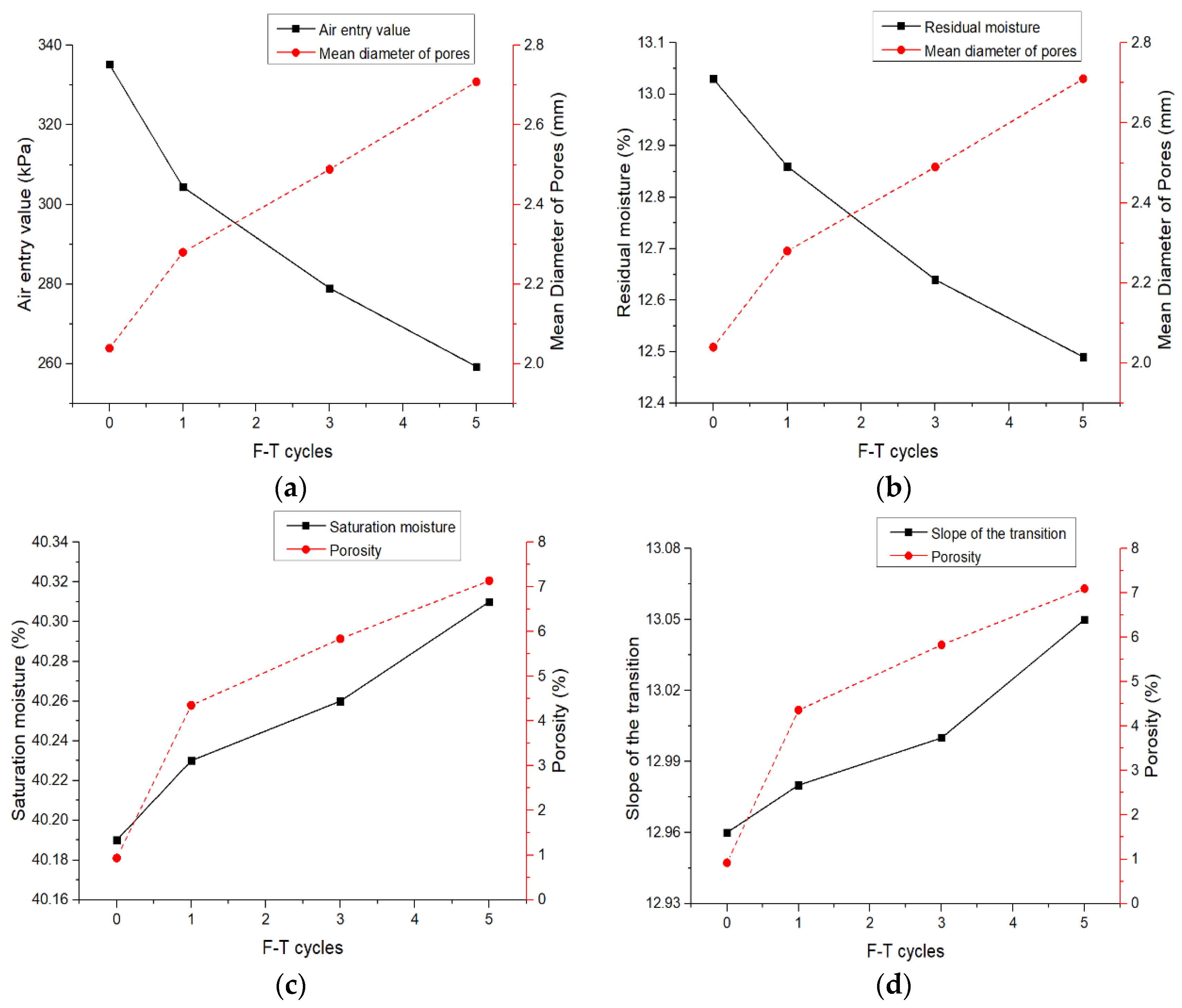
3.3. Prediction of Characteristic Parameters after F–T Cycles
4. Conclusions
- (1)
- The results of the aspiration test of low-liquid-limit silty clay matric at different densities indicate that a SWCC with high density soil SWCC has higher AEV and residual water content and lower saturated moisture content. In the transition section, the high-density soil sample has a lower moisture-loss rate under the same suction than the low-density soil sample. The high-density soil samples have smaller pores and better water retention; while their porosity is lower than that of low-density soils, the water content in saturated pores is smaller than that in low-density soils.
- (2)
- The characteristic parameters of a SWCC are negatively correlated with the number of F–T cycles. With the increase in the number of F–T cycles, the saturated water content and desorption rate of the transition section began to gradually increase. For the test soil samples, the AEV, residual moisture content and water holding capacity began to decrease. The sensitivity of the water in the pores to suction is increased, and became more susceptible to suction and began to dissipate. The first F–T cycle has the most severe effect on the characteristic parameters and then gradually decreases. This change is no longer obvious between five to seven F–T cycles.
- (3)
- The results of the SEM revealed that the original pore structure of the soil sample became looser. The plate-like overall structure of the soil sample gradually ruptured, and the crack gradually developed in the soil sample. In detail, the F–T cycles increase the large and medium pores in the soil and reduce the small pores. Overall, the porosity and average pore size of the soil sample are increased. This result explains the mechanism of the SWCC changes after the F–T cycles.
- (4)
- The characteristic parameters of a SWCC under different F–T cycles were fitted by a mathematical formula. The relationship between the characteristic parameters and the number of F–T cycles was established to predict the SWCC after n F–T cycles. Taking the correlation coefficient as the criterion, R2 is all above 0.98, which indicates that the fitting accuracy is outstanding.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Teng, J.; Kou, J.; Yan, X.; Zhang, S.; Sheng, D. Parameterization of soil freezing characteristic curve for unsaturated soils. Cold Reg. Sci. Technol. 2019, 170, 102928. [Google Scholar] [CrossRef]
- Ren, J.P.; Vanapalli, S.K.; Han, Z. Soil freezing process and different expressions for the soil-freezing characteristic curve. Sci. Cold Arid. Reg. 2017, 9, 43–50. [Google Scholar]
- Koopmans, R.W.R.; Miller, R.D. Soil freezing and soil water characteristic curves. Soil Sci. Soc. Am. J. 1966, 30, 680685. [Google Scholar] [CrossRef]
- Abraham, B.; Stoffels, S.M. Evaluation of Pavement Subgrade Long-Term Equilibrium Moisture with Suction Potential. KSCE J. Civ. Eng. 2019, 23, 147–159. [Google Scholar] [CrossRef]
- Chiu, C.F.; Yan, W.M.; Yuen, K.-V. Reliability Analysis of soil–water Characteristics Curve and its Application to Slope Stability Analysis. Engineering Geol. 2012, 135–136, 83–91. [Google Scholar] [CrossRef]
- Wijaya, M.; Leong, E.C.; Rahardjo, H. Effect of Shrinkage on Air-Entry Value of Soils. Soils Found. 2015, 55, 166–180. [Google Scholar] [CrossRef] [Green Version]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of Hysteresis on the Stability of Residual Soil Slope. Int. Soil Water Conserv. Res. 2019, 7, 226–238. [Google Scholar] [CrossRef]
- Li, X.; Li, J.H.; Zhang, L.M. Predicting Bimodal soil–water Characteristic Curves and Permeability Functions using Physically Based Parameters. Comput. Geotech. 2014, 57, 85–96. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the Soil-Water Characteristic Curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Fredlund, M.D.; Wilson, G.W.; Fredlund, D.G. Use of the Grain-Size Distribution for Estimation of the Soil-Water Characteristic Curve. Can. Geotech. J. 2002, 39, 1103–1117. [Google Scholar] [CrossRef] [Green Version]
- Gardner, W.R. Some Steady-State Solutions of the Unsaturated Moisture Flow Equation with Application to Evaporation from a Water Table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Stange, C.F.; Horn, R. Modeling the Soil Water Retention Curve for Conditions of Variable Porosity. Vadose Zone J. 2005, 4, 602–613. [Google Scholar] [CrossRef]
- Zhou, A.-N.; Sheng, D.; Carter, J.P. Modelling the Effect of Initial Density on Soil-Water Characteristic Curves. Geotechnique 2012, 62, 669–680. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Yu, J.; Yasufuku, N. Physically Based Soil Water Characteristic Curves Function for Soils with Inner Porosity. Arch. Agron. Soil Sci. 2019, 65, 537–548. [Google Scholar] [CrossRef]
- Satyanaga, A.; Rahardjo, H.; Leong, E.; Wang, J. Water Characteristic Curve of Soil with Bimodal Grain-Size Distribution. Comput. Geotech. 2013, 48, 51–61. [Google Scholar] [CrossRef]
- Raghuram, A.S.S.; Basha, B.M.; Raviteja, K.V.N.S. Variability Characterization of SWCC for Clay and Silt and its Application to Infinite Slope Reliability. J. Mater. Civ. Eng. 2021, 33, 4021180. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, J.; Li, Z. An Improved Prediction Method of Soil-Water Characteristic Curve by Geometrical Derivation and Empirical Equation. Math. Probl. Eng. 2021, 2021, 9956824. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Determination of soil–water Characteristic Curve Variables. Comput. Geotech. 2012, 42, 37–43. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Xiao, H.; Chen, Q.; Wan, J. Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data using Fractal Theory. Energies 2019, 12, 752. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Birle, E.; Cudmani, R. A New Framework to Determine General Multimodal Soil Water Characteristic Curves. Acta Geotech. 2021, 16, 3187–3208. [Google Scholar] [CrossRef]
- Bharat, T.V.; Gapak, Y. Soil-Water Characteristic Curves of Bentonites in Isochoric Conditions during Wetting: Measurement and Prediction. Can. Geotech. J. 2021, 58, 711–721. [Google Scholar] [CrossRef]
- Ren, W.; Yang, T.; Huang, M.; Zhang, A.; Wei, H.; Mi, W.; Wang, Y.; Hu, J. Optimal Mixing Ratio and SWCC Fitting of Lightweight Soil with Cotton Stalk Fibres. Soils Found. 2021, 61, 453–464. [Google Scholar] [CrossRef]
- Fu, Y.P.; Liao, H.J.; Chai, X.Q.; Li, Y.; Lv, L.L. A Hysteretic Model Considering Contact Angle Hysteresis for Fitting Soil-Water Characteristic Curves. Water Resour. Res. 2021, 57, 4. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Sheng, D.; Zhao, J. Estimation of Soil Suction from the Soil-Water Characteristic Curve. Can. Geotech. J. 2011, 48, 186–198. [Google Scholar] [CrossRef]
- Yang, H.; Rahardjo, H.; Leong, E.; Fredlund, D.G. Factors Affecting Drying and Wetting Soil-Water Characteristic Curves of Sandy Soils. Can. Geotech. J. 2004, 41, 908–920. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Leung, A.K. Measurements of Drying and Wetting Permeability Functions using a New Stress-Controllable Soil Column. J. Geotech. Geoenviron. Eng. 2011, 138, 58–68. [Google Scholar] [CrossRef]
- Wang, T.; Lu, J.; Yue, C. Soil-Water Characteristic Curve for Unsaturated Loess Considering Temperature and Density Effect. Rock Soil Mech. 2008, 29, 1–5. [Google Scholar]
- Li, S.; Shi, L.; Pei, W.; Lai, Y.; Yu, W. Thermodynamic Responses of a Crushed-Rock Interlayer Embankment on Sloping Permafrost Ground under Traffic Loads. Appl. Therm. Eng. 2018, 144, 670–680. [Google Scholar] [CrossRef]
- Ma, T.; Wei, C.; Xia, X.; Zhou, J.; Chen, P. Soil Freezing and Soil Water Retention Characteristics: Connection and Solute Effects. J. Perform. Constr. Facil. 2017, 31, 1–8. [Google Scholar] [CrossRef]
- Institute of Highway Science, Ministry of Communications. Code of Geotechnical Test for Highway: JTG E40-2007; People’s Communications Publishing House: Beijing, China, 2007. [Google Scholar]
- Zhang, Y.; Zhao, W.; Ma, W.; Wang, H.; Wen, A.; Li, P. Effect of Different Freezing Modes on the Water-Heat-Vapor Behavior in Unsaturated Coarse-Grained Filling Exposed to Freezing and Thawing. Cold Reg. Sci. Tech. 2020, 174, 103038. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper; ASTM International: West Conshohocken, PA, USA, 2010; Volume ASTM D5298-10. [Google Scholar]
- Liu, F.; Zhang, Z.; Zhou, D.; Zhao, X.; Zhu, L. Effects of Initial Density and Drying-Wetting Cycle on Soil Water Characteristic Curve of Unsaturated Loess. Rock Soil Mech. 2011, 32, 132–142. [Google Scholar]





| Liquid Limit (%) | Plastic Limit (%) | Plasticity (%) | Optimum Moisture (%) | Maximum Density (g/cm3) |
|---|---|---|---|---|
| 34.96 | 21.11 | 13.85 | 15.38 | 1.8 |
| Density | 1.73 g/cm3 | 1.67 g/cm3 | 1.61 g/cm3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F–T Cycles | 0 | 1 | 3 | 5 | 7 | 0 | 1 | 3 | 5 | 7 | 0 | 1 | 3 | 5 | 7 |
| 335.06 | 304.23 | 278.99 | 259.25 | 256.03 | 182.34 | 155.51 | 136.34 | 125.51 | 125.08 | 135.2 | 106.72 | 91.49 | 81.41 | 80.19 | |
| 12.96 | 12.98 | 13 | 13.05 | 13.06 | 13.4 | 13.44 | 13.5 | 13.51 | 13.51 | 13.51 | 13.58 | 13.62 | 13.63 | 13.63 | |
| 40.19 | 40.23 | 40.26 | 40.31 | 40.3 | 40.43 | 40.5 | 40.57 | 40.61 | 40.61 | 40.41 | 40.45 | 40.47 | 40.49 | 40.5 | |
| 13.03 | 12.86 | 12.64 | 12.49 | 12.47 | 12.65 | 12.39 | 12.2 | 12.15 | 12.14 | 12.34 | 12.21 | 12.1 | 12.03 | 12 | |
| F–T Cycles | Porosity (%) | Mean Diameter (mm) | Small Pore (%) | Medium Pore (%) | Large Pore (%) |
|---|---|---|---|---|---|
| 0 | 0.94 | 2.04 | 83.51 | 16.49 | 0 |
| 1 | 4.35 | 2.28 | 73.24 | 25.91 | 0.85 |
| 3 | 5.84 | 2.49 | 72.40 | 23.04 | 4.56 |
| 5 | 7.11 | 2.71 | 66.59 | 25.70 | 7.71 |
| ρ | 1.73 g/cm3 | 1.67 g/cm3 | 1.61 g/cm3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θs | θr | ψb | s1 | θs | θr | ψb | s1 | θs | θr | ψb | s1 | |
| R2 | 0.992 | 0.989 | 0.997 | 0.987 | 0.994 | 0.991 | 0.988 | 0.993 | 0.997 | 0.991 | 0.998 | 0.985 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, X.; Han, L. Variation Mechanism and Prediction of Soil–Water Characteristic Curve Parameters of Low-Liquid-Limit Silty Clay under Freeze–Thaw Cycles. Appl. Sci. 2022, 12, 10713. https://doi.org/10.3390/app122110713
Luan X, Han L. Variation Mechanism and Prediction of Soil–Water Characteristic Curve Parameters of Low-Liquid-Limit Silty Clay under Freeze–Thaw Cycles. Applied Sciences. 2022; 12(21):10713. https://doi.org/10.3390/app122110713
Chicago/Turabian StyleLuan, Xiaohan, and Leilei Han. 2022. "Variation Mechanism and Prediction of Soil–Water Characteristic Curve Parameters of Low-Liquid-Limit Silty Clay under Freeze–Thaw Cycles" Applied Sciences 12, no. 21: 10713. https://doi.org/10.3390/app122110713
APA StyleLuan, X., & Han, L. (2022). Variation Mechanism and Prediction of Soil–Water Characteristic Curve Parameters of Low-Liquid-Limit Silty Clay under Freeze–Thaw Cycles. Applied Sciences, 12(21), 10713. https://doi.org/10.3390/app122110713







