The Limit of the Lateral Fundamental Frequency and Comfort Analysis of a Straddle-Type Monorail Tour Transit System
Abstract
1. Introduction
2. Test Overview
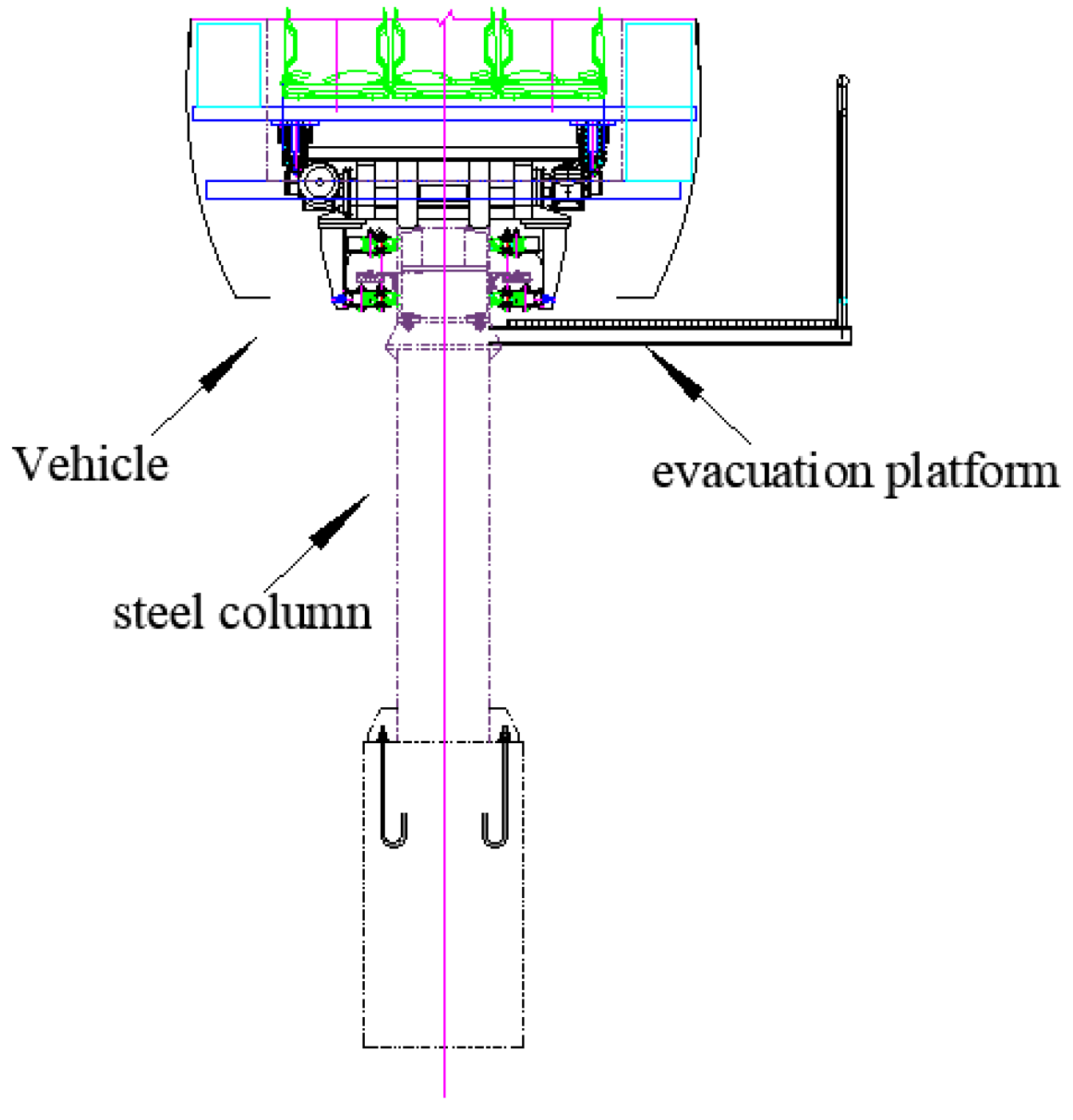
2.1. Project Introduction
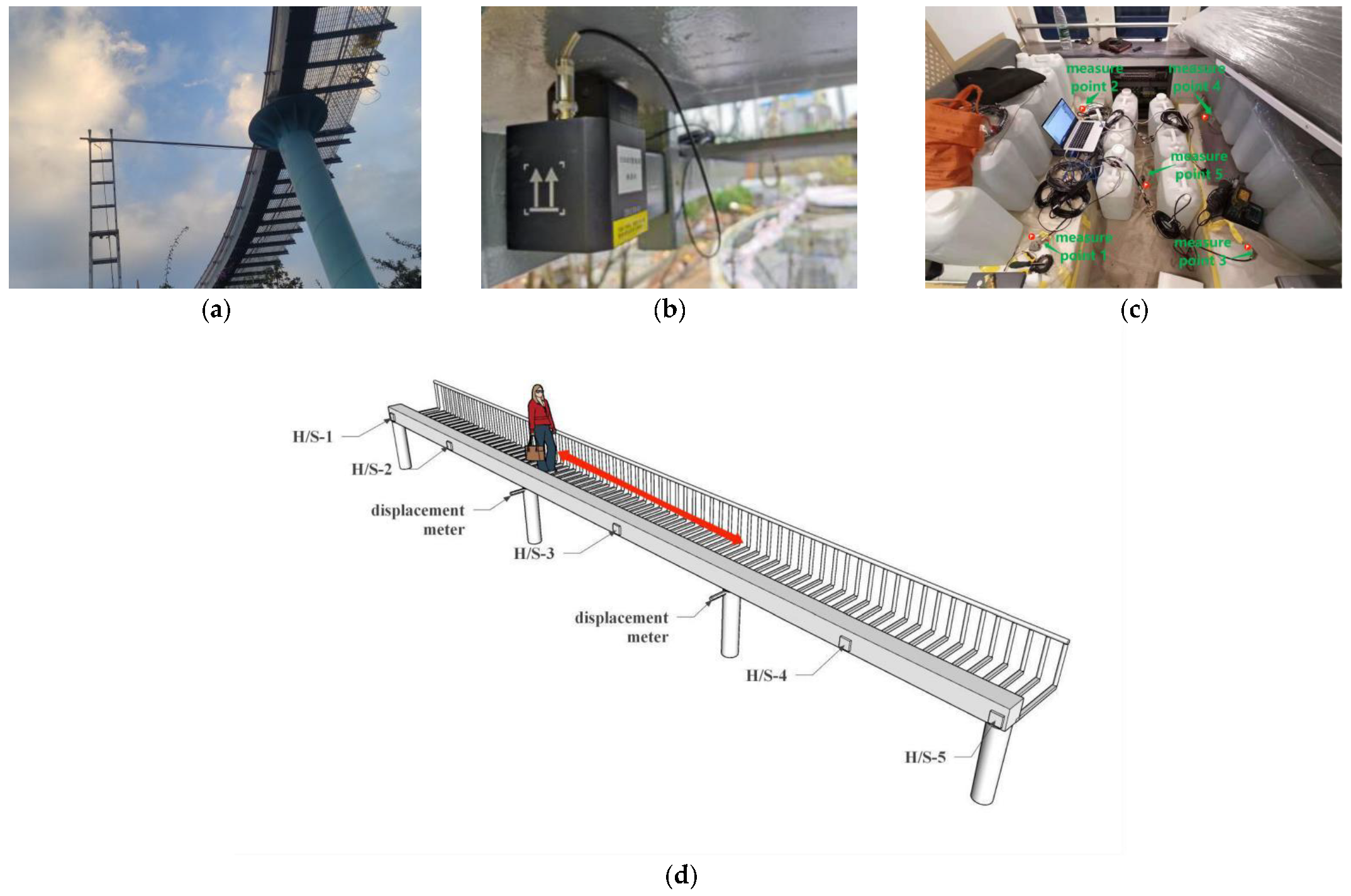
2.2. Test Content
2.3. Layout of Measuring Points
3. Dynamic Characteristics and Comfort Analysis
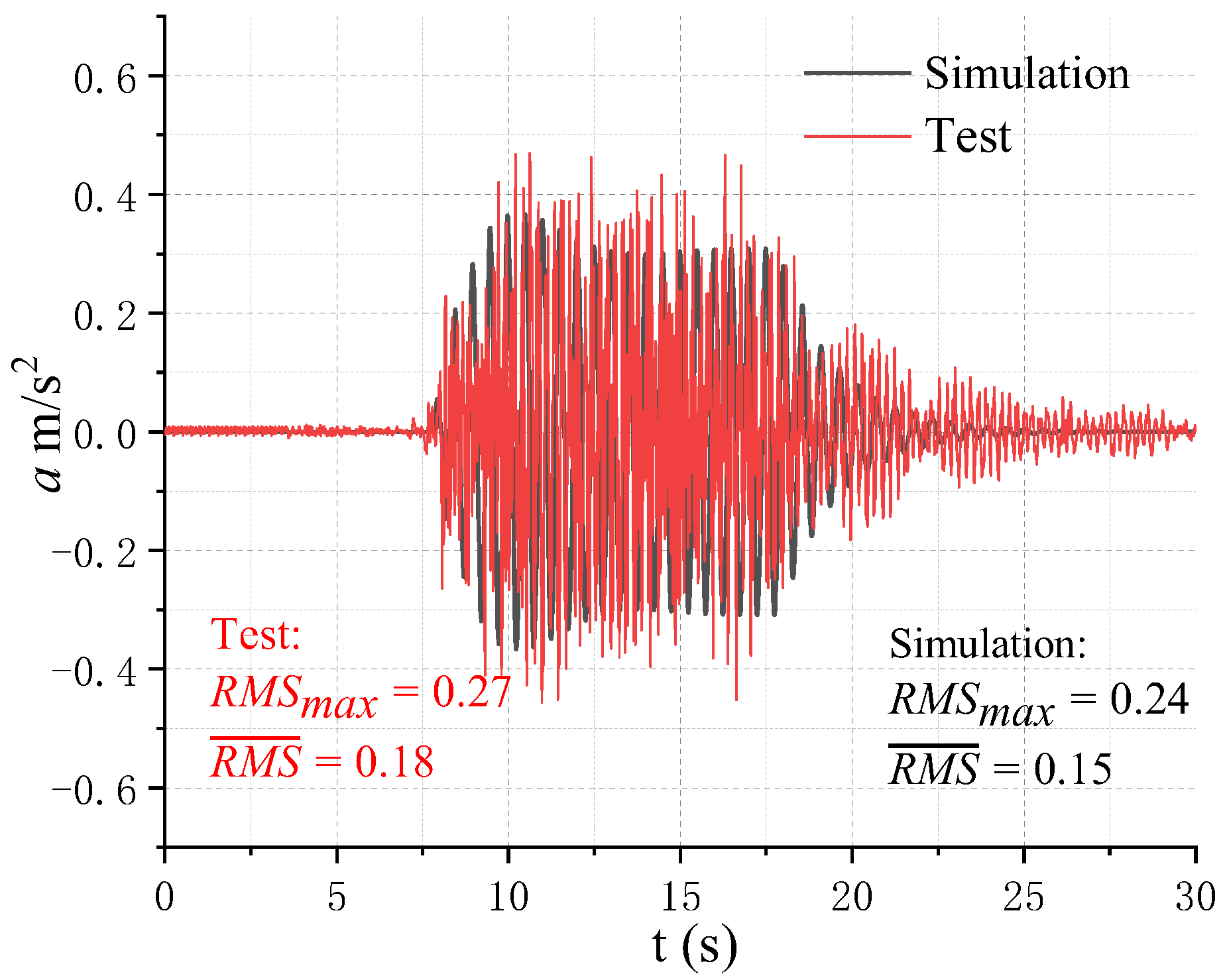
3.1. Dynamic Characteristics Analysis
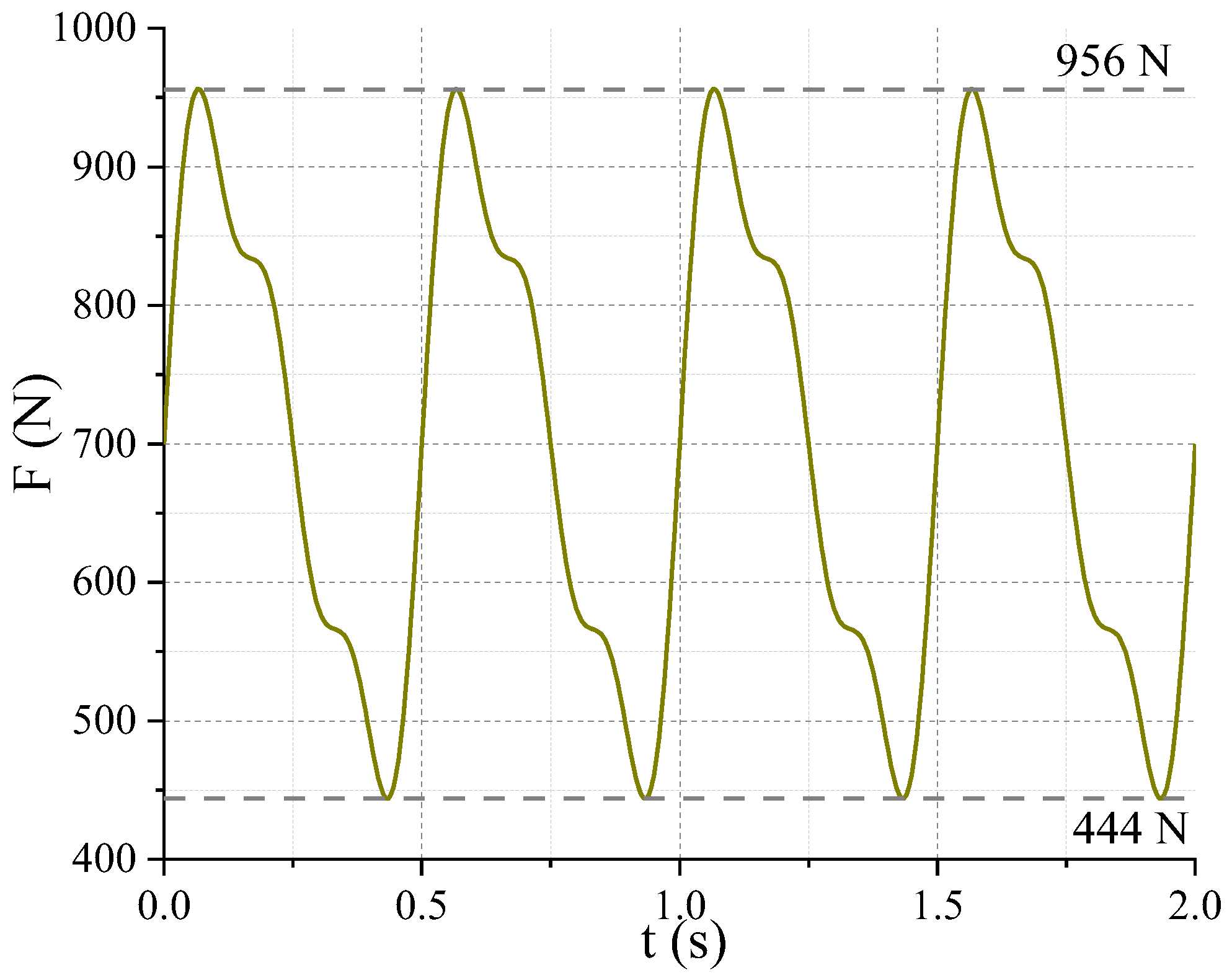
3.2. Vehicle Operation Performance Analysis
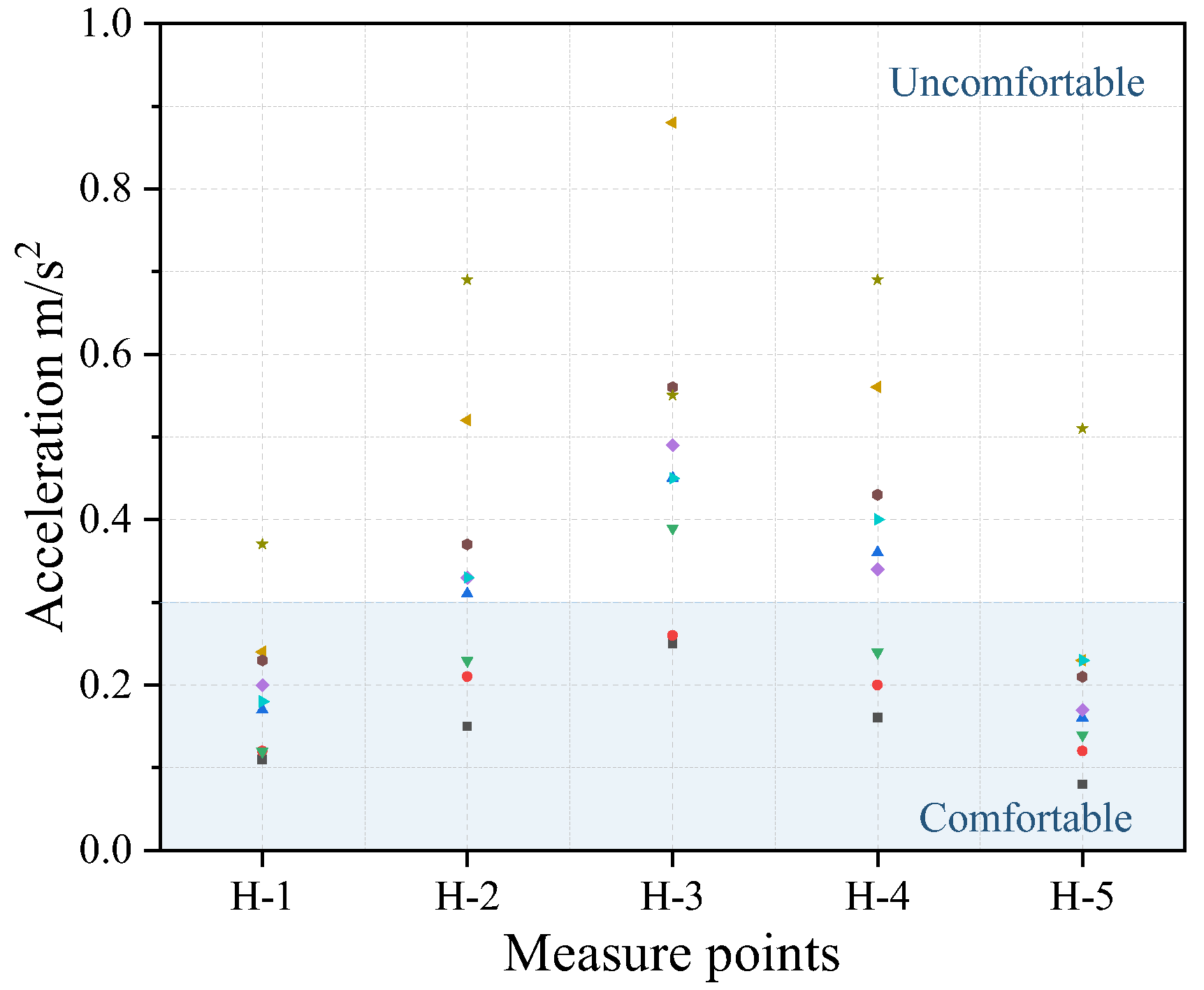
3.3. Human-Induced Vibration Analysis
4. Analysis of Different Parameters
4.1. Pedestrian Load Model
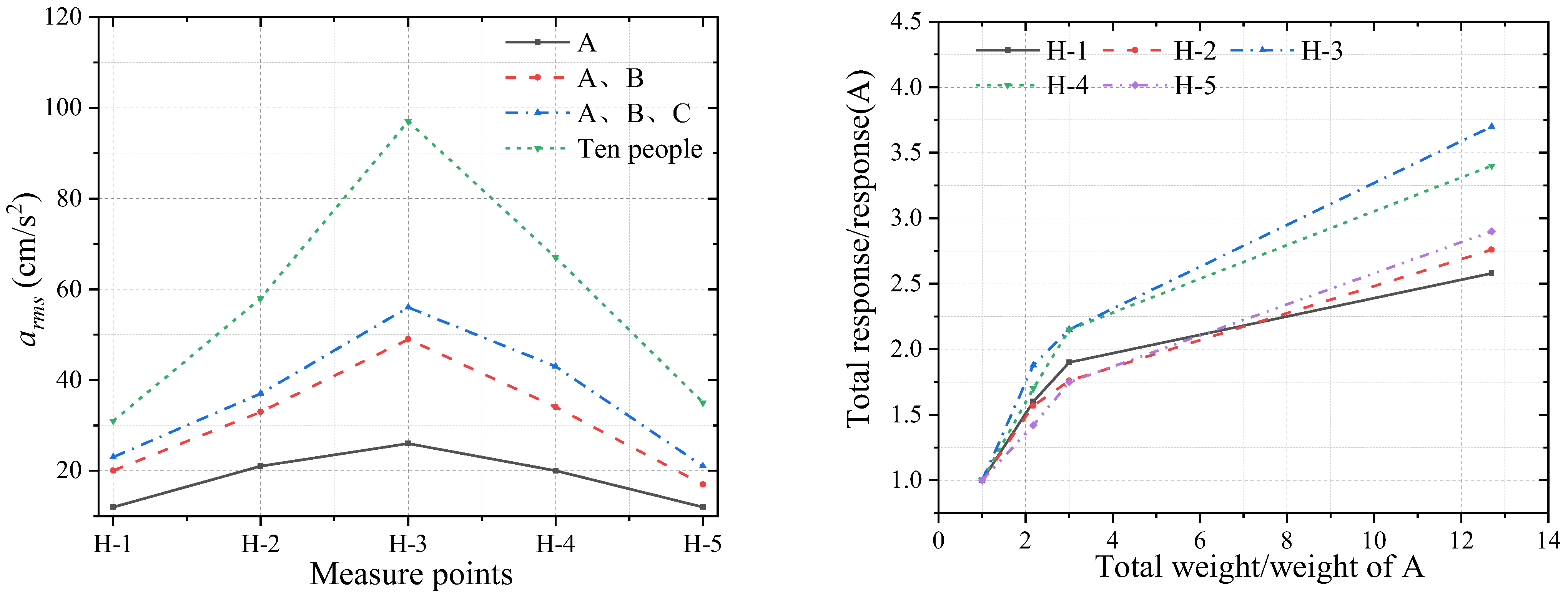
4.2. Influence of the Number of People on the Structural Response
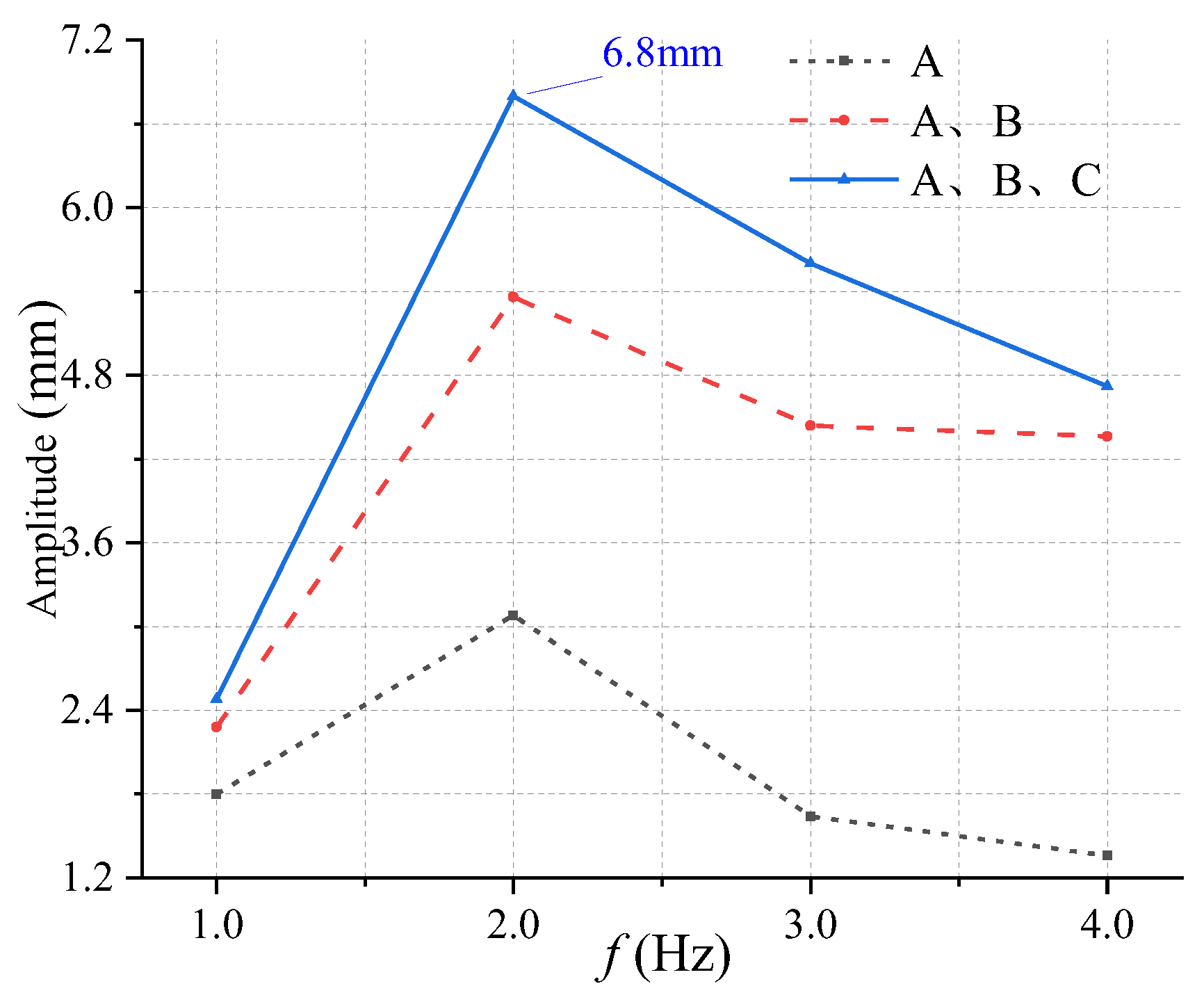
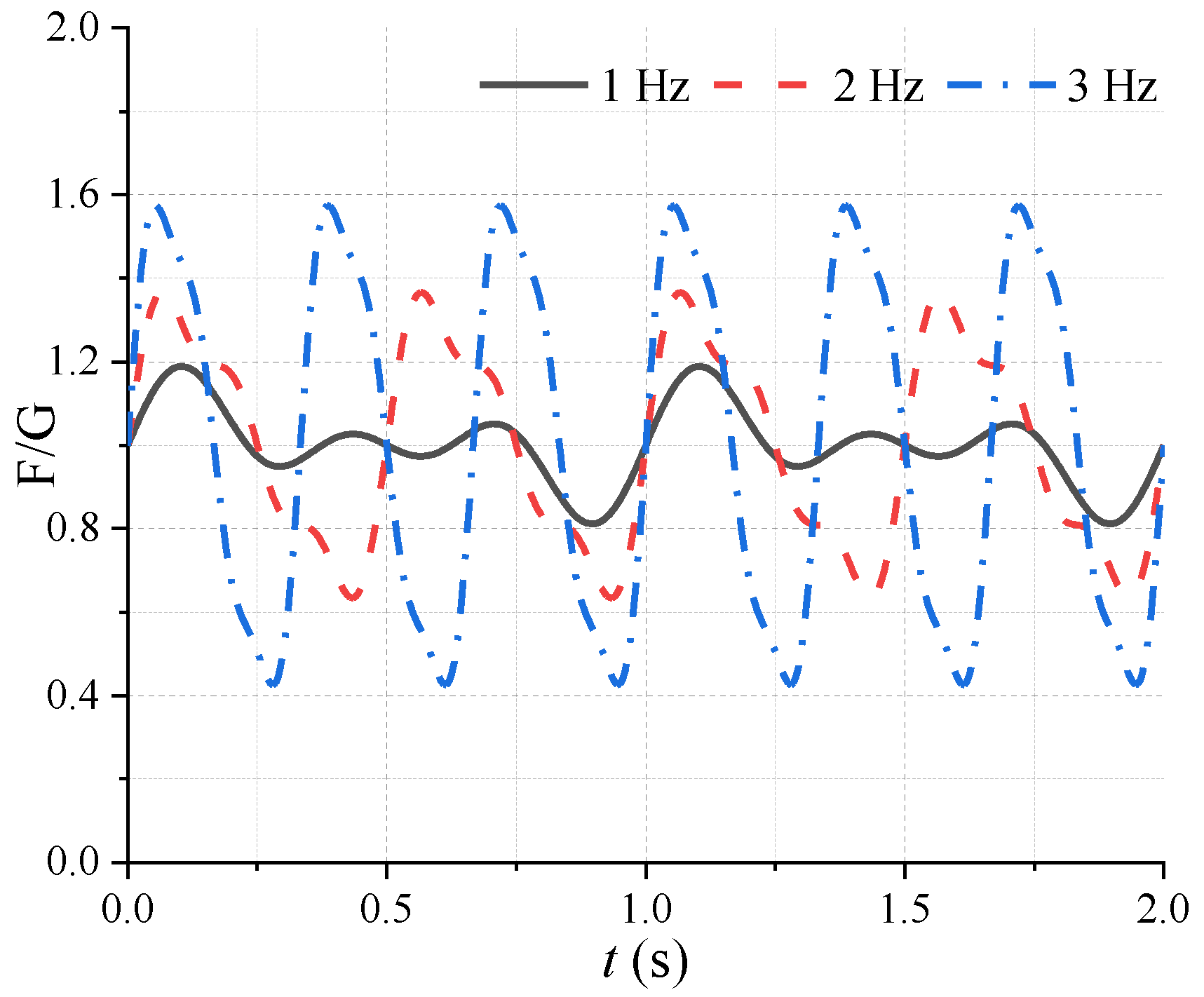
4.3. Influence of Walking Frequency on Structural Response
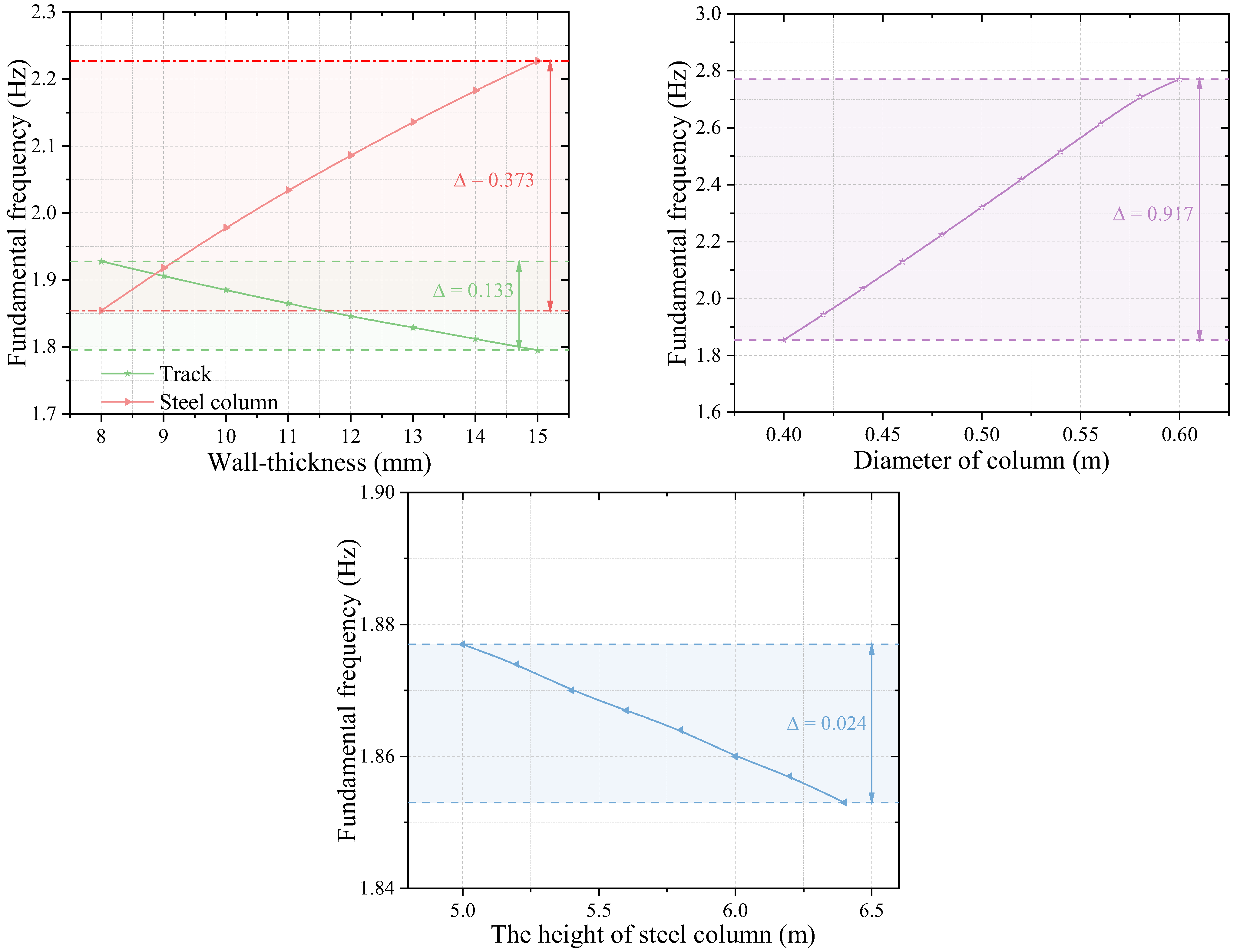
4.4. Methods of Increasing Structural Stiffness
5. Study on the Limit of the Fundamental Lateral Frequency
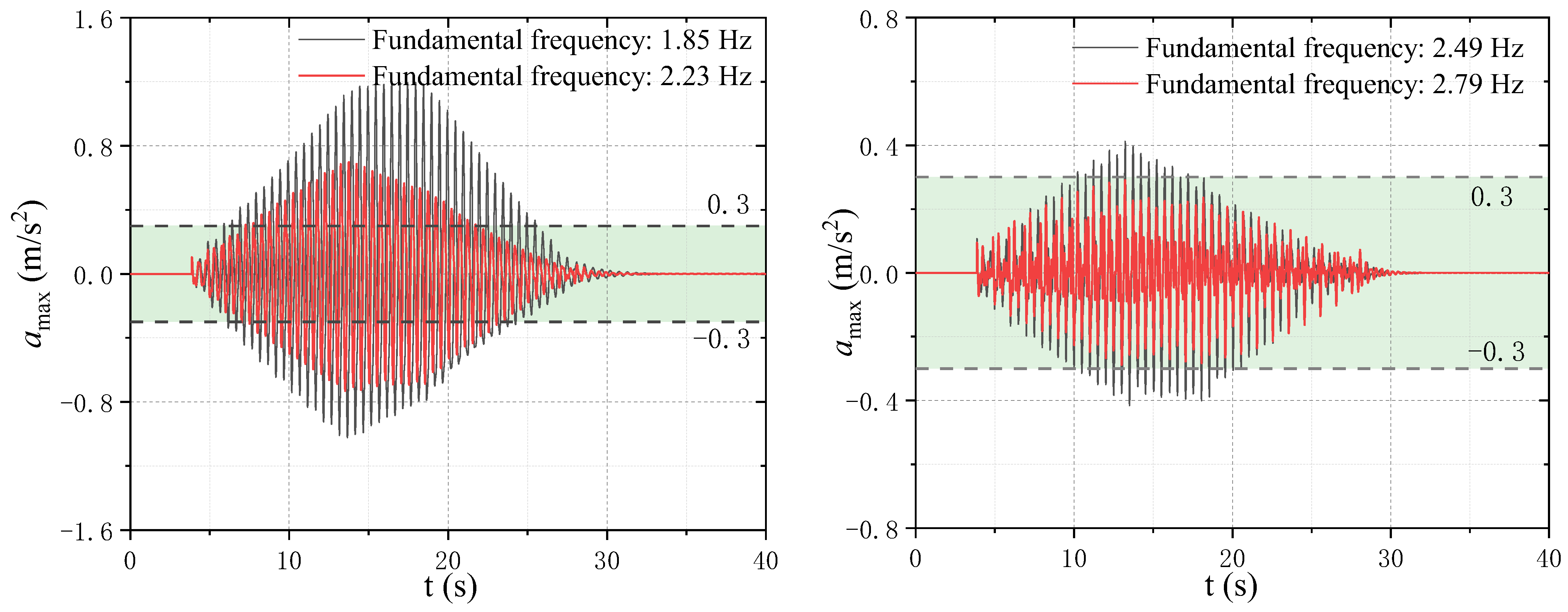
5.1. Analysis of Human-Induced Vibration
5.2. Discussion on the Limit of the Fundamental Frequency
6. Conclusions
- (i)
- When the running stability and riding comfort of the MTTS are good, the comfort of human-induced vibration may also be poor. The lateral stiffness of the track is weak, and the fundamental lateral frequency is close to the activity frequency of tourists, which easily causes resonance. Thus, the designer should focus on controlling the structure’s lateral stiffness;
- (ii)
- When pedestrians walk on the evacuation platform, the comprehensive response of the structure increases with the increase in walking frequency. The increase in the number of pedestrians or total weight increases the structural response, and the growth speed decreases with the increase in number or weight;
- (iii)
- The structural stiffness of the MTTS has a different sensitivity to different parameters and is most sensitive to the change in column diameter, followed by column wall thickness;
- (iv)
- According to the test and finite element analysis, for the 15 m, 18 m, and 25 m span of MTTS, this paper suggests that the lower limit of the fundamental lateral frequency for the span length of 15 m is 5.0 Hz, for 18 m it is 3.5 Hz, and for 25 m it is 2.8 Hz.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishikawa, K. Straddle-type monorail as a leading urban transport system for the 21st century. Hitachi Rev 2019, 48, 149–152. [Google Scholar]
- Timan, P.E. Why Monorail Systems Provide a Great Solution for Metropolitan Areas. Urban Rail Transit 2015, 1, 13–25. [Google Scholar] [CrossRef]
- Kikuchi, S.; Onaka, A. Monorail development and application in Japan. J. Adv. Transp. 1988, 22, 17–38. [Google Scholar] [CrossRef]
- Kato, M.; Yamazaki, K. Straddle-type monorail systems with driverless train operation system. Hitachi Rev. 2019, 53, 25–29. [Google Scholar]
- Guo, F.; Chen, K.; Gu, F.; Wang, H.; Wen, T. Reviews on current situation and development of straddle-type monorail tour transit system in China. J. Cent. South Univ. Sci. Technol. 2021, 52, 4540–4551. [Google Scholar]
- Wang, P. Study on Dynamic Response of Monorail Rapid-Transit Tour System Based on Measured Longitudinal Irregularity; Central South University: Changsha, China, 2021. [Google Scholar]
- Rahmatnezhad, K.; Zarastvand, M.R.; Talebitooti, R. Mechanism study and power transmission feature of acoustically stimulated and thermally loaded composite shell structures with double curvature. Compos. Struct. 2021, 276, 114557. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Asadijafari, M.H.; Talebitooti, R. Improvement of the low-frequency sound insulation of the poroelastic aerospace constructions considering Pasternak elastic foundation. Aerosp. Sci. Technol. 2021, 112, 106620. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Asadijafari, M.H.; Talebitooti, R. Acoustic wave transmission characteristics of stiffened composite shell systems with double curvature. Compos. Struct. 2022, 292, 115688. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. Prediction of acoustic wave transmission features of the multilayered plate constructions: A review. J. Sandw. Struct. Mater. 2022, 24, 218–293. [Google Scholar] [CrossRef]
- Gao, Q.; Cui, K.; Li, Z.; Li, Y. Numerical Investigation of the Dynamic Performance and Riding Comfort of a Straddle-Type Monorail Subjected to Moving Trains. Appl. Sci. 2020, 10, 5258. [Google Scholar] [CrossRef]
- Nakagawa, C.; Suzuki, H. Effects of Train Vibrations on Passenger PC Use. Q. Rep. RTRI 2005, 46, 200–205. [Google Scholar] [CrossRef][Green Version]
- Suzuki, H. Effects of the range and frequency of vibrations on the momentary riding comfort evaluation of a railway vehicle. Jpn. Psychol. Res. 1998, 40, 156–165. [Google Scholar] [CrossRef]
- Munawir, T.I.T.; Abu Samah, A.A.; Rosle, M.A.A.; Azlis-Sani, J.; Hasnan, K.; Sabri, S.; Ismail, S.; Yunos, M.N.A.M.; Bin, T.Y. A Comparison Study on the Assessment of Ride Comfort for LRT Passengers. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012039. [Google Scholar] [CrossRef]
- Orvanäs, A. Methods for Reducing Vertical Carbody Vibrations of a Rail Vehicle. Report in Railway Technology Stockholm; KTH Engineering Sciences Department of Aeronautical and Vehicle Engineering, Division of Rail Vehicles: Stockholm, Sweden, 2010. [Google Scholar]
- Takigami, T.; Tomioka, T. Investigation to Suppress Bending Vibration of Railway Vehicle Carbodies using Piezoelectric Elements. Q. Rep. RTRI 2005, 46, 225–230. [Google Scholar] [CrossRef]
- Kamada, T.; Kiuchi, R.; Nagai, M. Suppression of railway vehicle vibration by shunt damping using stack type piezoelectric transducers. Veh. Syst. Dyn. 2008, 46, 561–570. [Google Scholar] [CrossRef]
- Kamada, T.; Hiraizumi, K.; Nagai, M. Active vibration suppression of lightweight railway vehicle body by combined use of piezoelectric actuators and linear actuators. Veh. Syst. Dyn. 2010, 48, 73–87. [Google Scholar] [CrossRef]
- Tomioka, T.; Takigami, T. Reduction of bending vibration in railway vehicle carbodies using carbody–bogie dynamic interaction. Veh. Syst. Dyn. 2010, 48, 467–486. [Google Scholar] [CrossRef]
- Sugahara, Y.; Watanabe, N.; Takigami, T.; Koganei, R. Vertical vibration suppression system for railway vehicles based on primary suspension damping control—System development and vehicle running test results. Q. Rep. RTRI 2011, 52, 13–19. [Google Scholar] [CrossRef][Green Version]
- Tomioka, T. Reduction of car body elastic vibration using high-damping elastic supports for under-floor equipment. Railw. Technol. Avalanche 2012, 41, 245–270. [Google Scholar]
- Aida, K.-I.; Tomioka, T.; Takigami, T.; Akiyama, Y.; Sato, H. Reduction of Carbody Flexural Vibration by the High-damping Elastic Support of Under-floor Equipment. Q. Rep. RTRI 2015, 56, 262–267. [Google Scholar] [CrossRef][Green Version]
- Dumitriu, M. A new passive approach to reducing the carbody vertical bending vibration of railway vehicles. Veh. Syst. Dyn. 2017, 55, 1787–1806. [Google Scholar] [CrossRef]
- Schandl, G.; Lugner, P.; Benatzky, C.; Kozek, M.; Stribersky, A. Comfort enhancement by an active vibration reduction system for a flexible railway car body. Veh. Syst. Dyn. 2007, 45, 835–847. [Google Scholar] [CrossRef]
- Dumitriu, M. Ride comfort enhancement in railway vehicle by the reduction of the carbody structural flexural vibration. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012042. [Google Scholar] [CrossRef]
- Dumitriu, M. Study on Improving the Ride Comfort in Railway Vehicles Using Anti-Bending Dampers. Appl. Mech. Mater. 2018, 880, 207–212. [Google Scholar] [CrossRef]
- Dumitriu, M.; Stănică, D.I. An approach to improving the ride comfort of the railway vehicles. UPB Sci. Bull. Ser. D Mech. Eng. 2020, 82, 81–98. [Google Scholar]
- Zhang, G.; Ge, Y. Test and analysis of vibration characteristics of concrete continuous box girder pedestrian overpass. J. Vib. Shock 2009, 28, 102–106. [Google Scholar]
- He, H.; Yan, W.; Zhang, A. Study on the coupling action between beam plate structure and human body under pedestrian excitation. J. Vib. Shock 2008, 27, 130–133. [Google Scholar]
- Dumitriu, M.; I Stănică, D. Vertical bending vibration analysis of the car body of railway vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012104. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, C. Influences of Carbody Vertical Flexibility on Ride Comfort of Railway Vehicles. Arch. Mech. Eng. 2017, 64, 219–238. [Google Scholar] [CrossRef]
- Dumitriu, M.; Stănică, D.I. Influence of the Primary Suspension Damping on the Ride Comfort in the Railway Vehicles. Mater. Sci. Forum 2019, 957, 53–62. [Google Scholar] [CrossRef]
- Ministry of Communications. Technical Specification for Urban Pedestrian Overpass and Pedestrian Underpass. (CJJ69-95); China Communication Press: Beijing, China, 1995.
- Zhou, J. Study on Running Stability of Straddle Monorail Train in Chongqing; Beijing Jiaotong University: Beijing, China, 2007. [Google Scholar]
- State Railway Administration. Specification for Dynamic Performance Evaluation and Test Evaluation of Rolling Stock: GB/T5599-2019; China Standards Press: Beijing, China, 2019.
- Cheng, Y.C.; Hsu, C.T. Running Safety and Comfort Analysis of Railway Vehicles Moving on Curved Tracks. Int. J. Struct. Stab. Dyn. 2014, 14, 1450004. [Google Scholar] [CrossRef]
- International Union of Railways (UIC); European Committee for Standardization (CEN). UIC Code 513 Guidelines for Evaluating Passenger Comfort in Relation to Vibration in Railway Vehicles; International Union of Railways(UIC) & European Committee for Standardization(CEN): Paris, France, 1994. [Google Scholar]
- Guo, F.; Wang, P. Experimental Research Report on Mechanical Properties of Monorail Elevated Steel Structure Rapid Transit System; School of Civil Engineering, Central South University: Changsha, China, 2021; pp. 1–41. [Google Scholar]
- GB/T 51234-2017; Code for Design of Urban Rail Transit Bridges (with Description of Articles). China Architecture & Building Press: Beijing, China, 2017.
- Zhu, Q.; Ma, F.; Zhang, Q.; Du, Y. Experimental study on vertical dynamic coupling effect of pedestrian-structure. J. Build. Struct. 2020, 41, 125–133. [Google Scholar]
- Zhu, Q.; Li, H.; Du, Y.; Zhang, Q. Quantitative evaluation of vibration serviceability of pedestrian bridge under different walking speed. J. Eng. Mech. 2016, 33, 97–104. [Google Scholar]
- Luo, X.; Zhang, J.; Shen, Z.; Zhang, Q.; Liu, S. Human-induced vibration control of curved beam footbridge with single inclined cable arch. J. Vib. Shock. 2020, 39, 83–92. [Google Scholar]
- Dang, H.V. Influence of low-frequency vertical vibration on walking locomotion. J. Struct. Eng. 2016, 142, 04016120. [Google Scholar] [CrossRef]
- Ma, B. Analysis of pedestrian induced lateral vibration and comfort of a steel structure pedestrian bridge. China Munic. Eng. 2017, 8–11. [Google Scholar] [CrossRef]
- Guan, J.; Tan, L.; Chen, X.; Zhang, Z.; Chang, H. Vibration comfort analysis of an indoor large-span steel corridor considering human-structure coupling. Build. Struct. 2021, 51, 43–49. [Google Scholar]
- Cao, L.; Li, A.; Chen, X.; Zhang, Z. Vibration serviceability control of a long-span floor in large station room under crowd-induced excitation. China Civ. Eng. J. 2010, 43, 334–340. [Google Scholar]
- Fu, X.; Qu, J.; Chen, X. Walking comfort analysis and control for the Expectation Bridge using combined time history and frequency spectra method. China Civ. Eng. J. 2011, 44, 73–80. [Google Scholar]
- Xu, Q.; Li, A.; Zhang, Z.; Ding, Y. Research on vibration control of long-span suspension structure considering human comfort. J. Vib. Shock 2008, 27, 139–142. [Google Scholar]
- Lu, Y.; Cheng, Y.; Cheng, Z.; Lv, Q.; Liu, Y. Experimental study on vibration serviceability of composite floor in a suspended structure. J. Build. Struct. 2020, 41 (Suppl. 2), 263–269. [Google Scholar]
- Ma, F.; Zhang, Z.; Xiao, X.; Li, A. Vibration response measurement and analysis of large-span steel floor structure at high-speed rail station under moving train and crowd excitations. J. Build. Struct. 2018, 39, 109–119. [Google Scholar]

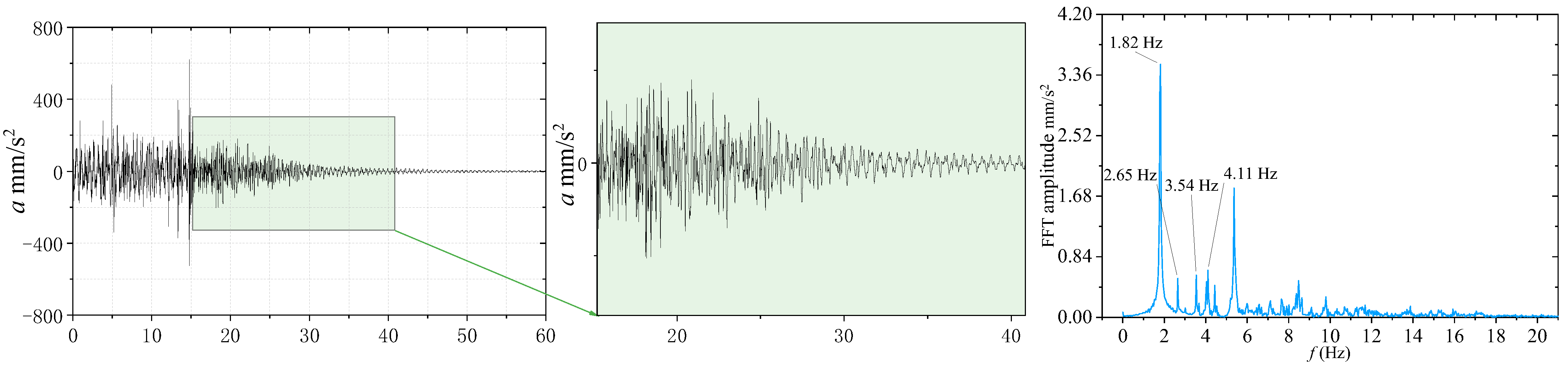
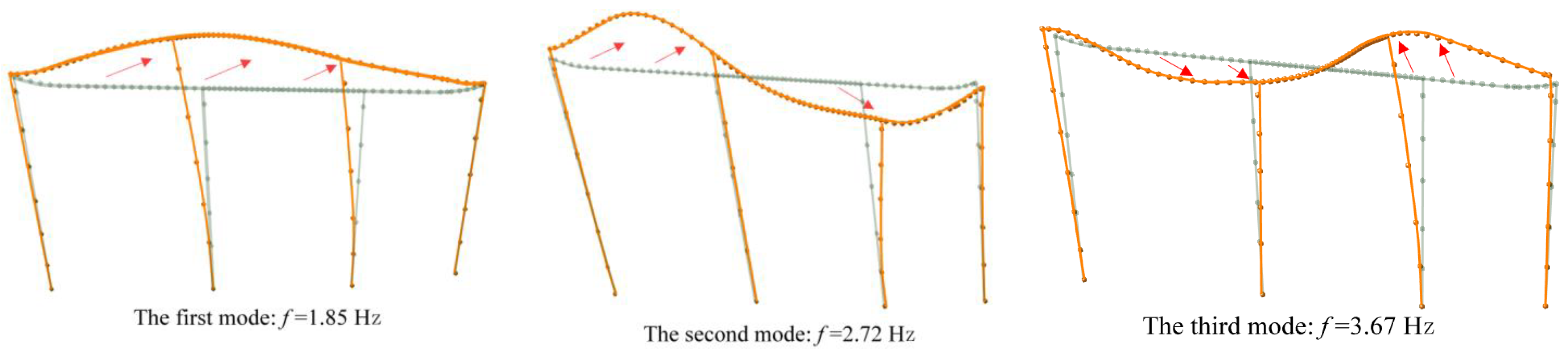





| Mode | Test | ANSYS | ||
|---|---|---|---|---|
| Lateral | Vertical | Lateral | Vertical | |
| 1 | 1.82 | 4.26 | 1.85 | 4.13 |
| 2 | 2.65 | 5.55 | 2.72 | 5.15 |
| 3 | 3.54 | 9.77 | 3.67 | 9.53 |
| 4 | 4.11 | 10.23 | 4.38 | 10.32 |
| Test | Conditions | f/Hz | Participants | Excitation Source |
|---|---|---|---|---|
| Number of people test | 1 | 2 | A | Walk |
| 2 | 2 | A, B | Walk in line | |
| 3 | 2 | A, B, C | Walk in line | |
| 4 | 2 | Ten people (70 kg/person) | Walk in line | |
| Walk frequency test | 5 | 1 | A | Walk |
| 1 | 2 | |||
| 6 | 3 | |||
| 7 | 1 | A, B | Walk in line | |
| 2 | 2 | |||
| 8 | 3 | |||
| 9 | 1 | A, B, C | Walk in line | |
| 3 | 2 | |||
| 10 | 3 | |||
| 11 | 1 | Ten people (70 kg/person) | Walk in line | |
| 4 | 2 | |||
| 12 | 3 |
| Current Codes | Evaluation Standard of Human-Induced Vibration Comfort | |
|---|---|---|
| Vertical | Lateral | |
| CJJ69-95 (China) | fvertical ≥ 3 Hz | - |
| BS5400 (Englind) | amax ≤ 0.5 fv10.5 m/s2 | - |
| EN03(2007) (Germany) | amax ≤ 1.0 m/s2 | amax < 1.0 m/s2 |
| Bro2004 (Sweden) | arms ≤ 0.5 m/s2 | - |
| Span/m | Excitation Source | Lateral Acceleration: amax (m/s2) | Fundamental Lateral Frequency (Hz) | The Limit of Fundamental Frequency | ||
|---|---|---|---|---|---|---|
| Based on Acceleration | Standard Value (PC Structure) | Recommended Value | ||||
| 15 | Full span crowd walking at 2 Hz | 1.21 | 1.87 | 5.0 | 4.7 | 5.0 |
| 0.29 | 4.93 | |||||
| 18 | 1.19 | 1.85 | 2.8 | 3.5 | 3.5 | |
| 0.29 | 2.79 | |||||
| 25 | 0.97 | 1.51 | 2.5 | 2.8 | 2.8 | |
| 0.28 | 2.42 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Ji, Y.; Liao, Q.; Liu, B.; Li, C.; Wei, S.; Xiang, P. The Limit of the Lateral Fundamental Frequency and Comfort Analysis of a Straddle-Type Monorail Tour Transit System. Appl. Sci. 2022, 12, 10434. https://doi.org/10.3390/app122010434
Guo F, Ji Y, Liao Q, Liu B, Li C, Wei S, Xiang P. The Limit of the Lateral Fundamental Frequency and Comfort Analysis of a Straddle-Type Monorail Tour Transit System. Applied Sciences. 2022; 12(20):10434. https://doi.org/10.3390/app122010434
Chicago/Turabian StyleGuo, Fengqi, Yanqiang Ji, Qiaoyun Liao, Bo Liu, Chenjia Li, Shiqi Wei, and Ping Xiang. 2022. "The Limit of the Lateral Fundamental Frequency and Comfort Analysis of a Straddle-Type Monorail Tour Transit System" Applied Sciences 12, no. 20: 10434. https://doi.org/10.3390/app122010434
APA StyleGuo, F., Ji, Y., Liao, Q., Liu, B., Li, C., Wei, S., & Xiang, P. (2022). The Limit of the Lateral Fundamental Frequency and Comfort Analysis of a Straddle-Type Monorail Tour Transit System. Applied Sciences, 12(20), 10434. https://doi.org/10.3390/app122010434








