Topp–Leone Modified Weibull Model: Theory and Applications to Medical and Engineering Data

Abstract

In this article, a four parameter lifetime model called the Topp–Leone modified Weibull distribution is proposed. The suggested distribution can be considered as an alternative to Kumaraswamy Weibull, generalized modified Weibull, extend odd Weibull Lomax, Weibull-Lomax, Marshall-Olkin alpha power extended Weibull and exponentiated generalized alpha power exponential distributions, etc. The suggested model includes the Topp-Leone Weibull, Topp-Leone Linear failure rate, Topp-Leone exponential and Topp-Leone Rayleigh distributions as a special case. Several characteristics of the new suggested model including quantile function, moments, moment generating function, central moments, mean, variance, coefficient of skewness, coefficient of kurtosis, incomplete moments, the mean residual life and the mean inactive time are derived. The probability density function of the Topp–Leone modified Weibull distribution can be right skewed and uni-modal shaped but, the hazard rate function may be decreasing, increasing, J-shaped, U-shaped and bathtub on its parameters. Three different methods of estimation as; maximum likelihood, maximum product spacing and Bayesian methods are used to estimate the model parameters. For illustrative reasons, applications of the Topp–Leone modified Weibull model to four real data sets related to medical and engineering sciences are provided and contrasted with the fit reached by several other well-known distributions.

1. Introduction and Motivation

Over the last four decades or more, a major amount of statistical research has developed a number of innovative statistical distributions. This criterion was inspired by theoretical concepts, real-world applications, or both. The most recent advancement is to build a larger range of statistical distributions by adding one (or more) shape parameters to a baseline distribution, which tends to improve the diversity of the statistical models developed. Particularly appropriate to data sets for researching reliability experiments, medical, clinical trials, finance, infant mortality rate, and engineering applications, among other things. The Weibull distribution is a well-liked distribution that may be used to predict how long a product will last, such as a ball bearing, a car part, or electrical insulation see [1,2,3,4,5,6,7,8,9,10]. It is also frequently employed in biological and medical applications. This distribution, however, lacks a bathtub or upside-down shaped hrf, making it ineffective for simulating the lifetime of some systems. To overcome this shortcoming, refs. [11,12,13] studied the modified Weibull (MW) distribution that can be used to describe various reliability models. It has three parameters, $\alpha$ and $\beta$ are two scale parameters and $\theta$ is the shape parameter. The distribution function (cdf), the probability density function (pdf), survival function (sf) and hazard rate function (hrf) of the MW distribution due to [13] are provided via

$$G(x,\alpha ,\beta ,\theta )=1-e^{-(\alpha x+\beta x^{\theta })},x>0,\alpha ,\beta ,\theta >0,$$

(1)

$$g(x,\alpha ,\beta ,\theta )=\left(\alpha +\theta \beta x^{\theta -1}\right)e^{-(\alpha x+\beta x^{\theta })},x>0,\alpha ,\beta ,\theta >0,$$

(2)

$$\overline{G}(x,\alpha ,\beta ,\theta )=e^{-(\alpha x+\beta x^{\theta })},x>0,\alpha ,\beta ,\theta >0,$$

(3)

and

$$h(x,\alpha ,\beta ,\theta )=\left(\alpha +\theta \beta x^{\theta -1}\right),x>0,\alpha ,\beta ,\theta >0.$$

(4)

Recently, many authors have proposed many generalizations of the MW distribution to improve its flexibility. For example, generalized MW by [14], beta MW by [15], exponentiated MW by [16], new MW by [17], transmuted MW by [18], McDonald MW by [19], Kumaraswamy MW [20], gamma MW by [21], Burr XII MW by [22], log-logistic MW by [23], half logistic MW by [24], beta exponentiated MW by [25] and sine MW by [26].

Topp–Leone ($TL$) distribution was proposed by [27]. Recently, statisticians have been showing interest on Topp–Leone ($TL$) distribution as a generator. This distribution has one parameter and its domain is restricted to $(0,1)$. Furthermore, this distribution is not particularly adaptable. It is an extension of the triangular distribution and can be used as an alternative in circumstances where a bounded distribution, such as the uniform, triangular, trapezoid, or beta, is acceptable. Ref. [28] introduced $TL$-generated ($TL$-G) family of distributions and the cdf of the TL-G can be defined as

$$F(x;\lambda )={(1-{\overline{G}}^2\left(x\right))}^{\lambda }=G^{\lambda }\left(x\right){\left[2-G\left(x\right)\right]}^{\lambda },x\in R,\lambda >0,$$

(5)

the associated pdf is available below

$$f(x;\lambda )=2\lambda g\left(x\right)\overline{G}\left(x\right){(1-{\overline{G}}^2\left(x\right))}^{\lambda -1}.$$

(6)

The sf and hrf of the $TL$-G are provided via

$$\overline{F}(x;\lambda )=1-{(1-{\overline{G}}^2\left(x\right))}^{\lambda },$$

(7)

and

$$h((x;\lambda )=\frac{2\lambda g\left(x\right)\overline{G}\left(x\right){(1-{\overline{G}}^2\left(x\right))}^{\lambda -1}}{1-{(1-{\overline{G}}^2\left(x\right))}^{\lambda }},$$

(8)

respectively.

Many researchers have recently suggested numerous generalizations of the TL-G to increase its versatility. For example, the $TL$ Weibull distribution, $TL$ inverse Weibull distribution, $TL$ Burr XII distribution, $TL$ geometric distribution, the transmuted TL-G family of distributions, $TL$ odd log-logistic family, $TL$ Lomax distribution, TL-G family of distributions, the TL-G generalized exponential power series distribution, $TL$ power series family of distributions, the type II TL-G family, the type II generalized TL-G family, the Fréchet TL-G family, among others. See [29] for elaborate references.

In this article, the Topp–Leone modified Weibull (TLMW) distribution, which has four parameters are introduced by connecting $G\left(x\right)$ in Equation (1) to the cdf in Equation (5). The TLMW distribution encompasses the behavior of and provides better fits than some well known lifetime distributions, such as Kumaraswamy Weibull, generalized modified Weibull, extend odd Weibull Lomax, Weibull-Lomax, Marshall-Olkin alpha power extended Weibull and exponentiated generalized alpha power exponential distributions, distributions. We are motivated to introduce the ($TLMW$) distribution because it is capable of modeling decreasing, increasing, J-shaped, U-shaped and bathtub hrf which are common in reliability studies and lifetime data analysis. It might be a useful option for fitting skewed data that other common distributions may not be able to correctly fit, and it may also be utilized in a range of challenges in diverse sectors such as biological investigations, industrial dependability, the suggested family have also an important utilisation in the insurance industry see; [30,31,32] and survival analysis.

The reminder of the paper is organized as follows: In Section 2, the Topp–Leone modified Weibull $\left(TLMW\right)$ distribution is defined. Also, an useful expansion of the $\left(TLMW\right)$ distribution and some sub-models are studied in the same section. Some statistical features of the $TLMW$ distribution are discussed in Section 3. In Section 4, the maximum likelihood (ML), maximum product spacing (MPS) and Bayesian estimators of the unknown parameters are obtained. Section 5 concerned with simulation results. Four illustrative applications based on real data sets related to medical and engineering sciences are investigated in Section 6. Finally, some conclusions are provided in Section 7.

2. Topp–Leone Modified Weibull Distribution

In this section, we introduce the Topp–Leone modified Weibull $\left(TLMW\right)$ distribution by taking $\overline{G}\left(x\right)$ in Equation (3) to the cdf of $TL$ in Equation (5). Hence, the cdf and pdf of $TLMW$ can indeed be expressed as

$$F_{{}_{{}_{TLMW}}}(x,\alpha ,\beta ,\theta ,\lambda )={\left[1-e^{-2(\alpha x+\beta x^{\theta })}\right]}^{\lambda }$$

(9)

and

$$f_{{}_{TLMW}}(x;\alpha ,\beta ,\theta ,\lambda )=2\lambda \left(\alpha +\theta \beta x^{\theta -1}\right)e^{-2(\alpha x+\beta x^{\theta })}{\left[1-e^{-2(\alpha x+\beta x^{\theta })}\right]}^{\lambda -1},$$

(10)

By writing $X\backsim TLMW\left(\phi \right)$ where $\phi =(\alpha ,\beta ,\theta ,\lambda )$ if the pdf of X can be written as (10).

The hrf is defined by

$$h_{{}_{TLMW}}(x,\phi )=\frac{2\lambda \left(\alpha +\theta \beta x^{\theta -1}\right)e^{-2(\alpha x+\beta x^{\theta })}{\left[1-e^{-2(\alpha x+\beta x^{\theta })}\right]}^{\lambda -1}}{1-{\left[1-e^{-2(\alpha x+\beta x^{\theta })}\right]}^{\lambda }}.$$

(11)

Figure 1 and Figure 2 shows the pdf and hrf for different values of $\lambda$ and $\theta$ and at $\alpha =\beta =0.5$. The plots shows the pdf can be decreasing, uni-modal and right skewness but the hrf can be decreasing, increasing, J-shaped, U-shaped and bathtub.

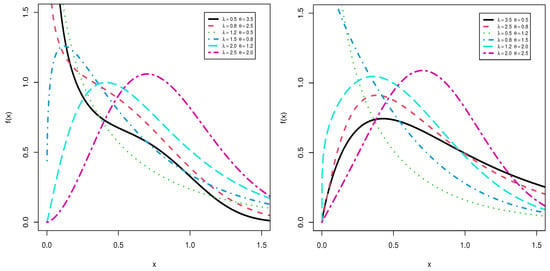
Figure 1. Plots of the pdf for TLMW model at $\alpha =\beta =0.5$.

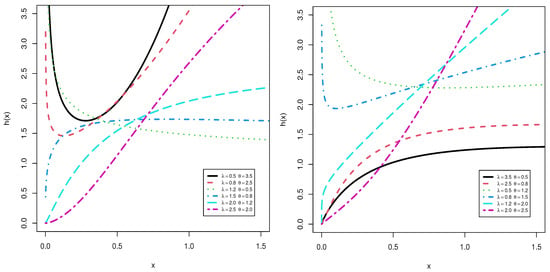
Figure 2. Plots of the hrf for TLMW model at $\alpha =\beta =0.5$.

A Useful Expansion for the Density Function

In this part, the pdf representation of the $TLMW$ distribution are discussed. The mathematical relation and the series representation are given below. If b is a positive real non-negative integer and $\left|z\right|<1$ then

$${(1-z)}^{b-1}=\sum _{i=0}^{\infty }{(-1)}^i\left(\genfrac{}{}{0pt}{}{b-1}{i}\right)z^i.$$

(12)

Inserting Equation (12) into Equation (10) then,

$$f_{{}_{TLMW}}(x;\phi )=2\lambda \sum _{i=0}^{\infty }{(-1)}^i\left(\genfrac{}{}{0pt}{}{\lambda -1}{i}\right)\left(\alpha +\theta \beta x^{\theta -1}\right)e^{-2(i+1)(\alpha x+\beta x^{\theta }).}$$

(13)

The series expansion of

$$e^{-2(i+1)\beta x^{\theta }}=\sum _{j=0}^{\infty }\frac{{\left[-2(i+1)\beta x^{\theta }\right]}^j}{j!},$$

(14)

by substituting Equation (14) into Equation (13) then,

$$\begin{array}{ccc}\hfill f_{{}_{TLMW}}(x;\phi )& =& 2\lambda \sum _{i,j=0}^{\infty }\frac{{(-1)}^{i+j}}{j!}{\left[2(i+1)\beta \right]}^j\left(\genfrac{}{}{0pt}{}{\lambda -1}{i}\right)\left(\alpha x^{\theta j}+\theta \beta x^{\theta (j+1)-1}\right)e^{-2(i+1)\left(\alpha x\right)}\hfill \\ & =& 2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left(\alpha x^{\theta j}+\theta \beta x^{\theta (j+1)-1}\right)e^{-2(i+1)\left(\alpha x\right)},\hfill \end{array}$$

(15)

where

$$\pi (i,j)=\frac{{(-1)}^{i+j}}{j!}{\left[2(i+1)\beta \right]}^j\left(\genfrac{}{}{0pt}{}{\lambda -1}{i}\right).$$

The $TLMW$ distribution is a very flexible model which contains the well-known models listed below as special models:

• If $\alpha =0$, the $TLMW$ distribution reduces to the $TL$ Weibull (TLW) distribution.
• If $\theta =2$, then Equation (9) the $TLMW$ distribution reduces to the $TL$ Linear failure rate (TLLFR) model.
• If $\beta =0$, the TLMW distribution reduces to the $TL$ exponential (TLE) distribution.
• If $\theta =2$ and $\alpha =0$, then Equation (9) the TLMW distribution reduces to the $TL$ Rayleigh (TLR) distribution.

3. Some Statistical Features

In this part, some of the statistical features of the $TLMW$ distribution such as; quantile function (QF), moments(Ms), M generating function (MGF), central Ms, mean, variance, coefficient of skewness (CS), coefficient of kurtosis (CK), incomplete Ms (INMs), the mean residual life (MRL) and the mean inactive time are computed.

3.1. Quantile Function

The qth QF $x_q$ of the $TLMW(\alpha ,\beta ,\theta ,\lambda )$ is the real solution of the following equation

$$\alpha x_q+\beta x_q^{\theta }+\frac{1}{2}ln\left(1-q^{\frac{1}{\lambda }}\right)=0.$$

(16)

In particular, setting $q=\frac{1}{2}$ in Equation (16), the median of X can be calculated. Also, using the QF given by Equation (16), the Bowley’s skewness (see [33]) and the Moors’ kurtosis (see [34]) can be determined as

$$B_{{}_S}=\frac{Q\left(\frac{3}{4}\right)-2Q\left(\frac{2}{4}\right)+Q\left(\frac{1}{4}\right)}{Q\left(\frac{3}{4}\right)-Q\left(\frac{1}{4}\right)}$$

and

$$M_k=\frac{Q\left(\frac{7}{8}\right)-Q\left(\frac{5}{8}\right)+Q\left(\frac{3}{8}\right)-Q\left(\frac{1}{8}\right)}{Q\left(\frac{6}{8}\right)-Q\left(\frac{2}{8}\right)}.$$

where $Q(.)$ is the QF provided in Equation (16). Table 1, provide the median, skewness and kurtosis, of the $TLMW$ distribution for various values of $\alpha$, $\beta$, $\theta$ and $\lambda$. It is clear from Table 1 that for fixed $\alpha$, $\beta$ and $\theta$ with increasing $\lambda$, median and kurtosis are decreasing but the skewness is increasing.

Table 1. Quantiles for $TLMW$ distribution.

Parameters				Quantiles
$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	Median	Skewness (${\mathit{B}}_{\mathit{s}}$)	Kurtosis (${\mathit{M}}_{\mathit{k}}$)
0.6	0.5	1.0	0.70	0.753263	−0.311058	6.59101
			1.0	0.667129	−0.268271	5.19103
			2.0	0.445061	−0.123186	3.49902
			7.0	0.0588123	0.49274	2.52725
1.0	1.0	2.0	0.70	0.838	−0.391413	6.32248
			1.0	0.77687	−0.348819	4.99573
			2.0	0.603527	−0.202834	3.3833
			7.0	0.17078	0.433166	2.46412

3.2. Moments and Moment Generating Function

The $r_{th}$ M of $TLMW$ distribution can be computed using the following expression

$$\begin{array}{ccc}\hfill {\mu }_r{}^{\prime }& =& {\int }_0^{\infty }{x}^{r}f(x,\phi )dx=2\lambda \sum _{i,j=0}^{\infty }\pi (i,j){\int }_0^{\infty }\left(\alpha x^{r+\theta j}+\theta \beta x^{r+\theta (j+1)-1}\right)e^{-2\alpha (i+1)x}dx\hfill \\ & =& 2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left[\frac{\alpha \Gamma (r+\theta j+1)}{{\left[2\alpha (i+1)\right]}^{r+\theta j+1}}+\theta \beta \frac{\Gamma (r+\theta (j+1\left)\right)}{{\left[2\alpha (i+1)\right]}^{r+\theta (j+1)}}\right].\hfill \end{array}$$

(17)

Further, the $r_{th}$ central Ms ${\mu }_r$ and cumulants ${\kappa }_r$ of the $TLMW$ distribution can be determined from ${\mu }_r={\displaystyle \sum _{m=0}^r}\left(\genfrac{}{}{0pt}{}{r}{m}\right){(-1)}^m{\mu }_1^{/m}$${\mu }_{r-m}^{/}$ and ${\kappa }_r={\mu }_r^{/}-{\displaystyle \sum _{m=1}^{r-1}}\left(\genfrac{}{}{0pt}{}{r-1}{m-1}\right){\kappa }_m$${\mu }_{r-m}^{/}$, respectively, where ${\kappa }_1={\mu }_1^{/}$, ${\kappa }_2={\mu }_2^{/}-$${\mu }_1^{/2}$, ${\kappa }_3={\mu }_3^{/}-3{\mu }_2^{/}$${\mu }_1^{/}+2{\mu }_1^{/3}$, and ${\kappa }_4={\mu }_4^{/}-4{\mu }_1^{/}{\mu }_3^{/}-3{\mu }_2^{/2}+12{\mu }_2^{/}{\mu }_1^{/2}-6{\mu }_1^{/4},$ etc. Additionally, $CS$ and $CK$ can be obtained according to the following relation $CS=\frac{{\kappa }_3}{\sqrt{{\kappa }_2^3}}$ and $CK=\frac{{\kappa }_4}{{\kappa }_2^2}$, respectively.

The MGF of $TLMW$ model is provided as below

$$\begin{array}{ccc}\hfill M_X\left(t\right)& =& {\int }_0^{\infty }{e}^{tx}f(x,\phi )dx=2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left(\alpha x^{\theta j}+\theta \beta x^{\theta (j+1)-1}\right)e^{-\left(2\alpha (i+1\right)-t)x}dx\hfill \\ & =& 2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left[\frac{\alpha \Gamma (\theta j+1)}{{\left[2\alpha (i+1)-t\right]}^{\theta j+1}}+\theta \beta \frac{\Gamma \left(\theta \right(j+1\left)\right)}{{\left[2\alpha (i+1)-t\right]}^{\theta (j+1)}}\right].\hfill \end{array}$$

(18)

Table 2 and Table 3 show the numerical values of ${\mu }_1{}^{\prime }$, ${\mu }_2{}^{\prime }$, ${\mu }_3{}^{\prime }$, ${\mu }_4{}^{\prime }$, variance (V), skewness (CS) and kurtosis (CK) of the $TLMW$ distribution.

Table 2. Moments for $TLMW$ distribution at $\alpha =\beta =0.5$.

$\mathit{\theta }$	$\mathit{\lambda }$	${\mathit{\mu }}_1{}^{\prime }$	${\mathit{\mu }}_2{}^{\prime }$	${\mathit{\mu }}_3{}^{\prime }$	${\mathit{\mu }}_4{}^{\prime }$	$\mathit{Variance}$	$\mathit{CS}$	$\mathit{CK}$
0.5	0.4	0.215	0.250	0.522	1.566	0.204	4.128	4.128
	0.8	0.383	0.481	1.028	3.112	0.335	3.037	3.037
	1.2	0.520	0.696	1.519	4.637	0.425	2.578	2.578
	1.6	0.636	0.897	1.997	6.144	0.492	2.317	2.317
	2.0	0.737	1.086	2.462	7.632	0.544	2.148	2.148
	2.4	0.825	1.265	2.915	9.104	0.585	2.027	2.027
	2.8	0.904	1.436	3.358	10.559	0.618	1.938	1.938
	3.2	0.976	1.599	3.792	11.999	0.646	1.868	1.868
	3.6	1.041	1.754	4.215	13.424	0.670	1.812	1.812
	4.0	1.101	1.903	4.631	14.834	0.691	1.766	1.766
	4.4	1.157	2.047	5.038	16.231	0.709	1.727	1.727
	4.8	1.208	2.185	5.437	17.614	0.725	1.694	1.694
	5.2	1.257	2.319	5.830	18.985	0.739	1.666	1.666
1.5	0.4	0.285	0.214	0.238	0.338	0.133	2.092	2.092
	0.8	0.460	0.388	0.452	0.658	0.176	1.507	1.507
	1.2	0.585	0.536	0.649	0.962	0.194	1.276	1.276
	1.6	0.680	0.664	0.831	1.254	0.202	1.153	1.153
	2.0	0.757	0.778	1.000	1.533	0.205	1.079	1.079
	2.4	0.821	0.881	1.159	1.802	0.207	1.030	1.030
	2.8	0.875	0.974	1.310	2.062	0.207	0.996	0.996
	3.2	0.923	1.060	1.452	2.313	0.207	0.971	0.971
	3.6	0.966	1.139	1.588	2.557	0.207	0.952	0.952
	4.0	1.003	1.213	1.717	2.793	0.206	0.938	0.938
	4.4	1.038	1.282	1.842	3.023	0.205	0.926	0.926
	4.8	1.069	1.347	1.961	3.247	0.204	0.917	0.917
	5.2	1.098	1.408	2.075	3.465	0.203	0.910	0.910
3.0	0.4	0.301	0.215	0.210	0.250	0.124	1.627	1.627
	0.8	0.480	0.383	0.394	0.481	0.152	1.077	1.077
	1.2	0.602	0.520	0.557	0.696	0.158	0.862	0.862
	1.6	0.692	0.636	0.704	0.897	0.157	0.752	0.752
	2.0	0.763	0.737	0.839	1.086	0.154	0.690	0.690
	2.4	0.822	0.825	0.962	1.265	0.150	0.653	0.653
	2.8	0.871	0.904	1.077	1.436	0.146	0.629	0.629
	3.2	0.913	0.976	1.184	1.599	0.143	0.613	0.613
	3.6	0.950	1.041	1.285	1.754	0.139	0.603	0.603
	4.0	0.982	1.101	1.380	1.903	0.136	0.596	0.596
	4.4	1.011	1.157	1.469	2.047	0.134	0.592	0.592
	4.8	1.038	1.208	1.555	2.185	0.131	0.589	0.589
	5.2	1.062	1.257	1.636	2.319	0.129	0.588	0.588

Table 3. Moments for $TLMW$ distribution at $\alpha =\beta =1.2$.

$\mathit{\theta }$	$\mathit{\lambda }$	${\mathit{\mu }}_1{}^{\prime }$	${\mathit{\mu }}_2{}^{\prime }$	${\mathit{\mu }}_3{}^{\prime }$	${\mathit{\mu }}_4{}^{\prime }$	$\mathit{Variance}$	$\mathit{CS}$	$\mathit{CK}$
0.5	0.4	0.061	0.024	0.018	0.019	0.020	4.751	4.751
	0.8	0.110	0.046	0.035	0.038	0.034	3.495	3.495
	1.2	0.152	0.067	0.051	0.056	0.044	2.962	2.962
	1.6	0.187	0.087	0.068	0.075	0.052	2.658	2.658
	2.0	0.218	0.106	0.084	0.093	0.059	2.457	2.457
	2.4	0.246	0.124	0.099	0.111	0.064	2.314	2.314
	2.8	0.271	0.142	0.115	0.129	0.068	2.206	2.206
	3.2	0.294	0.158	0.130	0.147	0.072	2.121	2.121
	3.6	0.315	0.174	0.145	0.165	0.075	2.052	2.052
	4.0	0.334	0.190	0.160	0.182	0.078	1.996	1.996
	4.4	0.352	0.205	0.174	0.199	0.081	1.948	1.948
	4.8	0.369	0.219	0.188	0.217	0.083	1.907	1.907
	5.2	0.385	0.233	0.202	0.234	0.085	1.872	1.872
1.5	0.4	0.137	0.051	0.029	0.021	0.032	2.196	2.196
	0.8	0.223	0.093	0.055	0.041	0.044	1.589	1.589
	1.2	0.284	0.129	0.079	0.060	0.049	1.347	1.347
	1.6	0.331	0.161	0.101	0.078	0.051	1.218	1.218
	2.0	0.369	0.189	0.122	0.095	0.052	1.139	1.139
	2.4	0.402	0.214	0.142	0.112	0.053	1.086	1.086
	2.8	0.429	0.238	0.161	0.128	0.053	1.049	1.049
	3.2	0.453	0.259	0.178	0.144	0.054	1.021	1.021
	3.6	0.474	0.279	0.195	0.160	0.054	1.000	1.000
	4.0	0.494	0.297	0.212	0.174	0.053	0.984	0.984
	4.4	0.511	0.314	0.227	0.189	0.053	0.971	0.971
	4.8	0.527	0.331	0.242	0.203	0.053	0.961	0.961
	5.2	0.542	0.346	0.257	0.217	0.053	0.952	0.952
3.0	0.4	0.171	0.074	0.043	0.030	0.045	1.608	1.608
	0.8	0.278	0.134	0.082	0.058	0.056	0.980	0.980
	1.2	0.352	0.182	0.115	0.083	0.058	0.705	0.705
	1.6	0.408	0.224	0.146	0.107	0.058	0.550	0.550
	2.0	0.452	0.260	0.173	0.129	0.056	0.453	0.453
	2.4	0.487	0.291	0.199	0.150	0.053	0.390	0.390
	2.8	0.517	0.319	0.222	0.170	0.051	0.346	0.346
	3.2	0.543	0.344	0.244	0.188	0.049	0.316	0.316
	3.6	0.565	0.367	0.264	0.206	0.047	0.296	0.296
	4.0	0.585	0.388	0.283	0.223	0.045	0.281	0.281
	4.4	0.603	0.407	0.301	0.239	0.044	0.271	0.271
	4.8	0.618	0.425	0.318	0.255	0.042	0.265	0.265
	5.2	0.633	0.441	0.334	0.270	0.041	0.261	0.261

3.3. Incomplete Moments

In terms of lifespan models, It is interesting to know the ${\mathrm{s}}_{th}$ lower and upper INMs of X defined by $v_s\left(t\right)=E(X^s\mid X<t)={\int }_0^t{x}^{s}f(x,\varphi )dx$ and ${\eta }_s\left(t\right)=E(X^s\mid X>t)={\int }_t^{\infty }{x}^{s}f(x,\varphi )dx$ respectively, for any real $s>0.$ The ${\mathrm{s}}_{th}$ lower INMs of $TLMW$ distribution is

$$\begin{array}{ccc}\hfill v_s\left(t\right)& =& {\int }_0^t{x}^{s}f\left(x\right)dx=2\lambda \sum _{i,j=0}^{\infty }\pi (i,j){\int }_0^t\left(\alpha x^{s+\theta j}+\theta \beta x^{s+\theta (j+1)-1}\right)e^{-2\alpha (i+1)x}dx\hfill \\ & =& 2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left[\frac{\alpha \gamma (s+\theta j+1,2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{s+\theta j+1}}+\theta \beta \frac{\gamma (s+\theta (j+1),2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{s+\theta (j+1)}}\right].\hfill \end{array}$$

(19)

Likewise, the ${\mathrm{s}}_{th}$ upper INMs of $TLMW$ distribution is

$$\begin{array}{ccc}\hfill {\eta }_s\left(t\right)& =& {\int }_t^{\infty }{x}^{s}f\left(x\right)dx=2\lambda \sum _{i,j=0}^{\infty }\pi (i,j){\int }_t^{\infty }\left(\alpha x^{s+\theta j}+\theta \beta x^{s+\theta (j+1)-1}\right)e^{-2\alpha (i+1)x}dx\hfill \\ & =& 2\lambda \sum _{i,j=0}^{\infty }\pi (i,j)\left[\frac{\alpha \Gamma (s+\theta j+1,2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{s+\theta j+1}}+\theta \beta \frac{\Gamma (s+\theta (j+1),2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{s+\theta (j+1)}}\right],\hfill \end{array}$$

(20)

where $\gamma (s,t)={\int }_0^t{x}^{s-1}{e}^{-x}dx$ and $\Gamma (s,t)={\int }_t^{\infty }{x}^{s-1}{e}^{-x}dx$ is the lower and upper incomplete gamma functions.

The MRL has many applications (see [35,36]). The MRL function is defined as

$$\mu \left(t\right)=E(X\mid X>t)=\frac{{\eta }_1\left(t\right)}{\overline{F}\left(t\right)}-t,$$

where ${\eta }_1\left(t\right)$ is the first INM of X and by putting $s=1$ in Equation (20), then

$$\mu \left(t\right)=\frac{2\lambda }{\overline{F}\left(t\right)}\sum _{i,j=0}^{\infty }\pi (i.j)\left[\frac{\alpha \Gamma (1+\theta j+1,2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{1+\theta j+1}}+\theta \beta \frac{\Gamma (1+\theta (j+1),2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{1+\theta (j+1)}}\right]-t.$$

Furthermore, the mean inactive time of X is determined as

$$\begin{array}{ccc}\hfill m\left(t\right)& =& E(X\mid X<t)=t-\frac{v_1\left(t\right)}{F\left(t\right)}\hfill \\ & =& t-\frac{2\lambda }{F\left(t\right)}\sum _{i,j=0}^{\infty }\pi (i,j)\left[\frac{\alpha \gamma (1+\theta j+1,2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{1+\theta j+1}}+\theta \beta \frac{\gamma (1+\theta (j+1),2\alpha (i+1\left)t\right)}{{\left[2\alpha (i+1)t)\right]}^{1+\theta (j+1)}}\right],t>0.\hfill \end{array}$$

4. Three Different Estimation Methods

In this part, ML approach, MPS approach, and Bayesian approach techniques are provided for $TLMW$ distribution parameters.

4.1. Maximum Likelihood Method

In this subsection, parameters estimates are derived using ML method. The log likelihood function for $TLMW$ distribution with the vector of parameters $\phi =(\alpha ,\beta ,\theta ,\lambda )$ is

$$\begin{array}{ccc}\hfill logL& =& nlog\left(2\lambda \right)+\sum _{i=1}^{n}log\left(\alpha +\theta \beta x_i^{\theta -1}\right)-2\sum _{i=1}^n(\alpha x_i+\beta x_i^{\theta })\hfill \\ & & +(\lambda -1)\sum _{i=1}^{n}log\left(1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right).\hfill \end{array}$$

(21)

The corresponding scoring function is supplied via

$$U_n\left(\phi \right)={\left[\frac{\partial L}{\partial \alpha },\frac{\partial L}{\partial \beta },\frac{\partial L}{\partial \theta },\frac{\partial L}{\partial \lambda }\right]}^T.$$

The components of the score vector are described as

$$\frac{\partial logL}{\partial \alpha }=\sum _{i=1}^n\frac{1}{\alpha +\theta \beta x_i^{\theta -1}}-2\sum _{i=1}^n{x}_i+(\lambda -1)\sum _{i=1}^n\frac{2x_i{e}^{-2(\alpha x_i+\beta x_i^{\theta })}}{1-e^{-2(\alpha x_i+\beta x_i^{\theta })}},$$

(22)

$$\frac{\partial logL}{\partial \beta }=\sum _{i=1}^n\frac{\theta x_i^{\theta -1}}{\alpha +\theta \beta x_i^{\theta -1}}-2\sum _{i=1}^n{x}_i^{\theta }+(\lambda -1)\sum _{i=1}^n\frac{2x_i^{\theta }{e}^{-2(\alpha x_i+\beta x_i^{\theta })}}{1-e^{-2(\alpha x_i+\beta x_i^{\theta })}},$$

(23)

$$\frac{\partial logL}{\partial \theta }=\sum _{i=1}^n\frac{\beta x_i^{\theta -1}(1+\theta ln\left(x_i\right))}{\alpha +\theta \beta x_i^{\theta -1}}-2\beta \sum _{i=1}^n{x}_i^{\theta }ln\left(x_i\right)+(\lambda -1)\sum _{i=1}^n\frac{2\beta x_i^{\theta }ln\left(x_i\right)e^{-2(\alpha x_i+\beta x_i^{\theta })}}{1-e^{-2(\alpha x_i+\beta x_i^{\theta })}},$$

(24)

and

$$\frac{\partial logL}{\partial \lambda }=\frac{n}{\lambda }+\sum _{i=1}^{n}log\left(1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right).$$

(25)

The $ML$ estimates (MLEs) of $\phi$, symbolize $\widehat{\phi }$ can indeed be produced by optimizing the log-likelihood function with regard to the involved parameters. In this approach, R-software packages such as nlm() and maxLik() might be useful (see [37,38]). Alternatively, the parameters can be found by concurrently solving four non-linear equations using an iterative process such as the Quasi Newton-Raphson method. Because the MLEs of the unknown parameters $\phi$ cannot be constructed in closed form, determining the exact distributions of the MLEs is difficult. As a result, specific confidence ranges can’t founded for the parameters. The large sample approximation must be used. It is known that the asymptotic distribution of the MLE $\widehat{\phi }$ is $(\widehat{\phi }-\phi )\to N(0,I^{-1}\left(\phi \right))$, see [39], where $I^{-1}\left(\phi \right)$, the inverse of the observed information matrix of the unknown parameters $\phi =(\alpha ,\beta ,\theta ,\lambda )$ is,

$$I^{-1}\left(\phi \right)={\left[\frac{{\partial }^{2}l}{\partial {\phi }^2}\right]}_{(\alpha ,\beta ,\theta ,\lambda )=(\widehat{\alpha },\widehat{\beta },\widehat{\theta },\widehat{\lambda })}^{-1},$$

and whose elements are given in Appendix A.

4.2. Maximum Product of Spacing Method

In this subsection, the MPS will be used, a substitute for the MLE method that is used to estimate the parameters of continuous uni-variate models. This method was developed by [40,41,42,43,44,45,46]. The uniform spacing of the TLMW distribution can be characterised as follows, $z_1<...<z_n$ assuming a random sample of size n:

$$\begin{array}{c}\hfill D_i\left(\phi \right)=F(z_{\left(i\right)},\phi )-F(z_{(i-1)},\phi );i=1,...,n+1,\end{array}$$

(26)

where $D_i\left(\phi \right)$ denotes to the uniform spacing, $F(z_{\left(0\right)},\phi )=0$, $F(z_{(n+1)},\phi )=1$ and ${\sum }_{i=1}^{n+1}{D}_i\left(\phi \right)=1$.

$$\begin{array}{c}\hfill G\left(\phi \right)=\frac{1}{n+1}\sum _{i=1}^{n+1}log\left\{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }\right\}.\end{array}$$

(27)

The MPS estimators (MPSE) of the TLMW distribution parameters may be constructed by maximizing Equation (27) with regards to $\alpha$ and $\delta$.

$$\frac{\partial G\left(\phi \right)}{\partial \alpha }=\frac{1}{n+1}\sum _{i=1}^{n+1}2\lambda \frac{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_i+\beta z_i^{\theta })}{z}_i-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}{z}_{i-1}}{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }},$$

(28)

$$\frac{\partial G\left(\phi \right)}{\partial \beta }=\frac{1}{n+1}\sum _{i=1}^{n+1}2\lambda \frac{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_i+\beta z_i^{\theta })}{z}_i^{\theta }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}{z}_{i-1}^{\theta }}{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }},$$

(29)

$$\frac{\partial G\left(\phi \right)}{\partial \theta }=\frac{1}{n+1}\sum _{i=1}^{n+1}2\beta \lambda \frac{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_i+\beta z_i^{\theta })}{z}_i^{\theta }ln\left(z_i\right)-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda -1}{e}^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}{z}_{i-1}^{\theta }ln\left(z_{i-1}\right)}{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }},$$

(30)

and

$$\frac{\partial G\left(\phi \right)}{\partial \lambda }=\frac{1}{n+1}\sum _{i=1}^{n+1}\frac{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }ln\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }ln\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}{{\left[1-e^{-2(\alpha z_i+\beta z_i^{\theta })}\right]}^{\lambda }-{\left[1-e^{-2(\alpha z_{i-1}+\beta z_{i-1}^{\theta })}\right]}^{\lambda }}.$$

(31)

Additionally, using the R application to solve Equations (28)–(31) to determine the MPSE of the parameters.

4.3. Bayesian Estimation

The Bayesian technique is extremely helpful in the analysis of reliability since it allows for the incorporation of previous knowledge into the research process. This is important because the restricted availability of data is one of the major issues with reliability analysis. By apply the insightful before to the $\alpha ,\beta ,\theta$, and $\lambda$ parameters, which are prior gamma distributions. $\alpha ,\beta ,\theta$, and $\lambda$ have independent joint prior density functions that look like this:

$$\Pi \left(\phi \right)\propto {\alpha }^{q_1-1}{\beta }^{q_2-1}{\lambda }^{q_3-1}{\theta }^{q_4-1}{e}^{-(w_1\alpha +w_2\beta +w_3\lambda +w_4\theta )};q_j,w_j>0;j=1,\cdots ,4.$$

(32)

By determining suitable and superior values for the independent joint prior’s hyper-parameters using the estimate and variance-covariance matrix of the MLE technique. By equating the gamma priors’ mean and variance as the following equations, the estimated hyper-parameters can be determined as follows:

$$q_j=\frac{{\left[\frac{1}{L}{\sum }_{i=1}^L{\widehat{\phi }}_i^j\right]}^2}{\frac{1}{L-1}{\sum }_{i=1}^L{\left[{\widehat{\phi }}_i^j-\frac{1}{L}{\sum }_{i=1}^L{\widehat{\phi }}_i^j\right]}^2},j=1,\cdots ,4,$$

(33)

$$w_j=\frac{\frac{1}{L}{\sum }_{i=1}^L{\widehat{\phi }}_i^j}{\frac{1}{L-1}{\sum }_{i=1}^L{\left[{\widehat{\phi }}_i^j-\frac{1}{L}{\sum }_{i=1}^L{\widehat{\phi }}_i^j\right]}^2},j=1,\cdots ,4,$$

(34)

where, L is the number of iteration and $\widehat{{\phi }^1}=\widehat{\alpha }$, $\widehat{{\phi }^2}=\widehat{\beta }$, $\widehat{{\phi }^4}=\widehat{\theta }$ and $\widehat{{\phi }^3}=\widehat{\lambda }$.

The likelihood function and joint prior function combine to form the joint posterior density function of $\phi$. The joint posterior of the TLMW distribution is thus written as

$$\begin{array}{cc}\hfill \Pi \left(\phi \right|x)\propto & e^{-2{\sum }_{i=1}^n(\alpha x_i+\beta x_i^{\theta })}\prod _{i=1}^n\left(\alpha +\theta \beta x_i^{\theta -1}\right){\left[1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right]}^{\lambda -1}\hfill \\ & {\alpha }^{q_1-1}{\beta }^{q_2-1}{\lambda }^{n+q_3-1}{\theta }^{q_4-1}{e}^{-(w_1\alpha +w_2\beta +w_3\lambda +w_4\theta )},\hfill \end{array}$$

(35)

utilising a function for squared error loss (SEL), which is the most typical function for symmetric loss. The Bayesian estimators of $\tilde{\phi }$ based on the SEL function.

$$\begin{array}{cc}\hfill S\left(\tilde{\phi }\right)=& E{\left(\tilde{\phi }-\phi \right)}^2\hfill \\ & {\int }_0^{\infty }...{\int }_0^{\infty }{\left(\tilde{\phi }-\phi \right)}^2\Pi \left(\phi \right|x)d{\phi }_{1}d{\phi }_{2}d{\phi }_{3}d{\phi }_4.\hfill \end{array}$$

(36)

The integrals provided by Equation (36) cannot be directly obtained, it should be emphasised. By employing the Markov chain Monte Carlo (MCMC) technique to estimate the value of integrals. Important sub-classes of MCMC approaches include Gibbs sampling and, within Gibbs samplers, a more generic Metropolis-Hesting. The Metropolis-Hasting (M-H) algorithm and Gibbs sampling are the two most often used MCMC applications. The MH technique, like acceptance-rejection sampling, presupposes that a candidate value can be generated from a proposal distribution for each iteration of the algorithm. The M-H algorithm claims that a candidate value from a normal proposal distribution can be generated for each iteration of the process, much like acceptance-rejection sampling claims. To obtain random samples of conditional posterior densities from the TLMW distribution, the M-H will be used inside Gibbs sampling. The conditional posterior distributions are as follows:

$$\begin{array}{cc}\hfill \Pi & \left(\alpha \right|\beta ,\lambda ,\theta ,x)\propto {\alpha }^{n+q_1-1}{e}^{-\alpha (2{\sum }_{i=1}^n{x}_i+w_1)}\prod _{i=1}^n{\left(1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right)}^{\lambda -1},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \Pi & \left(\beta \right|\alpha ,\lambda ,\theta ,x)\propto {\beta }^{n+q_2-1}{e}^{-\beta (w_2+2{\sum }_{i=1}^n{x}_i^{\theta })}\prod _{i=1}^n{x}_i^{\theta -1}{\left[1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right]}^{\lambda -1},\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \Pi & \left(\lambda \right|\alpha ,\beta ,\theta ,x)\propto {\lambda }^{n+q_3-1}{e}^{-w_3\lambda }\prod _{i=1}^n{\left[1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right]}^{\lambda -1},\hfill \end{array}$$

(39)

and

$$\begin{array}{cc}\hfill \Pi & \left(\theta \right|\alpha ,\beta ,\lambda ,x)\propto {\theta }^{n+q_4-1}{e}^{-w_4\theta }{e}^{-2\beta {\sum }_{i=1}^n{x}_i^{\theta }}\prod _{i=1}^n{x}_i^{\theta -1}{\left[1-e^{-2(\alpha x_i+\beta x_i^{\theta })}\right]}^{\lambda -1}.\hfill \end{array}$$

(40)

For further information, read [47]. The credible intervals (CIs) for Bayesian estimates are also known as the highest posterior density (HPD) intervals. Researchers utilized a well recognized approach to generate HPD ranges for unknown distribution characteristics. To generate estimates, samples are drawn using the proposed MH algorithm in this method; for information on the HPD algorithm, see [47].

5. Simulation

In this section, the purpose is to analyze the performance of the various estimation methods presented in sections above. Given a proposed model, a simulation study is used to analyse the behaviour of the offered methodologies and assess the statistical performances of the estimators. Calculations have been performed using the R-statistical programming language. Calculating MLEs and HPD intervals in R-language is done through utilizing the “maxLike” and “HDInterval” packages. Based on the following data produced by the TLMW distribution, where X is distributed as the TLMW distribution for various actual values of the parameters, Monte Carlo experiments were conducted:

• In Table 4, the actual values of the parameters are selected as first combination: $\alpha =0.5$, $\beta =0.6$, $\theta =2$ and $\lambda$ is 0.6 and 3.
• In Table 5, the actual values of the parameters are selected as second combination: $\alpha =2.5$, $\beta =2.5$, $\theta =2$ and $\lambda$ is 0.6 and 3.
• In Table 6, the actual values of the parameters are selected as third combination: $\alpha =0.5$, $\theta =0.75$, $\lambda =2$ and $\beta$ is 0.6 and 3.

Table 4. ML, MPS, Bayes estimation methods: RB, MSE, LACI and LCCI at first combination.

First Combination			ML			MPS			Bayesian
$\mathbf{\lambda }$	n		RB	MSEr	LACI	RB	MSEr	LACI	RB	MSEr	LCCI
0.6	30	$\alpha$	0.5590	0.2732	1.7321	0.1053	0.1775	1.6392	0.3274	0.1398	1.1151
		$\beta$	0.1203	0.7663	3.4215	−0.0980	0.2442	1.9244	0.0753	0.1159	1.2911
		$\theta$	0.7338	6.2504	7.9380	0.1212	0.9189	3.6374	0.2537	1.6512	4.3075
		$\lambda$	0.3275	0.1739	1.4427	0.0594	0.0747	1.0626	0.2622	0.0982	0.7599
	80	$\alpha$	0.5217	0.1971	1.4090	0.1017	0.1266	1.3764	0.2279	0.0912	0.9666
		$\beta$	−0.1170	0.3119	2.1839	−0.0919	0.1483	1.4949	0.0483	0.0626	1.0571
		$\theta$	0.5274	3.7303	6.3455	0.0638	0.5940	2.9812	0.1550	0.9555	3.2180
		$\lambda$	0.2829	0.1035	1.0716	0.0486	0.0487	0.8417	0.2037	0.0634	0.5619
	150	$\alpha$	0.5051	0.1140	0.8791	0.0923	0.0598	0.8492	0.1554	0.0322	0.6493
		$\beta$	−0.0971	0.0702	0.8203	−0.0916	0.0474	0.7690	−0.0266	0.0209	0.5862
		$\theta$	0.3542	1.2459	3.3828	0.0583	0.2675	1.9763	0.0823	0.2894	1.8616
		$\lambda$	0.1991	0.0232	0.3701	0.0411	0.0116	0.3331	0.1266	0.0214	0.2629
3	30	$\alpha$	−0.3465	0.3909	2.3600	−0.1871	0.1166	1.2902	0.2722	0.1569	1.3391
		$\beta$	0.4070	0.4790	2.5440	0.1221	0.1776	1.6305	−0.0107	0.0946	1.1588
		$\theta$	0.2691	2.1451	5.3509	0.0877	0.8827	3.6258	0.1040	2.0391	4.1324
		$\lambda$	0.1716	0.7055	2.6072	0.0834	0.4865	2.7104	0.6100	0.6178	2.1479
	80	$\alpha$	−0.3088	0.2280	1.7118	−0.1726	0.0775	0.9703	0.2377	0.1492	1.3171
		$\beta$	0.3988	0.3053	1.8913	0.1206	0.1237	1.2377	−0.0105	0.0937	1.0953
		$\theta$	0.0229	0.7876	3.4767	−0.0533	0.3438	2.2618	0.0253	0.6873	4.1040
		$\lambda$	0.1708	0.4688	1.7817	0.0789	0.2192	1.5084	0.1632	0.3885	1.2829
	150	$\alpha$	−0.2340	0.1448	1.3348	−0.1528	0.0608	0.7914	0.2133	0.1394	1.3147
		$\beta$	0.3963	0.1912	1.4394	0.1130	0.0946	0.9834	−0.0105	0.0926	1.0638
		$\theta$	−0.0215	0.3284	2.2118	−0.0495	0.1860	1.5192	0.0248	0.2511	2.1610
		$\lambda$	0.1422	0.2973	1.3326	0.0719	0.1340	0.9922	0.1157	0.2876	1.1344

Table 5. ML, MPS, Bayes estimation methods: RB, MSE, LACI and LCCI at second combination.

Second Combination			ML			MPS			Bayesian
$\mathbf{\lambda }$	n		RB	MSEr	LACI	RB	MSEr	LACI	RB	MSEr	LCCI
0.6	30	$\alpha$	0.0522	0.7978	3.4654	−0.1353	0.5969	2.7241	0.0647	0.6412	3.0449
		$\beta$	0.4818	5.4029	7.7970	−0.1623	1.2504	4.3427	0.1431	2.7290	5.1650
		$\theta$	0.1569	1.1422	4.0067	0.0574	0.6810	3.2363	0.1401	0.9200	3.5975
		$\lambda$	0.3607	0.3920	2.3041	0.1261	0.1188	1.3187	0.2241	0.0651	0.6844
	80	$\alpha$	0.0519	0.4446	2.4706	−0.0449	0.2686	1.9845	0.0461	0.4260	2.7081
		$\beta$	0.2506	2.7740	6.0522	−0.1008	0.6870	3.0968	0.1159	2.0343	4.1043
		$\theta$	0.1486	0.9200	3.4686	−0.0231	0.4395	2.5936	0.1341	0.5857	3.4668
		$\lambda$	0.1701	0.0571	0.8477	0.0858	0.0310	0.6605	0.1206	0.0536	0.3728
	150	$\alpha$	0.0511	0.2902	1.8065	0.0179	0.1315	1.4220	0.0398	0.2408	2.3326
		$\beta$	0.0757	1.1985	4.2289	−0.1001	0.4458	2.3754	0.0815	0.9543	4.0975
		$\theta$	0.1406	0.6086	2.7733	−0.0160	0.3022	2.1524	0.1234	0.4019	2.8139
		$\lambda$	0.1307	0.0297	0.6024	0.0778	0.0113	0.3746	0.1142	0.0246	0.2978
3	30	$\alpha$	0.0812	0.6413	3.0382	−0.0879	0.1829	1.4388	0.1867	0.5994	3.7191
		$\beta$	0.9488	9.9629	11.1623	−0.0559	0.9944	3.9028	0.0683	3.4979	6.6266
		$\theta$	0.4438	4.0650	7.0998	−0.1749	0.5279	2.7885	0.4153	1.9234	2.5075
		$\lambda$	0.4687	4.5403	6.2792	0.1385	0.9111	3.6076	0.3847	4.3673	5.8477
	80	$\alpha$	0.0810	0.5377	2.6483	−0.0613	0.0993	1.0804	0.1129	0.4705	2.3959
		$\beta$	0.6072	7.9721	10.1275	−0.0524	0.4115	2.4892	0.0502	2.5630	5.3703
		$\theta$	0.3501	2.9367	6.1343	−0.1180	0.3605	2.1970	0.3746	1.7163	2.2962
		$\lambda$	0.3784	2.2022	3.7487	0.1162	0.4354	2.1976	0.3197	1.1285	3.2517
	150	$\alpha$	0.0713	0.5263	2.6758	−0.0581	0.0960	1.0735	0.1024	0.3765	2.2545
		$\beta$	0.5767	2.4764	9.9199	−0.0421	0.3822	2.3893	0.0359	1.4837	5.2883
		$\theta$	0.3062	2.9222	6.0752	−0.1105	0.3461	2.1383	0.3080	0.4832	2.1480
		$\lambda$	0.3768	2.1278	3.6165	0.1017	0.4165	2.1209	0.2867	1.1131	3.1202

Table 6. ML, MPS, Bayes estimation methods: RB, MSE, LACI and LCCI at third combination.

Third Combination			ML			MPS			Bayesian
$\mathbf{\beta }$	n		RB	MSEr	LACI	RB	MSEr	LACI	RB	MSEr	LCCI
0.5	30	$\alpha$	−0.5339	0.2959	1.8619	−0.7322	0.3911	1.9920	0.2594	0.1048	1.0879
		$\beta$	0.8263	0.5700	2.4824	0.8859	0.5946	2.4794	−0.0114	0.1073	1.1189
		$\theta$	0.5756	0.9740	3.4866	0.1481	0.2823	2.0410	0.1133	0.1671	1.5405
		$\lambda$	0.3481	1.5059	3.9699	0.2444	0.7759	2.8788	0.3253	0.9005	3.0823
	80	$\alpha$	−0.4666	0.2516	1.4708	−0.6415	0.2177	1.3290	0.1847	0.0738	0.8989
		$\beta$	0.5956	0.5079	2.0725	0.8127	0.3687	1.7698	−0.0073	0.0947	1.0480
		$\theta$	0.2204	0.1608	1.4329	0.1200	0.0525	0.8260	0.1083	0.1601	1.3924
		$\lambda$	0.3090	1.3619	3.4023	0.2062	0.6508	2.4033	0.3155	0.8023	2.6051
	150	$\alpha$	−0.3593	0.1666	1.0996	−0.6019	0.1648	1.0687	0.0998	0.0505	0.7902
		$\beta$	0.4854	0.3347	1.5321	0.7994	0.2898	1.4141	0.0035	0.0669	0.9360
		$\theta$	0.1072	0.0351	0.6638	0.0725	0.0167	0.4591	0.0926	0.0234	0.5941
		$\lambda$	0.2345	0.8632	2.4374	0.1846	0.5588	1.9010	0.2360	0.7415	1.8685
3	30	$\alpha$	1.0510	3.1518	4.9250	1.4816	1.4329	3.6877	0.4612	0.3538	1.8668
		$\beta$	0.5033	3.9465	5.0629	0.3231	1.5708	3.1161	0.5670	1.4974	3.8887
		$\theta$	0.3385	0.4865	2.5479	0.1994	0.0549	0.7076	0.2919	0.1676	2.2720
		$\lambda$	0.7493	5.0224	6.5419	1.1926	6.5029	3.5369	0.7382	4.8340	5.9546
	80	$\alpha$	0.9208	1.3430	2.5436	1.3559	0.9532	2.3051	0.2860	0.2647	1.6196
		$\beta$	0.3678	1.5569	2.2854	0.3032	1.0617	1.8992	0.3258	1.2887	2.1018
		$\theta$	0.1766	0.2832	0.4069	0.1677	0.0262	0.4000	0.1607	0.1545	0.3666
		$\lambda$	0.6748	3.5248	7.1293	0.9328	4.5597	2.8017	0.6817	2.6870	4.4917
	150	$\alpha$	0.8160	1.3064	2.7226	0.9961	0.8072	1.5698	0.2892	0.2370	1.5071
		$\beta$	0.3576	1.2649	2.7693	0.2941	0.8905	1.3131	0.3148	0.8488	2.0209
		$\theta$	0.1575	0.1372	0.3922	0.1571	0.0226	0.3097	0.1332	0.1354	0.2539
		$\lambda$	0.4965	1.2215	4.9840	0.9337	2.5183	2.3962	0.4603	1.0261	3.0571

The sample sizes used in this simulation were 30, 80, and 150. The optimum method is one that minimises the relative bias (RB), mean squared error (MSEr), and length of confidence interval (LCI) of the estimator. In contrast to the LCI of MLE and MPS, which is the length of asymptotic confidence intervals (LACI), and Bayes calculates the length of confidence credible intervals (LCCI). Table 4, Table 5 and Table 6 provide the results of the simulation, and the following conclusion remakes are noted as a result.

• For techniques of estimation methods, the RBias, MSE, and the LCI related to the parameter estimations drop as n rises.
• It is noticed that the measures of the Bayesian estimation method are better than MLE method, as it is recognized.
• It is noticed that MPSE measures are, on average, more accurate than MLE and Bayesian estimate measures.
• Table 4, shows that the actual value of parameter $\lambda$ increases then the measures of $\beta$, $\theta$, $\lambda$ decreases.
• Table 6, show that the actual value of parameter $\beta$ increases then the measures of parameters increases.

A heatmap is a graphical representation of data that uses a system of color-coding to represent different values. Figure 3 and Figure 4 show heatmaps summarizing the results of the RB and MSE of simulation results. The dark red shading indicates RB and MSE with large value. The light yellow shading indicates RB and MSE with small value of parameters for TLMW under different estimation methods.

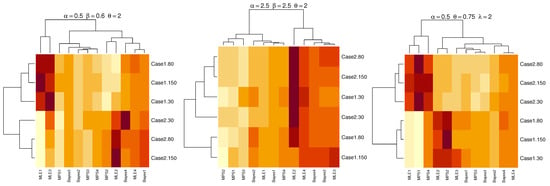
Figure 3. Heatmaps of RB for parameters under different estimation methods.

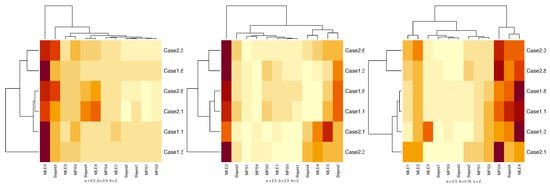
Figure 4. Heatmaps of MSEr for parameters under different estimation methods.

6. Applications

In this section, applications of the $TLMW$ distribution using four real data sets as COVID-19 data, survival rates sunaina Pigs, Waiting times of service of 100 bank customers, and Tensile strength for single carbon fibres (in GPa) in order to illustrate the potentiality of the $TLMW$ model are provided. The proposed distribution will be compared with other related lifetime models as Kumaraswamy Weibull (KW) by [48], generalized modified Weibull (GMW) by [14], extend odd Weibull Lomax (EOWL) by [49], Weibull-Lomax (WL) by [50], Marshall-Olkin alpha power extended Weibull (MOAPEW) by [51] and exponentiated generalized alpha power exponential (EGAPE) by [52].

When comparing distributions, we consider the following discriminating criteria: Akaike information criterion (AKIC), consistent AKIC (CAKIC), Bayesian information criterion (BIC) and Hannan–Quinn information criterion (HQIC), the Kolmogrov-Smirnov distance (KSD) with Pvalue (PVKS).

$$\begin{array}{cc}\hfill & AICc=-2logL+2p+2\frac{p(p+1)}{n-p-1},\hfill \\ & AIC=-2logL+2p,\hfill \\ & BIC=-2logL+plog\left(n\right),\hfill \\ & HQIC=-2logL+2plog\left(log\right(n\left)\right),\hfill \end{array}$$

(41)

where p is a number of parameters, and n is a sample size.

6.1. COVID-19 Data

The data set given as follows: 1, 1, 2, 4, 5, 1, 1, 3, 6, 6, 4, 1, 5, 6, 6, 8, 5, 7, 7, 9, 9, 15, 17, 11, 13, 5, 14, 5, 13, 9, 19, 15, 11, 14, 12, 11, 7, 13, 10, 20, 22, 21, 12, 14, 9, 14, 7, 16, 17, 13, 21, 11, 11, 8, 11, 12, 15, 21, 20, 18, 15, 14, 21, 16, 11, 28, 29, 19, 14, 19, 29, 34, 34, 46, 46, 47, 36.00, 38, 40, 32, 39, 34, 35, 36, 35, 45, 62. The most recent data, used by [4], revealed the daily fatality confirmed cases attributable to COVID-19. The data consists of 89 observed values, with 18.72 reported deaths on average every day.

By using equations Equations (22)–(25) to obtain the MLEs of the model parameters with standard error (SE) and the results are reported in Table 7. The estimated density with histogram of waiting times data for $TLMW$ distribution and other distributions are displayed in Figure 5. The estimated cumulative and the fitted $TLMW$ distribution and other distributions for the waiting times data set are displayed in Figure 6. The estimated PP and QQ plot for $TLMW$ distribution are displayed for waiting times data in Figure 7.

Table 7. MLE for parameters of $TLMW$ and comparative models for COVID-19 data.

Models		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$
TLMW	estimates	0.0106	0.0101	1.2689	1.2680
	SE	0.0740	0.0276	0.2493	1.0647
KW	estimates	1.2083	2.3127	0.0326	1.1786
	SE	0.9050	6.4453	0.0641	0.6493
GMW	estimates	0.0370	1.2290	0.0015	1.1750
	SE	0.0939	0.9993	0.0140	0.7523
WL	estimates	0.1965	1.4744	0.8391	4.3238
	SE	4.4704	0.8668	0.5010	70.5703
OLLMW	estimates	2.5199	0.0168	0.1754	0.3704
	SE	0.9641	0.0256	0.1080	0.2135

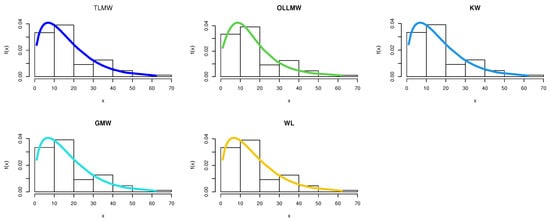
Figure 5. Pdf for different models for COVID-19 data.

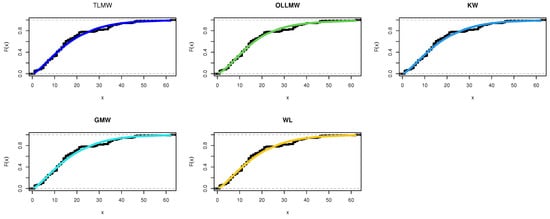
Figure 6. Cdf for different models for COVID-19 data.

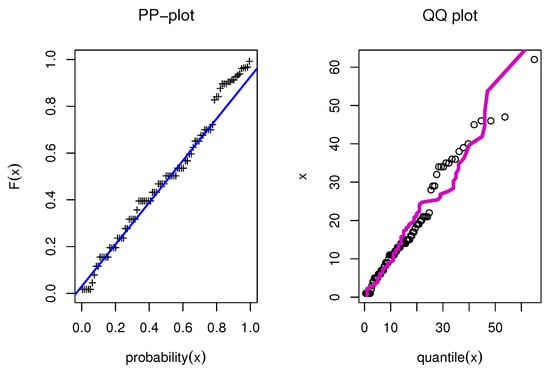
Figure 7. PP and QQ for $TLMW$ model for COVID-19 data.

Now, applying the formal goodness-of-fit tests in order to verify which distribution fits better to these data set. The measures AKIC, BIC, CAKIC, HQIC and the KSD with PVKS (See Table 8) are considered.

Table 8. Discrimination criteria and KS test of the TLMW model parameters for COVID-19 data.

Models	AKIC	BIC	CAKIC	HQIC	KSD	PVKS
TLMW	663.9288	673.7924	664.4166	667.9005	0.0740	0.7280
KW	663.9298	673.7984	664.4256	667.9996	0.0752	0.7090
GMW	663.9839	673.9776	664.9517	667.9857	0.0768	0.6834
WL	663.9706	673.8712	664.5954	667.9879	0.0750	0.7125
OLLMW	664.8357	674.6994	665.3235	668.8075	0.0764	0.7059

The $95\%$ CIs for the parameters $\alpha$, $\beta$, $\theta$ and $\lambda$ are presented for MLE and Bayesian estimation methods in Table 9. Figure 8 displayed contour plot of parameters for $TLMW$ model to check uniqueness and max-value of likelihood for COVID-19 data. While, Figure 9 confirmed convergence of MCMC results, which show the MCMC samples as a pairs plot, with the trace plot, and marginal frequency of proposed distribution as normal distribution for each parameter on the diagonal for parameters of $TLMW$ model for COVID-19 data. Figure 10 discussed Auto-correlation Function (ACF) test. Auto-correlation for MCMC is the correlation between a iteration series with a lagged version of itself. The ACF starts at a lag of 0, which is the correlation of the iteration series with itself and therefore results in a correlation of 1.

Table 9. MLE and Bayesian estimation methods of the $TLMW$ model parameters for COVID-19 data.

	MLE				Bayesian
	Estimates	SE	Lower	Upper	Estimates	SE	Lower	Upper
$\alpha$	0.0106	0.0740	0.0062	0.0831	0.0106	0.0005	0.0096	0.0115
$\beta$	0.0101	0.0276	0.0017	0.0371	0.0100	0.0014	0.0076	0.0129
$\theta$	1.2689	0.2493	1.0246	1.5133	1.2689	0.0125	1.2440	1.2936
$\lambda$	1.2680	1.0647	0.2246	2.3114	1.2676	0.0531	1.1618	1.3672

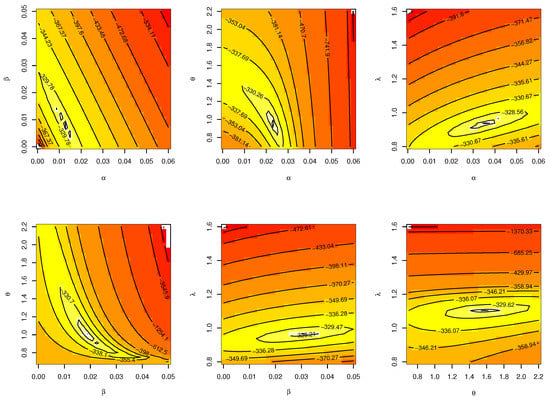
Figure 8. Contour plot for parameters of $TLMW$ model for COVID-19 data.

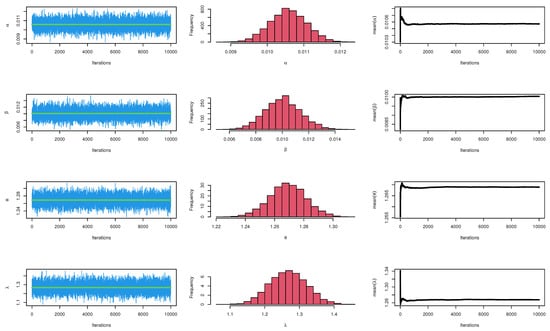
Figure 9. MCMC plots for parameters of $TLMW$ model for COVID-19 data.

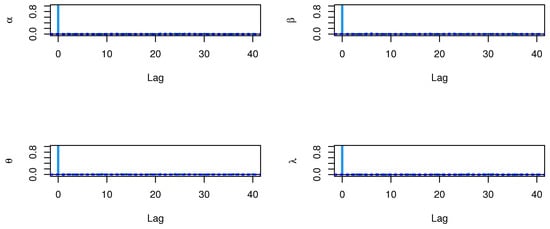
Figure 10. ACF test plots for parameters of $TLMW$ model for COVID-19 data.

6.2. Guinea Pigs Data

The set of data [53] shows survival rates for Guinea pigs infected with virulent tubercle bacilli. One of the reasons guinea pigs were chosen for this investigation is that they are thought to be highly susceptible to human tuberculosis. The data set given as follows: 0.10, 0.33, 0.440, 0.56, 0.59, 0.72, 0.74, 0.77, 0.920, 0.93, 0.96, 1.00, 1.00, 1.02, 1.05, 1.07, 1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.160, 1.200, 1.21, 1.22, 1.22, 1.24, 1.30, 1.34, 1.360, 1.390, 1.44, 1.46, 1.53, 1.59, 1.60, 1.63, 1.63, 1.680, 1.71, 1.72, 1.76, 1.83, 1.950, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.40, 2.45, 2.51, 2.53, 2.54, 2.54, 2.780, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.580, 5.55.

By using equations Equations (22)–(25) to obtain the MLEs of the model parameters and the results are reported in Table 10. The estimated density with histogram of waiting times data for $TLMW$ distribution and other distributions are displayed in Figure 11. The estimated cumulative and the fitted $TLMW$ distribution and other distributions for the Guinea Pigs data set are displayed in Figure 12. The estimated PP and QQ plot for $TLMW$ distribution are displayed for Guinea Pigs data in Figure 13.

Table 10. MLE for parameters of TLMW and comparative models for Guinea Pigs data.

Models		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	$\mathit{\delta }$
TLMW	estimates	0.2497	0.2004	1.2916	2.7723
	SE	0.9087	0.7554	0.7622	1.5924
KW	estimates	2.4052	0.7823	0.9365	1.2522
	SE	1.1901	0.1516	0.3952	0.8752
WL	estimates	11.2147	2.8862	0.2501	0.6035
	SE	27.0764	2.3091	0.2095	2.0505
MOAPEW	estimates	0.0106	0.6961	0.9662	0.4619	0.0332
	SE	0.0144	0.3549	0.1980	0.4283	0.0079
EGAPEx	estimates	2.8371	3.2962	16.2875	0.1090
	SE	0.9711	1.0053	2.9542	0.0265

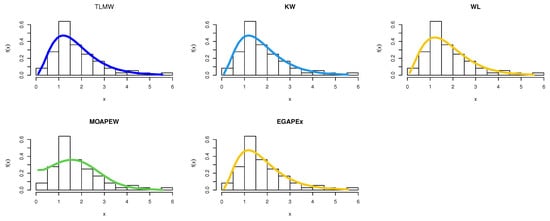
Figure 11. Pdf for different models for Guinea Pigs data.

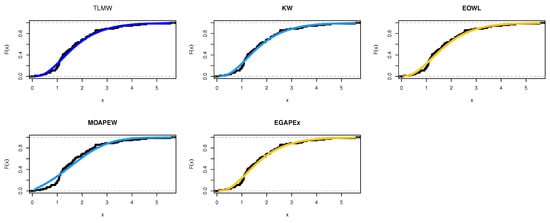
Figure 12. Cdf for different models for Guinea Pigs data.

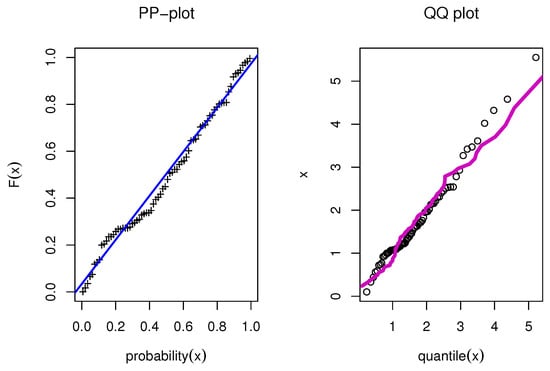
Figure 13. PP and QQ for $TLMW$ model for Guinea Pigs data.

Now, applying the formal goodness-of-fit tests in order to verify which distribution fits better to these data set. The measures AKIC, BIC, CAKIC, HQIC and the KSD with PVKS (See Table 11) are considered.

Table 11. Discrimination criteria and KS test of the TLMW model parameters for Guinea Pigs data.

Models	AKIC	BIC	CAKIC	HQIC	KSD	PVKS
TLMW	196.1265	205.2332	196.7235	199.7519	0.0885	0.6253
KW	196.2290	205.3357	196.8260	199.8544	0.0922	0.5737
WL	196.8496	205.9562	197.4466	200.4750	0.0955	0.5277
MOAPEW	210.8167	222.2000	211.7258	215.3484	0.1359	0.1398
EGAPEx	196.3202	205.4268	196.9172	199.9456	0.0907	0.5948

The $95\%$ CIs for the parameters $\alpha$, $\beta$, $\theta$ and $\lambda$ are presented for MLE and Bayesian estimation methods in Table 12. Figure 14 displayed contour plot of parameters for $TLMW$ model to check uniqueness and max-value of likelihood for Guinea Pigs data. While, Figure 15 confirmed convergence of MCMC results, which show the MCMC samples as a pairs plot, with the trace plot, and marginal frequency of proposed distribution as normal distribution for each parameter on the diagonal for parameters of $TLMW$ model for Guinea Pigs data. Figure 16 discussed ACF test. Auto-correlation for MCMC is the correlation between a iteration series with a lagged version of itself. The ACF starts at a lag of 0, which is the correlation of the iteration series with itself and therefore results in a correlation of 1.

Table 12. MLE and Bayesian estimation methods of the $TLMW$ model parameters for Guinea Pigs data.

	MLE				Bayesian
	Estimates	SE	Lower	Upper	Estimates	SE	Lower	Upper
$\alpha$	0.2497	0.9087	0.0378	0.4615	0.2501	0.0046	0.2410	0.2593
$\beta$	0.2004	0.7554	0.1326	0.2682	0.2146	0.0231	0.1838	0.2669
$\theta$	1.2916	0.7622	0.1723	2.4109	1.2962	0.0341	1.2292	1.3696
$\lambda$	2.7723	1.5924	0.5117	5.0330	2.7819	0.0719	2.6330	2.9210

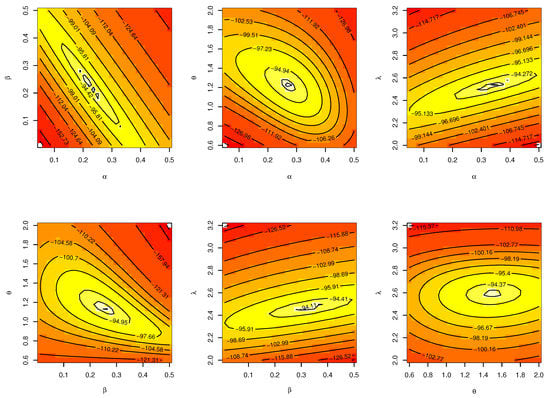
Figure 14. Contour plot for parameters of $TLMW$ model for Guinea Pigs data.

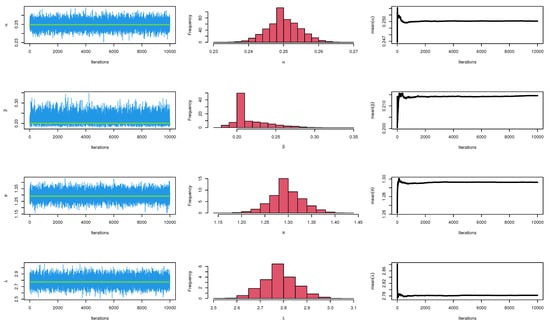
Figure 15. MCMC plots for parameters of $TLMW$ model for Guinea Pigs data.

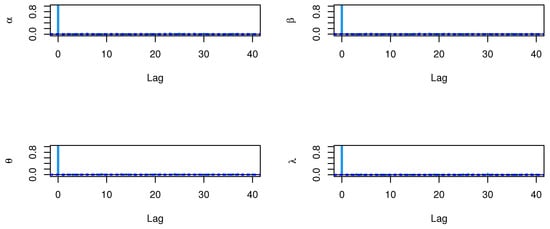
Figure 16. ACF test plots for parameters of $TLMW$ model for Guinea Pigs data.

6.3. Waiting Times of Service of 100 Bank Customers

The data set given in Table 13 represents the waiting times (in minutes) before service of 100 bank customers (see [54]).

Table 13. Waiting times (in minutes) before service of 100 bank customers.

0.8	0.8	1.3	1.5	1.8	1.9	1.9	2.1	2.6	2.7	2.9	3.1	3.2	3.3	3.5
3.6	4.0	4.1	4.2	4.2	4.3	4.3	4.4	4.4	4.6	4.7	4.7	4.8	4.9	4.9
5.0	5.3	5.5	5.7	5.7	6.1	6.2	6.2	6.2	6.3	6.7	6.9	7.1	7.1	7.1
7.1	7.4	7.6	7.7	8.0	8.2	8.6	8.6	8.6	8.8	8.8	8.9	8.9	9.5	9.6
9.7	9.8	10.7	10.9	11.0	11.0	11.1	11.2	11.2	11.5	11.9	12.4	12.5	12.9	13.0
13.1	13.3	13.6	13.7	13.9	14.1	15.4	15.4	17.3	17.3	18.1	18.2	18.4	18.9	19.0
19.9	20.6	21.3	21.4	21.9	23.0	27.0	31.6	33.1	38.5

Summary statistics of the Waiting times data set are presented in Table 14.

Table 14. Summary statistics of the Waiting times data set.

Median	$\mathit{E}\left(\mathit{X}\right)$	$\mathit{Var}\left(\mathit{X}\right)$	Kurtosis	Skewness
8.1	9.872	52.0875	1.44713	7.21717

Table 14, show that the distribution of this data set is positively skewed. By using equations Equations (22)–(25) to obtain the MLEs of the model parameters and the results are reported in Table 15.

Table 15. MLE for parameters of $TLMW$ and comparative models for waiting times.

Models		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	$\mathit{\delta }$
$TLMW$	estimates	0.0253	0.0905	0.8581	2.7331
	SE	0.6659	0.4810	1.9559	3.3520
KW	estimates	2.3386	0.3121	0.3319	1.1292
	SE	1.1505	0.7742	0.4551	0.4184
GMW	estimates	0.0934	1.7029	0.0070	1.1990
	SE	0.1679	1.3278	0.0216	0.6518
EOWL	estimates	2.2848	0.0719	0.4028	2.2202
	SE	2.9676	0.5081	1.0659	11.9778
WL	estimates	1.0497	2.0639	0.4387	2.8458
	SE	0.2157	0.3553	0.1099	0.4097
MOAPEW	estimates	0.2806	0.2616	0.5192	0.0064	0.0507
	SE	0.0956	0.0097	0.2034	0.0021	0.0423
EGAPEx	estimates	1.2516	2.0969	0.2248	0.7042
	SE	0.1157	0.3196	0.0399	0.0967

The estimated density with histogram of waiting times data for $TLMW$ distribution and other distributions are displayed in Figure 17. The estimated cumulative and the fitted $TLMW$ distribution and other distributions for the waiting times data set are displayed in Figure 18. The estimated PP and QQ plot for $TLMW$ distribution are displayed for waiting times data in Figure 19.

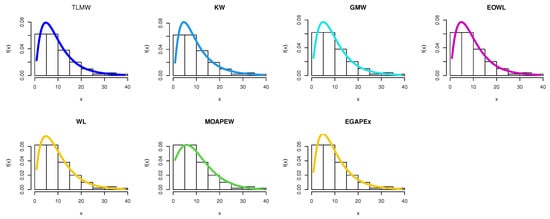
Figure 17. Pdf for different models for waiting times.

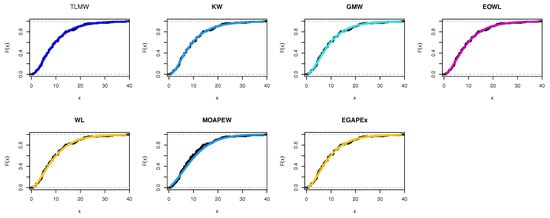
Figure 18. Cdf for different models for waiting times.

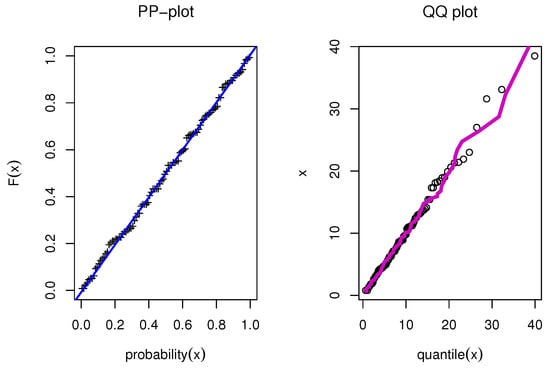
Figure 19. PP and QQ for $TLMW$ model for waiting times.

Now, applying the formal goodness-of-fit tests in order to verify which distribution fits better to these data set. The measures AKIC, BIC, CAKIC, HQIC and the KSD with PVKS (See Table 16) are considered.

Table 16. Discrimination criteria and KS test of the $TLMW$ model parameters for waiting times.

Models	AKIC	BIC	CAKIC	HQIC	KSD	PVKS
$TLMW$	642.067	652.488	642.489	646.285	0.036	0.999
KW	641.950	652.371	642.371	646.167	0.038	0.999
GMW	642.387	652.808	642.808	646.605	0.041	0.996
EOWL	642.231	652.652	642.652	646.449	0.038	0.999
WL	642.533	652.954	642.954	646.751	0.041	0.995
MOAPEW	652.324	665.350	652.963	657.596	0.082	0.509
EGAPEx	642.184	652.604	642.605	646.401	0.040	0.997

The $95\%$ CIs for the parameters $\alpha$, $\beta$, $\theta$ and $\lambda$ are presented for MLE and Bayesian estimation methods in Table 17. Figure 20 displayed contour plot of parameters for $TLMW$ model to check uniqueness and max-value of likelihood for waiting times. While, Figure 21 confirmed convergence of MCMC results, which show the MCMC samples as a pairs plot, with the trace plot, and marginal frequency of proposed distribution as normal distribution for each parameter on the diagonal for parameters of $TLMW$ model for waiting times. Figure 22 discussed ACF test. Auto-correlation for MCMC is the correlation between a iteration series with a lagged version of itself. The ACF starts at a lag of 0, which is the correlation of the iteration series with itself and therefore results in a correlation of 1.

Table 17. MLE and Bayesian estimation methods of the $TLMW$ model parameters for waiting times.

Method		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$
MLE	estimates	0.0253	0.0905	0.8581	2.7331
	SE	0.6659	0.4810	1.9559	3.3520
	Lower	0.0005	0.0419	0.4747	0.7041
	upper	1.3305	1.0334	4.6917	9.3031
Bayes	estimates	0.0252	0.0903	0.8580	2.7328
	SE	0.0050	0.0158	0.0652	0.1118
	Lower	0.0155	0.0608	0.7276	2.5096
	upper	0.0347	0.1227	0.9873	2.9423

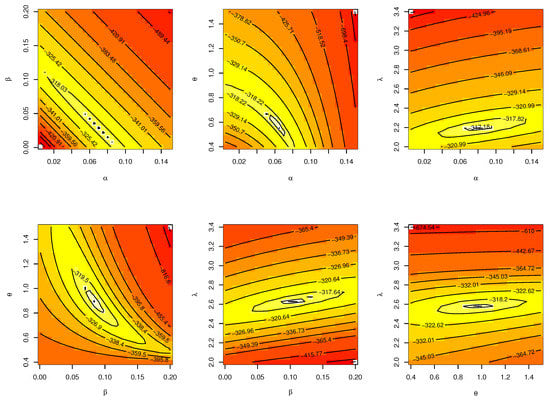
Figure 20. Contour plot for parameters of $TLMW$ model for waiting times.

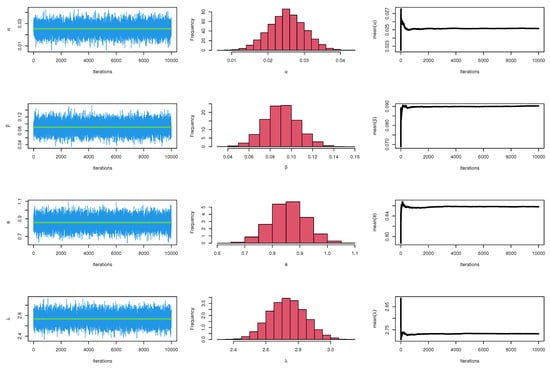
Figure 21. MCMC plots for parameters of $TLMW$ model for waiting times.

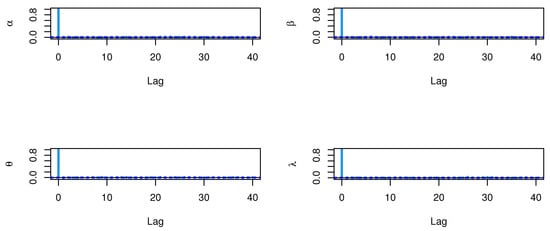
Figure 22. ACF test plots for parameters of $TLMW$ model for waiting times.

6.4. Tensile Strength for Single Carbon Fibres (in GPa)

The data set given in Table 18 contains the tensile strength for single carbon fibres (in GPa). The data set finds its source in [55].

Table 18. Tensile strength (with unit in GPa) for single carbon fibers.

0.312	0.944	1.063	1.272	1.434	1.566	1.697	1.848	2.128
0.314	0.958	1.098	1.274	1.435	1.57	1.726	1.88	2.233
0.479	0.966	1.14	1.301	1.478	1.586	1.77	1.954	2.433
0.552	0.997	1.179	1.301	1.49	1.629	1.773	2.012	2.585
0.7	1.006	1.224	1.359	1.511	1.633	1.8	2.067	2.585
0.803	1.021	1.24	1.382	1.514	1.642	1.809	2.084
0.861	1.027	1.253	1.382	1.535	1.648	1.818	2.09
0.865	1.055	1.27	1.426	1.554	1.684	1.821	2.096

We use equations Equations (22)–(25) to obtain the MLEs of the model parameters and the results are reported in Table 19.

Table 19. MLE for parameters of $TLMW$ and comparative models for single carbon fibers data.

Models		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	$\mathit{\delta }$
$TLMW$	estimates	0.2145	0.1057	3.2053	2.2749
	SE	0.1081	0.0346	0.7106	1.1533
OLLMW	estimates	28.7708	0.0560	0.6093	0.0125
	SE	39.8918	0.0814	0.1193	0.0310
KW	estimates	1.3752	0.1402	1.2141	3.0059
	SE	0.0409	0.0194	0.0306	0.0194
GMW	estimates	0.4864	4.4323	0.8582	0.3467
	SE	0.7405	8.6912	0.2825	1.0545
EOWL	estimates	2.6361	0.1152	8.7047	19.2595
	SE	0.4997	0.2885	4.9097	10.6442
WL	estimates	0.1399	2.5597	2.0355	2.1477
	SE	4.5871	2.4273	6.7471	31.2428
MAOPEW	estimates	0.8564	3.0230	0.0117	1.5489	0.0055
	SE	1.3615	0.8091	0.0091	0.3239	0.0036
EGAPEx	estimates	141.1326	2.4787	17.2979	0.4888
	SE	52.8014	0.9138	12.7006	0.1625

The estimated density with histogram of single carbon fibers data for $TLMW$ distribution and other distributions are displayed in Figure 23. The estimated cumulative and the fitted $TLMW$ distribution and other distributions for the second set are displayed in Figure 24. The estimated PP and QQ plot for $TLMW$ distribution are displayed for single carbon fibers data in Figure 25.

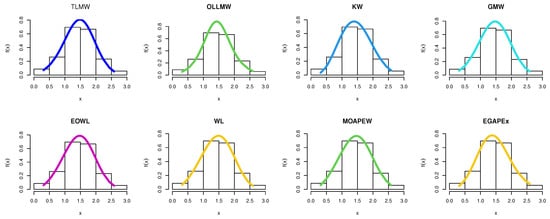
Figure 23. Pdf for different models for single carbon fibers data.

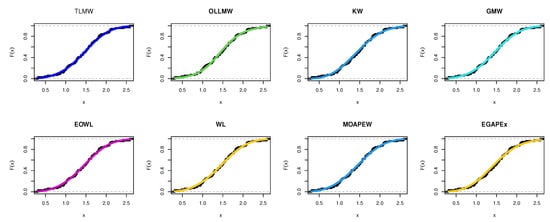
Figure 24. Cdf for different models for single carbon fibers data.

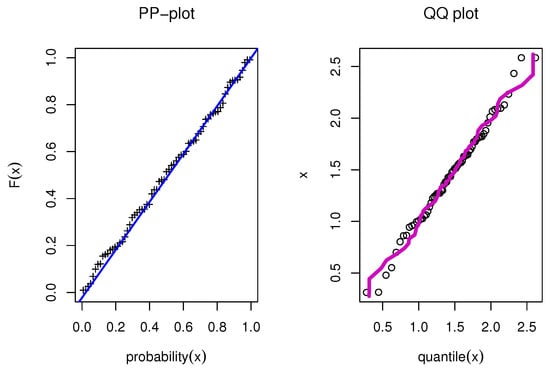
Figure 25. PP and QQ for $TLMW$ model for single carbon fibers data.

Now, applying the formal goodness-of-fit tests in order to verify which distribution fits better to single carbon fibers data set. The measures AKIC, BIC, CAKIC, HQIC and the KSD with PVKS (See Table 20) are considered.

Table 20. Discrimination criteria and KS test of the $TLMW$ model parameters for single carbon fibers.

Models	AKIC	BIC	CAKIC	HQIC	KSD	PVKS
$TLMW$	105.1709	114.1073	105.7959	108.7163	0.0406	0.9999
OLLMW	106.6756	115.6121	107.3006	110.2210	0.0468	0.9982
KW	107.4852	116.4217	108.1102	111.0306	0.0514	0.9932
GMW	105.4391	114.3755	106.0641	108.9844	0.0423	0.9997
EOWL	105.5875	114.5240	106.2125	109.1329	0.0435	0.9995
WL	105.6961	114.6326	106.3211	109.2415	0.0473	0.9978
MAOPEW	107.4438	118.6144	108.3962	111.8756	0.0496	0.9957
EGAPEx	107.0651	116.0015	107.6901	110.6105	0.0561	0.9817

The $95\%$ CIs for the parameters $\alpha$, $\beta$, $\theta$ and $\lambda$ are presented for MLE and Bayesian estimation methods in Table 21. Figure 26 displayed contour plot of parameters for $TLMW$ model to check uniqueness and max-value of likelihood for single carbon fibers data. While, Figure 27 confirmed convergence of MCMC results, which show the MCMC samples as a pairs plot, with the trace plot, and marginal frequency of proposed distribution as normal distribution for each parameter on the diagonal for parameters of $TLMW$ model for single carbon fibers. Figure 28 discussed ACF test. Auto-correlation for MCMC is the correlation between a iteration series with a lagged version of itself. The correlation between the iteration series and itself, which is where the ACF starts with a lag of 0, yields a correlation of 1.

Table 21. LE and Bayesian estimation methods of the $TLMW$ model parameters for single carbon fibers.

Method		$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$
MLE	estimates	0.2145	0.1057	3.2053	2.2749
	SE	0.1081	0.0346	0.7106	1.1533
	Lower	0.1897	0.0571	2.8219	0.2459
	upper	0.2393	0.1543	3.5887	4.3039
Bayes	estimates	0.2144	0.1057	3.2053	2.2745
	SE	0.0050	0.0039	0.0355	0.0866
	Lower	0.2048	0.0984	3.1342	2.1021
	upper	0.2242	0.1137	3.2757	2.4367

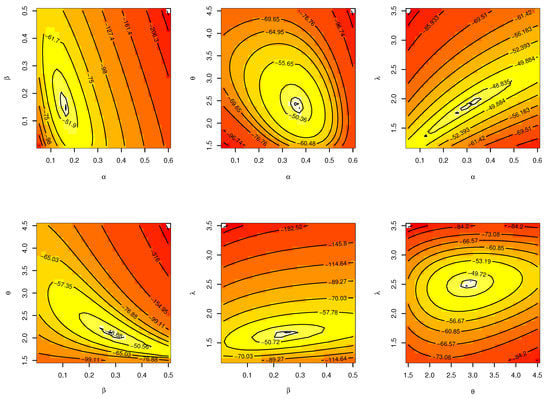
Figure 26. Contour plot for parameters of $TLMW$ model for single carbon fibers.

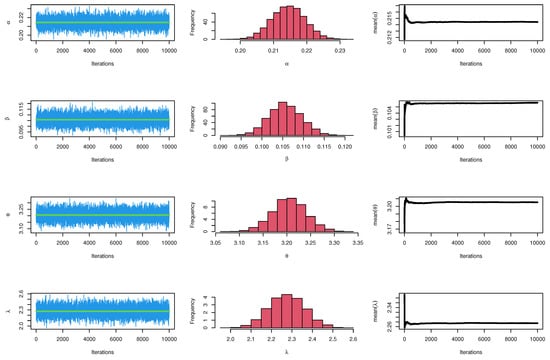
Figure 27. MCMC plots for parameters of $TLMW$ model for single carbon fibers.

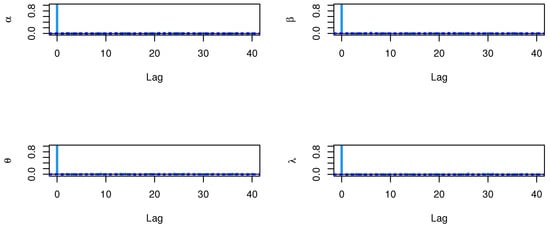
Figure 28. ACF test plots for parameters of $TLMW$ model for single carbon fibers.

7. Conclusions

In this paper, a four-parameter family of distributions called the Topp–Leone modified Weibull distribution ($TLMW$) is introduced. Some of its statistical and reliability features are derived. The $TLMW$ density function can decreasing, uni-modal and right skewed but, its hazard rate function can be decreasing, increasing, J-shaped, U-shaped and bathtub. Therefore, it can be used quite effectively in analyzing lifetime data. Three different methods of estimation as; maximum likelihood, maximum product spacing and Bayesian methods are used to estimate the model parameters. Additionally, the $TLMW$ model can be used as a substitute for many known distributions and in some cases it can provide better results (with respect to model fitting) than the models considered in the paper. The flexibility of this distribution is evaluated by applying it to four real data sets and comparing it to various other distributions. The findings of the tables and figures show that the suggested model regularly outperforms other competitor models for these four data sets as COVID-19 data, survival rates Guinea Pigs, Waiting times of service of 100 bank customers, and Tensile strength for single carbon fibres (in GPa). Finally, the $TLMW$ distribution will attract a broader range of applications, including medical, engineering, and social sciences, among others.