Early Ventricular Fibrillation Prediction Based on Topological Data Analysis of ECG Signal
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Pre-Processing
2.2. TDA Features Extraction
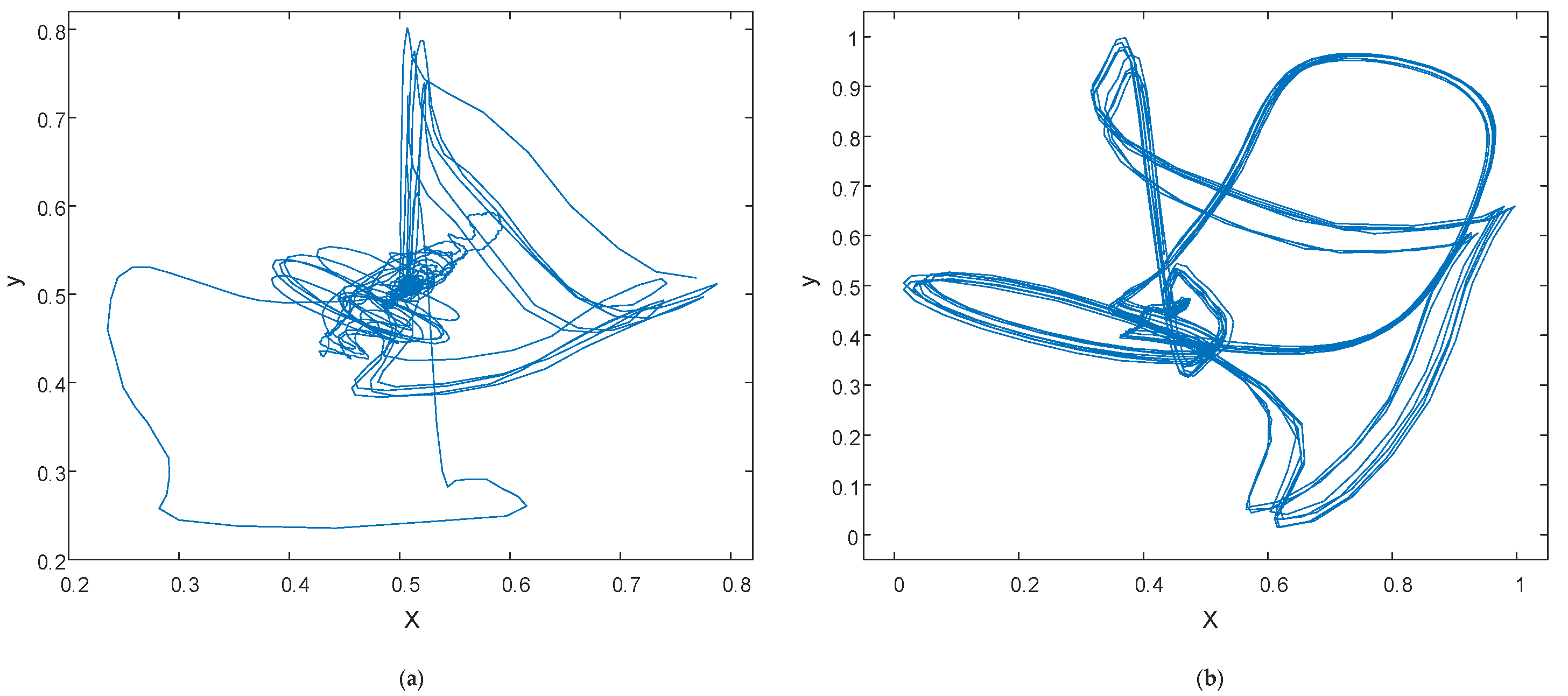
2.2.1. Phase Space Reconstruction
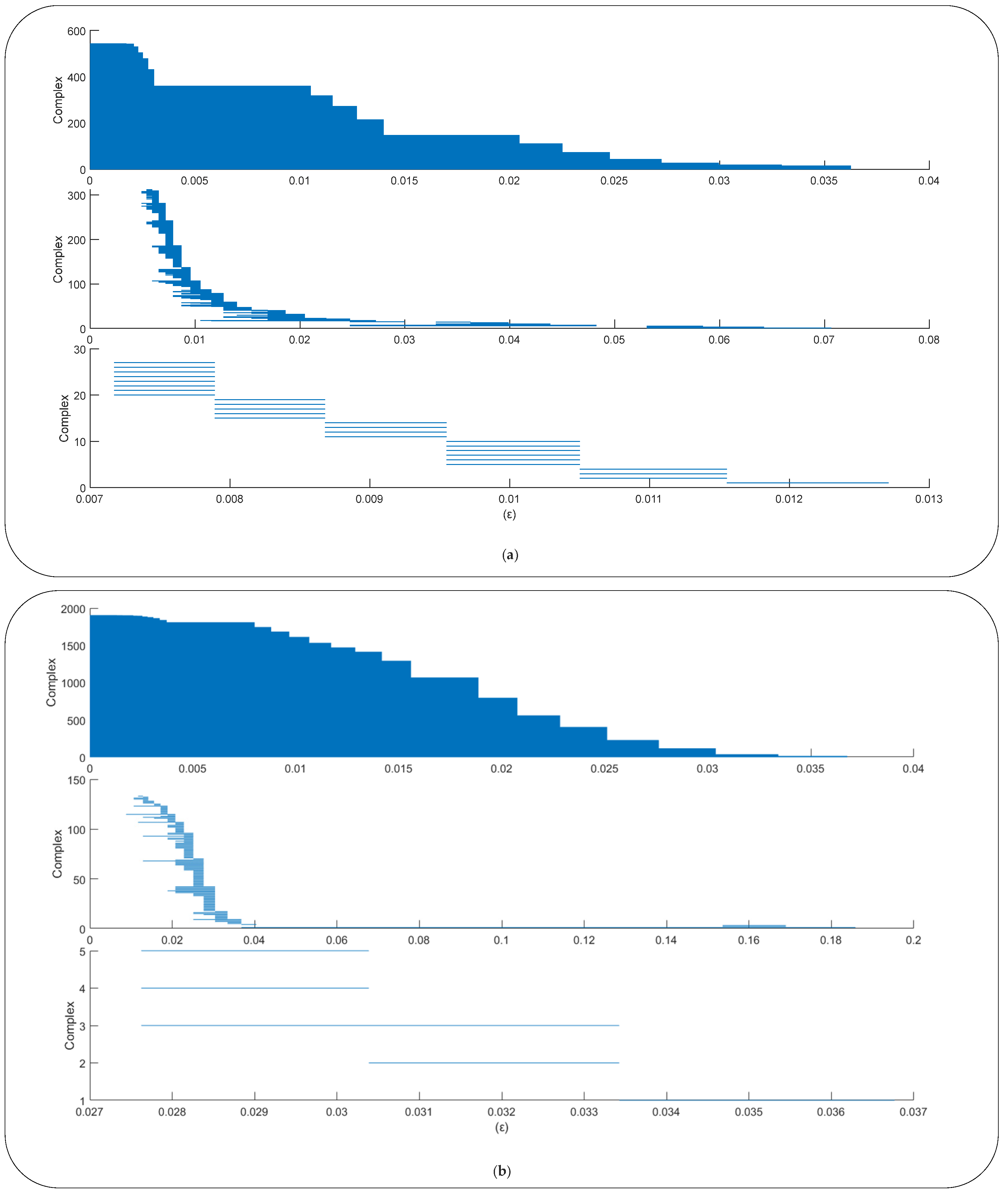
2.2.2. Topological Data Analysis
- Obtain the barcode from the point cloud;
- Calculate the PH duration length (PHDL) of each complex during the filtration process, which is defined as the difference between the radius when the complex disappears and the radius when the complex appears:where b is the Betti number, is the radius during the filtration process, and there are complexes in the barcodes; and,
- Finally, the three statistical features of PHDL in the barcodes with Betti number b are calculated as follows:
2.3. Other Features Extraction
2.3.1. Box-Counting Features
2.3.2. HRV Features
2.4. VF Prediction
3. Results
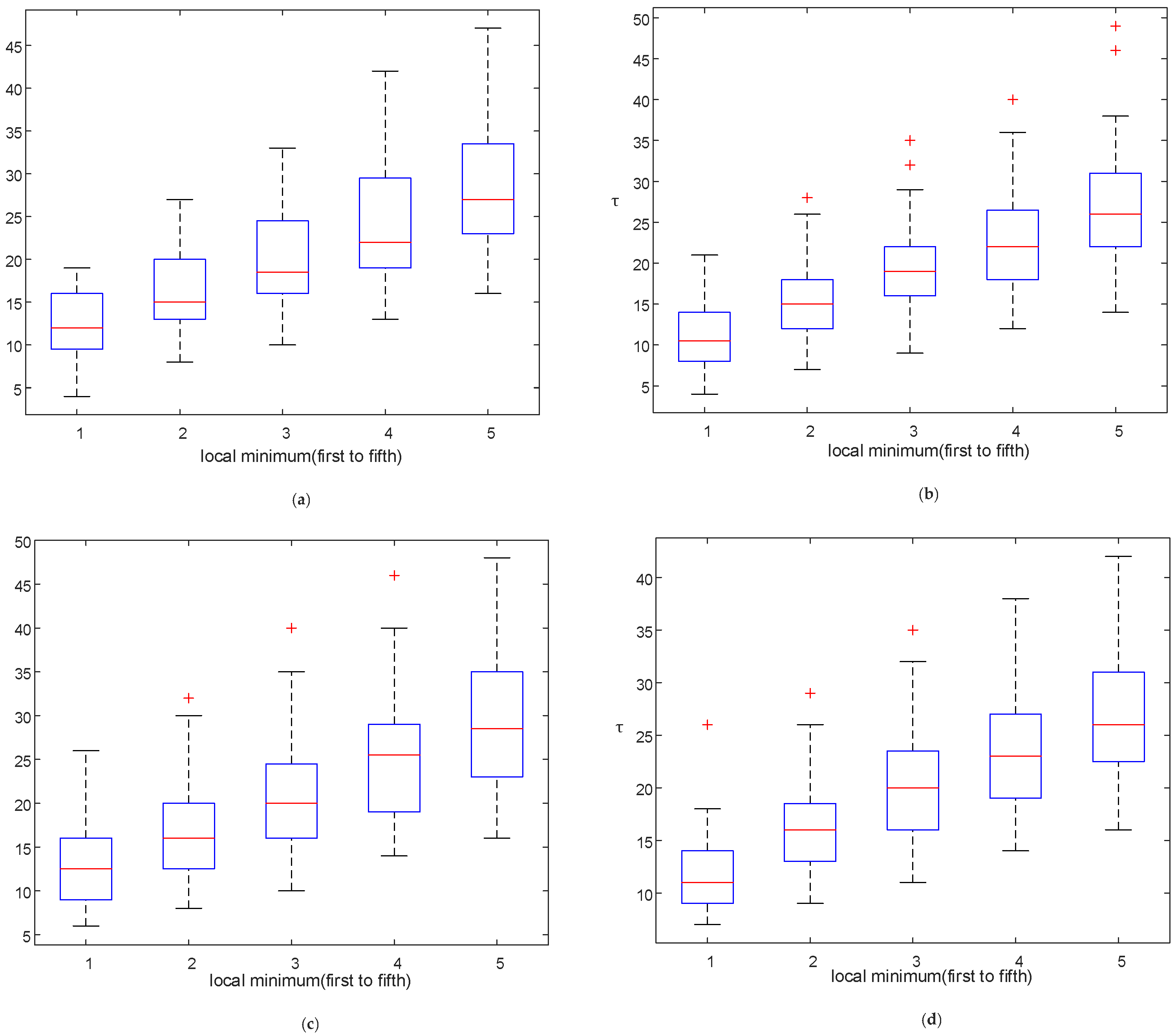
3.1. Reconstruction Parameter Determination
3.2. Split Frame Length Selection
3.3. Prediction Performance Comparison
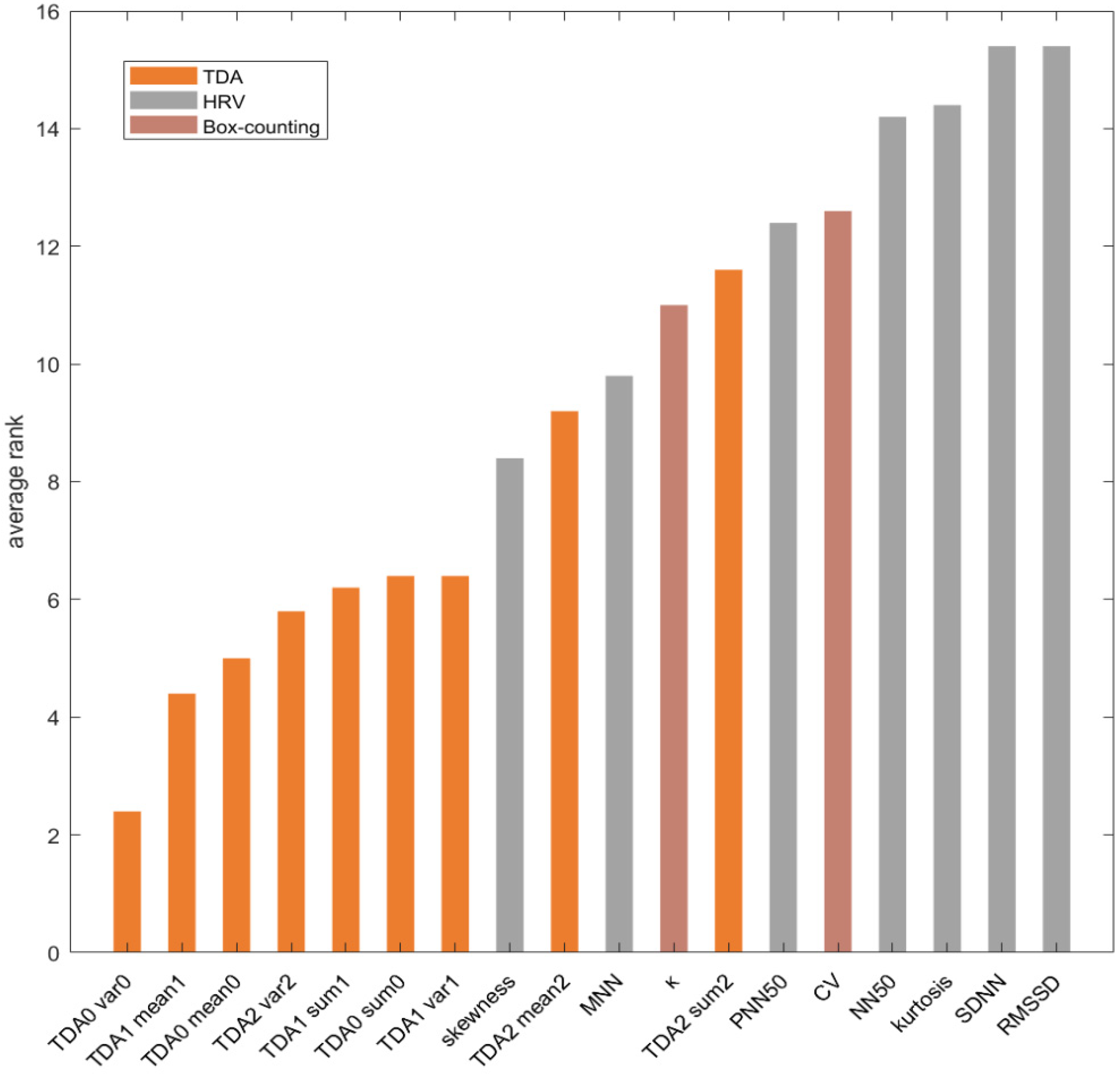
3.4. Features Ranking
4. Discussion
4.1. Effect of Reconstruction Parameters and Split Frame Length
4.2. Evaluation of TDA Features
4.3. Comparison with Previous Prediction Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zipes, D.P.; Wellen, H. Sudden Cardiac Death. Circulation 1998, 98, 2334–2351. [Google Scholar] [CrossRef] [PubMed]
- Bezzina, C.R.; Priori, S.G. Genetics of sudden cardiac death. Circ. Res. 2015, 116, 1919–1936. [Google Scholar] [CrossRef] [PubMed]
- Tseng, L.M.; Tseng, V.S. Predicting Ventricular Fibrillation Through Deep Learning. IEEE Access 2020, 8, 221886–221896. [Google Scholar] [CrossRef]
- Mandala, S.; Senar, M.S. ECG-based prediction algorithm for imminent malignant ventricular arrhythmias using decision tree. PLoS ONE 2020, 15, e0231635. [Google Scholar]
- Eeab, C.; Af, D. An optimal strategy for prediction of sudden cardiac death through a pioneering feature-selection approach from HRV signal. Comput. Methods Programs Biomed. 2019, 169, 19–36. [Google Scholar]
- Taye, G.T.; Shim, E.B. Machine learning approach to predict ventricular fibrillation based on QRS complex shape. Front. Physiol. 2019, 10, 1193. [Google Scholar] [CrossRef] [PubMed]
- Joo, S.; Choi, K.J. Prediction of spontaneous ventricular tachyarrhythmia by an artificial neural network using parameters gleaned from short-term heart rate variability. Expert Syst. Appl. 2012, 39, 3862–3866. [Google Scholar] [CrossRef]
- Mohammad, K.; Khadijeh, R. Early detection of sudden cardiac death using nonlinear analysis of heart rate variability. Biocybern. Biomed. Eng. 2018, 38, 931–940. [Google Scholar]
- Heng, W.W.; Ming, E.S.L. Investigating Phase Space Reconstruction of ECG for Prediction of Malignant Ventricular Arrhythmia. Int. J. Integr. Eng. 2020, 12, 187–196. [Google Scholar]
- Mandal, S.; Mondal, P. Detection of Ventricular Arrhythmia by using Heart rate variability signal and ECG beat image. Biomed. Signal Process. Control 2021, 68, 102692. [Google Scholar] [CrossRef]
- Sessa, F.; Anna, V. Heart Rate Variability as predictive factor for Sudden Cardiac Death. Aging 2018, 10, 166–177. [Google Scholar] [CrossRef]
- Jeong, D.U.; Taye, G.T. Optimal length of heart rate variability data and forecasting time for ventricular fibrillation prediction using machine learning. Comput. Math. Methods Med. 2021, 2021, 6663996. [Google Scholar] [CrossRef]
- Bassareo, P.P.; Mercuro, G. QRS complex enlargement as a predictor of ventricular arrhythmias in patients affected by surgically treated tetralogy of Fallot: A comprehensive literature review and historical overview. Int. Sch. Res. Not. 2013, 2013, 782508. [Google Scholar] [CrossRef]
- Riasi, A.; Mohebbi, M. Prediction of ventricular tachycardia using morphological features of ECG signal. In Proceedings of the International Symposium on Artificial Intelligence & Signal Processing, Mashhad, Iran, 3–5 March 2015. [Google Scholar]
- Fojt, O.; Holcik, J. Applying nonlinear dynamics to ECG signal processing. IEEE Eng. Med. Biol. Mag. 1998, 17, 96–101. [Google Scholar] [CrossRef]
- Small, M. Applied Nonlinear Time Series Analysis: Applications in Physics, Physiology and Finance; World Scientific: Singapore, 2005. [Google Scholar]
- Amann, A.; Tratnig, R. Detecting Ventricular Fibrillation by Time-Delay Methods. IEEE Trans. Biomed. Eng. 2007, 54, 174–177. [Google Scholar] [CrossRef]
- Cappiello, G.; Das, S. A Statistical Index for Early Diagnosis of Ventricular Arrhythmia from the Trend Analysis of ECG Phase-portraits. Physiol. Meas. 2014, 36, 107. [Google Scholar] [CrossRef][Green Version]
- Koulaouzidis, G.; Das, S. Prompt and accurate diagnosis of ventricular arrhythmias with a novel index based on phase space reconstruction of ECG. Int. J. Cardiol. 2015, 182, 38–43. [Google Scholar] [CrossRef]
- Roopaei, M.; Boostani, R. Chaotic based reconstructed phase space features for detecting ventricular fibrillation. Biomed. Signal Process. Control 2010, 5, 318–327. [Google Scholar] [CrossRef]
- Nolle, F.M.; Badura, F.K.; Catlett, J.M.; Bowser, R.W.; Sketch, M.H. CREI-GARD, a new concept in computerized arrhythmia monitoring systems. Comput. Cardiol. 1986, 13, 515–518. [Google Scholar]
- Greenwald, S.D. Development and Analysis of a Ventricular Fibrillation Detector. Master’s Thesis, MIT Dept of Electrical Engineering and Computer Science, Cambridge, MA, USA, 1986. [Google Scholar]
- Bousseljot, R.; Kreiseler, D. Use of the ECG signal database CARDIODAT of PTB via the Internet. Biomed. Tech. 1995, 40, 317–318. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick, 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Packard, N.H.; Crutchfield, J.P. Geometry from a Time Series. Phys. Rev. Lett. 2008, 45, 712. [Google Scholar] [CrossRef]
- Abarbanel, H.D.; Brown, R. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J. Reconstruction expansion as a geometry-based framework for choosing proper delay times. Phys. D Nonlinear Phenom. 1994, 73, 82–98. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Bukkuri, A.; Andor, N. Applications of Topological Data Analysis in Oncology. Front. Artif. Intell. 2021, 4, 38. [Google Scholar] [CrossRef]
- Safarbali, B.; Golpayegani, S.M.R.H. Nonlinear dynamic approaches to identify atrial fibrillation progression based on topological methods. Biomed. Signal Process. Control 2019, 53, 101563. [Google Scholar] [CrossRef]
- Dey, T.K.; Shi, D. SimBa: An Efficient Tool for Approximating Rips-Filtration Persistence via Simplicial Batch-Collapse. J. Exp. Algorithm. (JEA) 2019, 24, 1–16. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C. Feature selection method based on chi-square test and minimum redundancy. In Proceedings of the International Conference on Intelligent and Interactive Systems and Applications, Shanghai, China, 25–27 September 2020. [Google Scholar]
- Ding, C. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef] [PubMed]
- Darbellay, G. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 1315–1321. [Google Scholar] [CrossRef]
- Leo, B.; Jerome, H.F.; Richard, A. Classification and Regression Trees, 1st ed.; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Loh, W.Y. Regression Trees with Unbiased Variable Selection and Interaction Detection. Stat. Sin. 2002, 12, 361–386. [Google Scholar]
- Loh, W.Y. Split Selection Methods for Classification Trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Kononenko, I.; Šimec, E. Overcoming the myopia of inductive learning algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. An adaptation of Relief for attribute estimation in regression. In Proceedings of the Fourteenth International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]



| Database | Data | Sampling Rate |
|---|---|---|
| CUDB | ‘cu10′; ‘cu11′;‘cu13′;‘cu24′;‘cu17′;‘cu22′;‘cu23′; ‘cu05′;‘cu15′;‘cu19′;‘cu32′;‘cu33′;‘cu03′;‘cu14′;‘cu18 | 250 Hz |
| SDDB | 31;32;33;34;35;36;37;38;44;45;46;47;48;50;51 | 250 Hz |
| PTBDB | ‘s0552_re’;‘s0551_re’;‘s0543_re’;‘s0534_re’;‘s0533_re’;‘s0532_re’;‘s0531_re’;‘s0527_re’;‘s0526_re’;‘s0506_re’;‘s0504_re’;‘s0503_re’;’s0502_re’;’s0500_re’;’s0499_re’;’s0496_re’;’s0491_re’;‘s0487_re’;‘s0486_re’;‘s0481_re’;‘s0480_re’;‘s0479_re’;‘s0478_re’;‘s0474_re’;‘s0473_re’;‘s0472_re’;‘s0471_re’;‘s0470_re’;‘s0469_re’;‘s0468_re’ | 1000 Hz |
| Features | TDA 0 | TDA 1 | TDA 2 |
|---|---|---|---|
| Sum | sum 0 | sum 1 | sum 2 |
| Variance | var 0 | var 1 | var 2 |
| Mean | mean 0 | mean 1 | mean 2 |
| Features | Equation |
|---|---|
| The number of RRI sequences where the difference between adjacent terms is greater than 50 ms | |
| The ratio of the number of adjacent terms in RRI sequence whose difference is greater than 50 ms to the sequence length | |
| 5 s Split Frame | 8 s Split Frame | 10 s Split Frame | 15 s Split Frame | |
|---|---|---|---|---|
| 11 | 90.0% RF | 86.7% RF | 88.3% DT | 83.3% DT |
| 12 | 91.7% RF | 93.3% RF | 88.3% RF | 83.3% RF |
| ML Classifiers | Box-Counting Features | HRV Features | TDA Features | Fusion Features |
|---|---|---|---|---|
| Decision Trees | 70.0% | 61.7% | 86.7% | 91.7% |
| Logistic Regression | 65.0% | 56.7% | 53.3% | 55.0% |
| SVM | 71.7% | 71.7% | 55.0% | 55.0% |
| KNN | 63.3% | 66.7% | 55.0% | 53.3% |
| Radom Forest | 61.7% | 65.0% | 91.7% | 95.0% |
| Features | MI | Chi−Square | MRMR | Out-of-Bag | ReliefF |
|---|---|---|---|---|---|
| −0.06973 | 8.52156 | 0.14073 | 0.35355 | 0.22132 | |
| −0.05626 | 9.05480 | 0.16236 | 0.38521 | 0.26416 | |
| −0.26306 | 1.10083 | 0.05174 | 0.06355 | −0.04202 | |
| −0.02478 | 12.90666 | 0.36806 | 0.70518 | 0.58501 | |
| −0.08660 | 4.96328 | 0.13049 | 0.29902 | 0.20516 | |
| −0.05625 | 10.68233 | 0.26268 | 0.48215 | 0.26509 | |
| −0.03002 | 11.78756 | 0.29908 | 0.62190 | 0.40754 | |
| −0.12454 | 1.84986 | 0.12685 | 0.17107 | 0.12099 | |
| −0.13324 | 1.77568 | 0.10477 | 0.14286 | 0.08333 | |
| −0.39715 | 0.18215 | 0.00018 | −0.14286 | −0.14500 | |
| −0.83429 | 0.06164 | 3.49049 × 10−15 | −0.14286 | −0.15243 | |
| −0.31335 | 0.76527 | 0.00076 | −0.10643 | −0.12677 | |
| −0.27056 | 1.06271 | 0.04106 | 0.00000 | −0.07877 | |
| −0.31891 | 0.39783 | 0.00071 | −0.14286 | −0.13620 | |
| −0.09189 | 2.35361 | 0.13049 | 0.24026 | 0.13275 | |
| −0.27523 | 1.03846 | 0.02133 | −0.03349 | −0.09768 | |
| −0.13934 | 1.15556 | 0.05641 | 0.09654 | 0.07217 |
| Reference Index | Forecast Time | Database | Split Frame Length | ECG Features | Prediction Performance |
|---|---|---|---|---|---|
| [4] | 15 min | NSRDB 9 VFDB 9 | 60 s | 12 morphological features | Sensitivity 95% Specificity 90% |
| [5] | 13 min | SDDB 23 NSRDB 18 | 60 s | 23 HRV features | Accuracy 84.28% |
| [6] | 30 s | CUDB 27 PAFDB 22 NSRDB 6 | 120 s | 4 QRS features | Accuracy 98.6% |
| [7] | 10 s | MVTDB 78 | 5 min | 11 HRV features | Accuracy 92.2% |
| [8] | 5 min | SDDB 20 NSRDB 18 | 60 s | 13 HRV features | Accuracy 95% |
| [9] | 4 min 31 s | CUDB 32 PTBDB 32 | 10 heart beats | 2 box-counting features | Accuracy 98.44% |
| [12] | 0 s | CUDB 29 MVTDB 30 +29 PAFDB 12 NSRDB 18 | 20 s | 5 HRV features | Accuracy 88.64% |
| Our work | 5 min | CUDB 15 SDDB 15 PTBDB 30 | 5 s,8 s,10 s,15 s | 2 box-counting features 9 TDA features 7 HRV features | Accuracy 95% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, T.; Zhu, Z.; Zhang, Y.; Jiang, F. Early Ventricular Fibrillation Prediction Based on Topological Data Analysis of ECG Signal. Appl. Sci. 2022, 12, 10370. https://doi.org/10.3390/app122010370
Ling T, Zhu Z, Zhang Y, Jiang F. Early Ventricular Fibrillation Prediction Based on Topological Data Analysis of ECG Signal. Applied Sciences. 2022; 12(20):10370. https://doi.org/10.3390/app122010370
Chicago/Turabian StyleLing, Tianyi, Ziyu Zhu, Yanbing Zhang, and Fangfang Jiang. 2022. "Early Ventricular Fibrillation Prediction Based on Topological Data Analysis of ECG Signal" Applied Sciences 12, no. 20: 10370. https://doi.org/10.3390/app122010370
APA StyleLing, T., Zhu, Z., Zhang, Y., & Jiang, F. (2022). Early Ventricular Fibrillation Prediction Based on Topological Data Analysis of ECG Signal. Applied Sciences, 12(20), 10370. https://doi.org/10.3390/app122010370






