Hybrid Coded Excitation of the Torsional Guided Wave Mode T(0,1) for Oil and Gas Pipeline Inspection
Abstract
:1. Introduction
- The developed hybrid coded excitation technique is applied to the guided wave mode excitation for pipe inspection for the first time.
- The proposed method has been theoretically evaluated that has better performance than other common techniques.
- The experimental results that the proposed method has the best echo SNR and PSL at various frequencies (30 kHz–50 kHz).
- This work can be extended to other potential applications for a significant SNR improvement.
2. Methodology
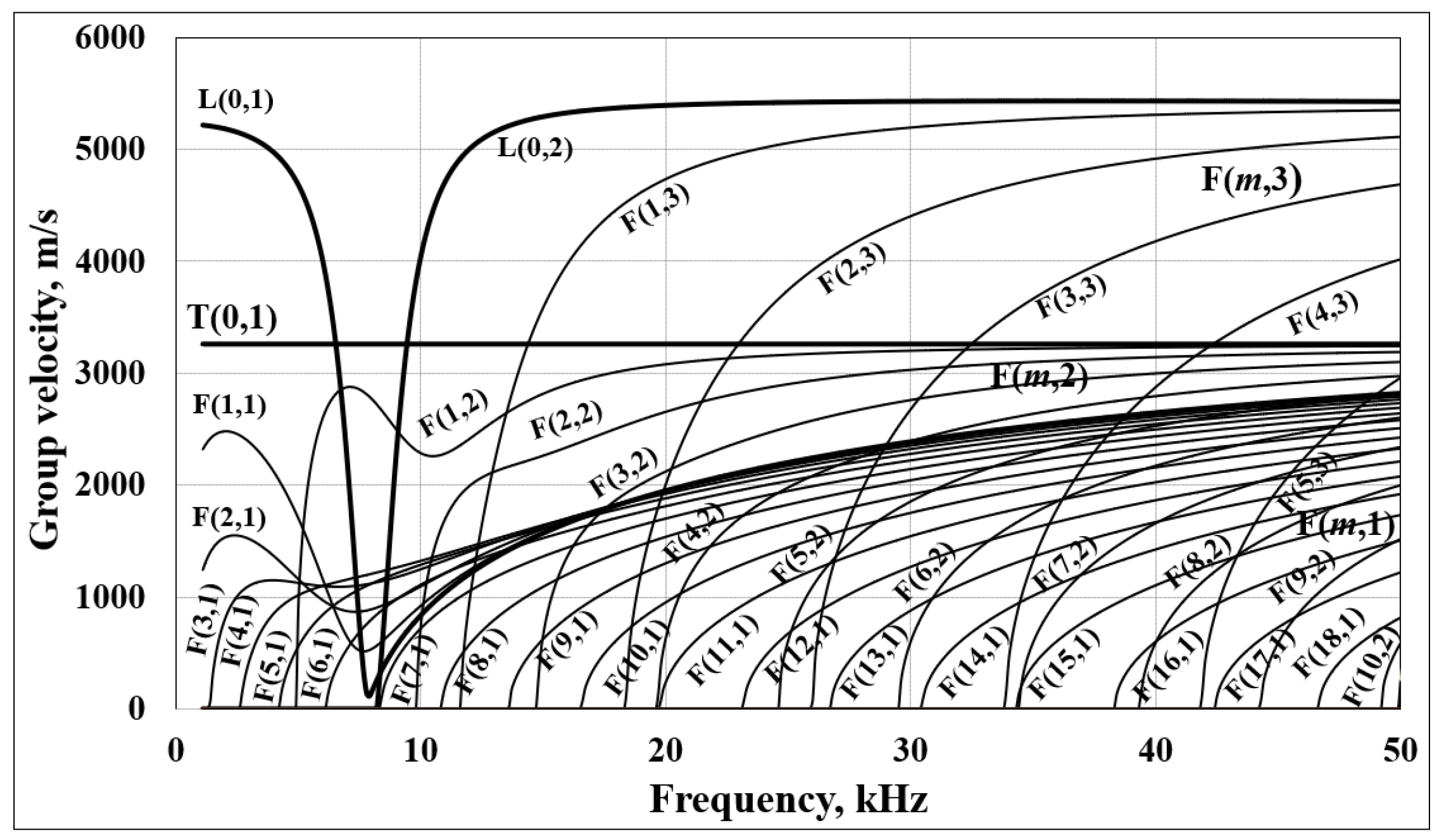
2.1. Dispersion Curves
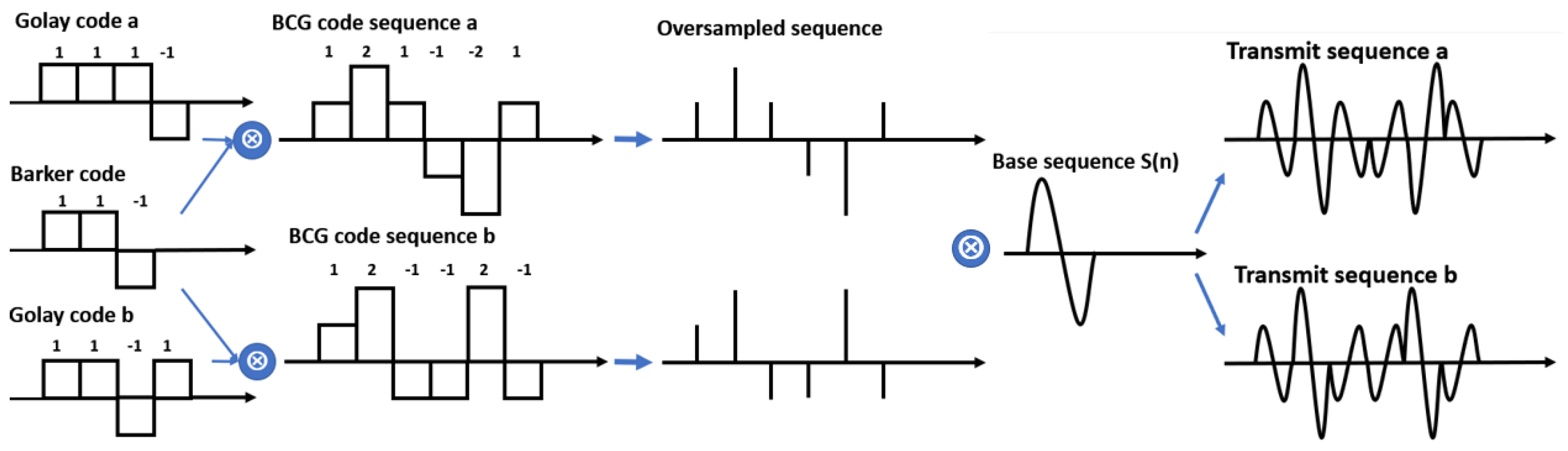
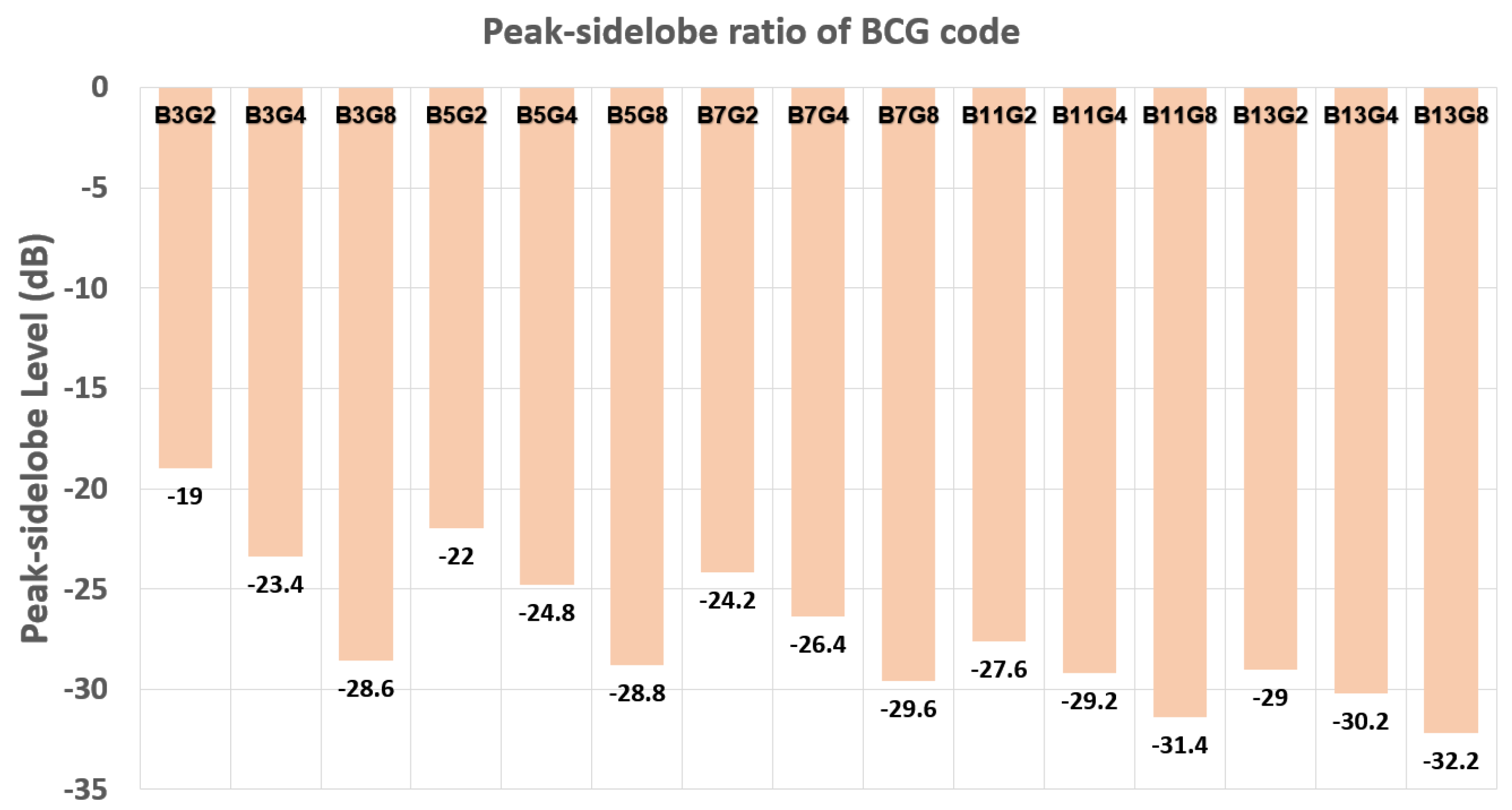
2.2. Code Generation and Compression
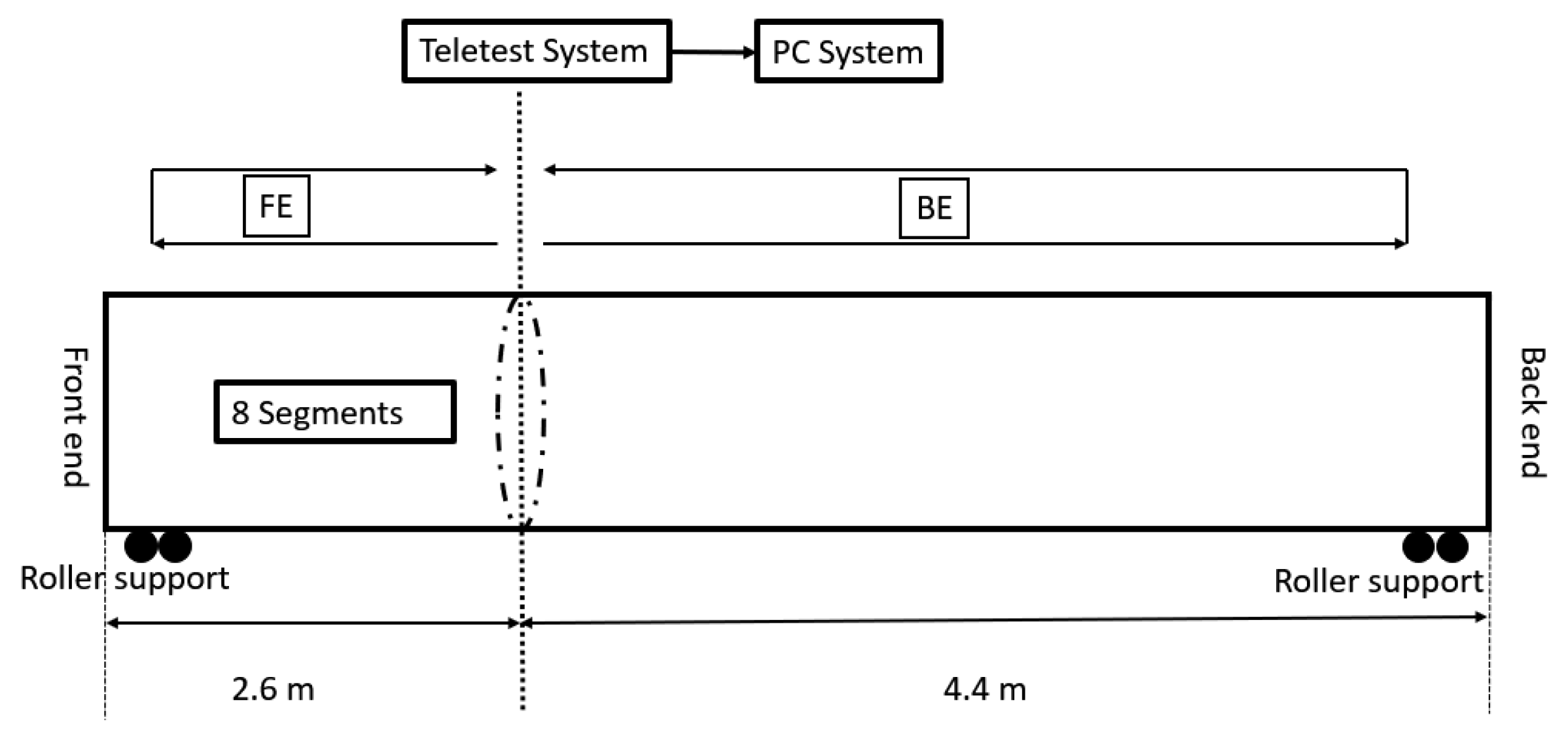
3. Laboratory Testing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lowe, M.J.; Alleyne, D.N.; Cawley, P. Defect detection in pipes using guided waves. Ultrasonics 1998, 36, 147–154. [Google Scholar] [CrossRef]
- Mahal, H.N.; Mudge, P.; Nandi, A.K. Comparison of coded excitations in the presence of variable transducer transfer functions in ultrasonic guided wave testing of pipelines. In Proceedings of the 9th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018; pp. 10–13. [Google Scholar]
- Cawley, P.; Lowe, M.; Alleyne, D.; Pavlakovic, B.; Wilcox, P. Practical long range guided wave inspection-applications to pipes and rail. Mater. Eval 2003, 61, 66–74. [Google Scholar]
- Song, X.; Ta, D.; Wang, W. A base-sequence-modulated Golay code improves the excitation and measurement of ultrasonic guided waves in long bones. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2580–2583. [Google Scholar]
- Fan, Z.; Rudlin, J.; Asfis, G.; Meng, H. Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing. Technologies 2019, 7, 72. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Karney, B. An overview of transient fault detection techniques. In Modeling and Monitoring of Pipelines and Networks; Springer: Cham, Switzerland, 2017; pp. 13–37. [Google Scholar]
- Meniconi, S.; Capponi, C.; Frisinghelli, M.; Brunone, B. Leak Detection in a Real Transmission Main Through Transient Tests: Deeds and Misdeeds. Water Resour. Res. 2021, 57, e2020WR027838. [Google Scholar] [CrossRef]
- Brunone, B.; Capponi, C.; Meniconi, S. Design criteria and performance analysis of a smart portable device for leak detection in water transmission mains. Measurement 2021, 183, 109844. [Google Scholar] [CrossRef]
- Joy, J.; Peter, S.; John, N. Denoising using soft thresholding. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 1027–1032. [Google Scholar]
- Gan, T.; Hutchins, D.; Billson, D.; Schindel, D. The use of broadband acoustic transducers and pulse-compression techniques for air-coupled ultrasonic imaging. Ultrasonics 2001, 39, 181–194. [Google Scholar] [CrossRef]
- Takeuchi, Y. An investigation of a spread energy method for medical ultrasound systems: Part one: Theory and investigation. Ultrasonics 1979, 17, 175–182. [Google Scholar] [CrossRef]
- O’Donnell, M. Coded excitation system for improving the penetration of real-time phased-array imaging systems. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 341–351. [Google Scholar] [CrossRef]
- Jedwab, J.; Parker, M.G. A construction of binary Golay sequence pairs from odd-length Barker sequences. J. Comb. Des. 2009, 17, 478–491. [Google Scholar] [CrossRef]
- Kim, P.; Jung, E.; Bae, S.; Kim, K.; Song, T.K. Barker-sequence-modulated golay coded excitation technique for ultrasound imaging. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Wang, M.; Cong, S.; Zhang, S. Pseudo Chirp-Barker-Golay coded excitation in ultrasound imaging. In Proceedings of the 2018 IEEE Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4035–4039. [Google Scholar]
- Hedayatrasa, S.; Poelman, G.; Segers, J.; Van Paepegem, W.; Kersemans, M. Novel discrete frequency-phase modulated excitation waveform for enhanced depth resolvability of thermal wave radar. Mech. Syst. Signal Process. 2019, 132, 512–522. [Google Scholar] [CrossRef]
- De Marchi, L.; Marzani, A.; Moll, J.; Kudela, P.; Radzieński, M.; Ostachowicz, W. A pulse coding and decoding strategy to perform Lamb wave inspections using simultaneously multiple actuators. Mech. Syst. Signal Process. 2017, 91, 111–121. [Google Scholar] [CrossRef]
- MUDEG, P. Field application of the Teletest; Long-range ultrasonic testing technique. Insight 2001, 43, 74–77. [Google Scholar]
- Lowe, M.; Cawley, P. Long Range Guided Wave Inspection Usage–Current Commercial Capabilities and Research Directions; Department of Mechanical Engineering, Imperial College London: London, UK, 2006. [Google Scholar]
- Silk, M.; Bainton, K. The propagation in metal tubing of ultrasonic wave modes equivalent to Lamb waves. Ultrasonics 1979, 17, 11–19. [Google Scholar] [CrossRef]
- Guan, R.; Lu, Y.; Duan, W.; Wang, X. Guided waves for damage identification in pipeline structures: A review. Struct. Control Health Monit. 2017, 24, e2007. [Google Scholar] [CrossRef]
- Wilcox, P.D. A rapid signal processing technique to remove the effect of dispersion from guided wave signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 419–427. [Google Scholar] [CrossRef]
- Niu, X.; Duan, W.; Chen, H.P.; Marques, H. Excitation and propagation of torsional T (0, 1) mode for guided wave testing of pipeline integrity. Measurement 2019, 131, 341–348. [Google Scholar] [CrossRef]
- Duan, W.; Kirby, R. A numerical model for the scattering of elastic waves from a non-axisymmetric defect in a pipe. Finite Elem. Anal. Des. 2015, 100, 28–40. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Hao, X. Coded excitation for diagnostic ultrasound: A system developer’s perspective. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 160–170. [Google Scholar] [CrossRef]
- Török, I.; Seller, R. Pulse compression in search radar. Period. Polytech. Electr. Eng. 1998, 42, 391–408. [Google Scholar]
- Ghavamian, A.; Mustapha, F.; Baharudin, B.; Yidris, N. Detection, localisation and assessment of defects in pipes using guided wave techniques: A review. Sensors 2018, 18, 4470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niu, X.; Tee, K.F.; Marques, H.R. Superposition model of mode shapes composed of travelling torsional guided waves excited by multiple circular transducer arrays in pipes. Ultrasonics 2021, 116, 106507. [Google Scholar] [CrossRef] [PubMed]



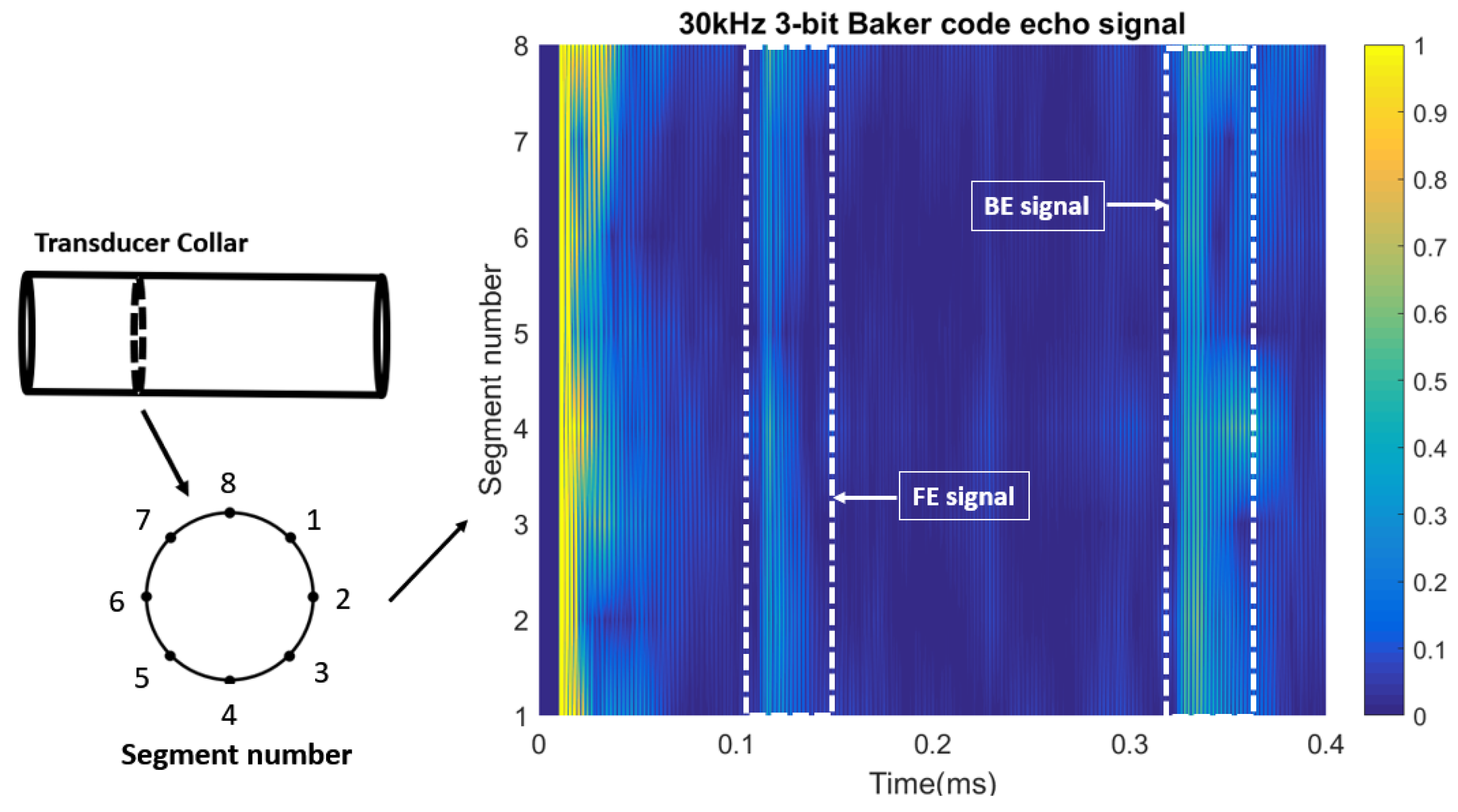
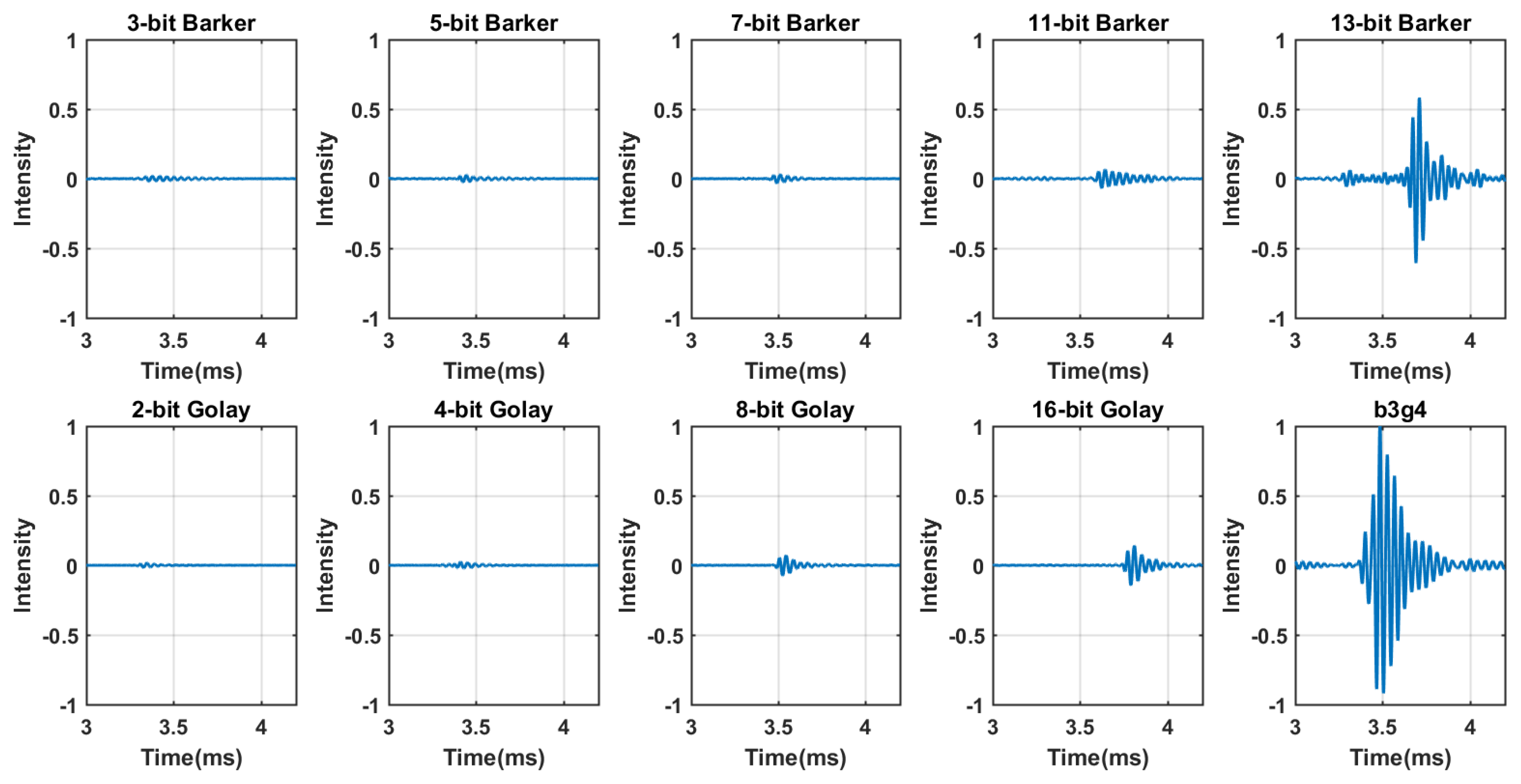
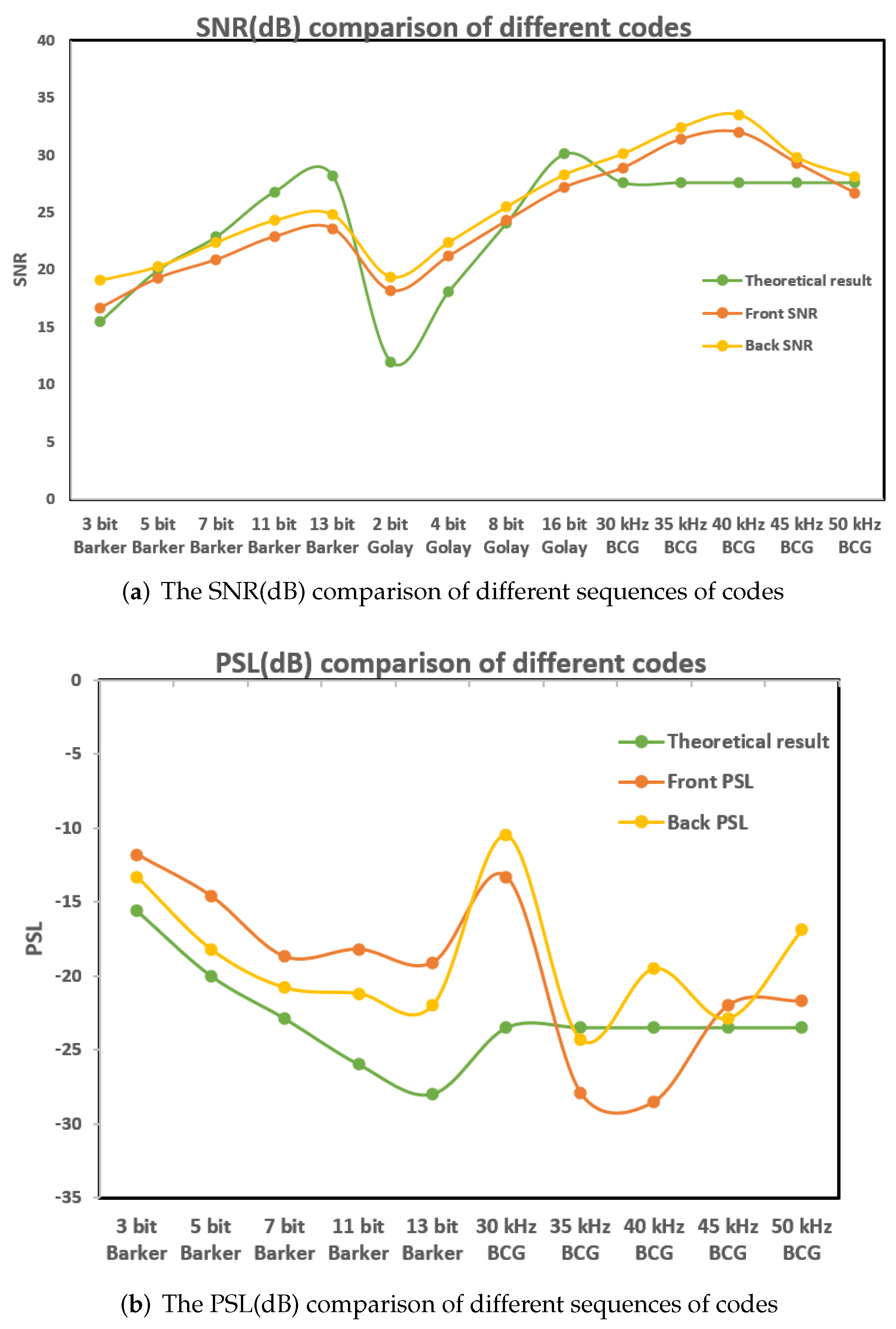
| Excitation Sequence | Characteristics | ||
|---|---|---|---|
| Carrier Frequency (kHz) | Duration (μs) | Binary Code | |
| 1-cycle sine | 30 | 33 | - |
| 3-bit Barker | 30 | 100 | 11-1 |
| 5-bit Barker | 30 | 160 | 111-11 |
| 7-bit Barker | 30 | 230 | 111-1 -11-1 |
| 11-bit Barker | 30 | 360 | 111-1-1-11-1-11-1 |
| 13-bit Barker | 30 | 430 | 11111-1-111-11-11 |
| 2-bit Golay | 30 | 66 | 11 & 1-1 |
| 4-bit Golay | 30 | 132 | 111-1 & 11-11 |
| 8-bit Golay | 30 | 264 | 111-111-11 & 111-1-1-11-1 |
| 16-bit Golay | 30 | 528 | 111-111-11111-1-1-11-1 |
| 111-111-11-1-1-1111-11 | |||
| 6-bit b3g4 | 30 | 198 | 121-1-21 & 12-1-12-1 |
| 6-bit b3g4 | 35 | 171 | 121-1-21 & 12-1-12-1 |
| 6-bit b3g4 | 40 | 150 | 121-1-21 & 12-1-12-1 |
| 6-bit b3g4 | 45 | 133 | 121-1-21 & 12-1-12-1 |
| 6-bit b3g4 | 50 | 120 | 121-1-21 & 12-1-12-1 |
| Code Bit | Front SNR (dB) | Front PSL (dB) | Back SNR (dB) | Back PSL (dB) |
|---|---|---|---|---|
| 3 | 16.7 | −11.8 | 19.1 | −13.3 |
| 5 | 19.3 | −14.6 | 20.3 | −18.2 |
| 7 | 20.9 | −18.7 | 22.4 | −20.8 |
| 11 | 22.9 | −18.2 | 24.3 | −21.2 |
| 13 | 23.6 | −19.1 | 24.8 | −22 |
| Code Bit | Front SNR (dB) | Back SNR (dB) |
|---|---|---|
| 2 | 18.2 | 19.4 |
| 4 | 21.2 | 22.4 |
| 8 | 24.3 | 25.5 |
| 16 | 27.2 | 28.3 |
| Frequency | Front SNR (dB) | Front PSL(dB) | Back SNR (dB) | Back PSL (dB) |
|---|---|---|---|---|
| 30 kHz | 28.9 | −13.3 | 30.1 | −10.5 |
| 35 kHz | 31.4 | −27.9 | 32.4 | −24.3 |
| 40 kHz | 32 | −28.5 | 33.5 | −19.5 |
| 45 kHz | 29.3 | −22 | 29.8 | −22.9 |
| 50 kHz | 26.7 | −21.7 | 28.1 | −16.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Niu, X.; Miao, B.; Meng, H. Hybrid Coded Excitation of the Torsional Guided Wave Mode T(0,1) for Oil and Gas Pipeline Inspection. Appl. Sci. 2022, 12, 777. https://doi.org/10.3390/app12020777
Fan Z, Niu X, Miao B, Meng H. Hybrid Coded Excitation of the Torsional Guided Wave Mode T(0,1) for Oil and Gas Pipeline Inspection. Applied Sciences. 2022; 12(2):777. https://doi.org/10.3390/app12020777
Chicago/Turabian StyleFan, Zeng, Xudong Niu, Baichun Miao, and Hongying Meng. 2022. "Hybrid Coded Excitation of the Torsional Guided Wave Mode T(0,1) for Oil and Gas Pipeline Inspection" Applied Sciences 12, no. 2: 777. https://doi.org/10.3390/app12020777
APA StyleFan, Z., Niu, X., Miao, B., & Meng, H. (2022). Hybrid Coded Excitation of the Torsional Guided Wave Mode T(0,1) for Oil and Gas Pipeline Inspection. Applied Sciences, 12(2), 777. https://doi.org/10.3390/app12020777







