Multi-Robot Formation Control Based on CVT Algorithm and Health Optimization Management
Abstract
:1. Introduction
2. Multi-Robot Formation Control
2.1. Problem Description
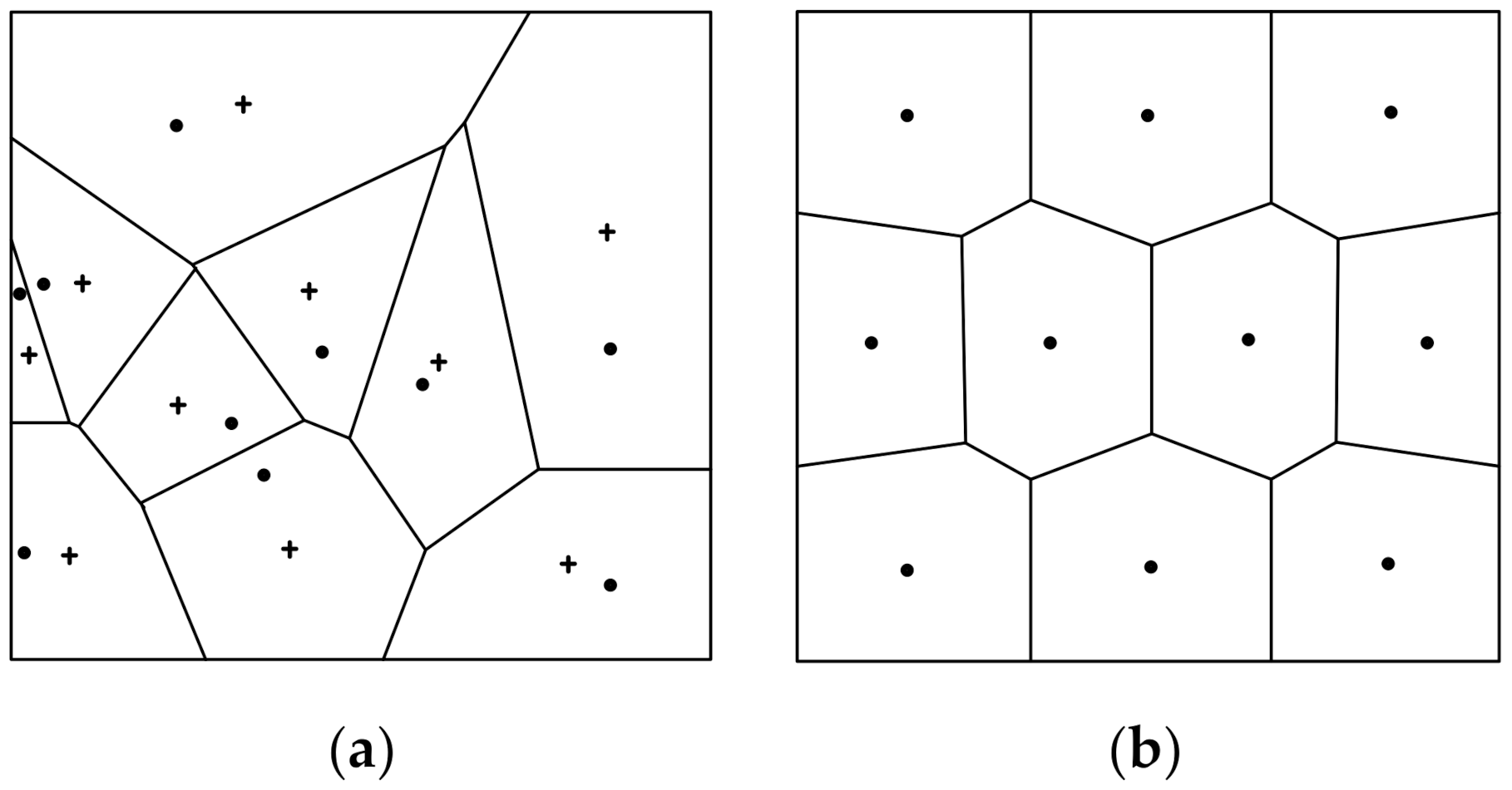
2.2. Cost Function Optimization
- The position change of the generated point is shown in Equation (9):
- 2.
- Simplifying Equation (9) to Equation (10):
- 3.
- Assuming that in Equation (10) tends to 0, we obtain:
- 4.
- Deforming Equation (11) into Equation (12):
- 5.
- If the derivative part is 0, as shown in Equation (13), the solution at this time is the minimum solution.
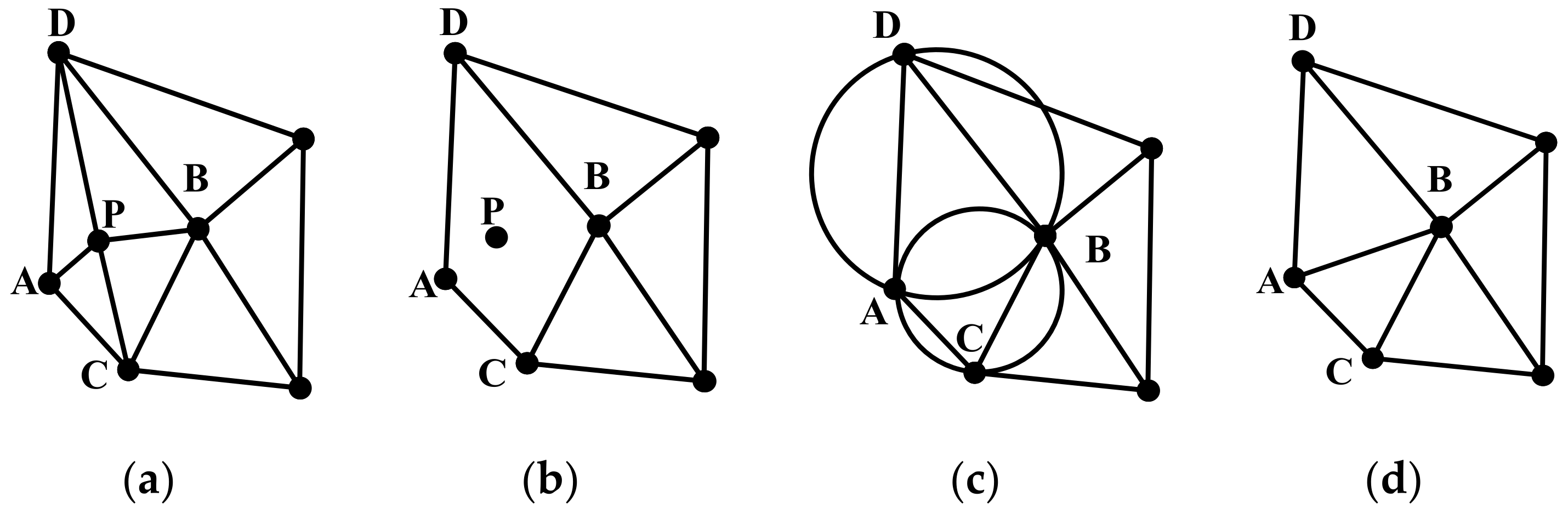
2.3. Formation Control Algorithm
2.4. System Stability Analysis
| Algorithm 1: The multi-robot formation control Algorithm 1 | |
| Require: The robot performs SLAM mapping and positioning; Set the initial area density function . Procedure: | |
| 1: | While |
| 2: | Construct a Delaunay triangulation that contains the initial positions of all robots; |
| Traverse the triangle list; | |
| 3: | if Triangles b,c,d have common sides with the current triangle a then |
| 4: | Connect the outer centers of triangles b,c,d to the outer centers of triangles a; |
| 5: | else |
| 6: | Calculate the outermost midline of the triangle; |
| 7: | end if |
| 8: | Store in Voronoi side list; |
| 9: | Construct Voronoi graph grid of region ; |
| 10: | Drive the robot to reach the corresponding centroid; |
| 11: | End While |
3. Health Optimization Management
Problem Description
| Algorithm 2: CVT-based multi-robot formation control and health optimization management Algorithm 2 | |
| Require: The initial position of a group of robots , , ; Boundary information of task area , area density function ; | |
| Procedure: | |
| 1: | Calculate the centroid of the Voronoi cell and of the robot position ; |
| 2: | While |
| 3: | Calculate and for each robot |
| 4: | if ≤ 0 then |
| 5: | Use the insert construction method to re-form and divide the area |
| 6: | end if |
| 7: | Calculate and for the entire formation |
| 8: | Drive the robot to the center-of-mass position ; |
| 9: | Generate a new set of robot positions ; |
| 10: | Calculate the new centroid and of the robot position set ; |
| 11: | End While |
4. Experiment and Simulation
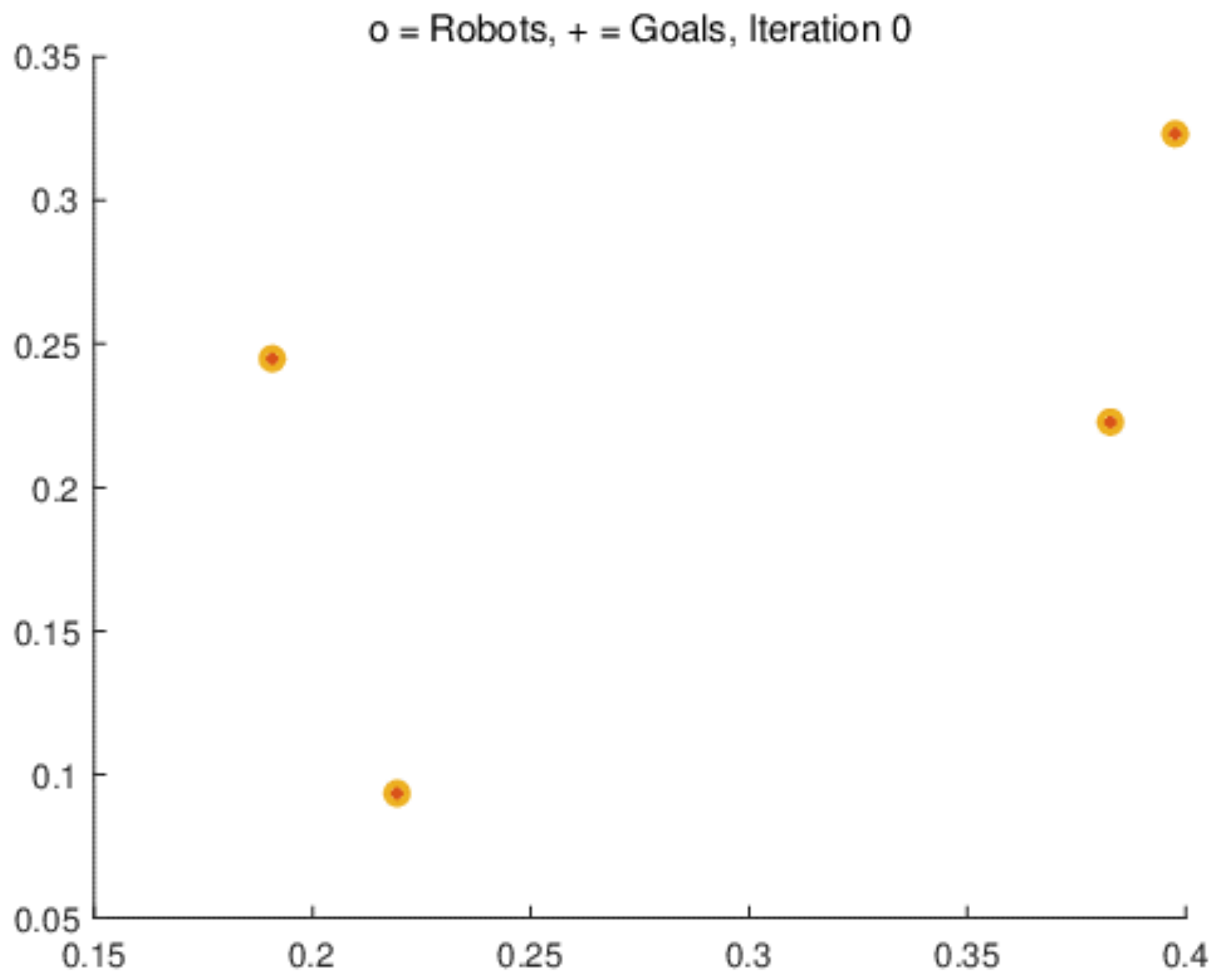
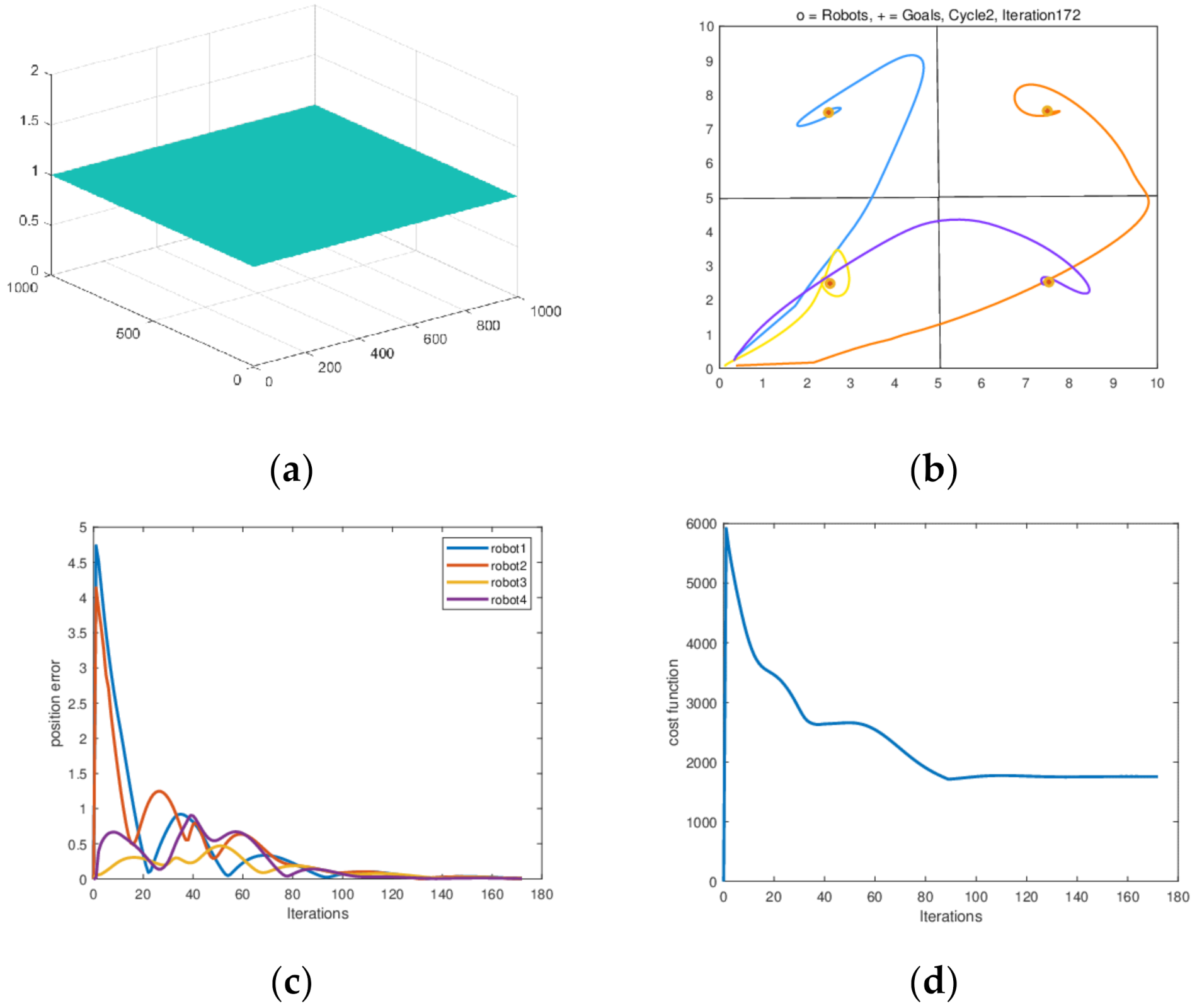
4.1. Multi-Robot Formation Control Simulation Experiment
4.1.1. Square Formation Simulation and Results Analysis
4.1.2. Simulation and Results Analysis for the Diamond Formation
4.1.3. Straight Line Formation Simulation and Results Analysis
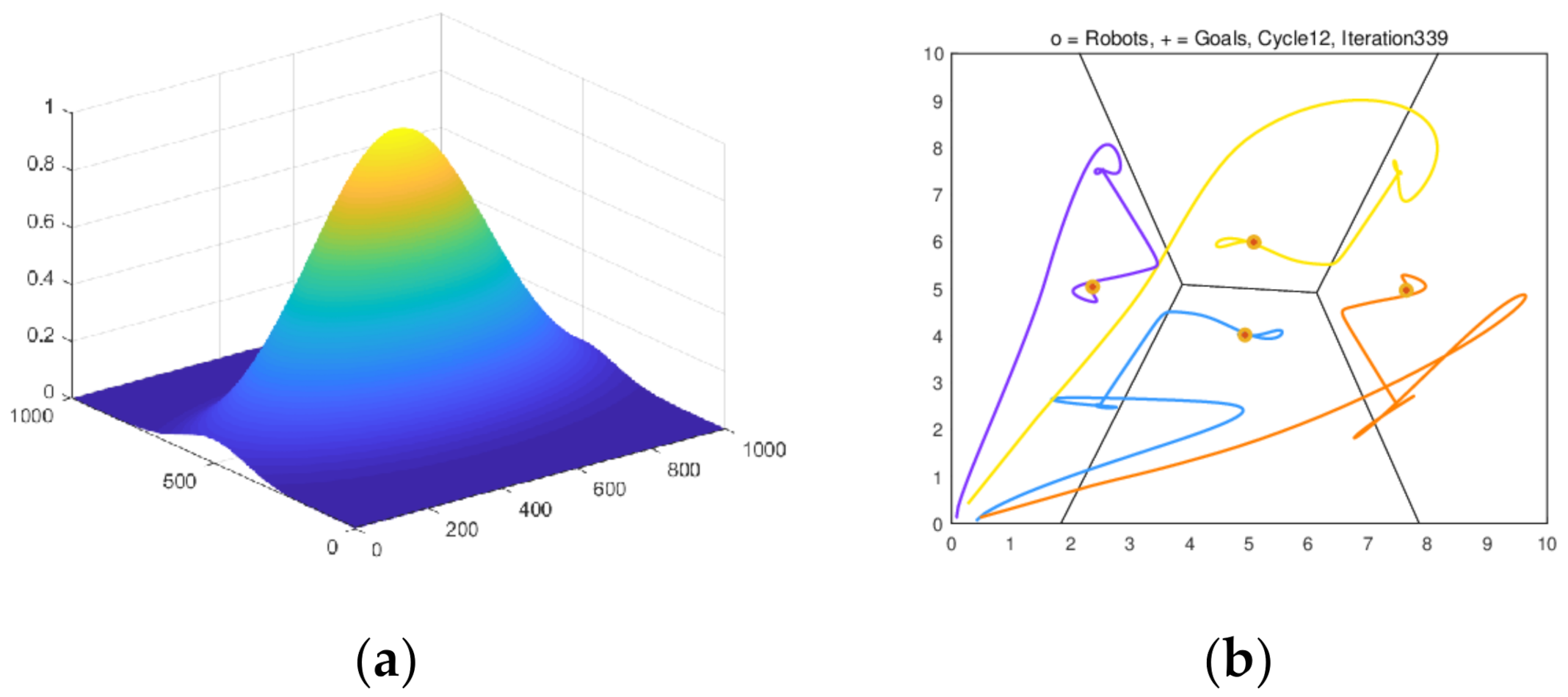
4.1.4. Simulation and Results Analysis of Dynamic Formation in Barrier-Free Scenes
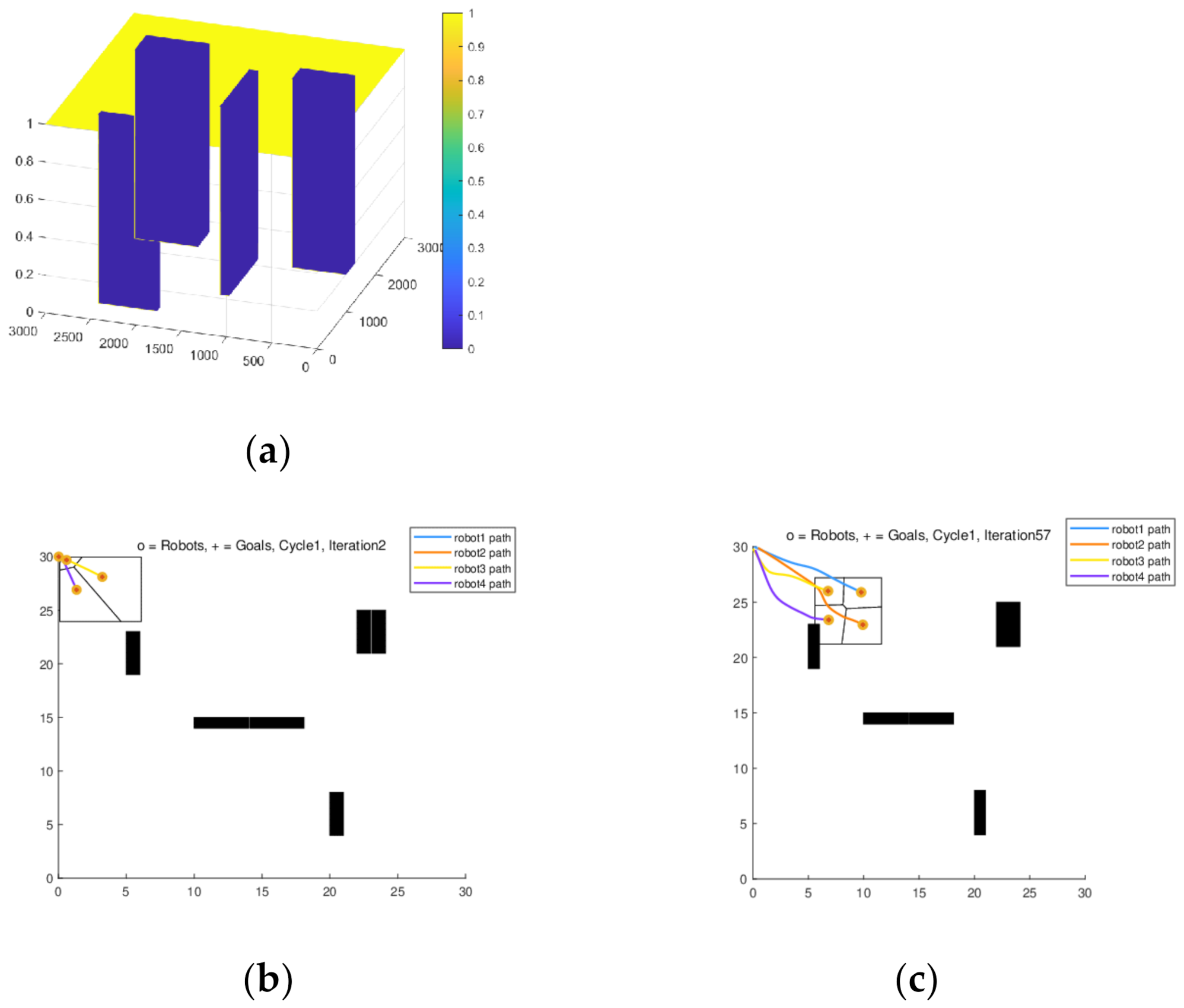
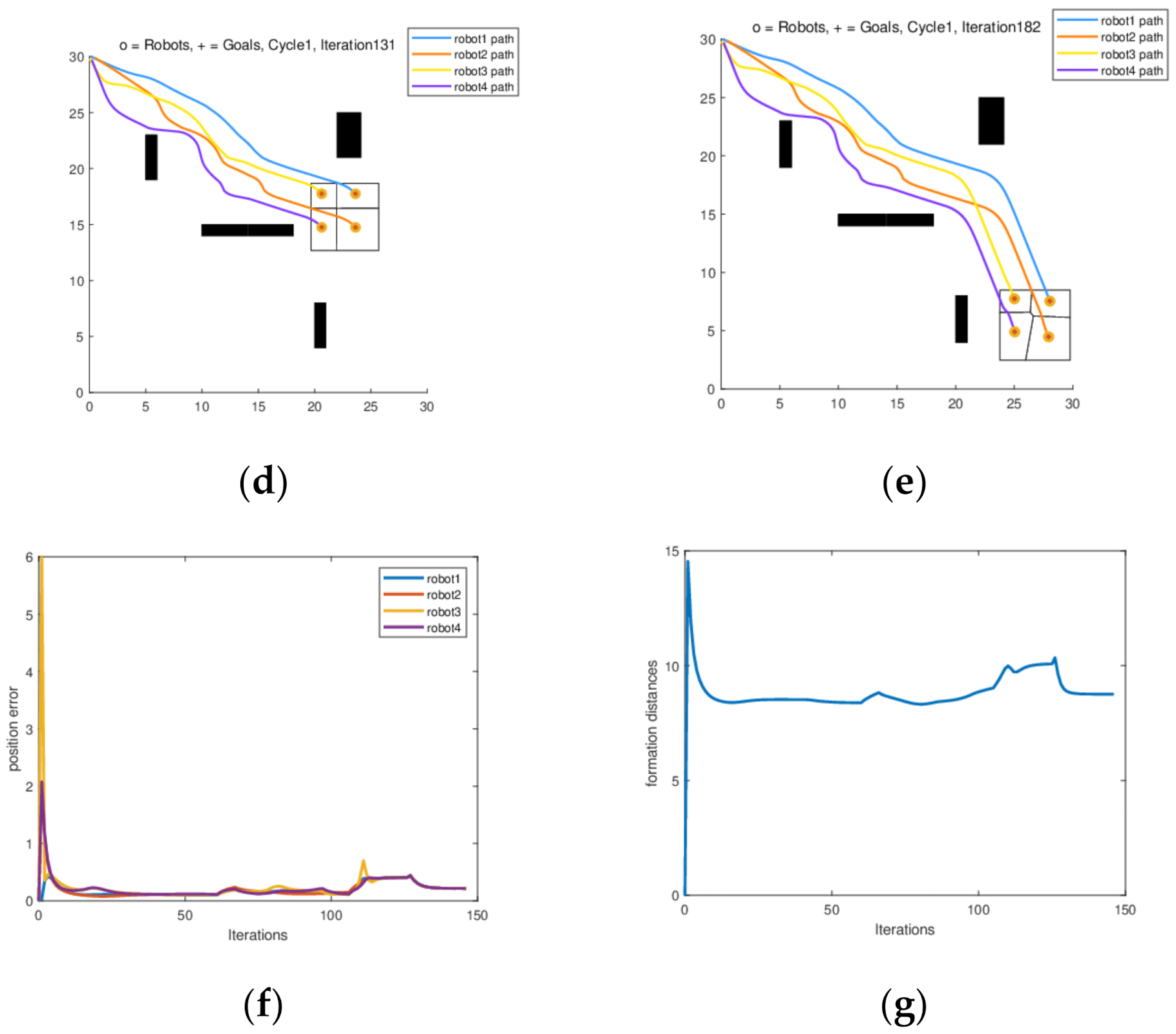
4.1.5. Dynamic Formation Simulation and Results Analysis under Random Obstacle Scenarios
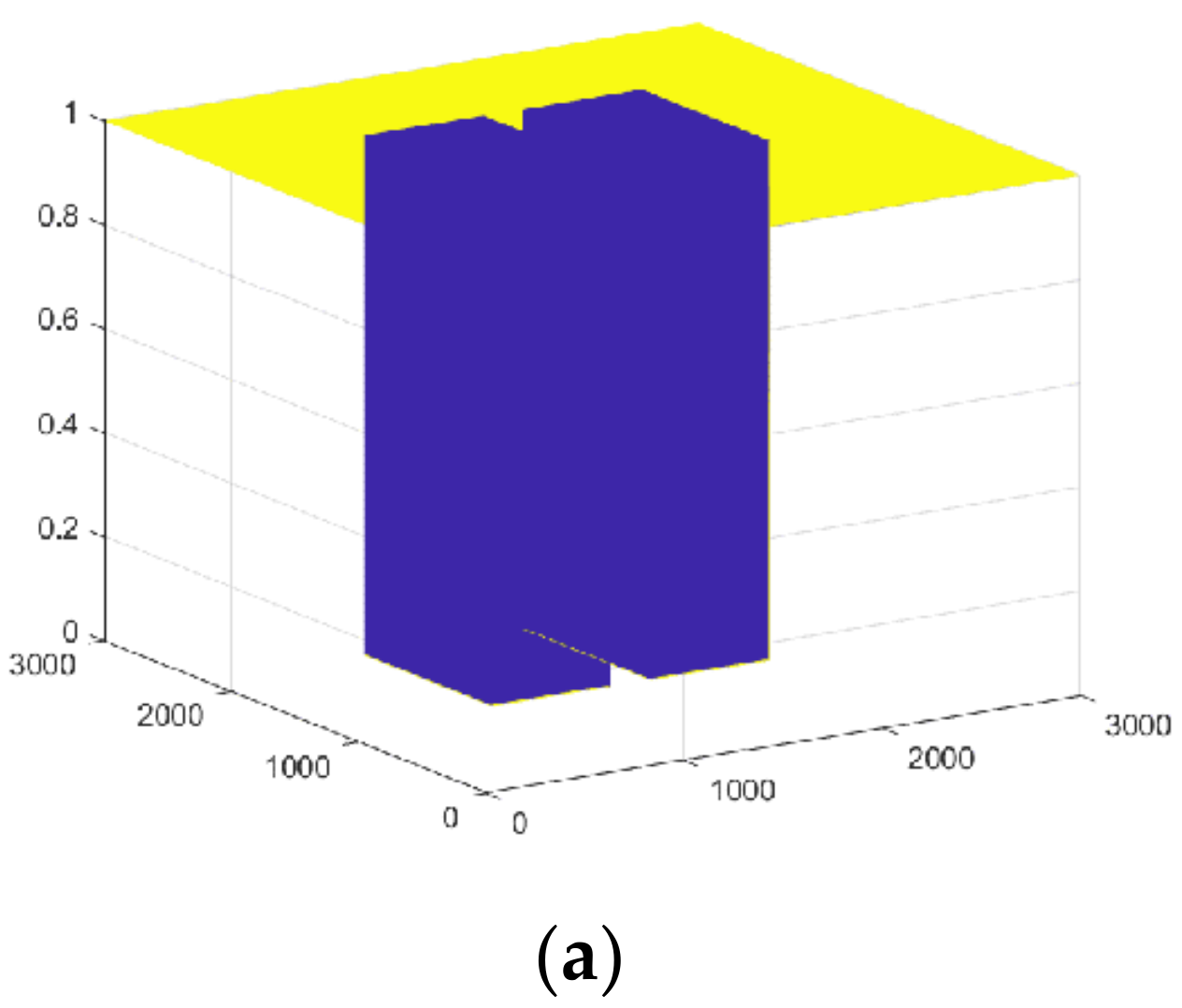
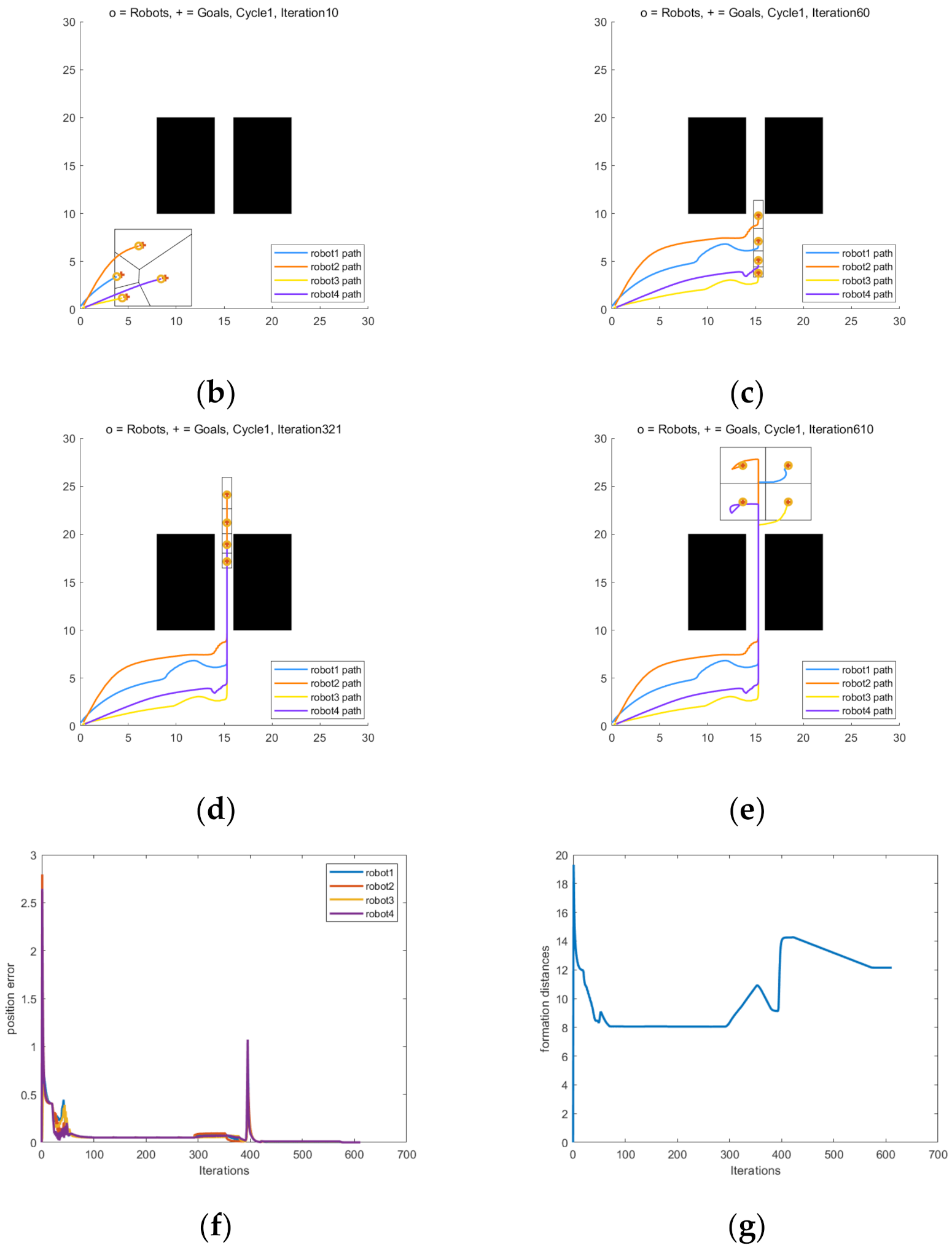
4.1.6. Simulation and Results Analysis of Dynamic Formation in Narrow Passage
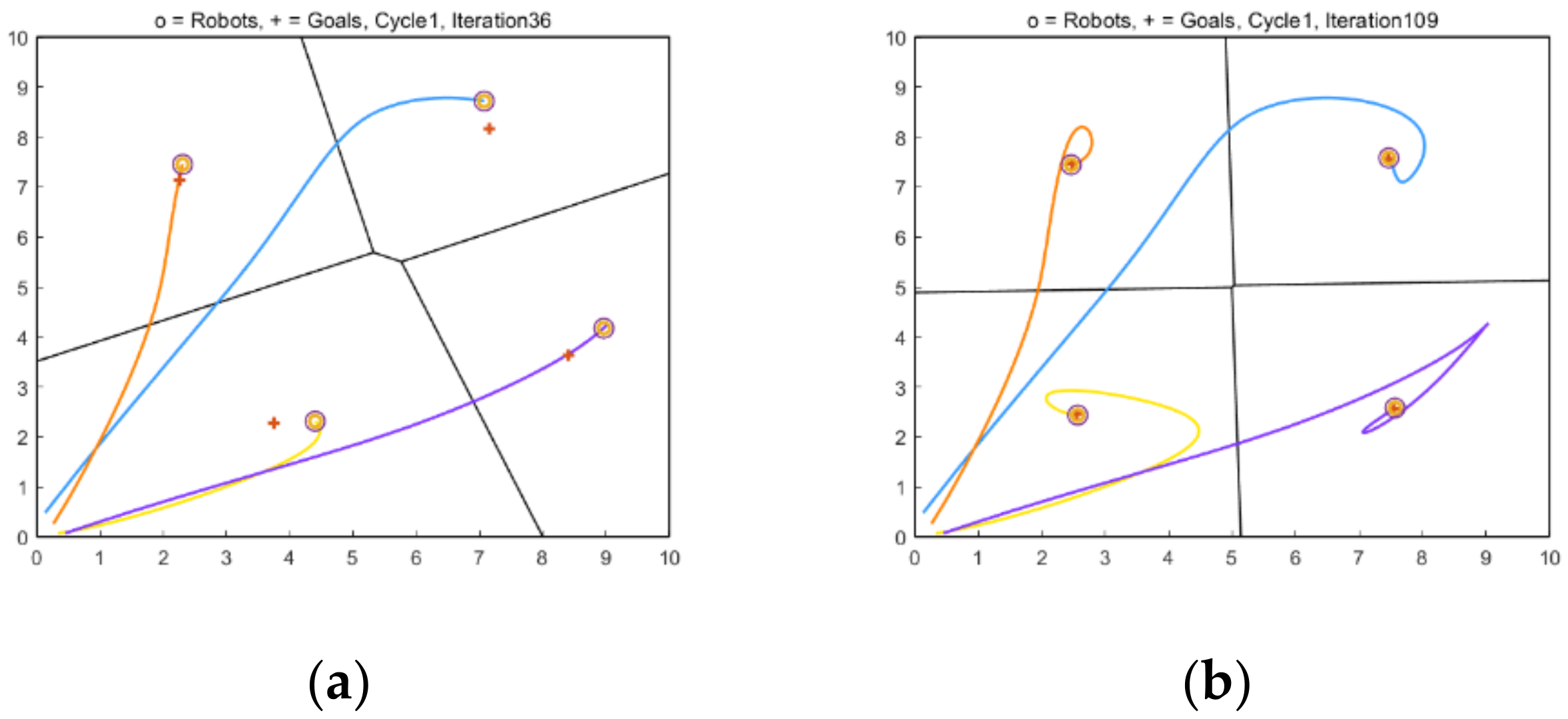
4.2. Simulation of Formation Health Optimization Management
- ①
- None of the robots in the group have any abnormal health behaviors;
- ②
- The health degradation rate of a single robot increases;
- ③
- The health value of a single robot at the beginning of the task is lower than other members of the group;
- ④
- The health of a single robot decreases suddenly.
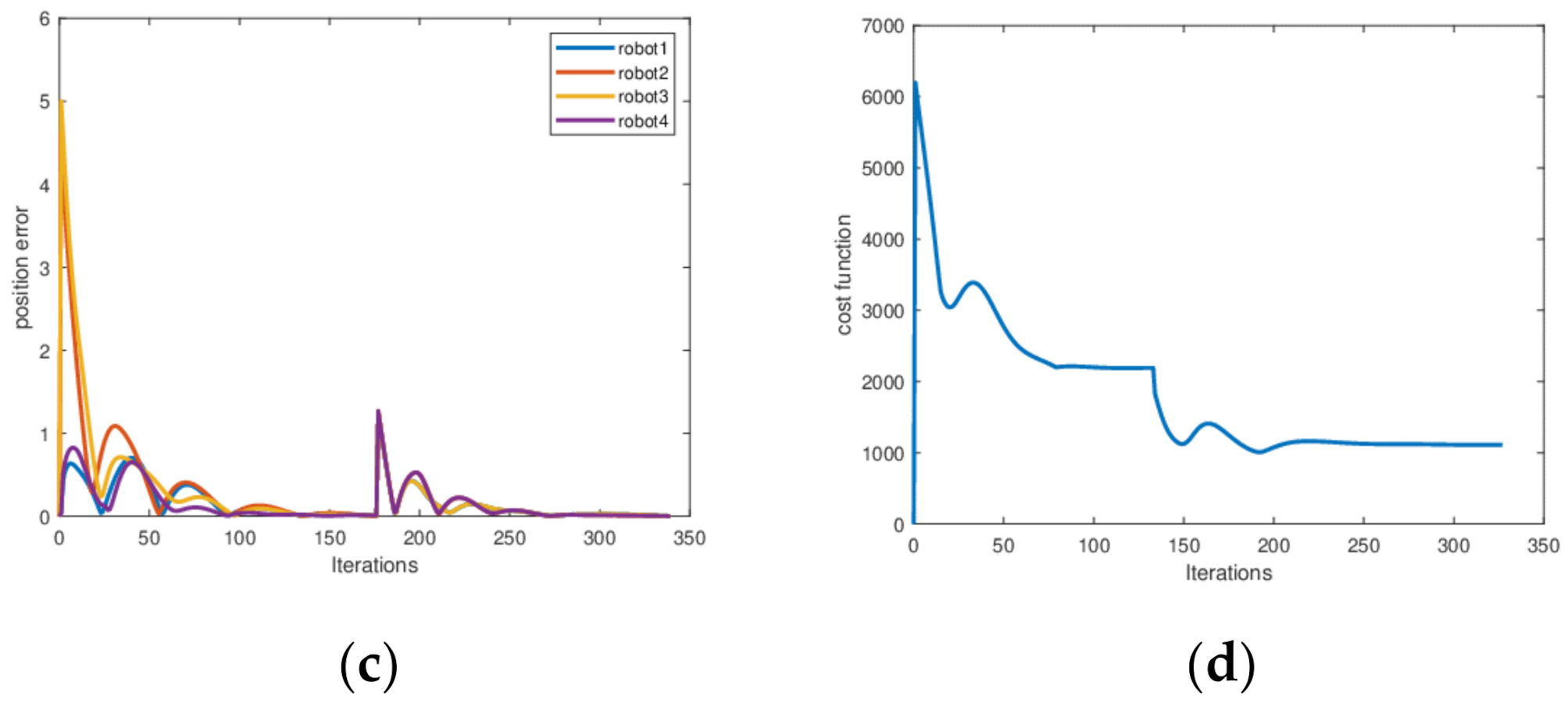
4.2.1. All Robots Are Healthy
4.2.2. The Initial Power of a Single Robot Is Lower than That of Other Robots, Resulting in a Decrease in Battery Life
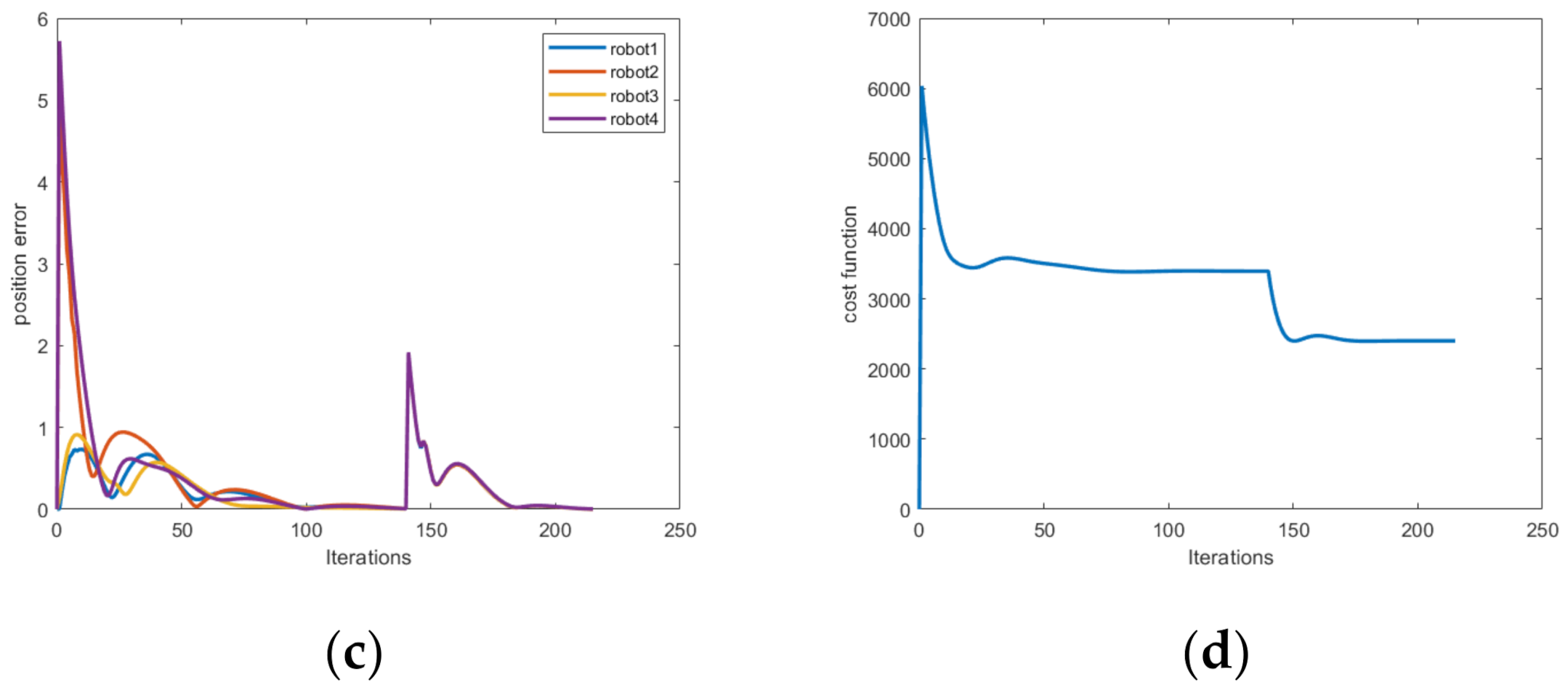
4.2.3. The Failure of a Single Robot Component Caused by the External Environment, Such as a Damaged Wheel That Causes a Sharp Deterioration in the Health of the Robot
4.2.4. Due to the Abnormal Fault of the Motor of a Single Robot, the Power Consumption Rate of the Robot Increases
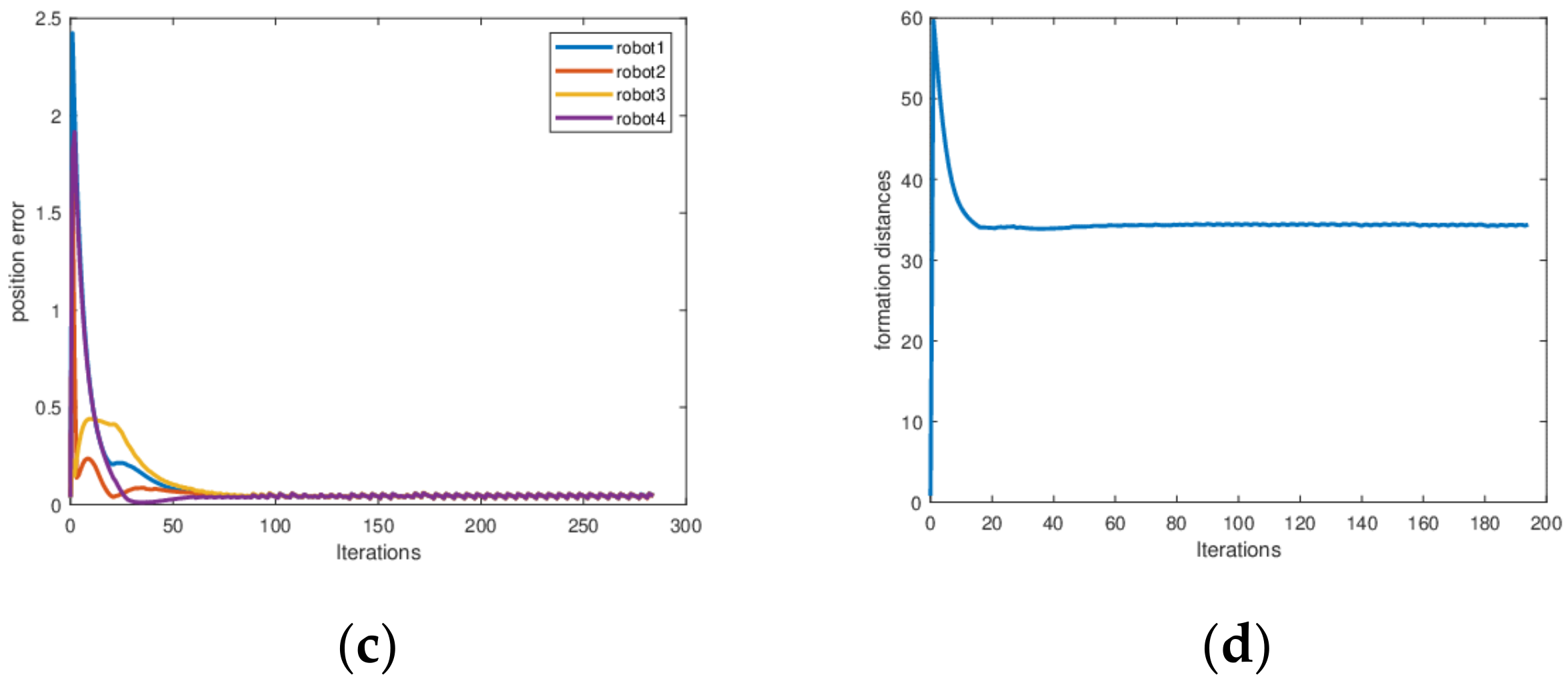
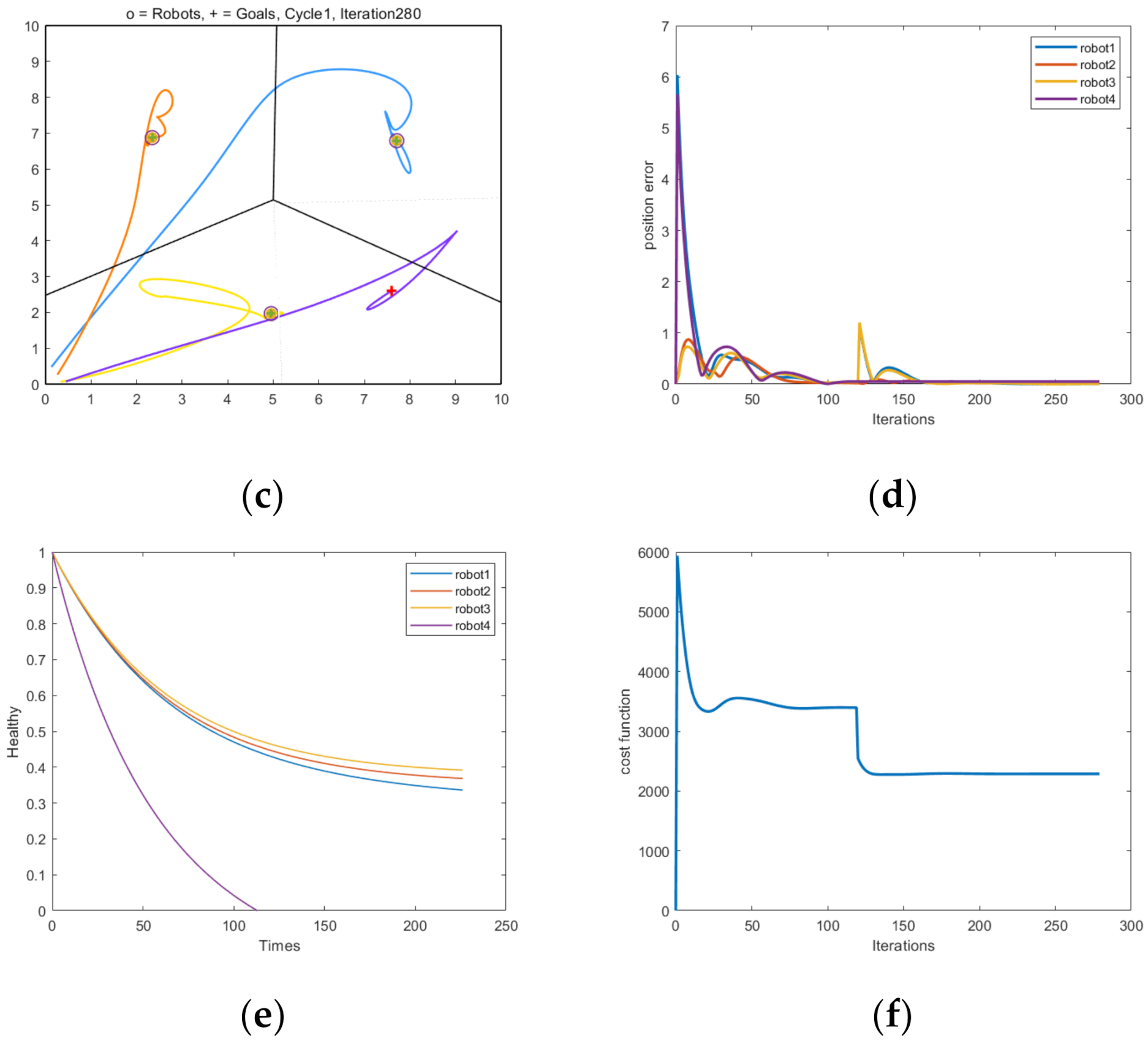
4.2.5. Formation Simulation and Results Analysis after Robot Stops Working
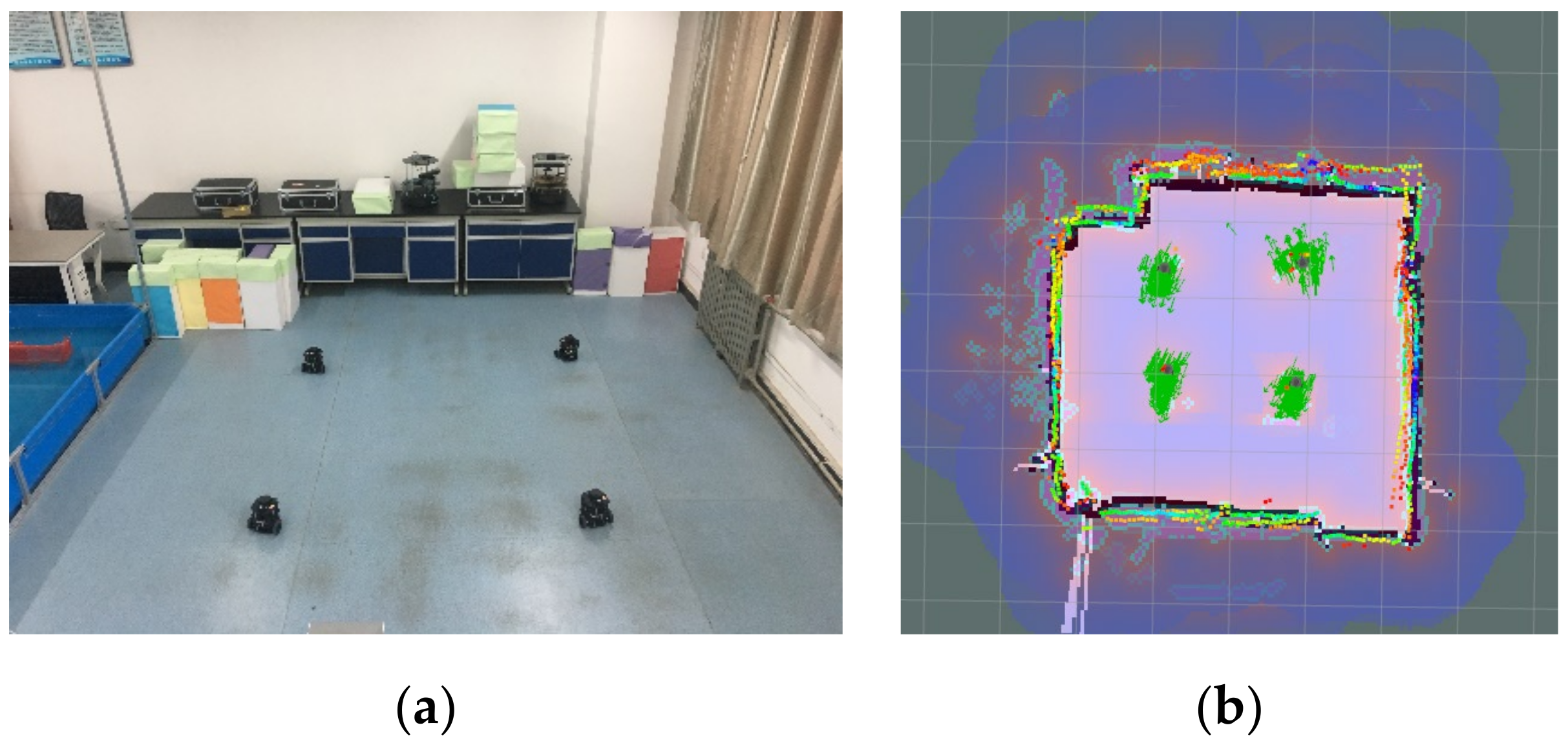
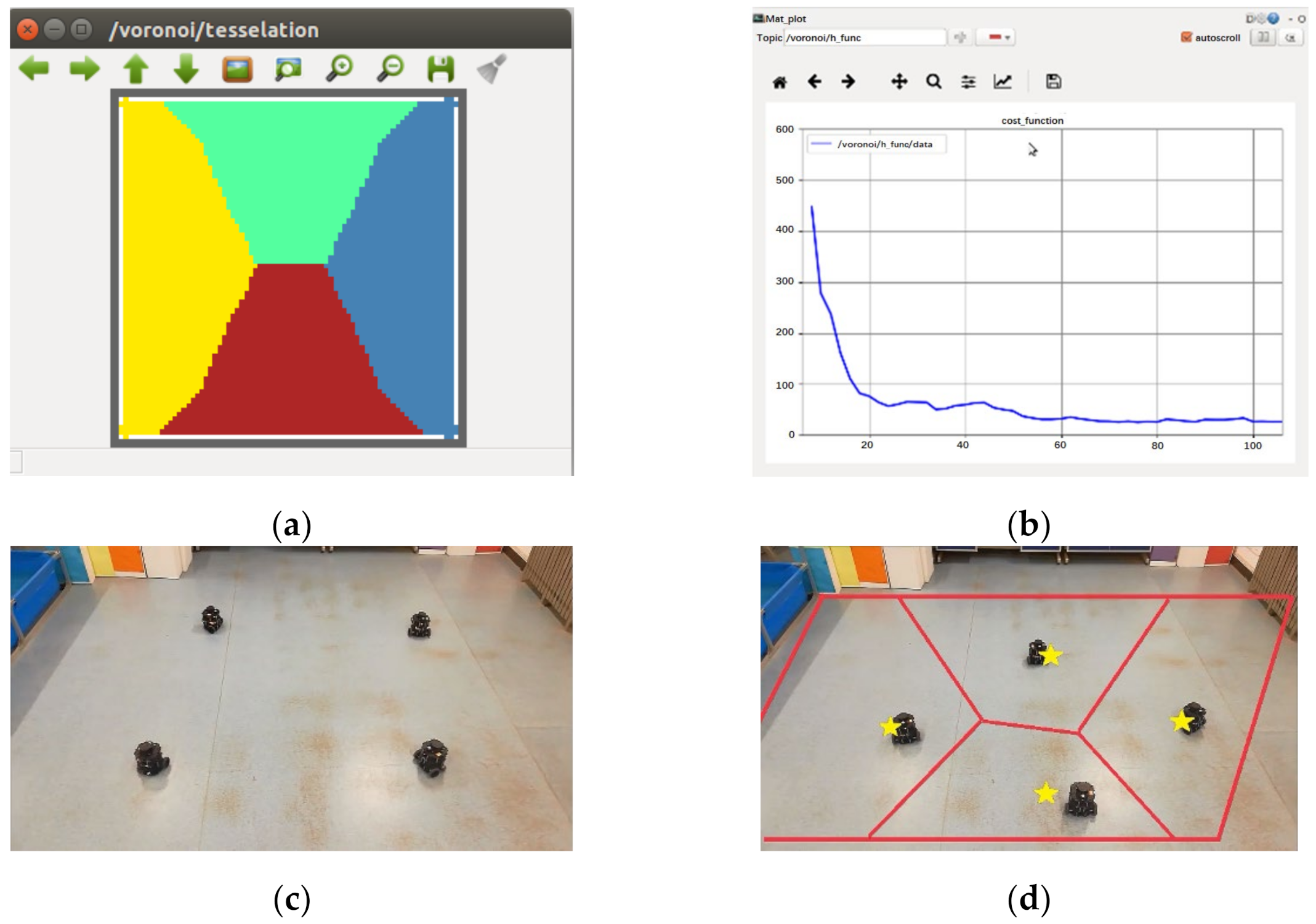
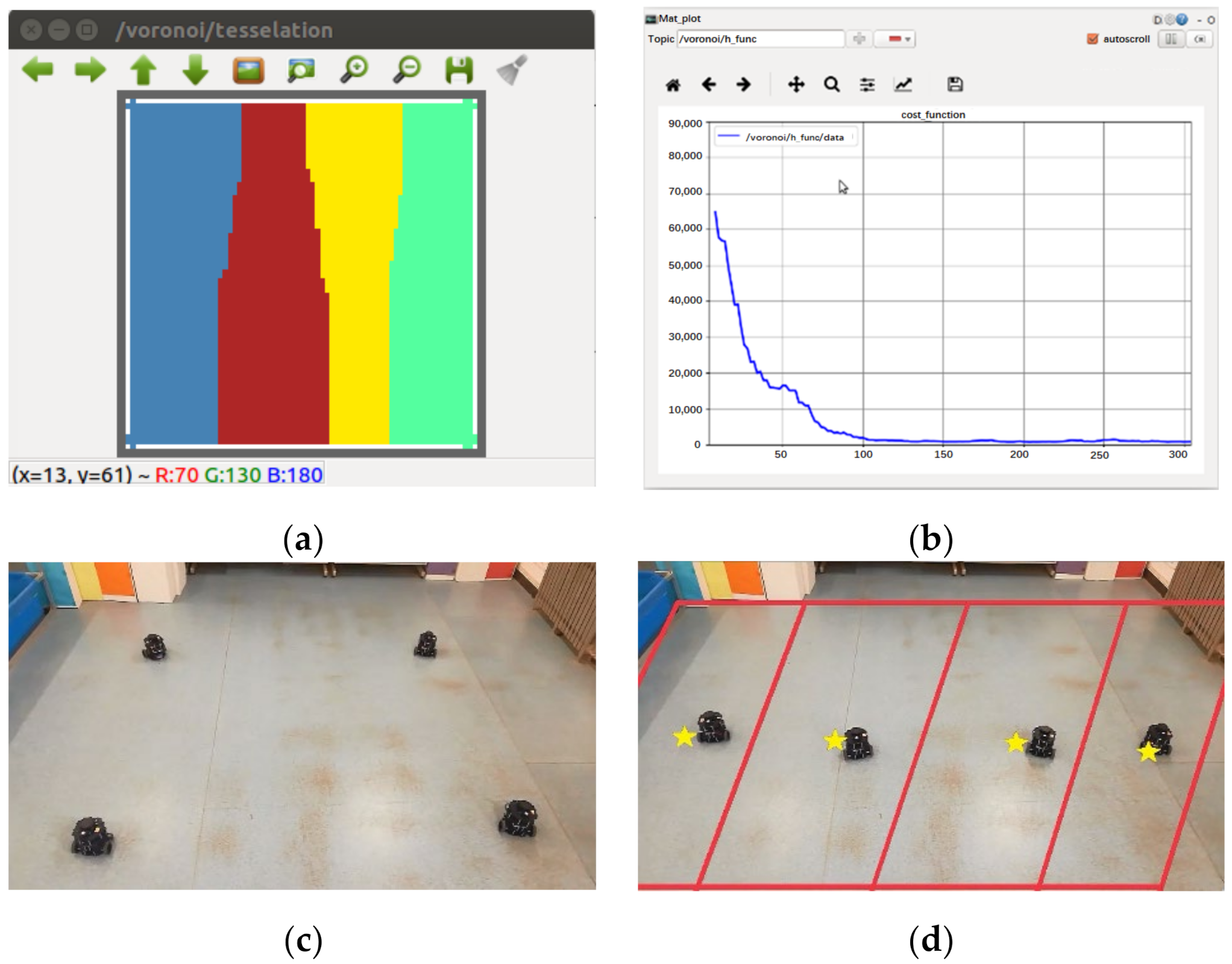
5. ROS Robot Experiment
5.1. Multi-Robot Formation Experiment
5.1.1. Square Formation Experiment
5.1.2. Diamond Formation Experiment
5.1.3. Linear Formation Experiment
5.2. Multi-Robot Dynamic Formation Experiment
5.2.1. Dynamic Formation Experiment in Obstacle-Free Scene
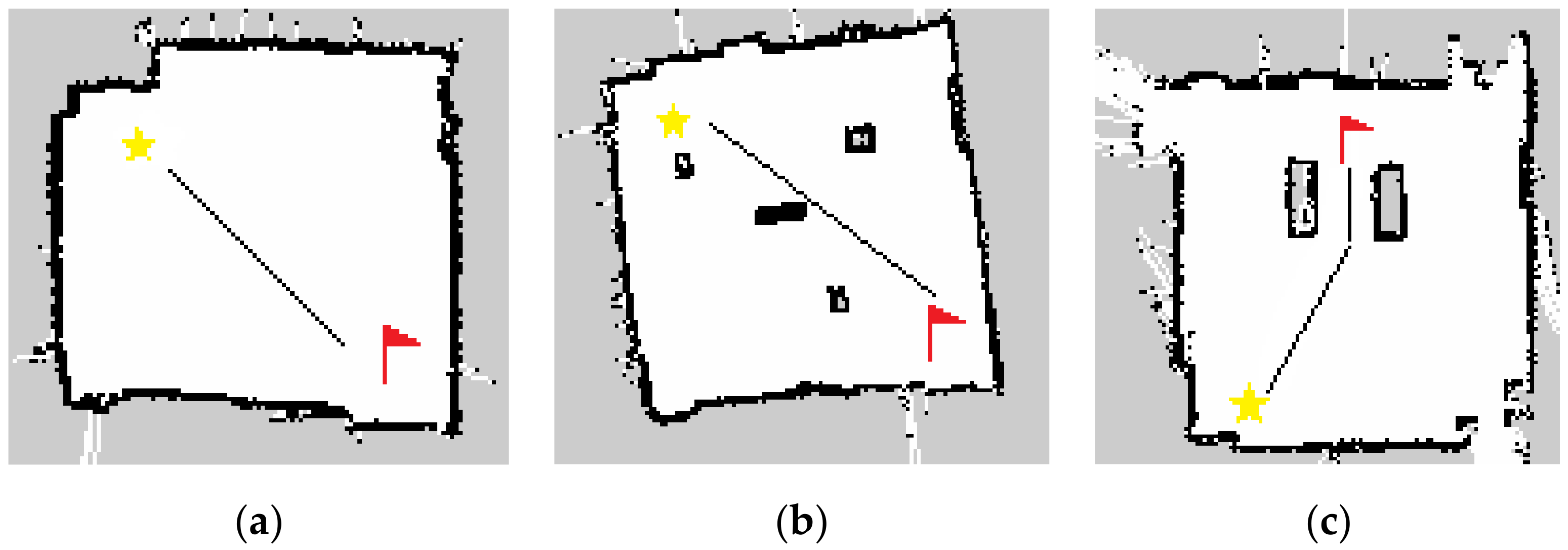
5.2.2. Dynamic Formation Experiment in Random Obstacle Scene
5.2.3. Dynamic Formation Experiment in Narrow Channel Scene
6. Summary and Outlook
- (1)
- The algorithm converges one robot to the center of mass of each Voronoi unit, which avoids collisions between robots to the greatest extent, making the multi-robots form the desired formation at the specified position according to the optimal distribution and proving the related theories.
- (2)
- Taking into account the existence of obstacles in the environment, by reducing the value of the density function of the obstacle position the robot can avoid the obstacle, improving the collision avoidance ability of the robot.
- (3)
- The health optimization management algorithm was used to maximize the endurance of unhealthy robots and improve the stability and robustness of the unhealthy robots under the premise of minor changes in the original framework. At the same time, the insertion construction method was introduced to make the robots in the formation more efficient. This enables a better response to changes in the environment.
- (4)
- In the simulations and experiments, through experimental verification using the MATLAB simulation platform and the ROS robot platform, it was verified that the method proposed in this paper can ensure that the robot can form the required formations according to the optimal distribution. In the designated area, the structural redundancy and internal carrying capacity of the multi-robot system were increased, and the formation was dynamically switched according to the external environment. At the same time, the health of the robots was better optimized and managed, which improves the flexibility and robustness of the formation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Queralta, J.P.; Mccord, C.; Gia, T.N.; Tenhunen, H.; Westerlund, T. Communication-free and index-free distributed formation control algorithm for multi-robot systems. Procedia Comput. Sci. 2019, 151, 431–438. [Google Scholar] [CrossRef]
- Freudenthaler, G.; Meurer, T. PDE-based multi-agent formation control using flatness and backstepping: Analysis, design and robot experiments. Automatica 2020, 115, 108897. [Google Scholar] [CrossRef] [Green Version]
- López-González, A.; Campaña, J.A.M.; Martínez, E.G.H.; Pablo, P.C. Multi robot distance-based formation using Parallel Genetic Algorithm. Appl. Soft Comput. 2020, 86, 105929. [Google Scholar] [CrossRef]
- Lu, Q.; Miao, Z.; Zhang, D.; Yu, L.; Ye, W.; Yang, S.X.; Su, C.Y. Distributed Leader-follower Formation Control of Nonholonomic Mobile Robots. IFAC-PapersOnLine 2019, 52, 67–72. [Google Scholar] [CrossRef]
- Franchi, A.; Giordano, P.R.; Michieletto, G. Online Leader Selection for Collective Tracking and Formation Control: The Second-Order Case. IEEE Trans. Control Netw. Syst. 2019, 6, 1415–1425. [Google Scholar] [CrossRef]
- Chen, Q.; Meng, Y.; Xing, J. Shape control of spacecraft formation using a virtual spring-damper mesh. Chin. J. Aeronaut. 2016, 29, 1730–1739. [Google Scholar] [CrossRef] [Green Version]
- Pan, W.W.; Jiang, D.P.; Pang, Y.J.; Zhang, Q. A multi-AUV formation algorithm combining artificial potential field and virtual structure. Acta Armamentarii 2017, 38, 326–334. [Google Scholar]
- Zhou, D.; Wang, Z.; Schwager, M. Agile coordination and assistive collision avoidance for quadrotor swarms using virtual structures. IEEE Trans. Robot. 2018, 34, 916–923. [Google Scholar] [CrossRef]
- Flores-Resendiz, J.F.; Meza-Herrera, J.; Aranda-Bricaire, E. Formation control with collision avoidance for first-order multi-agent systems: Experimental results. IFAC-PapersOnLine 2019, 52, 127–132. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Li, C.; Liu, M. Distributed coordinated control for satellite formation system with communication delay. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 1282–1287. [Google Scholar]
- Yao, X.Y.; Ding, H.F.; Ge, M.F. Synchronization control for multiple heterogeneous robotic systems with parameter uncertainties and communication delays. J. Frankl. Inst. 2019, 356, 9713–9729. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. A multi-objective pigeon-inspired optimization approach to UAV distributed flocking among obstacles. Inf. Sci. 2020, 509, 515–529. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Wang, Z.; Liang, J. Automatic dynamic flocking in mobile actuator sensor networks by central Voronoi tessellations. In Proceedings of the IEEE International Conference on Mechatronics & Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; pp. 1630–1635. [Google Scholar]
- Bhattacharya, S.; Ghrist, R.; Kumar, V. Multi-robot coverage and exploration on Riemannian manifolds with boundaries. Int. J. Robot. Res. 2014, 33, 113–137. [Google Scholar] [CrossRef]
- Boardman, B.; Harden, T.; Martínez, S. Limited range spatial load balancing in non-convex environments using sampling-based motion planners. Auton. Robot. 2018, 42, 1731–1748. [Google Scholar] [CrossRef]
- Teruel, E.; Aragues, R.; López-Nicolás, G. A distributed robot swarm control for dynamic region coverage. Robot. Auton. Syst. 2019, 119, 51–63. [Google Scholar] [CrossRef]
- Bethke, B.; How, J.P.; Vian, J. Group health management of UAV teams with applications to persistent surveillance. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 July 2008; pp. 3145–3150. [Google Scholar]
- Nigam, N. Dynamic Replanning for Multi-UAV Persistent Surveillance. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef]
- Sharifi, F.; Zhang, Y.; Aghdam, A.G. Coverage control in multi-vehicle systems subject to health degradation. In Proceedings of the International Conference on Unmanned Aircraft Systems, Atlanta, GA, USA, 28–31 May 2013; pp. 1119–1124. [Google Scholar]
- Pierson, A.; Schwarting, W.; Karaman, S.; Rus, D. Weighted Buffered Voronoi Cells for Distributed Semi-Cooperative Behavior. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5611–5617. [Google Scholar]
- Turanli, M.; Temeltas, H. Multi-Robot Energy-Efficient Coverage Control with Hopfield Networks. Stud. Inform. Control 2020, 29, 179–188. [Google Scholar] [CrossRef]



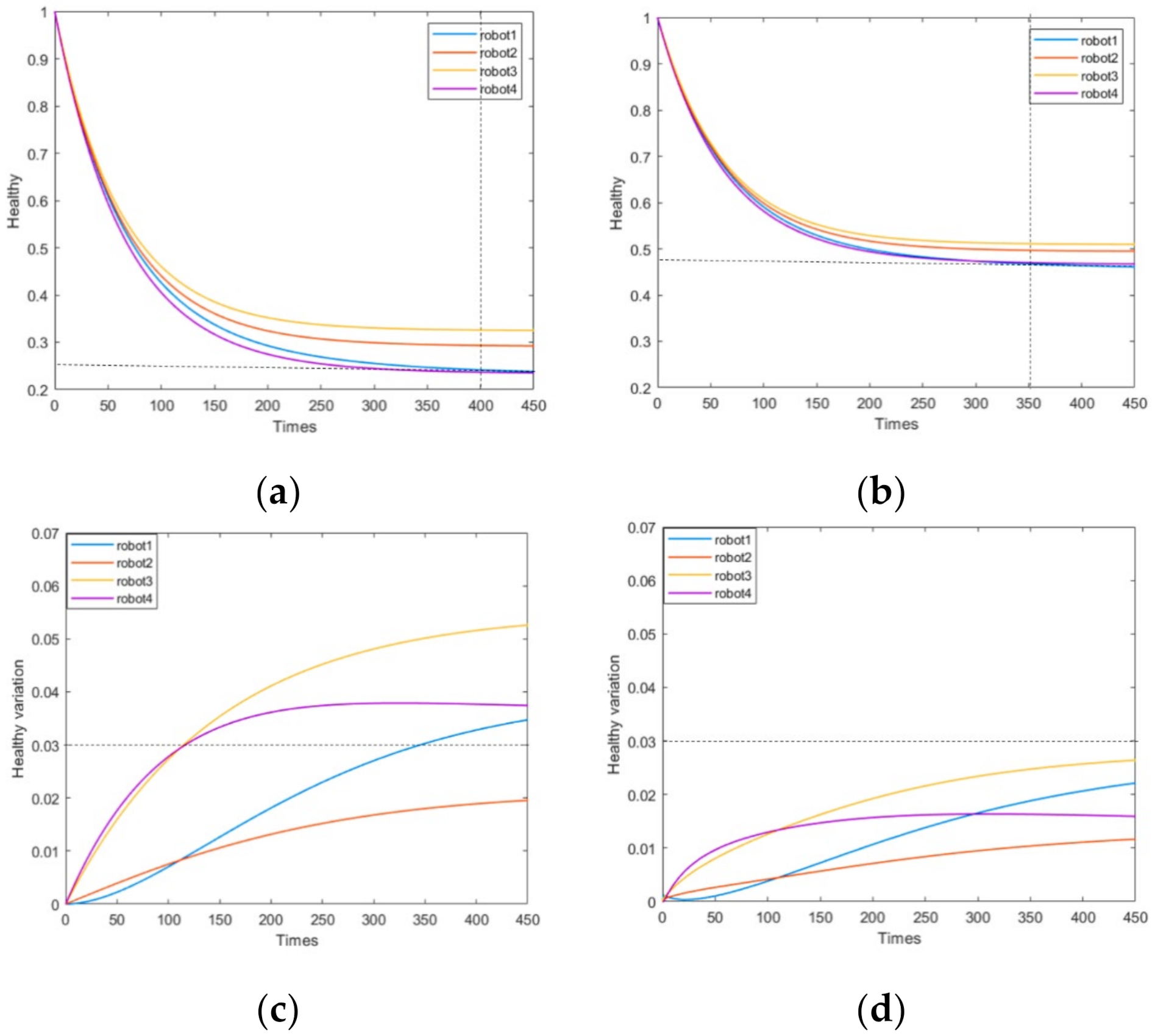
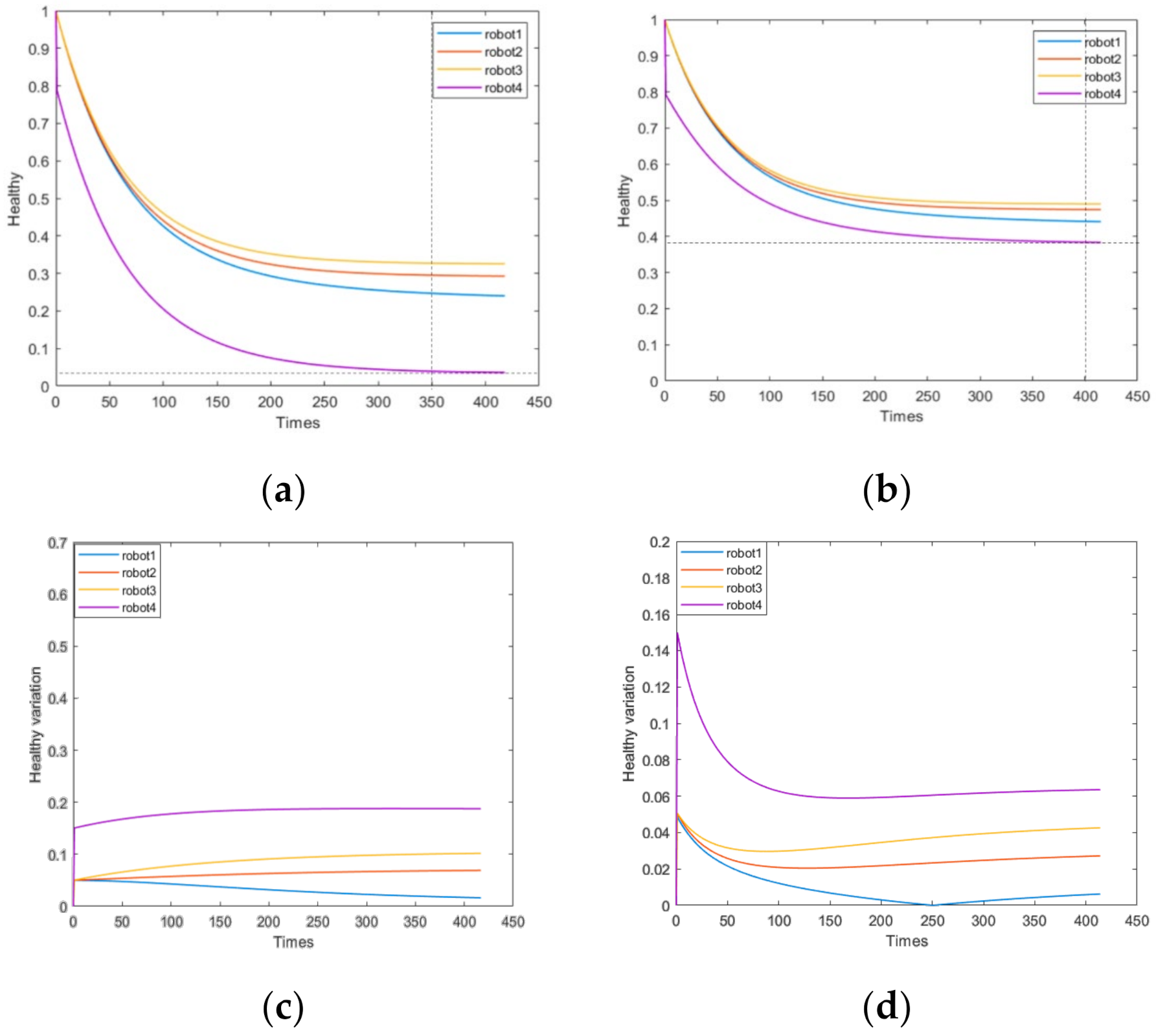

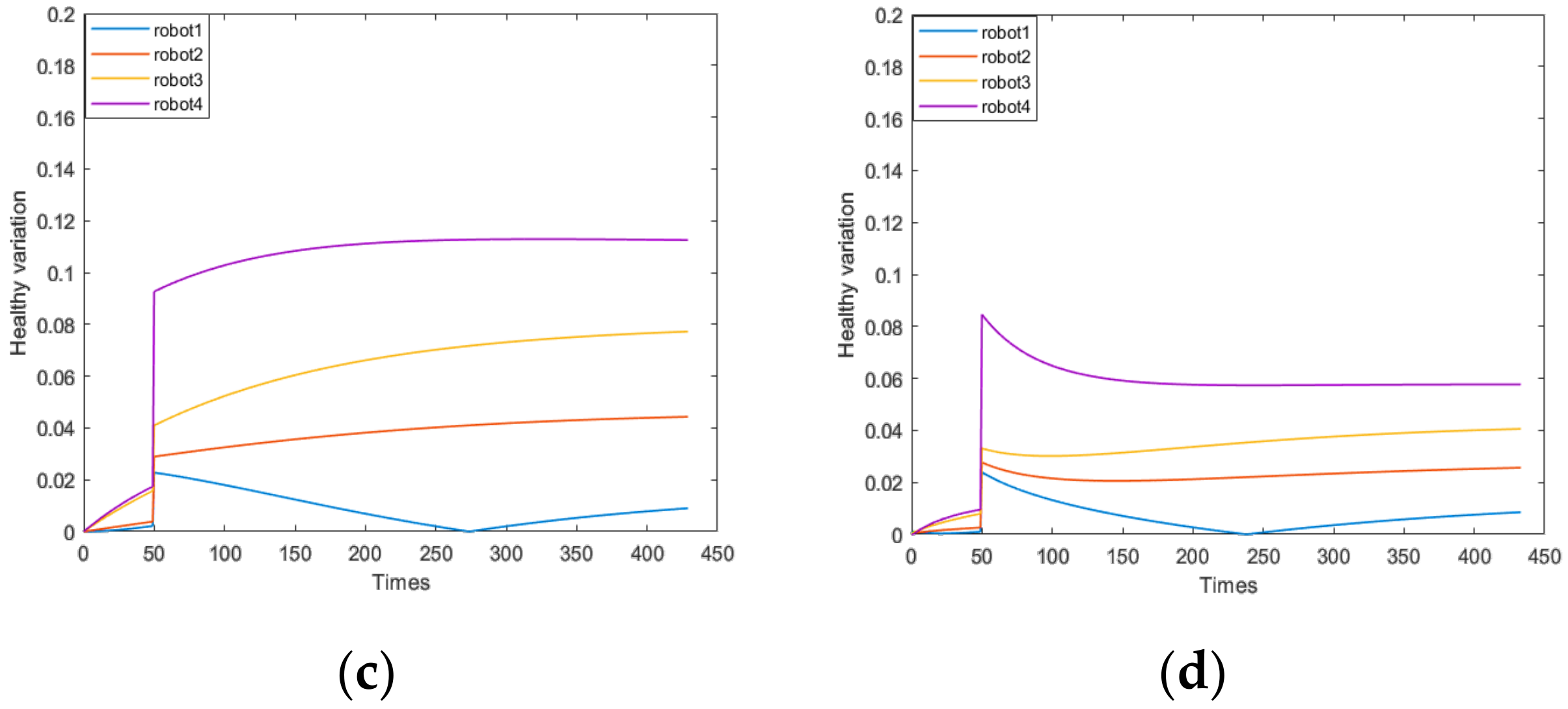
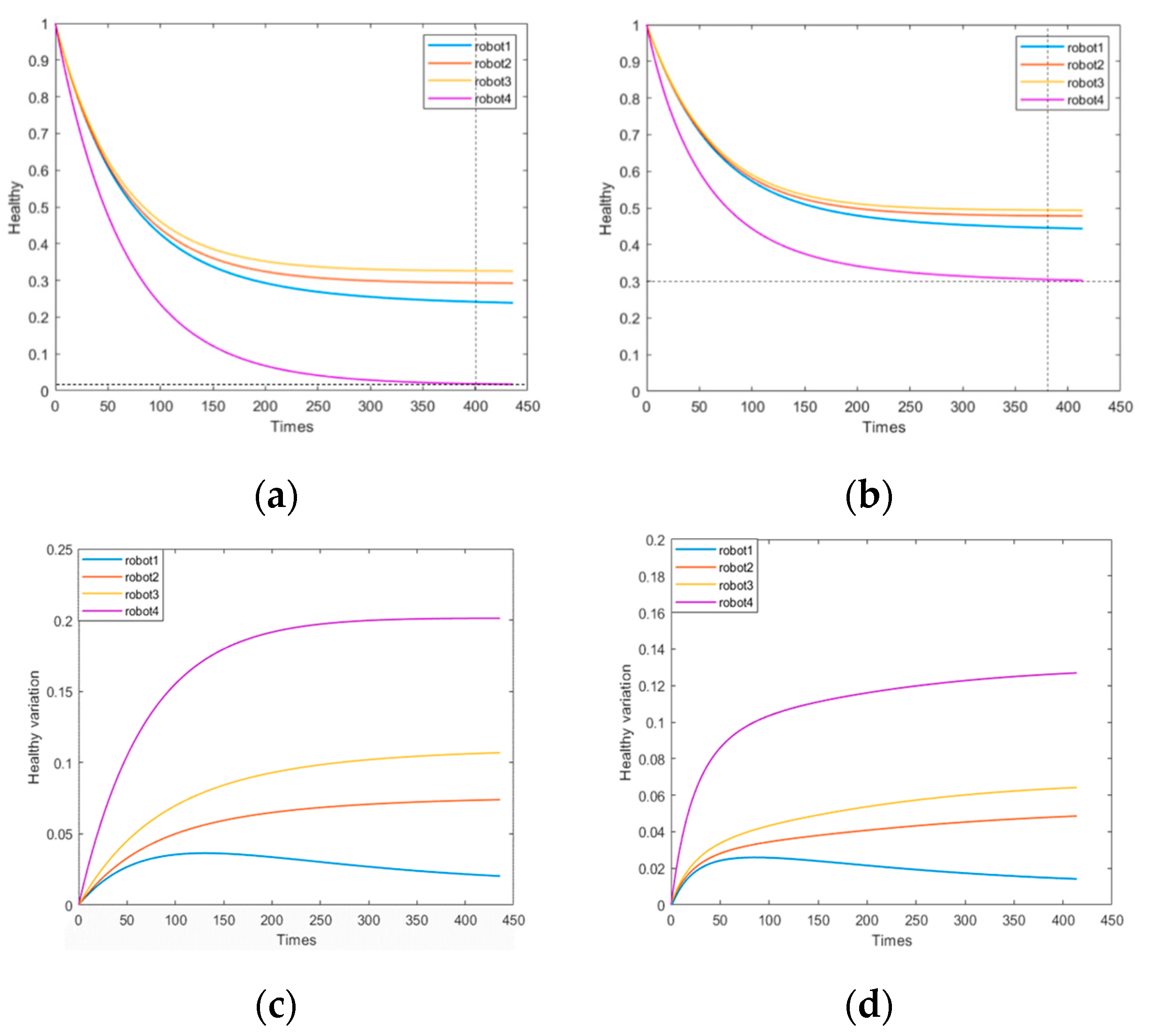





| hi(t) When the System Is Stable (Normal Situation) | hi(t) When the System Is Stable (HOM) | Percentage Increase in System Health Value | ||
|---|---|---|---|---|
| Scenario 1 | 0.26 | 0.48 | 22% | |
| Scenario 2 | 0.04 | 0.38 | 34% | |
| Scenario 3 | 0.15 | 0.40 | 25% | |
| Scenario 4 | 0.02 | 0.30 | 28% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, K.; Chen, Y.; Gao, S.; Zhang, H.; Dang, H. Multi-Robot Formation Control Based on CVT Algorithm and Health Optimization Management. Appl. Sci. 2022, 12, 755. https://doi.org/10.3390/app12020755
Cao K, Chen Y, Gao S, Zhang H, Dang H. Multi-Robot Formation Control Based on CVT Algorithm and Health Optimization Management. Applied Sciences. 2022; 12(2):755. https://doi.org/10.3390/app12020755
Chicago/Turabian StyleCao, Kai, Yangquan Chen, Song Gao, Hang Zhang, and Haixin Dang. 2022. "Multi-Robot Formation Control Based on CVT Algorithm and Health Optimization Management" Applied Sciences 12, no. 2: 755. https://doi.org/10.3390/app12020755
APA StyleCao, K., Chen, Y., Gao, S., Zhang, H., & Dang, H. (2022). Multi-Robot Formation Control Based on CVT Algorithm and Health Optimization Management. Applied Sciences, 12(2), 755. https://doi.org/10.3390/app12020755







