Ferrites and Nanocrystalline Alloys Applied to DC–DC Converters for Renewable Energies
Abstract
:Featured Application
Abstract
1. Introduction
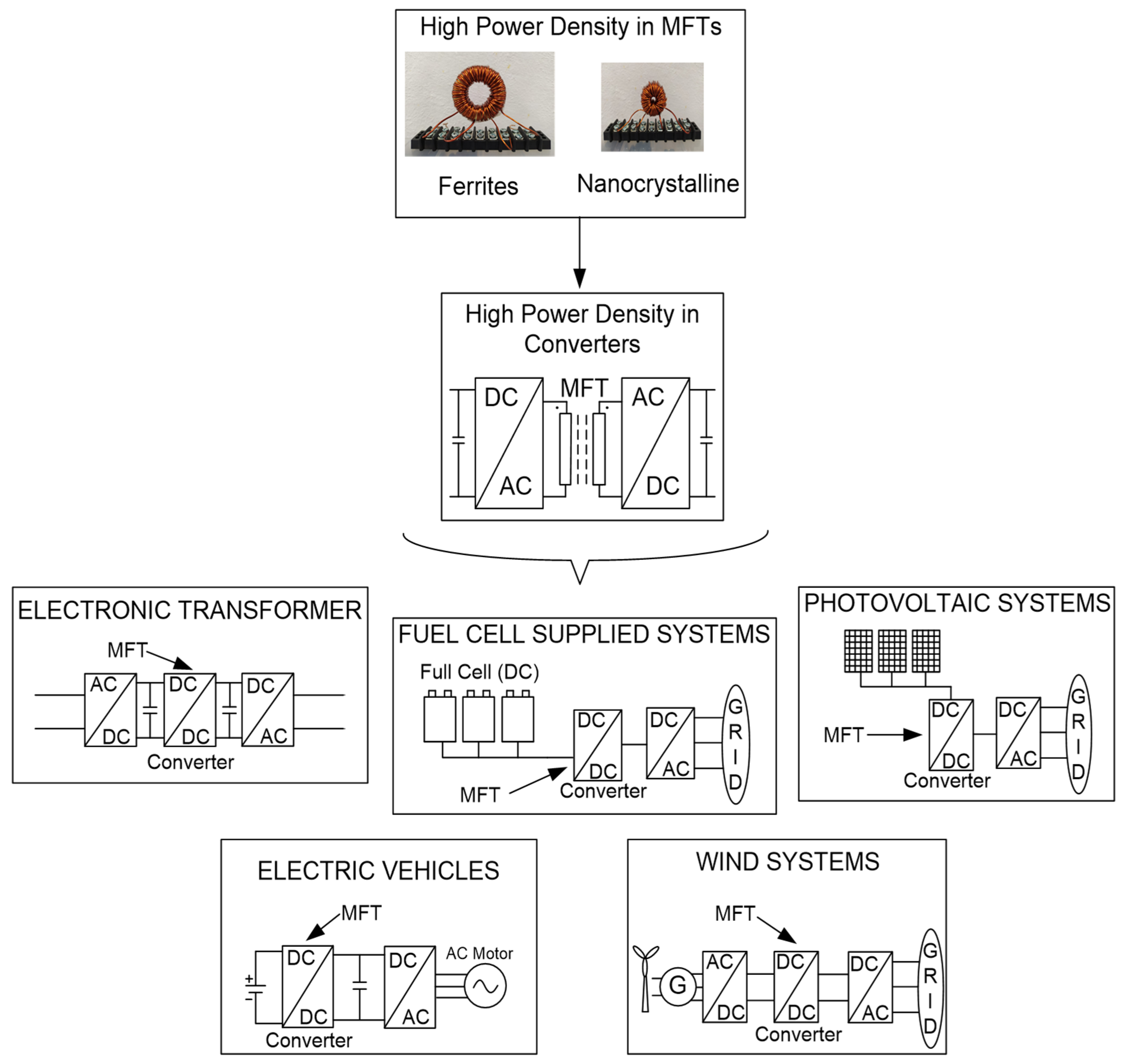
1.1. Motivation and Incitement
1.2. Literature Review
1.3. Contribution and Paper Organization
2. MFT Design and Magnetic Materials
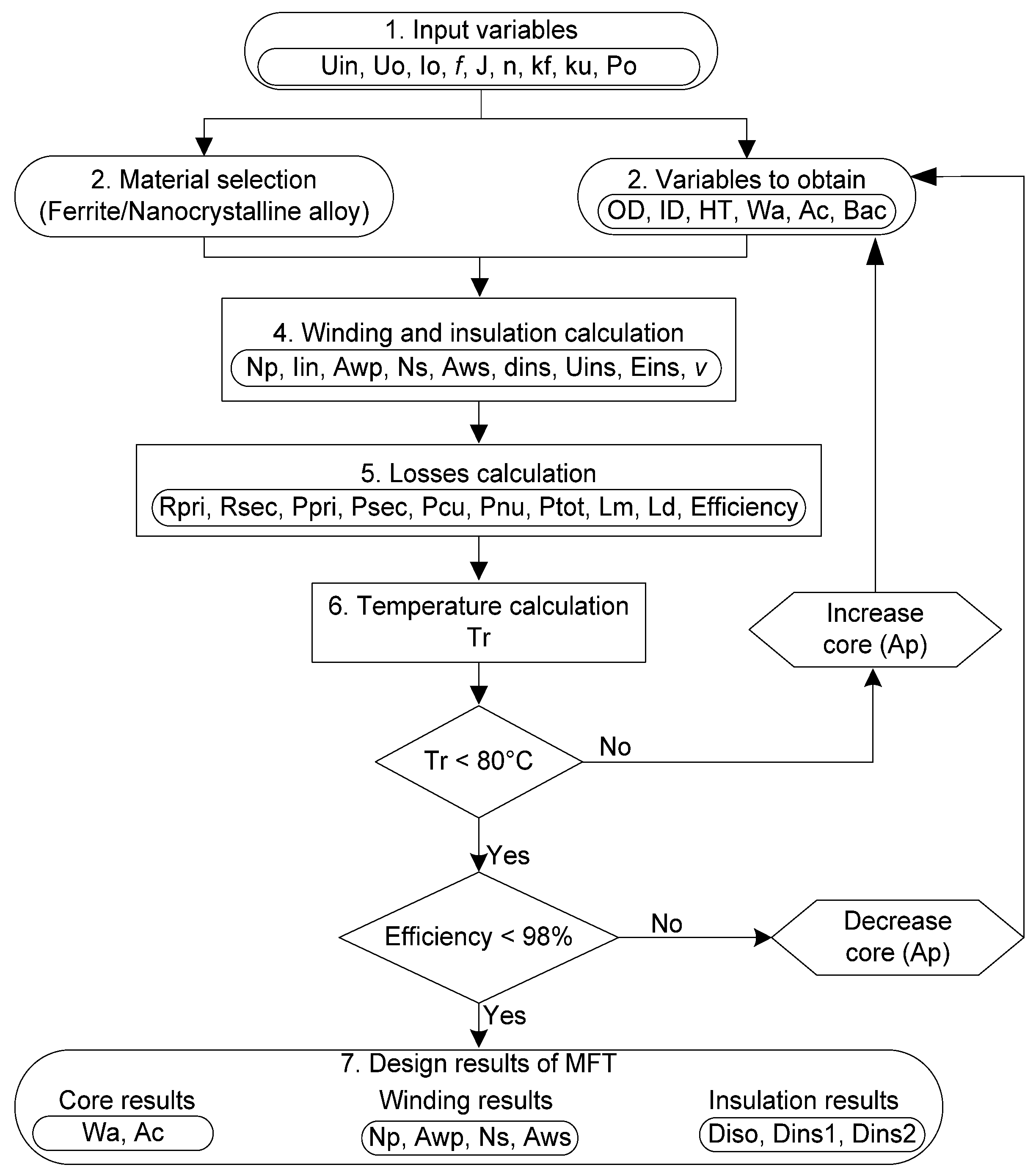
2.1. MFTs Design
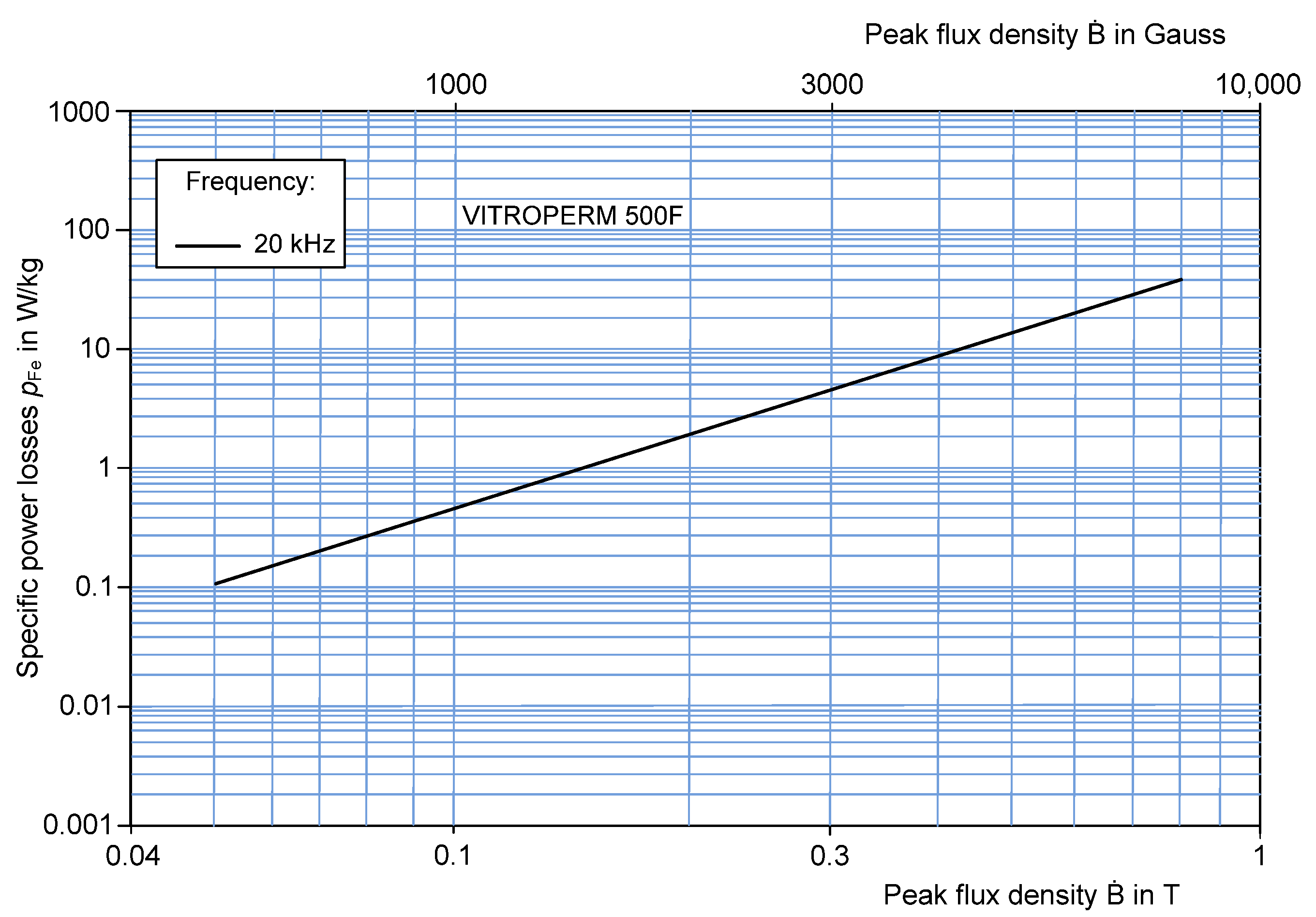
2.2. Magnetic Materials
3. Core Dimensions, Core Losses, and Winding Losses
3.1. Geometric Dimensions
3.2. Core Losses and Winding Losses
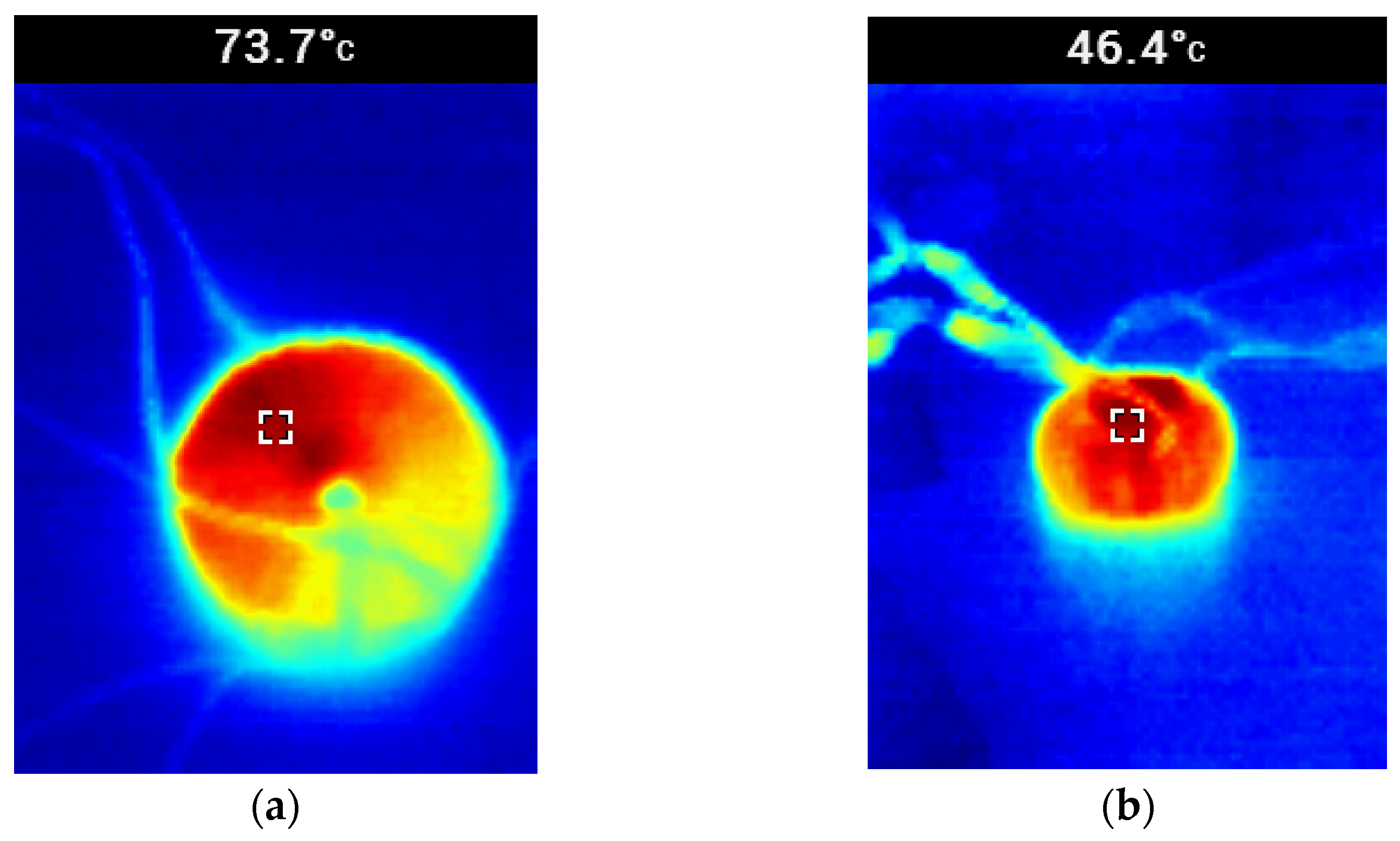
3.3. Temperature Rise
3.4. Calculation of the Dispersion Inductance
| = vacuum permeability | diso = isolation distance |
| dins1 = insulation distance between the layers of the primary | NL1 = turns per layer |
| dins2 = insulation distance between the layers of the secondary | hw = winding height |
| m1 = number of layers in the primary | dpri = thickness of the primary |
| m2 = number of layers in the secondary | dsec = thickness of the secondary |
| MLTiso = mean length of the isolation distance | ∆1 = penetration ratio of the primary, |
| MLTpri = mean length turns of primary portion | ∆2 = penetration ratio of the primary, |
| MLTsec = mean length turns of secondary portion | where is the skin depth |
4. Simulation
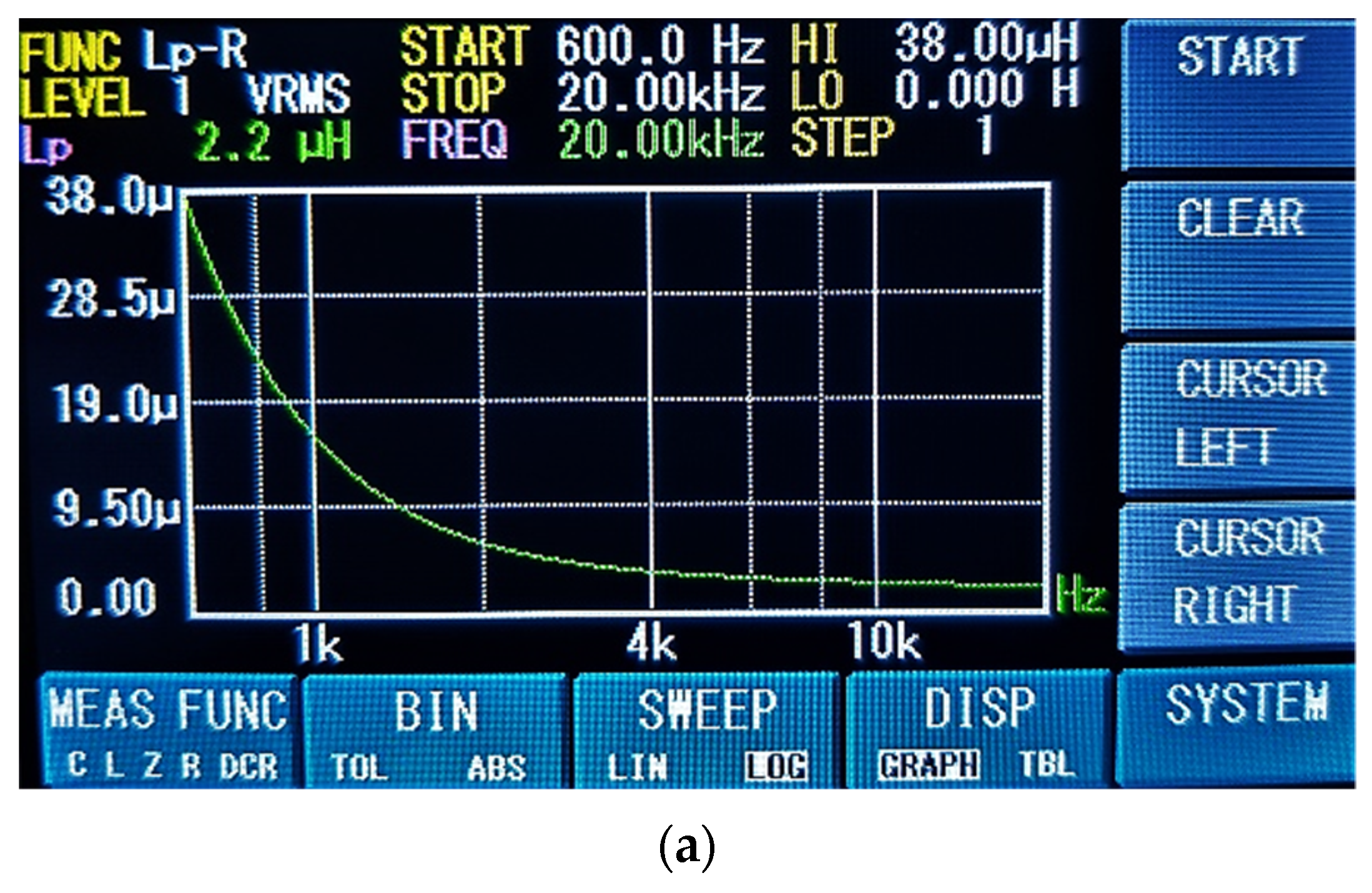
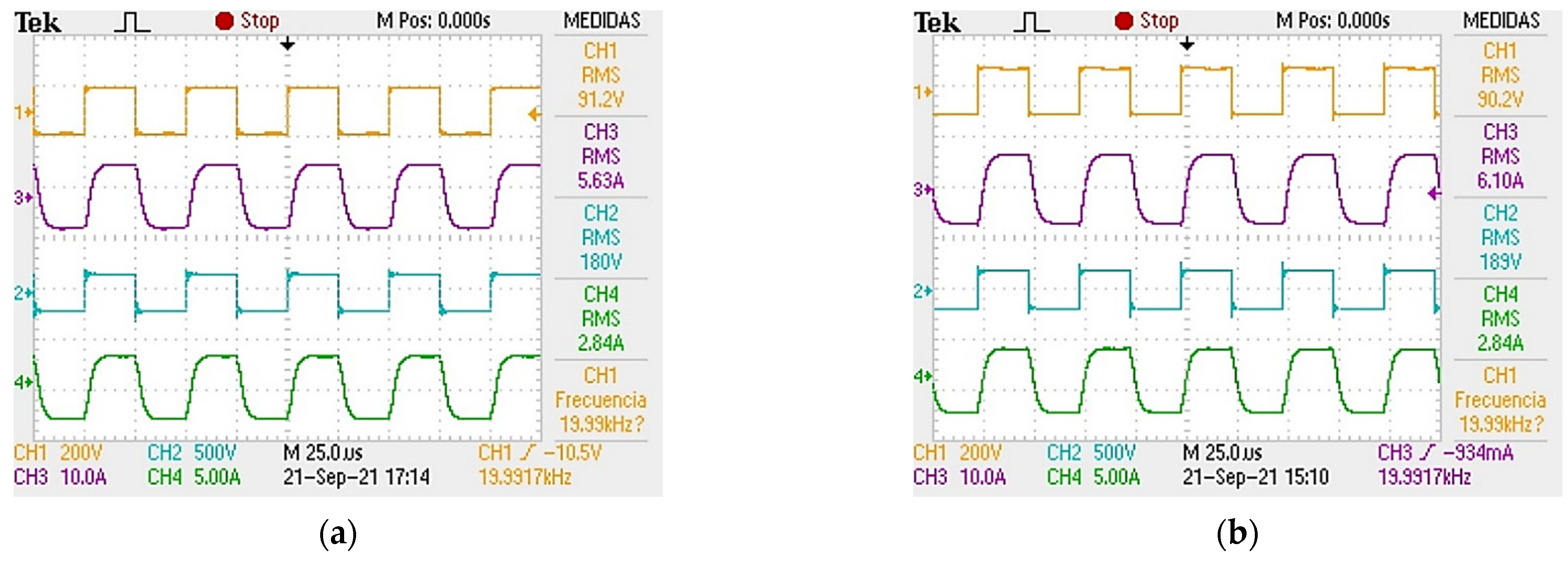
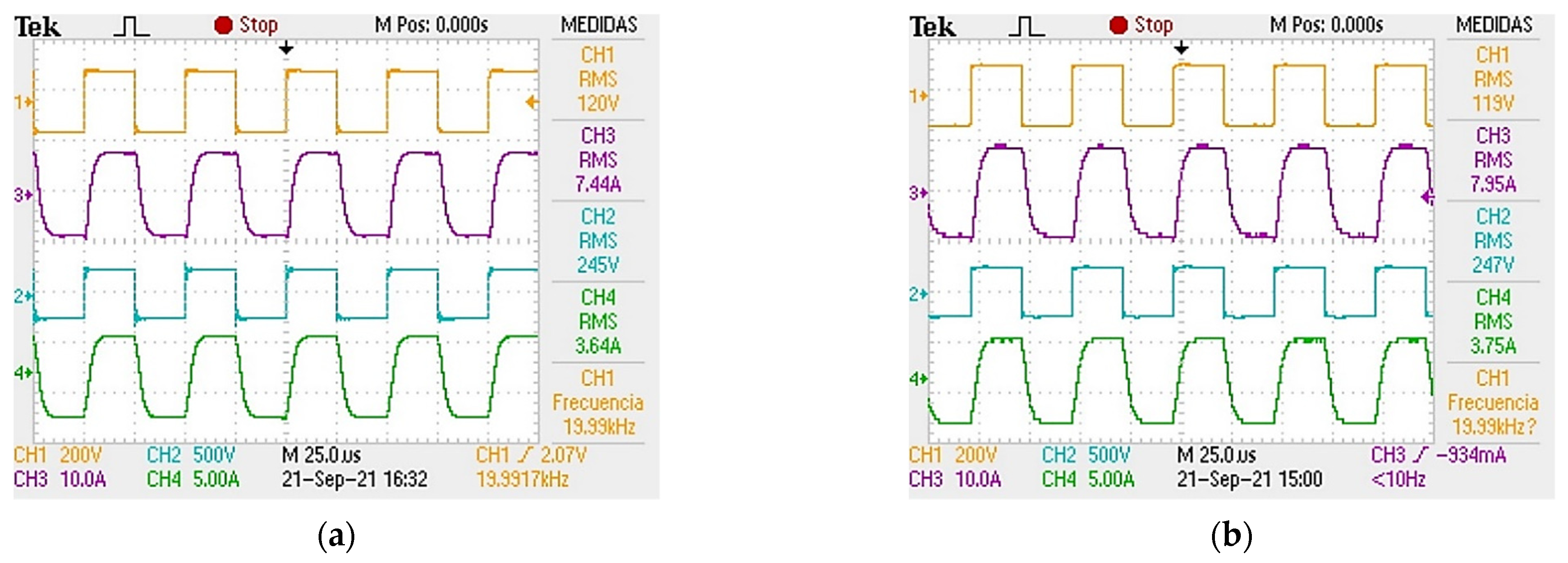
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kauder, T.; Belgrand, T.; Lemaitre, T.; Thul, A.; Hameyer, K. Medium-frequency power transformer using GOES for a three-phase dual active bridge. J. Magn. Magn. Mater. 2020, 504, 166672. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Q.; Yu, W.; Huang, A.Q. A Medium-Voltage Medium-Frequency Isolated DC–DC Converter Based on 15-kV SiC MOSFETs. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 100–109. [Google Scholar] [CrossRef]
- Tseng, S.; Fan, J. Sof-Switching Full-Bridge Converter with Multiple-Input Source for DC Distribution Applications. Symmetry 2021, 13, 775. [Google Scholar] [CrossRef]
- Zhang, F.; Yan, Y. Novel Forward–Flyback Hybrid Bidirectional DC–DC Converter. IEEE Trans. Ind. Electron. 2009, 56, 1578–1584. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q.; Burgos, R. Review of Solid-State Transformer Technologies and Their Application in Power Distribution Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 186–198. [Google Scholar] [CrossRef]
- Wei, Q.; Wu, B.; Xu, D.; Zargari, N.R. A Medium-Frequency Transformer-Based Wind Energy Conversion System Used for Current-Source Converter-Based Offshore Wind Farm. IEEE Trans. Power Electron. 2017, 32, 248–259. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.S.; Rana, D.; Garg, P.; Enjeti, P.N.; Pitel, I.J. Wind Turbine Generator–Battery Energy Storage Utility Interface Converter Topology With Medium-Frequency Transformer Link. IEEE Trans. Power Electron. 2014, 29, 4146–4155. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Future on Power Electronics for Wind Turbine Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.; Daniel, M.; Ramos-Ruiz, J.; Enjeti, P.; Liu, L.; Aeloiza, E. Isolated AC–DC Converter Using Medium Frequency Transformer for Off-Shore Wind Turbine DC Collection Grid. IEEE Trans. Ind. Electron. 2017, 64, 8939–8947. [Google Scholar] [CrossRef]
- Huang, P.; Mao, C.; Wang, D.; Wang, L.; Duan, Y.; Qiu, J.; Xu, G.; Cai, H. Optimal Design and Implementation of High-Voltage High-Power Silicon Steel Core Medium-Frequency Transformer. IEEE Trans. Ind. Electron. 2017, 64, 4391–4401. [Google Scholar] [CrossRef]
- Yu, J.; Yang, Z.; Kurths, J.; Zhan, M. Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry. Symmetry 2021, 13, 157. [Google Scholar] [CrossRef]
- Fan, H.; Li, H. High-Frequency Transformer Isolated Bidirectional DC–DC Converter Modules with High Efficiency Over Wide Load Range for 20 kVA Solid-State Transformer. IEEE Trans. Power Electron. 2011, 26, 3599–3608. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Q.; Lee, F.C.; Li, B. High-Frequency Transformer Design for Modular Power Conversion from Medium-Voltage AC to 400 VDC. IEEE Trans. Power Electron. 2018, 33, 7545–7557. [Google Scholar] [CrossRef]
- Balci, S.; Sefa, I.; Altin, N. Design and analysis of a 35 kVA medium frequency power transformer with the nanocrystalline core material. Int. J. Hydrogen Energy 2017, 42, 17895–17909. [Google Scholar] [CrossRef]
- Ozdemir, S.; Balci, S.; Altin, N.; Sefa, I. Design and performance analysis of the three-level isolated DC–DC converter with the nanocyrstalline core transformer. Int. J. Hydrogen Energy 2017, 42, 17801–17812. [Google Scholar] [CrossRef]
- Ruiz-Robles, D.; Venegas-Rebollar, V.; Anaya-Ruiz, A.; Moreno-Goytia, E.; Rodríguez-Rodríguez, J. Design and Prototyping Medium-Frequency Transformers Featuring a Nanocrystalline Core for DC–DC Converters. Energies 2018, 11, 2081. [Google Scholar] [CrossRef] [Green Version]
- Bahmani, M.A.; Thiringer, T.; Kharezy, M. Design Methodology and Optimization of a Medium-Frequency Transformer for High-Power DC–DC Applications. IEEE Trans. Ind. Appl. 2016, 52, 4225–4233. [Google Scholar] [CrossRef]
- Garcia-Bediaga, A.; Villar, I.; Rujas, A.; Mir, L.; Rufer, A. Multiobjective Optimization of Medium-Frequency Transformers for Isolated Soft-Switching Converters Using a Genetic Algorithm. IEEE Trans. Power Electron. 2017, 32, 2995–3006. [Google Scholar] [CrossRef]
- Ruiz-Robles, D.; Ortíz-Marín, J.; Venegas-Rebollar, V.; L Moreno-Goytia, E.; Granados-Lieberman, D.; R Rodríguez-Rodriguez, J. Nanocrystalline and Silicon Steel Medium-Frequency Transformers Applied to DC–DC Converters: Analysis and Experimental Comparison. Energies 2019, 12, 2062. [Google Scholar] [CrossRef] [Green Version]
- Kauder, T.; Hameyer, K. Performance Factor Comparison of Nanocrystalline, Amorphous, and Crystalline Soft Magnetic Materials for Medium-Frequency Applications. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Chen, B.; Liang, X.; Wan, N. Design Methodology for Inductor-Integrated Litz-Wired High-Power Medium-Frequency Transformer with the Nanocrystalline Core Material for Isolated DC-Link Stage of Solid-State Transformer. IEEE Trans. Power Electron. 2020, 35, 11557–11573. [Google Scholar] [CrossRef]
- Balci, S.; Sefa, I.; Altin, N. An Investigation of Ferrite and Nanocrystalline Core Materials for Medium-Frequency Power Transformers. J. Electron. Mater. 2016, 45, 3811–3821. [Google Scholar] [CrossRef]
- Hilzinger, R.; Rodewald, W. Magnetic Materials, 1st ed.; Publicis MCD Werbeagentur GmbH, Vaccumschmelze GmbH & Co. KG: Hanau, Germany, 2013. [Google Scholar]
- Bahmani, M.A.; Thiringer, T. Accurate Evaluation of Leakage Inductance in High-Frequency Transformers Using an Improved Frequency-Dependent Expression. IEEE Trans. Power Electron. 2015, 30, 5738–5745. [Google Scholar] [CrossRef]

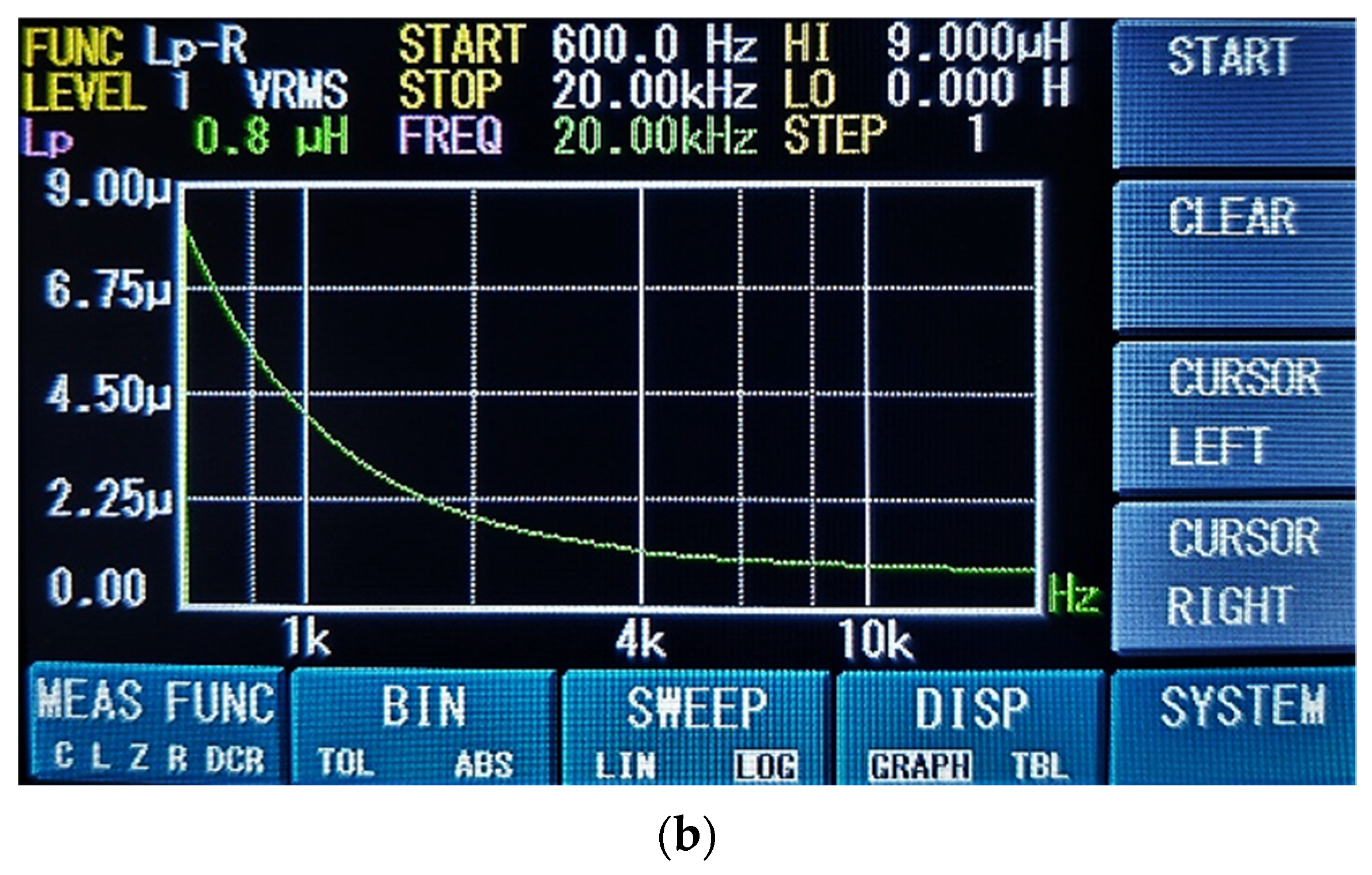
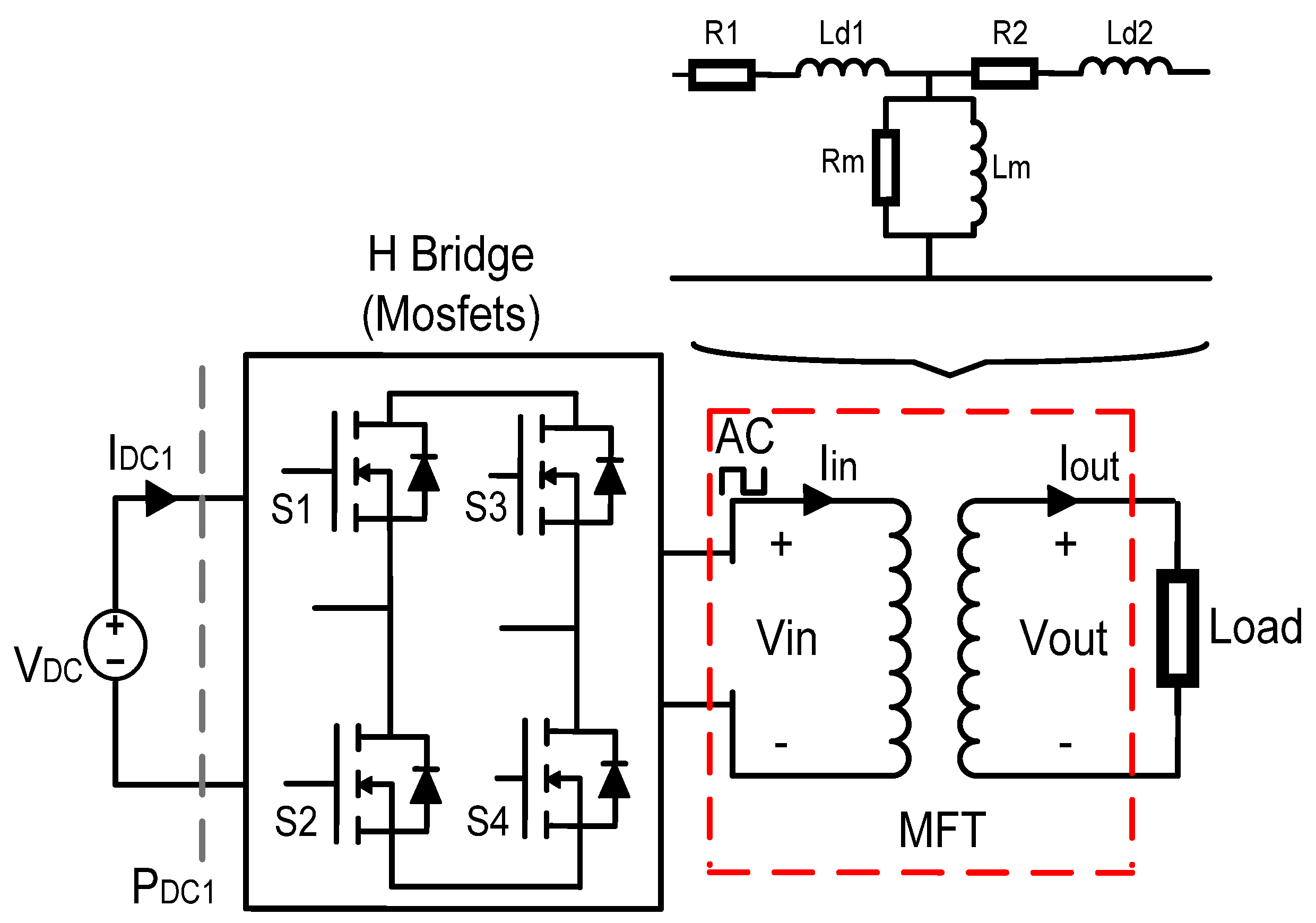




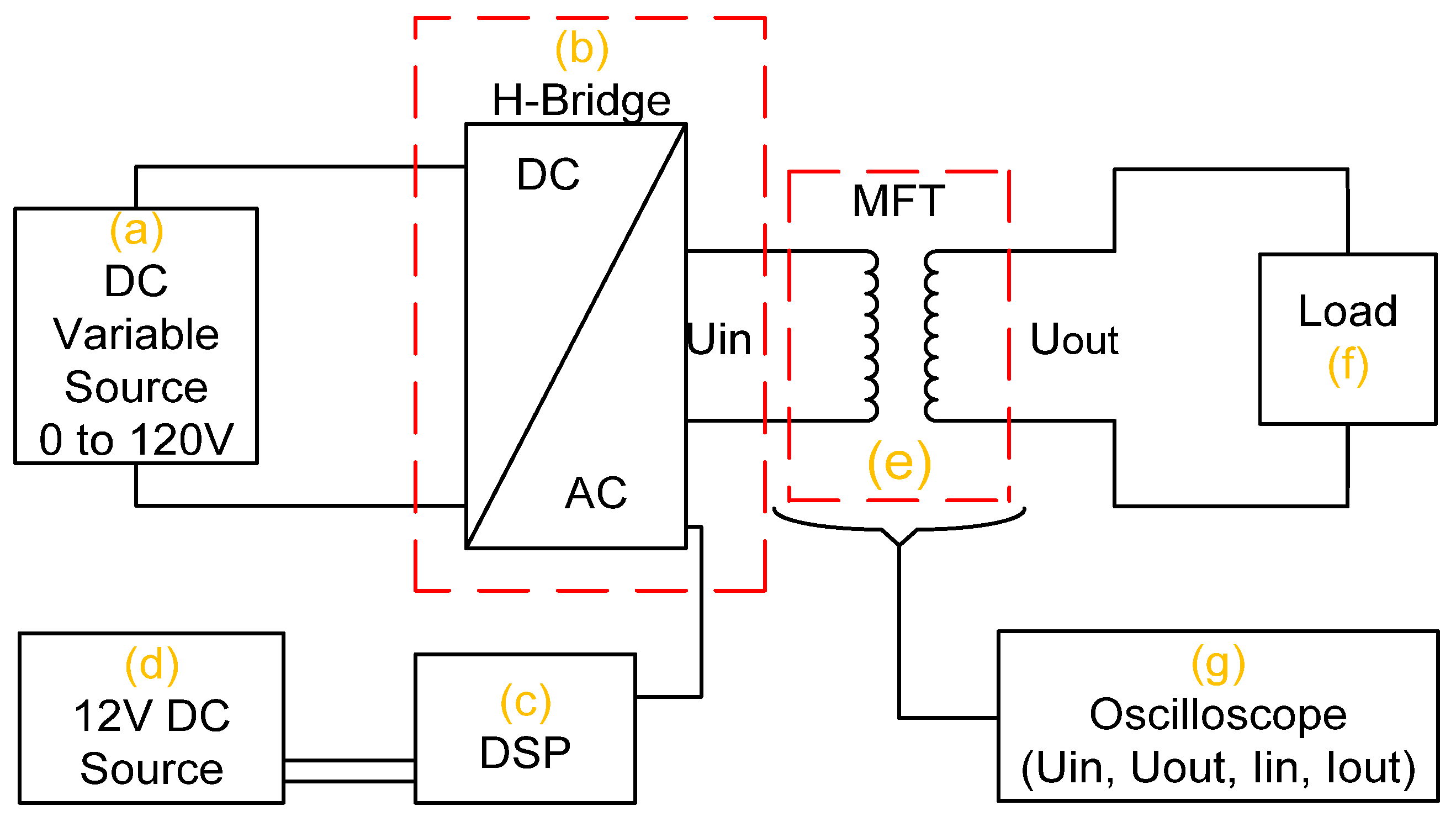

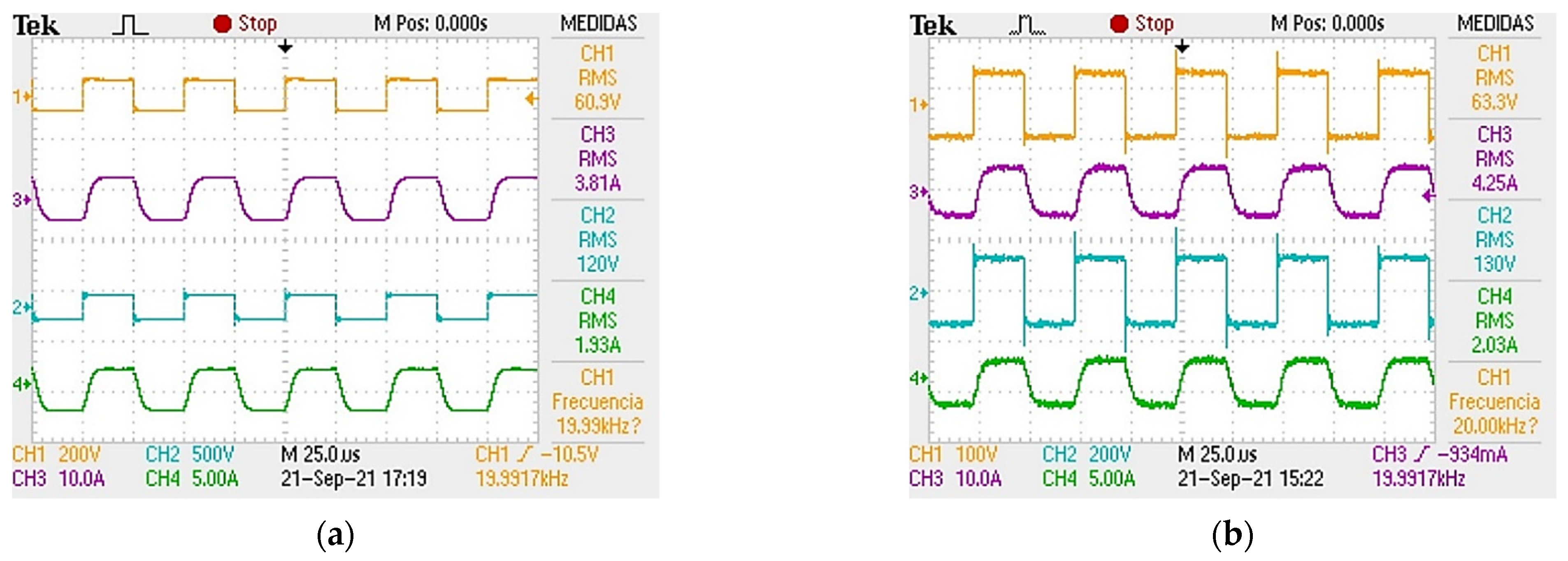
| Reference | Frequency (kHz) | Bac (T) | Core Material | Power (kVA) | Efficiency (%) | Power Density (kW/L) |
|---|---|---|---|---|---|---|
| [19] | 1 | 0.9 | Nanocrystalline | 1 | 80.2 | 2.50 |
| [21] | 10 | 0.46 | Nanocrystalline | 200 | 99.4 | 8.00 |
| [17] | 5 | 0.9 | Nanocrystalline | 50 | 99.5 | 11.50 |
| [16] | 5 | 0.9 | Nanocrystalline | 1 | 99.4 | 15.01 |
| [15] | 10 | 0.3 | Nanocrystalline | 5 | 96 | 19.90 |
| [22] | 10 | 0.3 | Nanocrystalline | 35 | 99.2 | 23.30 |
| [14] | 10 | 0.3 | Nanocrystalline | 35 | 98 | 23.30 |
| This proposal | 20 | 0.8 | Nanocrystalline | 1 | 99.7 | 36.91 |
| Parameter | Material 1 | Material 2 |
|---|---|---|
| Material | Ferrite (3C90) | Nanocrystalline (Vitroperm 500 F) |
| Core | Block core | Laminate (0.02 mm) |
| Maximum flux density | 0.35 T | 1.2 T |
| Permeability | 2000–4000 | 15,000–150,000 |
| Cost | Low | High |
| Parameter | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Vcore | 22.03 cm3 | 5.89 cm3 |
| Vwinding | 39.95 cm3 | 21.20 cm3 |
| Vtotal | 61.98 cm3 | 27.09 cm3 |
| Wcore | 100 grs | 32.9 grs |
| WMFT | 238 grs | 102 grs |
| MFT | Flux Density | Power Density (kW/L) |
|---|---|---|
| Ferrite core | 0.2 T | 16.13 |
| Nanocrystalline core | 0.8 T | 36.91 |
| MFT | MFT with Ferrite Core | MFT with Nanocrystalline Core |
|---|---|---|
| Lω | 4.83 W | 1.69 W |
| Pfe | 2.29 W | 1.32 W |
| Ltot | 7.12 W | 3.01 W |
| Efficiency | 99.28% | 99.69% |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Ld | 2.06 µH | 1.01 µH |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Vin | 120 V | 120 V |
| f | 20 kHz | 20 kHz |
| Load | 60 Ω | 60 Ω |
| Ld1 | 2.06 µH | 1.01 µH |
| Ld2 | 9.09 µH | 4.06 µH |
| R1 | 0.0300 Ω | 0.0114 Ω |
| R2 | 0.1222 Ω | 0.0465 Ω |
| Lm | 10.2 mH | 28.7 mH |
| Rm | 6288 Ω | 10,909 Ω |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Vin | 120 V | 120 V |
| Vo | 235.4 V | 237.8 V |
| Iin | 7.852 A | 7.936 A |
| Io | 3.924 A | 3.963 A |
| Efficiency | 98.03% | 98.96% |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Number of phases | 1-phase | 1-phase |
| Core type | Toroidal (3C90) | Toroidal (Vitroperm 500 F, W514) |
| Core dimensions | 5.1 × 3.2 × 1.9 cm | 3 × 2 × 1.5 cm |
| Number of turns of primary winding | 42 turns | 22 turns |
| Number of turns of secondary winding | 85 turns | 45 turns |
| Primary winding caliber | 13 AWG | 13 AWG |
| Secondary winding caliber | 16 AWG | 16 AWG |
| Flux density | 0.2 T | 0.8 T |
| Permeability | 3456 | 53,355 |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Vin | 119 V | 120 V |
| Vo | 247 V | 245 V |
| Iin | 7.95 A | 7.44 A |
| Io | 3.75 A | 3.64 A |
| Efficiency | 97.9% | 99.8% |
| Pnom | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| 6% | 93.5% | 98.4% |
| 25% | 98.1% | 99.8% |
| 50% | 97.7% | 99.6% |
| MFT | MFT with Ferrite Core | MFT with Nanocrystallyne Core |
|---|---|---|
| Power density | 16.1 kW/L | 36.9 kW/L |
| Core cost | USD 13.86 | USD 28.24 |
| Winding cost | USD 1.86 | USD 0.99 |
| Total cost of MFT | USD 15.72 | USD 29.23 |
| Reference | Material | Bac (T) | Frequency (kHz) | Power (kVA) | Efficiency (%) | Year | Power Density (kW/L) |
|---|---|---|---|---|---|---|---|
| [9] | Silicon Steel | 0.6 | 0.6 | 0.8 | 99 | 2017 | 1.29 |
| [19] | Nanoc./Silic. Steel | 0.9/0.1 | 1 | 1 | 80.2/99.1 | 2019 | 2.50/0.25 |
| [10] | Silicon Steel | 0.5 | 1 | 35 | 99.4 | 2017 | 2.96 |
| [21] | Nanocrystalline | 0.46 | 10 | 200 | 99.4 | 2020 | 8.00 |
| [18] | Ferrite | 0.35 | 20 | 10 | 99.2 | 2017 | 9.25 |
| [17] | Nanocrystalline | 0.9 | 5 | 50 | 99.5 | 2016 | 11.50 |
| [16] | Nanocrystalline | 0.9 | 5 | 1 | 99.4 | 2018 | 15.01 |
| [15] | Nanocrystalline | 0.3 | 10 | 5 | 96 | 2017 | 19.90 |
| [22] | Nanoc./Ferrite | 0.3/0.2 | 10 | 35 | 99.2/99.5 | 2016 | 23.30/11.7 |
| [14] | Nanocrystalline | 0.3 | 10 | 35 | 98 | 2017 | 23.30 |
| This proposal | Nanocrystalline | 0.8 | 20 | 1 | 99.8 | 2021 | 36.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz, D.; Ortíz, J.; Moreno, E.; Fuerte, C.; Venegas, V.; Vargas, A.; Vergara, H. Ferrites and Nanocrystalline Alloys Applied to DC–DC Converters for Renewable Energies. Appl. Sci. 2022, 12, 709. https://doi.org/10.3390/app12020709
Ruiz D, Ortíz J, Moreno E, Fuerte C, Venegas V, Vargas A, Vergara H. Ferrites and Nanocrystalline Alloys Applied to DC–DC Converters for Renewable Energies. Applied Sciences. 2022; 12(2):709. https://doi.org/10.3390/app12020709
Chicago/Turabian StyleRuiz, Dante, Jorge Ortíz, Edgar Moreno, Claudio Fuerte, Vicente Venegas, Alejandro Vargas, and Héctor Vergara. 2022. "Ferrites and Nanocrystalline Alloys Applied to DC–DC Converters for Renewable Energies" Applied Sciences 12, no. 2: 709. https://doi.org/10.3390/app12020709
APA StyleRuiz, D., Ortíz, J., Moreno, E., Fuerte, C., Venegas, V., Vargas, A., & Vergara, H. (2022). Ferrites and Nanocrystalline Alloys Applied to DC–DC Converters for Renewable Energies. Applied Sciences, 12(2), 709. https://doi.org/10.3390/app12020709






