Abstract
With the rise of technology in recent years, more people are studying distributed system architecture, such as the e-government system. The advantage of this architecture is that when a single point of failure occurs, it does not cause the system to be invaded by other attackers, making the entire system more secure. On the other hand, inner product encryption (IPE) provides fine-grained access control, and can be used as a fundamental tool to construct other cryptographic primitives. Lots of studies for IPE have been proposed recently. The first and only existing decentralized IPE was proposed by Michalevsky and Joye in 2018. However, some restrictions in their scheme may make it impractical. First, the ciphertext size is linear to the length of the corresponding attribute vector; second, the number of authorities should be the same as the length of predicate vector. To cope with the aforementioned issues, we design the first decentralized IPE with constant-size ciphertext. The security of our scheme is proven under the ℓ-DBDHE assumption in the random oracle model. Compared with Michalevsky and Joye’s work, ours achieves better efficiency in ciphertext length and encryption/decryption cost.
1. Introduction
Identity-based encryption (IBE) was first introduced by Shamir [1] in 1985, which allows a sender to use the recipient’s identity to encrypt a message. An identity is a unique string directly linking to a user, e.g., an email address, a student ID number, an employee ID, etc. The first IBE scheme was proposed by Boneh and Franklin [2] in 2001. Though IBE reduces the management cost for traditional public key infrastructures, a drawback of IBE is that an encrypted datum can be only shared at a coarse-grained control level. This may not be suitable in the real world because the sender should know the particular recipient in advance. In a system, there may be a lot of users, and the identities of recipients may be uncertain when a message is encrypted. To solve the issue, Katz, Sahai and Waters [3] conceptualized inner product encryption (IPE) in 2008. In an IPE scheme, each ciphertext is associated with an attribute vector that can be decrypted by a private key associated with a predicate vector if and only if the inner product of and is zero, denoted by . IPE can be viewed as the generalization for several cryptographic primitives. For example, given two identities, , we can encode it into two vectors, , and we have
Thus, we are able to represent the functionality of IBE using IPE. Since then, lots of IPE scheme have been proposed [4,5,6,7,8,9,10,11]. In additional to its theoretical value, IPE provides lots applications in fine-grained access control as well. Using the encoding technique, IPE can be converted into many types of one-to-many encryption, such as broadcast encryption [12,13,14], attribute-based encryption [15,16,17] and subset predicate encryption [18,19,20]. Therefore, by adopting IPE, one can realize multiple kinds of flexible access control using only a single cryptographic primitive. Recently, more applications for IPE have been developed, e.g., privacy-preserving video streaming [21], access control for WBAN [22], secure keyword searching [23] and outsourced data integration [24]. It shows the possibility for the application of IPE in various environments.
Traditionally, IPE is a centralized architecture, which needs a trusted server to issue private keys for all users. However, a centralized paradigm may not be practical in a real-world environment. In practice, the privileges of a user are usually given by different authorities. In addition, a centralized architecture would suffer from the problem of a single point of failure. To cope with these problems, Michalevsky and Joye gave the first Decentralized IPE (DIPE) scheme [25] in 2018. In a DIPE scheme, there are multiple authorities. For a user, each authority will output a partial private key for this user, without interaction with each other.
After studying the DIPE scheme of Michalevsky and Joye, we found two problems. One problem is the large ciphertext size. In their scheme, the ciphertext size is group elements, where n is the length of attribute/predicate vector and k is the parameter of k-linear assumption. Since k can be viewed as a part of the security parameter, which is a constant, the ciphertext size is linear to the length of attribute/predicate vector. Another problem is that, in their scheme, each authority is responsible for issuing a private key for only an element in the user’s predicate vector. This setting brings two disadvantages. First, unlike to decentralized attribute-based encryption [26,27,28], where the attributes of a user is independent to each other, the elements in a predicate vector for a user are usually closely bonded. Second, since each authority issues a partial private key for one element in a predicate vector, the number of authorities must equal to the length of predicate vector, which may not be practical, i.e., in the scheme of [25], an authority cannot responsible for multiple attributes, which is common in practice.
1.1. Contribution
In this manuscript, we propose a novel DIPE scheme with constant-size ciphertexts, and we give a formal security proof for the selective IND-CPA security under q-DBDHE assumption. We also modify the way an authority produces private keys from predicate vectors due to the aforementioned issue. In addition, we implement our construction in Python with Charm-Crypto library and C with PBC library to evaluate the performance.
1.2. Organization
In Section 2, we introduce the notations and complexity assumption used in our manuscript, and the definition of decentralized inner product encryption. The security of DIPE is defined in Section 2, as well. In Section 3, we describe our proposed scheme in detail and show the correctness. In Section 4, we give the formal security proof for our scheme. In Section 5, we show the comparison results between our scheme and the DIPE scheme in [25]. Finally, we conclude our work in Section 6.
2. Preliminaries
In this section, we introduce the definition and security requirements of decentralized inner product encryption. In addition, we demonstrate the notation and complexity assumption used in our work.
2.1. Notation
Given a set S, “randomly choose an element x from the set S” is denoted as . For algorithm A, we write to denote “x is the output by running A”. The symbol “⊥” means a failed decryption that recovers the certain message unsuccessfully. “PPT” algorithm means "probabilistic polynomial time" algorithm that can run in polynomial-bounded time.
2.2. Bilinear Maps and Complexity Assumption
Let and be two multiplicative cyclic groups with prime order p. A map e is called a bilinear map if the following properties hold:
- Bilinearity: For , and , the equation holds.
- Non-Degeneracy: Assume g is the generator of , then, .
- Computability: For , there exists an efficient algorithm to compute .
Next, we show the complexity assumption, the ℓ-decisional bilinear Diffie–Hellman exponent (ℓ-DBDHE) assumption [29,30], which the security of our scheme based on.
Definition 1
(The ℓ-Decisional Bilinear Diffie–Hellman Exponent Problem). Let be a group. g is a generator of , and are two integers. Given a tuple:
decide if or is a random element of .
Let . For an algorithm , the advantage of in solving the ℓ-DBDHE problem is defined as:
Definition 2
(The ℓ-Decisional Bilinear Diffie–Hellman Exponent Assumption). We say that the ℓ-decisional bilinear Diffie–Hellman exponent assumption holds if for all PPT algorithms, is negligible.
2.3. Definition of Decentralized Inner Product Encryption
The difference between DIPE and IPE is that a private key of DIPE is generated by multiple authorities, while a private key of IPE is generated by a centralized authority.
2.3.1. System Model
A DIPE scheme contains three roles, i.e., sender, receiver and authorities. A sender is a participant of the system who transfers the encrypted data to the receiver. The data are encrypted by an attribute vector before delivered to receiver. Authorities are responsible for issuing partial keys for receivers who make a request to obtain partial keys. The authorities will issue partial keys according to the predicate vector of the receiver. A receiver is a participant who wants to receive encrypted data. After a receiver receives all the partial keys from the authorities, the receiver will perform a decryption procedure to recover the data.
2.3.2. Definition of DIPE
A decentralized inner product encryption scheme consists of five PPT algorithms: , , , and . Unlike the single authority construction, in DIPE, the private key of a user is generated by multiple authorities. Each authority computes a “partial key ” of a user using its master secret key and the user’s predicate vector. The full private key of a user is , where n is the number of authorities:
- . An authority in the system or a third party will run the algorithm. Taking as input a security parameter , the algorithm outputs a public parameter .
- . All authorities will run the algorithm. Taking as inputs a public parameter , and a number i, the algorithm outputs a master secret key and a public key of each authority, where i is the index of authority.
- . All authorities will run the algorithm. Taking as inputs a public parameter , a master secret key , a global identity and a predicate vector , the algorithm outputs a partial key of the private key associated with generated by authority. Note that the description of will be included in the partial keys.
- . A sender will run the algorithm. Taking as inputs a public parameter , all the public keys of each authority , a message M and an attribute vector , the algorithm outputs a ciphertext C associated with . Note that the description of will be included in the ciphertext.
- . A receiver will run the algorithm. Taking as inputs all the partial key of private keys of each authority , a ciphertext C and an attribute vector , the algorithm outputs a message M or ⊥.
- Correctness. For , ,, , where , we have that:
- -
- If , then.
- -
- If , then.
2.3.3. Security Model
The security definition used in our manuscript is the security against indistinguishability under selective chosen-plaintext attacks (sIND-CPA). “Indistinguishability” means that given a ciphertext, which is the encryption of one of two messages chosen by an adversary, the adversary tries to tell which of the two messages is encrypted. In addition, “chosen-plaintext attacks” means that an adversary is allowed to obtain the ciphertext for the plaintext of its choice. Finally, “selective” means that an adversary chooses a target vector and submits to the challenger before Setup phase.
Definition 3 (The sIND-CPA Security).
Let be a probabilistic polynomial-time adversary. We define our security via the following interactive game between and a challenger :
- .chooses an attribute vector and sends to .
- .runs the Setup algorithm to generate and , where , is the index of authority. sends and to .
- .can make polynomially times queries of the following oracle.
- -
- KeyExtract oracle: sends a predicate vector and a global identity to , and returns the private key of . There is a restriction, that is, .
- .submits two distinct messages of the same length to . then randomly chooses and generates ciphertexts . Then, sends to .
- .Same as Phase1.
- .will output a bit and win the game if .The advantage of winning the game is defined as:
A DIPE scheme is sIND-CPA secure if for all PPT adversaries , is negligible.
3. The Proposed Scheme
In this section, we present our decentralized inner product encryption scheme with constant-size ciphertexts. The notations used in the proposed scheme are defined in Table 1.

Table 1.
Notations.
The algorithm performs the following steps:
- Randomly choose bilinear groups of prime order p with a generator ;
- Choose an one-way hash function, ;
- Output the public parameter .
Each authority in the system performs the following steps to generate its public key and its master secret key:
- Choose ;
- Choose ;
- Choose ;
- Output a public key of authority i, ;
- Output a master secret key of authority , .
Each authority in the system performs the following steps to generate a part of private key for receivers in the system"
- Return failure symbol ⊥ if ;
- Output the private key , where.
Unlike the KeyGen algorithm in [25], we use the entire predicate vector in performed by a single authority .
A sender computes the ciphertext for a message and an attribute vector by the following steps:
- Choose ;
- Output the ciphertexts as , where.
To decrypt, a receiver uses the private key to recover the message M from a ciphertext C as follows:
- If , perform the following computation; otherwise, return ⊥;
- Compute.
- Compute .
The correctness of the decryption algorithm is described as follows. For convenience, let , for . It is enough to show that
We first take a look at the numerator:
where . Using the fact that
we have:
Thus, the numerator is:
In addition, the denominator is:
Finally, we have:
4. Security Proof
In this section, we will prove the sIND-CPA security for the proposed under the ℓ-DBDHE assumption in the random oracle model.
Theorem 1.
The proposed DIPE scheme is sIND-CPA secure if the q-DBDHE assumption holds.
Proof .
Assume there is a polynomial-time adversary that can win the sIND-CPA game with a non-negligible advantage. Then, we construct a PPT challenger able to solve the ℓ-DBDHE problem as follows:
First of all, is given an instance of the q-DBDHE problem, that is,
where T is or a random element of . Then, interacts with in the game as follows.
Initialization.
first sends the target vector to .
Setup.
Without loss of generality, we may assume that can obtain the first master secret keys of authorities, where :
- Set . Define ;
- Choose ;
- Compute and ;
- For , , compute and following the AuthSetup shown in Section 3;
- Send to the public keys , and the master secret key s .
Here, we implicitly set
Phase1.
maintains a hash list, H-list, to store the mapping result of . Then, is allowed to query the following oracles:
- Hash oracle:This oracle takes and (global identity) as input and outputs an element of . If there exists a record in the H-list, return . Otherwise, the oracle performs the following steps:
- If , then randomly choose and return to ;
- Choose ;
- Implicitly setby computingThis can be efficiently computed with the instance of q-DBDHE problem;
- Return to and store into the H-list.
- KeyExtract oracle:Upon receiving a vector and a global identity from , where (As shown in Definition 3, is not allowed to make a KeyExtract query with , otherwise can break the security trivially.) performs as follows. For , can be easily computed using the algorithm shown in Section 3 since knows . As for , it can be computed from the instance of the ℓ-DBDHE problem by the following steps:
- Query and set . Let , whereNote that can be found in the H-list;
- For , computeOne can note that, in the exponent of ,the only unknown term is . However, the coefficient of isThus, can be easily computed using the knowledge of and the instance of the ℓ-DBDHE problem;
- ComputeOne can note that the exponent of isAgain, the coefficient of the unknown term isTherefore, can be also computed using the knowledge of and the instance of the ℓ-DBDHE problem.
Challenge.
submits two message and of the same length, and computes the challenge ciphertext as follows:
- Choose ;
- Set ;
- Compute
- Compute
- Output to .
Phase2.
Same as Phase1.
Guess.
outputs a bit . outputs 1 if ; otherwise, outputs 0.
If , then:
and hence is a valid ciphertext. Thus, we have:
and
If T is a random element from , then the message is completely hidden from the adversary’s view, since , and are all independently random elements. Therefore, the advantage of the adversary is:
and
Finally, the advantage of in solving the ℓ-DBDHE problem is:
Therefore, if there is an adversary that wins the sIND-CPA game with a non-negligible advantage, then we can construct an algorithm to solve the ℓ-DBDHE problem with a non-negligible advantage in polynomial time. □
5. Comparison
In this section, we compare our scheme with [3,5,8,11,25] in time complexity, space complexity and other security features. Among these works, [3,5,8,11] are IPE schemes and [25] is a DIPE scheme. In addition, we implement our scheme and the scheme of [25] in Python and C, and compare the execution time of our algorithms with theirs.
5.1. Asymptotic Comparisons
In Table 2, we show the encryption cost and decryption cost of each scheme. For encryption, the exponentiation computation cost is linear with the vector size, which is better than others, except [5]. In addition, we only need ℓ times exponentiation computations plus two pairing computations in decryption. Though our efficiency is not the best among [3,5,8,11], our scheme achieves decentralization while others do not. In [25], they need n times exponentiation computations plus pairing computations, where . Thus, both of the cost for our scheme in encryption and decryption algorithm is more efficient.

Table 2.
Comparison of time complexity.
The length of ciphertexts and private keys are shown in Table 3. Due to decentralization, it is normal that the private key length of DIPE is larger than that of IPE. In addition, though, we can see that [25] needs about elements in for a private key. Indeed, the value of k can be small in their work. However, in our work, the vector size could be large in reality. Therefore, our private key length is larger than others, which may need more storage. Nevertheless, if the value of k is greater or equal than our vector size. Then, we only need less storage than [25] in storing the private key. Note that the work of [11] achieves constant private key size. As a trade-off, their ciphertext size is , which might be longer then others in the respect of the curve used in implementation.

Table 3.
Comparison with the previous schemes in space complexity.
In the comparison of ciphertext length, both our work and [5] have the least ciphertext length and only needs two elements in plus an element in . It means that our ciphertext length is independent with the vector size and the number of the authorities. It can reduce the burden of connection between sender and receiver for transmitting ciphertext. However, the ciphertext length of [25] dependent on n and k. To the best of our knowledge, our work is the first DIPE scheme achieving a constant-size ciphertext.
In Table 4, only our work, as well as [25], achieves a decentralized framework. In order to avoid collusion between users, a and a predicate (or an attribute) vector are mapped to a value by a random oracle. Therefore, the security of ours and [25]’s are both proven in the random oracle model. As far as we know, there is no standard model for DIPE currently. In addition, although ours and [25]’s are both CPA secure, the latter achieves adaptive security, which is stronger than our selective model. Though all the works in Table 4 achieve CPA security, we should note that [11]’s security is proven in a relatively less used model, called a co-selective model, where an adversary outputs several vectors for querying the Key-Extract oracle in Phase 1 before seeing the system parameter. Although selective security and co-selective security are both weaker than full security, both notions are incomparable in general by definition.

Table 4.
Property comparison.
5.2. Experimental Result
In this section, we show the experimental results of our construction and the construction of [25] via Python and C languages, and analyze the execution time of the five algorithms.
Table 5 shows the system configuration and the chosen pairing group of Python. We implement our construction by Charm-Crypto library in Python. In our implementation, the pairing group is a symmetric pairing curve with a 512-bit-based field. The experiment is executed on Intel(R) Core(TM) i7-10875H CPU at 3.60GHz processor, 4 GB memory size and under the Ubuntu-16.04 operating system. In addition, we also implement our scheme and [25] in C with the pbc library, where a Type a1 pairing group is used. Table 6 shows the details for the system configuration of our C implementation.

Table 5.
System configuration and elliptic curve for Python.

Table 6.
System configuration and elliptic curve for C.
We analyze the time cost of each algorithm in our DIPE scheme below. In our experiment, the length of (global identity) is set to 10 bits for convenience. However, note that the length of a can be arbitrarily long since it is a input of the hash function. In [25], since each authority generates a partial key for an element of the predicate vector, therefore, the length of th vector size should be the same as the total number of authorities, ranging from 1 to 25 in our implementation. In addition, the value of k in [25] is set to one to minimize the cost of their work. The value of each point on the figure is obtained by executing the algorithm 1000 times and obtaining the value of the average execution time.
For the implementation using Python, Figure 1b shows that the time spent by [25] on the AuthSetup algorithm is more time-consuming than ours. In Figure 1d,e, we can note that the Encrypt and Decrypt algorithms are both growing linearly in two schemes when the number of authorities increases. However, ours has better performance than theirs. Then, Figure 1c exhibits that KeyGen is the most time-consuming algorithm due to the decentralized network. Nevertheless, we have relatively poorer performance than [25]. Since our decentralization is different from [25], in our scheme, each authority generates a partial key for a whole predicate vector instead of only an element. Therefore, the execution time of KeyGen is longer. Finally, in Figure 1a, the Setup algorithm only generates some generator of , some elements of and the description of a hash function in both schemes. Thus, execution time is independent of the total number of authorities and vector size. In addition, our scheme has one more advantage, that is, the length of the predicate vector does not need to bind with the total number of authorities with same value.
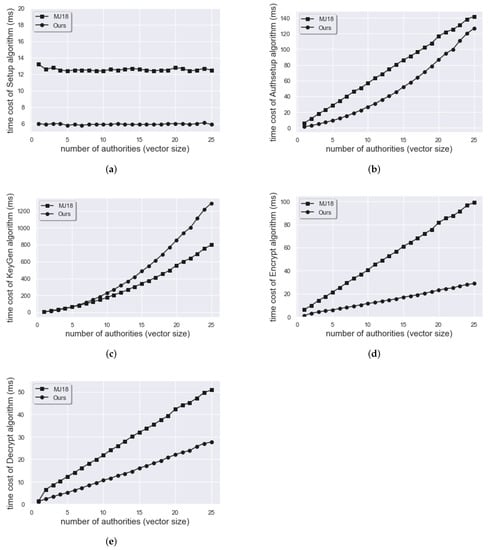
Figure 1.
The time cost for Python Implementation of (a) Setup, (b) Authsetup, (c) KeyGen, (d) Encrypt, (e) Decrypt algorithm. (Pairing group: SS512, =10, # of authorities = = = [1,…,25], k = 1).
In addition, Figure 2 shows the time cost of our scheme and [25] using C. Similar to the results using Python, Figure 2a,b show that in the comparison of the time costs of Setup and AuthSetup algorithms, our scheme is more efficient than [25]. As shown in Figure 2c,e, the costs for KeyGen and Decryption of ours are pretty close to those of [25]. Interestingly, the result of Encryption in C is opposite to that in Python. Figure 2d shows that the Encrypt algorithm of [25] is faster than ours. The reason for this might be due to the system configuration or the language. We will keep figuring out more details that may be inspired from this difference.
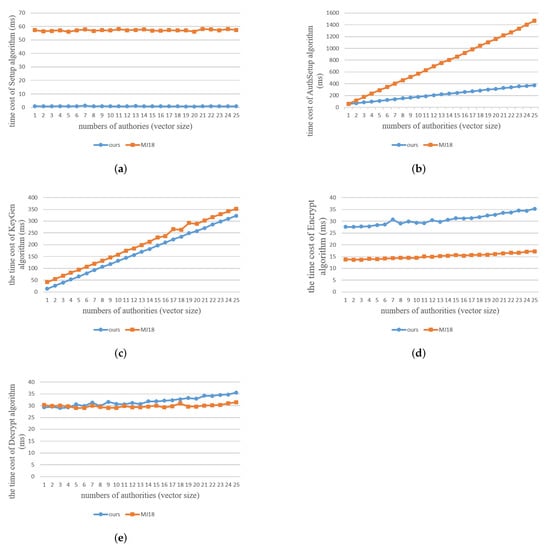
Figure 2.
The time cost for C Implementation of (a) Setup, (b) Authsetup, (c) KeyGen, (d) Encrypt, (e) Decrypt algorithm. (Pairing group: Type a1, = 10, # of authorities = = = [1,…,25], k = 1).
6. Conclusions
Thus far, there is only one decentralized inner product encryption, proposed by Michalevsky et al. in 2018. In their scheme, however, the length of ciphertexts are dependent on the number of authorities, which may become a bottleneck in the system. Therefore, we would like to solve this problem. In this manuscript, we present a novel decentralized inner product encryption which achieves constant-size ciphertexts. In addition, our scheme is proven to be selectively secure under the ℓ-DBDHE assumption. We further implement our scheme and the scheme of [25] to analyze the execution time. Except for the KeyGen algorithm, our work has better performance in the remaining four algorithms (Setup, AuthSetup, Encrypt, Decrypt). Yet, our scheme is the first DIPE scheme achieving constant-size ciphertext, and there are several potential improvements. One direction could be to upgrade the security to chosen-ciphertext security. Several generic methods [31,32,33,34,35] have been proposed in the literature, however, constructing a DIPE scheme with direct chosen-ciphertext security is an open problem. In addition, the security of our scheme is proven under the random oracle model. How to construct a DIPE scheme that is secure in the standard model is also a worth-fighting goal.
Author Contributions
Conceptualization, Y.-F.T. and S.-J.G.; methodology, Y.-F.T.; formal analysis, Y.-F.T.; investigation, Y.-F.T. and S.-J.G.; writing—original draft preparation, S.-J.G.; writing—review and editing, Y.-F.T.; supervision, Y.-F.T.; project administration, Y.-F.T.; funding acquisition, Y.-F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan (ROC), under grant numbers MOST 110-2221-E-004 -003-, MOST 110-2218-E-004-001-MBK, MOST 109-2221-E-004 -011 -MY3 and MOST 109-3111-8-004-001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Advances in Cryptology; Blakley, G.R., Chaum, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology—CRYPTO 2001; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Katz, J.; Sahai, A.; Waters, B. Predicate Encryption Supporting Disjunctions, Polynomial Equations, and Inner Products. In Advances in Cryptology—EUROCRYPT 2008; Smart, N., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 146–162. [Google Scholar]
- Lewko, A.; Okamoto, T.; Sahai, A.; Takashima, K.; Waters, B. Fully Secure Functional Encryption: Attribute-Based Encryption and (Hierarchical) Inner Product Encryption. In Advances in Cryptology—EUROCRYPT 2010; Gilbert, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 62–91. [Google Scholar]
- Attrapadung, N.; Libert, B. Functional Encryption for Inner Product: Achieving Constant-Size Ciphertexts with Adaptive Security or Support for Negation. In Public Key Cryptography—PKC 2010; Nguyen, P.Q., Pointcheval, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 384–402. [Google Scholar]
- Park, J.H. Inner-product encryption under standard assumptions. Des. Codes Cryptogr. 2011, 58, 235–257. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, W. A Predicate Encryption Scheme Supporting Multiparty Cloud Computation. In Proceedings of the 2015 International Conference on Intelligent Networking and Collaborative Systems, Taipei, Taiwan, 2–4 September 2015; pp. 252–256. [Google Scholar]
- Kim, I.; Hwang, S.O.; Park, J.H.; Park, C. An Efficient Predicate Encryption with Constant Pairing Computations and Minimum Costs. IEEE Trans. Comput. 2016, 65, 2947–2958. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Wang, Y. Efficient inner product encryption for mobile clients with constrained computation capacity. Int. J. Innov. Comput. Inf. Control 2019, 15, 209–226. [Google Scholar]
- Soroush, N.; Iovino, V.; Rial, A.; Roenne, P.B.; Ryan, P.Y.A. Verifiable Inner Product Encryption Scheme. In Public-Key Cryptography—PKC 2020; Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 65–94. [Google Scholar]
- Tseng, Y.F.; Liu, Z.Y.; Tso, R. Practical Inner Product Encryption with Constant Private Key. Appl. Sci. 2020, 10, 8669. [Google Scholar] [CrossRef]
- Fiat, A.; Naor, M. Broadcast Encryption. In Advances in Cryptology—CRYPTO’ 93; Stinson, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 480–491. [Google Scholar]
- Acharya, K. Secure and efficient public key multi-channel broadcast encryption schemes. J. Inf. Secur. Appl. 2020, 51, 102436. [Google Scholar] [CrossRef]
- Chen, L.; Li, J.; Zhang, Y. Anonymous Certificate-Based Broadcast Encryption With Personalized Messages. IEEE Trans. Broadcast. 2020, 66, 867–881. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Li, Y.; Wang, H.; Wang, H.; Wang, H.; Chen, J.; You, Z. An Efficient Attribute-Based Encryption Scheme With Policy Update and File Update in Cloud Computing. IEEE Trans. Ind. Inform. 2019, 15, 6500–6509. [Google Scholar] [CrossRef]
- Xue, L.; Yu, Y.; Li, Y.; Au, M.H.; Du, X.; Yang, B. Efficient attribute-based encryption with attribute revocation for assured data deletion. Inf. Sci. 2019, 479, 640–650. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Ning, J.; Huang, X.; Poh, G.S.; Wang, D. Attribute Based Encryption with Privacy Protection and Accountability for CloudIoT. IEEE Trans. Cloud Comput. 2020, 1. [Google Scholar] [CrossRef]
- Katz, J.; Maffei, M.; Malavolta, G.; Schröder, D. Subset Predicate Encryption and Its Applications. In Cryptology and Network Security; Capkun, S., Chow, S.S.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 115–134. [Google Scholar]
- Chatterjee, S.; Mukherjee, S. Large Universe Subset Predicate Encryption Based on Static Assumption (Without Random Oracle). In Topics in Cryptology—CT-RSA 2019; Matsui, M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 62–82. [Google Scholar]
- Tseng, Y.F.; Gao, S.J. Efficient Subset Predicate Encryption for Internet of Things. In Proceedings of the 2021 IEEE Conference on Dependable and Secure Computing (DSC), Edinburgh, UK, 22–24 June 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Rajan, M.; Varghese, A.; Narendra, N.; Singh, M.; Shivraj, V.; Chandra, G.; Balamuralidhar, P. Security and Privacy for Real Time Video Streaming Using Hierarchical Inner Product Encryption Based Publish-Subscribe Architecture. In Proceedings of the 2016 30th International Conference on Advanced Information Networking and Applications Workshops (WAINA), Crans-Montana, Switzerland, 23–25 March 2016; pp. 373–380. [Google Scholar] [CrossRef]
- Xiong, H.; Yang, M.; Yao, T.; Chen, J.; Kumari, S. Efficient Unbounded Fully Attribute Hiding Inner Product Encryption in Cloud-Aided WBANs. IEEE Syst. J. 2021, 1–9. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Mu, Y.; Hu, Y. Fully Secure Hierarchical Inner Product Encryption for Privacy Preserving Keyword Searching in Cloud. In Proceedings of the 2015 10th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Krakow, Poland, 4–6 November 2015; pp. 449–453. [Google Scholar] [CrossRef]
- Huang, K.C.; Chen, Y.C. Privacy Preserving Outsourced Data Integration from Inner Product Encryption. In Proceedings of the 2021 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Hualien City, Taiwan, 16–19 November 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Michalevsky, Y.; Joye, M. Decentralized Policy-Hiding ABE with Receiver Privacy. In Proceedings of the 23rd European Symposium on Research in Computer Security, ESORICS 2018, Barcelona, Spain, 3–7 September 2018; pp. 548–567. [Google Scholar]
- Chase, M. Multi-authority Attribute Based Encryption. In Theory of Cryptography; Vadhan, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 515–534. [Google Scholar]
- Lewko, A.; Waters, B. Decentralizing Attribute-Based Encryption. In Advances in Cryptology—EUROCRYPT 2011; Paterson, K.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 568–588. [Google Scholar]
- Zhang, L.; Gao, X.; Kang, L.; Liang, P.; Mu, Y. Distributed Ciphertext-Policy Attribute-Based Encryption With Enhanced Collusion Resilience and Privacy Preservation. IEEE Syst. J. 2021, 1–12. [Google Scholar] [CrossRef]
- Boneh, D.; Gentry, C.; Waters, B. Collusion Resistant Broadcast Encryption with Short Ciphertexts and Private Keys. In Advances in Cryptology—CRYPTO 2005; Shoup, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 258–275. [Google Scholar]
- Boneh, D.; Hamburg, M. Generalized Identity Based and Broadcast Encryption Schemes. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008. [Google Scholar]
- Canetti, R.; Halevi, S.; Katz, J. Chosen-Ciphertext Security from Identity-Based Encryption. In Advances in Cryptology—EUROCRYPT 2004; Cachin, C., Camenisch, J.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 207–222. [Google Scholar]
- Fujisaki, E.; Okamoto, T. Secure Integration of Asymmetric and Symmetric Encryption Schemes. In Advances in Cryptology—CRYPTO’ 99; Wiener, M., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 537–554. [Google Scholar]
- Fujisaki, E.; Okamoto, T. Secure Integration of Asymmetric and Symmetric Encryption Schemes. J. Cryptol. 2011, 26, 80–101. [Google Scholar] [CrossRef]
- Koppula, V.; Waters, B. Realizing Chosen Ciphertext Security Generically in Attribute-Based Encryption and Predicate Encryption. In Advances in Cryptology—CRYPTO 2019; Boldyreva, A., Micciancio, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 671–700. [Google Scholar]
- Yamada, S.; Attrapadung, N.; Hanaoka, G.; Kunihiro, N. Generic Constructions for Chosen-Ciphertext Secure Attribute Based Encryption. In Public Key Cryptography—PKC 2011; Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 71–89. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).