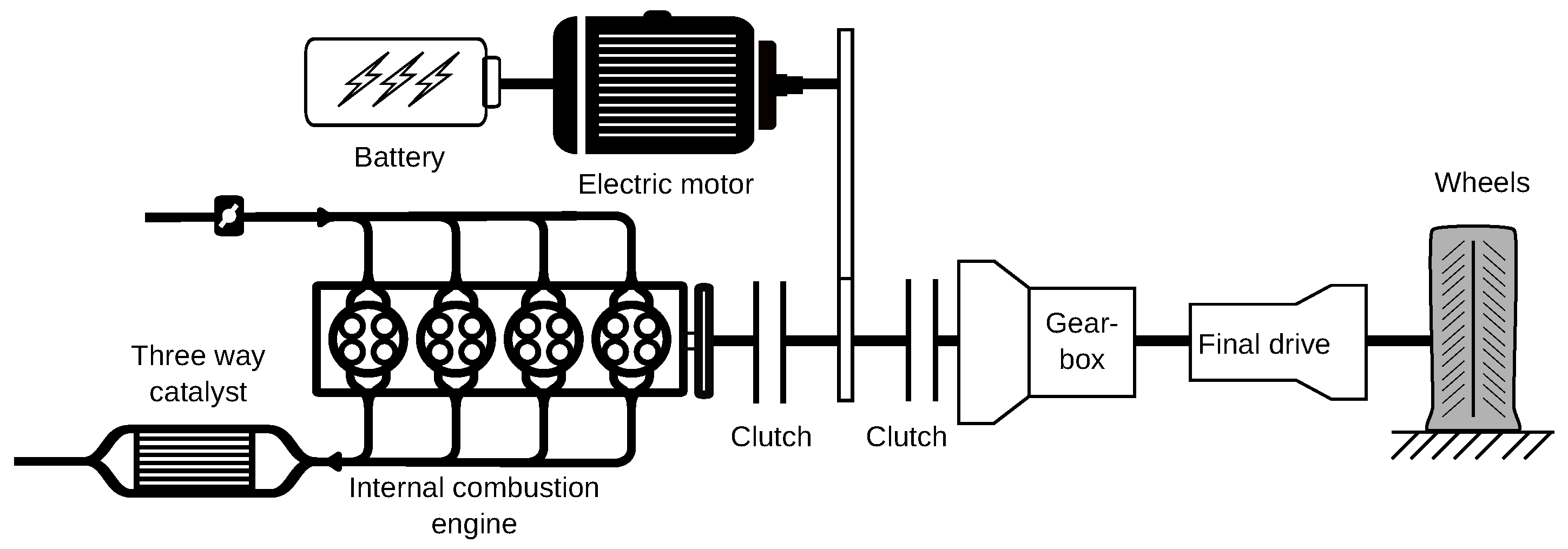
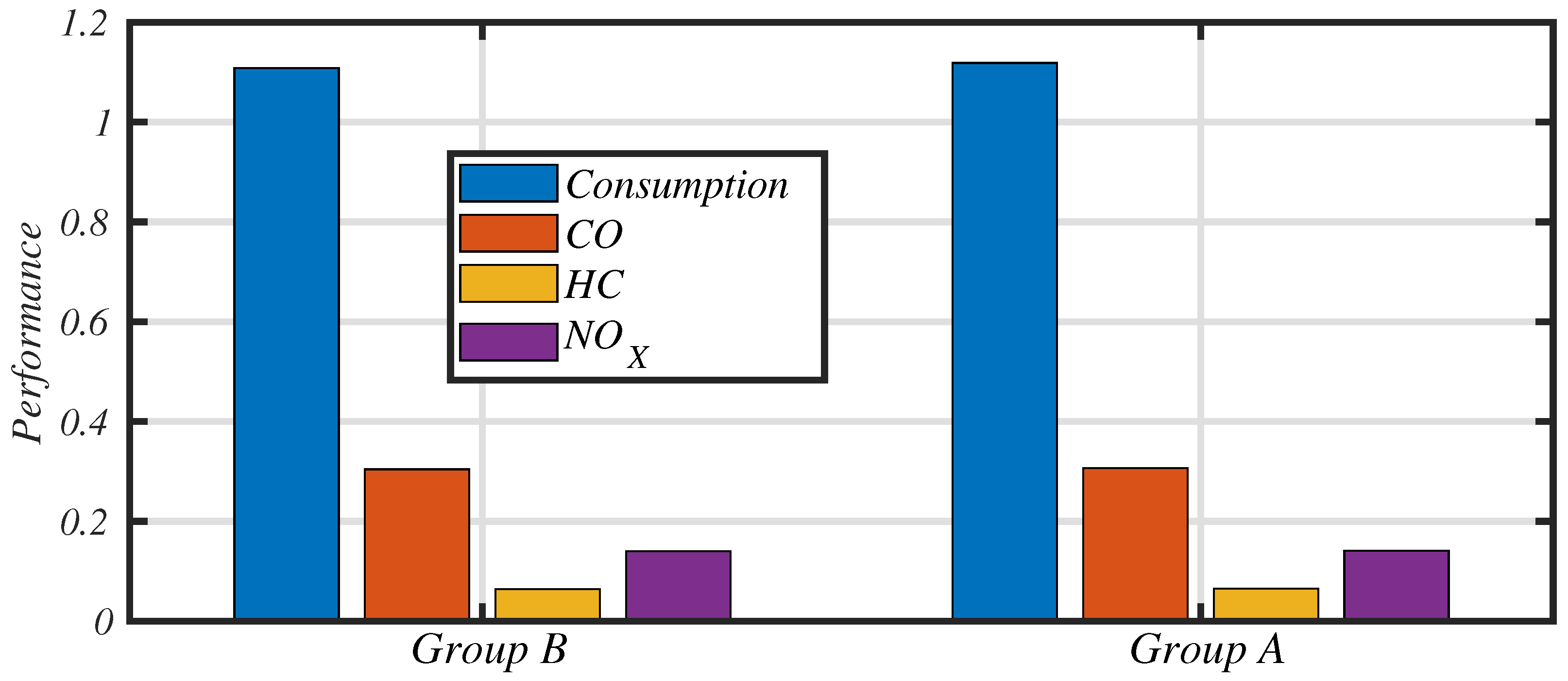1. Introduction
The Emissions Database for Global Atmospheric Research (EDGAR) is a global greenhouse gas inventory developed by the Joint Research Centre at the European Commission [
1]. Recent results show that global fossil CO
2 emissions increased by 1.9% in 2018 and 0.9% in 2019. The transportation sector is responsible for 21% of these emissions, with a slightly increasing trend. Several of the main CO
2 emitting countries reduced their emissions in 2019 compared to 2018, including the European Union (by 3.8%), United States (by 2.6%), Japan (by 2.1%), and Russia (by 0.8%). Conversely, China (3.4%) and India (1.6%) increased their emissions in 2019, representing 30.3%, and 6.8% of the global total, respectively.
The effect of global warming is particularly evident when you walk through the alps; the retreat of the glaciers is impressive. A recent study conducted by Vincent et al. [
2] shows that for the Intergovernmental Panel on Climate Change (IPCC) scenario RCP 4.5, in which greenhouse gas emissions decline after 2050 and concentrations stabilize towards the end of the 21st century, the Argentière glacier might disappear towards the end of the 21st century and the Mer de Glace surface area could decrease by 80%. The glaciers of the Alps will then almost all disappear within 80 years.
However, the transportation sector is not only responsible for a large part of global warming effects; it also impacts air pollution, which affects health. In 2018, the European Environment Agency estimated that nitrogen dioxide (NO
2) was linked to 54,000 premature deaths across the 27 EU member states and the United Kingdom. Particulate matter and black carbon also affect human health, from impairing the respiratory system to causing premature death [
3,
4]. In the case of France, the road transportation sector is responsible for 57% of total NO
x emission [
5]. Globally, fleet renewal leads to a decrease in emissions despite traffic growth. Emissions of particulate matter PM10, PM2.5, PM1.0, and black carbon (BC) from the road transportation sector include particulate from vehicle exhausts. It also encompasses PM from wear and tear on roads and certain vehicle components such as tires and brakes. The road sector is responsible for 15 to 20% of total PM emissions depending on their size, and 50% of black carbon is emitted by the combustion of fossil fuels in the vehicles.
“Is it really the end of internal combustion engines and petroleum in transport?” asked Pr Kalghatgi [
6]. Obviously, the balance is very unfavorable to fossil fuels. Helmers et al. [
7] made a life cycle assessment (LCA) of electric vehicles (EVs) versus conventional vehicles (CVs) using the ReCiPe characterization method. This method captures 18 impact categories and a single score endpoint. The results show that EVs are very advantageous with respect to climate change impacts. This is especially true when using all options, such as green electricity charging, battery production under green electricity supply, and battery second use. However, the study also reveals disadvantages of electric cars in several impact categories (e.g., human and freshwater toxicity, freshwater eutrophication, mineral resource depletion, and agricultural and urban land occupation).
Nevertheless, we have to be aware that at the time of writing, the share of renewables in global electricity generation jumped to nearly 28% in Q1 2020 from 26% in Q1 2019. The increase in renewables came mainly at the cost of coal and gas, though those two sources still represent close to 60% of the global electricity supply [
8]. Although this share will have to increase in the future to limit global warming [
9], a majority of our electricity still comes from fossil fuels.
Even if conventional vehicle will be replaced by all electric vehicle in the future, we must keep working on the combustion engine. There is still room for improvement. Leach et al. [
10] reviewed new developments that can improve engine efficiency. Among these, we can cite increasing the expansion ratio with respect to the compression ratio, reducing pumping work losses and throttle pressure drop with exhaust gas recirculation, downsizing, supercharging, etc. Furthermore, during this transition phase, hybrid electric vehicles (HEVs) will play a key role [
11]. In this context, it is of primary importance to find virtuous compromises between energy saving and pollutant emissions.
Some experiments conducted in our lab show that focusing on fuel economy can induce extra pollution. This is the case for eco-driving research, as shown by Mensing et al. in [
12]. In this study, the authors compared two eco-driving strategies on a hybrid vehicle equipped with an internal combustion engine controlled by a standard ECU (electronic control unit). The strategy that minimized fuel consumption runs at full throttle during part of the driving cycle. A slight enrichment of the fuel to air mixture occurs in this part of the cycle in order to reduce high chamber temperatures. This induces high CO and HC emissions.
Furthermore, special control parameters are adopted during cold start to shorten this stage, which emits a large amount of pollutants for several reasons: firstly, the catalyst is not efficient until it reaches its light-off temperature [
13,
14,
15]. Secondly, the HC concentration at low chamber temperatures is high due to flame quenching and misfires [
16,
17]. As a consequence, special control parameters of the ICE are used during this period. Usually, late ignition regarding optimal values is employed in order to bring more heat to the after-treatment system [
18,
19]. In this context, the energy management strategy must take into account the engine control parameters if we want to consider both fuel economy and pollutant emissions.
The article is mainly based on works by Mrs. Guille des Buttes during her PhD [
20] and pursues new developments on those works. Optimal control theory was adopted to show how the control parameters of the engine are actuated. A trade-off between fuel consumption and pollutant emissions during both cold start and normal operation of the engine was achieved. This work differs from what is usually described in the literature because here no arbitrary choices were made to find these compromises. The article is outlined as follow: after explaining the methodology in detail in
Section 2, we present the results in
Section 3.
Section 4 is a discussion of the results. In the last section, we briefly summarize our main results.
3. Results
3.1. Consumption Centered Scenario
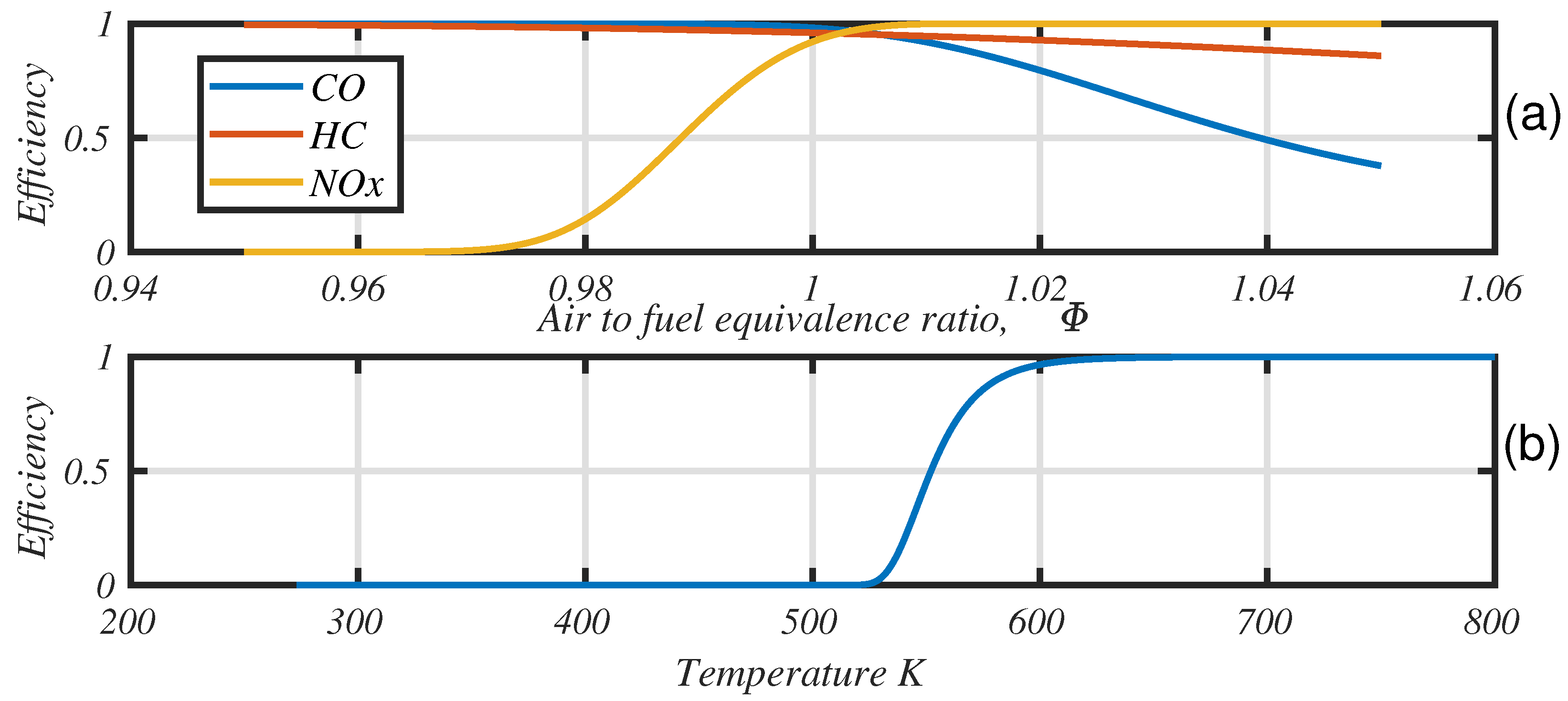
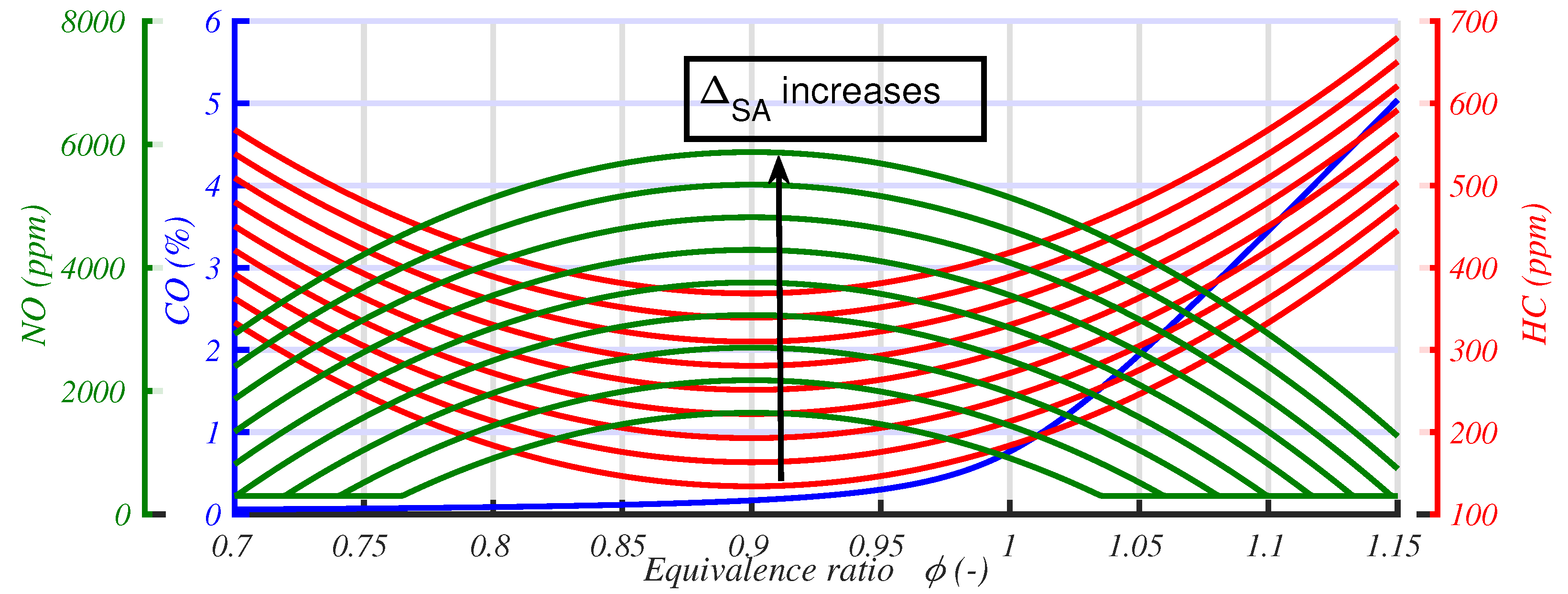
The best efficiency area lies at an equivalence ratio of
= 0.97 (the model is from [
29] and is fully developed in [
24]). However, the efficiency improvement is less than 2% between
= 0.97 and
= 1.0, and the value
= 0.97 emits a very large amount of NO
x (the NO
x conversion efficiency falls from 100% to almost 0 in this narrow window; see
Figure 4). Therefore, this strategy will not be studied.
The consumption centered scenario is calculated for stoichiometric combustion and an optimal spark advance. Results are presented in
Table 5.
These values must be compared to the CO
2 emissions targets for cars, established at 95 g CO
2/km, and the EU current regulations (EURO6) as given in
Table 2.
The first analysis shows that even very efficient sustaining hybrid drive trains have difficulties achieving the new regulations in term of CO2 emissions. In this example, the WLTC driving cycle consumes 20% more than its NEDC predecessor. This new cycle must be welcomed, as it is closer to real-world conditions, but it makes the 95 g CO2/km target all the more difficult to achieve.
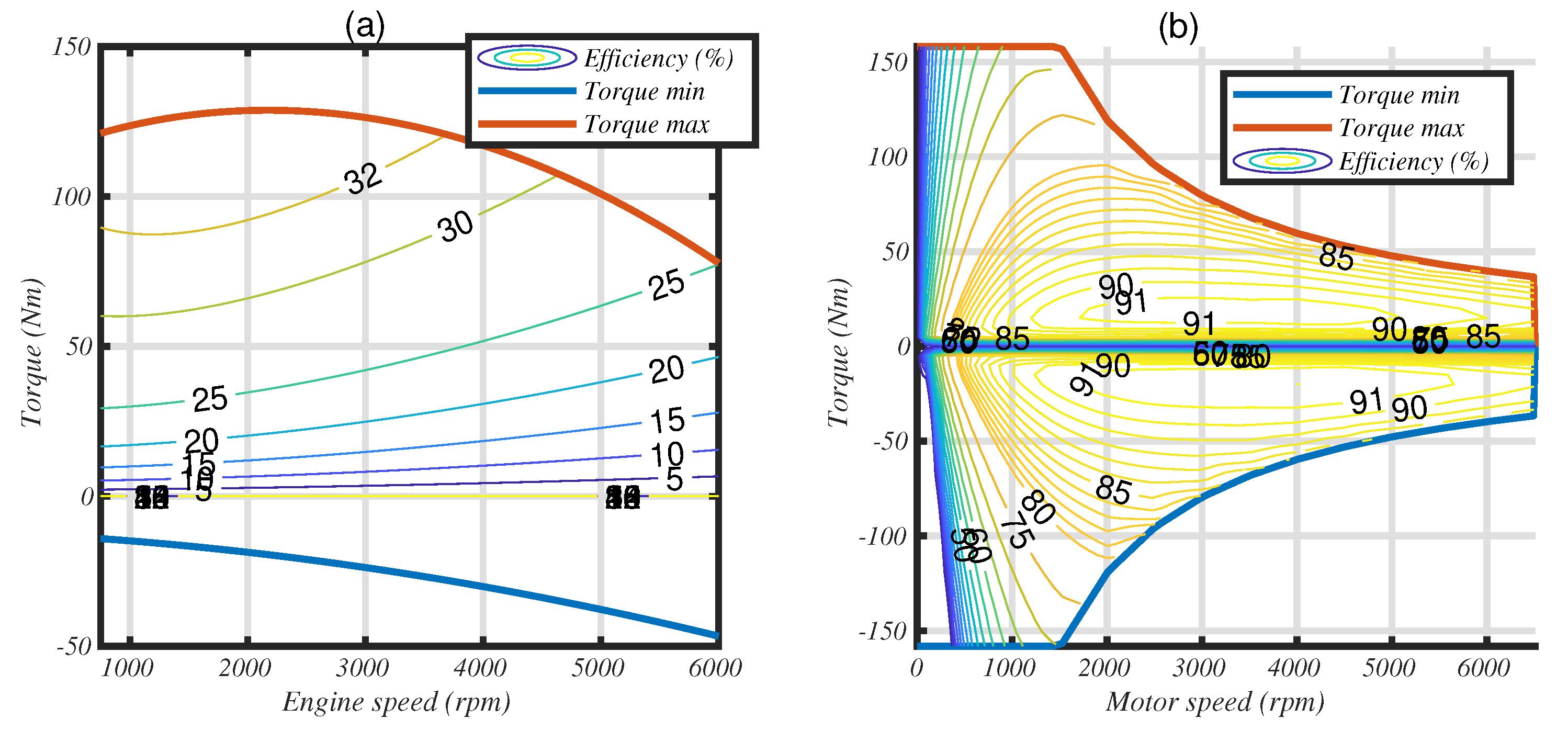
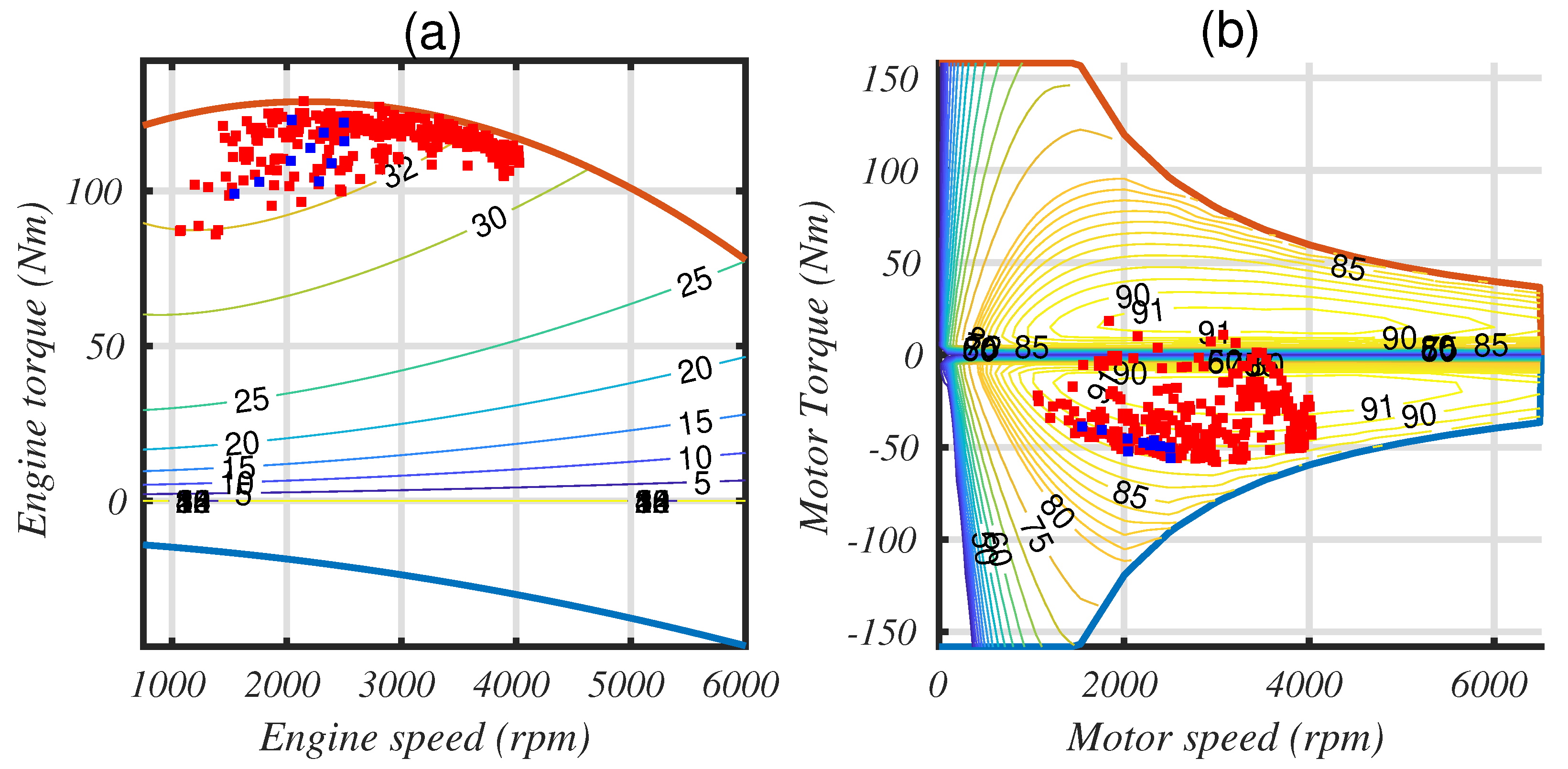
Figure 9 shows the efficiency maps of ICE and EM (the points correspond to the hybrid mode only; i.e., we do not represent the electrical machine operating points in all-electric mode).
Firstly, we notice that the best efficiency of the engine used in this article is 32% (which corresponds to a BSFC of 245 g/kWh). Better efficiency is currently possible; for example, a minimum BSFC value of 225 g/kWh is obtained with the Atkinson cycle engine that equips the Prius II (Model/Year 2004, see [
30]).
Secondly, we notice that the engine works in its best efficiency area, which is quite normal for this strategy. This is also the case for the electric machine.
A supplementary degree of freedom that is not in the scope of this work is the gearbox. Neither the number and ratios of the gears, nor the instances where the gears change have been optimized. This latter option can bring improvements in fuel consumption without sacrificing vehicle driveability [
31]. The five gear ‘20DP42’ gearbox used in this study is quite old and we currently see automated gearbox with six, seven, and even eight gears in today’s vehicle. This greatly improves fuel consumption, especially in highway mode [
32].
In term of emissions, CO or HC are very low compared to the current regulations. However, the NO
x level is almost three times higher than EURO6 limit.
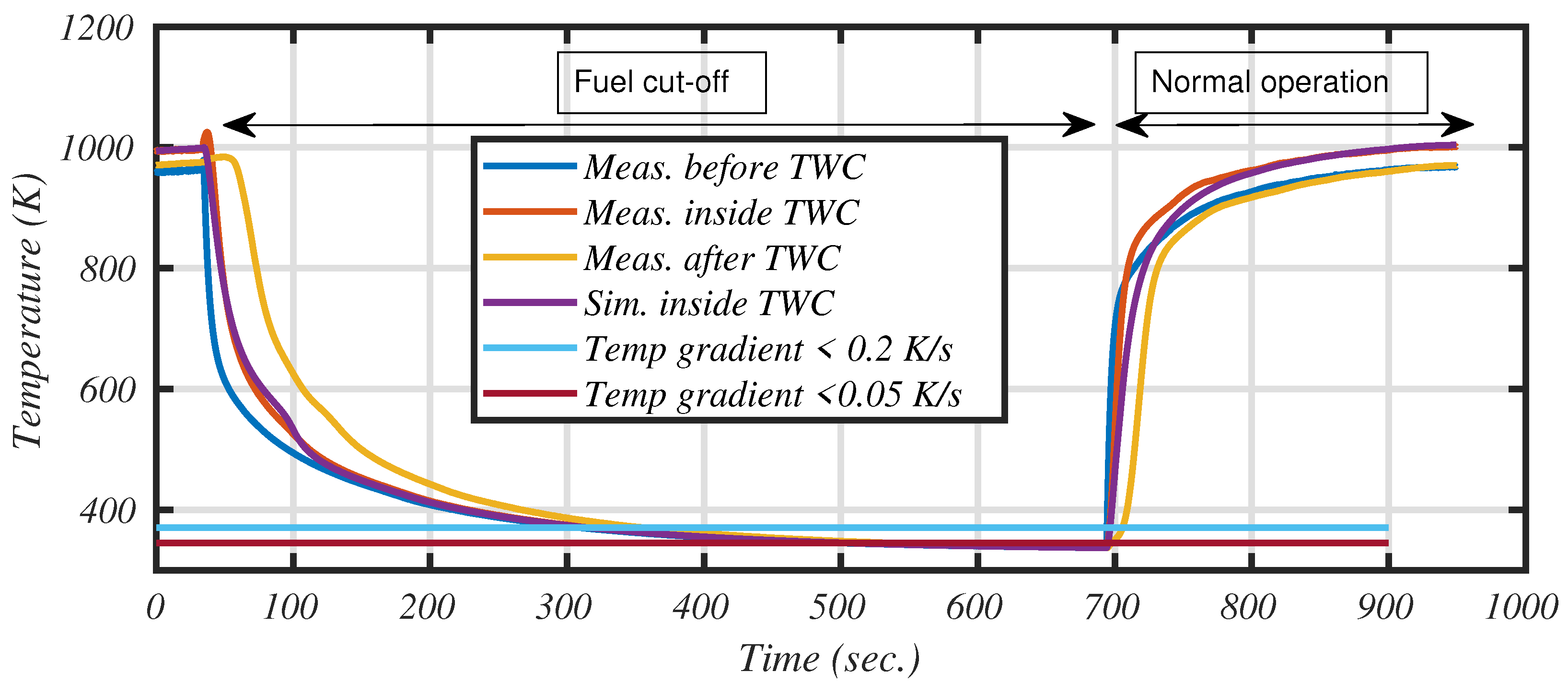
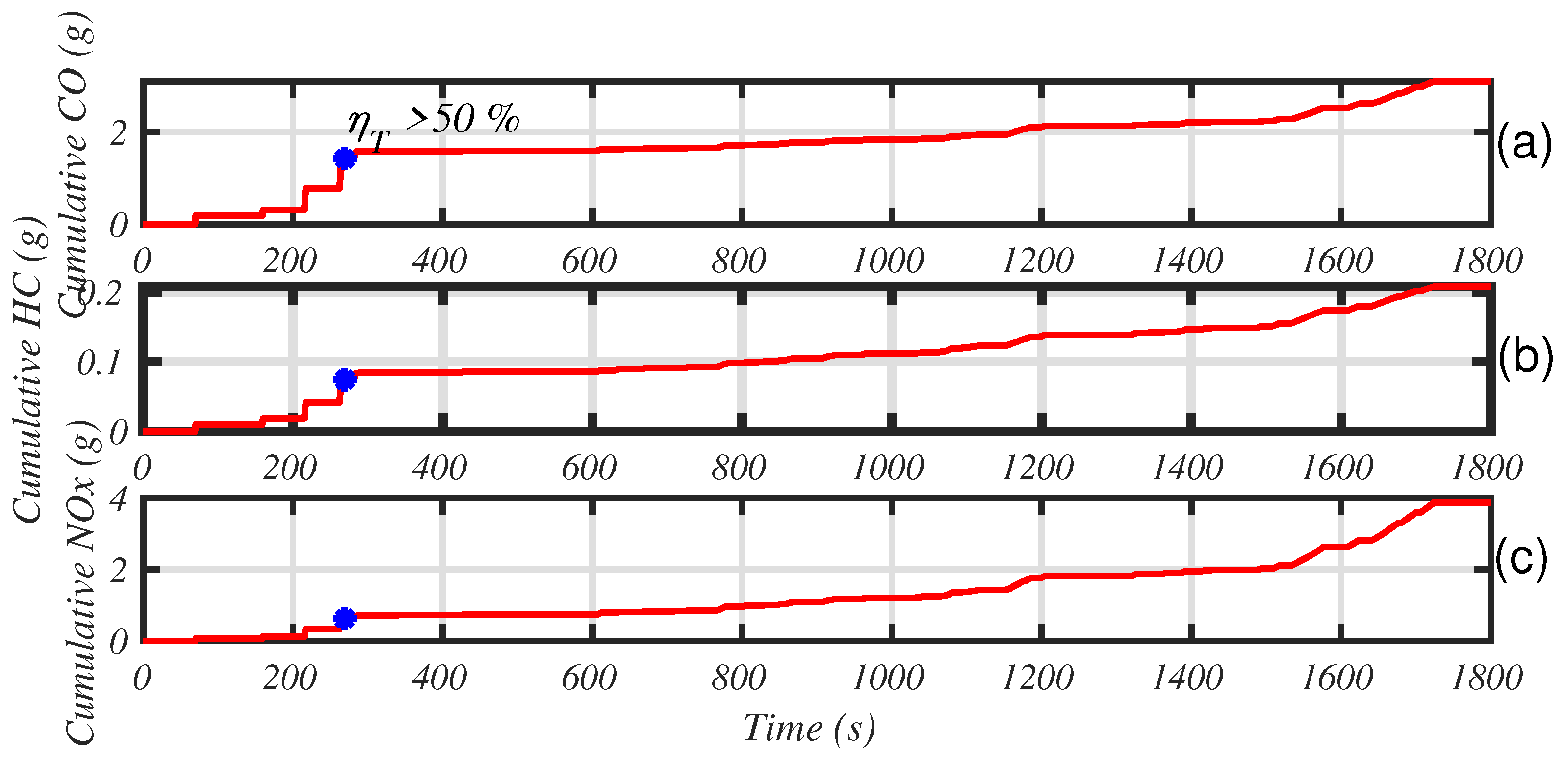
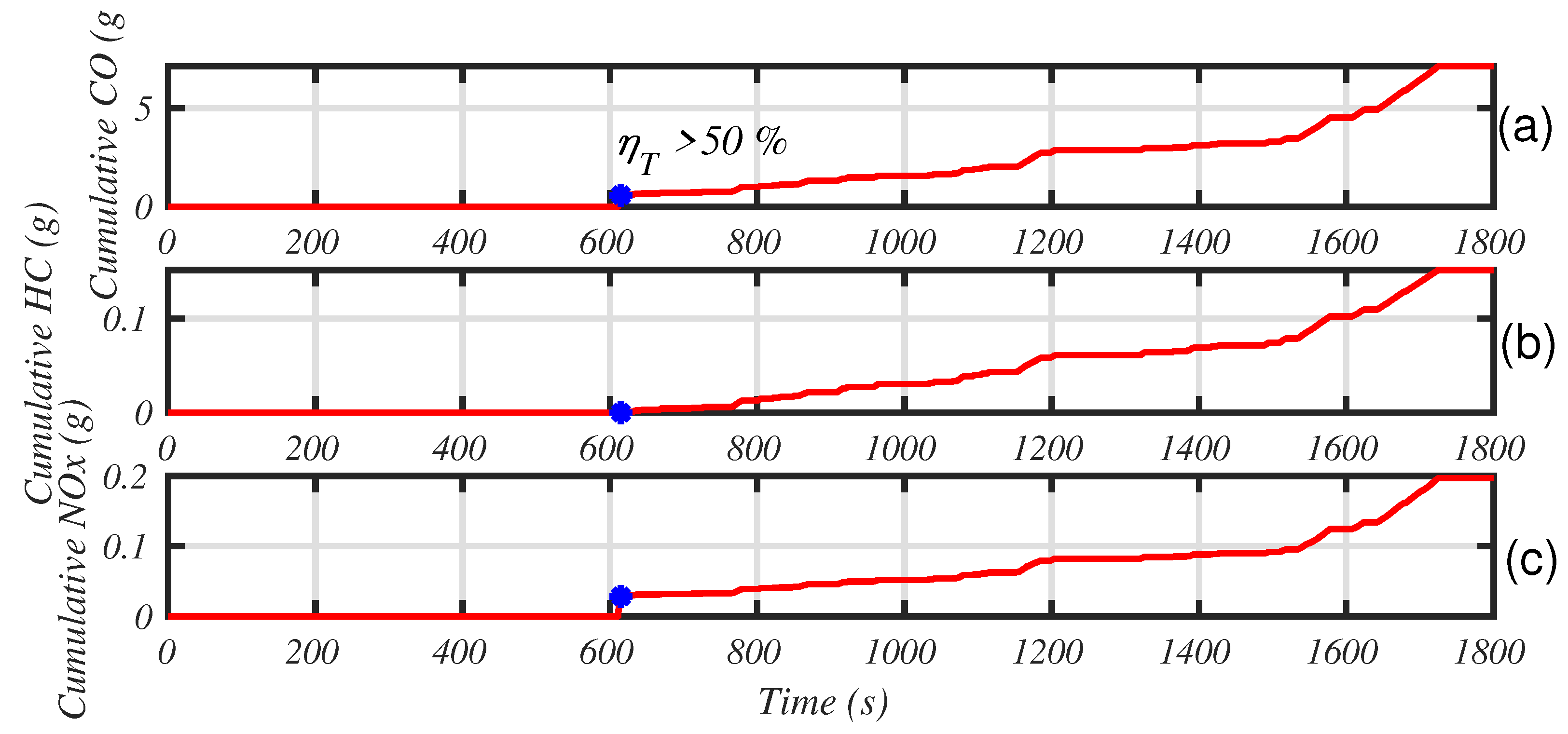
Figure 10 shows the cumulative emissions, while
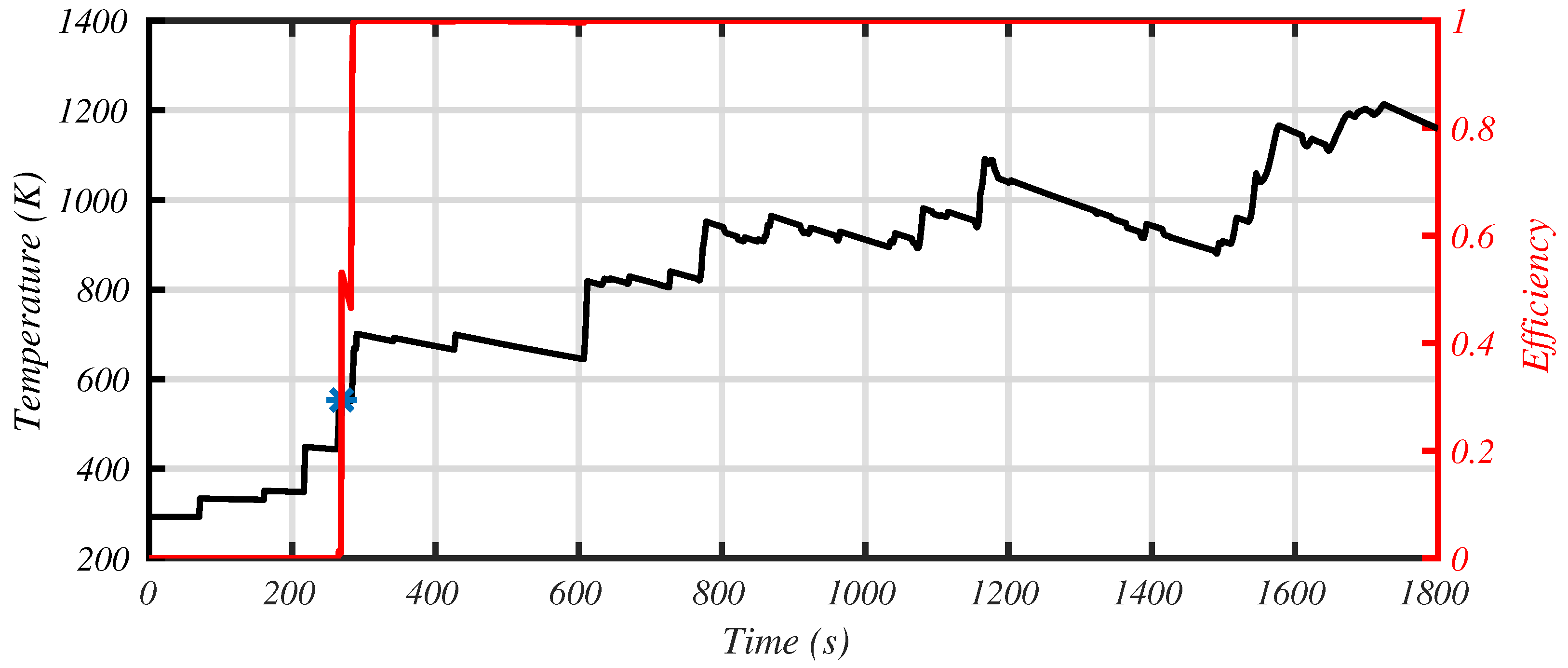
Figure 11 shows the temporal evolution of the catalyst temperature and efficiency.
Before the catalyst light off, almost half of the total amount of CO and HC has already been emitted. For the total NOx, 15% has already been dispersed in the environment.
Catalyst is primed after 250 s (the time when the efficiency exceeds 50%, symbolized with blue stars in
Figure 10 and
Figure 11), during which half of the urban part of the driving cycle has been performed. Between 250 and 600 s, the catalyst is cooling and is not far from being inefficient due to low temperature (light-off temperature is 550 K in our model). This can happen in real usage (stops or congested areas, for example) and must be managed by the engine ECU.
3.2. Emission-Centered Scenario
In this section, we consider a scenario in which the weighting parameters are equals (
, see Equation (
5)) and the Group A hypothesis concerning the optimization parameters is selected.
An analysis of the use of RAM on the computing machine has shown that the implementation of the method does not allow the use of more than 16 values of advance and/or equivalence ratio without reaching the limits of the available memory (256 GB) for the Group A parameters. Therefore, four values for the air to fuel equivalence ratio and four values for the relative spark advance are considered.
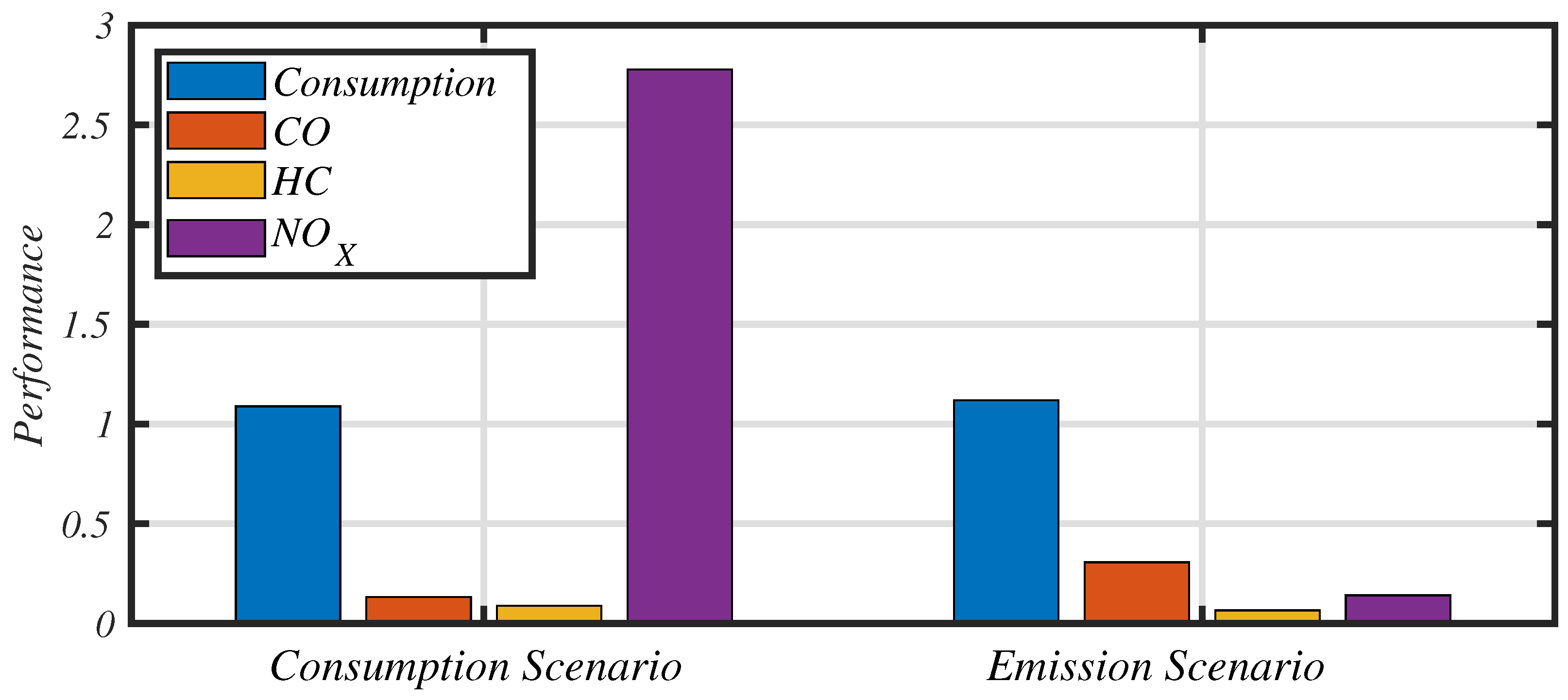
Global results are presented in
Table 7 and a comparison with the consumption-centered scenario is drawn in
Figure 12 for the WLTC driving cycle. In this drawing, the performance index is represented by the normalized value of the component. For example, the performance index of the fuel is:
(see Equation (
5)).
Aggregated results show that, whatever the driving cycle considered, a small increase in fuel consumption (between 3% to 5%) allows a great reduction in NOx emission (divided by a factor 20), thus passing the EURO6 rules (0.060 g/km). One can also notice that CO emissions increase, but still stay three times lower than EU limits.
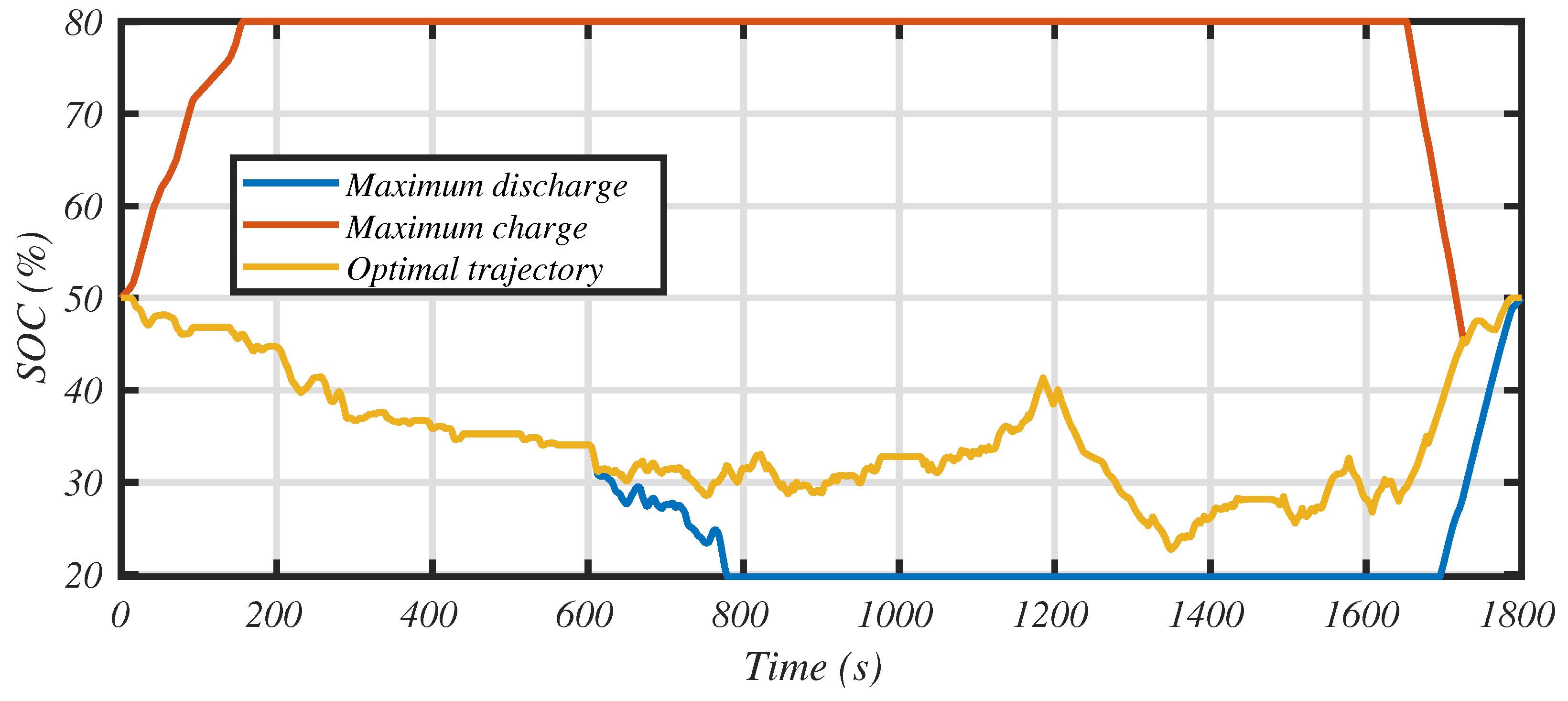
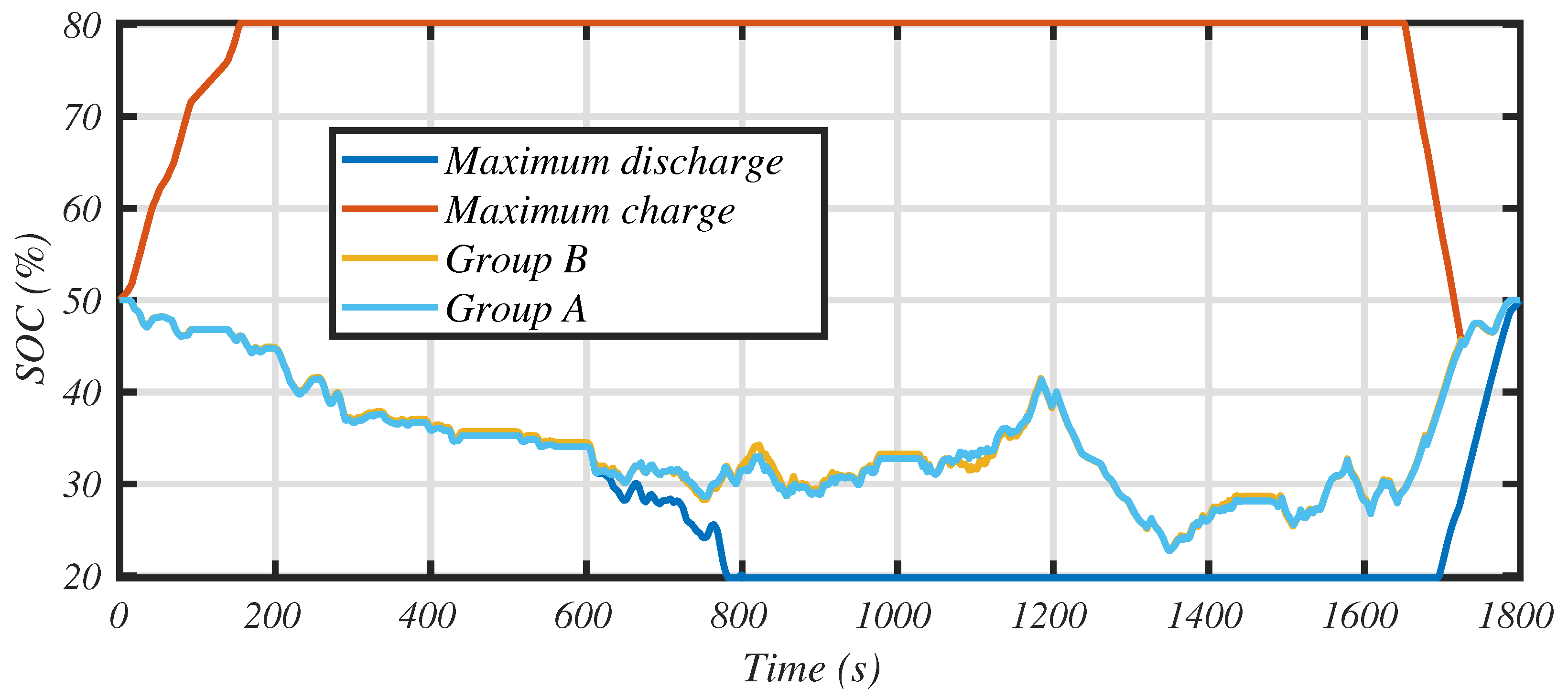
Figure 13 represents the variation of the state of charge of the battery. The lower bound (in blue line) corresponds to the strategy that maximizes the discharge of the battery (i.e., the all-electric mode), while the red curve represents its maximum charge (i.e., the engine is providing maximum power). Of course, because we are simulating a charge sustaining hybrid, the curve must converge at the end of the driving cycle. This surface defines the admissible operating area. The yellow line is the optimal trajectory regarding the objective function. We conclude that the first part of the driving cycle is made in all-electric mode. This is confirmed in
Figure 14, where we observe that the urban part is driven with the electric motor alone. We also notice that when the IC engine is started, the electric motor runs in recovery mode, thus recharging the battery. We also observe in
Figure 13 that the optimal strategy is not far from the maximum discharge rate. This is only due to the fact that the more aggressive part of the driving cycle happens at the end, which gives the right conditions for the ICE to develop high power and recharge the battery with the best global efficiency (see
Figure 14).
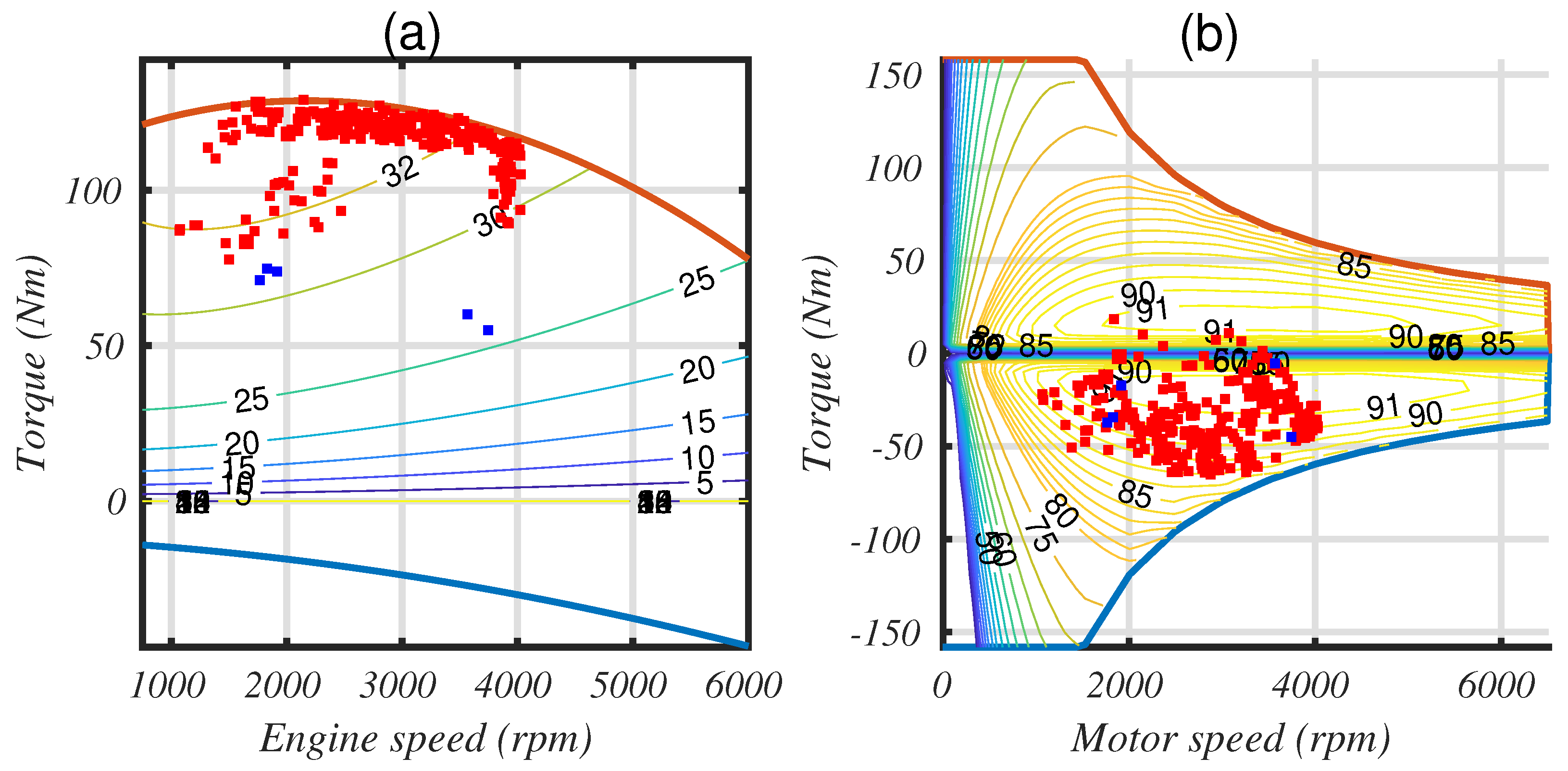
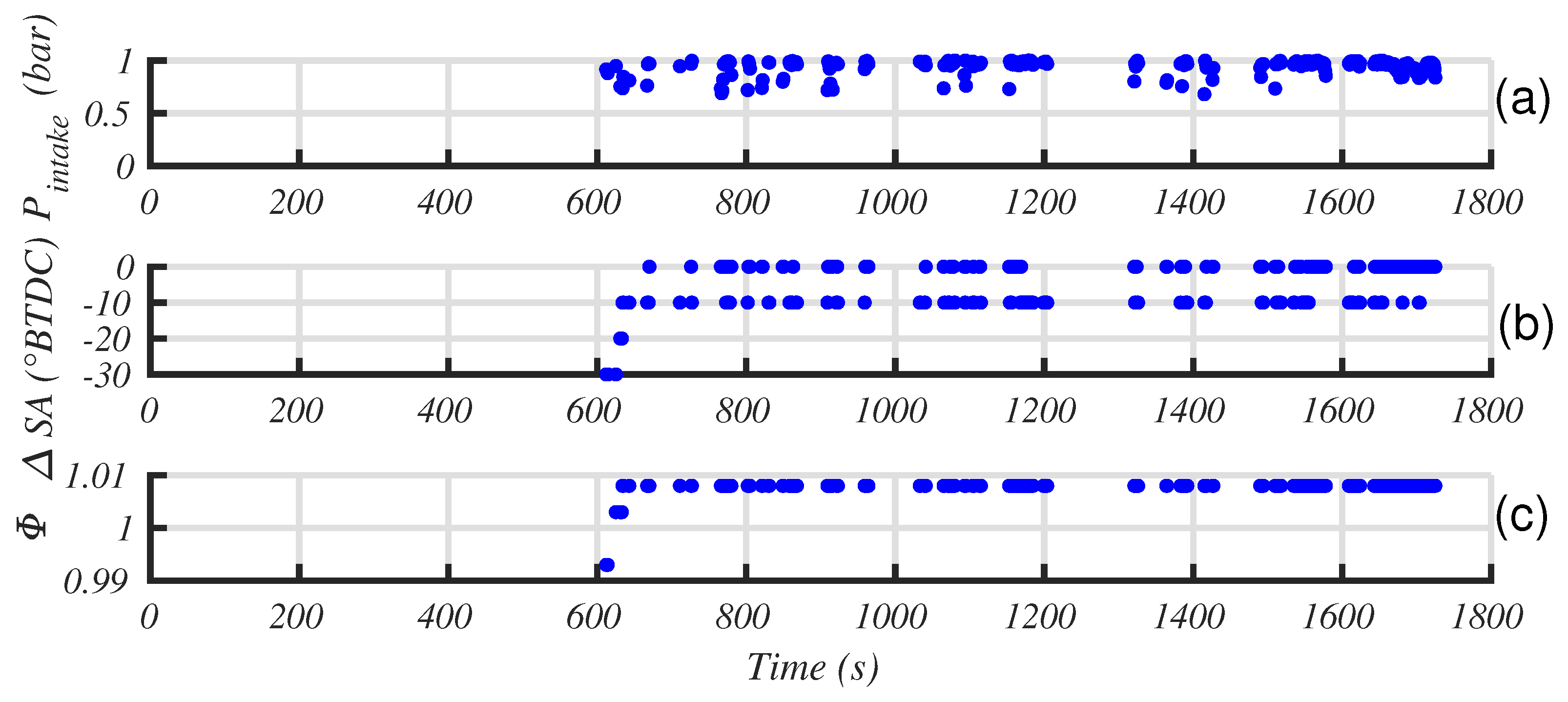
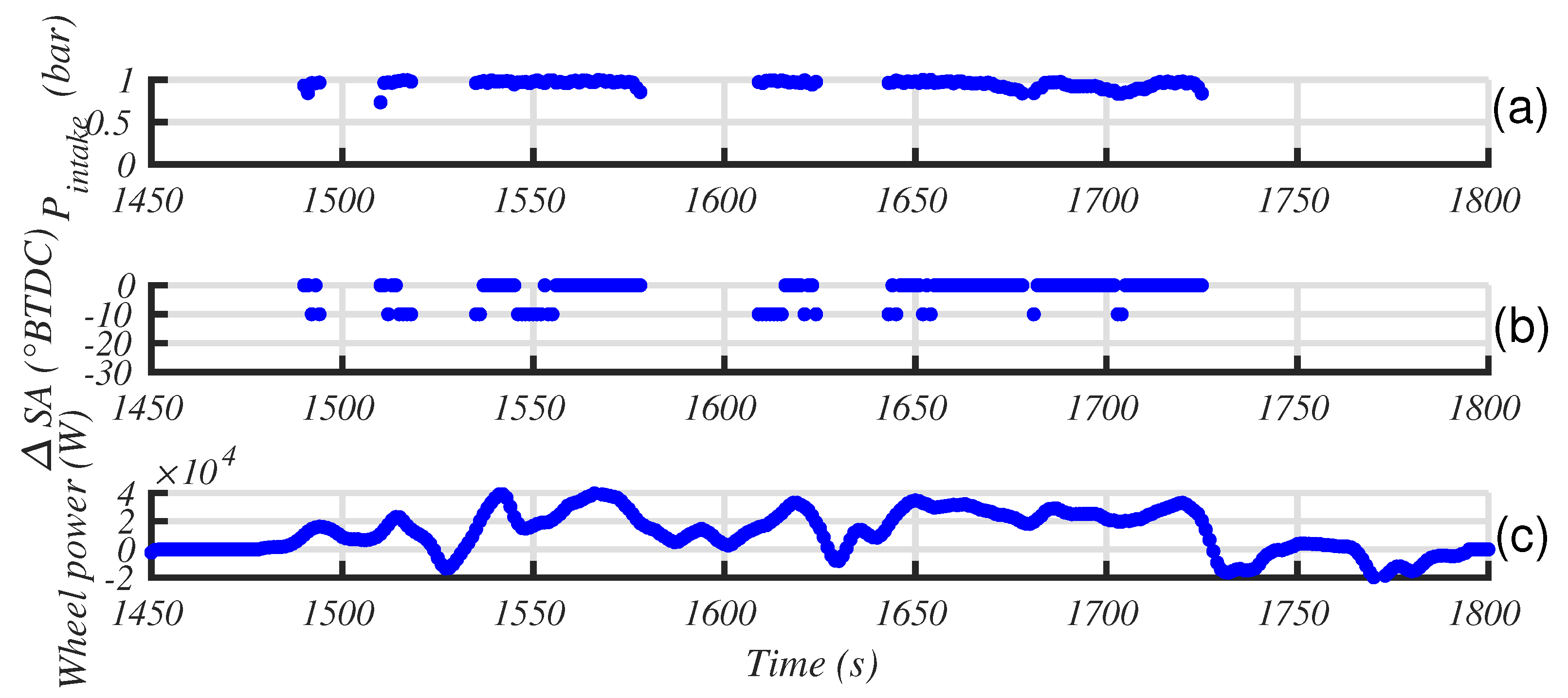
Figure 15 shows how the strategy operates regarding the operating points of the ICE and EM. First, we notice that a cloud of points is located near the full load of the ICE, which also matches with the best efficiency area. The blue points denote the operating point used with a cold and thus low efficiency catalyst. Although these points correspond to full open throttle (see intake pressure in
Figure 16, plot a), as the spark advance is delayed by 20 to 30 degrees (plot b), the resulting torque is low. During this stage, the strategy increases exhaust enthalpy in order to quickly warm the catalyst. Of course, these operating points present a low thermal efficiency, but this behavior last only a few seconds over the WLTC driving cycle, thus producing a minor impact on global fuel consumption. At the same time, engine admits a lean mixture (air to fuel equivalence ratio lower than 1, see
Figure 16, plot c), but as the catalyst is cold, it has no impact on its behavior. This has a small effect, but increases engine efficiency and exhaust temperature while reducing CO emissions at the engine outlet.
As soon as the catalyst is primed, the strategy has to conciliate conflicting constraints:
For the fuel, the major parameters will be the relative spark advance, which has to be close to its optimal value (). It is also clear that an intake pressure close to atmospheric pressure eliminates pressure drop at the intake valve, thus maximizing efficiency;
CO is not influenced by the spark advance, but only by the equivalent air to fuel ratio. A low value of is better for CO engine emission. That is not what we observed. Several factors explain this result:
- −
In this narrow window, CO emissions variation are low;
- −
CO efficiency is very high when catalyst is primed;
- −
The strategy greatly reduces CO emission before catalyst light-off (see
Figure 10).
The HC level is very low, and its performance index,
is less than 0.1 (see
Figure 12), so it has no impact on the control parameters;
NO
x clearly deeply influences the strategy; we observe a slight enrichment of the mixture (
= 1.008) that drives the catalyst efficiency to 0.995 (see
Figure 4). Conversely, we notice an alternation of the relative spark advance between 0 and −10°. This last value means firing later than is optimal, thus reducing the temperature in the combustion chamber and the feedgas NO level. Finally, the temporal distribution of the spark advance values is questionable. It seems to be correlated with the driving power; the strategy adopts a null relative spark advance when the driving power is high, and delays ignition when the wheel power decreases. This interpretation is highlighted in
Figure 18.
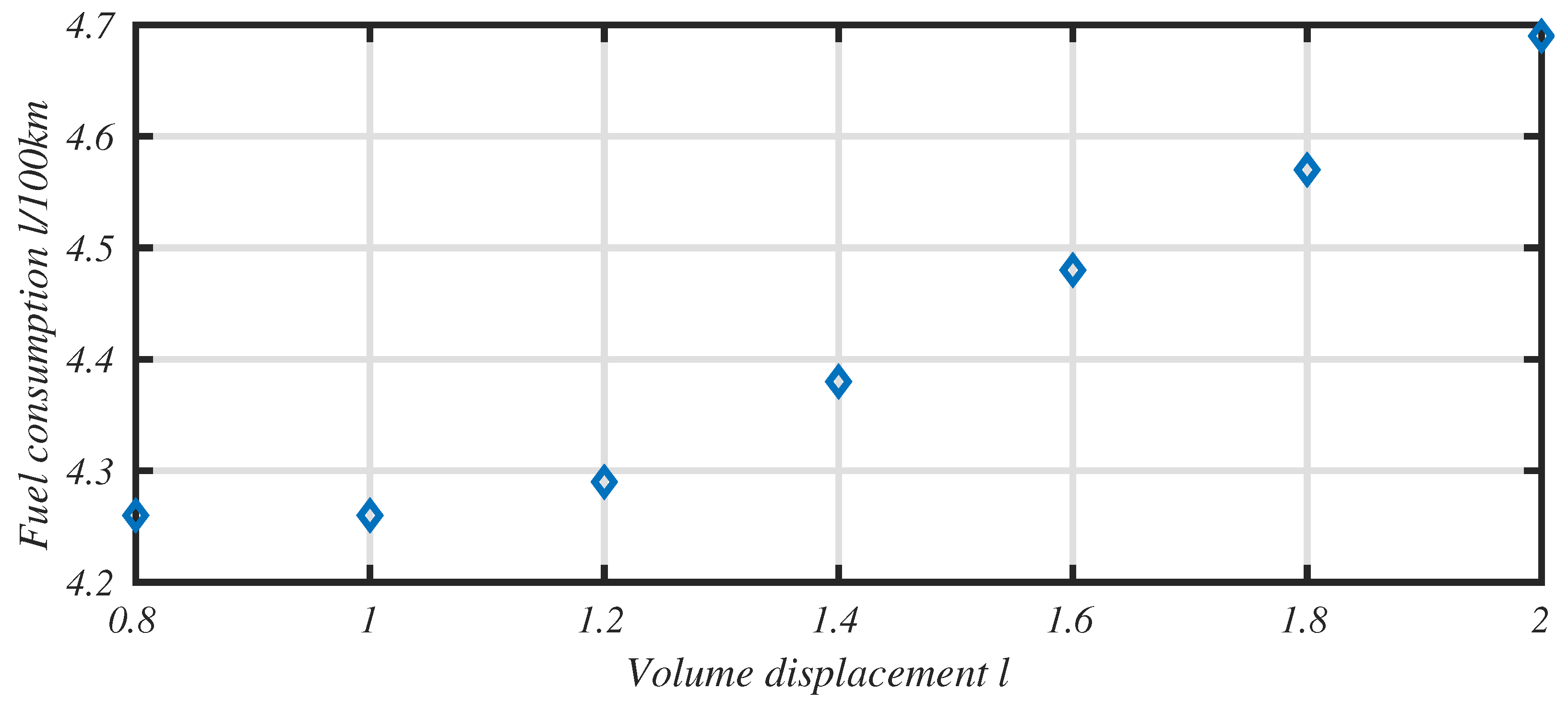
3.3. Parametric Study on Engine Displacement
We propose in this section to analyze the impact of engine displacement on the performance of the pollution-centered scenario. The displacement varies from 0.8 up to 2.0 L. Accordingly, the engine weight and its inertia vary with the same proportions. The computations are conducted with the Group B parameters values in the WLTC driving cycle (see
Table 8). Eight combinations of spark advance and air to fuel equivalence ratio are considered.
One can see on
Table 9 that emissions stay relatively stable while the engine displacement varies, but there is a certain gap in fuel consumption; indeed, there is an almost 10% increase in fuel economy between 2.0 and 1.0 L. The variation in global vehicle weight and inertia only explains 3 to 4%. This means that there is an optimal engine size that minimizes whole drive train losses; i.e., it allows the engine to run in its optimal operating range while lowering electric motor and battery losses.
We also compare, for the nominal case (i.e., engine displacement = 1.6 L) the result of the two simulations.
Figure 20 shows that the aggregated results are very close and this is the same for temporal behavior, as shown in
Figure 21. The last simulation runs eight times faster and consumes almost five times less memory. This is encouraging, as compromises can be found between the two groups of hypotheses.
4. Discussion
We chose to balance each pollutant with the same weighting factor in the objective function. The optimal strategy depends on these values used to scale and weight the emissions. Different compromises can be obtained, but the results presented in this paper show that with a small increase in fuel consumption (less than 3% for NEDC and 5% for WLTC), we observe a reduction of NOx emissions by a factor 20, and thus pass the EU6 regulation limits.
HC emissions are very low, even for the fuel consumption scenario. This is due to the fact that we do not take into account internal cylinder temperature during a cold start. This factor has an effect on the quality of combustion and increases HC emission before that the cylinder’s walls become hot. Moreover, to stabilize combustion during this phase, enrichment occurs, which promotes unburned hydrocarbons. This pollutant is very influenced by the cold start and less influenced by the operating parameters during the whole drive cycle [
33]. To take this phenomenon in account, we should add a new state variable simulating the cylinder mean temperature.
Given the verticality of the catalyst efficiency curves, especially the NOx one, a very small change in the equivalence ratio or efficiency S-curve shape can have a significant influence on the results. In practice, it is not possible to control the gas chemistry with such precision in a real engine, especially in the case of transient operations that are common with hybridization. Actual equivalence ratio control strategies usually consist of oscillating around the unit value of equivalence ratio to oxidize CO and HC on the one hand and reduce NO on the other. In addition, the catalyst has oxygen storage capabilities that allow small deviations during transient operations. The model of this equivalence ratio control loop is very complex and involves many state variables, so it is not realistic to take it into account when using dynamic programming.
Regarding the method used in this paper, we wanted to run the code with a step time of 1 s, as it is the necessary condition to limit the rounding errors due to quantization. We used a computer that was equipped with two processors running at 2.2 GHz and with 256 GB of RAM. We tried to limit the use of memory by storing only the variables that were mandatory to solve the graph. The conclusion is that the calculation time is long, resource intensive, and it is difficult to increase the combinatory on the control variables or add more state variables to the models.
Running the code with a step time of 2 s allows the use of natural cooling with a more reasonable temperature grid. Results presented on
Section 3.3 are promising, as the same results were observed while using almost five times less computer memory.
5. Conclusions
This study shows how to drive the control parameters of a port fuel injection engine in a hybrid architecture with respect to fuel consumption and pollutant emissions. It gives insight on how to use the degree of freedom represented by spark advance, air to fuel equivalence ratio, and intake pressure. It is known that delaying spark advance allows the early priming of the catalyst. However, our algorithm demonstrates when it should be done and the level of magnitude go bring it to optimality.
To summarize the work, we analyzed the influence of three parameters of close engine control: intake pressure (by the way of SOE), equivalence ratio, and ignition timing:
Over a wide range of variation, the equivalence ratio acts on the trade-off between the efficiency of the pollution control system and the fuel consumption because the optimal efficiency of the engine is with a lean mixture. However, when emissions are taken into account, the optimal range of variation of the equivalence ratio is reduced by a stoichiometric proportion. In this small range of variation, the equivalence ratio plays a role in the trade-off between the reduction of NO on one hand and of HC and CO on the other. As previously mentioned, a more precise model of the influence of this variable would be necessary to deepen this analysis of equivalence ratio control;
The optimal strategy degrades the ignition timing to optimize the catalyst priming phase, as in a conventional vehicle. Indeed, despite the reduction in the efficiency of the combustion engine, the ignition delay has a double positive effect on pollution. A significant delay in relation to optimal ignition increases the temperature of the gases at the engine outlet while reducing the concentrations of HC and NO. This ensures that the catalyst is primed as soon as possible while reducing emissions during this critical phase when the catalyst is not yet active. Once the catalyst is primed, the hybrid strategy taking into account pollutant emissions and therefore often tends to delay the advance. This impacts the temperature in the chamber and thus reduces NO emissions;
The intake pressure is directly linked to the power developed by the internal combustion engine and acts on the one hand on the concentration of NO and HC at the engine outlet and on the other hand on the efficiency of the engine. This latter effect is predominant in the optimal strategy, as the weighted factor for fuel is high in the objective function.
The work is conducted in a backward model environment that allows optimal methods to be deployed. This is a great improvement compared to trial-and-error methods, which are complex and time consuming when the search domain is wide. Dynamic programming is robust and supplies a reference on how to operate an engine in a hybrid vehicle. The drawback of this method is that the dynamic description of the engine has to be quite simple. Other optimization methods can now be explored in light of these results. Additional state variables can be introduced to the models. This work is a milestone that provides us with the opportunity to develop models and to move towards real-time applications.