High-Velocity Metal Fragment: Motion Characteristic and Optimization Design
Abstract
1. Introduction
2. Experimental System
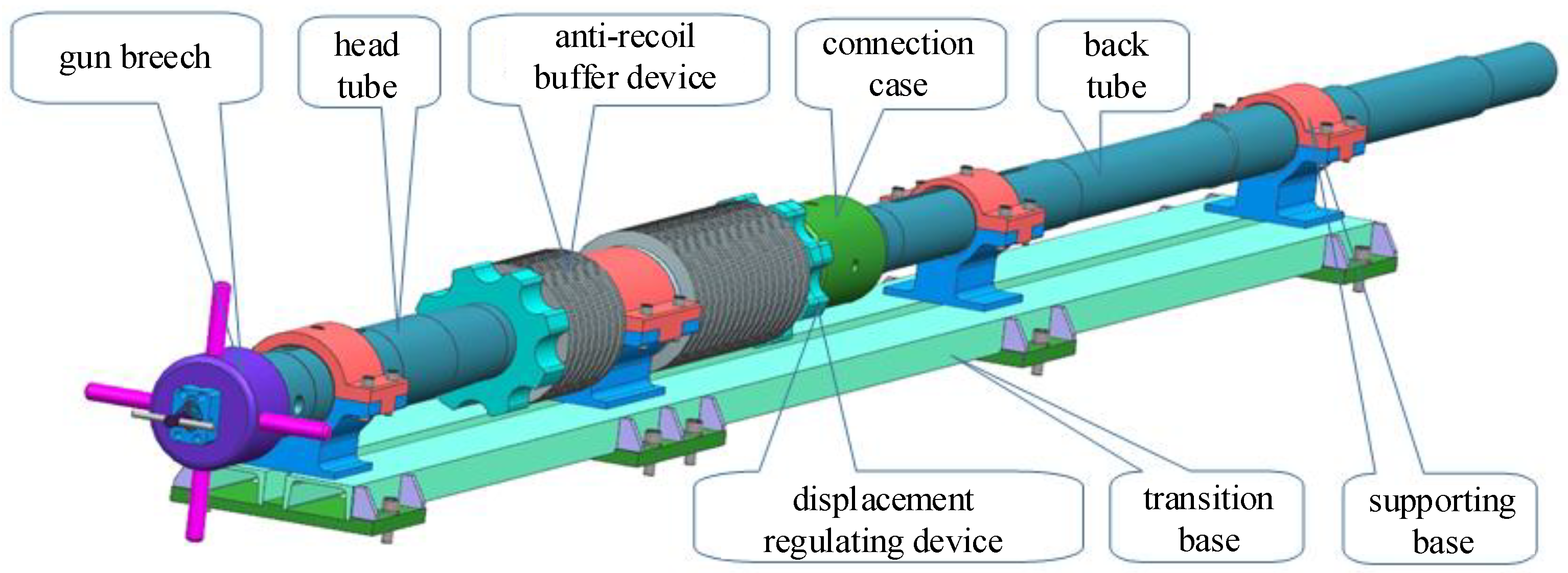
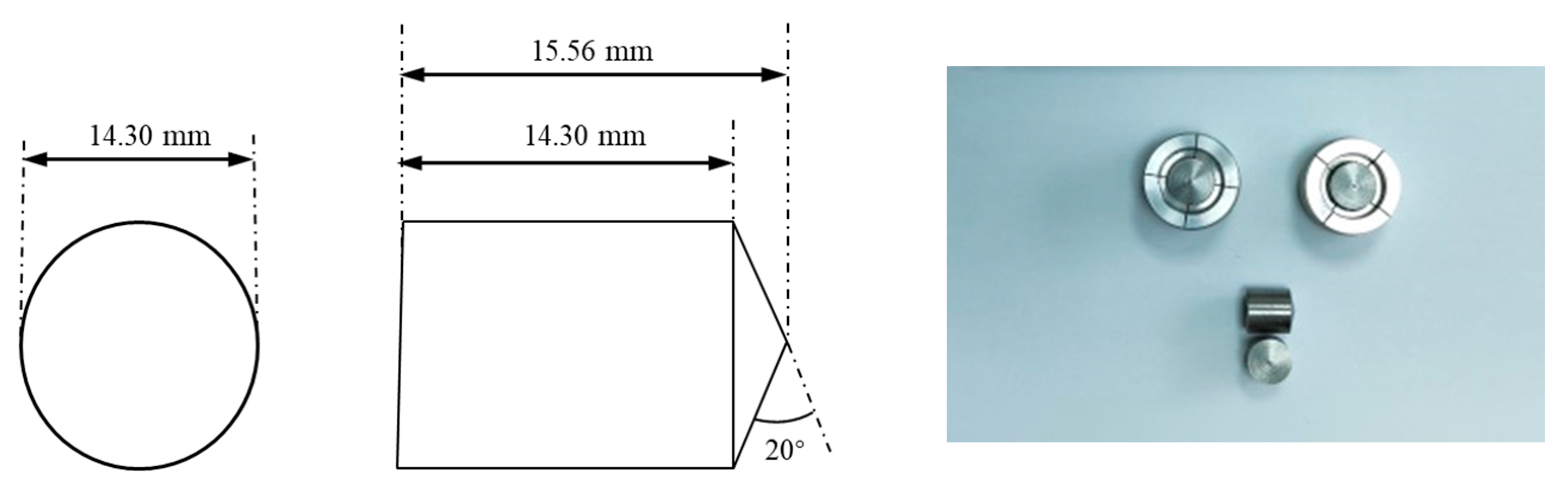
2.1. Experimental Device and Process
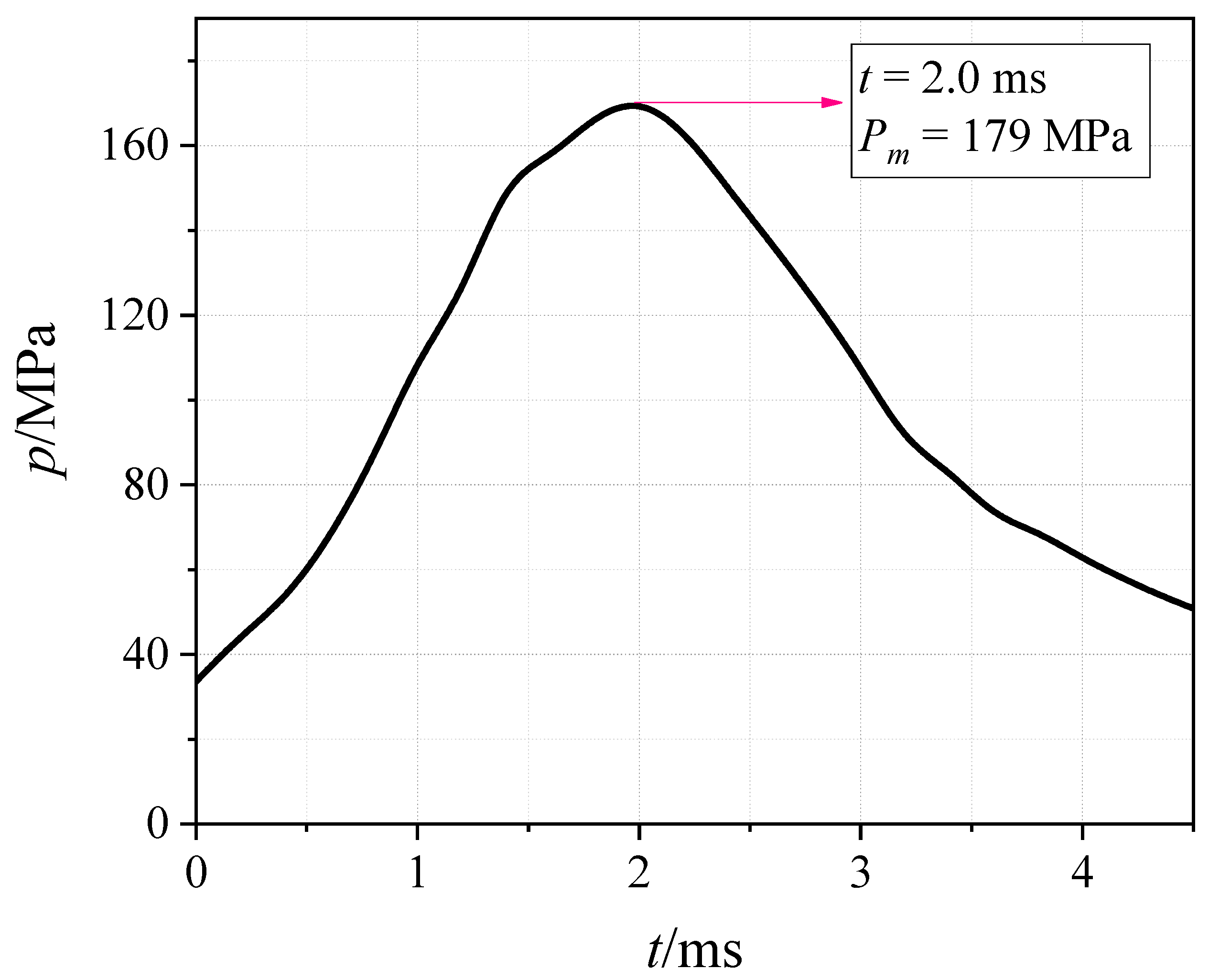
2.2. Experimental Results and Discussions
3. Optimization Calculation
3.1. Calculation Method
3.2. Verification of the Numerical Simulation
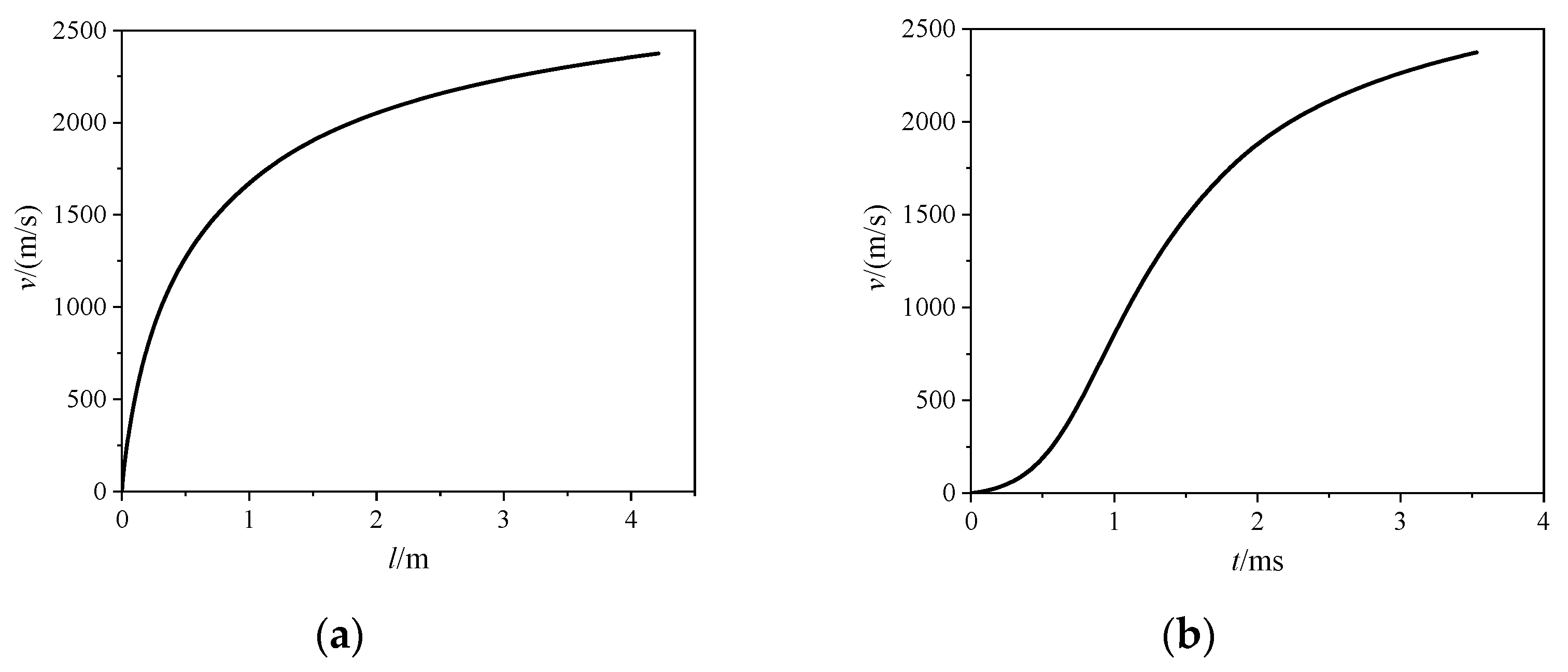
3.3. Optimization Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ignatova, A.M.; Yudin, M.V.; Voronov, V.L.; Ignatov, M.; Gladky, I.; Inozemtsev, A.; Naimark, O. Velocity characteristics of fracture fragments of mica-crystal materials under high-speed impact. Procedia Struct. Integr. 2022, 41, 589–597. [Google Scholar] [CrossRef]
- Baker, E.L.; Al-Shehab, N.; Miers, K.; Pudlak, D. Insensitive munitions fragment impact gun testing technology challenges. Propellants Explos. Pyrotech. 2016, 41, 572–579. [Google Scholar] [CrossRef]
- Felix, D.; Colwill, I.; Harris, P. A fast and accurate model for the creation of explosion fragments with improved fragment shape and dimensions. Def. Technol. 2022, 18, 159–169. [Google Scholar] [CrossRef]
- Davydova, M.M.; Uvarov, S.V.; Naimark, O.B. Scaling invariance in dynamic fragmentation of quarts. Phys. Mesomech. 2014, 17, 81–88. [Google Scholar] [CrossRef]
- Demay, S.C.; Thelen, C.J. Insensitive munitions propulsion progress. Int. J. Energ. Mater. Chem. Propuls. 1997, 4, 1–6. [Google Scholar]
- Liao, W.; Jiang, J.W.; Men, J.-B.; Wang, S.-Y.; Li, M.; Liu, H. Effect of the end cap on the fragment velocity distribution of a cylindrical cased charge. Def. Technol. 2021, 17, 1052–1061. [Google Scholar] [CrossRef]
- Ning, J.; Duan, Y.; Xu, X.; Ren, H. Velocity characteristics of fragments from prismatic casing under internal explosive loading. Int. J. Impact Eng. 2017, 109, 29–38. [Google Scholar] [CrossRef]
- Grady, D.E. Local inertial effects in dynamic fragmentation. J. Appl. Phys. 1982, 53, 322–325. [Google Scholar] [CrossRef]
- Kipp, M.E.; Grady, D.E. Dynamic fracture growth and interaction in one dimension. J. Mech. Phys. Solids 1985, 33, 399–415. [Google Scholar] [CrossRef]
- Kipp, M.E.; Grady, D.E.; Swegle, J.W. Experimental and Numerical Studies of High-Velocity Impact Fragmentation; Sandia National Laboratories Report SAND93–0773; U.S. Department of Energy, Office of Scientific and Technical Information: Washington, DC, USA, 1993.
- Kipp, M.E.; Grady, D.E.; Swegle, J.W. Numerical and experimental studies of high-velocity impact fragmentation. Int. J. Impact Eng. 1993, 14, 427–438. [Google Scholar] [CrossRef]
- Glenn, L.A.; Chudnovsky, A. Strain-energy effects on dynamic fragmentation. J. Appl. Phys. 1986, 59, 1379–1380. [Google Scholar] [CrossRef]
- Englmant, R.; Rivier, N.; Jaeger, Z. Fragment-size distribution in disintegration by maximum-entropy formalism. Philos. Mag. Part B 1987, 56, 751–769. [Google Scholar] [CrossRef]
- Grady, D.E.; Passman, S.L. Stability and fragmentation of ejecta in hypervelocity impact. Int. J. Impact Eng. 1990, 10, 197–212. [Google Scholar] [CrossRef]
- Sil’Vestrov, V.V. Fragmentation of a Steel Sphere by a High-Velocity Impact on a Highly Porous Thin Bumper. Combust. Explos. Shock. Waves 2004, 40, 238–252. [Google Scholar] [CrossRef]
- Cagle, C.B.; Hill, K.J.; Woodruff, C.; Pantoya, M.L.; Abraham, J.; Meakin, C. High Velocity Impact Testing for Evaluation of Intermetallic Projectiles. J. Dyn. Behav. Mater. 2020, 6, 236–245. [Google Scholar]
- Myagkov, N.N. Scaling invariance of spherical projectile fragmentation upon high-velocity impact on a thin continuous shield. J. Exp. Theor. Phys. 2017, 124, 57–69. [Google Scholar] [CrossRef]
- Teng, T.L.; Chu, Y.A.; Chang, F.A.; Shen, B.C. Design and implementation of a high-velocity projectile generator. Combust. Explos. Shock. Waves 2007, 43, 233–240. [Google Scholar] [CrossRef]
- Rabczuk, T.; Eibl, J.S.L. The SPH/MLSPH method for the simulation of high velocity concrete fragmentation. In International Workshop on Meshfree Methods for Partial Differential Equations; Springer: Berlin, Germany, 2003. [Google Scholar]
- Johnson, J.C.; Puvvada, S.; Lu, Y. Energy Dissipation and Fragmentation of Granite Core During High Velocity Impact. Min. Metall. Explor. 2019, 36, 839–849. [Google Scholar] [CrossRef]
- Johnson, J.C. The Hustrulid Bar-A Dynamic Strength Test and Its Application to the Cautious Blasting of Rock. Ph.D. Dissertation, The University of Utah, Salt Lake City, UT, USA, 2010. [Google Scholar]
- Myagkov, N.N.; Shumikhin, T.A. Critical Behavior and Energy Dependence of Mass Distribution in High-Velocity Impact Fragmentation. In III European Conference on Computational Mechanics; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Zelepugin, S.A.; Zelepugin, A.S. Modeling of the destruction of targets during a high-velocity impact. Russ. J. Phys. Chem. B 2008, 2, 246–250. [Google Scholar] [CrossRef]
- Kong, X.; Wu, W.; Li, J.; Liu, F.; Chen, P.; Li, Y. A numerical investigation on explosive fragmentation of metal casing using Smoothed Particle Hydrodynamic method. Mater. Des. 2013, 51, 729–741. [Google Scholar] [CrossRef]
- An, X.; Liu, J.; Ye, P.; Tian, C.; Feng, S.; Dong, Y. Axial distribution characteristics of fragments of the warhead with a hollow core. Int. J. Impact Eng. 2018, 122, 10–22. [Google Scholar] [CrossRef]
- Huang, G.; Li, W.; Feng, S. Fragment Velocity Distribution of Cylindrical Rings Under Eccentric Point Initiation. Powders Explos. Pyrotech. 2015, 40, 215–220. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, G.; Liu, C.; Feng, S.-S. Velocity axial distribution of fragments from non-cylindrical symmetry explosive-filled casing. Int. J. Impact Eng. 2018, 118, 1–10. [Google Scholar] [CrossRef]
- Arnold, W.; Rottenkolber, E. Fragment mass distribution of metal cased explosive charges. Int. J. Impact Eng. 2008, 35, 1393–1398. [Google Scholar] [CrossRef]
- Persson, P. The relationship between strain energy, rock damage, fragmentation, and throw in rock blasting. In Rock Fragmentation by Blasting; Mohanty, B., Ed.; CRC Press: London, UK, 1996; pp. 113–120. [Google Scholar]
- Espinosa, H.D.; Zavattieri, P.D.; Dwivedi, S.K. A finite deformation continuum/discrete model for the description of fragmentation and damage in brittle materials. J. Mech. Phys. Solids 1998, 46, 1909–1942. [Google Scholar] [CrossRef]
- Camancho, G.T.; Ortiz, M. Computational modeling of impact damage in brittle materials. Int. J. Solids Struct. 1996, 33, 2899–2938. [Google Scholar] [CrossRef]
- Miller, O.; Freund, L.B.; Needleman, A. Modeling and Simulation of Dynamic Fragmentation in Brittle Materials. Int. J. Fract. 1999, 96, 101–125. [Google Scholar] [CrossRef]
- Denoual, C.; Hild, F. A damage model for the dynamic fragmentation of brittle solids. Comput. Methods Appl. Mech. Eng. 2000, 183, 247–258. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Lu, Y.; Hong, H. Analysis of fragment size and ejection velocity at high strain rate. Int. J. Mech. Sci. 2004, 46, 27–34. [Google Scholar] [CrossRef]
- Yen, C.F. A ballistic material model for continuous-fiber reinforced composites. Int. J. Impact Eng. 2012, 46, 11–22. [Google Scholar] [CrossRef]
- Zhikharev, M.V.; Sapozhnikov, S.B. Two-scale modeling of high-velocity fragment GFRP penetration for assessment of ballistic limit. Int. J. Impact Eng. 2016, 101, 42–48. [Google Scholar] [CrossRef]
- Judge, R.; Yang, Z.; Jones, S.W.; Beattie, G.; Horsfall, I. Spiral strand cables subjected to high velocity fragment impact. Int. J. Impact Eng. 2017, 107, 58–79. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.T.; He, Y.T.; Zhang, T.; Fan, X.-H.; Zhang, T.-Y. Damage analysis of typical structures of aircraft under high-velocity fragments impact. Alex. Eng. J. 2022, 62, 431–443. [Google Scholar] [CrossRef]
- Grisaro, H.Y.; Dancygier, A.N. Model of fragmentation distribution over a protective wall. Int. J. Impact Eng. 2019, 128, 1–10. [Google Scholar] [CrossRef]
- Kljuno, E.; Catovic, A. Estimation of projected surface area of irregularly shaped fragments. Def. Technol. 2019, 15, 198–209. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldívar, D.; Cuevas, E.; Maciel-Castillo, O. An improved Simulated Annealing algorithm based on ancient metallurgy techniques. Appl. Soft Comput. 2019, 84, 105761. [Google Scholar] [CrossRef]
- Yu, C.; Heidari, A.A.; Chen, H. A quantum-behaved simulated annealing algorithm-based moth-flame optimization method. Appl. Math. Model. 2020, 87, 1–19. [Google Scholar] [CrossRef]




| No. | Tube Length (mm) | Pressure (MPa) | Inner Diameter (mm) | Outer Diameter (mm) | σi (MPa) | σe (MPa) | ni | ne |
|---|---|---|---|---|---|---|---|---|
| 1 | 0~200 | 400 | 54 | 130 | 700.15 | 166.82 | 1.49 | 6.23 |
| 2 | 200~715 | 310 | 30 | 120 | 454.67 | 41.33 | 2.29 | 25.16 |
| 3 | 715~960 | 230 | 30 | 106 | 346.72 | 40.05 | 3.00 | 25.97 |
| 4 | 960~2000 | 180 | 30 | 100 | 275.6 | 35.6 | 3.77 | 29.21 |
| 5 | 2000~2850 | 80 | 30 | 100 | 122.49 | 15.82 | 8.49 | 65.72 |
| 6 | 2850~3560 | 50 | 30 | 80 | 83.03 | 16.36 | 12.53 | 63.56 |
| 7 | 3560~3830 | 38 | 30 | 90 | 60.17 | 9.5 | 17.29 | 109.47 |
| 8 | 3830~4270 | 35 | 30 | 70 | 62.42 | 15.75 | 16.66 | 66.03 |
| 9 | 4270~4500 | 30 | 30 | 60 | 60 | 20 | 17.33 | 52 |
| No. | Group IVMDs | Distances (m) | Interval Time (ms) | Fragment Velocity (m/s) |
|---|---|---|---|---|
| 1 | 1–4 | 6.242 | 3.498 | 1784.4 |
| 2 | 2–3 | 5.8 | 3.25 | 1784.6 |
| 3 | 4–5 | 6.8 | 4.058 | 1675.7 |
| 4 | 5–8 | 5.199 | 3.295 | 1577.8 |
| 5 | 6–7 | 4.755 | 3.014 | 1577.6 |
| Grain Configuration | Powder Charge(g) | Muzzle Velocity (m/s) | Maximum Pressure (MPa) | ||
|---|---|---|---|---|---|
| Experiment | Simulation | Experiment | Simulation | ||
| 5/7 | 260 | 1770 | 1844 | 179 | 178 |
| 5/7 | 300 | 2080 | 2056 | 263 | 261 |
| No. | Muzzle Velocity (m/s) | Burning Rate Coefficient | Burning Rate Index | Gunpowder Impetus (kJ/kg) | Distance between Adjacent Holes (mm) | Diameter of Every Holes (mm) |
|---|---|---|---|---|---|---|
| 1 | 2132.0 | 1.56 × 108 | 0.8267 | 975.1 | 0.30 | 0.25 |
| 2 | 2224.2 | 1.43 × 108 | 0.8299 | 991.3 | 0.37 | 0.23 |
| 3 | 2299.5 | 1.70 × 108 | 0.8245 | 958.4 | 0.38 | 0.22 |
| 4 | 2303.8 | 1.64 × 108 | 0.8283 | 905.1 | 0.22 | 0.21 |
| 5 | 2315.8 | 1.69 × 108 | 0.8273 | 917.3 | 0.25 | 0.22 |
| 6 | 2342.3 | 1.54 × 108 | 0.8284 | 967.8 | 0.36 | 0.21 |
| 7 | 2362.8 | 1.73 × 108 | 0.8298 | 950.7 | 0.23 | 0.24 |
| 8 | 2373.6 | 1.72 × 108 | 0.8268 | 967.2 | 0.24 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Chen, H.; Yu, Y.; Xue, X.; Fu, Y. High-Velocity Metal Fragment: Motion Characteristic and Optimization Design. Appl. Sci. 2022, 12, 9922. https://doi.org/10.3390/app12199922
Hu J, Chen H, Yu Y, Xue X, Fu Y. High-Velocity Metal Fragment: Motion Characteristic and Optimization Design. Applied Sciences. 2022; 12(19):9922. https://doi.org/10.3390/app12199922
Chicago/Turabian StyleHu, Jie, Hua Chen, Yonggang Yu, Xiaochun Xue, and Yu Fu. 2022. "High-Velocity Metal Fragment: Motion Characteristic and Optimization Design" Applied Sciences 12, no. 19: 9922. https://doi.org/10.3390/app12199922
APA StyleHu, J., Chen, H., Yu, Y., Xue, X., & Fu, Y. (2022). High-Velocity Metal Fragment: Motion Characteristic and Optimization Design. Applied Sciences, 12(19), 9922. https://doi.org/10.3390/app12199922






