Measurement-Driven Synthesis of Female Digital Mannequin Using Convex Sub-Volumes
Abstract
1. Introduction
1.1. Context
1.2. Research Strategy and Scope
- : A set of measurements that describe the shape of a female body. With : Height, : Shoulder width, : Breast perimeter, : Waist perimeter, and : Hip perimeter.
- B: 3D mannequin approximation of a female body that satisfies a particular set of tailor measurements . B is a set of convex volumes.
1.3. Manuscript Structure
2. Literature Review
2.1. Non-Convex Example-Based Modeling
2.1.1. Deformation of a Single Template/Example Model
- Reference [8] imposes symmetric constraints to the ‘SCAPE’ parametric model. These symmetric constraints are defined as symmetry-related matrices and are applied during pose and shape deformation to provide a resulting symmetric model.
- Reference [9] proposes a tensor decomposition technique to model human bodies based on data (shape and pose) of multiple subjects. They use such data to train a deformation method that considers pose and shape parameters in conjunction rather than independently. This method is applied to a template model.
- Reference [10] proposes the segmentation of a template model (point-cloud) into regular intervals. These intervals are subsets of point-clouds to which shape control lines (SCL) are fitted. The SCLs are then modified by applying centroid-based and ratio-based scalings to produce variations of the template.
- Reference [11] extracts contour (features) from a scanned model. These contours are measured and translated vertically according to the template model’s height and the input height. The shape of the scanned model is then modified by applying linear anthropometric rules to produce an adaptive mannequin.
- Reference [12] extracts shape and measurement information from a template model. The authors identify key parameters that define the scaling for the global deformation (responsible for general shape) and feature factors for local deformation (of specific parts of the body). Nonlinear interpolation is used to deform the overall shape and critical parts of the template model based on the key parameters.
- Reference [13] extracts cross sections from a scanned dataset of a physical mannequin. The initial locations of the cross sections are obtained using statistical anthropometric data. These cross sections are deformed by resizing and relocating according to input anthropometric data (measurements) that describes the desired geometry.
- Reference [14] extracts cross sections and characteristic points (features) from a template model. Then, characteristic sizes are calculated (heights and circumferences) based on the features. Nineteen main control points are established and used to perform a three-dimensional lengthwise axial deformation. Radial deformation is used to perform girth-wise or area deformations.
- Reference [15] obtains parameter-to-geometry correlations by using radial-basis interpolation over a number of 3D scanned models. These correlations allow for the creation of deformation functions. A template model is then deformed through skeletal deformation, and geometric and energy-based processes are used to calculate vertex displacement.
- Reference [16] performs a manual segmentation of a template model and applies spline and radial-basis deformation functions and continuity filters to change the shape and size of the template model.
2.1.2. Synthesis through Multiple Example Models
- Reference [2] proposes the creation of a database from scanned models. Correlations between the meshes (feature points and curves) and semantic parameters are created and computed as a linear system of equations. The system of equations has its complexity reduced through PCA. New models are produced by modifying input models or finding and modifying similar models (from databases) to satisfy input measurements.
- References [17,18] preprocess 250 (125 females and 125 males) scanned models from the SizeKorea database. The models are categorized, and the correlations between body shape variation and body sizes are extracted through statistical analysis (PCA). With such correlations, new models are obtained through shape parameter optimization techniques and radial-basis function (RBF) deformation of a template surface.
- Reference [19] obtains a set of thousands of scans, for which they extract and correct landmarks. Then, PCA is performed to extract the parameters that define shape variation, which are stored in a database. Moreover, a system in which users can have access to individual 3D scanned data and personalized body-shape modeling is presented.
- Reference [20] presents a unified model that describes pose, shape, and muscular deformation. A set of 550 full-body scans of 114 subjects is obtained, registered, and encoded. Rotation-invariant encoding allows for the creation of semantic regression functions (PCA-based technique). The regression functions are used to generate arbitrary models.
- Reference [21] constructs a database of 160 (80 male and 80 female) body scans. PCA is then performed to parameterize the data and characterize the tendency of shape variation and modeling parameters, and their correlation with anthropometric parameters. Through such correlations and a non-linear error-optimization-based shape modeling method, an arbitrary model can be obtained from user-specified measurements.
- Reference [22] extracts feature points from a set of scanned models. The feature points are used to create feature curves, which are then parameterized. Using a numerical optimization-based scheme, a new model can be synthesized by interpolating certain examples from the database. These examples are selected through an optimization algorithm.
- Reference [23] proposes a learning-based method to define the relationship between feature curves (wireframes) and anthropometric measurements. Such a relationship is built using a deep neural network (DNN) based on a test dataset and used to build new wireframes. New meshes can be created by interpolating the new wireframes into patches.
- Reference [24] proposes a modeling scheme called SMPL, which uses 2100 female models from the CAESAR project database to train a set of parameters. Such parameters are used in linear blending functions (i.e., shape, skinning, and pose) and a regressor to reconstruct a new mesh from the vertex of a template mesh.
- Reference [25] proposes the extraction of measurements from 1024 bodies using VR controllers (i.e., HTC Vive). These measurements are then related to the SIMPL [24] model shape parameters. With such relations, the author train four regressors that allow the creation of new meshes from body measurements obtained with the VR controllers.
2.1.3. Feature Extraction from Photographs
- Reference [26] captures orthogonal pictures of a person and extracts silhouettes. Feature points are obtained from the silhouettes and used to define a linear affine mapping of the correlation between the template model and the silhouettes. This mapping is then used to define and apply shape deformation to the 3D template model.
- Reference [27] manually defines feature points on three orthogonal pictures of a person. From the feature points, a silhouette is extracted and a skeleton is automatically fitted by applying affine transformations and Barycentric interpolation. A template model’s skin (surface) is then deformed through piecewise affine transformations and 2D-to-3D mapping with the skeleton and silhouette information.
- Reference [28] applies a segmentation method on two orthogonal photographs of a subject to extract contours (silhouettes). The silhouettes are correlated to silhouettes of a template model, and feature points are extracted using morphology rules and template-based feature extraction algorithms. The authors use the model and silhouette photographs to perform view-dependent deformation of the template model.
- Reference [29] presents a modeling scheme in which the authors deform a template model to best fit the user’s shape. The first step consists of fitting the template to a user-generated point-cloud via 3D scans and feature-point extraction. The second uses low-resolution 2D images to estimate the shape and pose of the human body, assisted by boundary constraints.
- Reference [30] presents a method for rebuilding 3D models based on a set of seven template models and orthographic images of a subject. The method consists of extracting contours from the images and scaling contours from the template models according to the extracted contours.
- Reference [31] estimates the 3D shape and pose of a subject from a single image. This process consists of regressing the 3D positions of the vertices of a SMPL-template mesh via graph convolutional networks, avoiding the use of anthropometric parameters.
- Reference [32] propose the reconstruction of 3D meshes from a single image. A graph convolutional network (GCN) is used to directly predict the 3D locations of mesh vertices from the input image. Anthropometric parameters are integrated into the GCN to improve the reconstruction accuracy.
2.2. Anatomy-Based Modeling
2.3. Conclusions of Literature Review
3. Materials and Methods
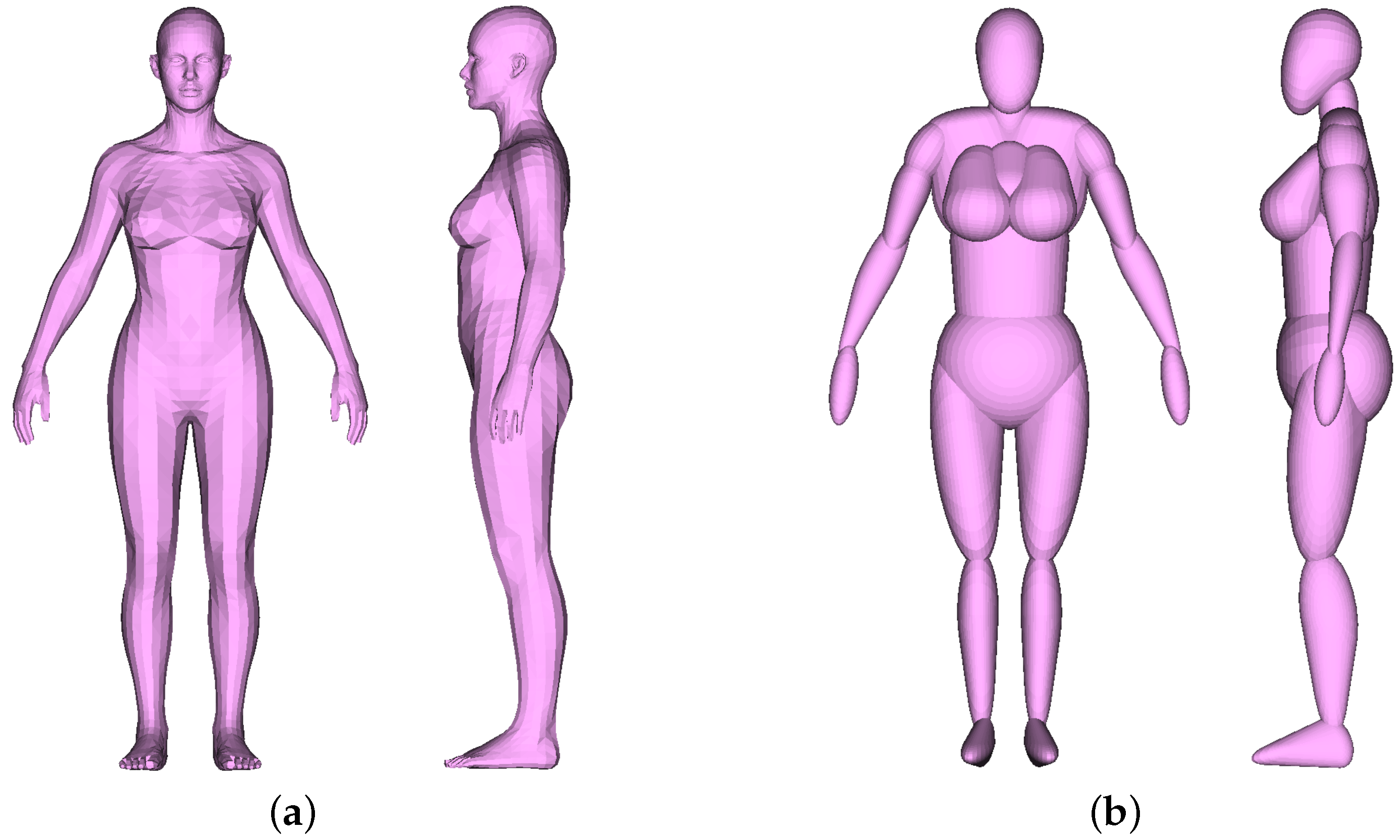
- A reference 3D model is manually approximated/traced with ellipsoids to produce a Base Mannequin (). Furthermore, an ellipsoid-to-cushion post-process is presented to improve the convex volume approximation after it has been parameterized. See Section 3.2.
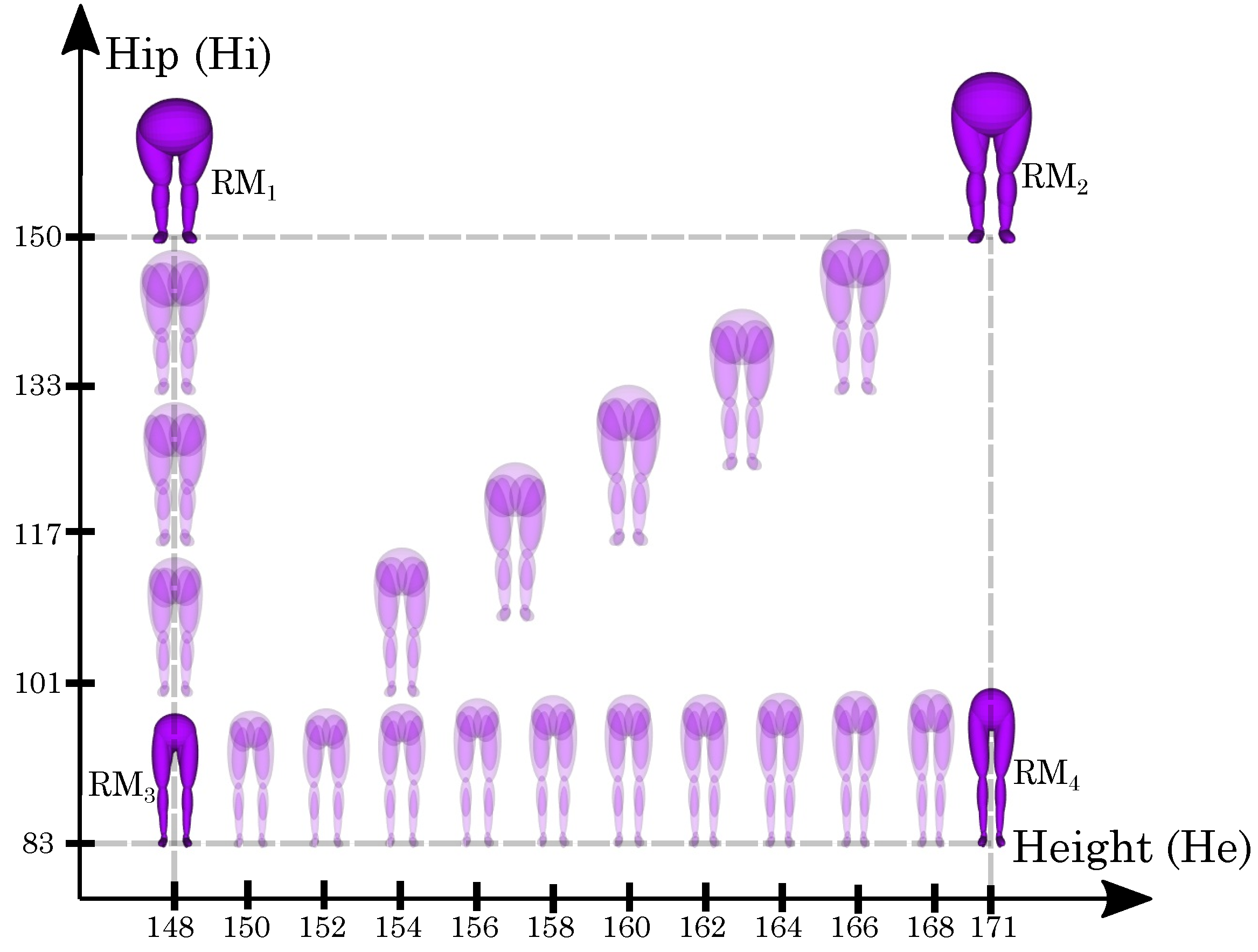
- The (set of ellipsoids) is then used to instance a set of Reference Mannequins (). Each one of these Reference Mannequins () satisfies a particular set of five tailor measurements. See Section 3.3.
- Based on the known data of (geometry and measurements), a set of functions is created. This set of functions synthesizes the geometry of a measurement-driven mannequin that in return satisfies the given measurements in . See Section 3.6.
- Finally, the measurement-driven mannequin can be synthesized by computing .
- A: A set of points in . Each component j of a point x (), with , represents a measurement of the human body in (e.g., height, shoulder width, etc.). The following conditions must be considered:
- (a)
- .
- (b)
- L: A set of q ordered pairs corresponding to the lower and upper limits of the components j of x.
- H: A set of sets of ellipsoids in . Each set of ellipsoids B, with , approximates the shape and size of a human body described by a point .
- (a)
- Each B has the same number m of ellipsoids and the same topology.
- (b)
- Each B satisfies the measurements of a specific point .
- (c)
- Each ellipsoid of B is defined by a homogeneous SO(3) coordinate system S and a triad D describing the dimensions of its semi-axes.
- : Function ; obtains the tailor measurements of any model .
- F: A set of functions , . More specifically, , such that applied to produces the measurements in x. F is a set of functions that, given a set of measurements x, synthesizes a model (geometry) B that satisfies x.
3.1. Rationale for the Mathematical Model
- Selection of ellipsoids due to their low geometrical complexity, low data-storage, and the benefits of convex volumes present in physics engines;
- Manual approximation of the 3D reference model by fitting a set of ellipsoids;
- Symmetrical location of ellipsoids with respect to the sagittal plane;
- Construction of a set of Reference Mannequins through rigid transformations of the set of ellipsoids;
- Compliance of Reference Mannequins to sets of tailor measurements;
- Data processing is performed over the set of Reference Mannequins in order to achieve:
- (a)
- Enforcement of symmetry with respect to the sagittal plane;
- (b)
- Enforcement of right-handedness in the ellipsoid coordinate systems;
- (c)
- Congruence of the coordinate system (definition of World Coordinate System);
- (d)
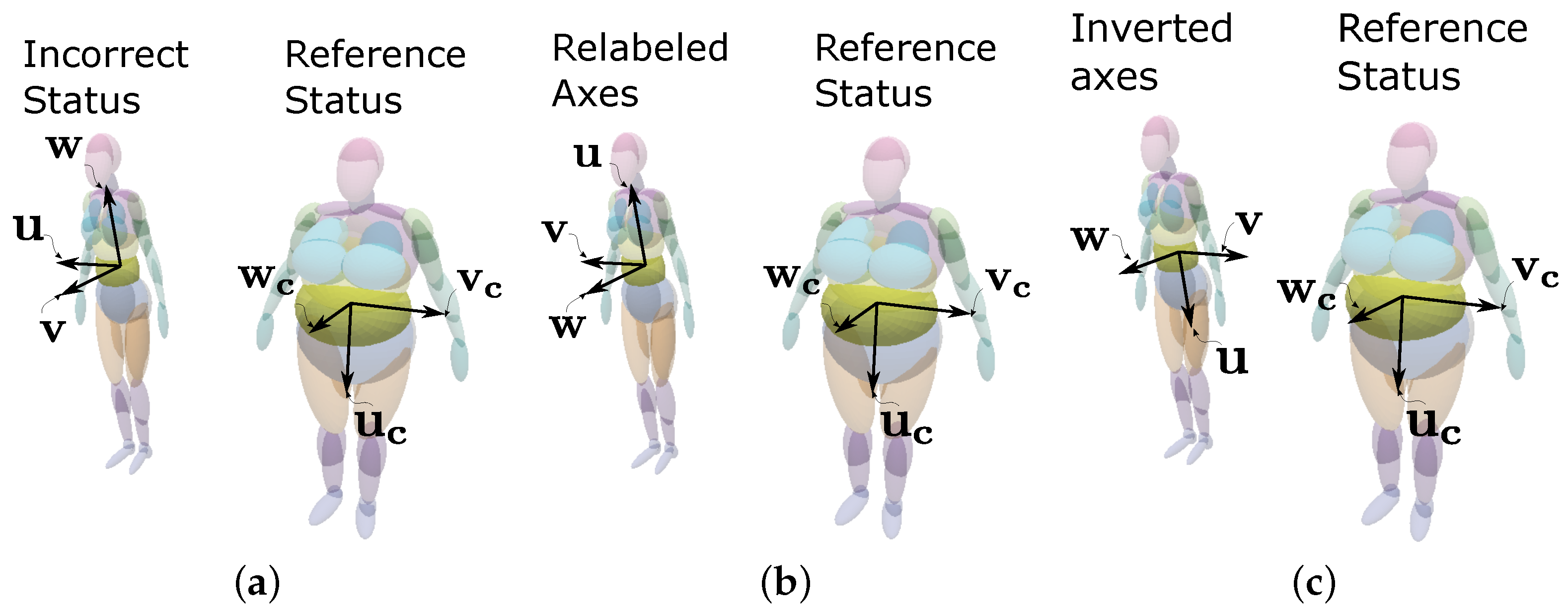
- Re-labeling of SO(3) coordinate systems (i.e., ellipsoid axes) to ensure minimal variation of the interpolation functions in set F.
- Selection of a multivariate weighted average (interpolation) method for the definition of F;
- Selection of inverse distance weighting (IDW) as the interpolation method due to its minimal tuning and boundary condition characteristics;
- Limitation of the dimension of the measurement space to reduce the complexity of the interpolation scheme;
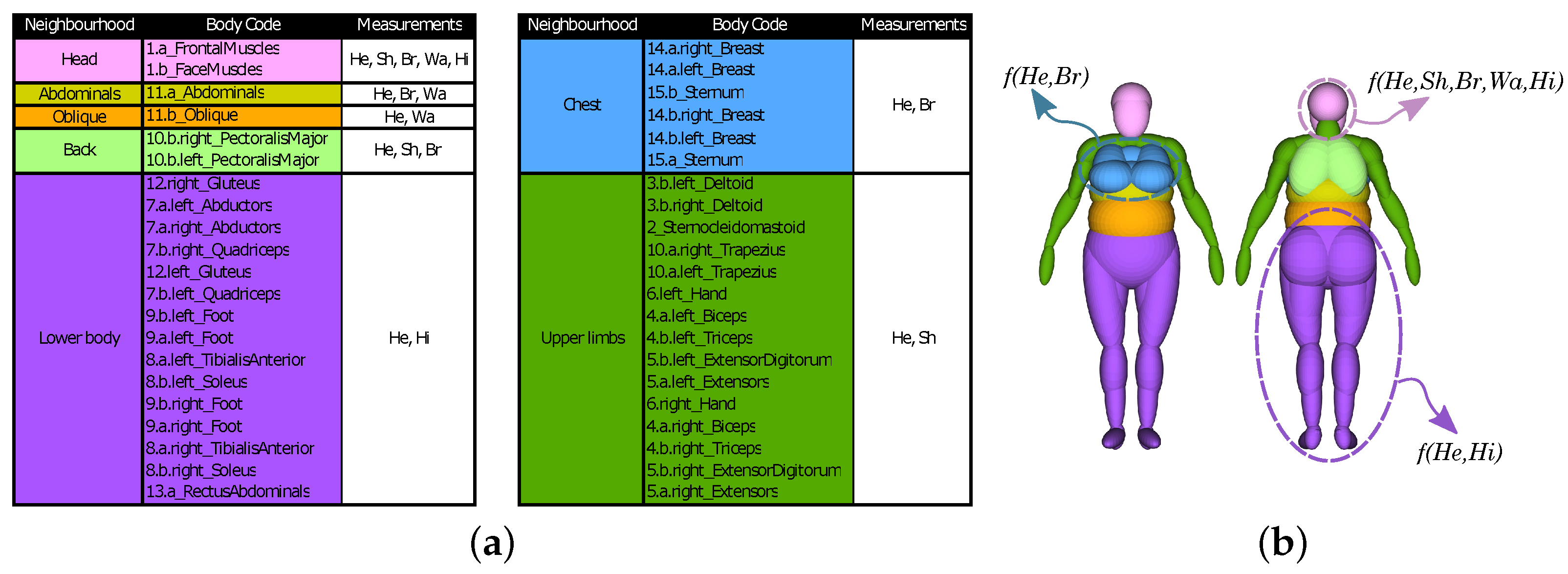
- Segmentation of the interpolation functions dictated by mannequin neighborhoods;
- Synthesis of neighborhoods by a subset of functions given a subset of measurements (e.g., shoulder width and height);
- Definition of neighborhoods based on a measurement dependency rationale.
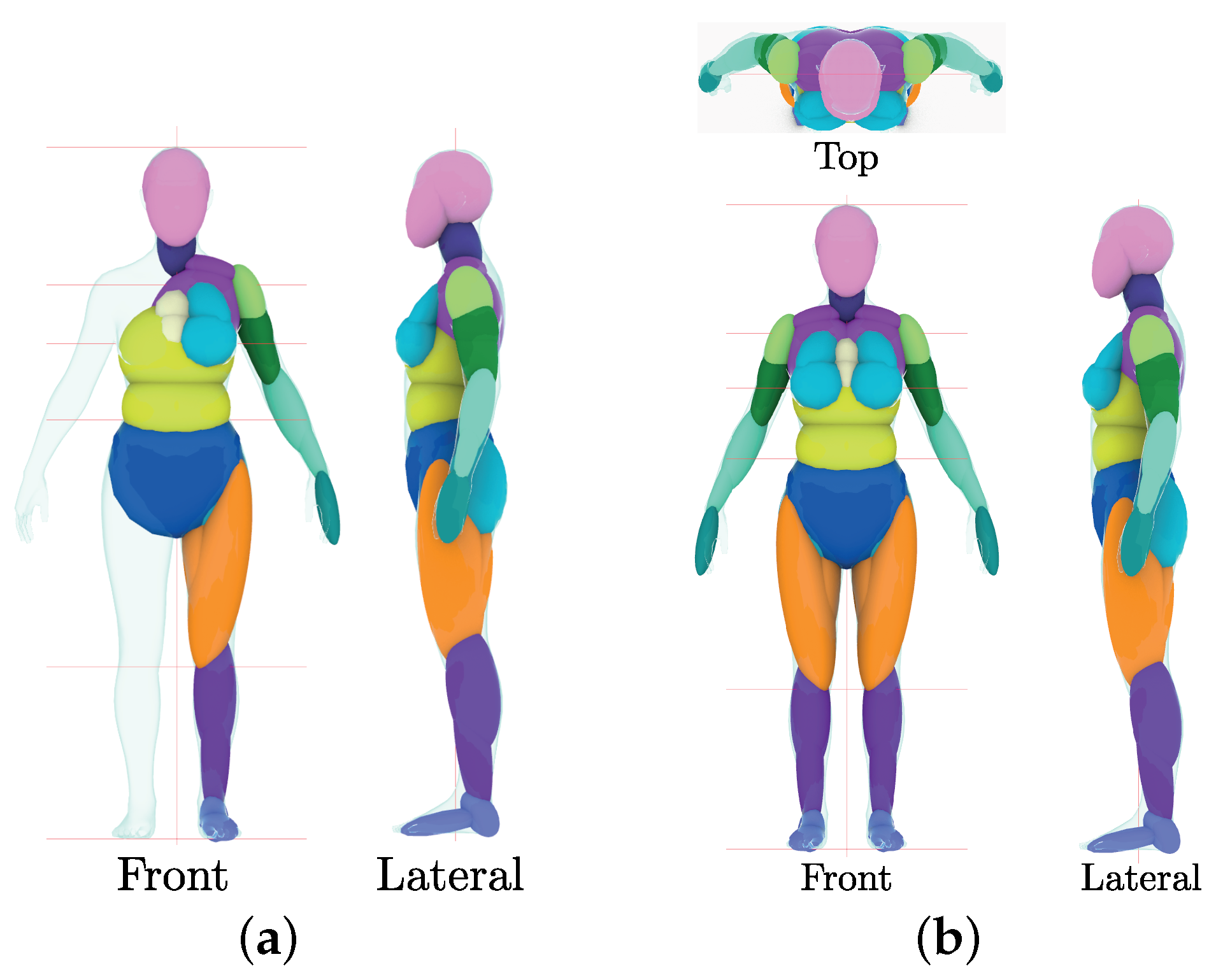
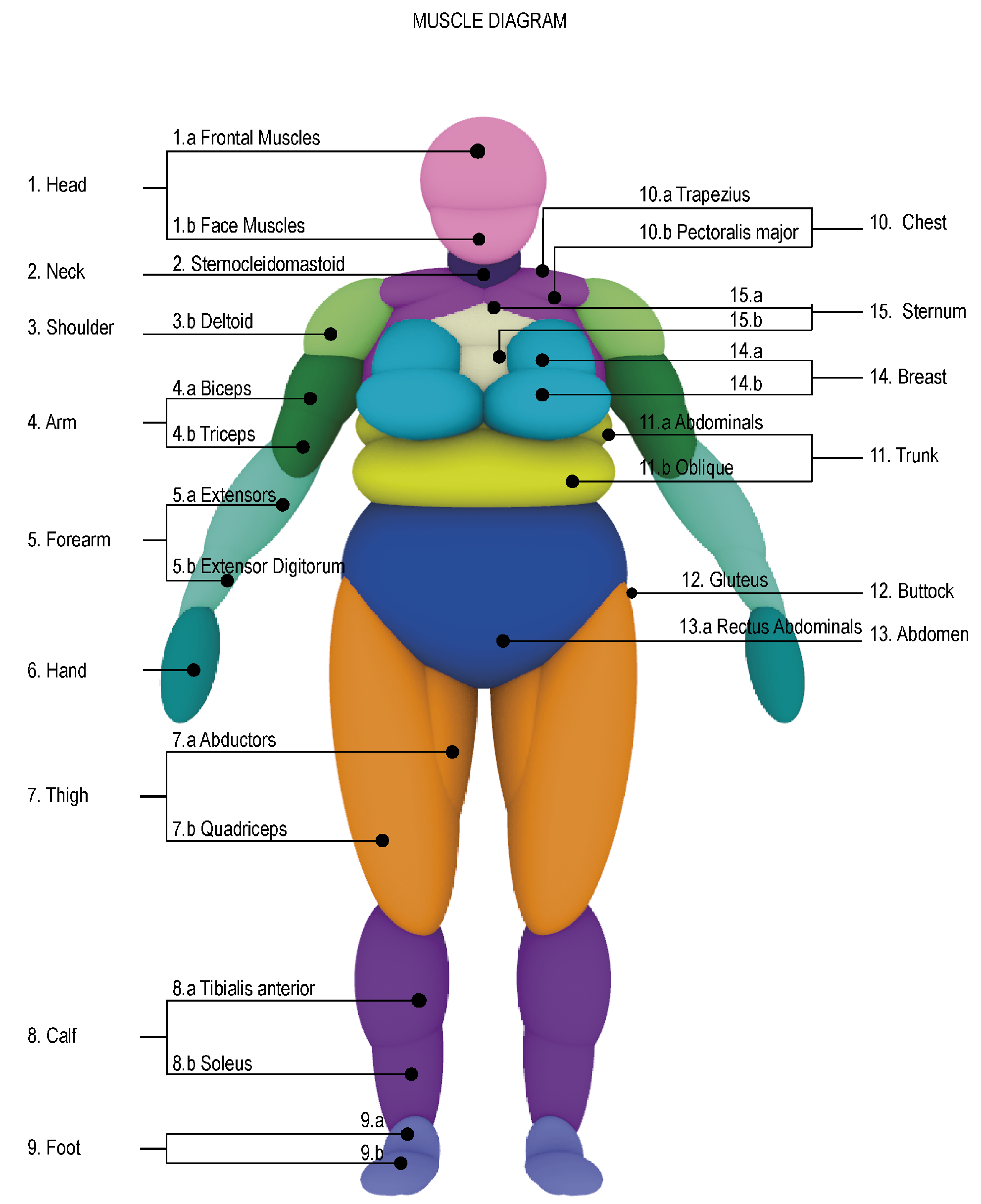
3.2. Creation of the Convex Volume Approximation
- Topology: Set of ellipsoids and rules that define the composition of the 3D mannequin;
- (a)
- The mannequin is conformed by a collection of convex volumes (ellipsoids), without boolean union among them;
- (b)
- The collection has a finite number of ellipsoids;
- (c)
- Each ellipsoid (singleton or pairs) approximates a particular part or area of the body;
- (d)
- Pairs of ellipsoids correspond to parts of the body with reflection (symmetry) along the sagittal plane (i.e., left and right);
- (e)
- Singleton ellipsoids are symmetric with respect to the sagittal plane.
- Geometry: Set of geometric properties S (position and orientation) and D (dimensions) that define each ellipsoid.
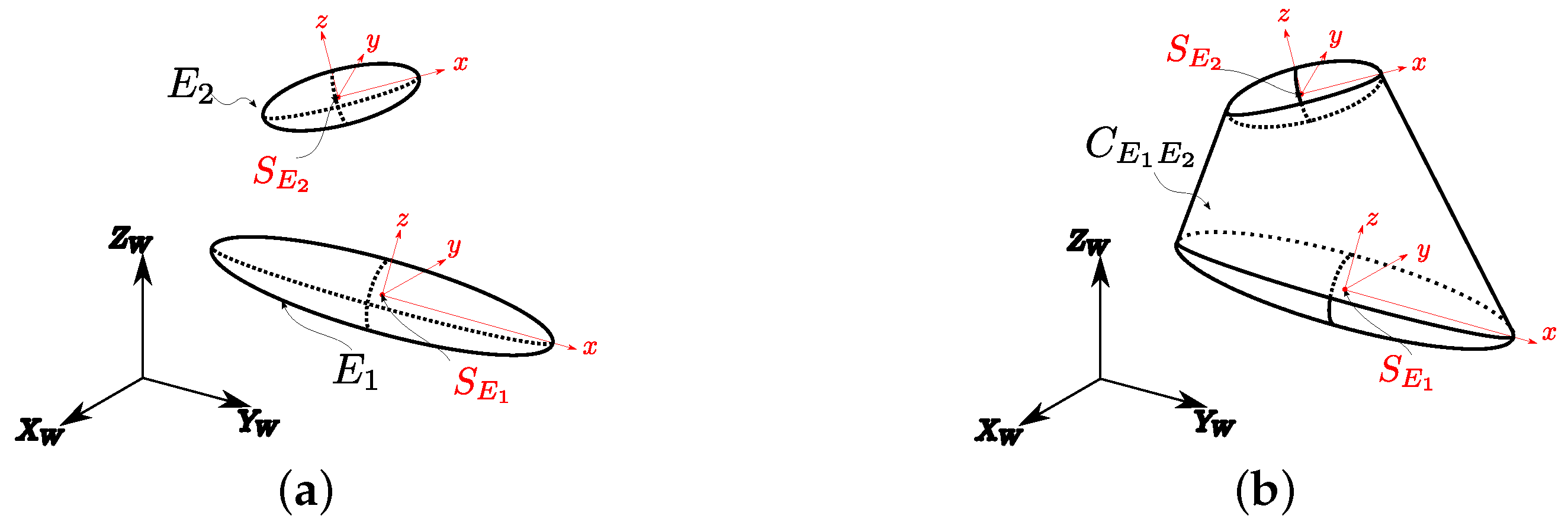
- : Point-clouds of ellipsoids in ;
- : SO(3) coordinate system of cushion , coincides with , the coordinate system of ellipsoid ;
- is defined as .
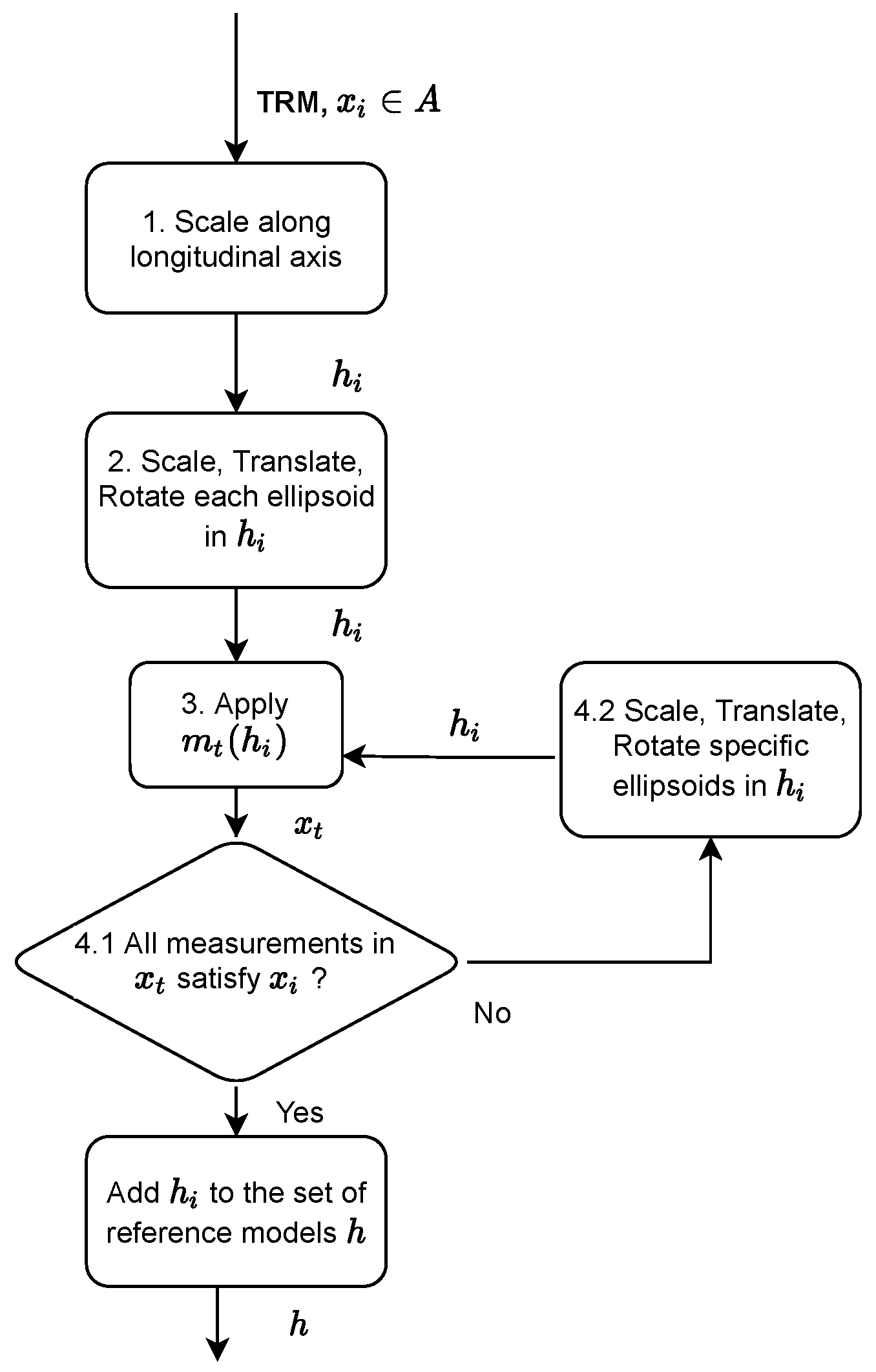
3.3. Construction of Reference Mannequins Based on the Base Mannequin
- Each ellipsoid is then manually modified (scaled, rotated, and translated) to obtain a mannequin that visually approximates the tailor measurements .
- Function is applied to obtain the current measurements () of the mannequin. See Section 3.5.
- If some cross section does not satisfy the desired measurement , the ellipsoids that influence it are manually modified (scaled, translated, and rotated) again.
- Steps 3 and 4 are repeated until the the measurements in Table 3 are satisfied.
3.4. Cleaning of Reference Mannequin Geometries
- A common SO(3) coordinate system (WCS) is defined;
- The position of each model is corrected according to WCS to ensure common placement;
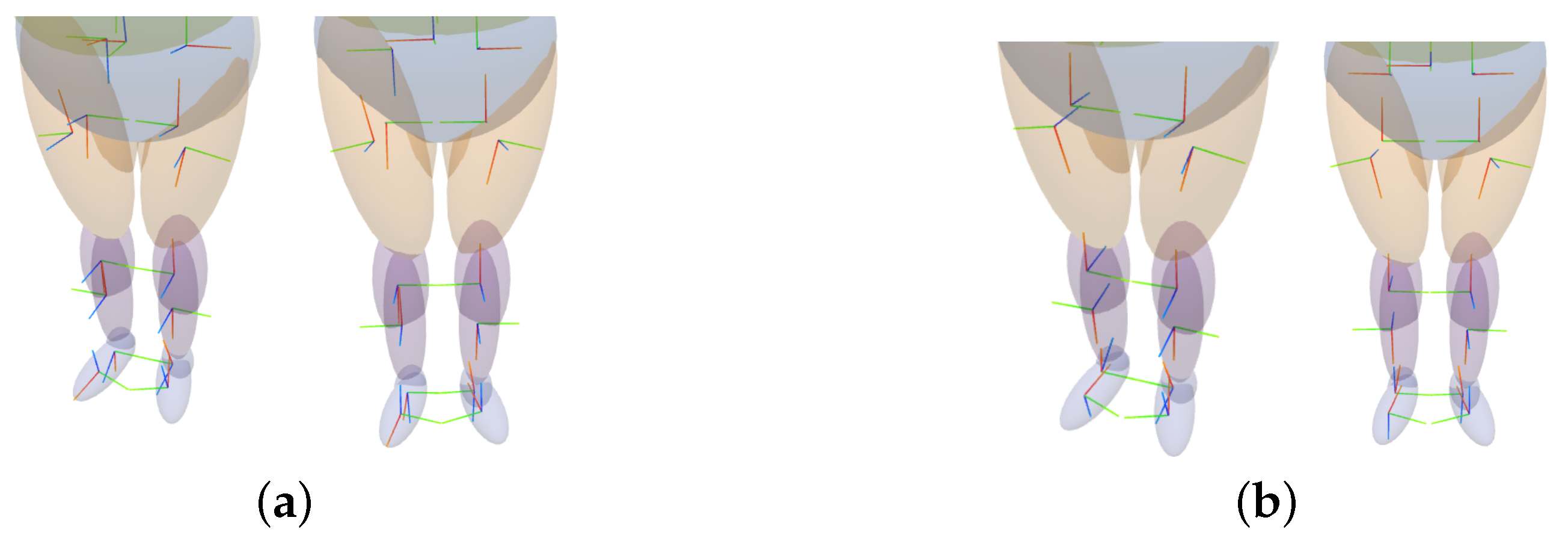
- The orientations of the sets of corresponding ellipsoids are corrected to ensure minimum variation between analogous axes;
- The ellipsoids in the right hemisphere are omitted and replaced by reflections (with respect to the sagittal plane) of the ellipsoids in the left hemisphere to obtain symmetry;
- Central ellipsoids are corrected in order to posses symmetry with respect to themselves along the sagittal plane.
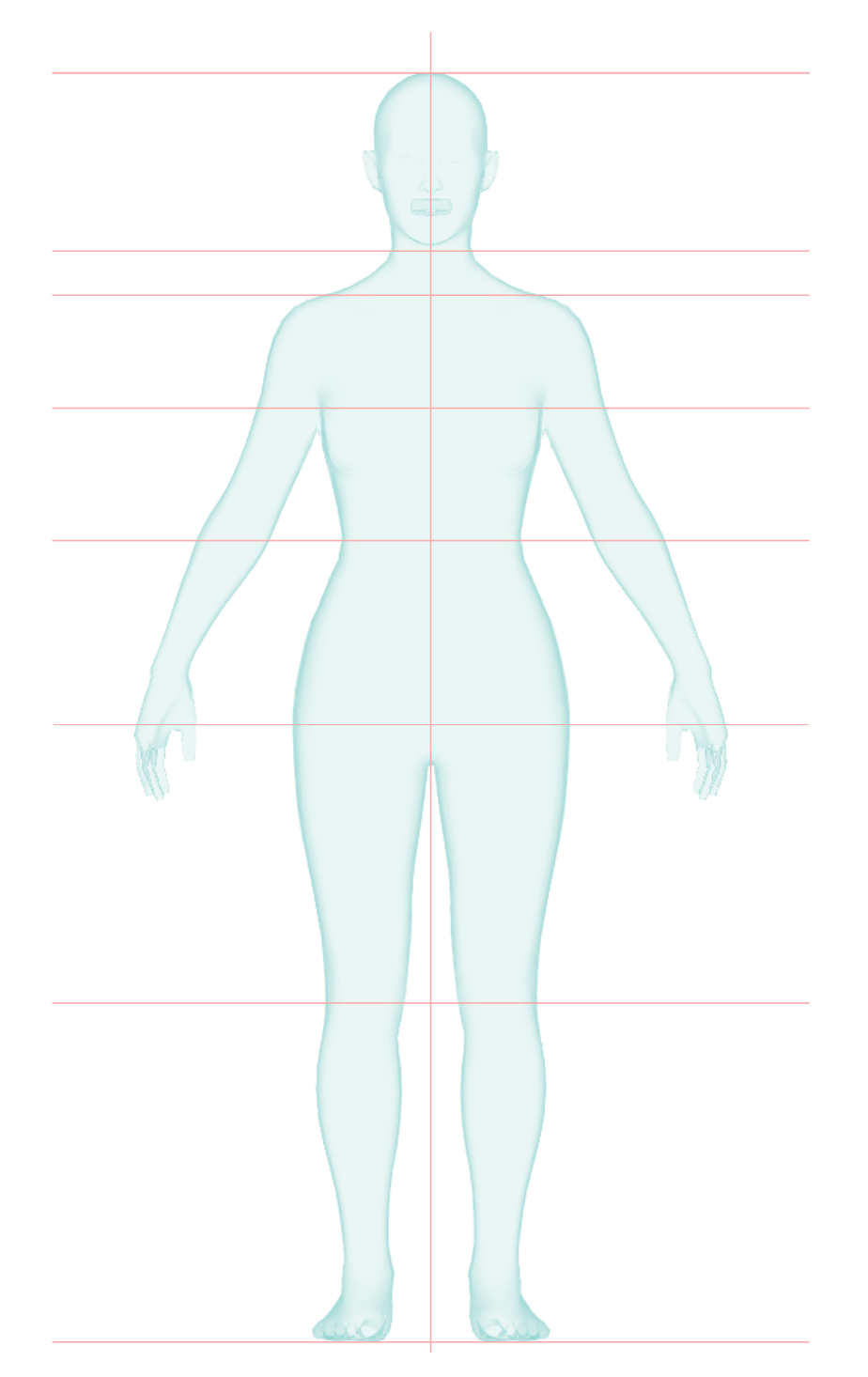
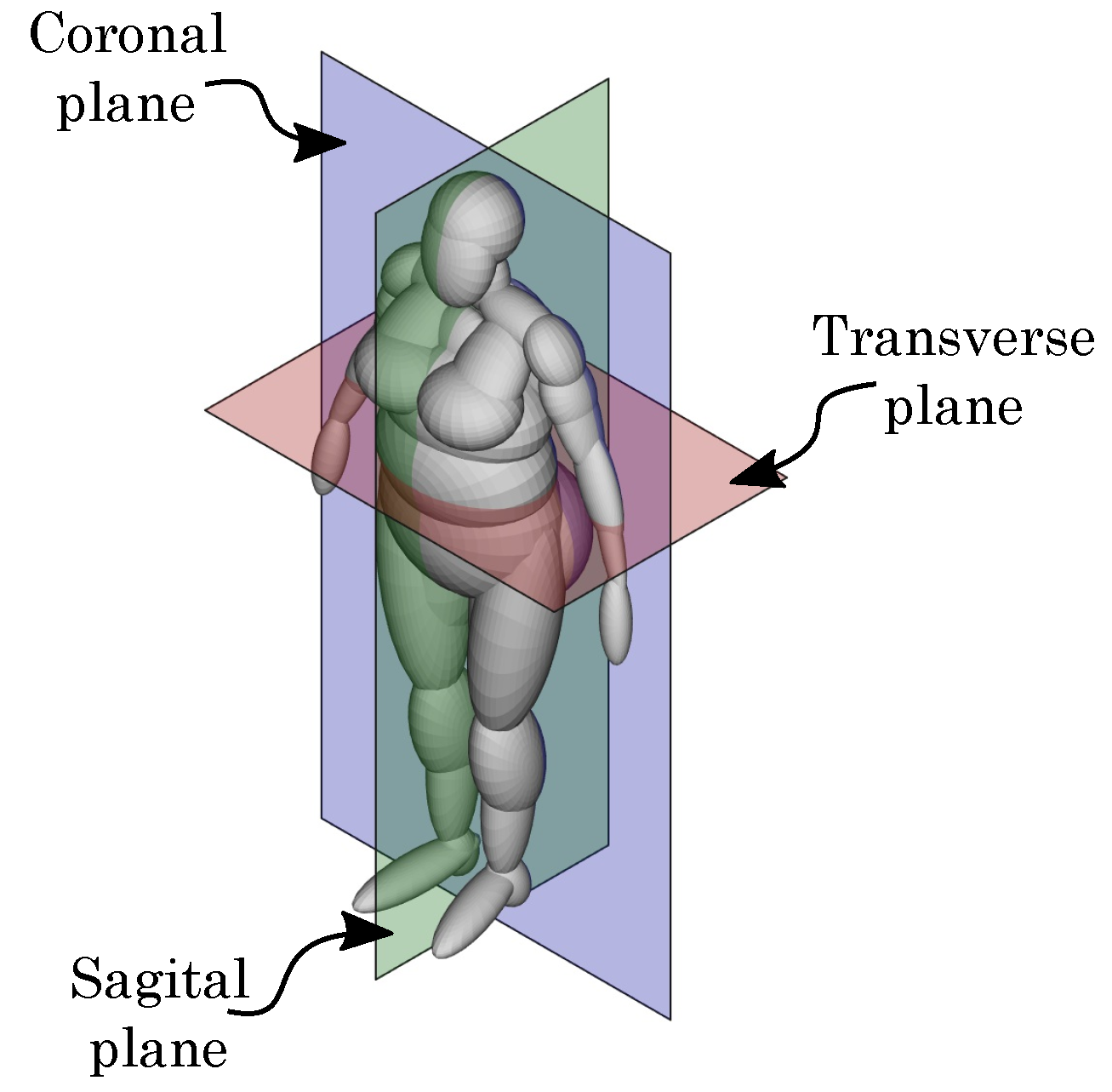
- Coronal plane: Perpendicular to the ground. Separates front from back.
- Transverse plane: Parallel to the ground. Separates head from feet.
- Sagittal plane: Perpendicular to the ground. Separates left from right.
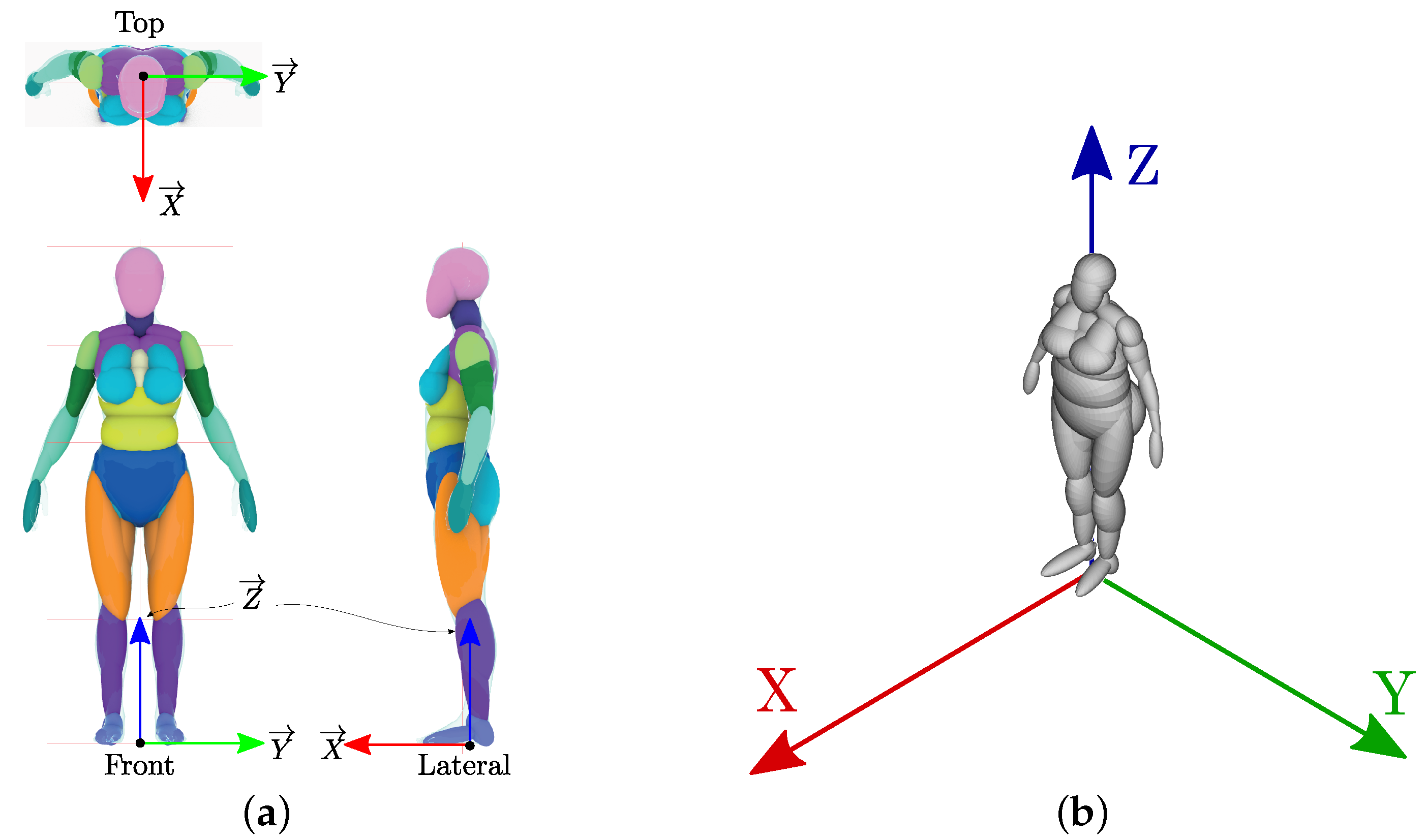
- In the direction, the origin is set in the lowest coordinate of the feet;
- In the direction, the origin is set in the centroid of the shoulder ellipsoids (10.a Trapezius) from the lateral view;
- In the direction, the origin is set in the middle point between shoulders (viewed from the front).
- For lateral ellipsoids, the right ellipsoids are omitted, and the analogous left ellipsoids are mirrored with respect to the sagittal plane.
- Due to the mirroring effect, the resulting coordinate systems are left-handed. Hence, the Z-axes have their direction inverted to preserve the SO(3) property. See Figure 13.
- For central ellipsoids, the X-axes are defined orthogonal to the sagittal plane.
- The Y-axes are projected to the sagittal plane, and the Z-axes are computed as . See Figure 14.
3.5. Extraction of Tailor Measurements from Models
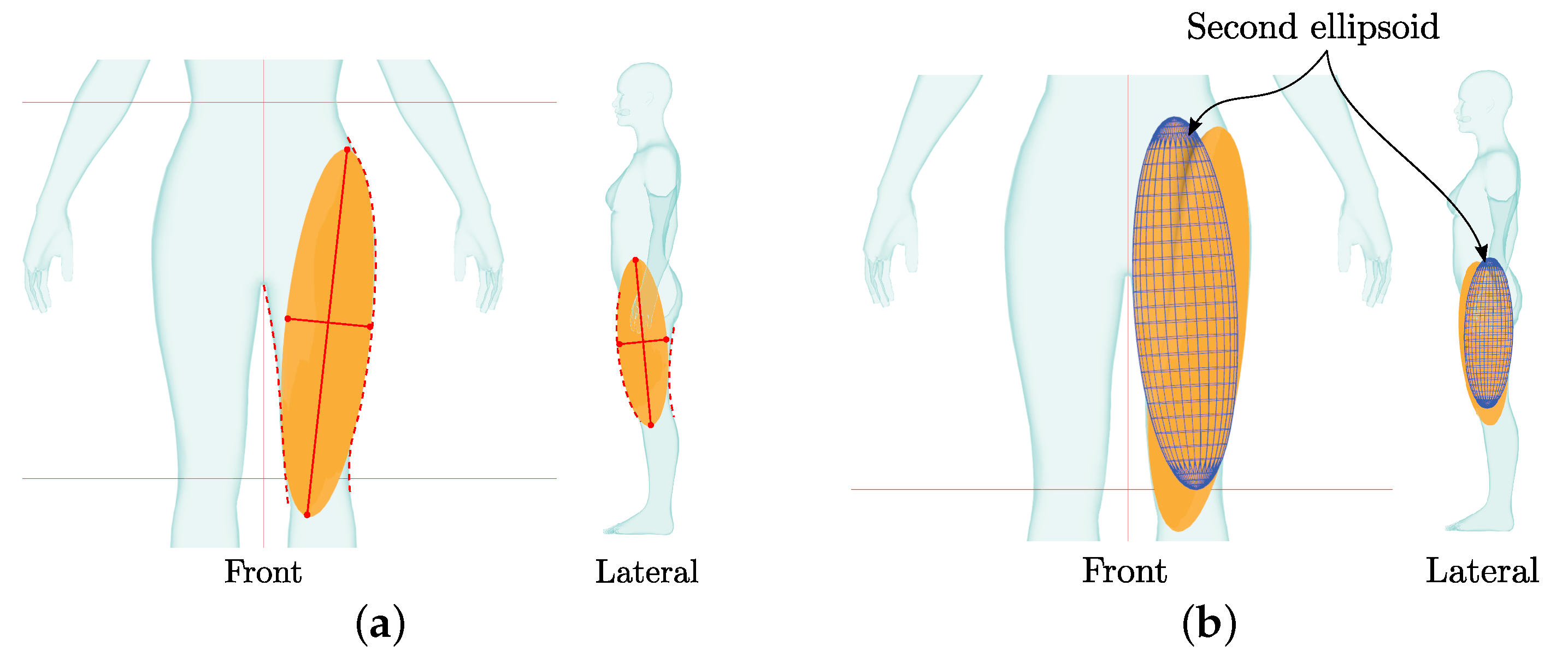
- Cross sections are obtained at specific heights (see Figure 15a) of mannequin B.
- A 2D () convex hull is computed for cross sections corresponding to , , and (see Figure 15b).
- The length of the perimeter of each convex hull in is calculated.
- Shoulder width is calculated as the distance between the two outermost points in the Y direction.
3.6. Synthesis of Mannequins from Tailor Measurements
- : set of n Reference Mannequins as a set of tuples .
- : point in containing the measurements of the jth Reference Mannequin , .
- : Set of ellipsoids . , with
- (a)
- k: the number of ellipsoids defined in the ;
- (b)
- ethe llipsoid defined by dimension and coordinate system (position and orientation), respectively.
- measurements of target model describing the shape of the desired female body.
- : Target model as a set of ellipsoids .
- : point in that describes the l measurements of that influence , with the synthesized model; .
- : point in that describes the l measurements of that influence , with ; .
- : known geometric property (i.e., or ) of with
- : euclidean distance between and .
- p: degree of the interpolation polynomial; .
- : interpolated property (i.e., or ) of ; with .
4. Results
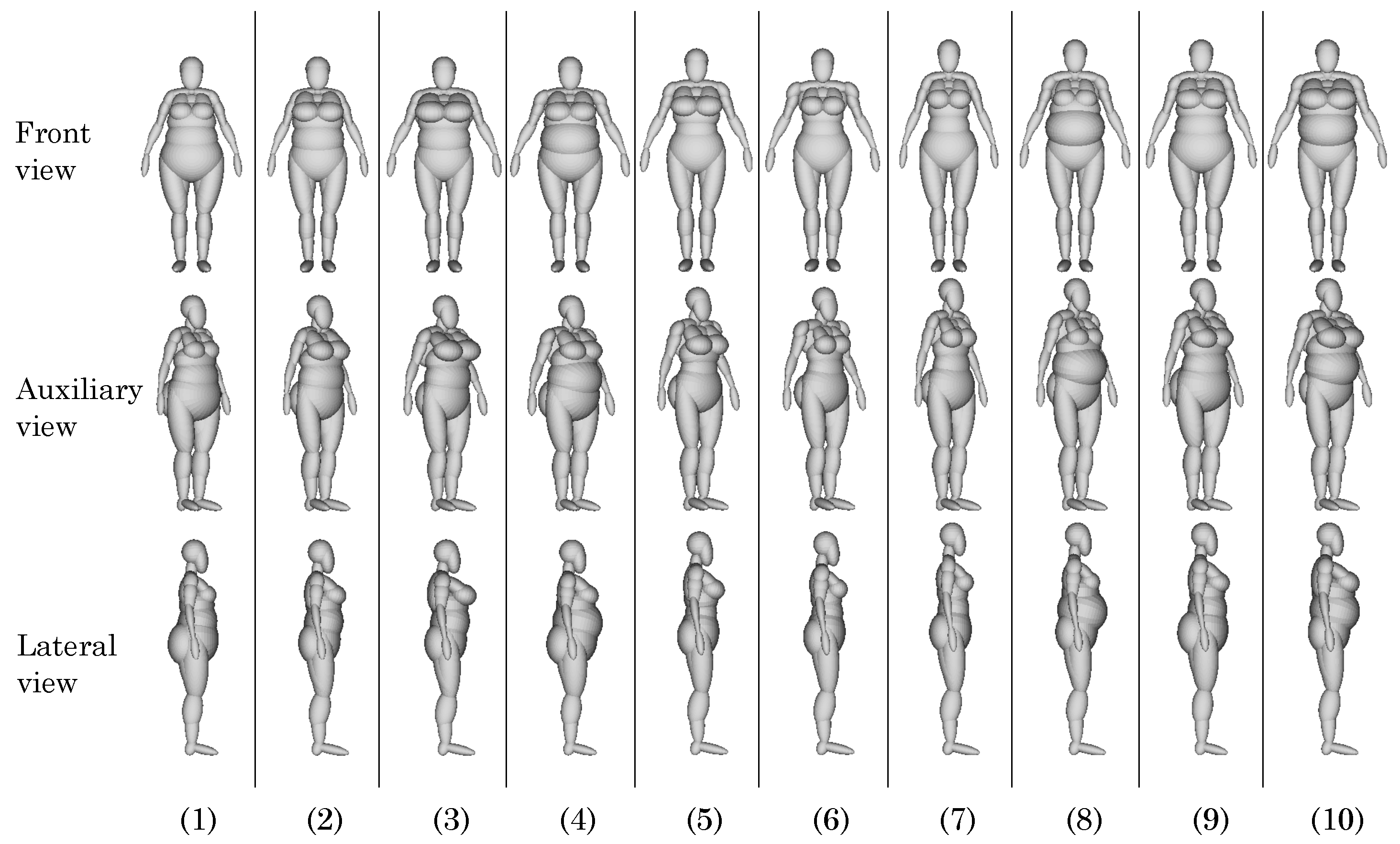
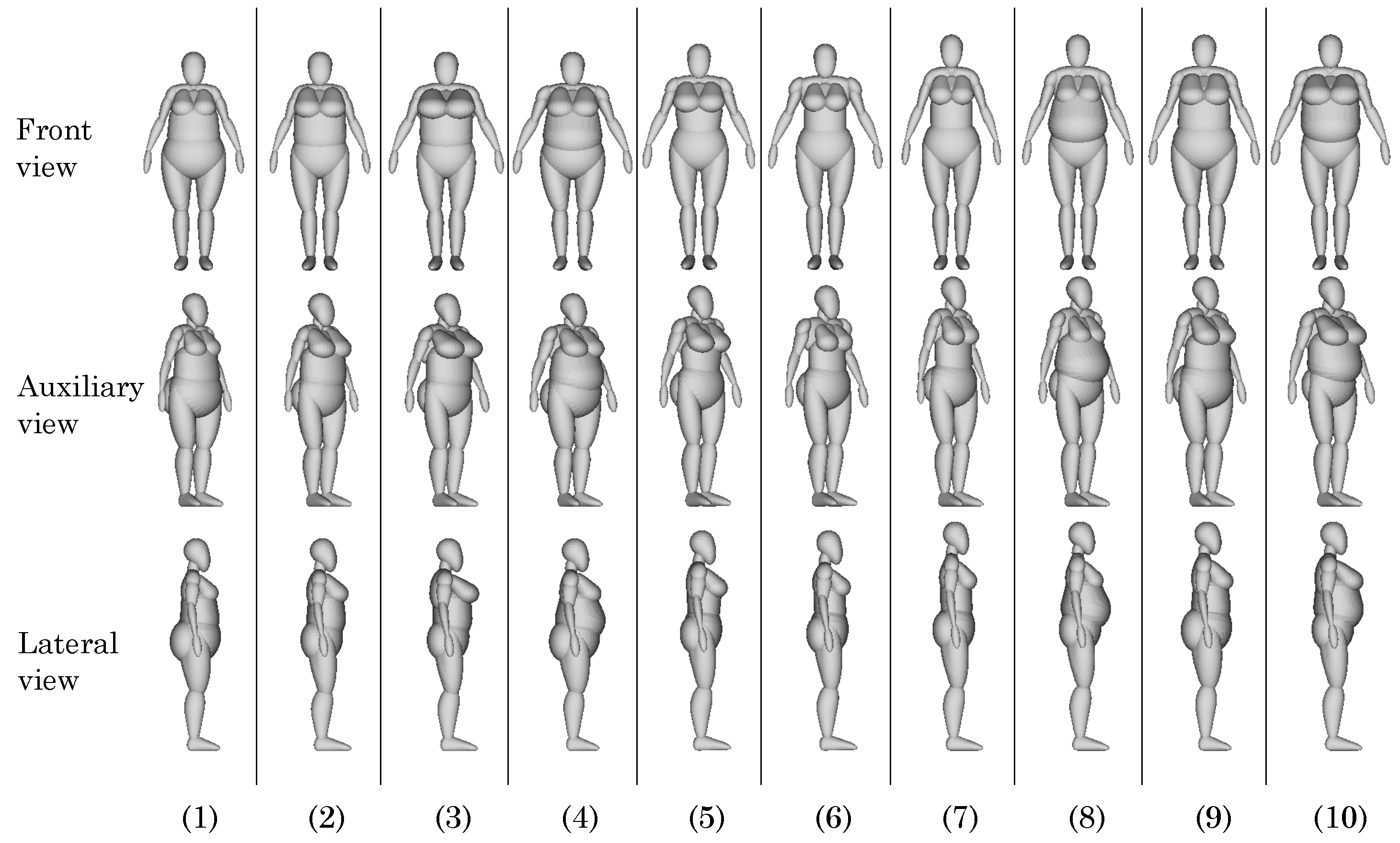
4.1. Measurement-Driven Models Generated via Interpolation
| Height () | Shoulder Width () | Breast Perimeter () | Waist Perimeter () | Hip Perimeter () | |
|---|---|---|---|---|---|
| Average Error (%) | 0.2 | 2.6 | 2.4 | 0.8 | 0.9 |
| Maximum Error (%) | 0.4 | 6.6 | 7.0 | 1.5 | 2.2 |
| Minimum Error (%) | 0.0 | 0.1 | 0.0 | 0.0 | 0.1 |
| Mannequin | Height () | Shoulder Width () | Breast Perimeter () | Waist Perimeter () | Hip Perimeter () |
|---|---|---|---|---|---|
| (1) | 153.75 | 35.75 | 101.25 | 102.5 | 134.75 |
| (2) | 153.75 | 35.75 | 118.5 | 102.5 | 117.5 |
| (3) | 153.75 | 41.5 | 135.75 | 102.5 | 117.5 |
| (4) | 153.75 | 47.25 | 118.5 | 122.25 | 134.75 |
| (5) | 159.5 | 41.5 | 118.5 | 82.75 | 117.5 |
| (6) | 159.5 | 47.25 | 101.25 | 82.75 | 117.5 |
| (7) | 165.25 | 35.75 | 101.25 | 82.75 | 117.5 |
| (8) | 165.25 | 41.5 | 101.25 | 122.25 | 117.5 |
| (9) | 165.25 | 41.5 | 118.5 | 102.5 | 134.75 |
| (10) | 165.25 | 47.25 | 135.75 | 122.25 | 117.5 |
4.2. Quantitative Comparison: Cushion-Based Mannequin vs. Mesh-Based Model
4.3. Interaction Simulation between Convex Volume Model and Garment
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Term | Description |
| A set of tailor measurements that describes the coarse shape and size of a female body. | |
| Height. | |
| Shoulder width. | |
| Breast perimeter. | |
| Waist perimeter. | |
| Hip perimeter. | |
| C | Cushion; 2-manifold mesh surface in . Computed as the convex hull of two ellipsoids (which can be the same) positioned and oriented arbitrarily in space. |
| SO(3) | Special Orthogonal Group. |
| RHCCS | SO(3) Right-Handed Canonical Coordinate System. |
| S | homogeneous matrix. SO(3) Right-Handed Canonical Coordinate System (RHCCS) defines the position and orientation of an ellipsoid in . |
| D | Point in . , . Defines the measurements of the semi-axes of an ellipsoid in . |
| A | A set of points in . Different sets of tailor measurements. |
| x | An element from A containing a set of particular tailor measurements . An instance of . |
| L | A set of n-ordered pairs that define the upper and lower limits of the components of point . |
| B | A set of ellipsoids in that approximates the shape and size of a female human body. B satisfies a particular set of tailor measurements . Each ellipsoid in B is described by a particular S and D (geometry). B is conformed of topology and geometry data. Synthesized mannequins B are displayed in gray color. |
| H | A set of different values of B that approximate the shape and size of different female human bodies. Each is described by the measurements of a specific point . |
| List of n tuples representing the Reference Mannequins. . , with an ellipsoidal model (geometry data) that satisfies the measurements in , with . Each is defined by a combination of the values of L. | |
| Set of functions . Set of heuristics to obtain the tailor measurements of a digital model B. | |
| Set of synthesis functions . A particular . Set of functions that produce a digital mannequin B that satisfies a set of measurements based on known data points . Weighted average of the form of Equation (1). | |
| 3D mannequin | 3D digital model that approximates the female human body as a set of convex volumes (ellipsoids and cushions). |
| 3D model | 3D non-convex mesh that represents the female human body. |
| Base Mannequin. A 3D mannequin instance. Template mannequin used to construct . |
References
- Cheng, Z.Q.; Chen, Y.; Martin, R.R.; Wu, T.; Song, Z. Parametric modeling of 3D human body shape—A survey. Comput. Graph. 2018, 71, 88–100. [Google Scholar] [CrossRef]
- Chu, C.H.; Tsai, Y.T.; Wang, C.C.; Kwok, T.H. Exemplar-based statistical model for semantic parametric design of human body. Comput. Ind. 2010, 61, 541–549. [Google Scholar] [CrossRef]
- Liu, K.; Zeng, X.; Bruniaux, P.; Wang, J.; Kamalha, E.; Tao, X. Fit evaluation of virtual garment try-on by learning from digital pressure data. Knowl.-Based Syst. 2017, 133, 174–182. [Google Scholar] [CrossRef]
- Wu, N.; Deng, Z.; Huang, Y.; Liu, C.; Zhang, D.; Jin, X. A fast garment fitting algorithm using skeleton-based error metric. Comput. Animat. Virtual Worlds 2018, 29, e1811. [Google Scholar] [CrossRef]
- AMMO.JS—JavaScript Physics Engine. Port from Bullet. Available online: https://github.com/kripken/ammo.js/ (accessed on 10 December 2020).
- Dang, L.M.; Min, K.; Wang, H.; Piran, M.J.; Lee, C.H.; Moon, H. Sensor-based and vision-based human activity recognition: A comprehensive survey. Pattern Recognit. 2020, 108, 107561. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 2012, 15, 1192–1209. [Google Scholar] [CrossRef]
- Chen, Y.; Song, Z.; Xu, W.; Martin, R.R.; Cheng, Z.Q. Parametric 3D modeling of a symmetric human body. Comput. Graph. 2019, 81, 52–60. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Zhang, Z. Tensor-based human body modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 105–112. [Google Scholar]
- Cho, Y.; Okada, N.; Park, H.; Takatera, M.; Inui, S.; Shimizu, Y. An interactive body model for individual pattern making. Int. J. Cloth. Sci. Technol. 2005, 17, 91–99. [Google Scholar] [CrossRef]
- Cichocka, A.; Bruniaux, P.; Frydrych, I. 3D Garment Modelling-Creation of a Virtual Mannequin of the Human Body; Instytut Biopolimerów i Włókien Chemicznych (IBWCh): Łódź, Polska, 2014. [Google Scholar]
- Huang, L.; Gao, C. Nonuniform Parametric Human Body Based on Model Reuse. In Proceedings of the 2014 5th International Conference on Digital Home, Guangzhou, China, 28–30 November 2014; pp. 406–411. [Google Scholar]
- Kim, S.; Park, C.K. Parametric body model generation for garment drape simulation. Fibers Polym. 2004, 5, 12–18. [Google Scholar] [CrossRef]
- Peng, J.; Jiang, G.; Cong, H. Rapid parametric human modeling in 3D garment simulation. Autex Res. J. 2019, 19, 60–67. [Google Scholar] [CrossRef]
- Seo, H.; Magnenat-Thalmann, N. An automatic modeling of human bodies from sizing parameters. In Proceedings of the 2003 Symposium on Interactive 3D Graphics, Monterey, CA, USA, 27–30 April 2003; pp. 19–26. [Google Scholar]
- Kasap, M.; Magnenat-Thalmann, N. Parameterized human body model for real-time applications. In Proceedings of the 2007 International Conference on Cyberworlds (CW’07), Hannover, Germany, 24–26 October 2007; pp. 160–167. [Google Scholar]
- Baek, S.Y.; Lee, K. Parametric human body shape modeling framework for human-centered product design. Comput.-Aided Des. 2012, 44, 56–67. [Google Scholar] [CrossRef]
- Baek, S.Y.; Lee, K. Parametric human body modelling system for virtual garment fitting. Int. J. Comput. Aided Eng. Technol. 8 2013, 5, 242–261. [Google Scholar] [CrossRef]
- Goncharenko, I.; Takashiba, K.; Mochimaru, M.; Kouchi, M.; Usui, S.; Odahara, M. Low-parametric control of human body shape modelling via the web using 3D scan data. Int. J. Hum. Factors Model. Simul. 1 2012, 3, 187–203. [Google Scholar] [CrossRef]
- Hasler, N.; Stoll, C.; Sunkel, M.; Rosenhahn, B.; Seidel, H.P. A statistical model of human pose and body shape. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2009; Volume 28, pp. 337–346. [Google Scholar]
- Koo, B.Y.; Park, E.J.; Choi, D.K.; Kim, J.J.; Choi, M.H. Example-based statistical framework for parametric modeling of human body shapes. Comput. Ind. 2015, 73, 23–38. [Google Scholar] [CrossRef]
- Wang, C.C. Parameterization and parametric design of mannequins. Comput.-Aided Des. 2005, 37, 83–98. [Google Scholar] [CrossRef]
- Huang, J.; Kwok, T.H.; Zhou, C. Parametric design for human body modeling by wireframe-assisted deep learning. Comput.-Aided Des. 2019, 108, 19–29. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. Graph. (TOG) 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Pujades, S.; Mohler, B.; Thaler, A.; Tesch, J.; Mahmood, N.; Hesse, N.; Bülthoff, H.H.; Black, M.J. The virtual caliper: Rapid creation of metrically accurate avatars from 3D measurements. IEEE Trans. Vis. Comput. Graph. 2019, 25, 1887–1897. [Google Scholar] [CrossRef]
- Hilton, A.; Beresford, D.; Gentils, T.; Smith, R.; Sun, W.; Illingworth, J. Whole-body modelling of people from multiview images to populate virtual worlds. Vis. Comput. 2000, 16, 411–436. [Google Scholar] [CrossRef]
- Lee, W.; Gu, J.; Magnenat-Thalmann, N. Generating animatable 3D virtual humans from photographs. In Computer Graphics Forum; Blackwell Publishers Ltd.: Oxford, UK; Boston, MA, USA, 2000; Volume 19, pp. 1–10. [Google Scholar]
- Wang, C.C.; Wang, Y.; Chang, T.K.; Yuen, M.M. Virtual human modeling from photographs for garment industry. Comput.-Aided Des. 2003, 35, 577–589. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, W.; Zhu, Y.; Dong, L.; Zhou, H.; Zhang, Q. Building high-fidelity human body models from user-generated data. IEEE Trans. Multimed. 2020, 23, 1542–1556. [Google Scholar] [CrossRef]
- Gu, L.; Istook, C.; Ruan, Y.; Gert, G.; Liu, X. Customized 3D digital human model rebuilding by orthographic images-based modelling method through open-source software. J. Text. Inst. 2019, 110, 740–755. [Google Scholar] [CrossRef]
- Kolotouros, N.; Pavlakos, G.; Daniilidis, K. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4501–4510. [Google Scholar]
- Xie, H.; Zhong, Y.; Yu, Z.; Hussain, A. Non-parametric anthropometric graph convolutional network for virtual mannequin reconstruction. IEEE Access 2019, 8, 3539–3550. [Google Scholar] [CrossRef]
- Scheepers, F.; Parent, R.E.; Carlson, W.E.; May, S.F. Anatomy-based modeling of the human musculature. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 3–8 August 1997; pp. 163–172. [Google Scholar]
- Wilhelms, J.; Van Gelder, A. Anatomically based modeling. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 3–8 August 1997; pp. 173–180. [Google Scholar]
- Qin, K.; Zhuang, Y.; Wu, F. Parameterizing 3D Human Model in Garment CAD. J. Comput. Aided Des. Comput. Graph. 2004, 16, 5. [Google Scholar]
- Seo, H.; Magnenat-Thalmann, N. An example-based approach to human body manipulation. Graph. Model. 2004, 66, 1–23. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. (TOG) 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Ouahabi, A. Signal and Image Multiresolution Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kaneflame3d. Realistic White Male and Female Low Poly: 3D Model. Available online: https://www.cgtrader.com/free-3d-models/character/anatomy/realistic-white-male-and-female-low-poly (accessed on 12 August 2021).
- Coyte, J.L.; Stirling, D.; Du, H.; Ros, M. Seated whole-body vibration analysis, technologies, and modeling: A survey. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 725–739. [Google Scholar] [CrossRef]
- THREE.JS—JavaScript 3D Library. Available online: https://threejs.org/ (accessed on 10 December 2020).
- Backenhof, A. Automatic Generation of Collision Hulls for Polygonal Objects; Linkoping University Electronic Press: Linkoping, Sweden, 2011. [Google Scholar]
- Bäcklund, H.; Neijman, N. Automatic Mesh Decomposition for Real-Time Collision Detection; Linköping University: Linköping, Sweden, 2014. [Google Scholar]
- Chowriappa, A.; Wirz, R.; Ashammagari, A.R.; Kesavadas, T. A convex decomposition methodology for collision detection. In Proceedings of the 2013 IEEE Virtual Reality (VR), Lake Buena Vista, FL, USA, 18–20 March 2013; pp. 57–58. [Google Scholar]
- Ghosh, M.; Amato, N.M.; Lu, Y.; Lien, J.M. Fast approximate convex decomposition using relative concavity. Comput.-Aided Des. 2013, 45, 494–504. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W.; Latecki, L.J. Convex shape decomposition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 97–104. [Google Scholar]
- Mamou, K.; Ghorbel, F. A simple and efficient approach for 3D mesh approximate convex decomposition. In Proceedings of the 2009 16th IEEE international conference on image processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 3501–3504. [Google Scholar]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef]



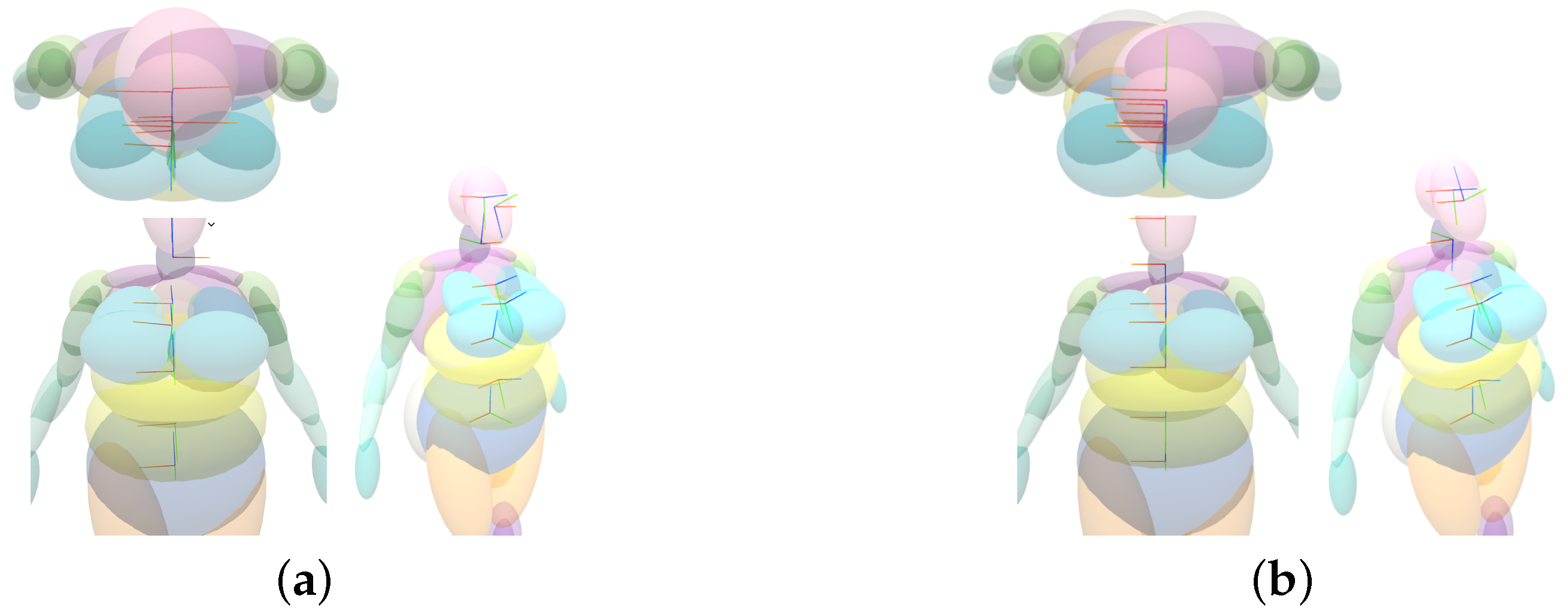


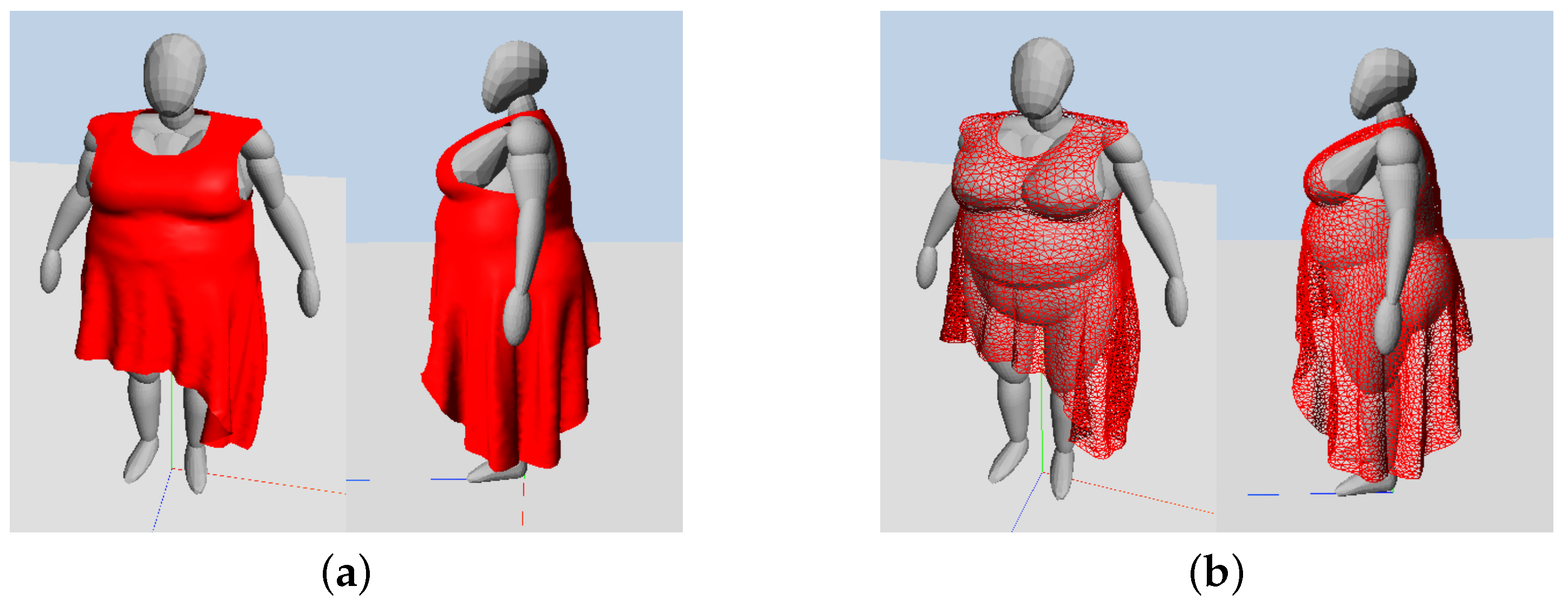
| Approach | Refs. | Advantages | Disadvantages |
|---|---|---|---|
| Non-Convex Example-Based Synthesis Approach | [2,8,9,10,11,12,13,14,15,16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,35,36] | (1) Models with intricate details can be reproduced. (2) Continuity of mesh surface is achieved. (3) Anatomic fidelity of the model. | (1) A non-convex model is produced. (2) Needs further processing steps to generate a ready-to-simulate model. (3) Expensive algorithms for deformation and surface-fitting. (4) Pose limitation or need to recompute/deform surfaces for pose changes. (5) Dependent on hardware and/or a large database of examples. |
| Non-Convex Anatomy Based Approach: Bone, Muscle, Tissue Construction | [33,34] | (1) Anatomic fidelity of the model. (2) High kinematic fidelity can be achieved. | (1) A non-convex model is produced. (2) High computation expenses. (3) Construction of unnecessary internal elements to reproduce external surfaces. (4) Phenotype limitation. |
| Synthesis Based on Convex Volumes | Our approach | (1) Low computational costs. (2) No intermediate steps for the preparation of the model for physics simulation. (3) Simple and straightforward parameterization with minimal tuning. (4) Reduced storage of data. (5) No need of re-computations of surfaces to change poses. | (1) Low model resolution, leaving out intricate details of the body. (2) Model surface does not have surface continuity. |
| Name | Origin | Number of Faces | Number of Vertex | Borders | Manifold |
|---|---|---|---|---|---|
| Reference 3D Model | [39] | 4984 | 4986 | 0 | True |
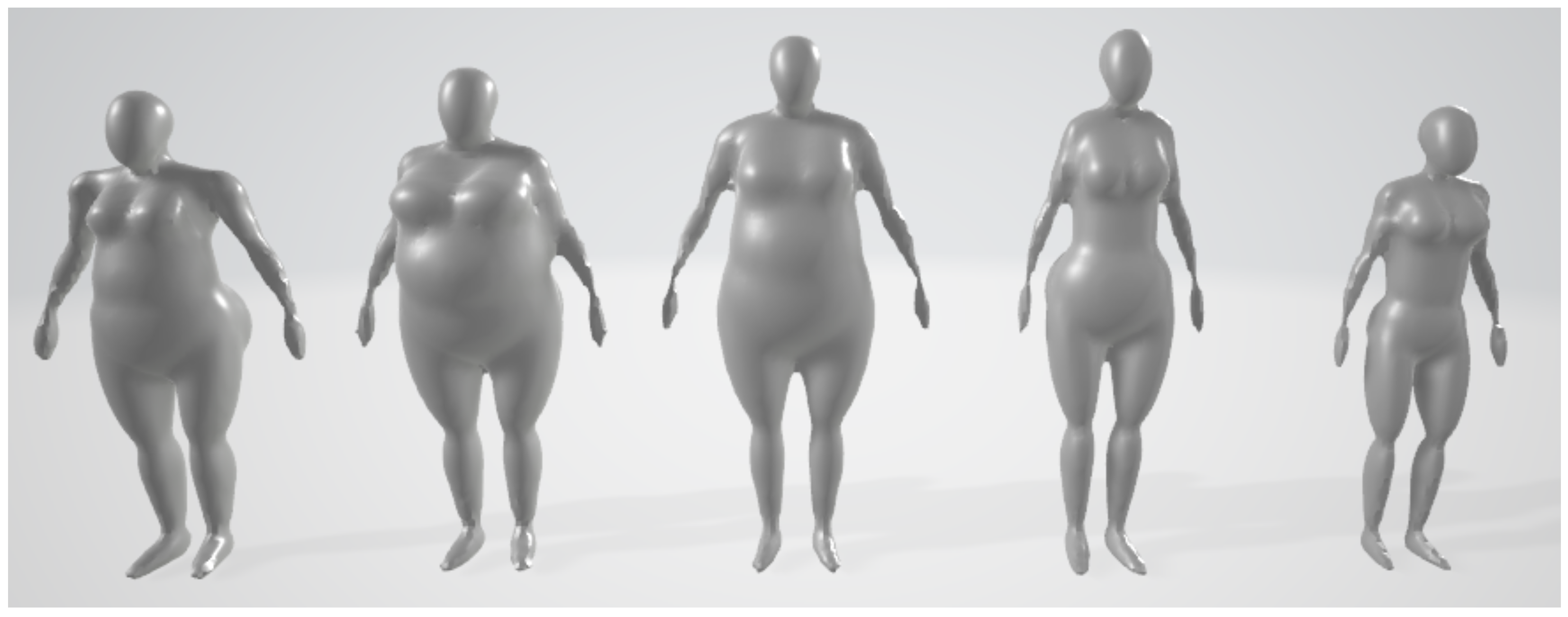
| Measurement/Model | Small Slim | Tall Slim | Small Chubby | Tall Chubby | Average |
|---|---|---|---|---|---|
| Height () | 148 | 171 | 148 | 171 | 159 |
| Shoulder Width () | 31 | 30 | 45 | 53 | 43 |
| Breast Perimeter () | 85 | 84 | 147 | 153 | 117 |
| Waist Perimeter () | 63 | 63 | 142 | 142 | 104 |
| Hip Perimeter () | 83 | 84 | 152 | 150 | 117 |
| Height (He) | Shoulder Width (Sh) | Breast Perimeter (Br) | Waist Perimeter (Wa) | Hip Perimeter (Hi) | |
|---|---|---|---|---|---|
| Mesh-based Model | 170 | 42.8 | 99.8 | 72.5 | 99.7 |
| Cushion-based Mannequin | 170.4 | 43.3 | 104.2 | 67.2 | 97.2 |
| Error (%) | 0.2 | 1.2 | 4.4 | 7.3 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velez-Sanin, S.; Gutierrez, J.; Correa, J.; Builes-Roldan, C.; Ruiz-Salguero, O. Measurement-Driven Synthesis of Female Digital Mannequin Using Convex Sub-Volumes. Appl. Sci. 2022, 12, 9742. https://doi.org/10.3390/app12199742
Velez-Sanin S, Gutierrez J, Correa J, Builes-Roldan C, Ruiz-Salguero O. Measurement-Driven Synthesis of Female Digital Mannequin Using Convex Sub-Volumes. Applied Sciences. 2022; 12(19):9742. https://doi.org/10.3390/app12199742
Chicago/Turabian StyleVelez-Sanin, Samuel, Juan Gutierrez, Jorge Correa, Carolina Builes-Roldan, and Oscar Ruiz-Salguero. 2022. "Measurement-Driven Synthesis of Female Digital Mannequin Using Convex Sub-Volumes" Applied Sciences 12, no. 19: 9742. https://doi.org/10.3390/app12199742
APA StyleVelez-Sanin, S., Gutierrez, J., Correa, J., Builes-Roldan, C., & Ruiz-Salguero, O. (2022). Measurement-Driven Synthesis of Female Digital Mannequin Using Convex Sub-Volumes. Applied Sciences, 12(19), 9742. https://doi.org/10.3390/app12199742






