A Separated-Flow Model for 2-D Viscous Flows around Bluff Bodies Using the Panel Method
Abstract
1. Introduction
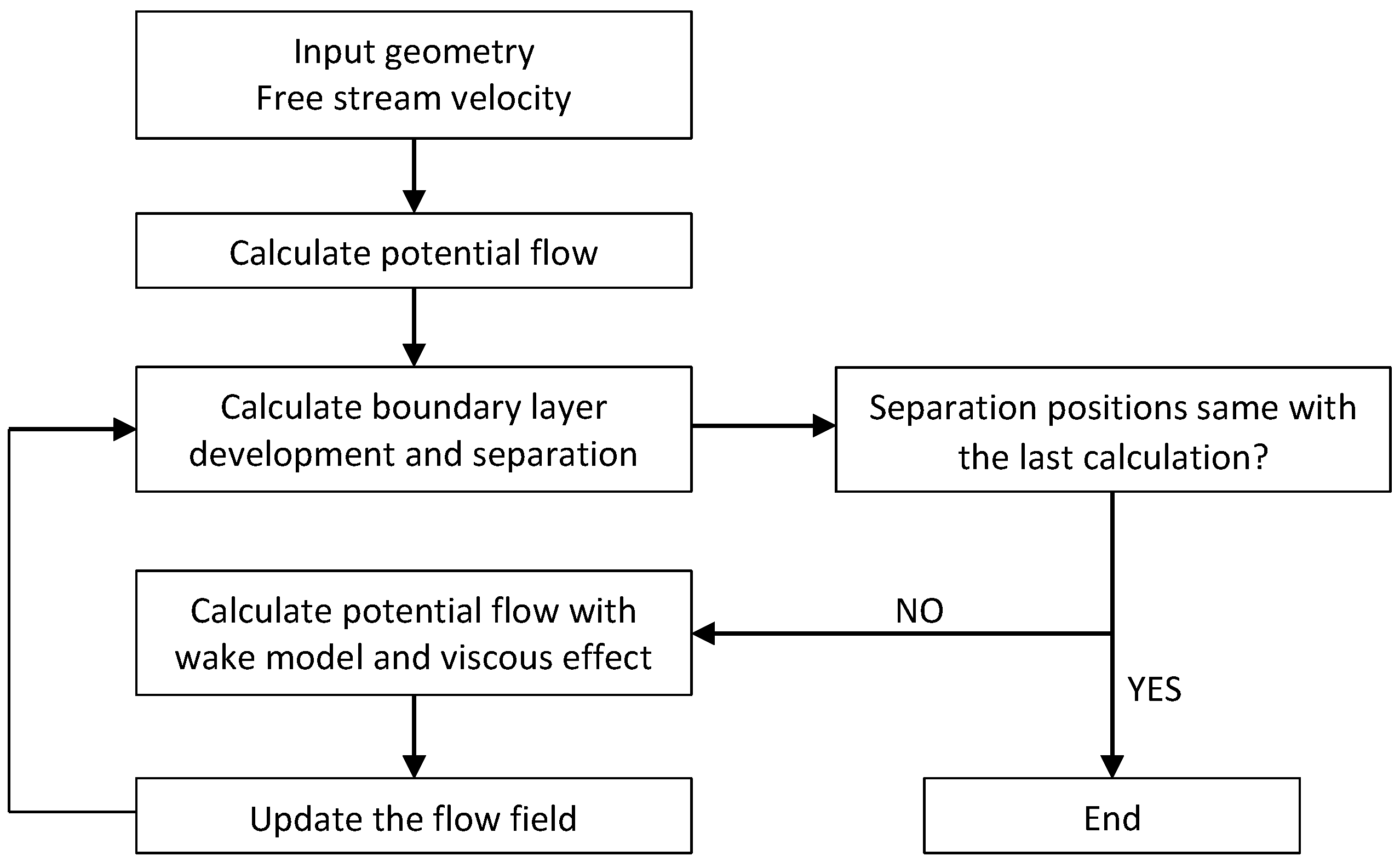
2. Methods
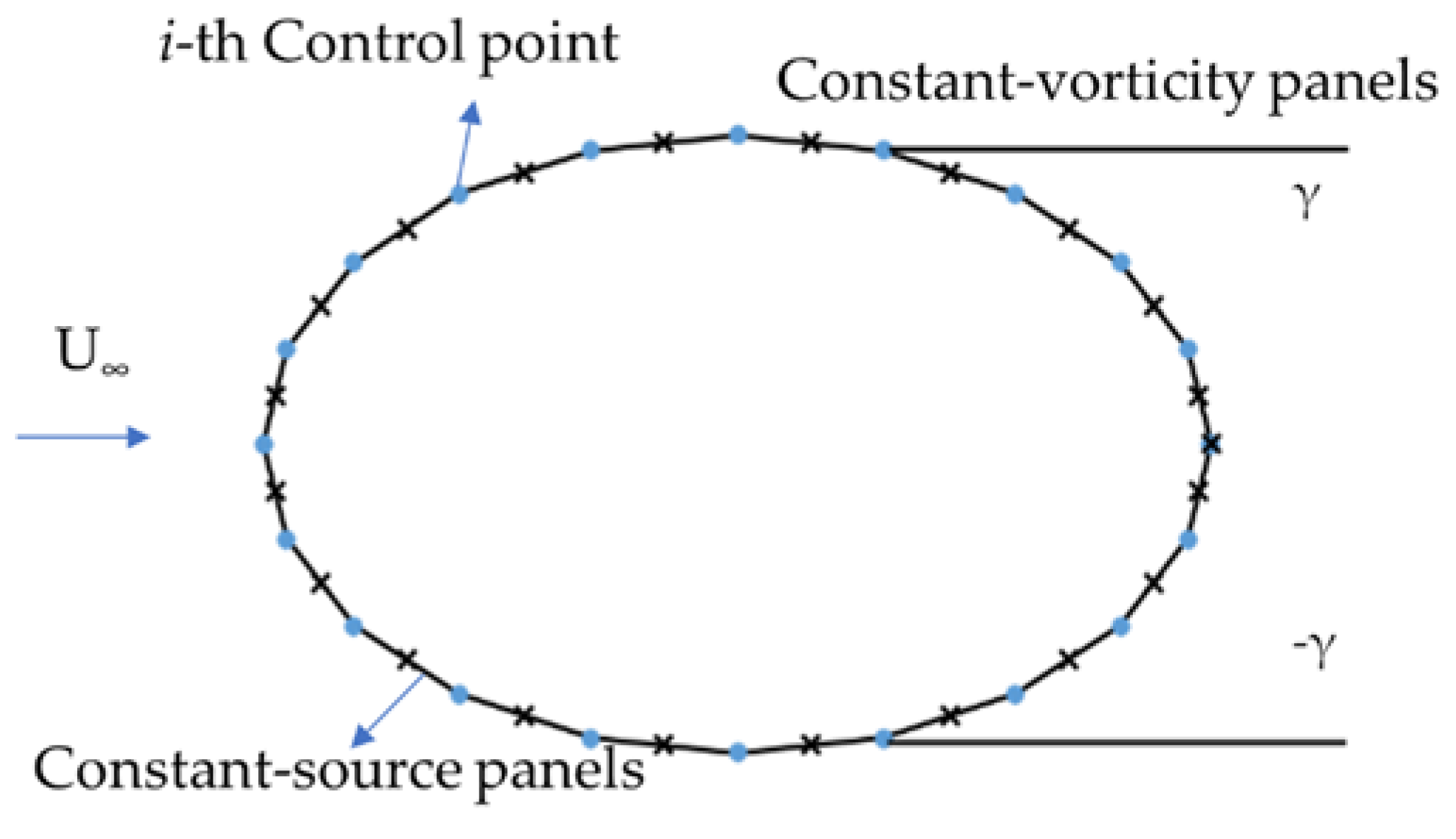
2.1. Potential Flow Calculation
2.2. Boundary-Layer Prediction
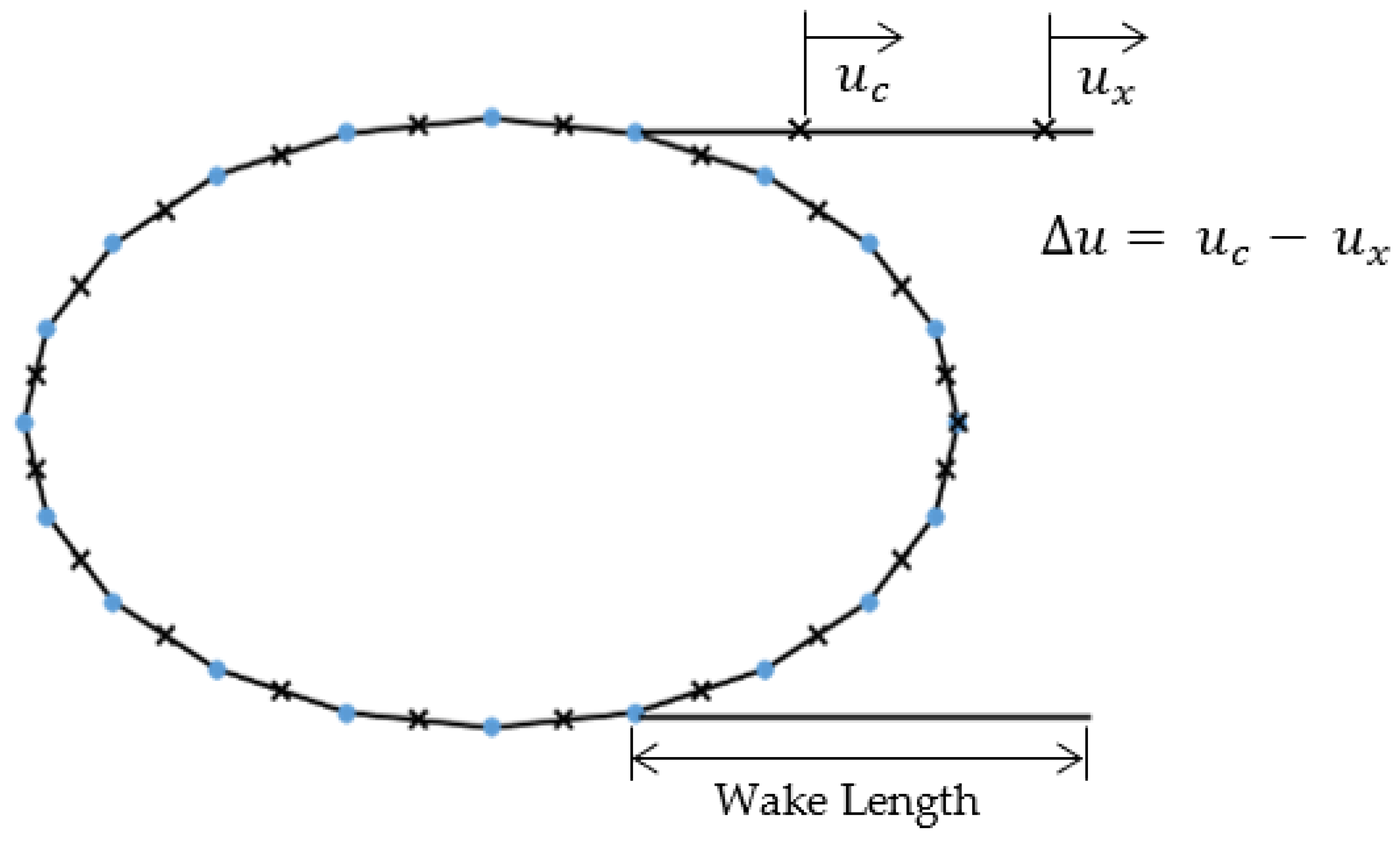
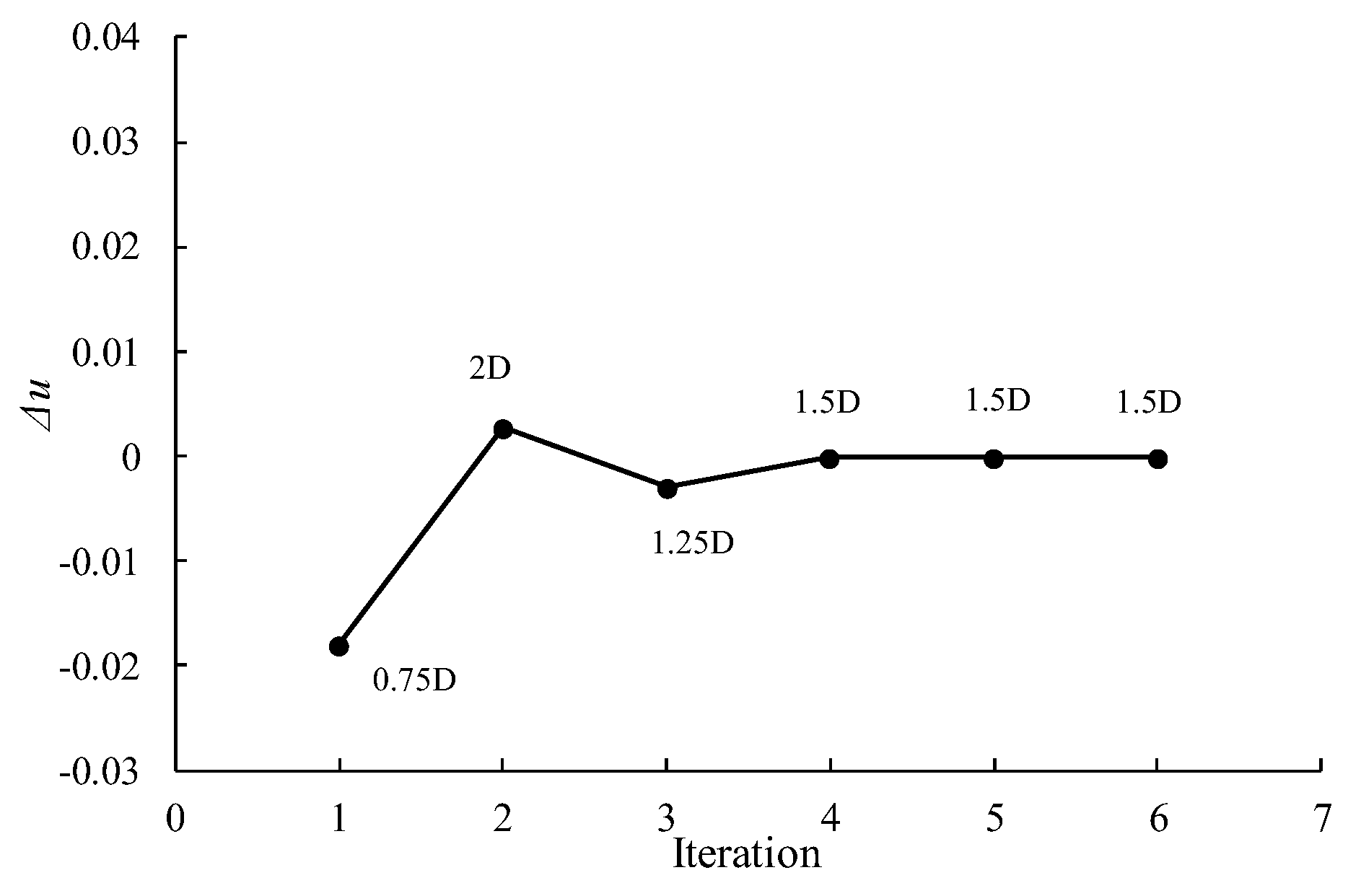
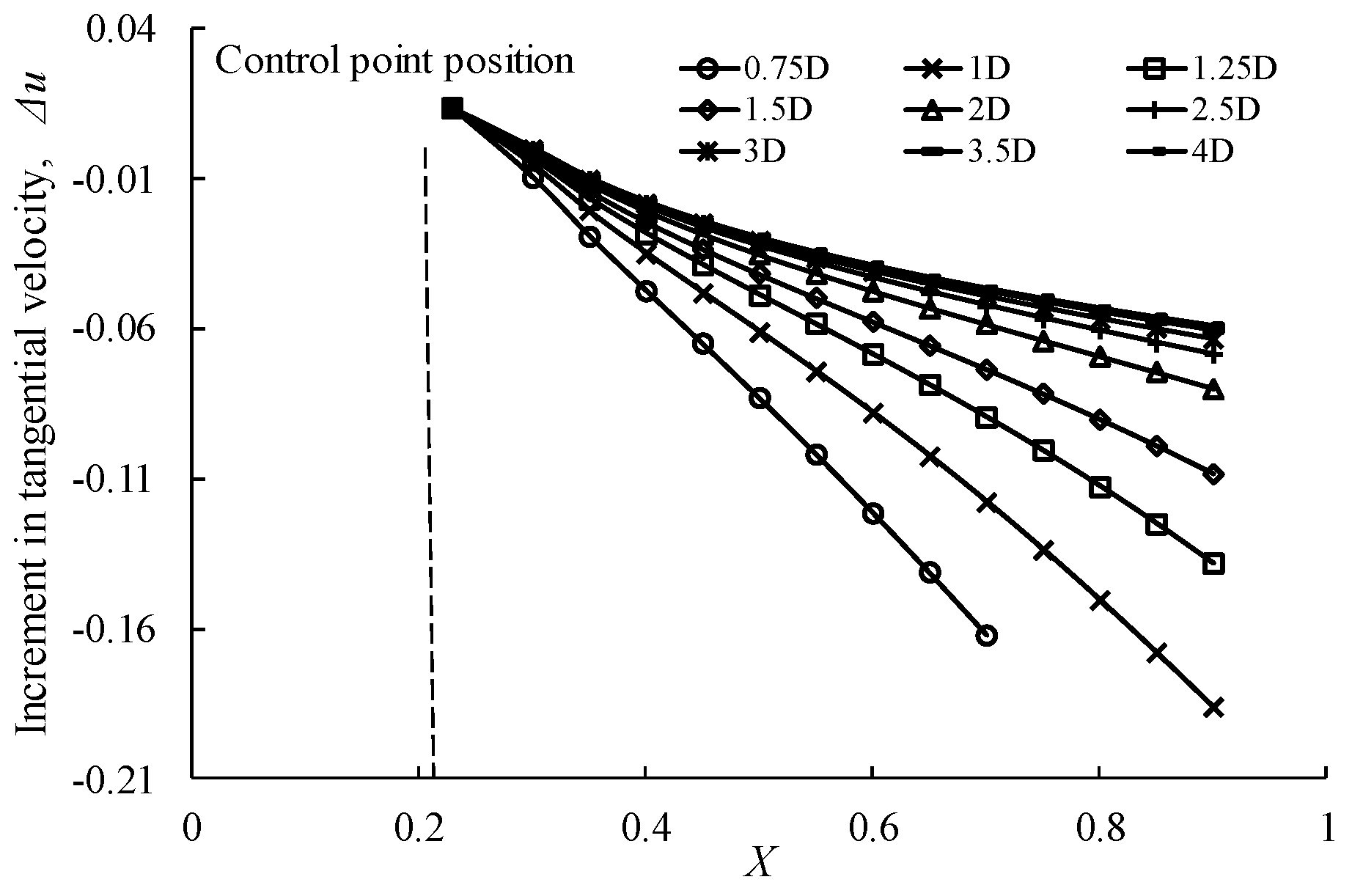
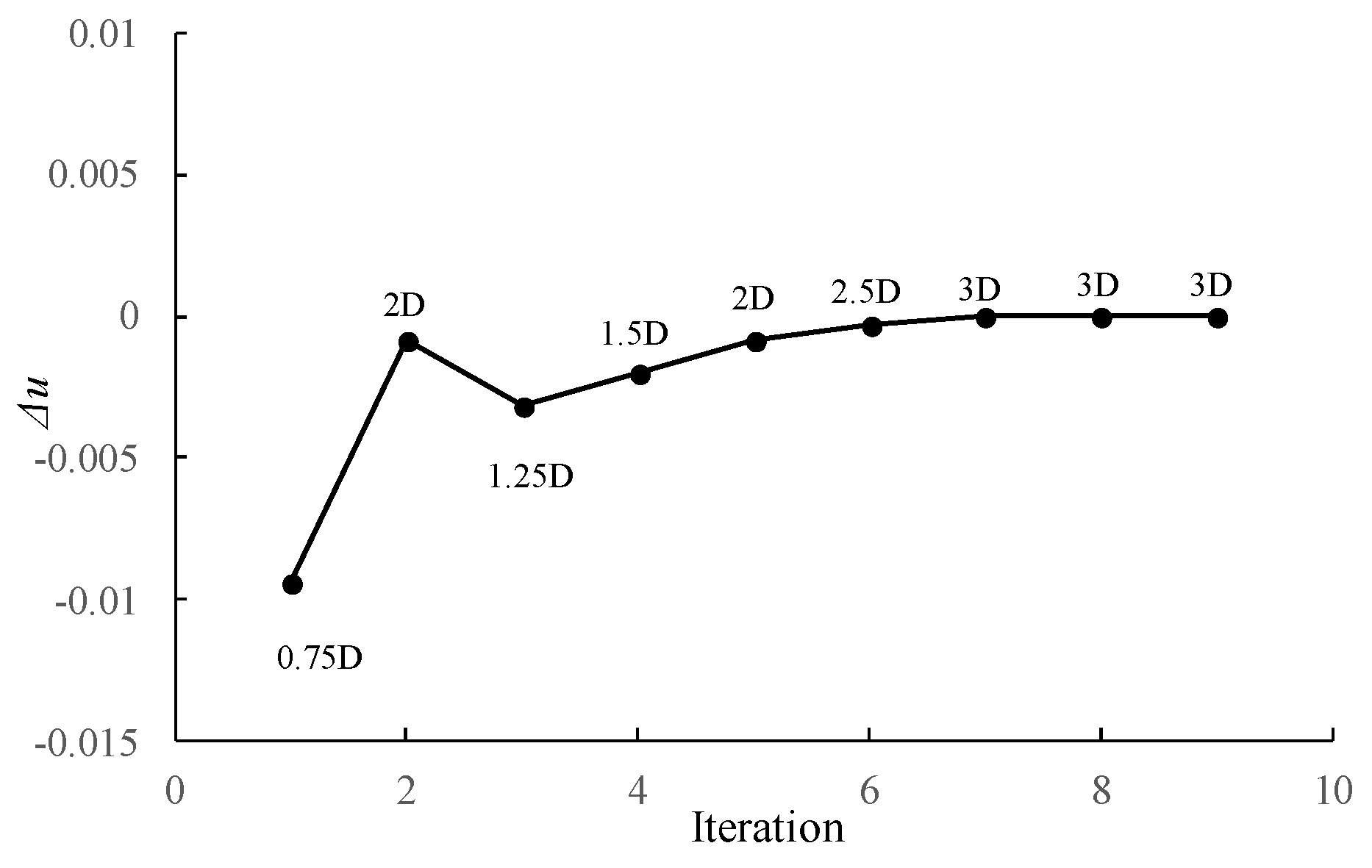
2.3. Separated-Flow Model
3. Results
3.1. Flow Past the Cylinder
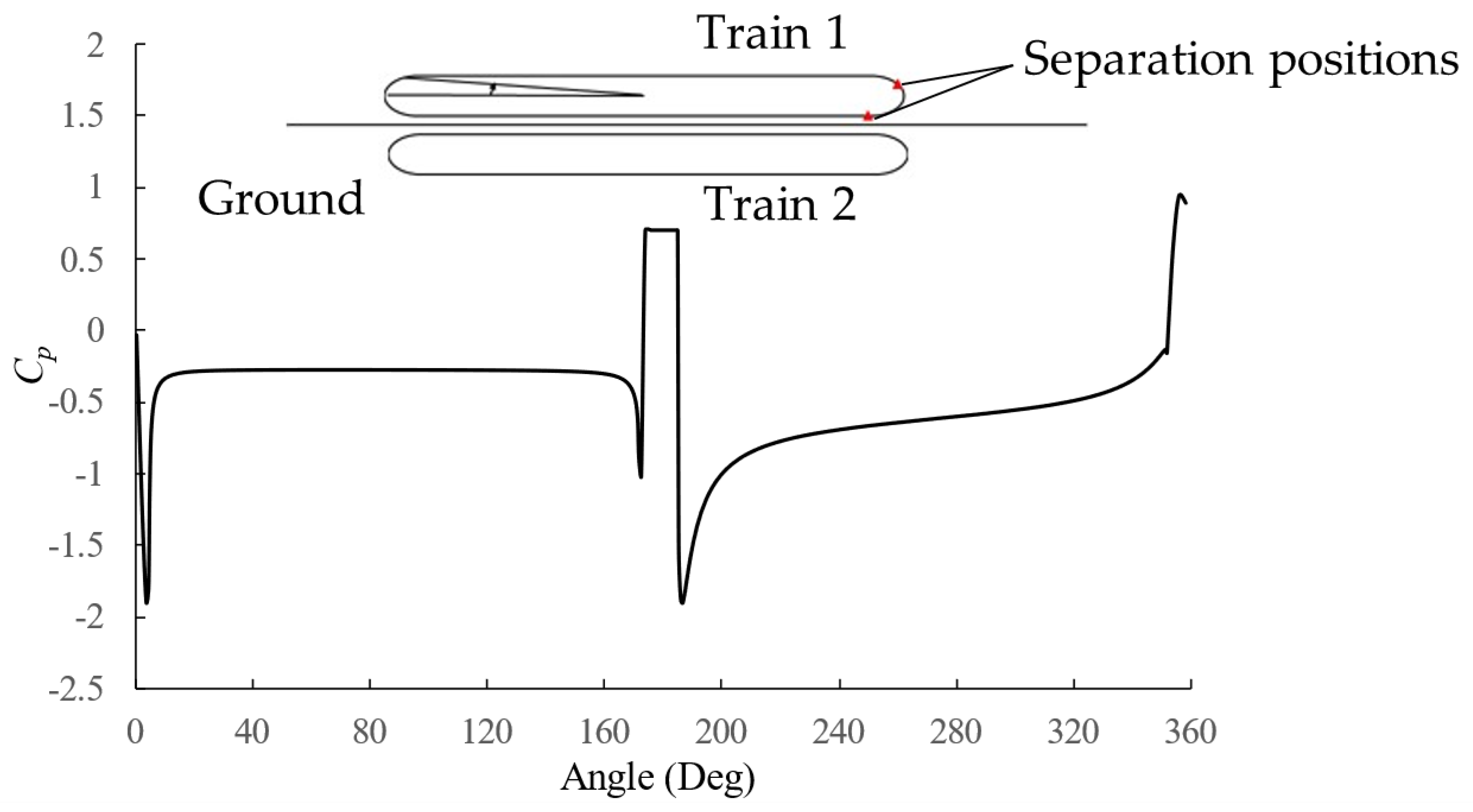
3.2. Flow Past the Train
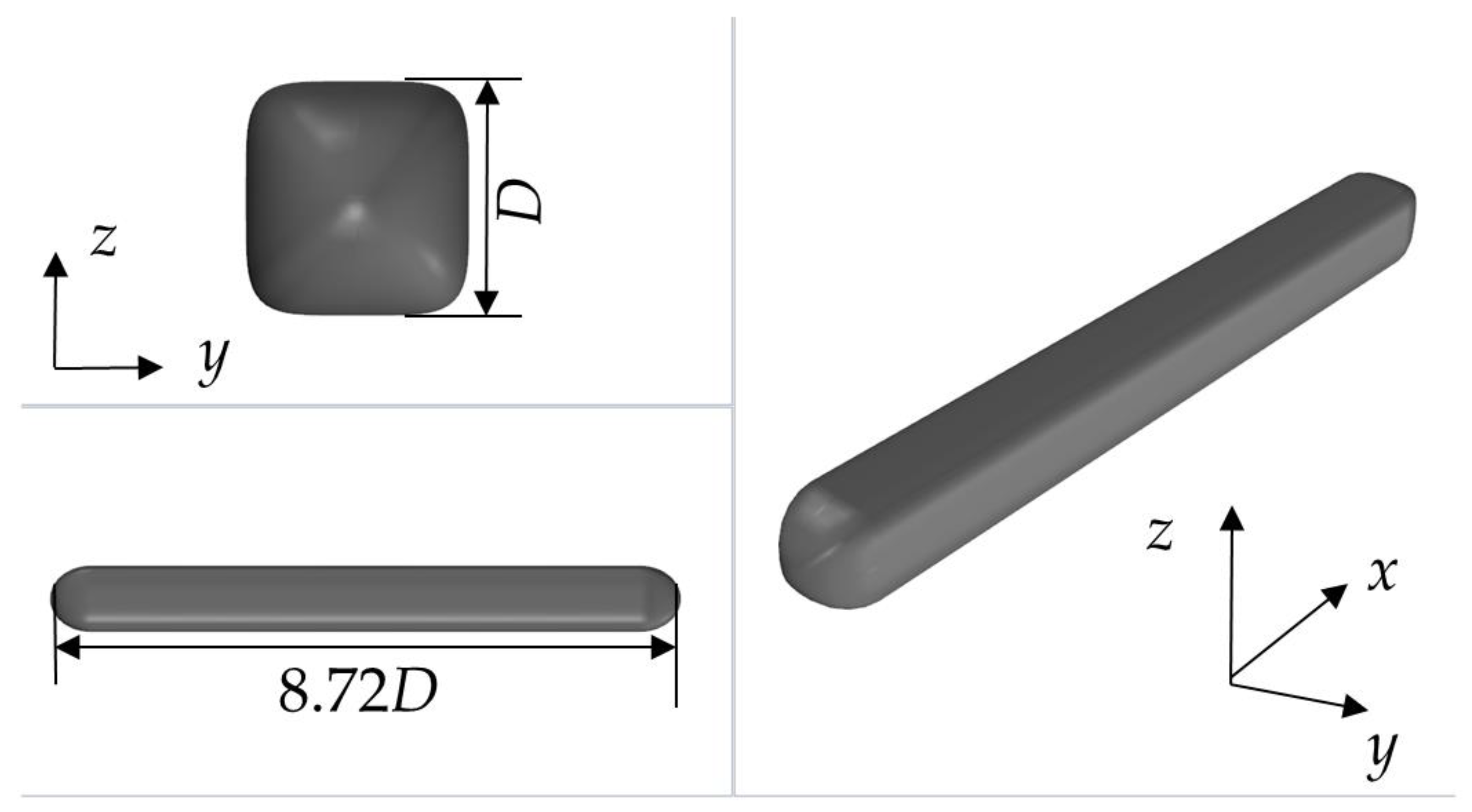
3.2.1. Physical Model
3.2.2. Pressure Loads on the Train
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buresti, G. Bluff-Body Aerodynamics; International Advanced School on Windexcited and Aeroelastic Vibrations of Structures: Genoa, Italy, 2000. [Google Scholar]
- Bearman, P. Bluff Body Flow Research with Application to Road Vehicles. In The Aerodynamics of Heavy Vehicles II: Trucks, Buses, and Trains; Lecture Notes in Applied and Computational Mechanics; Browand, F., McCallen, R., Ross, J., Eds.; Springer: Berlin, Heidelberg, 2009; Volume 41, pp. 3–13. [Google Scholar] [CrossRef]
- Flynn, D.; Hemida, H.; Soper, D.; Baker, C. Detached-eddy simulation of the slipstream of an operational freight train. J. Wind. Eng. Ind. Aerodyn. 2014, 132, 1–12. [Google Scholar] [CrossRef]
- Li, T.; Hemida, H.; Zhang, J.; Rashidi, M.; Flynn, D. Comparisons of Shear Stress Transport and Detached Eddy Simulations of the Flow Around Trains. J. Fluids. Eng. T ASME 2018, 140. [Google Scholar] [CrossRef]
- Morden, J.; Hemida, H.; Baker, C. Comparison of RANS and Detached Eddy Simulation Results to Wind-Tunnel Data for the Surface Pressures Upon a Class 43 High-Speed Train. J. Fluids Eng. 2015, 137. [Google Scholar] [CrossRef]
- Hemida, H.; Baker, C. Large-eddy simulation of the flow around a freight wagon subjected to a crosswind. Comput. Fluids 2010, 39, 1944–1956. [Google Scholar] [CrossRef]
- Hemida, H.; Krajnović, S. Exploring flow structures around a simplified ICE2 train subjected to a 30° side wind using LES. Eng. Appl. Comput. Fluid Mech. 2009, 3, 28–41. [Google Scholar] [CrossRef]
- Hemida, H.; Krajnović, S. LES study of the influence of the nose shape and yaw angles on flow structures around trains. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 34–46. [Google Scholar] [CrossRef]
- Krajnović, S. Large eddy simulation of flows around ground vehicles and other bluff bodies. Philos. Trans. Royal Soc. A 2009, 367, 2917–2930. [Google Scholar] [CrossRef]
- Baker, C.; Johnson, T.; Flynn, D.; Hemida, H.; Quinn, A.; Soper, D.; Sterling, M. Train Aerodynamics, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar] [CrossRef]
- Jin, G.; Zou, L.; Jiang, Y.; Zong, Z.; Sun, Z. A circle theorem technique to handle 2-D flows around arbitrary cylinders in discrete vortex method. J. Wind. Eng. Ind. Aerodyn. 2021, 209, 104496. [Google Scholar] [CrossRef]
- Mukesh, R.; Lingadurai, K.; Selvakumar, U. Airfoil shape optimization using non-traditional optimization technique and its validation. J. King Saud Univ. Sci. 2014, 26, 191–197. [Google Scholar] [CrossRef]
- Rakhsha, M.; Kees, C.E.; Negrut, D. Lagrangian vs. Eulerian: An Analysis of Two Solution Methods for Free-Surface Flows and Fluid Solid Interaction Problems. Fluids 2021, 6, 460. [Google Scholar] [CrossRef]
- Moraes, P.G.; Alcântara Pereira, L.A. Surface Roughness Effects on Flows Past Two Circular Cylinders in Tandem Arrangement at Co-Shedding Regime. Energies 2021, 14, 8237. [Google Scholar] [CrossRef]
- Bellenoue, M.; Moriniere, V.; Kageyama, T. Experimental 3-D simulation of the compression wave, due to train–tunnel entry. J. Fluids Struct. 2002, 16, 581–595. [Google Scholar] [CrossRef]
- Yoon, T.S.; Lee, S.; Hwang, J.H.; Lee, D.H. Prediction and validation on the sonic boom by a high-speed train entering a tunnel. J. Sound Vib. 2001, 247, 195–211. [Google Scholar] [CrossRef][Green Version]
- Rivero, J.M.; González-Martínez, E.; Rodríguez-Fernández, M. A methodology for the prediction of the sonic boom in tunnels of high-speed trains. J. Sound Vib. 2019, 446, 37–56. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Influence of ballast on wave steepening in tunnels. J. Sound Vib. 2000, 238, 595–615. [Google Scholar] [CrossRef]
- Ku, Y.C.; Rho, J.H.; Yun, S.H.; Kwak, M.H.; Kim, K.H.; Kwon, H.B.; Lee, D.H. Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave. Struct. Multidisc. Optim. 2010, 42, 965–976. [Google Scholar] [CrossRef]
- Hess, J. Panel methods in computational fluid dynamics. Annu. Rev. Fluid Mech. 1990, 22, 255–274. [Google Scholar] [CrossRef]
- Baker, C. The flow around high speed trains. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 277–298. [Google Scholar] [CrossRef]
- Baker, C. A review of train aerodynamics Part 1—Fundamentals. Aeronaut. J. 2014, 118, 201–228. [Google Scholar] [CrossRef]
- Hemida, H.; Baker, C.; Gao, G. The calculation of train slipstreams using large-eddy simulation. Proc. Inst. Mech. Eng. Pt. F J. Rail Rapid Transit. 2014, 228, 25–36. [Google Scholar] [CrossRef]
- Steinheuer, J. Aerodynamische Wirkungen Von Schnellfahrenden Schienenfahrzeugen Auf Die Umgebung; DFVLR-Bericht IB: Göttingen, Germany, 1981; pp. 129–181. [Google Scholar]
- Sanz-Andrés, A.; Santiago-Prowald, J.; Baker, C.; Quinn, A. Vehicle-induced loads on traffic sign panels. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 925–942. [Google Scholar] [CrossRef]
- Sanz-Andrés, A.; Laverón, A.; Cuerva, A.; Baker, C. Vehicle-induced force on pedestrians. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 185–198. [Google Scholar] [CrossRef][Green Version]
- Sanz-Andrés, A.; Laverón, A.; Baker, C.; Quinn, A. Vehicle induced loads on pedestrian barriers. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 413–426. [Google Scholar] [CrossRef][Green Version]
- Sanz-Andrés, A.; Santiago-Prowald, J. Train-induced pressure on pedestrians. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1007–1015. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Sanz-Andrés, A. Aeroelastic effects in a traffic sign panel induced by a passing vehicle. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 298–303. [Google Scholar] [CrossRef][Green Version]
- Rutschmann, S.; Ehenfried, K.; Dillmann, A. Validation of a potential flow model for the prediction of the aerodynamic loads on track side objects. In Proceedings of the World Congress on Rail Research, Sydney, Australia, 25–28 November 2013. [Google Scholar]
- Rutschmann, S.; Ehrenfried, K.; Dillmann, A. Aerodynamic loads induced by passing trains on track side objects. Notes Numer. Fluid Mech. Multidiscip. Des. 2014, 124, 343–351. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- Hermanns, L.; Giménez, J.; Alarcón, E. Efficient computation of the pressures developed during high-speed train passing events. Comput. Struct. 2005, 83, 793–803. [Google Scholar] [CrossRef]
- Takei, Y.; Izumi, Y.; Yamada, S.; Iida, M.; Kikuchi, K. Evaluation method for air pressure variation and station facility member deterioration caused by high-speed train passage in stations. Q. Rep. RTRI 2008, 49, 89–95. [Google Scholar] [CrossRef]
- Kikuchi, K.; Uchida, K.; Nakatani, K.; Yoshida, Y.; Maeda, T.; Yanagizawa, M. Numerical Analysis of Pressure Variation due to Train Passage Using the Boundary Element Method. Q. Rep. RTRI 1996, 37, 231–237. [Google Scholar]
- Khandhia, Y.; Gaylard, A.; Johnson, T. CFD simulation of three-dimensional unsteady train aerodynamics. Veh. Aerodyn. 1996, 10, 82–93. [Google Scholar]
- Johnston, G.; Seshagiri, B.; Ellis, N. Aerodynamic Interference of High Speed Ground Vehicles. In UTIAS Report, No. 185; University of Toronto: Toronto, ON, Canada, 1976; Available online: https://repository.tudelft.nl/islandora/object/uuid%3Acc2955c7-7f39-4c43-951c-8becc39c1530 (accessed on 11 September 2022).
- Morrow, T. Prediction of the Pressure Distribution on Vehicles Moving Near the Ground; Report No. TT72R05; Department of Transport Technology, Loughborough University of Technology: Loughborough, UK, 1972. [Google Scholar]
- Reinhardt-Piéchowiak, A.; Ducruet, C. Inviscid fluid flow around high-speed trains passing by in open air. Proc. Inst. Mech. Eng. Pt. F J. Rail Rapid Transit. 1999, 213, 105–116. [Google Scholar] [CrossRef]
- Bérenger, T.; Grégoire, R. Part 2: Panel Method Applied to Problems of European High-speed Train Interoperability. In TRANSAERO—A European Initiative on Transient Aerodynamics for Railway System Optimisation. Notes on Numerical Fluid Mechanics and Multidisciplinary Design (NNFM); Schulte-Werning, B., Grégoire, R., Malfatti, A., Matschke, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 79. [Google Scholar] [CrossRef]
- Bérenger, T.; Kessler, A.; Grégoire, R. Part 1: Panel Method Applied to the Prediction of Unsteady Effects Caused by High-speed Trains Passing in the Open Air. In TRANSAERO—A European Initiative on Transient Aerodynamics for Railway System Optimisation. Notes on Numerical Fluid Mechanics and Multidisciplinary Design (NNFM); Schulte-Werning, B., Grégoire, R., Malfatti, A., Matschke, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 79. [Google Scholar] [CrossRef]
- Farhan, I. Theoretical and Experimental Aerodynamic Analysis for High-Speed Ground Vehicles. Ph.D. Thesis, Department of Aeronautical and Automotive Engineering, Loughborough University, Loughborough, UK, 1991. Available online: https://hdl.handle.net/2134/22236 (accessed on 11 September 2022).
- Mahomedali, F. Two-dimensional potential flow calculations applied to train cross-section. In Internal Memorandum, IM AERO 67; British Railways Board, Research and Development Division, Aerodynamics Section: London, UK, 1973. [Google Scholar]
- Copley, J. The Three-Dimensional Flow around Railway Trains. Ph.D. Thesis, Department of Engineering, University of Cambridge, Cambridge, UK, 1985. [Google Scholar]
- Copley, J. The Three-Dimensional Flow around Railway Trains. J. Wind. Eng. Ind. Aerodyn. 1987, 26, 21–52. [Google Scholar] [CrossRef]
- Chiu, T. Aerodynamic Loads on a Railway Train in a Cross-Wind at Large Yaw Angles. Ph.D. Thesis, Churchill College, University of Cambridge, Cambridge, UK, 1990. [Google Scholar]
- Chiu, T. A two-dimensional second-order vortex panel method for the flow in a cross-wind over a train and other two-dimensional bluff bodies. J. Wind. Eng. Ind. Aerodyn. 1991, 37, 43–64. [Google Scholar] [CrossRef]
- Chiu, T. Prediction of the aerodynamic loads on a railway train in a cross-wind at large yaw angles using an integrated two- and three-dimensional source/vortex panel method. J. Wind. Eng. Ind. Aerodyn. 1995, 57, 19–39. [Google Scholar] [CrossRef]
- Tyll, J. Concurrent Aerodynamic Shape/Cost Design of Magnetic Levitation Vehicles Using Multidisciplinary Design Optimization Techniques. Ph.D. Thesis, Aerospace Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1997. [Google Scholar]
- Dvorak, F.; Maskew, B.; Woodward, F. Investigation of Three-Dimensional Flow Separation on Fuselage Configurations; US Army AMRDL Report TR-77-4; Analytical Methods Inc.: Bellevue, WA, USA, 1997. [Google Scholar]
- Balleur, J. Strong matching method for computing transonic viscous flows including wakes and separations. La Recherche Aérospatiale 1981, 3, 21–45. [Google Scholar]
- Drela, M.; Giles, M. Viscous-inviscid analysis of transonic and low Reynolds number airfoils. AIAA J. 1987, 25, 1347–1355. [Google Scholar] [CrossRef]
- White, F. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Thwaites, B. Approximate Calculation of the Laminar Boundary Layer. Aeronaut. Q. 1949, 1, 245–280. [Google Scholar] [CrossRef]
- Whitfield, D.; Swafford, T.; Jacocks, J. Calculation of turbulent boundary layers with separation and viscous-inviscid interaction. AIAA J. 1981, 19, 1315–1322. [Google Scholar] [CrossRef]
- Smith, A. Transition, Pressure Gradient and Stability Theory; Report ES 26388; Douglas Aircraft Co.: Santa Monica, CA, USA, 1956; Available online: https://ci.nii.ac.jp/naid/10008210731 (accessed on 11 September 2022).
- Van Ingen, J. A suggested semi-empirical method for the calculation of the boundary layer transition region. In Technische Hogeschool Delft, Vliegtuigbouwkunde, Rapport VTH-74; Delft University of Technology: Delft, The Netherlands, 1956. [Google Scholar]
- Green, J.; Weeks, D.; Brooman, J. Prediction of Turbulent Boundary Layers and Wakes in Compressible Flow by a Lag-Entrainment Method; R&M Report 3643; Aeronautical Research Council, HMSO: London, UK, 1973; Available online: https://apps.dtic.mil/sti/citations/ADA041015 (accessed on 11 September 2022).
- Head, M.; Patel, V. Improved Entrainment Turbulent Boundary Method for Calculating Layer Development; R&M Report 3791; Aeronautical Research Council, HMSO: London, UK, 1968; Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/2913 (accessed on 11 September 2022).
- Drela, M. Aerodynamics of Viscous Flows (Draft); Massachusetts Institute of Technology: Cambridge, MA, USA, 2016. [Google Scholar]
- Roshko, A. Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 1961, 10, 345–356. [Google Scholar] [CrossRef]
- Chiu, T.; Squire, L. An experimental study of the flow over a train in a crosswind at large yaw angles up to 90°. J. Wind. Eng. Ind. Aerodyn. 1992, 45, 47–74. [Google Scholar] [CrossRef]


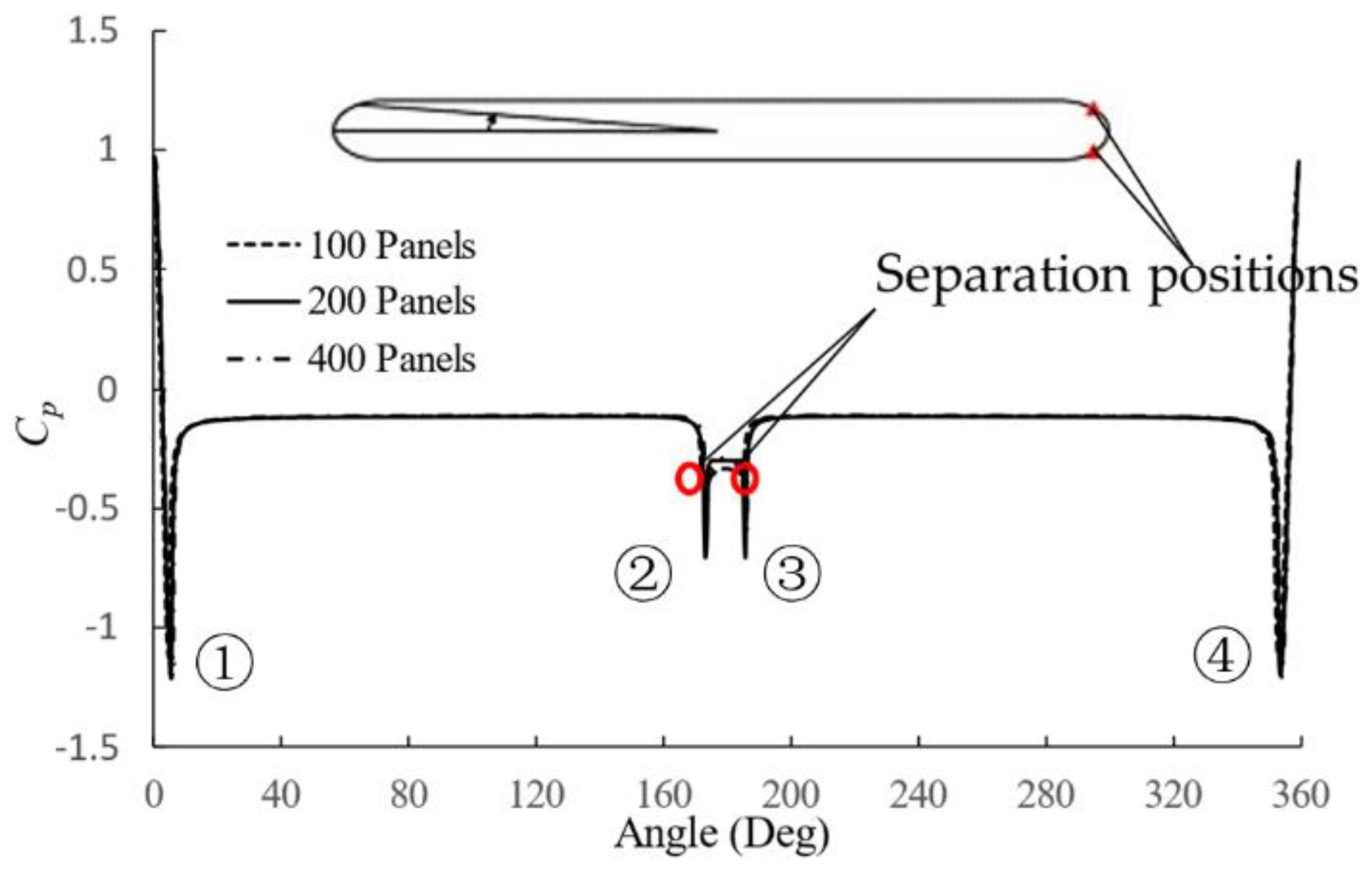
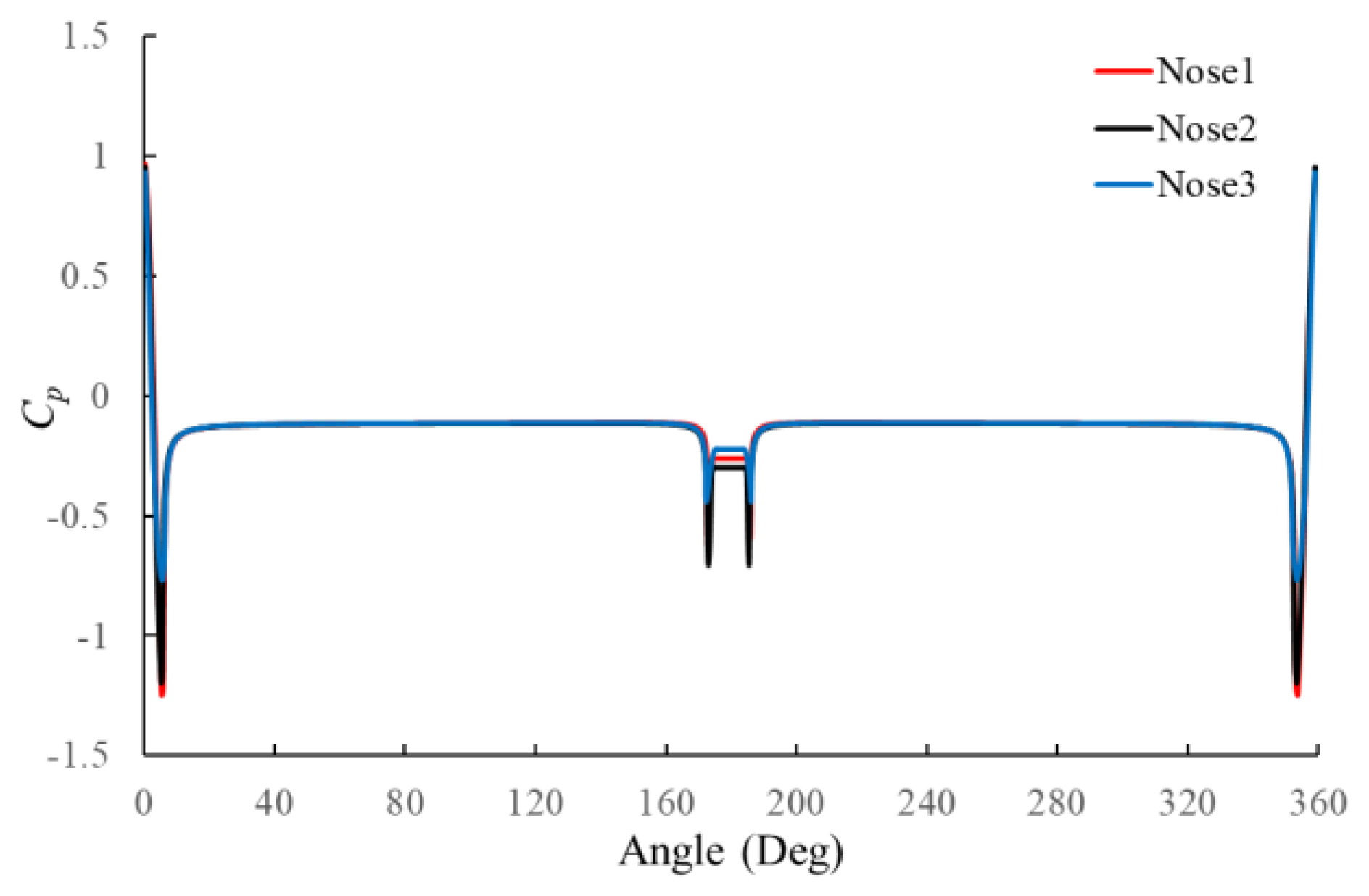

| Position | 100 Panels | 200 Panels | 300 Panels | |||
|---|---|---|---|---|---|---|
| Cp | Position | Cp | Position | Cp | Position | |
| 1 | −1.12 | 4.6° | −1.19 | 5.2° | −1.21 | 5.4° |
| 2 | −0.41 | 171.8° | −0.7 | 173.0° | −0.6 | 173.4° |
| 3 | −0.41 | 185° | −0.7 | 185.5° | −0.6 | 185.8° |
| 4 | −1.12 | 352.6° | −1.19 | 353.5° | −1.21 | 353.9° |
| Base pressure | −0.34 | −0.3 | −0.36 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Soper, D.; Xu, J.; Jia, Y.; Niu, J.; Hemida, H. A Separated-Flow Model for 2-D Viscous Flows around Bluff Bodies Using the Panel Method. Appl. Sci. 2022, 12, 9652. https://doi.org/10.3390/app12199652
Li R, Soper D, Xu J, Jia Y, Niu J, Hemida H. A Separated-Flow Model for 2-D Viscous Flows around Bluff Bodies Using the Panel Method. Applied Sciences. 2022; 12(19):9652. https://doi.org/10.3390/app12199652
Chicago/Turabian StyleLi, Rui, David Soper, Jianlin Xu, Yongxing Jia, Jiqiang Niu, and Hassan Hemida. 2022. "A Separated-Flow Model for 2-D Viscous Flows around Bluff Bodies Using the Panel Method" Applied Sciences 12, no. 19: 9652. https://doi.org/10.3390/app12199652
APA StyleLi, R., Soper, D., Xu, J., Jia, Y., Niu, J., & Hemida, H. (2022). A Separated-Flow Model for 2-D Viscous Flows around Bluff Bodies Using the Panel Method. Applied Sciences, 12(19), 9652. https://doi.org/10.3390/app12199652








