Abstract
The wake of a wind turbine has an important influence on the output power of wind farms. Staggered height layout is an emerging method for the layout optimization of wind farms. In order to study the effect of a staggered height layout on the overall power output of wind farms in depth, we established a combination of two large wind turbines and three small wind turbines arranged laterally between the two large wind turbines, and set four working conditions with different distances between the small wind turbines and the downstream large wind turbines as the research objects. The wind turbine array is analyzed by numerical simulation The layouts add three small wind turbines between the two large wind turbines, and each row of small wind turbines has a different distance from the downstream large wind turbines. The results show that as the distance from the upstream large wind turbine increases, the power of the three small wind turbines on the downstream wind turbine tends to be positive. The numerical simulation suggests that under the inflow wind speed, the closer to the downstream large wind turbine, the higher the wind speed is at the hub height.
1. Introduction
Wind energy is one of the important forms of clean energy utilization. It can be used by northern China as an important measure to reduce carbon emissions, such as heating [1]. A method to improve the power efficiency of wind turbines is to install vortex generators on the blades [2] and increase the power generation of downstream wind turbines by controlling the yaw angle of wind turbines [3], so as to maximize the power of wind farms [4].
The hub height is one way to control the kilowatt hour cost of the wind farm [5]. As the wake of wind turbines, such as the terrain, affects the power of the wind farm [6,7], the number and height of wind turbines in the wind farm need to go through a detailed design process. Ying et al. [8] studied the operation of a staggered height wind farm from the factors of power output, cost and profit, and pointed out that a staggered height wind farm is completely feasible. Stanley et al. [5] discussed in detail the arrangement of wind turbine stands in wind farms with different hub height differences, and optimized the two wind turbine height groups in wind farms with different capacities and sizes with the goal of per kilowatt hour power cost. At the same time, the number of wind turbines with different heights was also discussed to improve the utilization of wind energy. Vasel-Be-Hagh et al. [9] studied the improvement in output power of two wind turbines placed in the front and back at different hub heights, and found that the power output of wind farms with staggered height arrangements increased by 5.4%, discussed in detail the operation of wind farms composed of multiple wind turbines placed in this way, and tested the effectiveness of wind turbines with different hub heights under actual conditions. Wang et al. [10] proposed and compared the power prediction of three wake models for wind turbines with different hub heights, and improved the accuracy of the numerical simulation method for wind turbines with different hub heights, evaluated the applicable scope of the wind farm optimization method using a staggered height arrangement, and determined the number of wind turbines that are the most suitable for the staggered height optimization method. Mo et al. [11] used the large eddy simulation method to simulate a virtual wind tunnel to study the wake condition and structure behind the wind turbine, observed the extension and instability of the wake, and pointed out that the wake effect is still quite obvious at the extreme distance behind the wind turbine, but the wake structure is extremely unstable for a period of time after the wind turbine.
The method of using an actuator disk in the simulation has also been used in wind-turbine-related research such as that by Sanne et al. [12] and Bontempo et al. [13] As well, this method is widely used in the study of wake of wind turbines [14,15]. For example, Ingrid et al. [16] and others used the actuator disk model to simulate and study the turbulence in the wake field of wind turbines, and included the simulation results of the wind tunnel in the wake field in order to compare the two. Hamlaoui et al. [17] used the actuator to simulate the wake of a Horizontal Axis Wind Turbine (HAWT) to study the factors affecting wake development. Mehtab et al. [18] studied the impact of the height increase and decrease of wind turbines on a wind farm on the overall power output of the wind farm by using an actuator disk model, and simulated the relationship between the horizontal layout change of the wind farm and the power output. Yu et al. [19] paid more attention to the differences of different spatial points in the wake flow field and studied the causes of the velocity differences of different spatial points. Stevens et al. [20] compared the results of an actuator disk model with the results of the wind tunnel test, explored appropriate simulation methods for different positions in the wind farm, and improved the accuracy of the wind farm simulation.
At the same time, the research on wake effects using the numerical simulation method is gradually increasing around the world [21,22]. For example, Wu [23] used the Large Eddy Simulation (LES) method to simulate the wake of wind turbines and then studied the relationship between the wake and power loss. Lee et al. [24] simulated the wind turbine in a yaw state by LES, used the coupling of the Nonlinear Vortex Lattice Method (NVLM) and time-accurate Vortex Particle Method (VPM), and compared it with the measurement results for verification. Stevens [20] compared the results obtained by large eddy simulation with those obtained by actual wind tunnel experiments to increase the accuracy of the results and data. Mereu [25] and others used OpenFOAM (using the dynamic type solver pimpleDyMFoam) software to simulate the wind farm array to study the impact of various parameters of the wind farm on power generation efficiency, and pointed out that the spacing and incident angle of wind turbines have a significant impact on the power generation of the wind farm. Rajagopal [26] used OpenFOAM to simulate the operation of wind turbine arrays and study the layout of the wind turbine array with the highest power generation efficiency (OpenFOAM solvers are based on the Finite Volume Method (FVM) and the fluid flow is governed by the Navier–Stokes equations). Shayesteh [27] used OpenFOAM to simulate the wake of a wind turbine in Mexico under different inflow conditions.
The above algorithms or numerical simulations show that wind farms with different hub heights have a positive effect on their power generation. In this paper, the influence of adding a row of small wind turbines on the power of large wind turbines downstream is studied by numerical calculation. Section 2 of the paper details an overview of the simulation and wind turbine layouts. Section 3 discusses the results of downstream wind turbine power when a layout of small wind turbines was placed at the middle of two large turbines. Lastly, Section 4 summarizes the main outcomes of the study.
2. Project Overview
2.1. Simulation
The numerical experiments are conducted using the open-source wind farm modeling tool “Simulator for Wind Farm Applications” (SOWFA) [28] developed by the National Renewable Energy Laboratory (NREL), together with a transient solver for incompressible turbulent flow provided in the OpenFOAM (v2206) CFD toolbox [29]. More specifically, the standard k-ε model is employed for the turbulence modeling in unsteady Reynolds-averaged simulations (URANS), and the actuator-line model is used to model the rotating wind turbines and their wake flows. Thus, the governing equations of the fluid flow can be expressed as
where ρ is the fluid velocity, u and p are the Reynolds-averaged velocity and pressure, respectively; f is the body force resulting from the rotating wind turbine blade, and k is the kinematic energy. The notation μeff stands for an effective viscosity coefficient defined as the sum of the molecular viscosity coefficient (denoted by μ) and the turbulent viscosity (denoted by μt). In the standard k-ε model, μt is computed with
where Cμ is a constant (usually taken as 0.09), and ε is the energy dissipation rate. The kinematic energy k and the dissipation rate ε are obtained by solving the equations of
with
where Pk is the production of k induced by the rate-of-strain tensor of u; Cε1, Cε2, σk and σε are the constants (respectively taken as 1.44, 1.92, 1.0 and 1.3 in this study) of the standard k-ε model. The body force f on the right-hand side of (1-1) is given by
where x is the three-dimensional coordinate, F is the actuator line element force and g is a projection function. In this study, we employ an isotropic Gaussian projection function given by
where Δ is the Gaussian projection width and x0 is the location at which the Gaussian projection is being applied.
In the area, two types of wind turbines are considered in the numerical experiments. The larger one is the NREL 5-MW baseline turbine, which has a rotor diameter of 126 m and a rated wind speed of 11.4 m/s. The smaller one is also a hypothetical wind turbine, which is obtained by scaling the properties of the NREL 5-MW baseline turbine in terms of a size ratio of 1:3 accordingly (yielding a rotor diameter of 42 m). The hub height of the two different turbines is assumed to be 150 m and 37 m, respectively. Two large wind turbines and three small wind turbines are arranged vertically and crosswise, as shown in Figure 1. By changing the position of the small wind turbines, the change in the power generation of the large wind turbines downstream and the vertical velocity distribution in the flow field are analyzed. A single transverse row of three small wind turbines is arranged within the 9D longitudinal separation between the two large wind turbines. The center small wind turbine is located on the centerline of the upstream large wind turbine, and downstream separation of the row is varied (see Table 1). The simulated working conditions include: case 0 is the working condition when there is no small wind turbine running. The first working condition is that the small wind turbine is arranged 2D away from the upstream large wind turbine. From the second working condition to the fourth working condition, 5d is added one by one on the basis of the previous working condition.
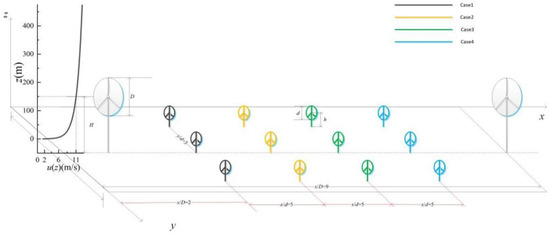
Figure 1.
Sketch of the wind turbine layout for different cases.

Table 1.
Wind farm and turbine parameters and layout.
The inflow of the numerical experiments is assumed to be a two-dimensional neutral equilibrium atmospheric boundary layer and employs log-law-type ground-normal inlet boundary conditions [30,31] with a surface roughness length (denoted by z0) of 0.1 m. The wind velocity magnitude, kinematic energy and dissipation rate on the inflow are respectively given by
where z is the ground-normal coordinate, u* is the friction velocity and κ is the von Kármán constant. All numerical experiments are carried out at the same velocity, which has a magnitude of 11.2 m/s (slightly lower than the rated wind speed of 11.4 m/s) at the hub height of the NREL 5-MW baseline turbine.
The computation domain of the numerical experiments is a rectangular of the dimension 2400 m × 960 m × 320 m in the stream-wise, cross-stream-wise and elevational directions, respectively. The employed boundary conditions corresponding to different flow variable fields are listed in Table 2. We employ both the blockMesh and the refineMesh utilities in OpenFOAM v2206 for the mesh generation of the computational domain. More specifically, the blockMesh utility is first used to generate a hexahedral background mesh, and the refineMesh utility is then applied to selected regions to refine the mesh cells adjacent to the rotating wind turbines. The background mesh employs uniform grid spacing in the streamwise and cross-streamwise directions. In the elevational direction, the grid spacing has an exponential distribution for the z-coordinate ranging from 0 m to 20 m or 240 m to 360 m, while there is a uniform distribution for the z-coordinate ranging from 20 m to 240 m. Figure 2 plots the three selected refinement regions inside the computational domain, in which the cell size within the 3rd level refinement region is one eighth of the background cell size in the streamwise and cross-streamwise directions.

Table 2.
Boundary conditions employed for the computational domain: the names of the boundary conditions are listed in accordance with the boundary condition notation in OpenFOAM.
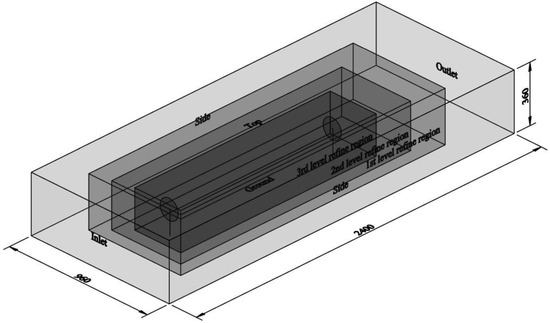
Figure 2.
A sketch of the computational domain and the mesh refinement scheme (unit, m).
A mesh-independence analysis is then conducted to determine to the appropriate grid spacing of the mesh. The analysis is carried out by simulating two NREL 5-MW baseline turbine (with a distance of 1134 m in the streamwise direction) on four different mesh respectively and comparing their power output afterwards. The four considered mesh employ the same mesh refinement scheme (see Figure 2) but different grid spacing for their initial background mesh. By doing so, the grid spacing adjacent to the wind turbines in these mesh are of sizes 1.5 m, 2.0 m, 2.5 m and 3.0 m, respectively.
Table 3 summarizes the time-averaged power output (over 150 s) of the two wind turbines on these mesh. The convergence of the power output results with the decrease of grid spacing can be clearly noted from the table.

Table 3.
Parameters and results of the mesh-independence analysis.
After the mesh-independence analysis, we select the mesh of case 2 (in Table 2) for later numerical experiments. All experiments are simulated for 20,000 time-steps with a time-step size of 0.025 s, yielding a time length of 500 s in total. At the employed time-step size, the CFL number in the computational domain has a mean value around 0.05 and a maximum value around 0.15 in all experiments. Finally, the desired statistics concerning the considered wind turbines (such as the generator power of wind turbines and the mean velocity of the wake flow) are averaged over the last 6000 time-steps.
2.2. Wind Tunnel Test
The size of the wind tunnel test section is 24 m × 4 m × 3 m. The wind speed range is continuously adjustable within 0.5~30 m/s. The layout of wind turbines in the experiment was the same as that in the simulation, as shown in Figure 3. Table 4 summarizes the parameters of the experimental wind turbines. In addition to that, Experimental measurement equipment is detailed in Zhao et al. [3].

Figure 3.
The layout of large and small wind turbines in the experiment, size of wind turbine and measurement equipment.

Table 4.
Experimental wind turbine parameters.
3. Results and Discussions
3.1. Power of Large Wind Turbines
Table 5 shows the power output of two large wind turbines under different operating conditions. It can be seen from Table 5 that the small wind turbines under different working conditions are gradually close to the downstream large wind turbines. Compared with Case 0, the power of downstream large wind turbines from Case 1 to Case 4 increases gradually. Although Case 1 to Case 3 have negative growth, the power of downstream large wind turbines increases by 0.5% for Case 4. Although the total power of the small wind turbines decreases gradually with increasing distance from the large upstream wind turbine, the total power of the small and large wind turbines increases gradually in comparison.

Table 5.
Comparison of the power of downstream large wind turbines under different number simulation cases (unit: kW).
Table 6 shows the power comparison of downstream wind turbines with different configurations in the wind tunnel experiment. Compared with the original working condition, the power output of the downstream large wind turbine increased by 0.69%. As the small wind turbine gradually approached the downstream large wind turbine, the power output trend of the downstream large wind turbine was consistent with the simulated situation and also gradually increased.

Table 6.
Comparison of the power of downstream large wind turbines under different wind tunnel test cases (unit: W).
3.2. Vertical Velocity Distribution in the Flow Field
According to Formula (11), the wind turbine power is mainly determined by the wind speed at the wind turbine location. By analyzing the vertical velocity distribution in the flow field, we can have a deep understanding of the characteristics of the flow field. The actuator disk model of OpenFOAM software is used to conduct numerical research on the flow field, and the vertical velocity distribution at the feature position is extracted for comparison, as shown in Figure 4, Figure 5, Figure 6 and Figure 7.
(: Power;: Power Coefficient;: Density;: Rotor Swept Area;: Wind Velocity).
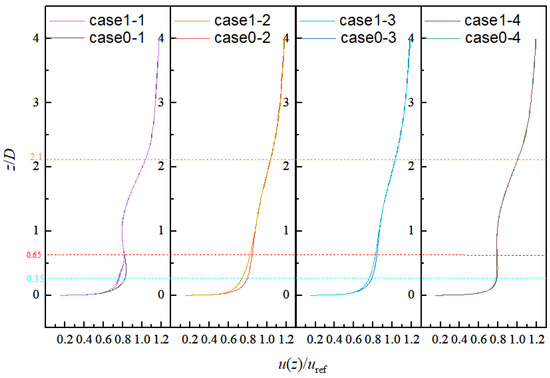
Figure 4.
Comparison of vertical velocity wind profiles between Case 1 and Case 0.
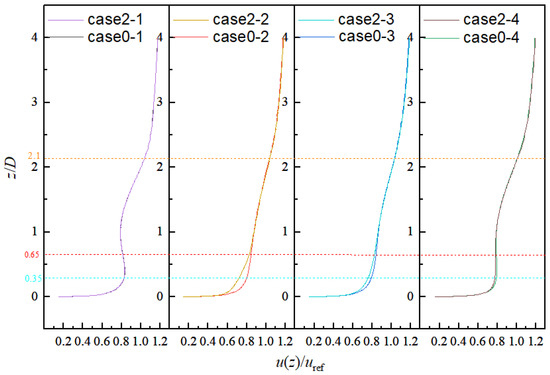
Figure 5.
Comparison of vertical velocity wind profiles of Case 2 and Case 0.
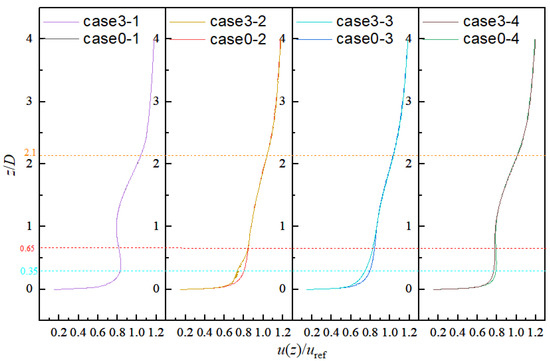
Figure 6.
Comparison of vertical velocity wind profiles of Case 3 and Case 0.
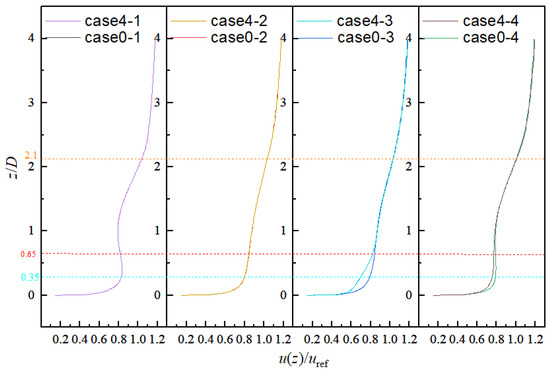
Figure 7.
Comparison of vertical velocity wind profiles of Case 4 and Case 0.
Figure 4 compares and analyzes the dimensionless velocity in the vertical direction at 2D, 2D + 5d, 2D + 10d and 2D + 15d in the flow field under Case 0 and Case 1 conditions. It is found that under the Case 1 working condition, the speed within the height of z/D = [0, 0.65], that is, within the height range of a small wind turbine; in the figure, we can see that the curve of Case 1-1 shifts significantly upstream in this region compared to the curve of Case 0-1. We calculate the results for both operating conditions at z/D = 0.35 and find that Case 1-1 has a loss of about 3.34% compared to Case 0-1, decreasing by approximately 3.34%. However, at the positions of 2D + 5d, 2D + 10d and 2D + 15d, the loss gradually weakened. This indicates that the surface roughness in the flow field is increased under Case 1 conditions. In addition, within the range of z/D = [0.65, 2.10] of the large wind turbine, the wake of the wind turbine gradually recovers, and the influence of the small wind turbine on the vertical speed gradually weakens.
Figure 5, Figure 6 and Figure 7 respectively show the dimensionless velocity analysis of Case 2, Case 3, Case 4 and Case 0 in the vertical direction. By comparing and analyzing the above three groups of data, the velocity reduction of Case 2, Case 3 and Case 4 gradually decreases with the increase in distance between the small wind turbine and large upstream wind turbine. Its speed loss is divided into 5.40%, 3.8% and 2.92% compared with Case 0.
3.3. Velocity Field Distribution under Different Operating Conditions
We compare the power change caused by the downstream wind turbine under the influence of the small wind turbine’s wake, as shown in Figure 8 and Figure 9. Figure 8 shows the influence of the wake of the small wind turbine on the flow field near the downstream wind turbine under different working conditions; Figure 9 shows the change in the vertical velocity wind profile of the flow field in front of the downstream wind turbine.
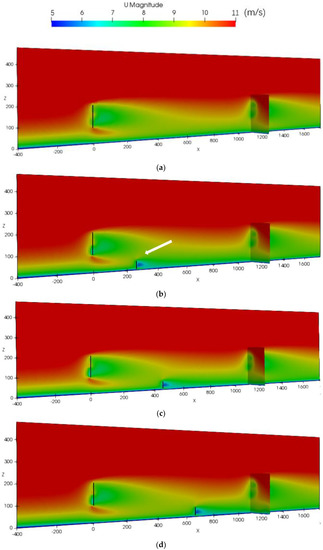
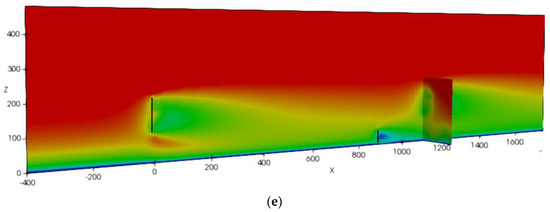
Figure 8.
Streamwise mean velocity in the YZ and XZ planes. (a) Case 0. (b) Case 1. (c) Case 2. (d) Case 3. (e) Case 4.
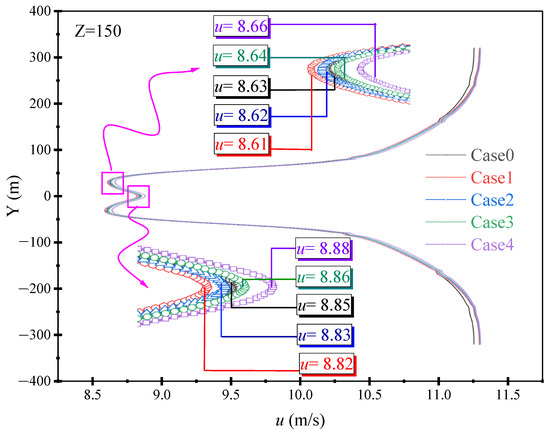
Figure 9.
The effect of the change in the position of the small wind turbine on the wind speed from the large downstream wind turbine at Z = 150 m.
A comprehensive comparison between Case 1–4 and Case 0 shows that the small wind turbine plays a certain role in improving the airflow, and its principle is similar to the deflector of vertical axis wind turbines [32]. As can be seen by the position of the white arrow in case 1 in Figure 8b, as the small wind turbine gradually approaches the downstream large wind turbine, the air flow lifting effect generated by it gradually increases. This strengthening effect can be understood as: when there are certain obstacles in front of the wind turbine, the air flow lifting effect generated by it can better improve the incoming speed of the wind turbine [33], while when the distance is long, this air flow lifting effect is very small, resulting in the negative impact of the turbulent wake of the small wind turbine taking the dominant position.
It can be seen from Figure 8 that as the small wind turbine gradually approaches the downstream wind turbine, the vertical velocity of the flow field in front of the wind turbine is increased. From the quantitative results in Figure 8, it can be seen that Case 4 condition has the largest increase in the speed in front of the downstream wind turbine, about 0.793%.
According to Figure 9, it is easy to see that as the small wind turbine gradually moves downstream, the wind speed at the center of the hub of the large downstream wind turbine gradually increases.
When the small wind turbine is far away from the large downstream wind turbine (Case 1, Case 2), the incoming wind speed at the hub of the large downstream wind turbine decreases slightly compared to Case 0 (u = 8.85 m/s → u = 8.82 m/s) due to the influence of the small wind turbine. Taking Case 1 as an example, due to its distance from the large downstream wind turbine, the wake of the three small wind turbines is fully developed. As the small wind turbines gradually approach the large wind turbines downstream, the wake of the small wind turbines becomes fully developed before they offset each other, and this offsetting effect gradually increases, resulting in the lifting effect of the small wind turbines.
In contrast, when the small wind turbine is closer to the large downstream wind turbine, the incoming wind speed at the center of the hub of the large downstream wind turbine has a certain increase effect compared with Case 0 (u = 8.85 m/s → u = 8.88 m/s). Take Case 4 as an example: because the small wind turbine is closer to the downstream large wind turbine, the wake flows cancel each other more fully, and the wind speed at the center of the downstream large wind turbine hub is promoted by the lifting effect of the airflow of the small wind turbine.
4. Conclusions
In this paper, OpenFOAM software is used to study the wake of three small wind turbines added to two wind turbines in a series. In addition, we carried out experimental verification in the wind tunnel. The influence of different distances between each row of small wind turbines and the upstream large wind turbines on the power of the downstream wind turbines is studied. After analyzing the vertical velocity wind profile and regional flow field, the following conclusions are obtained:
- (1)
- Small wind turbines with different distances have an impact on the power output of downstream wind turbines. The power of the downstream large wind turbine increases by about 0.5% when the small and large wind turbines are 2D + 15d away from the upstream large wind turbines, as in Case 4. The wind tunnel experiment results also show that the power of the downstream large wind turbine increases by 0.69%.
- (2)
- At the height of the small wind turbine, the velocity distribution of the wake obviously attenuates, and this attenuation will weaken as it moves downstream; however, the wind speed at the higher position of the small wind turbine will increase, and this increase effect will be captured by the adjacent downstream large wind turbine, resulting in an increase in the output power of the downstream large wind turbine.
Author Contributions
Conceptualization, S.K.; methodology, J.W.; formal analysis, H.T.; Writing—original draft preparation, W.T.; writing—review and editing, W.T. and Y.Z.; visualization, X.Z.; supervision, S.K.; project administration, W.T.; funding acquisition, S.K. and L.Z.; wind tunnel test, S.W.; verification, L.Z. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Jilin Provincial Science and Technology Department of Science and Technology Key Research and Development Projects (Grant number 20200403141SF) and the Open Project of State Key Laboratory (Grant number D2020Y004-3, HB2021Y003). National key r&d program (Grant number 2019YFB1503701), National Natural Science Foundation of China (Grant number 52078251, 52108456), Jiangsu Outstanding Youth Science Fund Project (Grant number BK20211518), Jiangsu Natural Science Foundation (Grant number BK20210309) and The Fundamental Research Funds for the Central Universities through grant no (Grant number NS2021050, NE2020007).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, L.D.; Li, Y.; Zhang, H.; Xu, X.D. A review of the potential of district heating system in Northern China. Appl. Therm. Eng. 2021, 188, 116605. [Google Scholar] [CrossRef]
- Zhao, Z.Z.; Jiang, R.F.; Feng, J.X.; Liu, H.W. Researches on vortex generators applied to wind turbines: A review. Ocean Eng. 2022, 253, 111266. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Hu, T.Y.; Zhang, L.D.; Yang, Z.L. Experimental study on the characteristics of wind turbine wake field considering yaw conditions. Energy Sci. Eng. 2021, 9, 2333–2341. [Google Scholar] [CrossRef]
- Ali, C.K.; Ryozo, N. A quantitative review of wind farm control with the objective of wind farm power maximization. J. Wind Eng. Ind. Aerodyn. 2019, 192, 45–73. [Google Scholar]
- Stanley, A.; Ning, A.; Dykes, K. Optimization of turbine design in wind farms with multiple hub heights, using exact analytic gradients and structural constraints. Wind Energy 2019, 22, 605–619. [Google Scholar] [CrossRef]
- Mao, Y.; Shi, C.Y.; Liu, H.Y. Day-ahead wind power forecasting based on the clustering of equivalent power curves. Energy 2021, 218, 119515. [Google Scholar]
- Li, X.Y.; Qiu, Y.N.; Feng, Y.H.; Wang, Z. Wind turbine power prediction considering wake effects with dual laser beam LiDAR measured yaw misalignment. Appl. Energy 2021, 299, 117308. [Google Scholar] [CrossRef]
- Chen, Y.; Li, H.; Jin, K.; Elkassabgi, K. Investigating the possibility of using different hub height wind turbines in a wind farm. Int. J. Sustain. Energy 2017, 36, 142–150. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A.; Archer, C.L. Wind farm hub height optimization. Appl. Energy 2017, 195, 905–921. [Google Scholar] [CrossRef]
- Wang, L.Y. Effectiveness of optimized control strategy and different hub height turbines on a real wind farm optimization. Renew. Energy 2018, 126, 819–829. [Google Scholar] [CrossRef]
- Mo, J.; Choudhry, A.; Arjomandi, M.; Lee, Y. Large eddy simulation of the wind turbine wake characteristics in the numerical wind tunnel model. J. Wind Eng. Ind. Aerodyn. 2013, 112, 11–24. [Google Scholar] [CrossRef]
- Sanne, J.H.; Magnus, K.V.; Antonio, S.; Nicholas, A. A comparison of lab-scale free rotating wind turbines and actuator disks. J. Wind Eng. Ind. Aerodyn. 2021, 209, 104485. [Google Scholar]
- Bontempo, R.; Manna, M. A ring-vortex actuator disk method for wind turbines including hub effects. Energy Convers. Manag. 2019, 195, 672–681. [Google Scholar] [CrossRef]
- Abdolrahim, R.; Micallef, D. Wake interactions of two tandem floating offshore wind turbines: CFD analysis using actuator disc model. Renew. Energy 2021, 179, 859–876. [Google Scholar]
- Daniel, M.; Carlos, F.; Iván, H.; Leo, H. Assessment of actuator disc models in predicting radial flow and wake expansion. J. Wind Eng. Ind. Aerodyn. 2020, 207, 104396. [Google Scholar]
- Ingrid, N.; Michael, H.; Jonathan, W.; Joachim, P. Comparison of the turbulence in the wakes of an actuator disc and a model wind turbine by higher order statistics: A wind tunnel study. Renew. Energy 2021, 179, 1650–1662. [Google Scholar]
- Hamlaoui, M.N.; Smaili, A.; Dobrev, I.; Pereira, M. Numerical and experimental investigations of HAWT near wake predictions using Particle Image Velocimetry and Actuator Disk Method. Energy 2022, 238, 121660. [Google Scholar] [CrossRef]
- Mehtab, A.K.; Adeel, J.; Sehar, S.; Abdul, H.S. Optimization of a wind farm by coupled actuator disk and mesoscale models to mitigate neighboring wind farm wake interference from repowering perspective. Appl. Energy 2021, 298, 117229. [Google Scholar]
- Yu, W.; Ferreira, C.; Kuik, G.A.M. The dynamic wake of an actuator disc undergoing transient load: A numerical and experimental study. Renew. Energy 2019, 132, 1402–1414. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Martínez-Tossas, L.; Meneveau, C. Comparison of wind farm large eddy simulations using actuator disk and actuator line models with wind tunnel experiments. Renew. Energy 2018, 116, 470–478. [Google Scholar] [CrossRef]
- Jiang, R.; Zhao, Z.; Liu, H.; Wang, T.; Chen, M.; Feng, J.; Wang, D. Numerical study on the influence of vortex generators on wind turbine aerodynamic performance considering rotational effect. Renew. Energy 2022, 186, 730–741. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Sotiropoulos, F. Turbulent flow inside and above a wind farm: A wind-tunnel study. Energies 2011, 4, 1916–1936. [Google Scholar] [CrossRef]
- Wu, Y.T.; Fernando, P. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D. Wake impact on aerodynamic characteristics of horizontal axis wind turbine under yawed flow conditions. Renew. Energy 2019, 136, 383–392. [Google Scholar] [CrossRef]
- Mereu, R.; Federici, D.; Ferrari, G.; Schito, P. Parametric numerical study of Savonius wind turbine interaction in a linear array. Renew. Energy 2017, 113, 1320–1332. [Google Scholar] [CrossRef]
- Rajagopal, V.B.; Santanu, M.; Pankaj, K. An OpenFOAM based study of Savonius turbine arrays in tunnels for power maximisation. Renew. Energy 2021, 179, 1345–1359. [Google Scholar]
- Shayesteh, A.; Mahmood, R.; Esmail, M.; Andres, J. Mohammad Hossein Abbaspour-Fard, Numerical simulation of the Mexico wind turbine using the actuator disk model along with the 3D correction of aerodynamic coefficients in OpenFOAM. Renew. Energy 2021, 163, 2029–2036. [Google Scholar]
- Churchfield, M.; Lee, S. NWTC Design Codes. Available online: http://wind.nrel.gov/designcodes/simulators/SOWFA (accessed on 5 September 2022).
- OpenFOAM. The Open Source CFD Toolbox. 2013. Available online: http://www.openfoam.com (accessed on 20 August 2022).
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering. J. Wind Eng. Ind. Aerodyn. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Hargreaves, D.M.; Wright, N.G. On the use of the k–ε model in commercial CFD software to model the neutral atmospheric boundary layer. J. Wind Eng. Ind. Aerodyn. 2007, 95, 355–369. [Google Scholar] [CrossRef]
- Li, Y.; Tong, G.; Zhao, B.; Feng, F.; Tagawa, K. Study on aerodynamic performance of a straight-bladed VAWT using a wind-gathering device with polyline hexagonal pyramid shape. Front. Energy Res. 2022, 10, 790777. [Google Scholar] [CrossRef]
- Liu, L.; Stevens, R.J.A.M. Enhanced wind-farm performance using windbreaks. Phys. Rev. Fluids 2021, 6, 074611. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).