Helicopter Takeoff and Landing Point Location in Cities for Emergency Services

Abstract

In low-altitude rescue, civilian helicopters, relying on their speed, efficiency and flexibility, play at center stage. Due to the terrain restrictions of the disaster area, it is difficult for helicopters to carry out safe and efficient rescue in cities. In order to facilitate emergency rescue, fixed helicopter takeoff and landing points for rescue missions must be selected strategically and wisely. However, the traditional method is to analyze the satellite data and conduct field surveys manually, which is rather subjective. A scientific, simple and efficient method of location selection is in urgent need. This paper analyzes the normativeness of the location of the helicopter’s take-off and landing point and establishes a model of the slope and undulation of the landing site. It utilizes ArcGIS software to build layers and selects for the terrain element models that meet the specifications. It also studies the rescue radius commonly used in the world and then maximizes the location range of the take-off and landing point based on the greedy algorithm. Considering the construction cost, the final optimized site selection result is obtained. The results show that the use of GIS space technology can effectively select suitable take-off and landing points and gain valuable time for low-altitude rescue.

1. Introduction

With a vast territory and complex geographical and climatic conditions, China is a country prone to frequent natural disasters. In recent years, the National Health Department in China has made profound plans for low-altitude emergency rescue. The selection of the take-off and landing points for rescue services has become one of the bottlenecks.

GIS (Geographical Information Systems), its database and software and numerical analysis may be useful for establishing geographical positions for takeoff and landing points. Geographical locations are very important for many transport systems and vehicles [1,2]. To know the geographical locations is to know the potential for a rescue operation. ArcGIS 10.8 is software that comprehensively integrates the GIS database, software engineering and AI and IT technology. It can offer a solution package for location selection problems. Scholars used to rely on satellite data and field surveys to decide the location. They were subjective and inefficient. The application of ArcGIS could potentially help with the selection of takeoff and landing points for helicopter rescue operations in cities to make it simpler, more efficient and more scientific. A lot of research was carried out around the rescue site location in order to improve the quality of low-altitude rescue services. In terms of helicopter low-altitude rescue research, it can be roughly divided into two types: land rescue and water rescue. As the land rescue pays more attention to the flatness of the site, this kind of research was mostly developed with GIS-related software [3,4,5]. For water rescue, due to the complicated water surface environment, most of the temporary take-off and landing activities were carried out on ships. Therefore, it is necessary to make more detailed research on the attitude of the helicopter, the movement of the ship and the changes of the water surface environment [6,7,8,9,10]. It can be seen that most of the research based on land rescue was focused on the evaluation of the take-off and landing site. Because of its applicability, there was no guarantee that it would actually be timely and effective. In the literature on water rescue, a large number of methods and models were demonstrated to solve the problem of safe and efficient landing on mobile platforms. Most of the research was performed through simulation, focusing on selected aspects of the mission. Therefore, the factors affecting the take-off, landing and operation should be fully considered to maximize the efficiency. Simple implementation methods should be explored.

In the research on locations, the interception problem mainly studied the problem of customer demand on the route and was mainly used in traffic planning, service, etc. [11,12]. Other research directions include research in the direction of total cost minimization [13,14]. It can be seen that the past research mainly selected locations randomly. The selection was highly subjective, which increased the uncertainty of the results. The location results did not analyze the terrain characteristics and could not be applied to aviation, especially for general aviation and other fields with harsh geographical environment. This paper hopes to further optimize the take-off and landing point selection model based on the existing research, reduce the overall cost and maximize the efficiency of low-altitude emergency rescue.

The research on the algorithms on location optimization can be divided into two categories, namely, exact algorithms and heuristic algorithms. Zhou [15] proposed an efficient hybrid genetic method including an improved wavelet propagation algorithm for solving multi-path optimization problems and a genetic algorithm for optimizing facility location problems. Inspired by the human immune system, Vikas [16] analyzed the optimal location of distributed power stations in the existing grid. Srinivasa [17] proposed a fuzzy multi-objective method based on the two-stage grasshopper optimization algorithm (GOA). To sum up, past studies have applied one or more meta-heuristic algorithms to comprehensively analyze location problems for different needs. This paper believes that the selection of the optimization algorithm should be practical. It should be able to maximize the coverage and reduce the number of base points as much as possible.

In the Sections following, Section 2 will discuss the constraints of the simulation environment. Then, in Section 3, based on ArcGIS and data collected, terrain and weather information is imposed and filtered. Results of possible sites selection are presented and discussed in Section 4. Additionally, the greedy algorithm is used to optimize the results in this part. Conclusions are made in Section 5.

2. Operation Scenario Setting

2.1. Description

This paper studies the selection of fixed takeoff and landing sites for helicopters in a low-altitude rescue environment. The city of Nanjing was chosen to be the sample. To ensure the authenticity of the experimental results and to cover all the complex and variable practical factors, this paper describes the problem as follows according to the currently applicable rules.

• Aircraft: According to the requirements of the CAAC for general aviation rescue, helicopter Mi-8 was selected for analysis.
• Flight regulations and rescue missions: In a low-altitude environment, pilots use visual flight rules to perform rescue missions. In this paper, the search and rescue points and hospitals in the rescue area were set, and the rescue tasks were mainly to transport materials and transfer the people.
• Grid division: For terrain data processing, 30 m-precision elevation data was used to divide the grid, the WGS-84 coordinate system (World Geodetic System-1984 Coordinate System) was used to depict all the latitude and longitude coordinates. The WGS-84 system is a well-accepted coordinate system and suitable for GIS. It has a wide range of applications in navigation, search and rescue. It is a fit system for the study. Raster data are obtained from files containing raster graphics, such as TIFF, which are available on the Geospatial Data Cloud website. We projected the raster data in the corresponding coordinate system; all raster data were georeferenced and mask extracted and could be directly used for analysis.
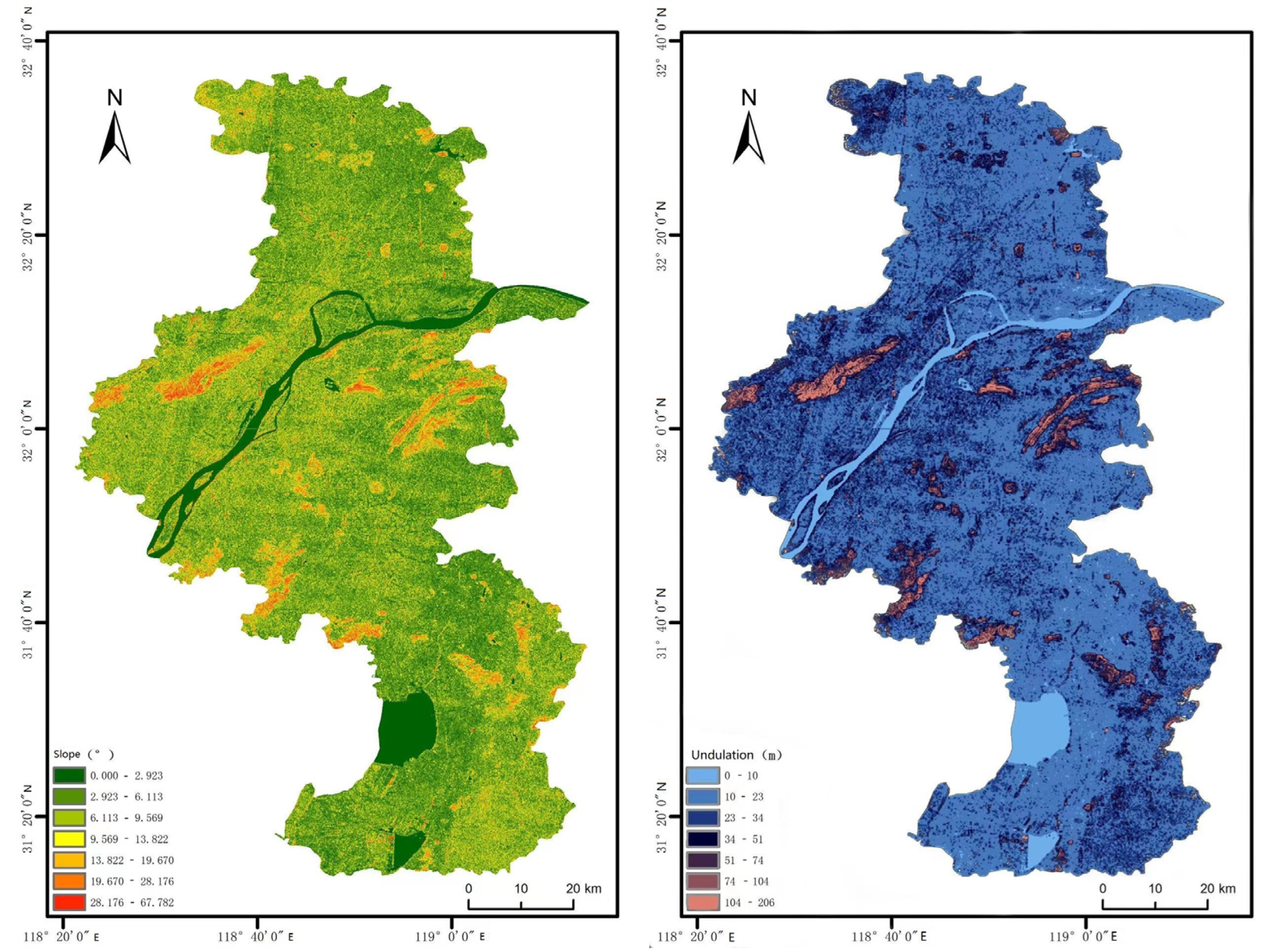
• Environmental factors: For the terrain slope, for the sake of simplicity, the requirement was limited to no more than 5 degrees, which is the only criteria stipulated by the regulation. As for hillside, longitudinal profile, and relief complexity, they will be studied in a further study. Additionally, slope, elevation(H) and undulation(F) were also considered. Road network and other restricted areas were also included in the study. These factors are discussed in detail in the following section.

2.2. Environmental Factors

• Terrain

According to relevant technical standards in China [18], land heliports and water platforms should have at least one final approach and take-off (FATO) area. When helicopters take off and land with Class 1 performance, the local slope of any area should be less than or equal to 5°. The aircraft selected in this paper is a multi-engine helicopter, and the flight mission is performed in a populated area that meets the helicopter’s level 1 performance operation standards. The slope of all grids in the take-off and landing area needs to conform to Formula (1):

$$Slope\le 5°$$

(1)

In addition, this paper also considers the undulation factor to ensure that the take-off and landing site is flat. In the general take-off and landing field, the undulation accuracy is required to be relatively high, which should conform to Formula (2):

$$F\le 0.5 \mathrm{m}$$

(2)

In practice, the slope and undulation factors selected in different directions are mostly used as constraint variables to define that the flatness of the site conforms to the specification.

2.

Area requirement

According to the technical requirements, the smallest circular temporary stop area needs to be not less than 2C (C is the outer clearance of the helicopter landing gear, and C is selected as 4.5 m in this paper); the area of square temporary stop area should be not less than 2C × 2C (In this paper, the area is rounded up to 85 m²).

3.

Barrier buffer

Due to the fact that obstacles, such as road networks and river networks, exist that may affect the safe operation of helicopters when a forced stop occurs, this paper sets a safe distance. Theoretically, the safe area should be at least 3D or greater (D is the length of the entire fuselage of the helicopter and is set at 13.46 m in this paper). To ensure safety, the safety distance is appropriately increased for buildings or tall obstacles according to their heights.

2.3. Basic Principles

2.3.1. Surface Flatness

Slope value expresses the steepness of the raster surface in each image element. The smaller the slope, the flatter the terrain. There are two calculation methods for the slope. The plane method is used in this paper, and the slope data is fitted by a uniform 3 × 3 DEM local grid, as shown in Figure 1. The 3 × 3 grid is only a specific example for calculating the slope, which is convenient for intuitive feeling and understanding. In the software, the slope can be calculated directly from the elevation data.

Figure 1. 3 × 3 grid calculation slope map.

The center of each grid is an elevation point, and the slope of the center point e is calculated [19]. See Formula (3):

$$\begin{array}{c}Slope=arctan\sqrt{{\left(\frac{dz}{dx}\right)}^2+{\left(\frac{dz}{dy}\right)}^2}\\ \frac{dz}{dx}=\frac{4\left(e9+2e6+e3\right)/\overline{w1}-4\left(e7+2e4+e1\right)/\overline{w2}}{8G}\\ \frac{dz}{dy}=\frac{4\left(e1+2e2+e3\right)/\overline{w3}-4\left(e7+2e8+e9\right)/\overline{w4} }{8G}\end{array}$$

(3)

In the formula: e1–e9 are the grid point elevations; $\overline{w1}-\overline{w4}$ is the weighted count of the area where the effective pixels are located; G is the resolution of the DEM grid.

The undulation is a quantitative indicator used to describe the landform, reflecting the maximum relative elevation difference of all grids in the selected area. It is widely used in land utility evaluation and ecological environment evaluation. Topographic undulation can be used as an important reference indicator for the division of topographic forms and is suitable for macro-topographic analysis. This paper intends to use the height difference method to calculate the undulation. See Formula (4):

$$F=H_{\max }-H_{\min }$$

(4)

where $F$ is the height difference; $H_{\max }$ and $H_{\min }$ represent the elevations of the highest and lowest points in the selected area, respectively.

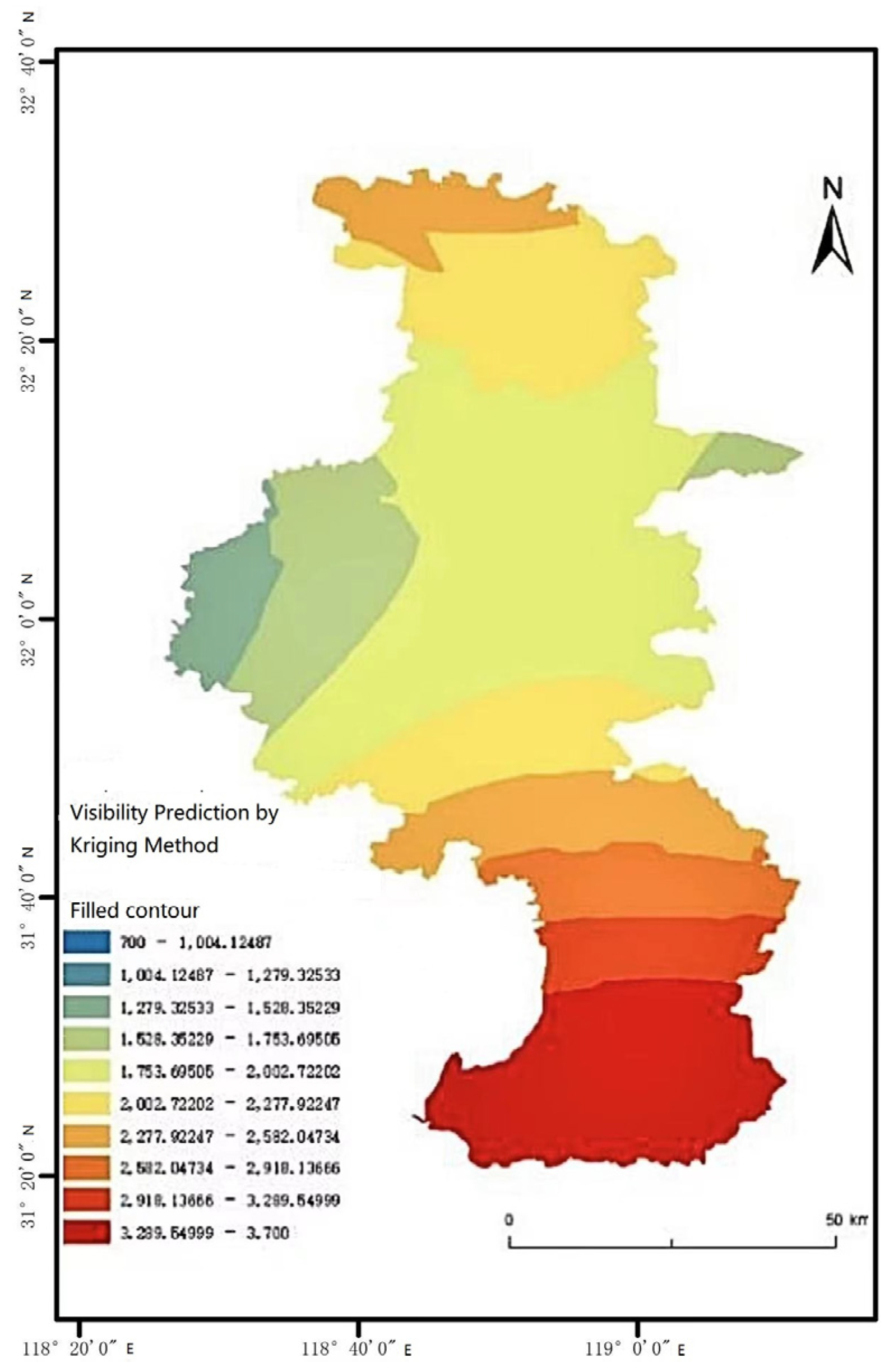
2.3.2. Visibility

Since the visibility information in this paper is obtained from weather stations, it is scattered and has basic errors. It is appropriate to use the ordinary Kriging interpolation method. For a given dataset $X={\left\{x^1,x^2,···x^n\right\}}^T$, the corresponding objective function is $y={\left\{y^1,y^2,···y^n\right\}}^T$. The Kriging method assumes that all data are subject to an n-dimensional normal distribution, so the objective function is a random process, and each variable $y^i$ in it is random.

According to estimation prediction research [20], it is assumed that there are n data points and 1 prediction point. The result of Formula (5) is obtained.

$$\begin{array}{c}\{\begin{array}{c}\widehat{y}\left(x\right)=\widehat{\mu }+r^T{C}^{-1}\left(y-1\widehat{\mu }\right)\\ s^2\left(x\right)=\widehat{\sigma }[1-r^T{C}^{-1}r+\frac{{\left(1-1^T{C}^{-1}r\right)}^2}{1^T{C}^{-1}1}]\end{array}\\ \{\begin{array}{c}\widehat{\mu }=\frac{1^T{C}^{-1}y}{1^T{C}^{-1}1}\\ {\widehat{\sigma }}^2=\frac{{\left(y-1\widehat{\mu }\right)}^T{C}^{-1}\left(y-1\widehat{\mu }\right)}{n}\end{array}\end{array}$$

(5)

where $\widehat{y}\left(x\right)$ and $s^2\left(x\right)$ represent the mean and variance of the required prediction points respectively; $r$ is the covariance matrix between the data points $X$ and the prediction points $x$; $C$ is the covariance matrix between the data points $X$; $y$ is the target value of the data points; $1$ is the n*1 matrix; $\widehat{\mu }$ and ${\widehat{\sigma }}^2$ are intermediate variables.

In conclusion, for the helicopter take-off and landing point, the following requirements must be met, see Table 1.

Table 1. Technical requirements for helicopter take-off and landing point.

Item	Core Parameter	Tech Requirement	Remarks
Site evenness	Slope/°	≤5	surface rock and hard soil
	F/m	≤0.5
Area of temporary stop area	S/m2	≥85	equivalent area for square
Visibility	v/m	≥1600	visual flight requirement under 1000 ft
Safe clearance of obstacles	H ≥ 3D	≥41	theoretical value
	H ≤ 10	≥50	actual operating value
	H > 10	≥80

3. Data Processing Using ArcGIS and Methods

3.1. Data Preparation

• Terrain data

We logged into the Geospatial Data Cloud website (http://www.gscloud.cn, accessed on 22 January 2021) to obtain the elevation information of Nanjing City, and the data accuracy is 30 m. The latitude range is 31.14–32.37, the longitude range is 118.22–119.14, and the city covers an area of 6587 square kilometers.

2.

Meteorological data

We logged into the Meteorological Data Network of China (http://data.cma.cn, accessed on 22 January 2021) to obtain the geographic information of weather stations in Nanjing and surrounding cities. See Table 2. With all these weather stations, the whole area of Nanjing could be covered. Using the data from these stations, a whole picture of the weather situation in the city could be depicted.

Table 2. Weather station data.

Code	Name	Longitude/°	Latitude/°	Elevation/m
58238	Nanjing	118.90	31.93	36.4
58235	Luhe	118.85	32.37	12.3
58237	Pukou	118.58	32.07	46.6
58339	Gaochun	118.90	31.33	20.9
58340	Lishui	119.03	31.65	27.0
58242	Yizhen	119.17	32.30	23.5
58344	Jurong	119.20	31.97	35.0
58331	Hexian	118.37	31.73	23.5
58336	Ma’anshan	118.57	31.70	81.2

As severe winter weather prevails in the middle and lower reaches of the Yangtze River, in order to obtain better location results to meet the actual needs, the meteorological data in the winter afternoon with mist or intermittent showers, which is the worst-case scenario, are selected. The following is the meteorological data reported by Nanjing Weather Station for every 3 h on 24 January 2022, see Table 3 (9999 represents no observation data).

Table 3. 24-h observation data of Nanjing Weather Station.

Time	Rainfall/mm	Visibility/m	Cloudage/%	Wind Speed/ m/s	Ceiling/m
0200	4.0	2100	100	9	600~1000
0500	3.0	1900	100	9	1000~1500
0800	3.0	1700	100	8	600~1000
1100	1.0	1500	100	8	600~1000
1400	0.2	1300	100	8	1000~1500
1700	0.1	1100	100	8	600~1000
2000	0	1700	100	6	1000~1500
2300	0	3400	100	6	9999

3.2. Data Processing

3.2.1. Extraction of Terrain Factors

The high-precision DEM data are processed to establish a gradient grading layer and a terrain undulation grading layer, as shown in Figure 2.

Figure 2. Slope grading layer and terrain undulation grading layer.

3.2.2. Building of Terrain Obstacle Buffer Zone

Considering the existence of road networks, rivers and other factors that may affect the safe operation of aircraft, this paper selects the main traffic lines in Nanjing and the banks of the Yangtze River to establish a buffer zone with a width of 50 m to prevent helicopter take-off and landing points from falling into the buffer zone. In this part, the buffer is set linearly. The road network and river information are downloaded from the Resource and Environmental Science and Data Center of the Chinese Academy of Sciences and can be directly applied to the software, as shown in Figure 3.

Figure 3. Highway and river buffer zone in Nanjing.

3.2.3. Visibility Interpolation

We extracted the data of the nine weather stations mentioned above on 24 January 2022, selected the time of 14:00 and made a table of elements. We analyzed whether the data at each site approximately conformed to the normal distribution. The outliers were eliminated by the Thiessen polygon, and then the trend analysis was performed to estimate the surface that could be fitted. Since visibility can be affected by environmental variables such as precipitation and air pollutants, forecasting is required. The results obtained are shown in Figure 4.

Figure 4. Visibility prediction by the Kriging interpolation method.

3.2.4. Feature Layers Filtering

The first three layers are comprehensively superimposed and erased, and the slope and undulation terrain that meet the requirements are selected. Areas that affect flight safety are filtered to obtain the take-off and landing point location layer. We set constraints (S ≥ 85 m²) in the location layer, selected locations that met the conditions and output the geographic coordinates of their centers. There were 56 spots and all met the requirements of terrain undulation, visibility and safe landing dimension. The results can partly be found in Table 4.

Table 4. Spot center coordinates (partial).

No.	Longitude/°	Latitude/°
1	119.0928	32.2183
2	119.0301	31.3250
3	119.0066	32.2029
4	118.9946	32.2005
5	118.9172	32.0416
6	118.8749	31.8023
7	118.7983	32.0703
8	118.7896	32.0699
9	118.7872	32.0827
10	118.7852	32.0711
11	118.7601	32.2026
12	118.7191	32.0662
13	118.4501	32.0317
14	118.3416	31.3601

3.2.5. Analysis of Results

Most of the take-off and landing points of the low-altitude rescue helicopters studied in this paper are on the water, and according to the relevant rules and regulations, the construction of the water platform should also meet other necessary conditions. According to the “Operation Requirements for Rotorcraft Water Platforms” issued by the CAAC [21], additional restrictions are imposed on the lighting and navigation aids, signs and safety facilities of the water platform. To ensure the safe and efficient operation of helicopters, pilots should receive strict training, including but not limited to more than 100 h of water flight experience, at least 50 complete water platform take-offs and landings and 90 days of flying day and night on water. After relevant theoretical and technical assessments, pilots can be certified to engage in flying activities such as take-off and landing on the water platform. In addition to the above requirements on platform construction and special trainings, the minimum area that can take off and land, meteorological conditions and operation specifications are basically consistent with the characteristic equations designed in this paper. Therefore, the method described in this paper can be applied to the study of the location problem of water take-off and landing operations for helicopters.

4. Optimization of Selection Based on the Greedy Algorithm

4.1. Rescue Radius Selection

The international rescue service radius for helicopters is 50 km. Considering the current shortage of helicopters in China, this indicator can be appropriately enlarged. For example, Japan currently implements a 100 km forward detection and rescue service radius [22]. However, due to the considerable uncertainty and limitations of terrain and environment in low-altitude rescue, in order to maximize the survival rate of rescues and reduce the severity of the injuries, the rescue scope of helicopters should be combined with the actual situation and cover densely populated areas as much as possible.

According to the golden rescue time, for different diseases, geological disasters and traffic accidents, medical treatment should be sought as soon as possible. The medical community generally recommends 30 min. Regarding factors such as the approval of the helicopter temporary route and the preparation of the helicopter crew, the above pre-rescue time was set at 15 min. Under the constraints of rescue time, the maximum rescue radius should not exceed 50 km (estimated at a level flight speed of 203 km/h under the maximum weight of Mi-8).

In order to accurately obtain the relationship between the medical coverage and the rescue radius, the geographic coordinates of the preliminary screening results were extracted by using GIS technology, and the ground surface was divided into small squares of 1 km². If the distance between the coordinates and the center of the square is lower than the rescue radius, it is considered that the area is within rescue range, and this square is within the coverage. We calculated the percentage of the squares within the coverage, and coverage rate was acquired. On this basis, this paper calculates the relationship between the rescue radius of the take-off and landing point and the coverage rate and obtains the approximate variation law of the two, as shown in Figure 5.

Figure 5. Change pattern in rescue radius and coverage rate.

Taking the above factors into consideration, when the rescue radius is selected as 28 km, a coverage rate of 96.87% can be achieved, and the helicopter pre-rescue time can be greatly reduced, which in turn, buys valuable time for follow-up rescue work.

4.2. Construction of the Greedy Algorithm Model

The greedy algorithm is a top-down approach that reduces the original problem to a smaller scale. In terms of the complexity of solving the problem and the difficulty of calculating the results, the greedy algorithm has more advantages than dynamic programming. Considering the above factors, this paper adopts greedy algorithm to optimize the initial selection of take-off and landing points to improve the efficiency of site selection.

Based on the objects studied in this paper, the following greedy strategies are made:

• Cost of helicopter transportation is proportional to the distance;
• Site with the largest coverage area is selected first;
• Newly added coverage must intersect with the covered surface;
• Terminate when the coverage is greater than 95%.

According to the above strategy, the required constraint function $\Gamma$ is constructed, and the simulation algorithm is shown in Table 5.

Table 5. Basic greedy algorithm framework.

Greedy Algorithm Framework for Location
Step 1:	Input all initial location coordinate sets $\mathsf{\Omega }$, constraint function $\Gamma$
Step 2:	Set the number of nodes k
Step 3:	Set the initial location point coordinate set ${\mathrm{A}}_0ϵ\mathsf{\Omega }$
Step 4:	$\mathrm{for}\mathrm{i}ϵ1,2,\dots ,\mathrm{k}-1\mathrm{do}$
	(1) ${\mathsf{\omega }\mathrm{argmax}}_{\mathrm{j}ϵ\mathsf{\Omega }\backslash {\mathrm{A}}_{\mathrm{i}}}\Gamma ({\mathrm{A}}_{\mathrm{i}}{\displaystyle \cup }\left\{\mathrm{j}\right\})-\Gamma \left({\mathrm{A}}_{\mathrm{i}}\right)$
	(2) ${\mathrm{A}}_{\mathrm{i}+1}={\mathrm{A}}_{\mathrm{i}}+\left\{\mathsf{\omega }\right\}$
Step 5:	end for
Step 6:	Coverage C ≥ 95%?
	(Yes) return Step7
	(No) p = p + 1, return Step2
Step 7:	Output coverage C and optimization results ${\mathrm{A}}_{\mathrm{k}}$

4.3. Location Optimization

4.3.1. Initial Location Optimization

According to the previous research on location optimization using the greedy algorithm [5], the optimal rescue radius is usually selected first. The optimization purpose of this section is to make the rescue range of the take-off and landing point cover the urban area of Nanjing as much as possible.

In order to further simplify the optimization simulation, this section selects the center point coordinates of the conforming area to replace the entire surface. The geographic data of the initial location is iteratively analyzed according to the above algorithm, and finally, the minimum facility distribution is obtained. After comparison, when the rescue radius is 30 km, five helicopter take-off and landing points need to be built, achieving 98.7% coverage, which basically meets the experimental expectations. The results are shown in Table 6.

Table 6. Optimized locations within a 30 km rescue radius.

Possible Location	Longitude/°	Latitude/°
1	118.7191	32.0662
2	119.0066	32.2029
3	118.4501	32.0317
4	118.8749	31.8023
5	118.3416	31.3601

4.3.2. Promotion of Optimized Location

From past experimental data, the average cost of constructing a take-off and landing platform is approximately 500,000 yuan [23], and because there aren’t many helicopters in China, it is difficult to achieve full coverage for large-scale low-altitude rescue in the short term. In order to further improve the utilization rate of helicopters and reduce the initial construction funds, this paper expands the rescue radius. We explore the possibility of carrying out cross-city rescue by increasing the rescue range of helicopters. On the premise of not affecting the survival rate of victims, the rescue radius is expanded to 50 km. After algorithm iteration, only two take-off and landing bases are needed, which can basically cover the whole area of Nanjing. As shown in Table 7.

Table 7. Optimized locations with 50 km rescue radius.

Possible Location	Longitude/°	Latitude/°
1	118.9172	32.0416
2	119.0301	31.3250

5. Conclusions

Starting from the selection of low-altitude rescue take-off and landing points, this paper studies how to optimize the selection based on the requirements of civil aviation regulations and considering the actual construction situation. With terrain and weather information, applying ArcGIS and the greedy algorithm, possible sites were selected and optimized. It shows great potential for future practice.

For meteorological elements, this paper proves that the Kriging method can be used for spatial interpolation analysis. For the problem of the maximum coverage area of site selection, this paper suggests that a more realistic rescue range could be adopted according to the specific situation to reduce helicopter requirements and costs.

However, during the location optimization, the simplification of the coordinates of the center point of the initial screening area selection may not be consistent with the actual situation; terrain restrictions such as hillside, longitudinal profile and relief properties are not considered; specific problems need to be analyzed in detail. Additionally, the worst-case scenario is considered alone with only daily/hourly weather data. In the future, yearly/seasonal data could be studied. The population factor could be taken into account in the optimization so that the helicopter allocation can be carried out with priorities within the scope of rescue coverage.