Unfrozen Skewed Turbulence for Wind Loading on Structures
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Surface Layer Turbulence Modelling
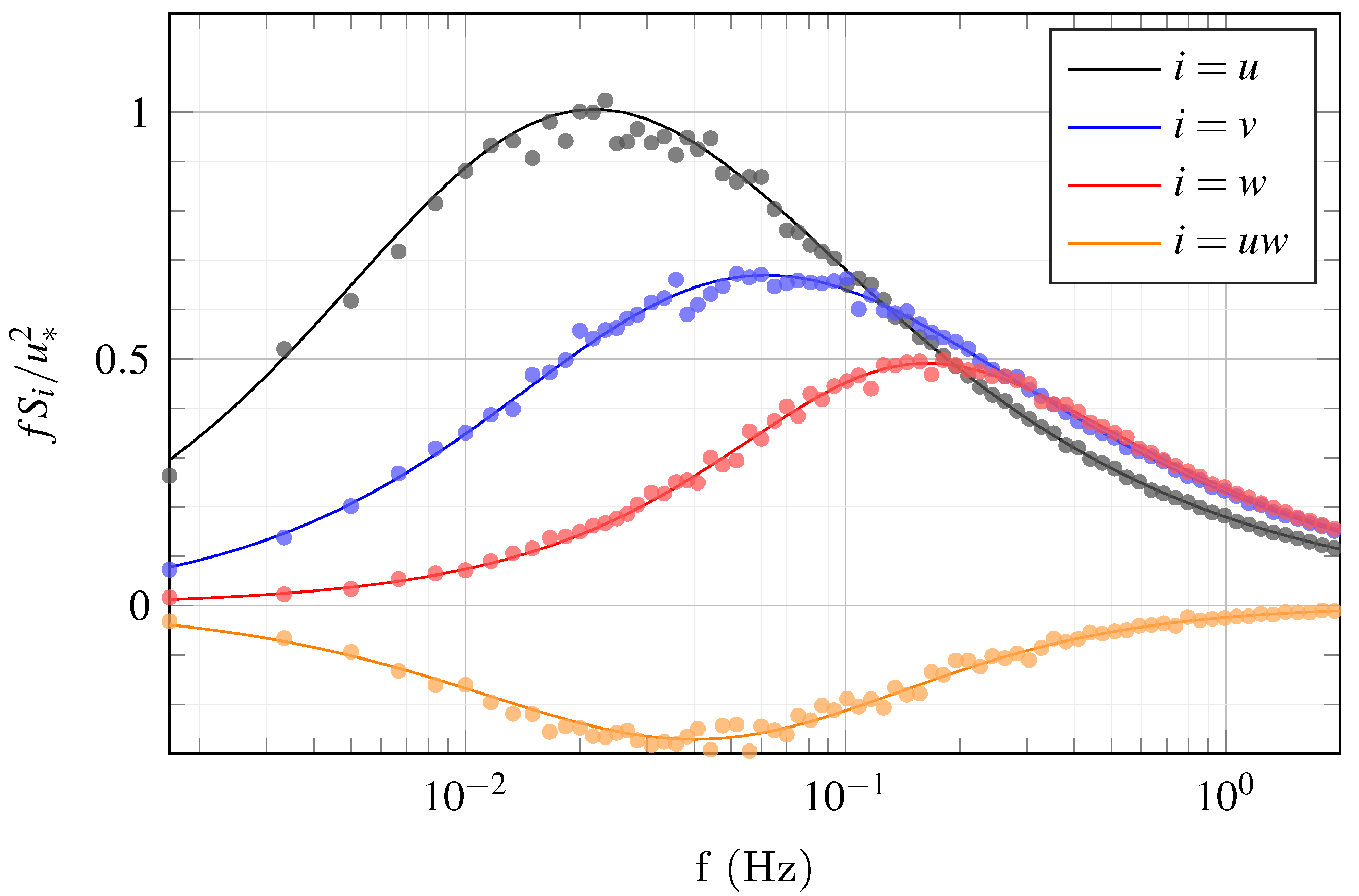
2.2. One-Point Velocity Spectra
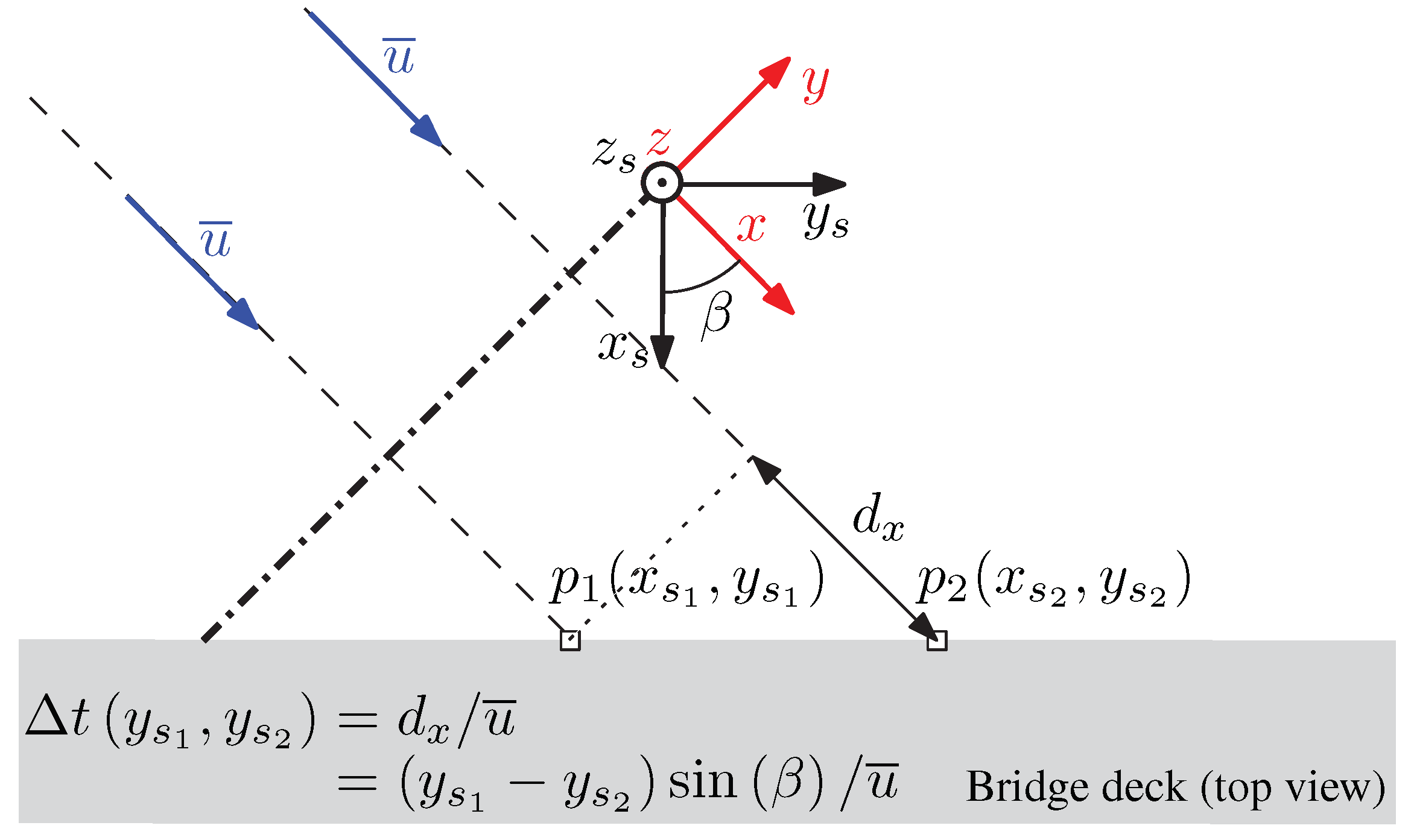
2.3. Taylor’s Hypothesis of Frozen Turbulence
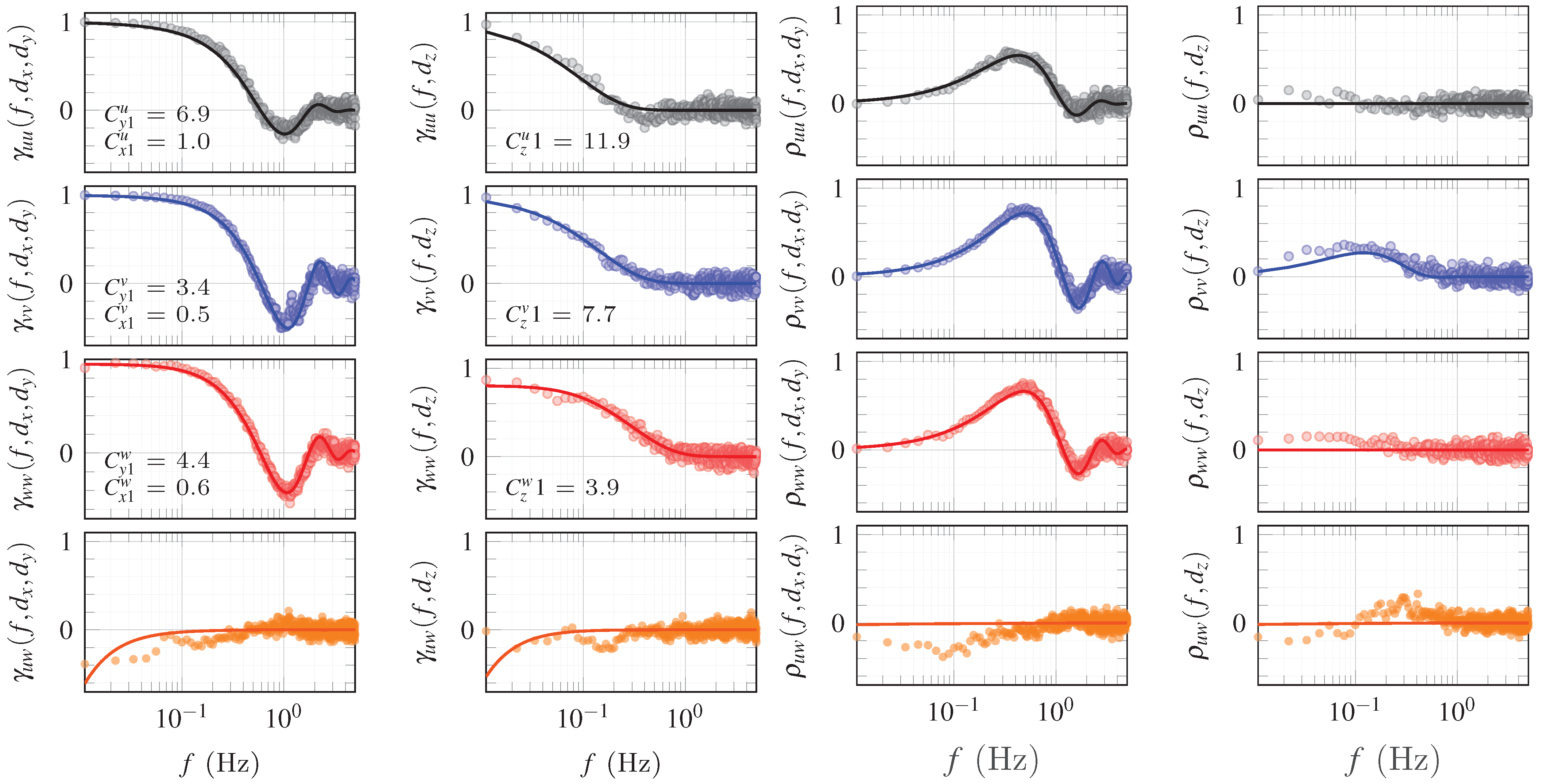
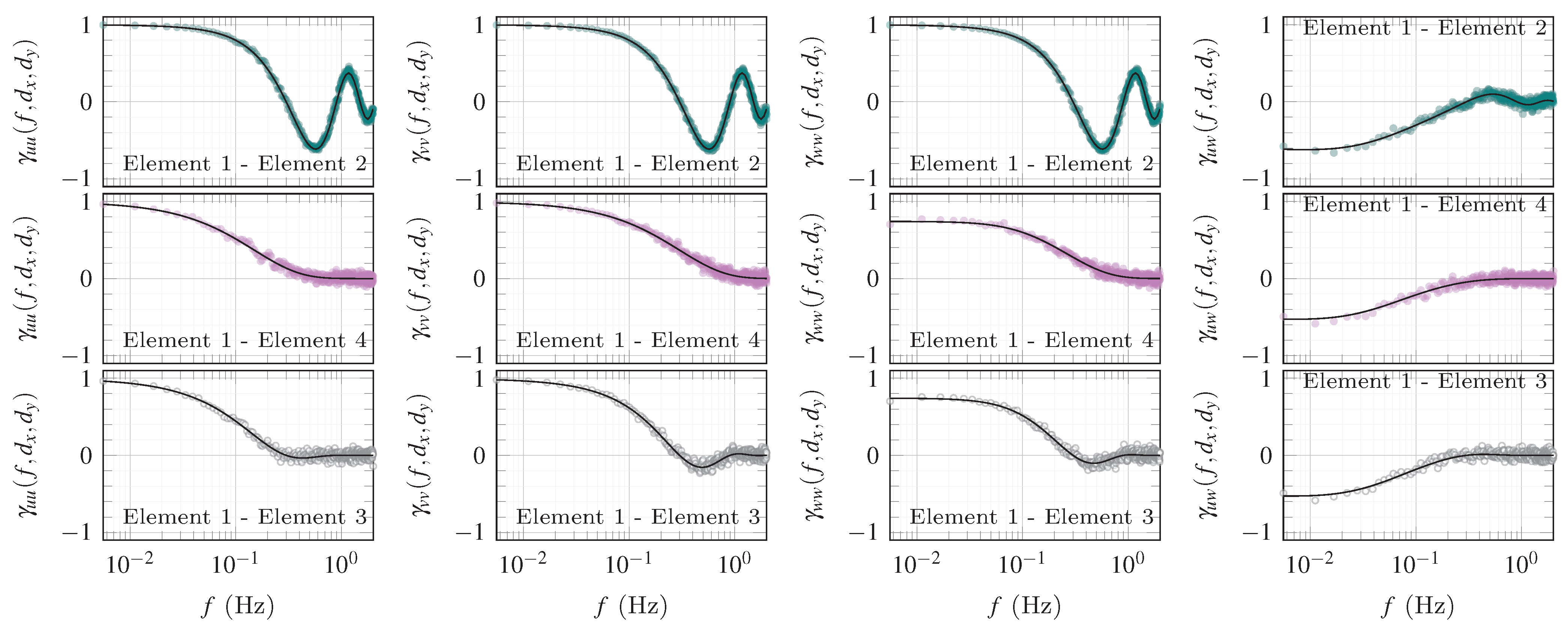
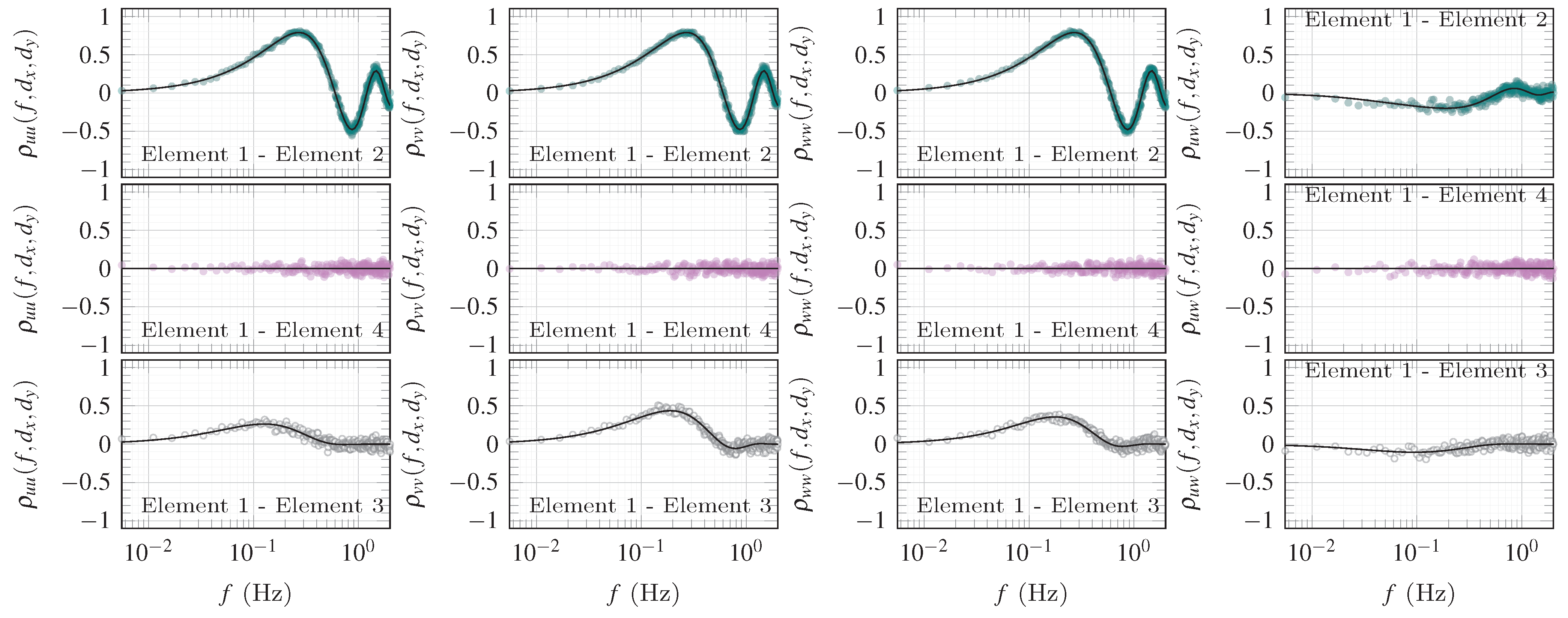
2.4. Coherence Modelling
3. Computation of Turbulent Time-Histories
4. Results
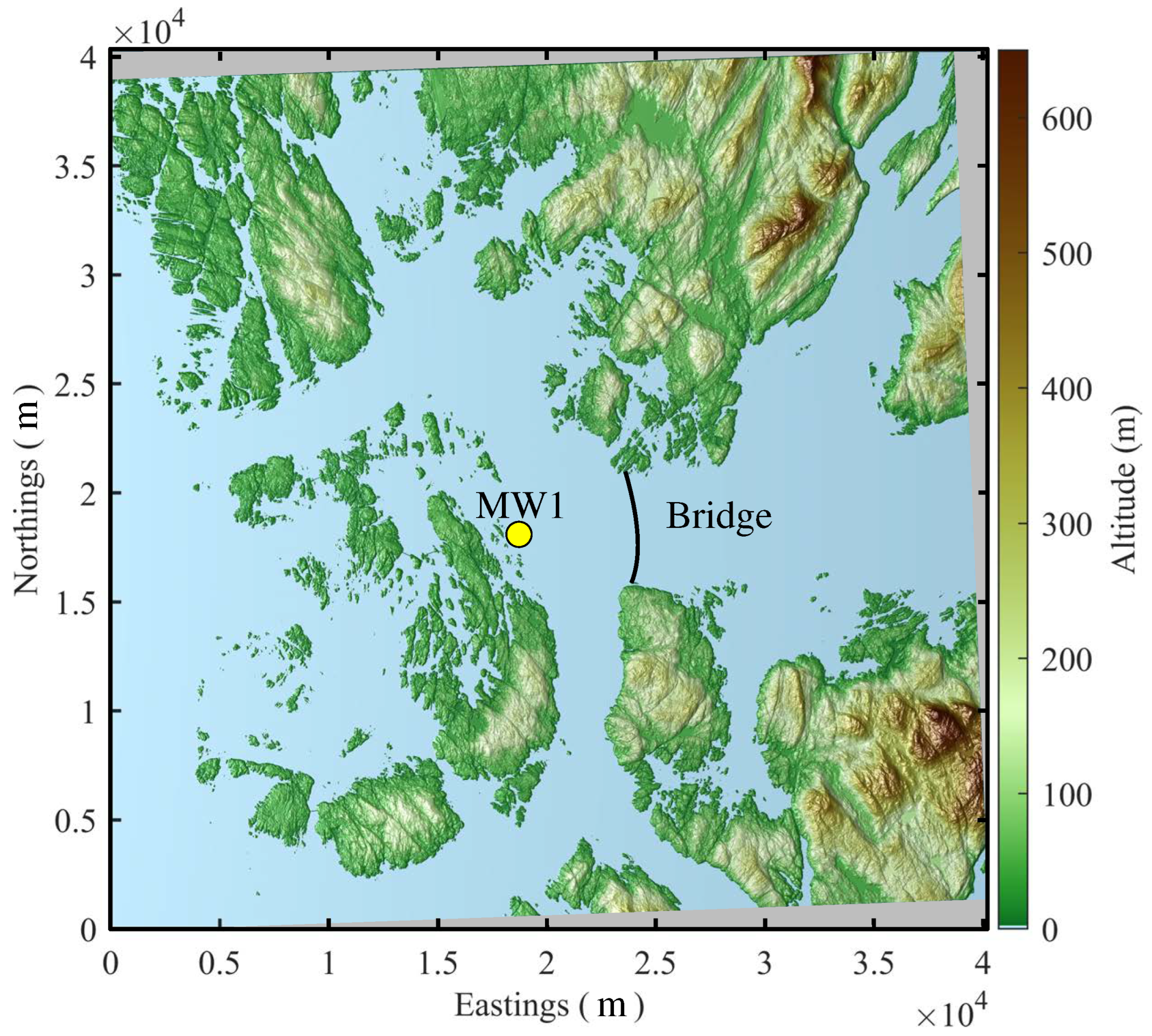
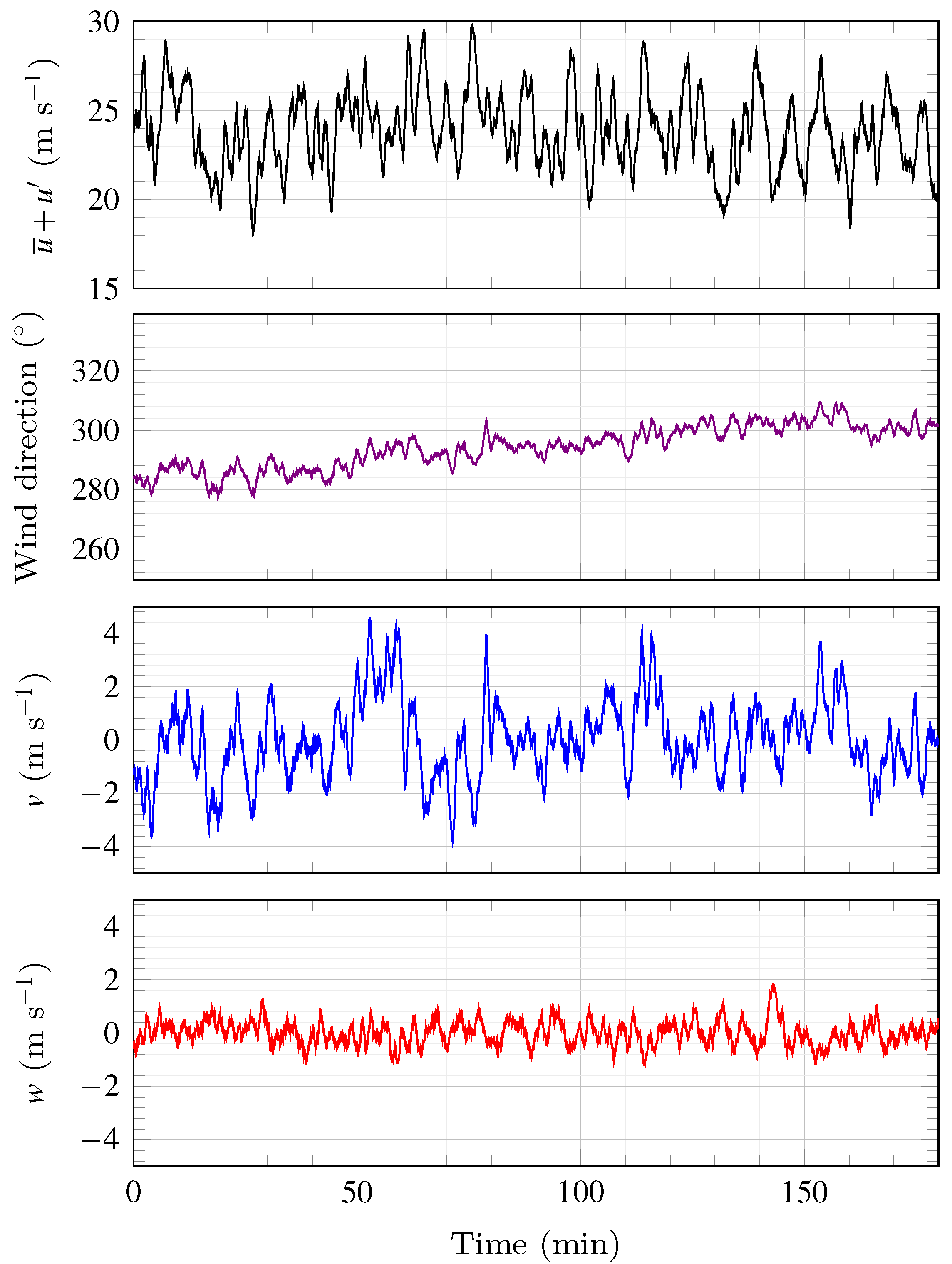
4.1. Flow Characteristics of Wind Storm Aina (2017)
4.2. One-Point Velocity Spectra
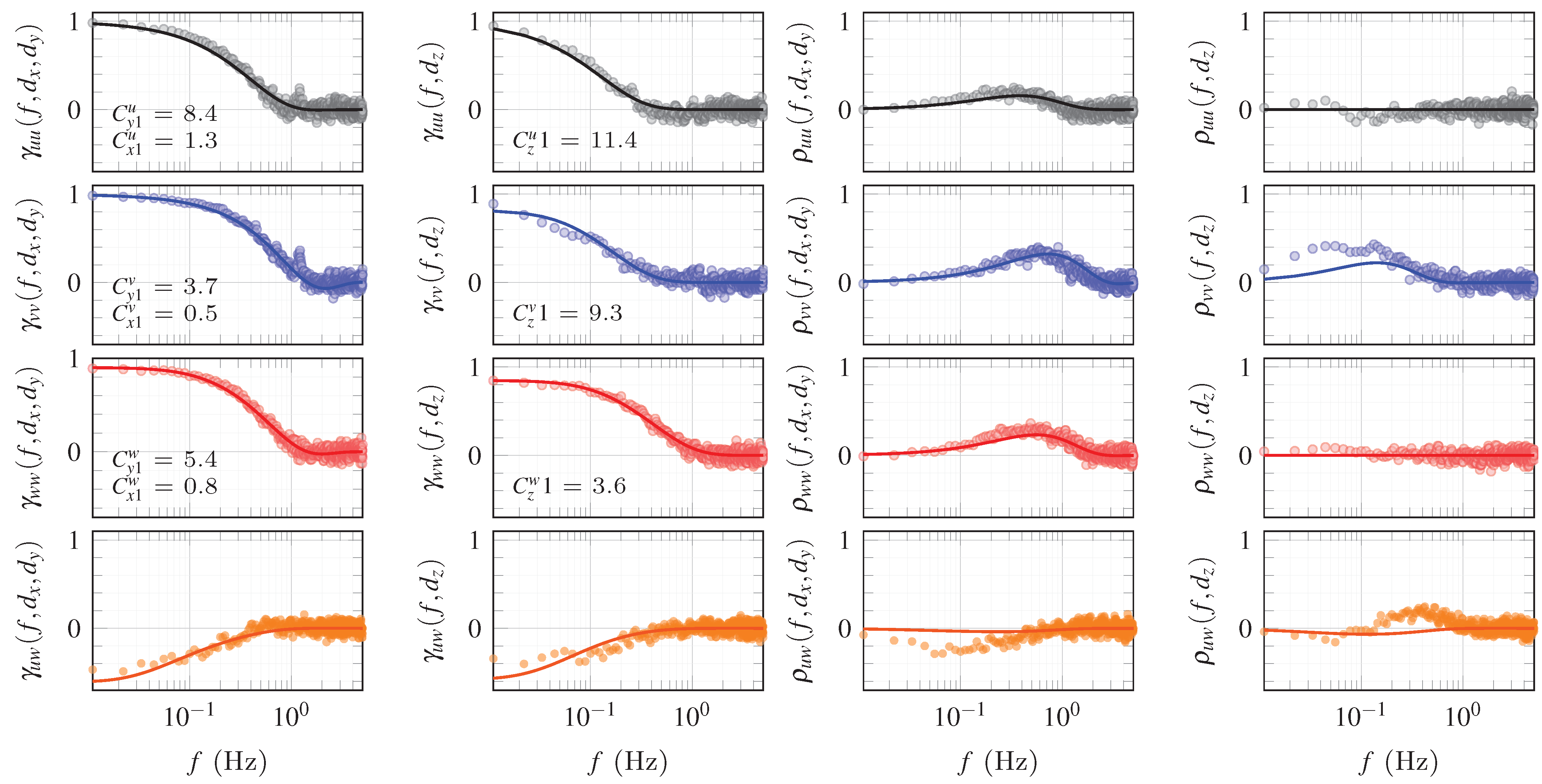
4.3. Coherence Estimates
5. Discussion and Conclusions
5.1. Skewed Turbulence Generation on a Diamond Geometry
5.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, J.; Tanaka, H.; Wardlaw, R.; Savage, M. Buffeting analysis of long span bridges to turbulent wind with yaw angle. J. Wind Eng. Ind. Aerodyn. 1991, 37, 65–77. [Google Scholar] [CrossRef]
- Xu, Y.L.; Zhu, L. Buffeting response of long-span cable-supported bridges under skew winds. Part II: Case study. J. Sound Vib. 2005, 281, 675–697. [Google Scholar] [CrossRef]
- Diana, G.; Falco, M.; Bruni, S.; Cigada, A.; Larose, G.L.; Darnsgaard, A.; Collina, A. Comparisons between wind tunnel tests on a full aeroelastic model of the proposed bridge over Stretto di Messina and numerical results. J. Wind Eng. Ind. Aerodyn. 1995, 54, 101–113. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, M.; Wang, D.; Guo, Z.; Cao, F. Flutter and buffeting performances of Third Nanjing Bridge over Yangtze River under yaw wind via aeroelastic model test. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1579–1606. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, Y.L.; Zhang, F.; Xiang, H. Tsing Ma bridge deck under skew winds—Part I: Aerodynamic coefficients. J. Wind Eng. Ind. Aerodyn. 2002, 90, 781–805. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Zasso, A.; Belloli, M.; Rocchi, D. Effects of the yaw angle on the aerodynamic behaviour of the Messina multi-box girder deck section. Wind Struct. 2004, 7, 41–54. [Google Scholar] [CrossRef]
- Davenport, A.G. The response of slender, line-like structures to a gusty wind. In Proceedings of the Institution of Civil Engineers; Thomas Telford-ICE Virtual Library: London, UK, 1962; Volume 23, pp. 389–408. [Google Scholar]
- Larose, G.L. The spatial distribution of unsteady loading due to gusts on bridge decks. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1431–1443. [Google Scholar] [CrossRef]
- Kristensen, L.; Jensen, N. Lateral coherence in isotropic turbulence and in the natural wind. Bound.-Layer Meteorol. 1979, 17, 353–373. [Google Scholar] [CrossRef]
- Solari, G.; Piccardo, G. Probabilistic 3-D turbulence modeling for gust buffeting of structures. Probabilistic Eng. Mech. 2001, 16, 73–86. [Google Scholar] [CrossRef]
- Strømmen, E.; Hjorth-Hansen, E. Static and dynamic section model tests of the proposed Hardanger fjord suspension bridge. In Proceedings of the Bridges into the 21st Century, Hong Kong, China, 2–5 October 1995; p. 8. [Google Scholar]
- Zhu, L.; Xu, Y.L. Buffeting response of long-span cable-supported bridges under skew winds. Part I: Theory. J. Sound Vib. 2005, 281, 647–673. [Google Scholar] [CrossRef]
- Jafari, M.; Sarkar, P.P. Wind-induced response characteristics of a yawed and inclined cable in ABL wind: Experimental-and numerical-model based study. Eng. Struct. 2020, 214, 110681. [Google Scholar] [CrossRef]
- Raeesi, A.; Cheng, S.; Ting, D.S.K. Application of a three-dimensional aeroelastic model to study the wind-induced response of bridge stay cables in unsteady wind conditions. J. Sound Vib. 2016, 375, 217–236. [Google Scholar] [CrossRef]
- Robertson, A.N.; Shaler, K.; Sethuraman, L.; Jonkman, J. Sensitivity analysis of the effect of wind characteristics and turbine properties on wind turbine loads. Wind Energy Sci. 2019, 4, 479–513. [Google Scholar] [CrossRef]
- Sanchez Gomez, M.; Lundquist, J.K. The effect of wind direction shear on turbine performance in a wind farm in central Iowa. Wind Energy Sci. 2020, 5, 125–139. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, C.; Wu, Y.; Flay, R.G.; Zhang, K. Investigation on the effects of twisted wind flow on the wind loads on a square section megatall building. J. Wind Eng. Ind. Aerodyn. 2019, 191, 127–142. [Google Scholar] [CrossRef]
- Feng, C.; Gu, M.; Zheng, D. Numerical simulation of wind effects on super high-rise buildings considering wind veering with height based on CFD. J. Fluids Struct. 2019, 91, 102715. [Google Scholar] [CrossRef]
- ESDU. ESDU 86010, Characteristics of Atmospheric Turbulence Near the Ground. Part III: Variations in Space and Time for Strong Winds (Neutral Atmosphere); IHS Inc.: London, UK, 2002. [Google Scholar]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. Lond. Ser.-Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Simley, E.; Pao, L.Y. A longitudinal spatial coherence model for wind evolution based on large-eddy simulation. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 3708–3714. [Google Scholar]
- Cheynet, E.; Jakobsen, J.; Snæbjörnsson, J.; Mann, J.; Courtney, M.; Lea, G.; Svardal, B. Measurements of Surface-Layer Turbulence in a Wide Norwegian Fjord Using Synchronized Long-Range Doppler Wind Lidars. Remote Sens. 2017, 9, 977. [Google Scholar] [CrossRef]
- Shinozuka, M.; Deodatis, G. Simulation of Stochastic Processes by Spectral Representation. Appl. Mech. Rev. 1991, 44, 191. [Google Scholar] [CrossRef]
- Eidem, M.E. Overview of floating bridge projects in Norway. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, American Society of Mechanical Engineers, Trondheim, Norway, 25–30 June 2017; p. 8. [Google Scholar]
- da Costa, B.M.; Wang, J.; Jakobsen, J.B.; øiseth, O.A.; þór Snæbjörnsson, J. Bridge buffeting by skew winds: A quasi-steady case study. J. Wind Eng. Ind. Aerodyn. 2022, 227, 105068. [Google Scholar] [CrossRef]
- Zerva, A.; Zervas, V. Spatial variation of seismic ground motions: An overview. Appl. Mech. Rev. 2002, 55, 271–297. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Liu, W.; Xie, W.C.; Pandey, M.D. Modeling of spatially correlated, site-reflected, and nonstationary ground motions compatible with response spectrum. Soil Dyn. Earthq. Eng. 2013, 55, 21–32. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, e187. [Google Scholar]
- Kaimal, J.; Wyngaard, J.; Izumi, Y.; Coté, O. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Panofsky, H.; Dutton, J. Atmospheric Turbulence: Models and Methods for Engineering Applications; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Barthelmie, R. The effects of atmospheric stability on coastal wind climates. Meteorol. Appl. A J. Forecast. Pract. Appl. Train. Tech. Model. 1999, 6, 39–47. [Google Scholar] [CrossRef]
- Olesen, H.R.; Larsen, S.E.; Højstrup, J. Modelling velocity spectra in the lower part of the planetary boundary layer. Bound.-Layer Meteorol. 1984, 29, 285–312. [Google Scholar] [CrossRef]
- Tieleman, H.W. Universality of velocity spectra. J. Wind Eng. Ind. Aerodyn. 1995, 56, 55–69. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 1941, 30, 299–303. [Google Scholar]
- Peña, A.; Dellwik, E.; Mann, J. A method to assess the accuracy of sonic anemometer measurements. Atmos. Meas. Tech. Discuss. 2018, 2018, 1–23. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Snæbjörnsson, J. Flow distortion recorded by sonic anemometers on a long-span bridge: Towards a better modelling of the dynamic wind load in full-scale. J. Sound Vib. 2019, 450, 214–230. [Google Scholar] [CrossRef]
- Weber, R.O. Remarks on the definition and estimation of friction velocity. -Bound.-Layer Meteorol. 1999, 93, 197–209. [Google Scholar] [CrossRef]
- Haugen, D.; Kaimal, J.; Bradley, E. An experimental study of Reynolds stress and heat flux in the atmospheric surface layer. Q. J. R. Meteorol. Soc. 1971, 97, 168–180. [Google Scholar] [CrossRef]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Högström, U. Review of some basic characteristics of the atmospheric surface layer. Bound.-Layer Meteorol. 1996, 78, 215–246. [Google Scholar] [CrossRef]
- Burlando, M.; Carassale, L.; Georgieva, E.; Ratto, C.F.; Solari, G. A simple and efficient procedure for the numerical simulation of wind fields in complex terrain. Bound.-Layer Meteorol. 2007, 125, 417–439. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The making of the new european wind atlas—Part 2: Production and evaluation. Geosci. Model Dev. 2020, 13, 5079–5102. [Google Scholar] [CrossRef]
- Haakenstad, H.; Breivik, ø.; Furevik, B.R.; Reistad, M.; Bohlinger, P.; Aarnes, O.J. NORA3: A Nonhydrostatic High-Resolution Hindcast of the North Sea, the Norwegian Sea, and the Barents Sea. J. Appl. Meteorol. Climatol. 2021, 60, 1443–1464. [Google Scholar] [CrossRef]
- Øiseth, O.; Rönnquist, A.; Sigbjörnsson, R. Effects of co-spectral densities of atmospheric turbulence on the dynamic response of cable-supported bridges: A case study. J. Wind Eng. Ind. Aerodyn. 2013, 116, 83–93. [Google Scholar] [CrossRef]
- ESDU. ESDU 85020, Characteristics of Atmospheric Turbulence Near the Ground. Part II: Single Point Data for Strong Winds (Neutral Atmosphere); IHS Inc.: London, UK, 2001. [Google Scholar]
- EN 1991-1-4; Eurocode 1: Actions on Structures–Part1-4: General Actions-Wind Actions. Comité Européen de Normalization (CEN): Brussels, Belgium, 2005.
- Norwegian Public Road Administration. N400 Handbook for Bridge Design; Directorate of Public Roads: Oslo, Norway, 2015.
- Hill, R. Corrections to Taylor’s frozen turbulence approximation. Atmos. Res. 1996, 40, 153–175. [Google Scholar] [CrossRef]
- Monin, A. Turbulence in the atmospheric boundary layer. Phys. Fluids 1967, 10, S31–S37. [Google Scholar] [CrossRef]
- Higgins, C.W.; Froidevaux, M.; Simeonov, V.; Vercauteren, N.; Barry, C.; Parlange, M.B. The effect of scale on the applicability of Taylor’s frozen turbulence hypothesis in the atmospheric boundary layer. Bound.-Layer Meteorol. 2012, 143, 379–391. [Google Scholar] [CrossRef]
- Tong, C. Taylor’s hypothesis and two-point coherence measurements. Bound.-Layer Meteorol. 1996, 81, 399–410. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Tennekes, H.; Panofsky, H. Horizontal coherence of wind fluctuations. Bound.-Layer Meteorol. 1973, 5, 353–363. [Google Scholar] [CrossRef]
- Burghelea, T.; Segre, E.; Steinberg, V. Validity of the Taylor hypothesis in a random spatially smooth flow. Phys. Fluids 2005, 17, 103101. [Google Scholar] [CrossRef]
- Sjöholm, M.; Mikkelsen, T.; Kristensen, L.; Mann, J.; Kirkegaard, P. Spectral analysis of wind turbulence measured by a Doppler LIDAR for velocity fine structure and coherence studies. In Proceedings of the 15th International Symposium for the Advancement of Boundary Layer Remote Sensing, Paris, France, 28–30 June 2010; p. 5. [Google Scholar]
- Davoust, S.; von Terzi, D. Analysis of wind coherence in the longitudinal direction using turbine mounted lidar. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 753, p. 072005. [Google Scholar]
- Debnath, M.; Brugger, P.; Simley, E.; Doubrawa, P.; Hamilton, N.; Scholbrock, A.; Jager, D.; Murphy, M.; Roadman, J.; Lundquist, J.K.; et al. Longitudinal coherence and short-term wind speed prediction based on a nacelle-mounted Doppler lidar. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1618, p. 032051. [Google Scholar]
- Chen, Y.; Schlipf, D.; Cheng, P.W. Parameterization of Wind Evolution using Lidar. Wind Energy Sci. Discuss. 2020, 6, 61–91. [Google Scholar] [CrossRef]
- Kristensen, L.; Panofsky, H.A.; Smith, S.D. Lateral coherence of longitudinal wind components in strong winds. Bound.-Layer Meteorol. 1981, 21, 199–205. [Google Scholar] [CrossRef]
- Bowen, A.J.; Flay, R.G.; Panofsky, H.A. Vertical coherence and phase delay between wind components in strong winds below 20 m. Bound.-Layer Meteorol. 1983, 26, 313–324. [Google Scholar] [CrossRef]
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. Q. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Pielke, R.; Panofsky, H. Turbulence characteristics along several towers. Bound.-Layer Meteorol. 1970, 1, 115–130. [Google Scholar] [CrossRef]
- Hjorth-Hansen, E.; Jakobsen, A.; Strømmen, E. Wind buffeting of a rectangular box girder bridge. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1215–1226. [Google Scholar] [CrossRef]
- Minh, N.N.; Miyata, T.; Yamada, H.; Sanada, Y. Numerical simulation of wind turbulence and buffeting analysis of long-span bridges. J. Wind Eng. Ind. Aerodyn. 1999, 83, 301–315. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jan, C.M. Digital simulation of random processes and its applications. J. Sound Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Veers, P.S. Three-Dimensional Wind Simulation; Technical report; Sandia National Labs.: Albuquerque, NM, USA, 1988. [Google Scholar]
- Shinozuka, M.; Deodatis, G. Simulation of Multi-Dimensional Gaussian Stochastic Fields by Spectral Representation. Appl. Mech. Rev. 1996, 49, 29. [Google Scholar] [CrossRef]
- Jonkman, B.J.; Buhl, M.L., Jr. TurbSim User’s Guide; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2006. [Google Scholar]
- Mann, J. Wind field simulation. Probabilistic Eng. Mech. 1998, 13, 269–282. [Google Scholar] [CrossRef]
- Benowitz, B.A.; Deodatis, G. Simulation of wind velocities on long span structures: A novel stochastic wave based model. J. Wind Eng. Ind. Aerodyn. 2015, 147, 154–163. [Google Scholar] [CrossRef]
- de Maré, M.; Mann, J. On the space-time structure of sheared turbulence. Bound.-Layer Meteorol. 2016, 160, 453–474. [Google Scholar] [CrossRef]
- Hémon, P.; Santi, F. Simulation of a spatially correlated turbulent velocity field using biorthogonal decomposition. J. Wind Eng. Ind. Aerodyn. 2007, 95, 21–29. [Google Scholar] [CrossRef]
- Ashcraft, C.; Grimes, R.G.; Lewis, J.G. Accurate symmetric indefinite linear equation solvers. SIAM J. Matrix Anal. Appl. 1998, 20, 513–561. [Google Scholar] [CrossRef]
- Duff, I.S. MA57-a New Code for the Solution of Sparse Symmetric Definite Systems; Technical Report; CM-P00045911; CLRC: Oxford, UK, 2002. [Google Scholar]
- Mann, J. The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Chougule, A.; Mann, J.; Kelly, M.; Sun, J.; Lenschow, D.; Patton, E. Vertical cross-spectral phases in neutral atmospheric flow. J. Turbul. 2012, 13, 36. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.; Snæbjörnsson, J.; Ágústsson, H.; Harstveit, K. Complementary use of wind lidars and land-based met-masts for wind measurements in a wide fjord. JPhCS 2018, 1104, 012028. [Google Scholar] [CrossRef]
- Rommetveit, A. Ekstremværet Aina Kan Bli Farlig. 2017. Available online: https://www.yr.no/artikkel/ekstremvaeret-aina-kan-bli-farlig-1.13814154 (accessed on 7 December 2017).
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Klipp, C. Turbulent friction velocity calculated from the Reynolds stress Tensor. J. Atmos. Sci. 2018, 75, 1029–1043. [Google Scholar] [CrossRef]
- Midjiyawa, Z.; Cheynet, E.; Reuder, J.; Ágústsson, H.; Kvamsdal, T. Potential and challenges of wind measurements using met-masts in complex topography for bridge design: Part I–Integral flow characteristics. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104584. [Google Scholar] [CrossRef]
- Busch, N.E.; Panofsky, H.A. Recent spectra of atmospheric turbulence. Q. J. R. Meteorol. Soc. 1968, 94, 132–148. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Reuder, J. Velocity spectra and coherence estimates in the marine atmospheric boundary layer. Bound.-Layer Meteorol. 2018, 169, 429–460. [Google Scholar] [CrossRef]
- Midjiyawa, Z.; Cheynet, E.; Reuder, J.; Ágústsson, H.; Kvamsdal, T. Potential and challenges of wind measurements using met-masts in complex topography for bridge design: Part II—Spectral flow characteristics. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104585. [Google Scholar] [CrossRef]
- Harstveit, K. Full scale measurements of gust factors and turbulence intensity, and their relations in hilly terrain. J. Wind Eng. Ind. Aerodyn. 1996, 61, 195–205. [Google Scholar] [CrossRef]
- Nybø, A.; Nielsen, F.G.; Reuder, J.; Churchfield, M.J.; Godvik, M. Evaluation of different wind fields for the investigation of the dynamic response of offshore wind turbines. Wind Energy 2020, 23, 1810–1830. [Google Scholar] [CrossRef]



| Characteristics | (m s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.14 | 0.11 | 0.08 | 1.36 | 2.43 | 1.96 | 1.34 | 0.81 | 0.55 |
| Characteristics | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 0.07 | 0.15 | 2.7 | 3.2 | 3.3 |
| Coefficients | |||||
|---|---|---|---|---|---|
| Values | 118 | 24 | 3.6 | 12 | 9 |
| Component i | |||||
|---|---|---|---|---|---|
| u | 1 | 8 | 0.01 | 11 | 0.03 |
| v | 1 | 4 | 0.01 | 9 | 0.30 |
| w | 1 | 5 | 0.36 | 4 | 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheynet, E.; Daniotti, N.; Bogunović Jakobsen, J.; Snæbjörnsson, J.; Wang, J. Unfrozen Skewed Turbulence for Wind Loading on Structures. Appl. Sci. 2022, 12, 9537. https://doi.org/10.3390/app12199537
Cheynet E, Daniotti N, Bogunović Jakobsen J, Snæbjörnsson J, Wang J. Unfrozen Skewed Turbulence for Wind Loading on Structures. Applied Sciences. 2022; 12(19):9537. https://doi.org/10.3390/app12199537
Chicago/Turabian StyleCheynet, Etienne, Nicolò Daniotti, Jasna Bogunović Jakobsen, Jónas Snæbjörnsson, and Jungao Wang. 2022. "Unfrozen Skewed Turbulence for Wind Loading on Structures" Applied Sciences 12, no. 19: 9537. https://doi.org/10.3390/app12199537
APA StyleCheynet, E., Daniotti, N., Bogunović Jakobsen, J., Snæbjörnsson, J., & Wang, J. (2022). Unfrozen Skewed Turbulence for Wind Loading on Structures. Applied Sciences, 12(19), 9537. https://doi.org/10.3390/app12199537









