Extensive Discussions of the Eddy Dissipation Concept Constants and Numerical Simulations of the Sandia Flame D
Abstract
:1. Introduction
2. Reaction Rates
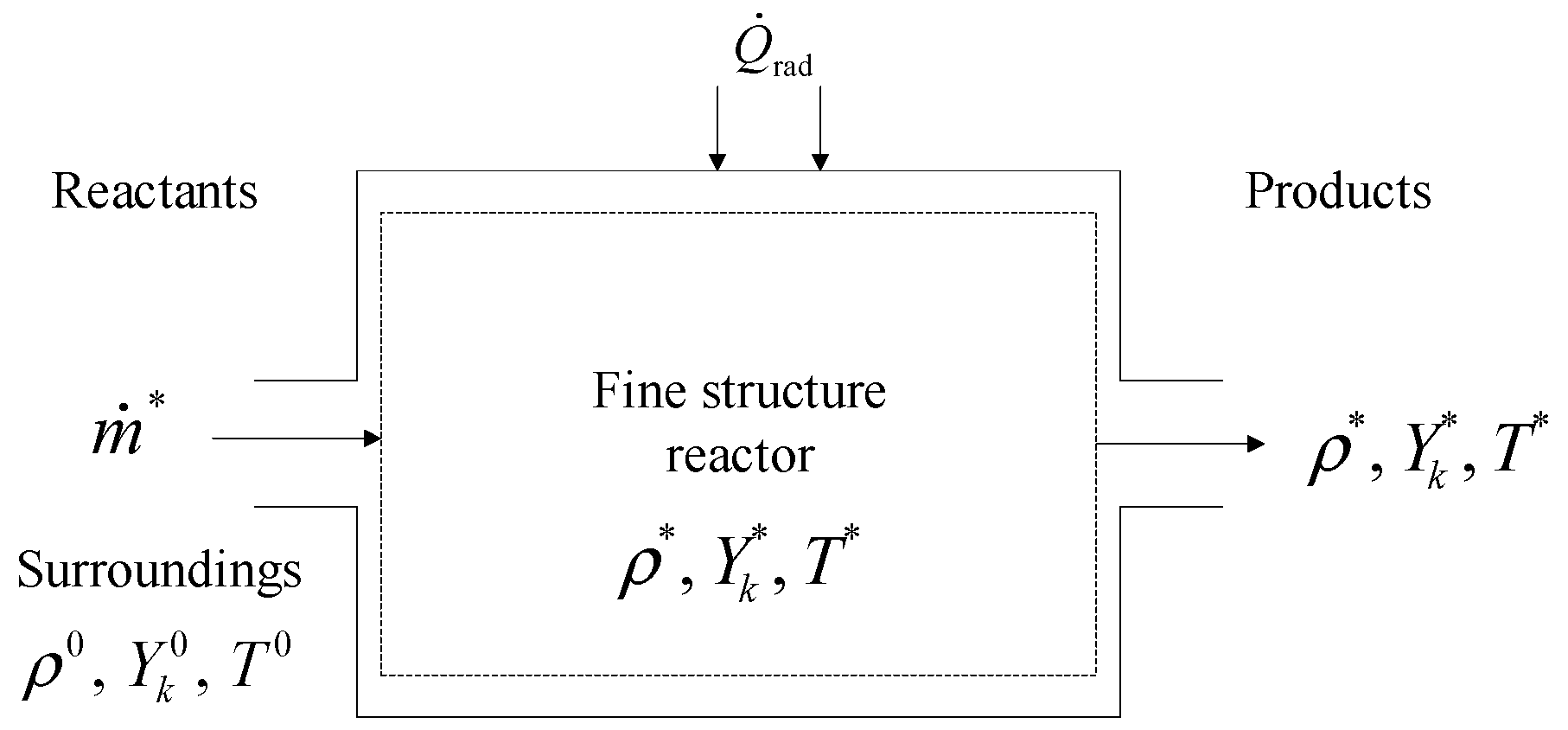
3. Fine-Structures Model
4. EDC Model Constants and the Effects on Reaction Rate
5. Results and Discussion
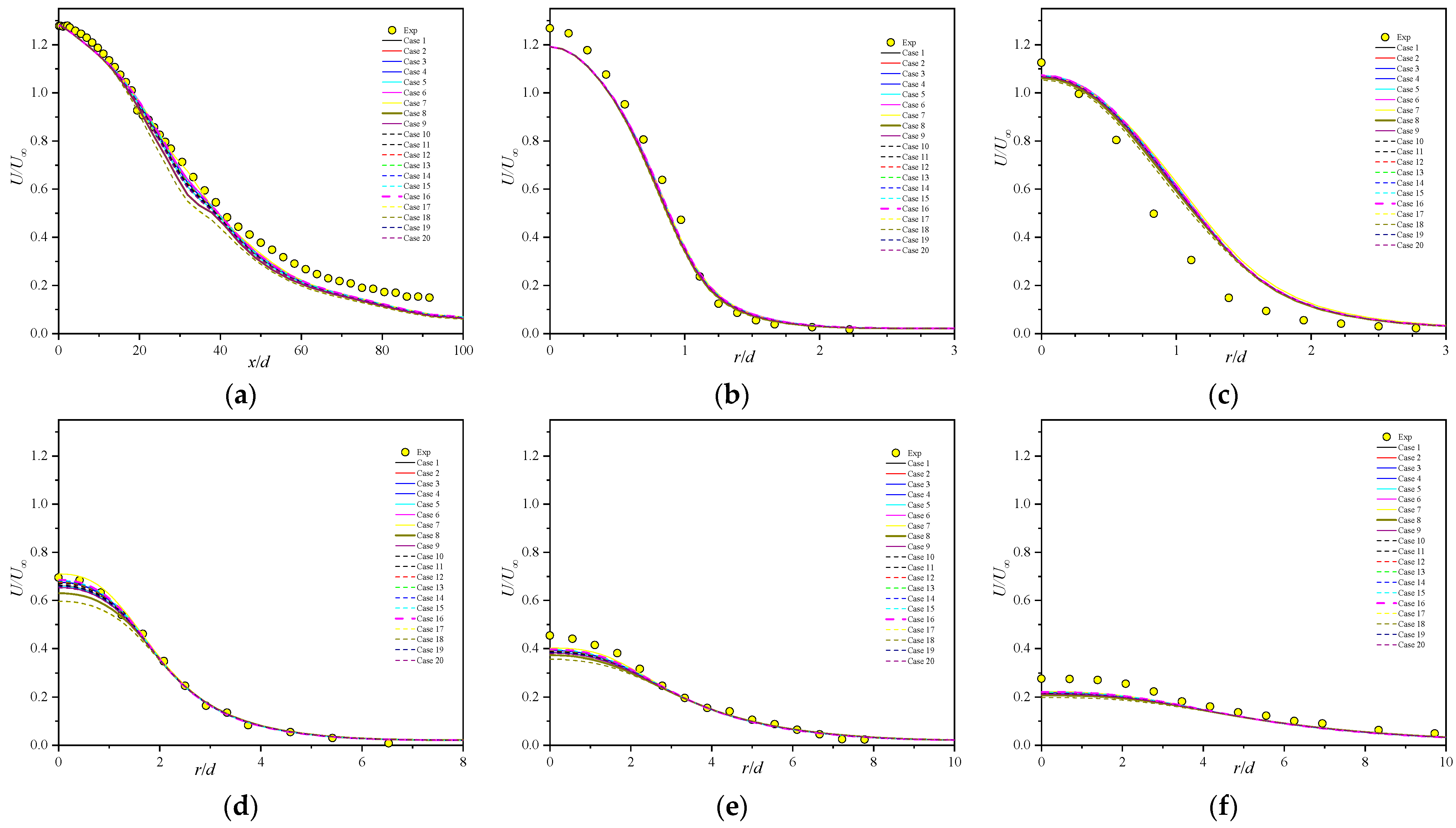
5.1. Axial Velocity Profiles
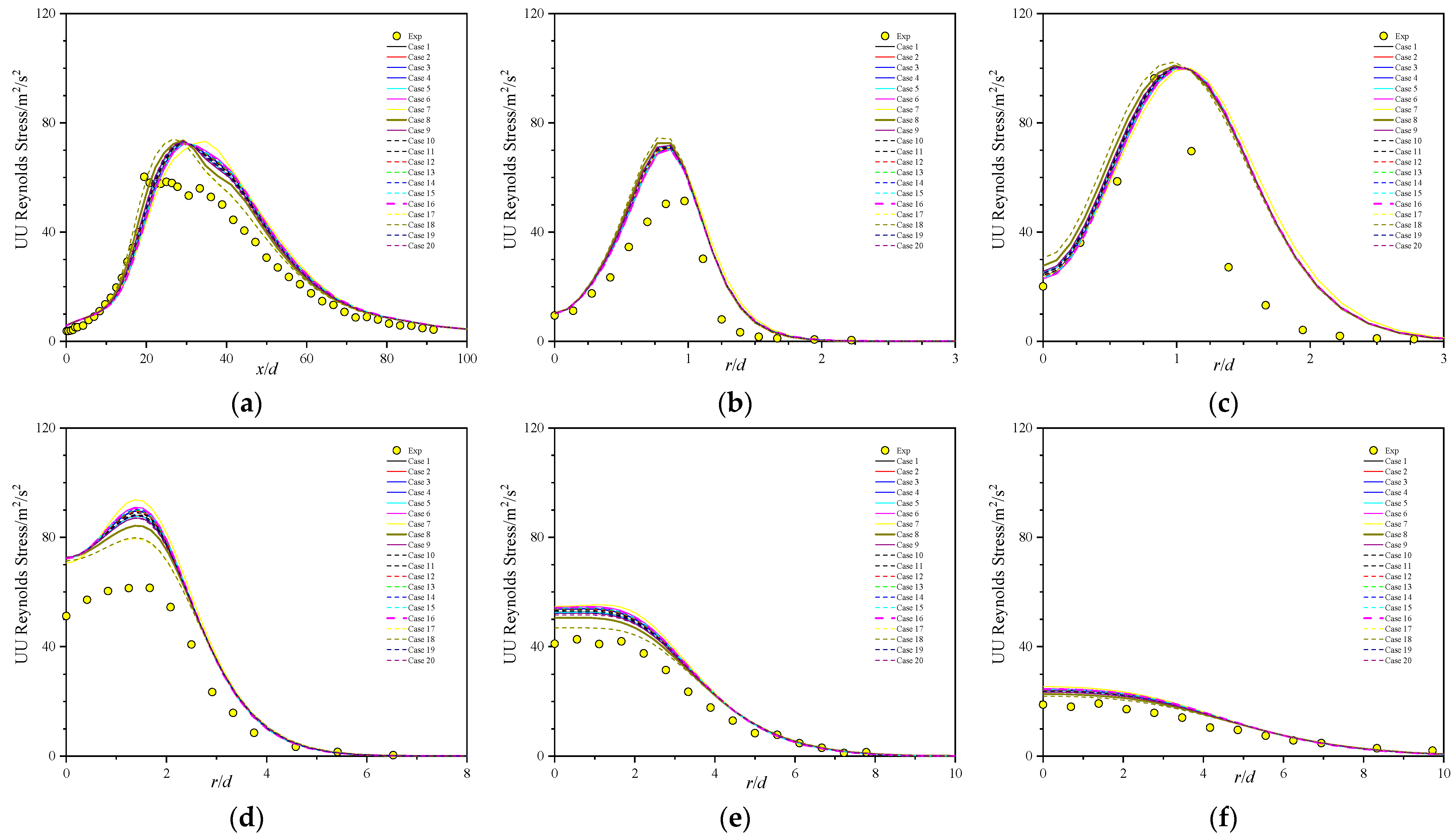
5.2. Reynolds Normal Stress Profiles
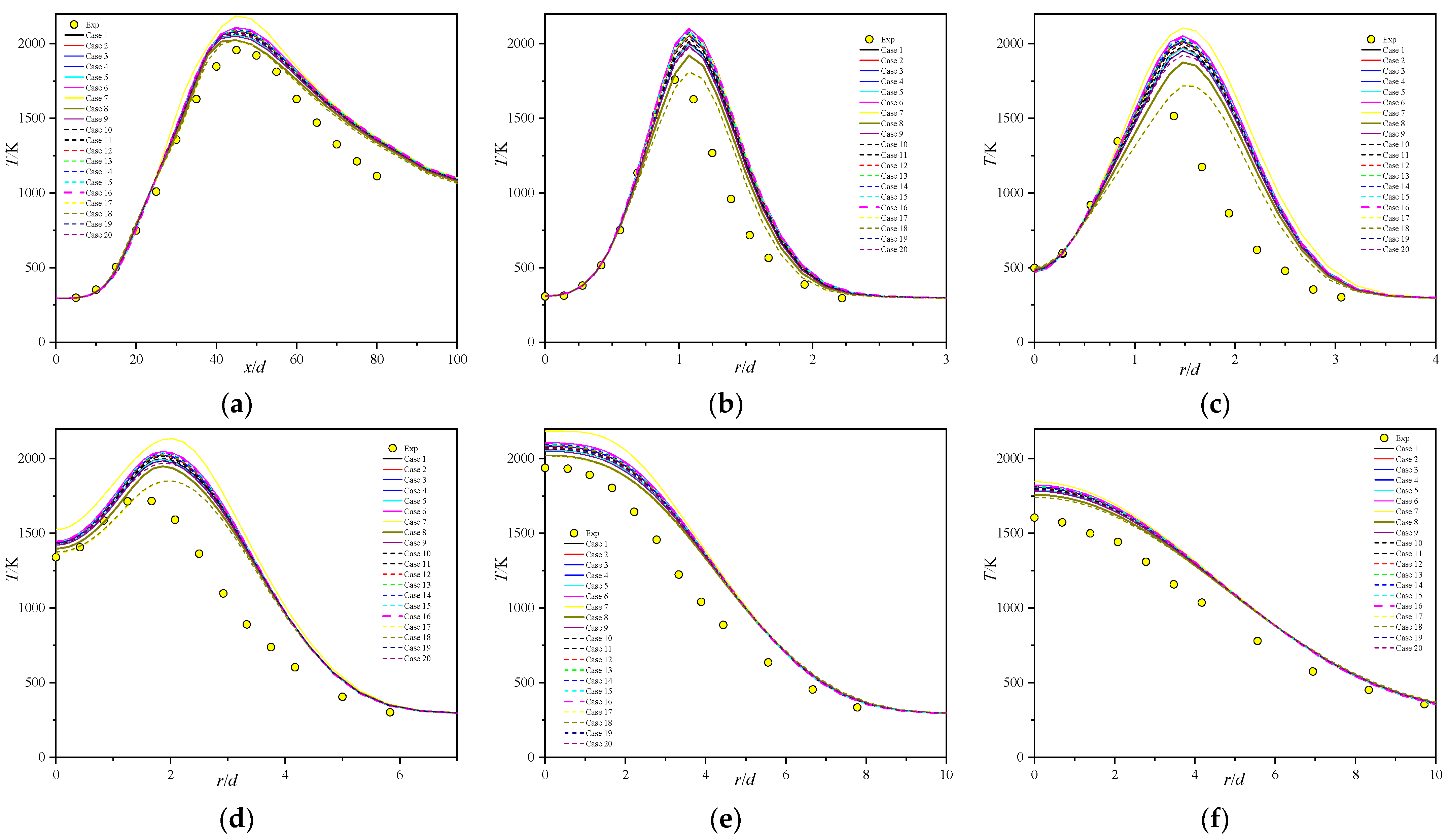
5.3. Mean Temperature Profiles
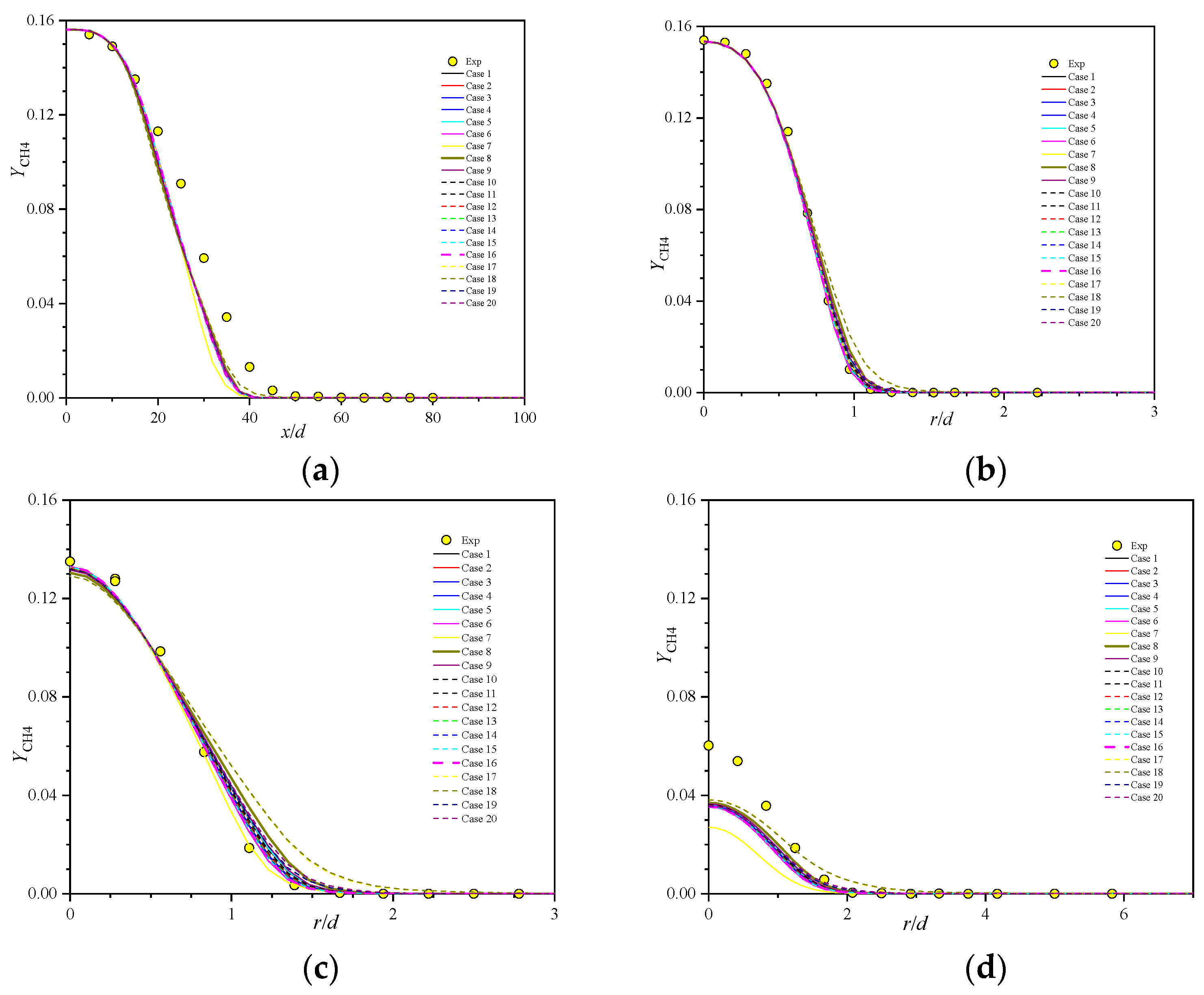
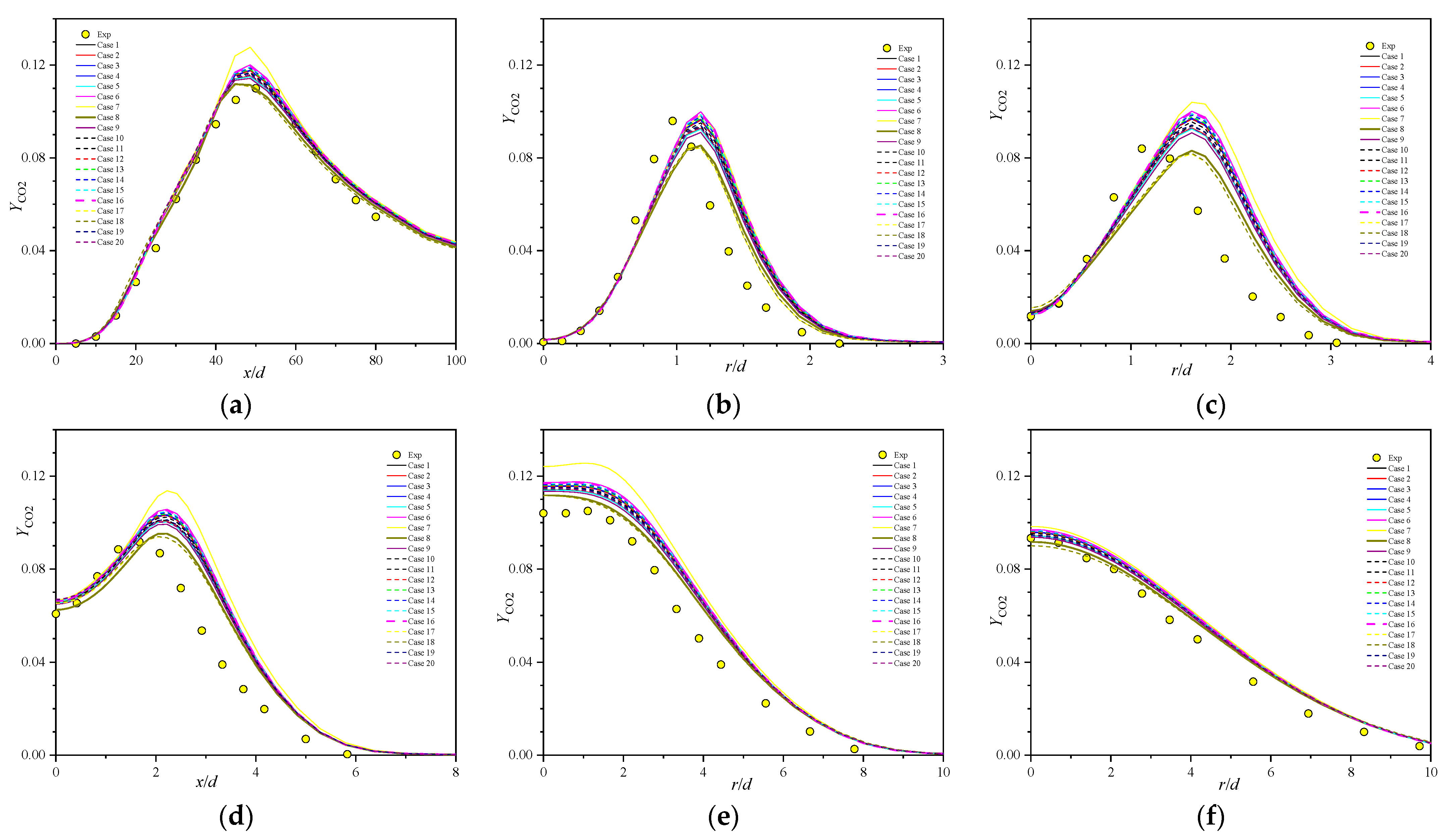
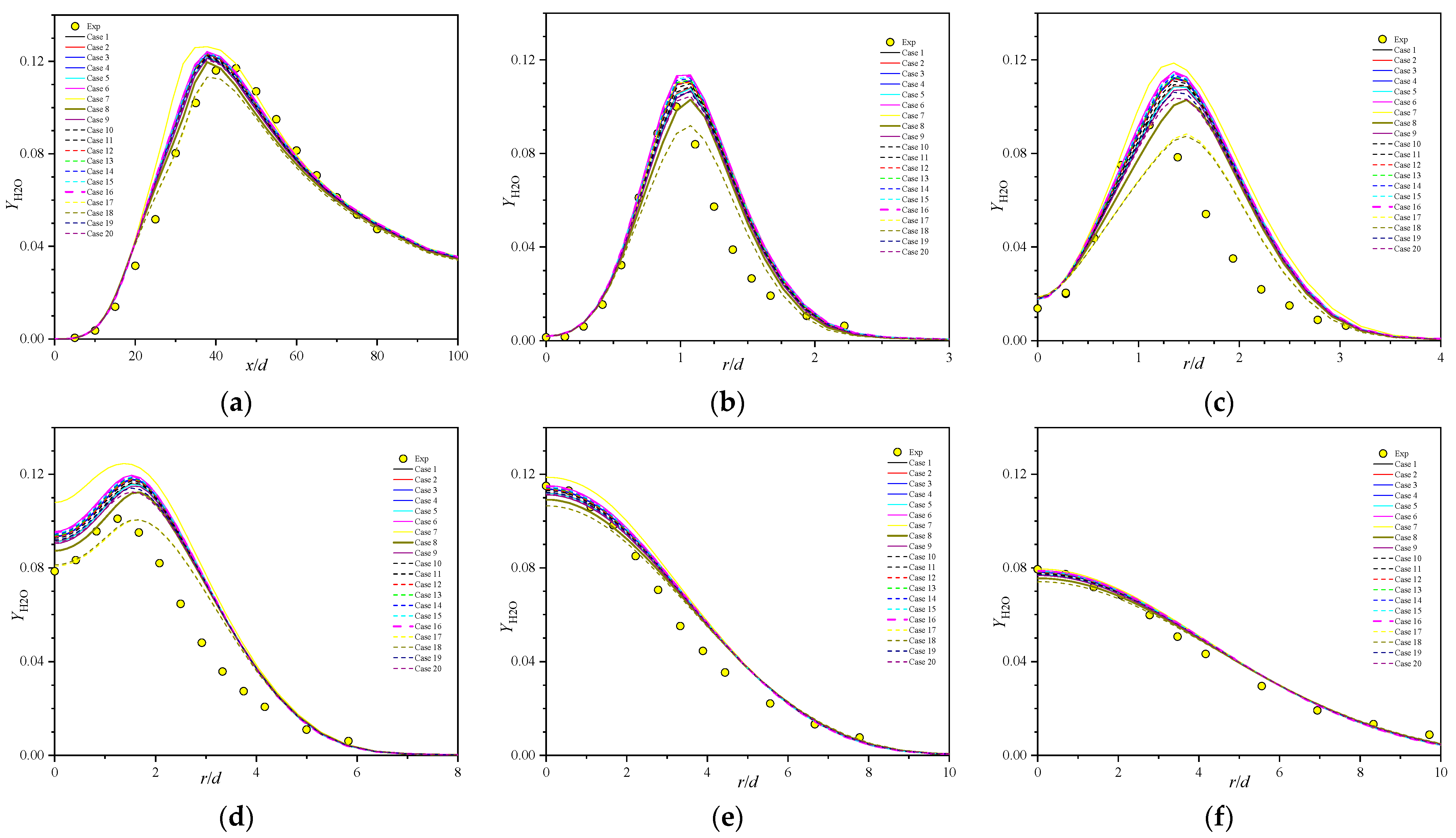
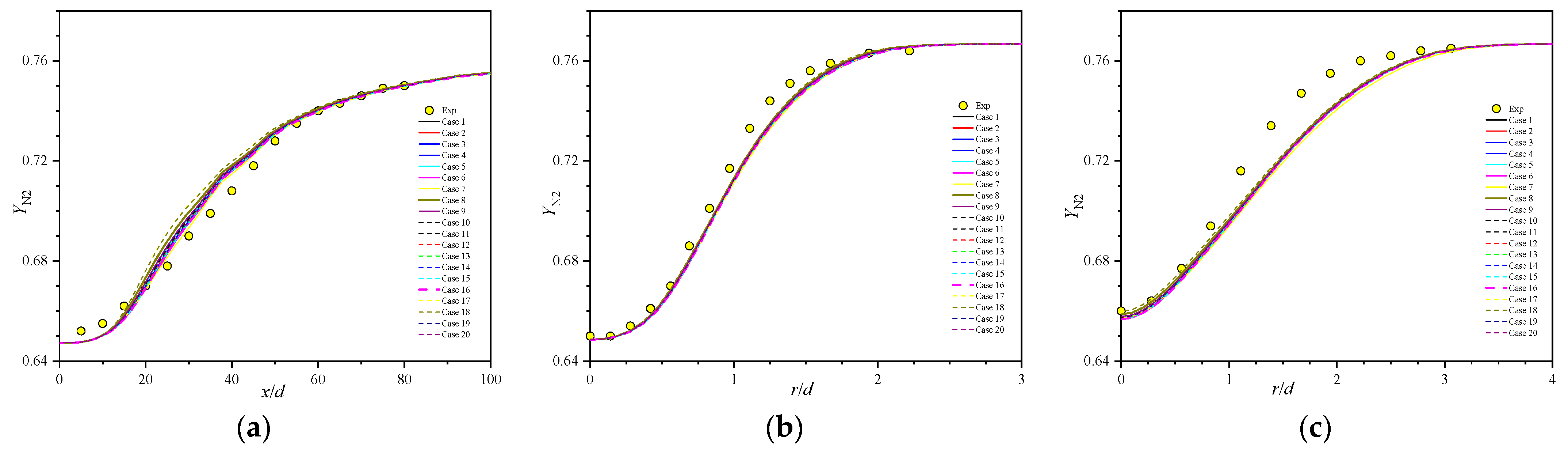
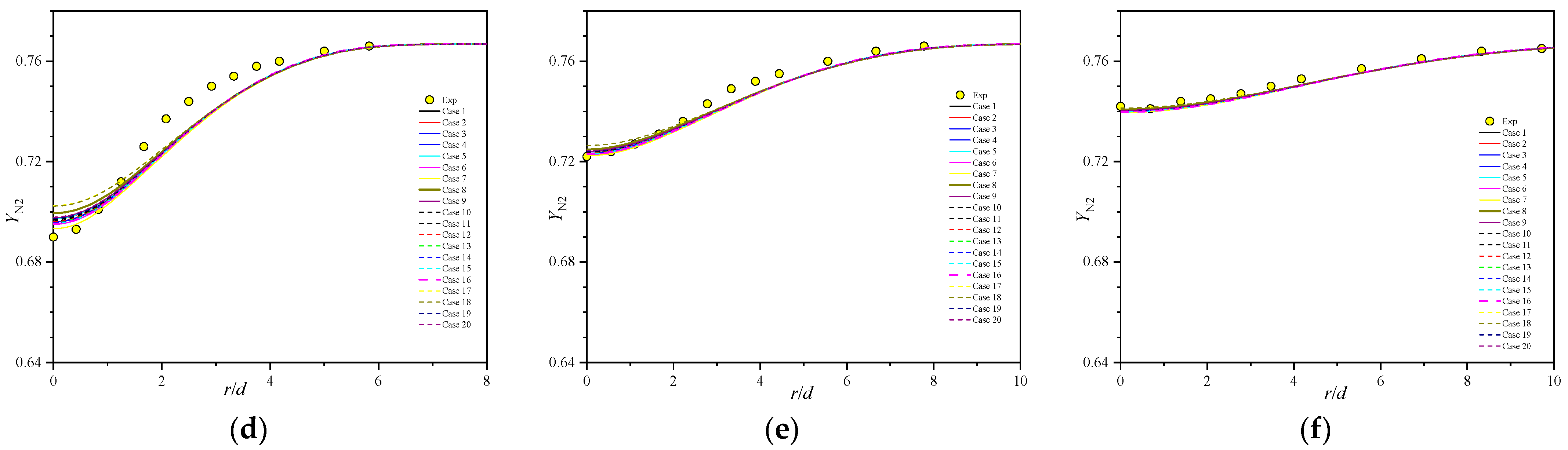
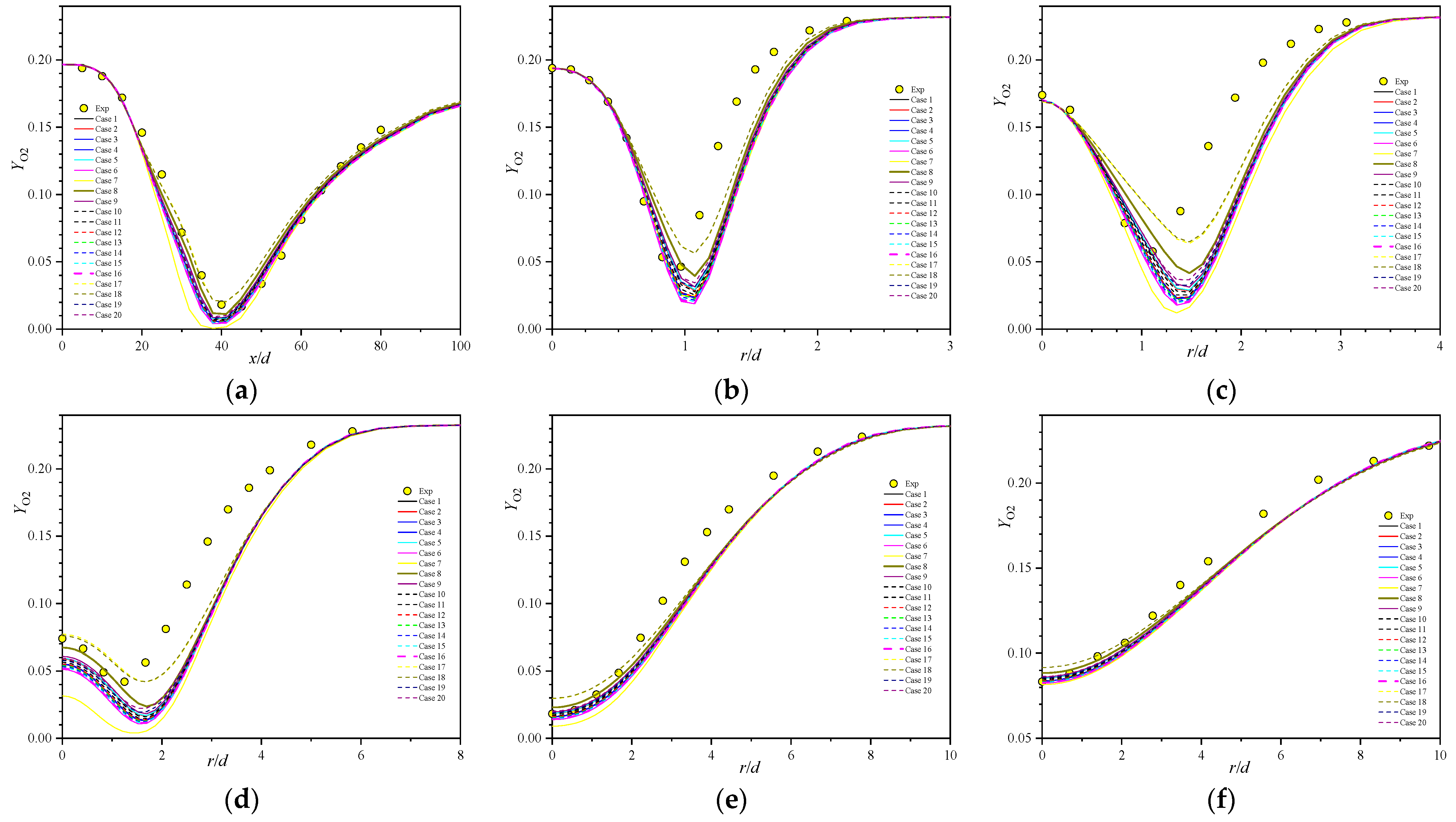
5.4. Major Species Profiles
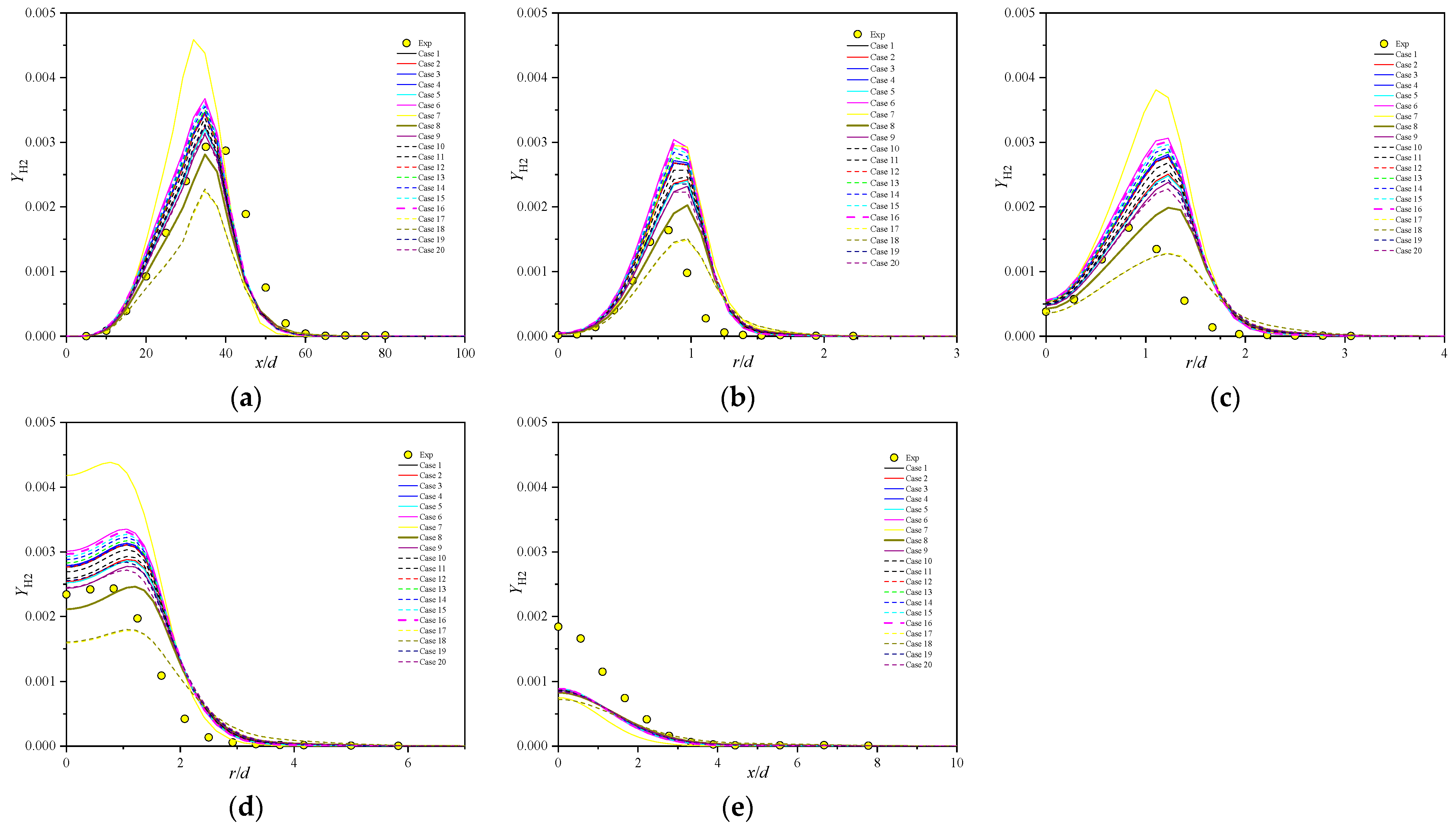
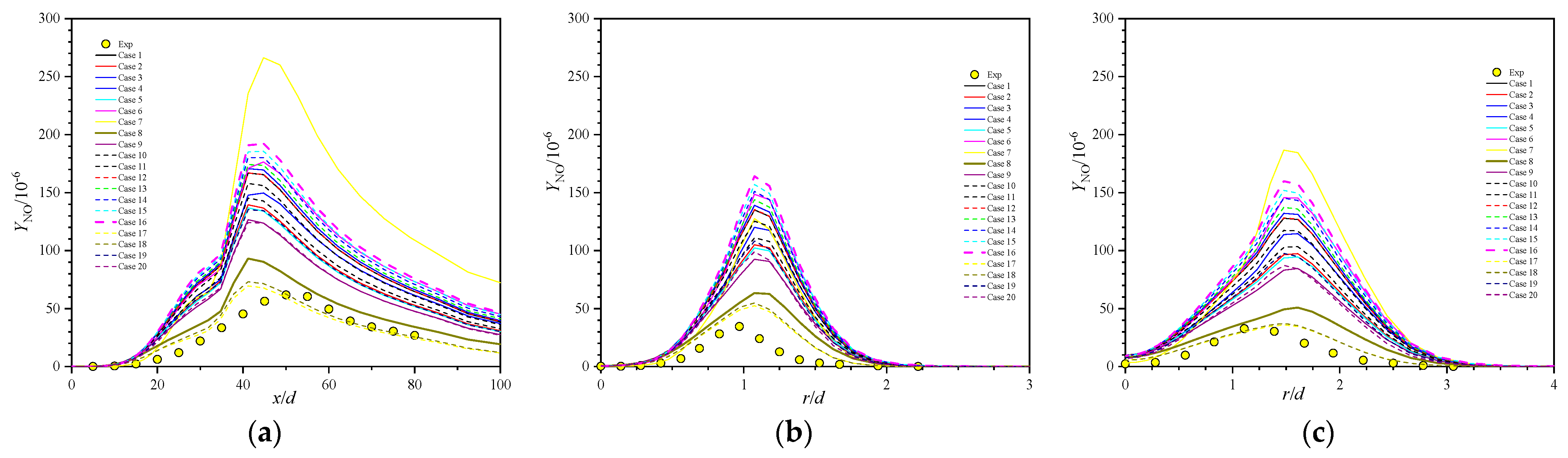
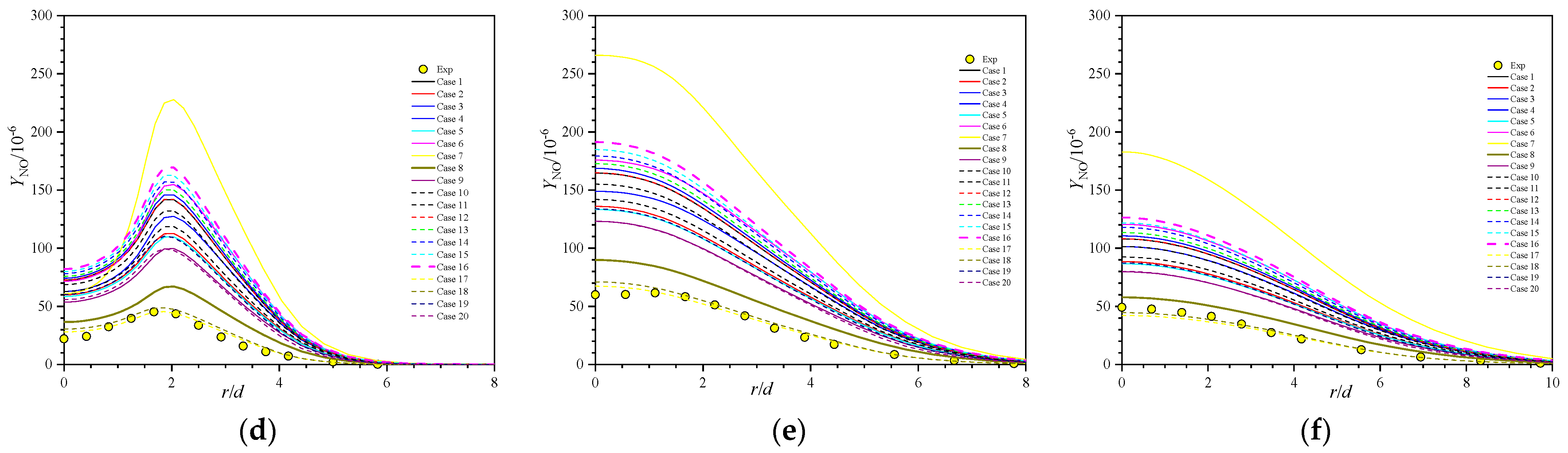
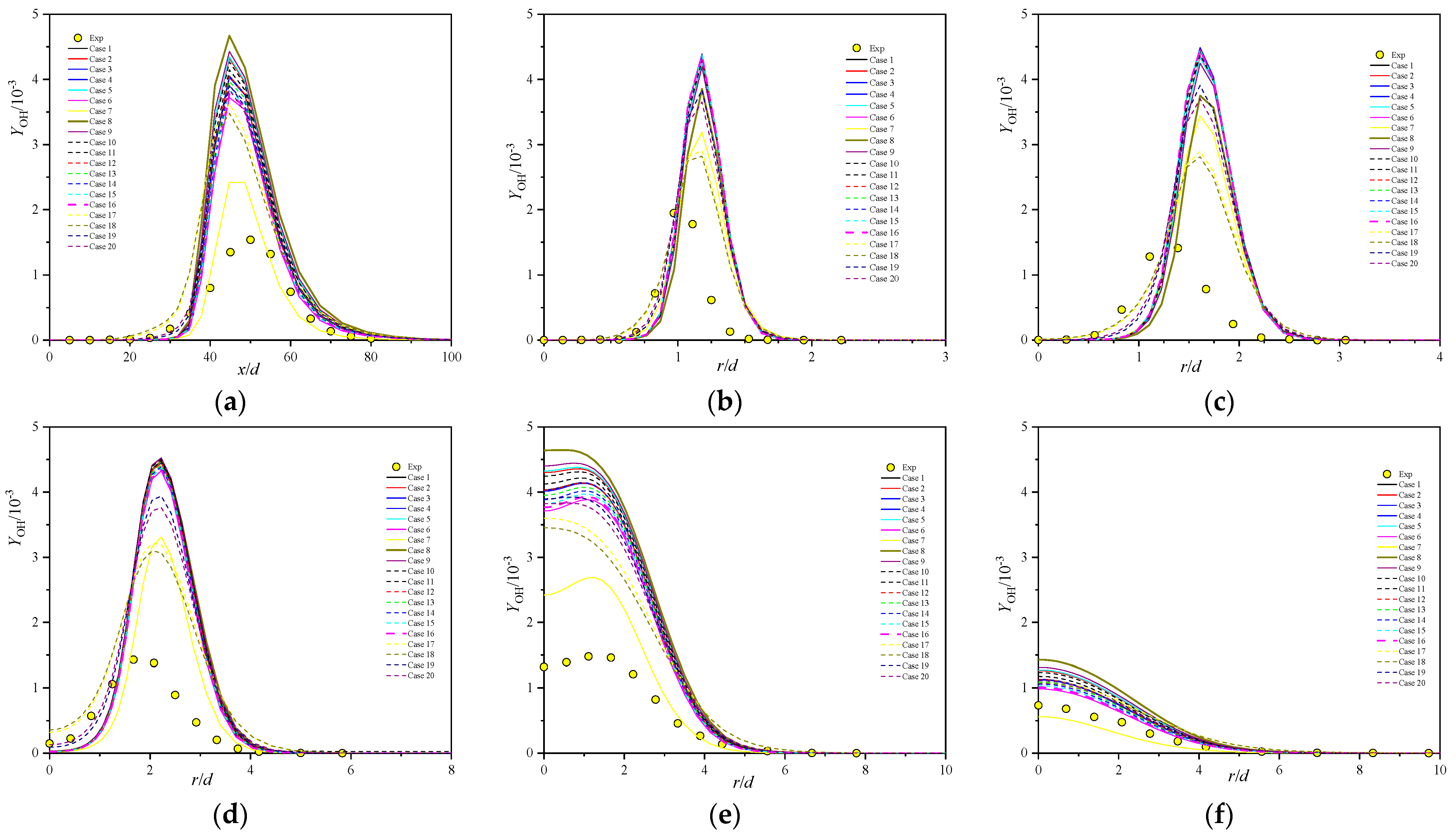
5.5. Minor Species Profiles
6. Conclusions
- (1)
- (2)
- The limiting Reynolds number for the validity of EDC is concluded. Thus, the turbulent Reynolds number should be larger than with different combinations of the primary EDC constants and , or the EDC constants need to be adjusted according to the criteria.
- (3)
- The secondary constant, , should be less than unity with the proposed EDC constant combinations because it is the time–scale ratio of the fine structure to the Kolmogorov scale. The upper limit of is determined from the unity .
- (4)
- The mean reaction rate is expressed as a function of the secondary constants, and its dependence on the EDC constant is presented. The dependence shows that decreasing the mean reaction rate requires deceases in or , and vice versa.
- (5)
- Comprehensive comparison of the predictions of axial velocity, Reynolds stress, temperature, and major and minor species with experimental data shows that case 8, with the secondary constant or the primary constants and can properly reproduce the Sandia flames D.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| , , , | - | primary constants of EDC |
| , , , , | - | secondary constants of EDC |
| k | m2/s2 | turbulence energy |
| L | m | length scale |
| s−1 | mass inflow rate to EDC reactor per reactor mass | |
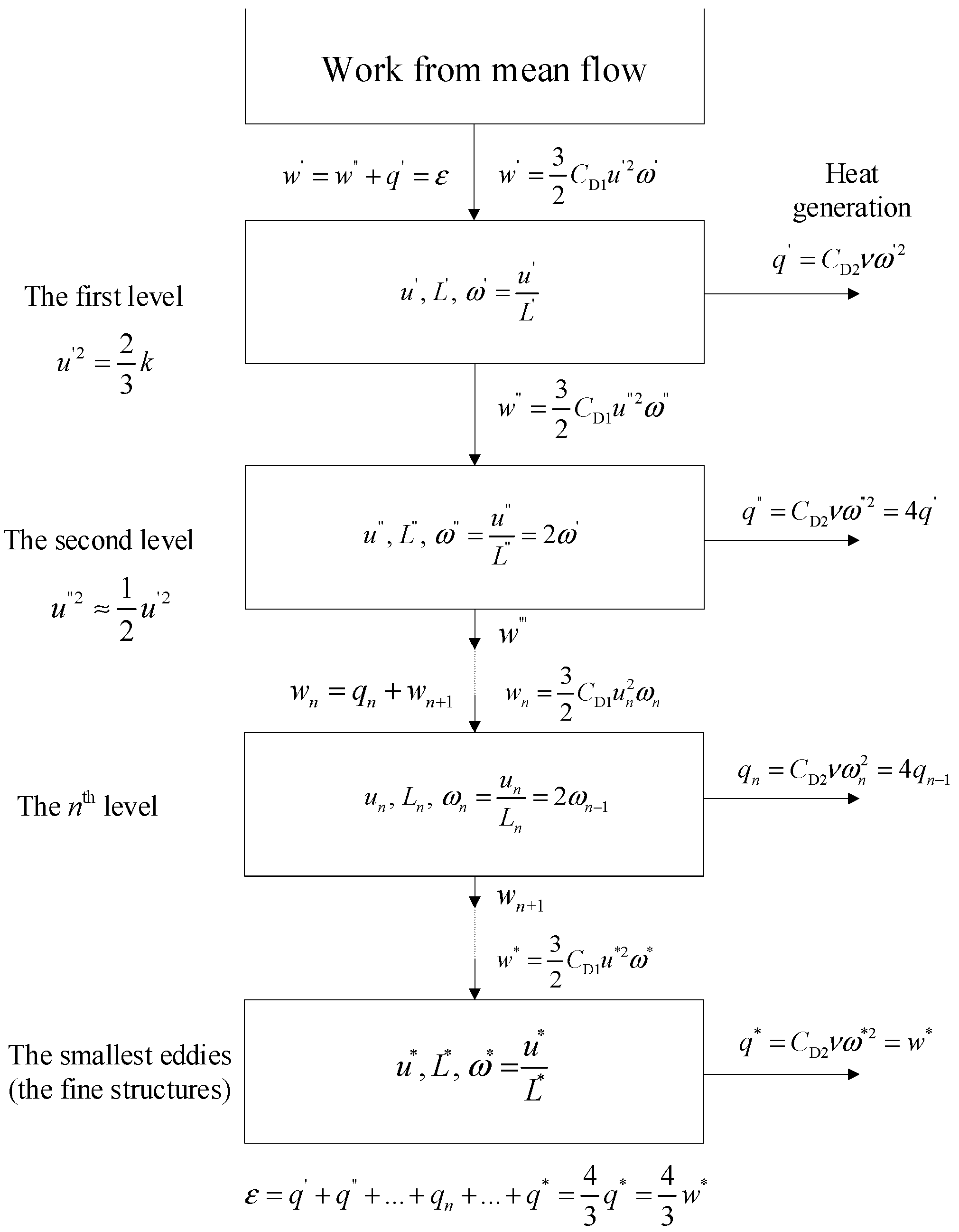
| q | m2/s3 | mechanical work rate dissipated into heat in the energy cascade model, Figure 2 |
| kg/(s·m3) | volumetric reaction rate of species k | |
| Re | - | Reynolds number |
| ReT | - | turbulence Reynolds number, |
| T | K | temperature |
| u | m/s | velocity scale |
| w | m2/s3 | mechanical work rate transferred in the energy cascade model, Figure 2 |
| Yk | - | mass fraction of species k |
| Greeks | ||
| - | mass of fine structures divided by total mass | |
| - | mass of fine-structure regions divided by total mass | |
| ε | m2/s3 | turbulence energy dissipation rate |
| - | numerical constant | |
| η | m | Kolmogorov length scale |
| ν | m2/s | kinematic viscosity |
| ρ | kg/m3 | mass density |
| τ | s | Time scale |
| m/s | Kolmogorov velocity scale | |
| χ | - | reacting fraction of fine structures |
| ω | s−1 | turbulence strain rate or frequency |
| Superscripts | ||
| - | average | |
| ~ | mass-weighted (Favre) average | |
| * | fine-structure (reactor) quantity of EDC | |
| 0 | surroundings of EDC fine-structure reactor | |
References
- Magnussen, B.F. On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow. In Proceedings of the 19th AIAA Aerospace Science Meeting, St. Louis, MO, USA, 12–15 January 1981. [Google Scholar]
- Magnussen, B.F. Modeling of NOx and soot formation by the eddy dissipation concept. In Proceedings of the International Flame Research Foundation, 1st Topic Oriented Technical Meeting, Amsterdam, The Netherlands, 17–19 October 1989. [Google Scholar]
- Gran, J.R.; Magnussen, B.F. A numerical study of a bluff-body stabilized diffusion flame. Part 1. Influence of turbulence modeling and boundary conditions. Comb. Sci. Technol. 1996, 119, 171–190. [Google Scholar] [CrossRef]
- Gran, J.R.; Magnussen, B.F. A numerical study of a bluff-body stabilized diffusion flame. Part 2. Influence of combustion modeling and finite-rate chemistry. Comb. Sci. Technol. 1996, 119, 191–217. [Google Scholar] [CrossRef]
- Ertesvåg, I.S.; Magnussen, B.F. The Eddy dissipation turbulence energy cascade model. Combust. Sci. Technol. 2000, 159, 213–236. [Google Scholar] [CrossRef]
- Magnussen, B.F. The Eddy dissipation concept—A bridge between science and technology. In Proceedings of the ECCOMAS Thematic Conference on Computational Combustion, Lisboa, Portugal, 21–24 June 2005. [Google Scholar]
- Rehm, M.; Seifert, P.; Meyer, B. Theoretical and numerical investigations on the EDC-model for turbulence-chemistry interaction at gasification conditions. Comp. Chem. Eng. 2009, 33, 402–407. [Google Scholar] [CrossRef]
- De, A.; Oldenhof, E.; Sathiah, P.; Roekaerts, D. Numerical simulation of Delft-jet-in-hot-coflow (DJHC) flames using the Eddy dissipation concept model for turbulence-chemistry interaction. Flow Turbul. Combust. 2011, 87, 537–567. [Google Scholar] [CrossRef]
- Aminian, J.; Galletti, C.; Shahhosseini, S.; Tognotti, L. Numerical investigation of a MILD combustion burner: Analysis of mixing field, chemical kinetics and turbulence-chemistry interaction. Flow Turbul. Combust. 2012, 88, 597–623. [Google Scholar] [CrossRef]
- Graça, M.; Duarte, A.; Coelho, P.J.; Costa, M. Numerical simulation of a reversed flow small-scale combustor. Fuel Process. Technol. 2013, 107, 126–137. [Google Scholar] [CrossRef]
- Xu, Y.; Dai, Z.; Li, C.; Li, X.; Zhou, Z.; Yu, G.; Wang, F. Numerical simulation of natural gas non-catalytic partial oxidation reformer. Int. J. Hydrogen Energy 2014, 39, 9149–9157. [Google Scholar] [CrossRef]
- Evans, M.J.; Medwell, P.R.; Tian, Z.F. Modeling lifted jet flames in a heated coflow using an optimized Eddy dissipation concept model. Combust. Sci. Technol. 2015, 187, 1093–1109. [Google Scholar] [CrossRef]
- Wang, F.; Li, P.; Mi, J.; Wang, J.; Xu, M. Chemical kinetic effect of hydrogen addition on ethylene jet flames in a hot and diluted coflow. Int. J. Hydrogen Energy 2015, 40, 16634–16648. [Google Scholar] [CrossRef]
- Farokhi, M.; Birouk, M. Application of Eddy dissipation concept for modeling biomass combustion, Part 1: Assessment of the model coefficients. Energy Fuels 2016, 30, 10789–10799. [Google Scholar] [CrossRef]
- Farokhi, M.; Birouk, M. Application of Eddy dissipation concept for modeling biomass combustion, Part 2: Gas-phase combustion modeling of a small-scale fixed bed furnace. Energy Fuels 2016, 30, 10800–10808. [Google Scholar] [CrossRef]
- Farokhi, M.; Birouk, M. A new EDC approach for modeling turbulence/chemistry interaction of the gas-phase of biomass combustion. Fuel 2018, 220, 420–436. [Google Scholar] [CrossRef]
- Shabanian, S.R.; Medwell, P.R.; Rahimi, M.; Frassoldati, A.; Cuoci, A. Kinetic and fluid dynamic modeling of ethylene jet flame in diluted and heated oxidant stream combustion condition. Appl. Therm. Eng. 2013, 52, 538–554. [Google Scholar] [CrossRef]
- Parente, A.; Malik, M.R.; Contino, F.; Cuoci, A.; Dally, B.B. Extension of the Eddy dissipation concept for turbulence/chemistry interactions to MILD combustion. Fuel 2016, 163, 98–111. [Google Scholar] [CrossRef]
- Mardani, A. Optimization of the Eddy Dissipation Concept (EDC) model for turbulence-chemistry interactions under hot diluted combustion of CH4/H2. Fuel 2017, 191, 114–129. [Google Scholar] [CrossRef]
- Li, Z.; Cuoci, A.; Sadiki, A.; Parente, A. Comprehensive numerical study of the Adelaide jet in hot-coflow burner by means of RANS and detailed chemistry. Energy 2017, 139, 555–570. [Google Scholar] [CrossRef]
- Ertesvåg, I.S. Analysis of Some Recently Proposed Modifications to the Eddy Dissipation Concept (EDC). Combust. Sci. Technol. 2020, 192, 1108–1136. [Google Scholar] [CrossRef]
- Barlow, R.S.; Frank, J.H. Effects of turbulence on species mass fractions in methane/air jet flames. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1998; Volume 27, pp. 1087–1095. [Google Scholar]
- Schneider, C.; Dreizler, A.; Janicka, J.; Hassel, E.P. Flow field measurements of stable and locally extinguishing hydrocarbon-fuelled jet flames. Combust. Flame 2003, 135, 185–190. [Google Scholar] [CrossRef]
- Barlow, R.S.; Frank, J.H. SandiaPilotDoc21.pdf. Available online: https://tnfworkshop.org/data-archives/pilotedjet/ch4-air/ (accessed on 1 May 2022).
- Barlow, R.S.; Frank, J.H.; Karpetis, A.N.; Chen, J.-Y. Piloted Methane/Air Jet Flames: Scalar Structure and Transport Effects. Combust. Flame 2005, 143, 433–449. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, J.W.C.; et al. GRI-Mech 3.0. 1999. Available online: http://combustion.berkeley.edu/gri_mech/ (accessed on 1 May 2022).
- He, D.; Yu, Y.S.; Kuang, Y.C.; Wang, C.J. Analysis of EDC constants for predictions of methane MILD combustion. Fuel 2022, 324, 124542. [Google Scholar] [CrossRef]
- ANSYS. Fluent Release 2021 R1, Fluent 2021R1 Documentation; Fluent Inc.: Philadelphia, PA, USA, 2021. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Magnussen, B.F.; Hjertager, B.H.; Olsen, J.G.; Bhaduri, D. Effects of turbulent structure and local concentrations on soot formation and combustion in C2H2 diffusion flames. Symp. (Int.) Combust. 1979, 17, 1383–1393. [Google Scholar] [CrossRef]
- He, D.; Yu, Y.S.; Zhang, X.W.; Kang, Y.J.; Ma, C.Q.; Wang, C.J. Analyses of EDC Model and Simulations of Jet-in-Hot-Coflow Flames with the Fuel Jet Reynolds Number-Based Constant Modifications. Submitted to Combust Flame. Unpublished work.
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Perot, J.B.; de Bruyn Kops, S.M. Modeling turbulent dissipation at low and moderate Reynolds numbers. J. Turbul. 2006, 7, N69. [Google Scholar] [CrossRef]
- He, D.; Yu, Y.S.; Kuang, Y.C.; Wang, C.J. Model Comparisons of Flow and Chemical Kinetic Mechanisms for Methane-Air Combustion for Engineering Applications. Appl. Sci. 2021, 11, 4107. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the Development of a Reynolds-Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Gibson, M.M.; Launder, B.E. Ground Effects on Pressure Fluctuations in the Atmospheric Boundary Layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Launder, B.E. Second-Moment Closure: Present… and Future. Int. J. Heat Fluid Flow 1989, 10, 282–300. [Google Scholar] [CrossRef]
- Saini, R.; Prakash, S.; De, A.; Yadav, R. Investigation of NOx in pilot stabilized methane-air diffusion flames using finite-rate and infinitely-fast chemistry based combustion models. Therm. Sci. Eng. Prog. 2018, 5, 144–157. [Google Scholar] [CrossRef]
- Pitsch, H.; Steiner, H. Large-Eddy simulation of a turbulent piloted methane/air diffusion flame (Sandia Flame D). Phys. Fluids 2000, 12, 2541–2554. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Numerical Simulations of the Sandia Flame D Using the Eddy Dissipation Concept. Flow Turbul. Combust. 2014, 93, 665–687. [Google Scholar] [CrossRef]
- Sheikhi, M.R.H.; Drozda, T.G.; Givi, P.; Jaberi, F.A.; Pope, S.B. Large eddy simulation of a turbulent nonpremixed piloted methane jet flame (Sandia flame D). Proc. Combust. Inst. 2004, 30, 549–556. [Google Scholar] [CrossRef]
- Mardani, A.; Nazari, A. Dynamic adjustment of the Eddy Dissipation Concept model for turbulent/combustion interactions in mixed combustion regimes. Combust. Flame 2022, 241, 111873. [Google Scholar] [CrossRef]
- Aminian, J.; Galletti, C.; Shahhosseini, S.; Tognotti, L. Key modeling issues in prediction of minor species in diluted-preheated combustion conditions. Appl. Therm. Eng. 2011, 31, 3287–3300. [Google Scholar] [CrossRef]
- Frank, J.H.; Barlow, R.S.; Lundquist, C. Radiation and nitric oxide formation in turbulent non-premixed jet flames. Proc. Combust. Inst. 2000, 28, 447–454. [Google Scholar] [CrossRef]
- Wang, C.J.; Ge, W.J.; Modest, M.F.; He, B.S. A full-spectrum k-distribution look-up table for radiative transfer in nonhomogeneous gaseous media. J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 46–56. [Google Scholar] [CrossRef]
- Wang, C.J.; Modest, M.F.; He, B.S. Improvement of Full-Spectrum k-Distribution Method Using Quadrature Transformation. Int. J. Therm. Sci. 2016, 108, 100–107. [Google Scholar] [CrossRef]
- Wang, C.J.; Modest, M.F.; He, B.S. Full-spectrum k-distribution look-up table for nonhomogeneous gas-soot mixtures. J. Quant. Spectrosc. Radiat. Transf. 2016, 176, 129–136. [Google Scholar] [CrossRef]
- Wang, C.J.; He, B.S.; Modest, M.F.; Ren, T. Efficient Full-Spectrum Correlated-k-distribution Look-Up Table. J. Quant. Spectrosc. Radiat. Transf. 2018, 219, 108–116. [Google Scholar] [CrossRef]
- Wang, C.J.; Modest, M.F.; He, B.S. Full-spectrum correlated-k-distribution look-up table for use with radiative Monte Carlo solvers. Int. J. Heat Mass Transf. 2019, 131, 167–175. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.J.; He, B.S.; Modest, M.F. Full-Spectrum Correlated-k-Distribution Look-Up Table for Radiative Transfer in Nonhomogeneous Participating Media with Gas-Particle Mixtures. Int. J. Heat Mass Transf. 2019, 137, 1053–1063. [Google Scholar] [CrossRef]
- Wang, C.J.; Modest, M.F.; Ren, T.; Cai, J.; He, B.S. Comparison and refinement of the various full-spectrum k-distribution and spectral line weighted-sum-of-gray-gases models for nonhomogeneous media. J. Quant. Spectrosc. Radiat. Transf. 2021, 271, 107695. [Google Scholar] [CrossRef]
- Smith, T.F.; Shen, Z.F.; Friedman, J.N. Evaluation of Coefficients for the Weighted Sum of Gray Gases Model. J. Heat Transf. Trans. ASME 1982, 104, 602–608. [Google Scholar] [CrossRef]

| Case | Ref. | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1350 | 0.5000 | 2.1298 | 0.4082 | 11.11 | 27 | 0.0900 | 0.54 | 21 | 1.42 | 2.47 | 222 | 0.2825 | 0.8264 | 20.6 | [2,5] |
| 2 | 0.1350 | 0.2700 | 1.8257 | 0.3000 | 11.11 | 15 | 0.0900 | 0.46 | 11 | 0.89 | 1.33 | 120 | 0.1930 | 0.7718 | 11.1 | [21] |
| 3 | 0.1296 | 0.4860 | 2.1584 | 0.4025 | 11.57 | 29 | 0.0864 | 0.54 | 22 | 1.42 | 2.50 | 234 | 0.2909 | 0.8306 | 21.7 | [1,2] |
| 4 | 0.1340 | 0.5000 | 2.1377 | 0.4082 | 11.19 | 28 | 0.0893 | 0.54 | 21 | 1.43 | 2.49 | 226 | 0.2848 | 0.8276 | 20.9 | [5] |
| 5 | 0.1340 | 0.2500 | 1.7976 | 0.2887 | 11.19 | 14 | 0.0893 | 0.45 | 10 | 0.85 | 1.24 | 113 | 0.1850 | 0.7655 | 10.4 | [19] |
| 6 | 0.1340 | 1.0000 | 2.5420 | 0.5773 | 11.19 | 56 | 0.0893 | 0.64 | 42 | 2.40 | 4.97 | 451 | 0.4004 | 0.8747 | 41.8 | |
| 7 | 0.1340 | 27.0000 | 5.7950 | 3.0000 | 11.19 | 1504 | 0.0893 | 1.46 | 1128 | 28.39 | 134.33 | 12,180 | 0.8335 | 0.9745 | 1127.8 | |
| 8 | 0.1357 | 0.1100 | 1.4549 | 0.1915 | 11.05 | 6 | 0.0905 | 0.37 | 4 | 0.45 | 0.54 | 48 | 0.0973 | 0.6661 | 4.5 | [21] |
| 9 | 0.1357 | 0.2100 | 1.7101 | 0.2646 | 11.05 | 11 | 0.0905 | 0.43 | 9 | 0.74 | 1.03 | 92 | 0.1607 | 0.7445 | 8.6 | |
| 10 | 0.1357 | 0.3100 | 1.8850 | 0.3215 | 11.05 | 17 | 0.0905 | 0.47 | 13 | 0.99 | 1.52 | 136 | 0.2101 | 0.7842 | 12.6 | |
| 11 | 0.1357 | 0.4100 | 2.0215 | 0.3697 | 11.05 | 22 | 0.0905 | 0.51 | 17 | 1.22 | 2.01 | 180 | 0.2503 | 0.8093 | 16.7 | |
| 12 | 0.1357 | 0.5100 | 2.1349 | 0.4123 | 11.05 | 28 | 0.0905 | 0.54 | 21 | 1.44 | 2.51 | 224 | 0.2840 | 0.8272 | 20.8 | |
| 13 | 0.1357 | 0.6100 | 2.2326 | 0.4509 | 11.05 | 33 | 0.0905 | 0.56 | 25 | 1.64 | 3.00 | 268 | 0.3128 | 0.8407 | 24.8 | |
| 14 | 0.1357 | 0.7100 | 2.3189 | 0.4865 | 11.05 | 39 | 0.0905 | 0.58 | 29 | 1.84 | 3.49 | 312 | 0.3380 | 0.8514 | 28.9 | |
| 15 | 0.1357 | 0.8100 | 2.3966 | 0.5196 | 11.05 | 44 | 0.0905 | 0.60 | 33 | 2.03 | 3.98 | 356 | 0.3602 | 0.8602 | 33.0 | |
| 16 | 0.1357 | 0.9100 | 2.4674 | 0.5508 | 11.05 | 49 | 0.0905 | 0.62 | 37 | 2.22 | 4.47 | 400 | 0.3800 | 0.8675 | 37.1 | |
| 17 | 0.6108 | 6.4827 | 1.9000 | 1.4700 | 2.46 | 17 | 0.4072 | 0.48 | 13 | 4.56 | 7.08 | 141 | 0.2145 | 0.7872 | 13.0 | [18] |
| 18 | 0.6638 | 9.3987 | 2.0000 | 1.7700 | 2.26 | 21 | 0.4425 | 0.50 | 16 | 5.78 | 9.44 | 173 | 0.2439 | 0.8057 | 16.0 | |
| 19 | 0.2686 | 2.0172 | 2.1400 | 0.8200 | 5.58 | 28 | 0.1791 | 0.54 | 21 | 2.87 | 5.01 | 227 | 0.2855 | 0.8279 | 21.0 | |
| 20 | 0.3275 | 3.0000 | 2.1400 | 1.0000 | 4.58 | 28 | 0.2184 | 0.54 | 21 | 3.49 | 6.11 | 227 | 0.2855 | 0.8280 | 21.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, D.; Yu, Y.; Ma, H.; Liang, H.; Wang, C. Extensive Discussions of the Eddy Dissipation Concept Constants and Numerical Simulations of the Sandia Flame D. Appl. Sci. 2022, 12, 9162. https://doi.org/10.3390/app12189162
He D, Yu Y, Ma H, Liang H, Wang C. Extensive Discussions of the Eddy Dissipation Concept Constants and Numerical Simulations of the Sandia Flame D. Applied Sciences. 2022; 12(18):9162. https://doi.org/10.3390/app12189162
Chicago/Turabian StyleHe, Di, Yusong Yu, Hao Ma, Hongbo Liang, and Chaojun Wang. 2022. "Extensive Discussions of the Eddy Dissipation Concept Constants and Numerical Simulations of the Sandia Flame D" Applied Sciences 12, no. 18: 9162. https://doi.org/10.3390/app12189162
APA StyleHe, D., Yu, Y., Ma, H., Liang, H., & Wang, C. (2022). Extensive Discussions of the Eddy Dissipation Concept Constants and Numerical Simulations of the Sandia Flame D. Applied Sciences, 12(18), 9162. https://doi.org/10.3390/app12189162







